扩展功能
文章信息
- 王婉秋, 肖凌云, 马明辉, 钱宇彬
- WANG Wan-qiu, XIAO Ling-yun, MA Ming-hui, QIAN Yu-bin
- 基于NSGA_Ⅱ的双车道公路弯道驾驶人模型
- Driver Models in Curves of Two-lane Highway Based on NSGA_Ⅱ
- 公路交通科技, 2021, 38(12): 131-138, 146
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(12): 131-138, 146
- 10.3969/j.issn.1002-0268.2021.12.015
-
文章历史
- 收稿日期: 2021-01-04
2. 国家市场监督管理总局, 北京 100101
2. State Administration for Market Regulation, Beijing 100101, China
双车道公路弯道是事故多发的路段。双车道公路弯道事故机理的研究离不开双车道公路弯道驾驶行为的研究。驾驶人的驾驶行为影响因素众多,包括弯道的三维线形、车辆的动力学特性以及作为一个复杂生物的驾驶人的感知、判断,驾驶行为是各因素综合作用的产物。PRAKASH[1]根据驾驶人期望车速,建立基于人工神经网络的驾驶人速度控制模型;LI[2]研究受弯道坡度和曲率影响的驾驶人的速度模型;JALALI[3]建立基于PID控制策略的多点预瞄速度控制模型,前视距离考虑驾驶人的反应时间和速度的影响;LEE[4]研究纵向速度控制模型和横向转向模型,横向转向模型考虑驾驶人由于手臂肌肉引起的延迟时间,以及受速度和曲线半径影响的前视距离;GUAN[5]以逼近于理想解(TOPSIS)的方法将驾驶人的模糊感知能力引入系统模型的建立;ZHUANG[6]引用基于误差消除算法的人工神经网络方法寻求驾驶人的最优前视时间。部分学者将驾驶人的模糊感知能力引入模型,但未考虑驾驶人的主观特性,部分学者在轨迹跟踪模型中考虑了驾驶人前视时间随驾驶环境实时变化的特性,然而速度控制模型却以跟随期望车速为主,未考虑驾驶人随着前方道路信息动态确定速度的特性。本研究在文献[7]中研究了驾驶人的模糊感知,主观决策行为在双车道公路驾驶行为中的影响,并进行了建模,然而文献[7]中前方道路线形对驾驶人行为的影响进行了一定的假设,假设前方道路线形首先影响驾驶人的速度控制行为,然后在速度决策下,驾驶人进行方向控制,然而实际驾驶中,驾驶人的速度控制行为和方向控制行为往往是同步进行。考虑驾驶行为是驾驶人综合考虑前方道路线形,结合车辆动力性能、自身的模糊分析和主观判断的结果,驾驶人有基于多个决策因素对多个目标进行优化决策的能力,本研究选择多目标遗传优化算法研究驾驶人的目标决策过程。
首先研究受前方道路线形影响的决策因素和对应目标集的初始样本,决策因素的初始样本考虑驾驶人的主观倾向性,选取Beta分布抽样和拉丁超立方抽样;为了增加不同速度和转角条件下目标集因素的可比性,基于熵权方法和模糊理论建立目标集的相对指标值;然后引入NSGA_Ⅱ多目标遗传算法,研究染色体编码、交叉和变异操作、数据越界处理以及精英保留策略等若干关键问题,得到决策因素的Pareto最优解集;基于多目标模糊优选算法得到决策因素的最优解;最后选取试验路段,通过2种仿真方法的仿真结果与实测结果的对比分析验证模型的有效性。
1 决策变量初始样本的获取基于文献[7]的研究,弯道的决策因素为车速V与方向盘转角δ,目标集为行驶轨迹弧长L,侧向偏移d,横向力系数μ。初始样本的获取分为速度V的初始样本的获取和方向盘转角δ的初始样本的获取。
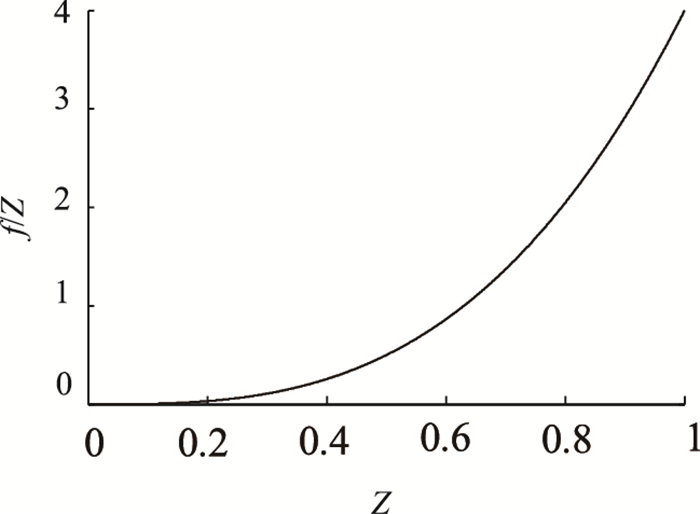
参考文献[7]的速度范围[Vmin, Vmax],考虑驾驶人在保证安全条件下追求较高车速的特性,车速V的初始样本抽样选取Beta分布随机抽样方法。Beta分布是定义在[0, 1]区间的连续概率分布族,属于偏态分布,形状参数α=4,β=1,如图 1中曲线所示,其概率密度函数为:
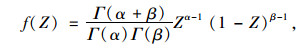
|
(1) |
|
| 图 1 Beta分布曲线(α=4,β=1) Fig. 1 Beta distribution curve (α=4, β=1) |
| |
式中,随机变量Z∈[0, 1], Γ表示gamma函数。基于Beta分布抽样的结果Zk, k=1, 2, …, M位于区间[0, 1]间,需将其换算为区间[Vmin, Vmax]的值,即
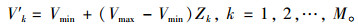
|
(2) |
对应速度V′k的方向盘转角范围为[δkmin, δkmax],δkmin,δkmax为瞬时行驶轨迹圆弧与前方线形影响范围存在交点的最小、最大方向盘转角。方向盘转角δ的初始样本采用均匀分层抽样的拉丁超立方抽样方法,在[0, 1]中随机抽取N个样本点Δkt,t=1, 2, …, N,再将其换算为[δkmin, δkmax]区间的值,如式3所示,式中k=1, 2, …, M,t=1, 2, …, N。
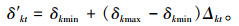
|
(3) |
为了统一速度和方向盘转角的标号,将速度样本进行变换,V′kt=V′k,k=1, 2, …, M,t=1, 2, …, N,将决策变量以矩阵形式表示[Vi, δi], i=1, 2, …, MN,其中Vi=V′kt,δi=δ′kt,i=1, 2, …, MN,k=1, 2, …, M,t=1, 2, …, N。
2 目标集的计算依据文献[7]中目标集的计算方法,计算Vi, δi(i=1, 2, …, MN)条件下的目标集中行驶轨迹弧长li、横向力系数μi和侧向偏移di(i=1, …, MN)。其中目标集的指标为绝对指标,考虑速度V和方向盘转角δ的差异性,为了增加目标集之间的可比性,依据式(4),将目标集的指标变换为相对指标。
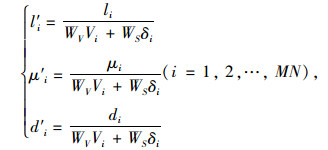
|
(4) |
式中, WV,WS分别为速度V和方向盘转角δ的权重,采用熵权法[8-9]计算。该法依据指标的变异性大小确定权重,即指标的变异性越大,其信息熵越小,则权重越大。将Vi,δi(i=1, 2, …, MN)进行标准化处理后得V′i,δ′i(i=1, 2, …, MN),其对应信息熵EV, ES计算式为式(5)。
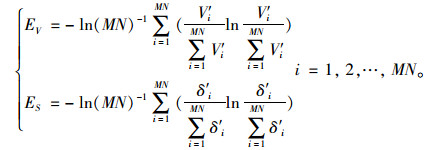
|
(5) |
通过信息熵,由式(6)计算速度V和方向盘转角δ的权重WV,WS。
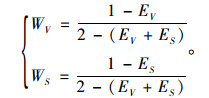
|
(6) |
考虑驾驶人对目标集相对指标l′i,μ′i,d′i(i=1, 2, …, MN)的感受具有模糊性,即行驶轨迹弧长l′i具有越长越好的模糊性,横向力系数μ′i和侧向偏移d′i具有越小越好的模糊性。“越……,越……”的模糊性用相对隶属度[10]进行描述,计算式为式(7)。
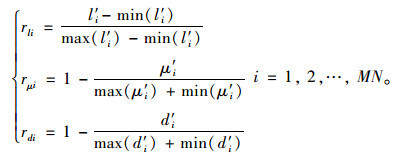
|
(7) |
式中,rli, rμi, rdi分别为目标集相对指标l′i,μ′i,d′i的相对隶属度。
3 NSGA_Ⅱ多目标遗传算法涉及2个决策、3个目标的优化问题的数学模型描述为如下优化模型:
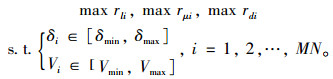
|
(8) |
本研究采用非支配的精英策略遗传算法NSGA_Ⅱ对模型8进行优化。该方法包括染色体编码、交叉和变异操作、数据越界处理以及精英保留策略等若干关键问题。
3.1 染色体编码依据第1节,第2节决策集、目标集初始样本的获取方法,种群染色体以向量形式进行编码,如式(9),染色体包括7个基因,基因以实数表示。
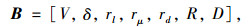
|
(9) |
式中, 基因rl,rμ,rd,R,D由基因V,δ计算得到。基因V,δ为个体的决策集信息,在约束条件里按Beta分布和拉丁超立方分布随机取值,如1节所示;基因rl,rμ,rd为个体的目标集相对指标信息,计算方法如2节所示;基因R为个体的非支配等级,通过擂台法[11]构造Pareto非支配集,并按非支配排序[12]计算得到;基因D为个体的拥挤距离值[12],即D=Dl+Dμ+Dd,其中Dl,Dμ,Dd分别为基因rl,rμ,rd的拥挤距离值。
基于种群染色体的编码B,得到初始种群矩阵M=[B1, B2, …, BMN]T,Bi=[Vi, δi, rli, rμi, rdi, Ri, Di],i=1, 2, …, MN。
3.2 交叉和变异操作 3.2.1 种群选择采用锦标赛法[12]从初始种群M选择适合繁殖的父代进入竞标池。每次随机选择2个相异个体Bi,Bj,i≠j,比较其非支配等级Ri和Rj。若Ri≠Rj,留下max (Ri, Rj)的个体;若Ri=Rj,则比较拥挤距离值Di, Dj,选择max(Di, Dj)的个体。
3.2.2 交叉算子鉴于染色体基因以实数表示,针对竞标池内选定的父代采用模拟二进制交叉法[13-14]生成子代,该方法基于二进制串的单点交叉工作原理,将其作用于以实数表示的染色体。考虑基因V,δ是染色体内其他基因的计算基础,交叉操作首先考虑基因V,δ的交叉操作,式(10)中以W符号代表基因V,δ的值,Wp1t,Wp2t代表竞标池中随机抽取的第t代父代个体p1,p2的基因值,Wc1t+1,Wc2t+1代表第t+1代子代个体c1、c2的基因值。
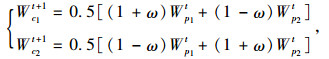
|
(10) |
式中,ω为传播因子,定义为第t代父代个体p1,p2的解码实数值差值与第t+1代子代个体c1,c2解码实数值差值的比值。由第t代父代个体p1,p2的二进制串分割位点的随机性,得满足一定概率u的ω值计算式(11)。
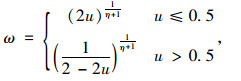
|
(11) |
式中,u在[0, 1]之间随机取值,η>0为分布指数,其值大小表示第t+1代子代逼近第t代父代个体的程度,值越大则子代逼近父代的概率越大。本研究为了提高算法的收敛速度,根据目标值的收敛程度动态确定分布指数η。首先设置门槛值为G,计算第t代父代种群的个体目标值rl,rμ,rd的均值之和Mt=rlt+rμt+rdt,t=1, 2, 3, …, q,其中q为总进化代数,若|Mt+1-Mt|≥G,则η=1,即η取较小值,对t+1代子代染色体基因V,δ的值实行较分散搜索;若|Mt+1-Mt| < G,则η=5,即对t+1代染色体基因V,δ的值在第t代父代个体的基因值附近实现小范围的集中搜索,提高收敛速度。
基于1.1节染色体编码一节的内容,第t+1代染色体的基因rl(t+1),rμ(t+1),rd(t+1),Rt+1,Dt+1的交叉值由第t+1代染色体基因Vt+1,δt+1的交叉值计算得到。
3.2.3 变异算子变异算子采用多项式变异[15-16],该方法是研究多目标优化时主要使用的一种变异算子。变异操作类似于交叉操作,变异操作主要针对染色体基因V,δ的变异, 第t+1代染色体的基因rl(t+1),rμ(t+1),rd(t+1),Rt+1,Dt+1的变异值由t+1代染色体基因Vt+1,δt+1的变异值计算得到。以Qi代表Vi,δi,变异形式表示为Qit+1=Qit+γi,i=1, 2, …, MN,其中γi为变异值,由式(12)计算获得。
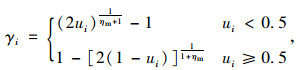
|
(12) |
式中,ui为[0, 1]区间内的随机数;ηm为分布指数,ηm>0。
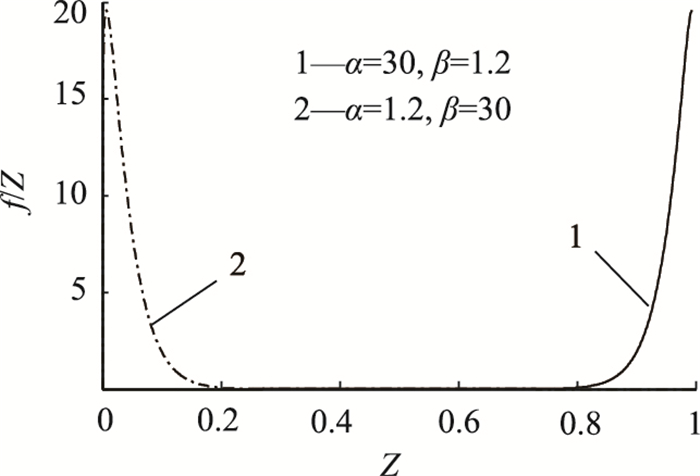
3.2.4 越界处理依据染色体的基因V,δ取值的约束条件δ∈[δmin, δmax], V∈[Vmin, Vmax],经过交叉和变异操作的第t+1代染色体基因值V,δ存在越界处理。鉴于本研究优化目标数为3,每代种群的最优解为Pareto解集,常规取端点值的越界处理方法,会造成种群Pareto解集在在边界过于集中,从而影响种群的多样性,本研究提出基于Beta分布抽样的越界处理方法。Beta分布的偏态分布特性,使得越界基因值V,δ在边界附近取值的概率大,保证了基因V,δ值接近端点值的特性,而且随机抽样方法也保证了种群的多样性。以S代表V,δ,针对S>Smax的越界情况,兼顾种群的多样性和端点值的逼近性,Beta分布形状参数取α=30、β=1.2,如图 2中曲线1,基于Beta分布抽样的结果,将其换算为区间[Smin, Smax]的值,越界基因值S在边界Smax附近取值的概率大;针对S < Smin的越界情况,Beta分布形状参数取α=1.2, β=30,如图 2中曲线2,同样基于Beta分布抽样的结果,将其换算为区间[Smin, Smax]的值,越界基因值S在边界Smin附近取值的概率大。
|
| 图 2 Beta分布 Fig. 2 Beta distribution |
| |
3.3 精英保留策略
为了保留父代种群Mft=[B1t, B2t, …, BMNt]T和子代种群Mct=[B1(t+1), B2(t+1), …, BMN(t+1)]T的优良个体,将其合并为R(t+1)=[B1t, …, BMNt, B1(t+1), …, BMN(t+1)]T,基于3.2.1节的精英保留策略从R(t+1)中选择MN个精英个体组成新一代种群。
4 多目标模糊优选决策由NSGA_Ⅱ多目标遗传算法获得Pareto最优解集MP=[Bp1, …, BpMN]T,Bpi=[Vi, δi, rli, rμi, rdi, Ri, Di]i=1, 2, …, MN,驾驶人从Pareto最优解集Mp中挑选最优解Bpi的决策因素是目标集相对隶属度指标rli,rμi,rdi,i=1, 2, …, MN,其决策过程需考虑驾驶人的模糊感知、主观决策能力。本研究引用文献[7]的相关研究成果,基于最优解集Mp中个体Bpi的目标集相对隶属度指标rli, rμi, rdi,i=1, 2, …, MN,建立多目标模糊优选决策模型,权重的确定采用文献[7]主客观权重确定方法,客观权重采用灰色关联分析法[17-18],驾驶人对权重的主观感受通过主观倾向性曲线模型[7]对相对指标l′,μ′和d′进行无量纲化的方法引入。主观倾向性曲线模型见式(13),以m代表相对指标l′,μ′和d′的值,W为m对应的无量纲值,mmax,a为待定参数,mmax代表相对指标l′,μ′和d′的边界因子mlmax,mμmax和mdmax,a为主观倾向因子。基于多目标模糊优选决策模型选择最优个体Bpi,从而获得驾驶人t时刻的最优速度Vp和最优方向盘转角δp。
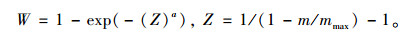
|
(13) |
本研究选取安徽省合肥市境内的S311(合水公路),采集5处曲线路段过往车辆的车速与行驶轨迹,数据采集方法参见文献[7],不再赘述。初始观测断面为直线和前缓和曲线交点前60 m的位置,其上采集的85%分位统计车速作为试验路段的初始车速,其余观测断面(直线和前缓和曲线交点ZH、前缓和曲线和圆曲线交点HY、圆曲线和后缓和曲线交点YH和后缓和曲线与直线交点HZ)的特征车速V85,以及观测断面(圆曲线中点QZ)和观测断面(HY和HZ)附近的行车轨迹侧向偏移最大值Δdmax作为驾驶人模型验证的数据来源[7]。
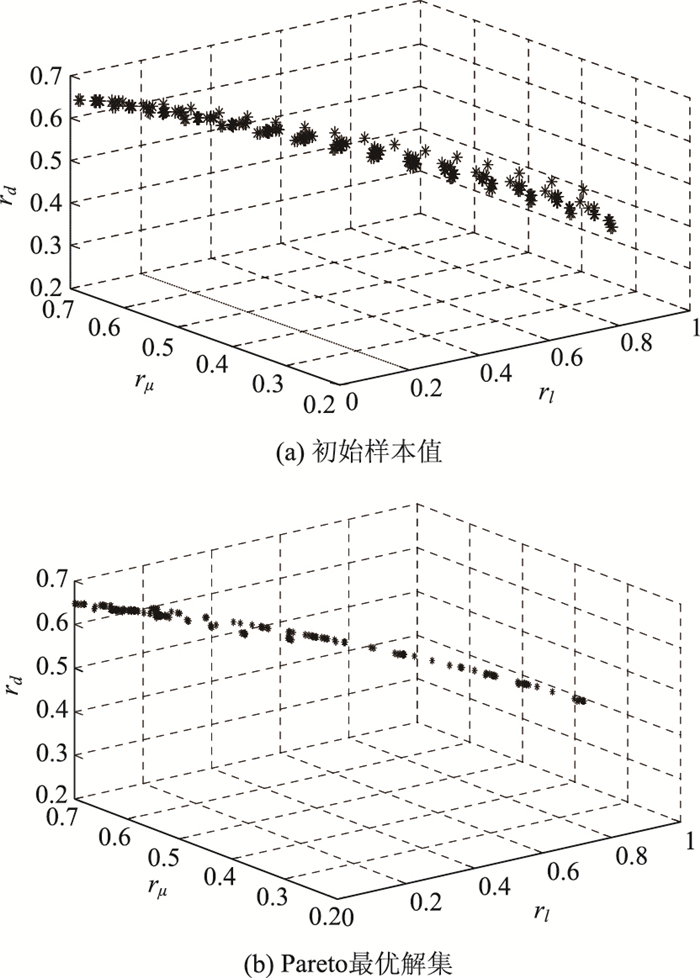
参数M=20,N=20,初始种群大小为MN=400,最大迭代次数为100,交叉概率Pc=0.9,变异概率Pm=0.1,分布指数ηm=10。试验弯道的曲线半径R=160 m,前缓和曲线长度60 m,圆曲线长160 m,后缓和曲线长60 m,圆曲线超高6%,初始车速V0=61.52 km/h,最大加速度amax=0.55g,最大减速度a′max=-0.1g,缓和曲线和圆曲线内的前方线形影响范围l=[0,0.3V],直线路段前方线形影响范围l=[0.3V,0.6V]。采用本研究中NSGA_Ⅱ多目标遗传算法,编程完成试验路段驾驶人模型的建立和求解。本研究抽取位于前缓和曲线路段、圆曲线路段、后缓和曲线路段内的3个特征断面,其里程桩号分别为208.40,304.46,371.90 m,3个特征断面的目标集相对隶属度指标rl,rμ,rd的初始样本值与Pareto最优解集如图 3~图 5中(a)、(b)所示。
|
| 图 3 208.40 m里程点的目标集初始样本值与Pareto最优解集 Fig. 3 Initial sample values and Pareto optimal solutions of target set at 208.40 m mileage point |
| |
|
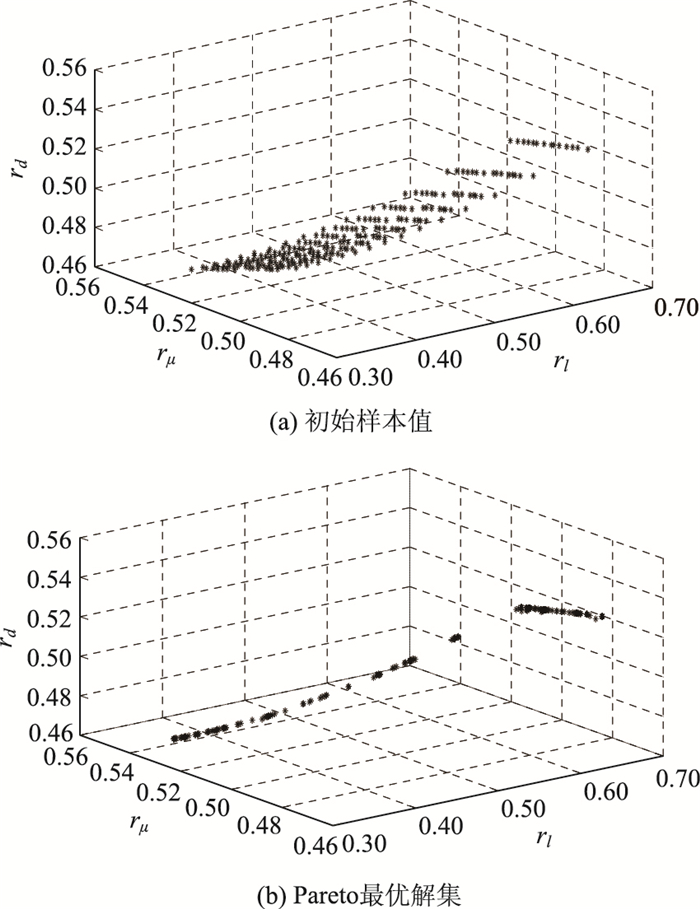
| 图 4 304.46 m里程点目标集初始样本值与Pareto最优解集 Fig. 4 Initial sample values and Pareto optimal solutions of target set at 304.46 m mileage point |
| |
|
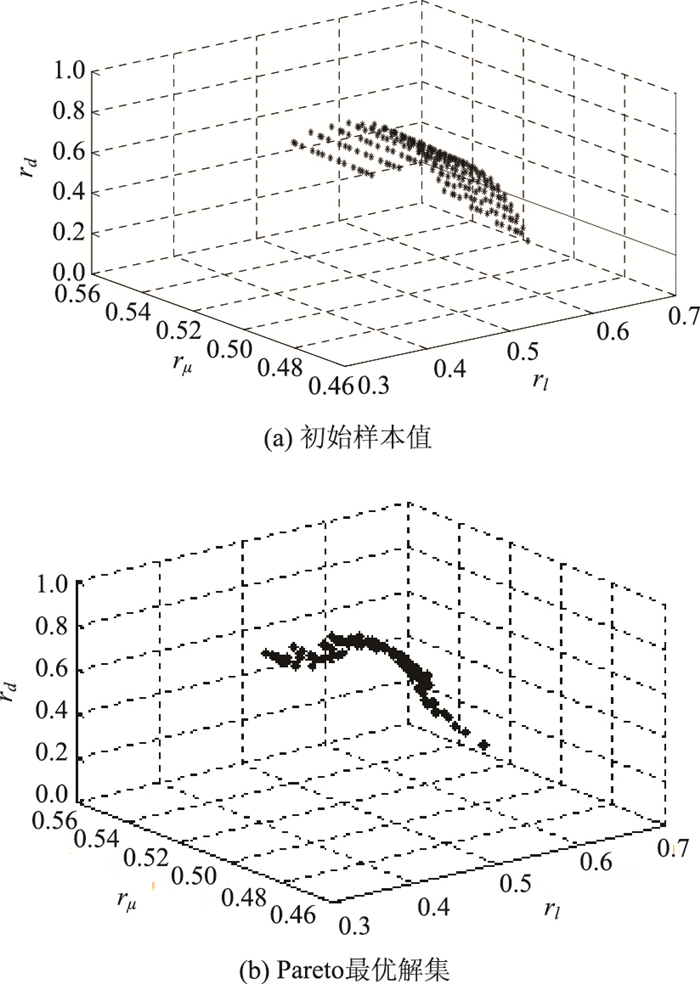
| 图 5 里程点371.90 m目标集的初始样本值与Pareto最优解集 Fig. 5 Initial sample values and Pareto optimal solutions of target set at 371.90 m mileage point |
| |
从图 3、图 4、图 5(b)中Pareto最优解集知,当车辆处于前缓和曲线路段和后缓和曲线路段时,随着rl的增大,rμ,rd的值减小;当车辆位于圆曲线段内,随着rl的增大,rμ值减小,rd值增大。目标集相对隶属度指标rl,rμ,rd在试验段内不会同时达到最优。针对Pareto最优解集采用多目标模糊优选决策算法获得最优解,其中目标集相对指标l′,μ′,d′的主观倾向性模型参数值由试算法获得,使特征断面的运行车速和行驶轨迹仿真值尽可能的接近于实测值,通过试算,mlmax=0.7l′max,mμmax=1.2μ′max,mdmax=1.2d′max(其中l′max,μ′max,d′max为相对指标l′,μ′,d′的最大值),主观倾向因子a=2.0。试验路段的决策变量V,δ的仿真数据和实测数据的对比如图 6所示。
|
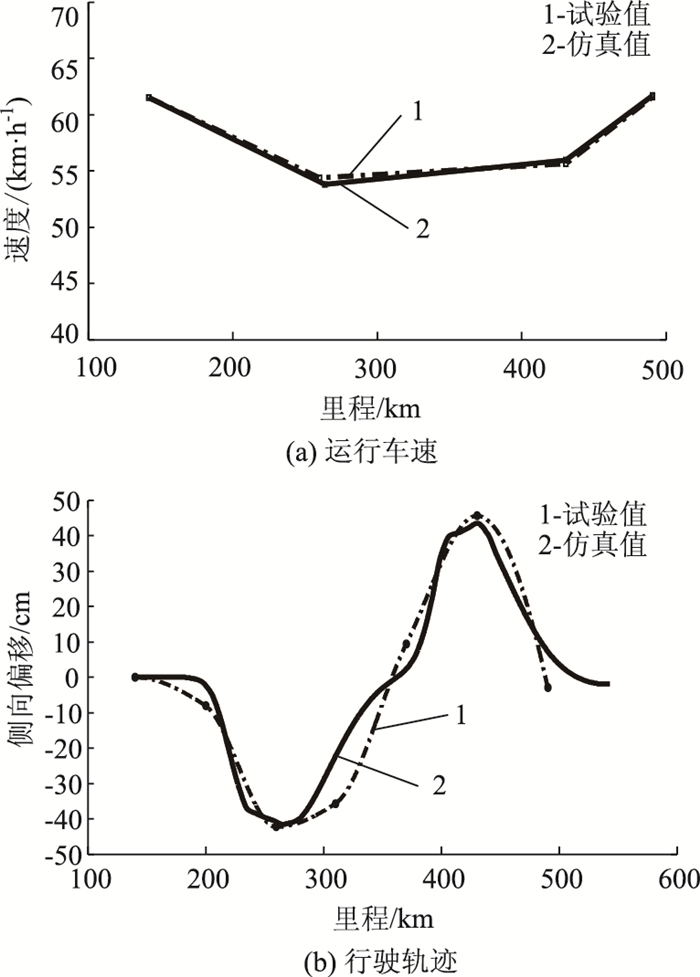
| 图 6 R=160 m试验段运行车速和行驶轨迹试验值与基于NSGA_Ⅱ多目标遗传算法的仿真值对比 Fig. 6 Comparison of experimental vehicle speeds and trajectory values and simulation values based on multi- objective NSGA_Ⅱ in R=160 m experimental section |
| |
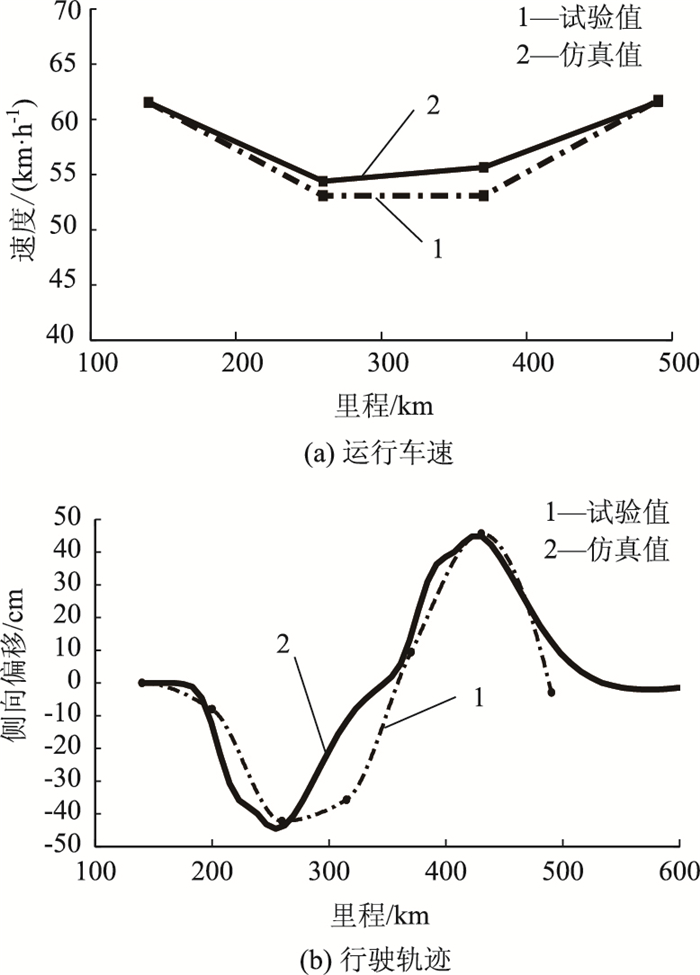
从图 6可以看出,融合NSGA_Ⅱ多目标遗传算法和模糊优选决策算法的驾驶人模型较好地模拟了驾驶人的运行车速和行驶轨迹,其值与实测值差异性较小,特别在圆曲线路段, 车速仿真值存在小幅度的加速行为,其值与试验数据较为接近。整个弯道车速总平均误差为0.46%,行驶轨迹误差最大点(QZ点附近)的误差值为37%,如图 6(a)、(b)图所示。与此对应,将文献[7]中多目标模糊优选决策算法应用于此试验路段,仿真结果与实测数据的对比如图 7所示,圆曲线路段,车辆基本处于匀速行驶状态。在图 7中,运行车速和行驶轨迹的仿真值与实测值的差异性较大,车速仿真值与试验值的总平均误差为1.83%,行驶轨迹误差最大点(QZ点附近)的误差值为67%,均大于本研究方法的仿真误差值。这与文献[7]中将驾驶人模型进行了一定的假设和简化计算有关,其假设驾驶人的速度控制行为先于轨迹跟踪行为完成,决策Vi的目标值视为综合值,即在速度Vi下,m个方向盘转角δk∈X。
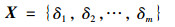
|
|
| 图 7 R=160 m试验段运行车速和行驶轨迹试验值与基于NSGA_Ⅱ多目标模糊优选决策算法的仿真值对比 Fig. 7 Comparison of experimental vehicle speeds and trajectory values and simulation values based on NSGA_Ⅱ and fuzzy optimization decision-making in R=160 m experimental section |
| |
对应的目标值的综合值,忽视了决策Vi,δk∈X引起的目标值的微观变化。
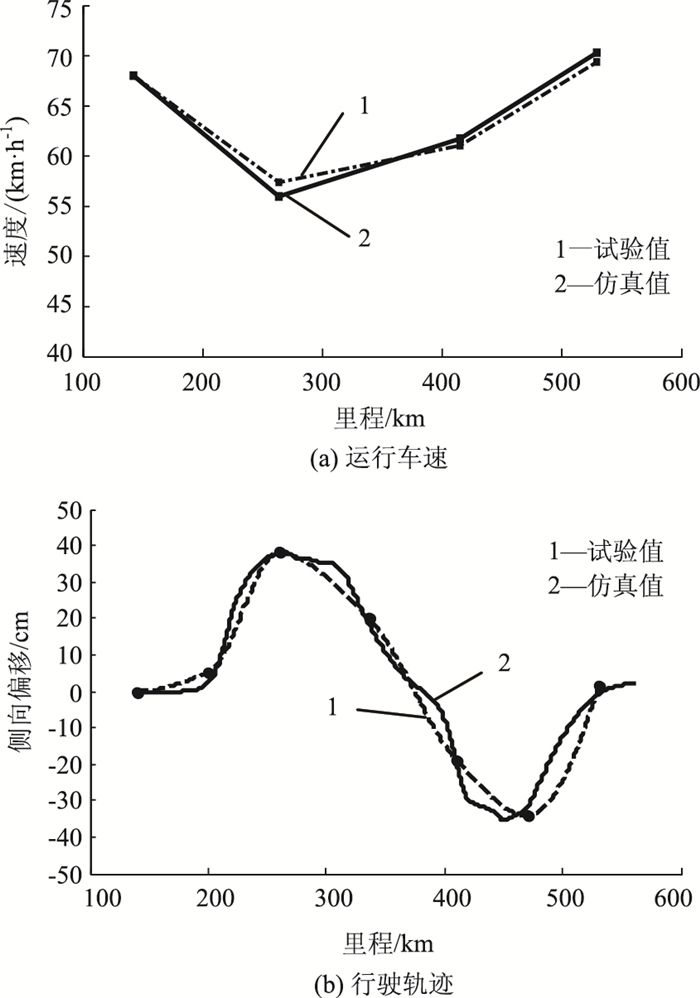
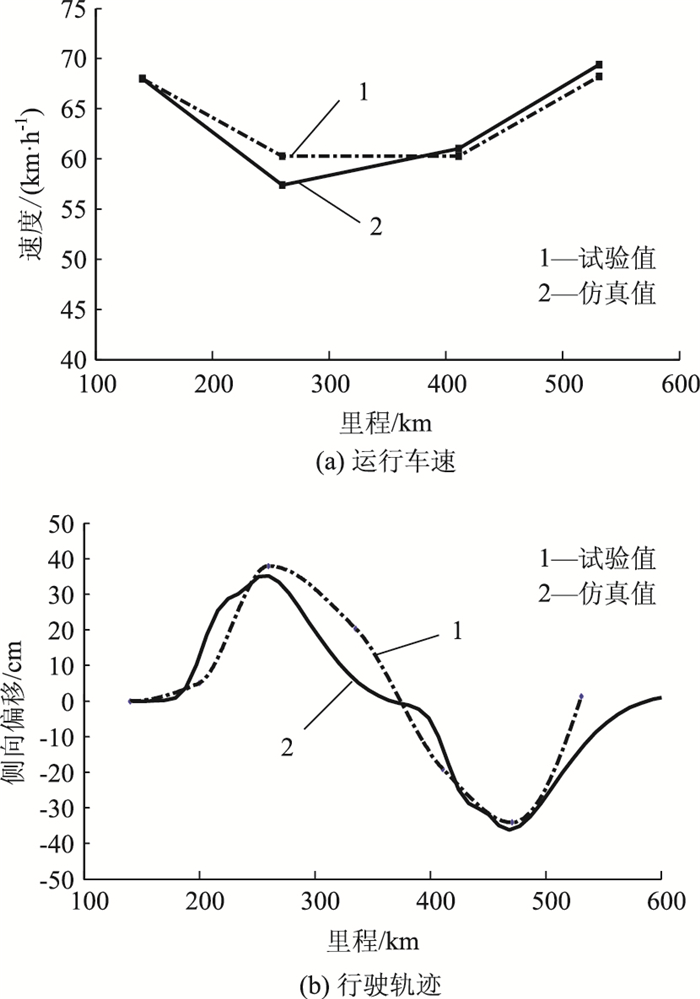
选择曲线半径R=240 m的试验路段,依据本研究中2种仿真方法对其进行仿真计算,试验值与仿真值的对比如图 8、9所示,车速仿真值与试验值的总平均误差分别为1.2%和2.0%,行驶轨迹误差最大点(QZ点附近)的误差值分别为7.0%和48%。同理可知,采用融合NSGA_Ⅱ多目标遗传算法和模糊优选决策算法的仿真结果优于单纯采用多目标模糊优选决策算法的仿真结果,其较好地模拟了驾驶人的运行车速和行驶轨迹,与试验数据较为接近。其余试验路段受篇幅限制不再赘述。
|
| 图 8 R=240 m试验段运行车速和行驶轨迹试验值与基于NSGA_Ⅱ多目标遗传算法的仿真值对比 Fig. 8 omparison of experimental vehicle speeds and trajectory values and simulation values based on multi- objective NSGA_Ⅱ in R=240 m experimental section |
| |
|
| 图 9 R=240 m试验段运行车速和行驶轨迹试验值与基于NSGA_Ⅱ多目标模糊优选决策算法的仿真值对比 Fig. 9 Comparison of experimental vehicle speeds and trajectory values and simulation values based on NSGA_Ⅱ and fuzzy optimization decision-making in R=240 m experimental section |
| |
6 结论
本研究针对双车道公路驾驶人模型中2个决策变量、3个相互冲突目标的多目标优化问题,研究了基于NSGA_Ⅱ的多目标遗传优化算法,算法中涉及了初始样本的抽样、目标值的计算、交叉和变异算法、数据越界处理等若干关键问题的分析和求解;采用多目标模糊优选决策算法对优化结果进行决策得到最优解。通过2种仿真方法与试验数据的对比分析,验证了本研究提出的模型及算法的有效性。结果表明,采用基于NSGA_Ⅱ和模糊优选决策联合优化算法的仿真结果试实验数据具有较好的一致性。
| [1] |
PRAKASH A K, AMOL P, KALYANI U. Artificial Neural Network Based Driver Modeling for Vehicle Systems[EB/OL]. (2013-11-27)[2020-12-15]. https://www.sae.org/publications/technical-papers/content/2013-01-2860/.
|
| [2] |
LI J M, SMITH D. Modeling the Impact of Road Grade and Curvature on Truck Driving for Vehicle Simulation[EB/OL]. (2014-04-01)[2020-12-15]. https://www.sae.org/publications/technical-papers/content/2014-01-0879/.
|
| [3] |
JALALI K, LAMBERT S, MCPHEE J. Development of a Path-following and a Speed Control Driver Model for an Electric Vehicle[J]. SAE International Journal of Passenger Cars-Electronic and Electrical Systems, 2012, 5(1): 100-113. |
| [4] |
LEE T, KANG J, YI K. Integration of Longitudinal and Lateral Human Driver Models for Evaluation of the Vehicle Active Safety Systems[EB/OL]. (2010-04-12)[2020-12-15]. https://www.sae.org/publications/technical-papers/content/2010-01-0084/.
|
| [5] |
GUAN H, GAO Z H, GUO K H, et al. A Driver Direction Control Model and Its Application in the Simulation of Driver-vehicle-road Closed-loop System[EB/OL]. (2000-06-06)[2020-12-15]. https://www.sae.org/publications/technical-papers/content/2000-01-2184/.
|
| [6] |
ZHUANG D J, YU F, LI D F. An Optimal Preview ANN Driver Model Based on Error Elimination Algorithm[EB/OL]. (2005-11-01)[2020-12-15]. https://www.sae.org/publications/technical-papers/content/2005-01-3495/.
|
| [7] |
王婉秋, 陈雨人, 钱宇彬. 双车道公路弯道驾驶人模糊优选决策模型与实验验证[J]. 中南大学学报: 自然科学版, 2015, 46(1): 332-341. WANG Wan-qiu, CHEN Yu-ren, QIAN Yu-bin. Driver's Fuzzy Optimal Decision-making Models in Curves of Two-lane Highway and Experimental Validation[J]. Journal of Central South University: Science and Technology Edition, 2015, 46(1): 332-341. |
| [8] |
徐艳艳, 李国柱, 徐喆, 等. 北京市交通环境承载力动态评价及障碍因子诊断[J]. 公路交通科技, 2017, 34(6): 122-128. XU Yan-yan, LI Guo-zhu, XU Zhe, et al. Dynamic Evaluation of Traffic Environment Bearing Capacity of Beijing and Diagnosis of Obstacle Factor[J]. Journal of Highway and Transportation Research and Development, 2017, 34(6): 122-128. |
| [9] |
姜福川, 周师, 吴增彤, 等. 基于熵权-TOPSIS法的煤矿安全投入决策分析[J]. 中国安全科学学报, 2021, 31(7): 24-29. JIANG Fu-chuan, ZHOU Shi, WU Zeng-tong, et al. Analysis of Coal Mine Safety Investment Decision Based on Entropy Weight-TOPSIS Method[J]. China Safety Science Journal, 2021, 31(7): 24-29. |
| [10] |
张哲, 王会利, 石磊, 等. 桥梁方案多层多目标模糊优选模型及其应用[J]. 哈尔滨工业大学学报, 2006, 38(9): 1567-1571. ZHANG Zhe, WANG Hui-li, SHI Lei, et al. Application of Multi-levels and Multi-objectives Fuzzy Optimization Model of Bridge Type Selection[J]. Journal of Harbin Institute of Technology, 2006, 38(9): 1567-1571. |
| [11] |
郑金华, 蒋浩, 邝达, 等. 用擂台赛法则构造多目标Pareto最优解集的方法[J]. 软件学报, 2007, 18(6): 1287-1297. ZHENG Jin-hua, JIANG Hao, KUANG Da, et al. An Approach of Constructing Multi-objective Pareto Optimal Solutions Using Arena's Principle[J]. Journal of Software, 2007, 18(6): 1287-1297. |
| [12] |
屠传运, 陈韬伟, 余益民, 等. 膜系统下的一种多目标优化算法[J]. 智能系统学报, 2017, 12(5): 678-683. TU Chuan-yun, CHEN Tao-wei, YU Yi-min, et al. Multi-objective Optimization Algorithm Based on Membrane System[J]. CAAI Transactions on Intelligent Systems, 2017, 12(5): 678-683. |
| [13] |
胡成玉, 余果, 代立国, 等. 知识驱动的高维多目标优化算法研究[J]. 华中科技大学学报: 自然科学版, 2020, 48(6): 19-25. HU Cheng-yu, YU Guo, DAI Li-guo, et al. Research on Knowledge-driven Many-objective Optimization Algorithm[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2020, 48(6): 19-25. |
| [14] |
DEB K, GOYAL M. A Combined Genetic Adaptive Search (Gene AS) for Engineering Design[J]. Journal of Computer Science and Informatics, 1996, 26: 30-45. |
| [15] |
AGRAWAL R B, DEB K, AGRAWAL R B. Simulated Binary Crossover for Continuous Search Space[J]. Complex Systems, 1994, 9(3): 115-148. |
| [16] |
王之仓, 李和成. 采用多项式变异策略和分解方法的多目标进化算法[J]. 微电子学与计算机, 2021, 38(1): 95-100. WANG Zhi-cang, LI He-cheng. Multi-objective Evolutionary Algorithm Using Decomposition Method and Polynomial Mutation Operator[J]. Microelectronics & Computer, 2021, 38(1): 95-100. |
| [17] |
鲍正壮, 周捷, 鲁丹丹, 等. 基于改进灰色关联度的弹力针织物吸湿速干性评价[J]. 西安工程大学学报, 2020, 34(1): 1-7. BAO Zheng-zhuang, ZHOU Jie, LU Dan-dan, et al. Evaluation of Moisture Absorption and Quick Drying of Elastic Knitted Fabric Based on Improved Grey Correlation Degree[J]. Journal of Xi'an Polytechnic University, 2020, 34(1): 1-7. |
| [18] |
胡超, 包惠明. 高岭土矿粉沥青混合料的灰色关联分析[J]. 公路交通科技, 2020, 37(7): 24-31. HU Chao, BAO Hui-ming. Grey Correlation Analysis on Kaolin Mineral Powder Asphalt Mixture[J]. Journal of Highway and Transportation Research and Development, 2020, 37(7): 24-31. |
 2021, Vol. 38
2021, Vol. 38
