扩展功能
文章信息
- 谢佳鑫, 俞卫琴
- XIE Jia-xin, YU Wei-qin
- 张量加权Schatten范数交通数据补全估计
- Estimation on Tensor Weighted Schatten Norm for Missing Traffic Data Completion
- 公路交通科技, 2021, 38(12): 122-130
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(12): 122-130
- 10.3969/j.issn.1002-0268.2021.12.014
-
文章历史
- 收稿日期: 2021-02-08
随着智慧交通概念的提出,城市道路上部署了大量的感知器不间断地采集具有相关时间地点信息的交通数据,这些数据被用来监测城市交通运行状态和进行通行时间预测等。由于采集到的时空交通数据规模与维数越来越大,并且数据采集过程中不可避免地发生数据丢失等情况,实际使用这些原始观测数据时,难免会受到缺失数据的影响,使得数据集的有效性降低。数据丢失的原因可能是由于传感器故障或传输丢包等设备因素,也可能是感知器的覆盖范围有限造成的。因此,数据缺失可分为以下两种情形:一种是连续时间状态下,随机记录点的缺失,即随机缺失情形;另一种是传感器不工作状态下,此区间段的数据丢失,即非随机缺失情形。可见对缺失数据进行合理补全成为交通数据应用前的关键步骤。
过去的工作中,低秩矩阵补全和低秩张量补全在图像领域取得了显著成功[1-2]。由于现实中大多数交通数据集也具有低秩性,所以可将低秩矩阵/张量补全用于交通数据集。Yu等[3]基于车辆轨迹数据建立了时空速度矩阵,使用Schatten p-norm实现了缺失数据矩阵的估计,并可以用作全市范围的交通数据估计和流量的动态监测。当采用矩阵结构来建模交通数据时,矩阵结构无法充分利用数据的时空信息,且在数据丢失率较大时,矩阵方法的恢复效果就会下降。鉴于交通数据与时间和空间高度相关,选择张量结构能很好地保留数据的时空特性。Asif和Tan等[4-5]均提出使用低秩张量补全的方法来解决交通数据的估算。鉴于交通数据集存在强时空相关性(如传感器在不同天的同一时间具有相似的读数,在不同星期观察的趋势也彼此相似),低秩模型往往能在一定准确度上对此类数据集进行建模并恢复。
在低秩逼近(Low Rank Approximation, LRA)中,核范数是最典型的低秩约束,其定义为给定矩阵的奇异值之和,即给定矩阵
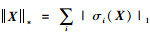
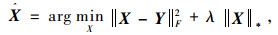
|
(1) |
式中,λ为一个平衡参数。在一定条件下,核范数可以完美恢复低秩矩阵[6]。Liu等[7]提出了HaLRTC(High accuracy Low Rank Tensor Completion)算法,采用张量展开的核范数和最小化算法进行数据补全。继而有学者提出使用Schatten p-范数作为低秩约束,其定义为奇异值的lp范数,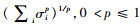
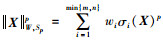
总体来说,交通数据补全领域多用核范数相关方法,于是本研究提出张量加权Schatten p-范数最小化(Tensor Weighted Schatten p-Norm Minimization, TWSNM)模型,结合交替方向乘子法和贝叶斯优化算法,用于广州城市交通数据的补全估计,并给出TWSNM模型的准确性与有效性。
1 基于低秩张量补全的优化模型 1.1 低秩张量补全低秩张量补全(Low Rank Tensor Completion, LRTC)是张量补全体系中的一个分支。针对时空交通数据具有低秩结构这一先验假设,本研究将构建1个三阶张量模型。对于缺失张量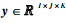
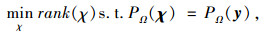
|
(2) |
式中,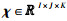
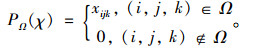
|
(3) |
LRTC模型中秩最小化的问题在计算上是非常困难的,因此需要寻找一个合适的凸松弛来逼近秩函数。常用的方法是利用核范数来代替秩函数,即:
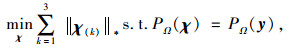
|
(4) |
式中,χ(k)为对应的k阶张量展开矩阵,核范数的定义是对于任何矩阵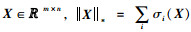
首先介绍关于矩阵的加权Schatten p-范数的常用定义。
定义1:矩阵的Schatten p-范数[20]。给定一个矩阵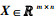
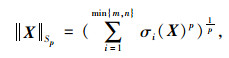
|
(5) |
即:
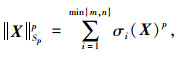
|
(6) |
式中,σi(X), i=1, 2, …, min{m, n}是矩阵X的第i个奇异值。奇异值的排序为σ1≥σ2≥…≥σr≥…≥σmin{m, n}≥0。
由于矩阵的Schatten p-范数定义并不能直接用于多维张量,并且奇异值的大小会对模型产生影响,于是在张量上定义加权的Schatten p-范数。
定义2:张量加权Schatten p-范数。对于任意d阶张量χ,张量加权Schatten p-范数定义为:
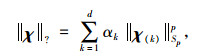
|
(7) |
式中,α1, α2, …, αd分别为施加在张量展开矩阵χ(1), χ(2), …, χ(d)上的权重参数,且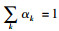
由定义2,当权重参数αk适当的设置,每个张量模态展开矩阵χ(k)将被分配权重。现用张量加权Schatten p-范数替换式(4)中的标准核范数,则LRTC模型变形为:
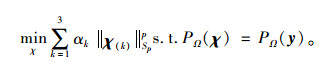
|
(8) |
事实上,以不同模态展开的张量不能保证变量的稳定性。因此,引入一个辅助张量δ和一组新的约束,将模型改写为:
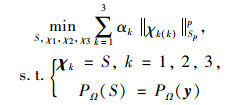
|
(9) |
式中,引入δ是为了保留观测信息,并将这些信息广播到变量χk, k=1, 2, 3,建立辅助变量δ与现有观测量y之间的关系。
1.3 算法设计为了解决优化式(9),本研究采用交替方向乘子法(Alternating Direction Method of Multipliers, ADMM),给出增广拉格朗日函数[9, 21-22]:
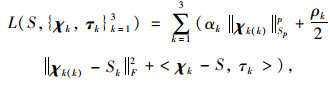
|
(10) |
式中 < ·, ·>为内积,τ1, τ2, τ3∈ 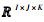
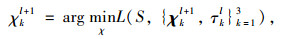
|
(11) |
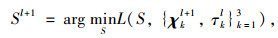
|
(12) |
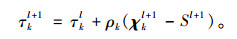
|
(13) |
遵循的更新顺序为χ1l+1→…→χ3l+1→Sl+1→τ1l+1→…→τ3l+1。
基于增广拉格朗日函数(10),得到χkl+1的最优解为:
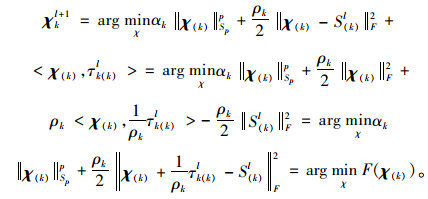
|
(14) |
考虑到模型的凸性,为使式(14)收敛到期望的全局最优解,基于定理1本研究给出引理1,得到封闭形式的最优解或者次优解。
定理1 (Von-Neumann [23]):对于任意m×n矩阵A和B,对应的奇异值分别为σ(A)=[σ1(A), σ2(A), …, σr(A)]T,σ(B)=[σ1(B), σ2(B), …, σr(B)]T,r=min{m, n},可得tr(ATB)≤tr(σ(A)Tσ(B)),当且仅当同时找到U, V时,取得等号。
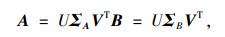
|
(15) |
式中ΣA, ΣB为有序对角奇异值矩阵。
引理1:对于任意α, ρ>0, 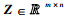
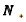
由引理1,最小化目标函数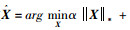
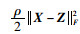
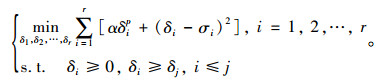
|
(16) |
则χkl+1可以通过式(17)进行更新:
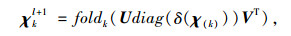
|
(17) |
式中foldk(·)为一个折叠运算符,将以k阶展开的矩阵再转换为高阶张量,即foldk(χ(k))=χ。同理,可以计算出辅助张量Sl+1。
2 算例分析 2.1 数据准备从CERN数据中心的公开数据集中选取广州城市交通速度数据作为试验数据集,其时间跨度为2016年8月1日—2016年9月30日,共61天。从214个路段收集平均行车速度,时间窗间隔为10 min,则一天可分为144个时间间隔。张量结构为“位置×天×时间窗”,其大小为214×61×144;展开成矩阵结构时为“位置×时间”,其大小为214×8 784, 数据的缺失率为1.29%。
2.2 对比模型本研究选取以下模型与提出的TWSNM模型进行比较:
(1) HaLRTC:高精度低阶张量补全[7]。其为低秩补全模型,使用核范数最小化估计缺失数据。
(2) LRTC-TNN:截断核范数张量补全[9]。其为低秩补全模型,使用截断的核范数来估计缺失数据。
(3) BGCP:贝叶斯高斯CP分解[11]。其为全贝叶斯高斯张量分解模型,使用马尔可夫链蒙特卡洛方法来学习低秩结构。
2.3 试验设定为了评估模型表现,将已观察到的数据掩盖为“缺失”数据。采用两种数据缺失模式,即随机缺失(Random Missing, RM)和非随机缺失(Non-random Missing, NM),对这些“缺失”数据进行逼近估计。选取平均百分比误差(Mean Absolute Percentage Error, MAPE)和均方根误差(Root Mean Square Error, RMSE)作为评价指标:
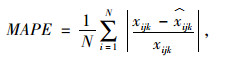
|
(18) |
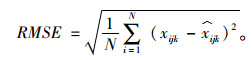
|
(19) |
其中非随机缺失情形更具有挑战性,数据会被严重破坏。
许多算法依赖于各种参数选择和设置,如滤波器组的大小,分类器正则化的强度等,这些设置会对系统性能产生巨大影响且这些参数是至关重要的。而调整参数的过程往往依赖于个人经验和直觉,难以量化或者描述。本研究采用的参数搜索方法是TPE (Tree of Parzen Estimators) 优化后的贝叶斯算法[24]。相较于随机搜索,TPE是用高斯混合模型(GMM)替代随机节点。在每次迭代中,对于每个超参数,TPE将匹配最小损失函数值相关的超参数值集。采用TPE算法目的是用可重复和无偏优化过程取代手工调优,其广泛地探索了一个单一参数化的模型族,产生从偶然到最优表现的分类性能,于是特定的搜索过程通常可以在给定的时间内发现最佳配置。贝叶斯优化,又叫序贯模型优化(Sequential Model-Based Optimization, SMBO),是有效的函数优化方法之一。与共轭梯度下降法等标准优化策略相比,SMBO具有自适应性且可以利用平滑性而无需计算梯度。TWSNM模型中需要设置参数的搜索空间,其中α1, α2, α3是3个展开张量的权重。在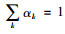
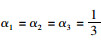
在随机缺失(RM)和非随机缺失(NM)两种数值缺失模式下,通过可视化搜索过程研究参数和模型的关系。横坐标为各参数的数值,纵坐标为RMSE值。通过图 1中展示的散点分布,可以看到TWSNM模型寻优过程中的趋势。在非随机缺失模式中,散点的分布要多于随机缺失模式,可以理解为在非随机缺失模式下算法需要进行更多的尝试,这一表现也符合现实逻辑。当点从均匀分布到集中在某一块区域,表明优化算法开始是在整个范围中均匀选择参数值,来学习目标值整体分布,最后找到最优分布区域和最优值。
|
| 图 1 TWSNM模型在两种数值缺失模式下参数寻优过程 Fig. 1 Parameters optimization process of TWSNM model in 2 missing modes |
| |
针对广州城市交通速度数据集,表 1总结了4个模型的数据插补性能,其中BGCP属于张量分解,HaLRTC、LRTC-TNN以及TWSNM模型属于低秩框架下的插补模型。
| 缺失率 | BGCP | HaLRTC | LRTC-TNN | TWSNM |
| 10%RM | 0.103 5/4.31 | 0.076 8/3.16 | 0.071 4/3.03 | 0.056 6/2.48 |
| 20%RM | 0.103 0/4.30 | 0.081 0/3.31 | 0.074 3/3.15 | 0.058 6/2.56 |
| 30%RM | 0.102 6/4.32 | 0.084 7/3.46 | 0.077 0/3.27 | 0.060 8/2.66 |
| 40%RM | 0.102 4/4.32 | 0.088 4/3.60 | 0.079 7/3.38 | 0.063 5/2.77 |
| 50%RM | 0.103 9/4.40 | 0.092 8/3.76 | 0.082 7/3.51 | 0.066 2/2.89 |
| 60%RM | 0.105 4/4.45 | 0.098 0/3.95 | 0.086 1/3.65 | 0.070 5/3.07 |
| 70%RM | 0.110 3/4.84 | 0.104 3/4.17 | 0.089 7/3.79 | 0.076 2/3.29 |
| 80%RM | 0.112 4/4.82 | 0.113 4/4.48 | 0.093 5/3.96 | 0.084 2/3.59 |
| 90%RM | 0.137 7/6.33 | 0.129 6/5.04 | 0.098 4/4.16 | 0.098 9/4.13 |
| 10%NM | 0.099 4/4.37 | 0.102 9/4.15 | 0.093 2/3.95 | 0.099 7/4.15 |
| 20%NM | 0.101 7/4.72 | 0.104 2/4.20 | 0.093 7/3.97 | 0.100 3/4.18 |
| 30%NM | 0.103 4/4.70 | 0.105 8/4.27 | 0.094 3/4.02 | 0.100 8/4.22 |
| 40%NM | 0.108 3/5.03 | 0.108 6/4.37 | 0.095 4/4.07 | 0.102 1/4.28 |
| 50%NM | 0.113 8/5.31 | 0.112 8/4.51 | 0.097 4/4.16 | 0.104 6/4.38 |
| 60%NM | 0.121 5/5.75 | 0.117 8/4.68 | 0.099 2/4.24 | 0.106 9/4.48 |
| 70%NM | 0.132 0/6.21 | 0.126 3/4.95 | 0.121 2/6.70 | 0.112 8/4.68 |
| 80%NM | 0.147 1/7.01 | 0.141 6/5.54 | 0.179 6/9.96 | 0.130 8/5.49 |
| 90%NM | 0.159 1/7.22 | 0.204 3/8.49 | 0.438 6/21.84 | 0.208 5/8.97 |
由图 2,可以看出TWSNM在随机缺失场景下各个缺失率中的指标表现都优于其他插补模型。随着缺失率上升,MAPE和RMSE也在上升。与随机缺失场景相比,非随机缺失场景更具挑战性。结果显示,在60%非随机缺失率之前,TWSNM模型仅次于低秩框架下的LRTC-TNN模型,但两者之间的差异非常小,RMSE相差0.2左右,说明TWSNM模型依然具有竞争性。在60%~80%缺失率的区间,TWSNM模型要优于其他模型,而此时LRTC-TNN模型的波动较大,变得不稳定,从而反映出TWSNM模型具有鲁棒性。在90%缺失率时贝叶斯模型显示出一定优势。
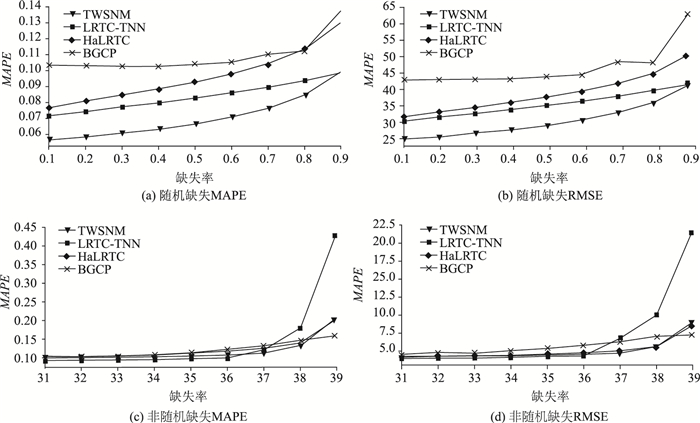
|
| 图 2 在不同缺失率情形下MAPE/RMSE的对比图 Fig. 2 Comparison of MAPE/RMSEs under different data missing rates |
| |
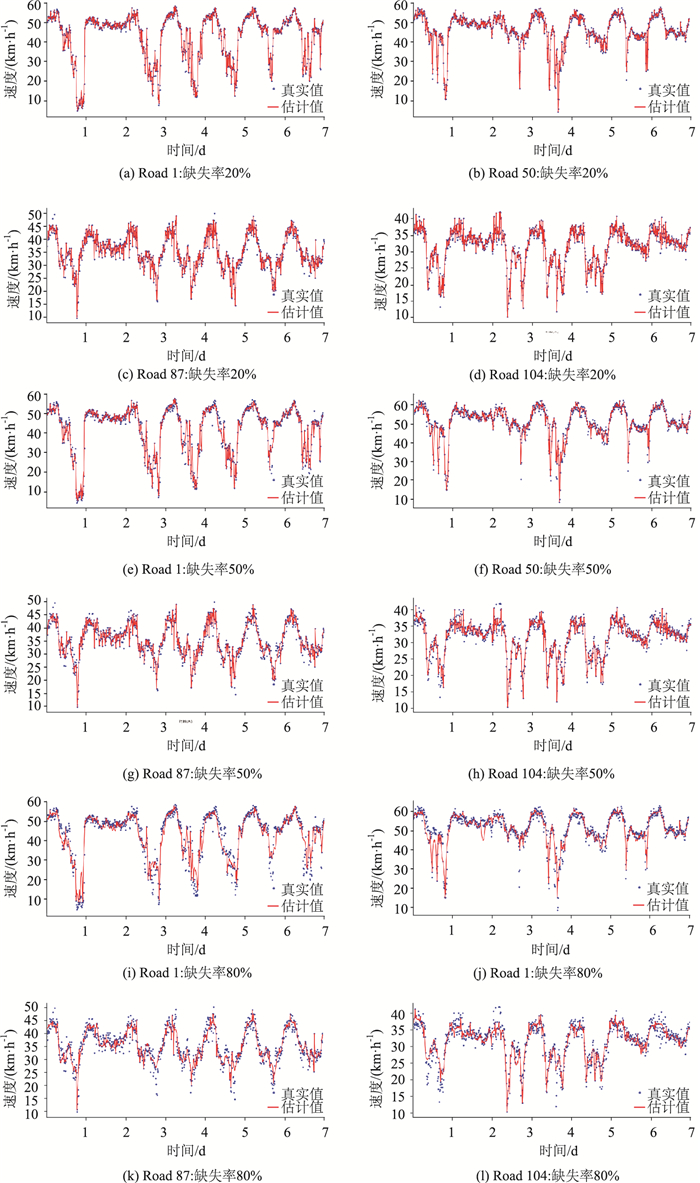
本研究选取4个不同路段,分别在缺失率20%,50%和80%场景下,展示TWSNM模型补全后的时间序列数据与实际时间序列数据的比较,如图 3所示。圆点表示实际时间序列数据,线条表示TWSNM模型补全后的时间序列数据。能看出线条可以基本覆盖圆点数据点,即使在缺失率大的场景下,也能做到趋势吻合。可见TWSNM模型可以进行高质量的数据补全估计。
|
| 图 3 实际时间序列数据与TWSNM模型估计序列数据对比 Fig. 3 Comparison of actual time series data with estimated series data of TWSNM model |
| |
4 结论
缺失交通数据的补全可以提高数据的利用率。本研究提出了一种基于非凸最小化的低秩张量补全模型——TWSNM模型,结合交替方向乘子法和贝叶斯优化算法来估计广州城市交通数据集中的缺失值。试验表明,TWSNM模型在随机缺失场景中不同缺失率情况下的表现都优于其他插补模型;在非随机缺失场景中低缺失率情形下TWSNM模型的表现与其他模型相比具有竞争性,在高缺失率情形下也有较好的表现并具有鲁棒性。可见TWSNM模型对实际缺失交通数据具有很好的补全效果。
| [1] |
DONG J, XUE Z, GUAN J, et al. Low Rank Matrix Completion Using Truncated Nuclear Norm and Sparse Regularizer[J]. Signal Processing: Image Communication, 2018, 68: 76-87. |
| [2] |
GU S, ZHANG L, ZUO W, et al. Weighted Nuclear Norm Minimization with Application to Image Denoising[C]//Proceedings of 2014 IEEE Conference on Computer Vision and Pattern Recognition. Columbus: IEEE, 2014: 2862-2869.
|
| [3] |
YU J, STETTLER M E J, ANGELOUDIS P, et al. Urban Network-wide Traffic Speed Estimation with Massive Ride-sourcing GPS Traces[J]. Transportation Research Part C: Emerging Technologies, 2020, 112: 136-152. |
| [4] |
ASIF M T, MITROVIC N, GARG L, et al. Low-dimensional Models for Missing Data Imputation in Road Networks[C]//2013 IEEE International Conference on Acoustics, Speech and Signal Processing. Vancouver: IEEE, 2013: 3527-3531.
|
| [5] |
TAN H, FENG J, CHEN Z, et al. Low Multilinear Rank Approximation of Tensors and Application in Missing Traffic Data[J]. Advances in Mechanical Engineering, 2014, 1: 1-12. |
| [6] |
CAI J F, CANDES E J, SHEN Z. A Singular Value Thresholding Algorithm for Matrix Completion[J]. SIAM Journal on Optimization, 2010, 20(4): 1956-1982. |
| [7] |
LIU J, MUSIALSKI P, WONKA P, et al. Tensor Completion for Estimating Missing Values in Visual Data[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 35(1): 208-220. |
| [8] |
LIU J, MUSIALSKI P, WONKA P. Exact Minimum Rank Approximation via Schatten p-norm Minimization[J]. Journal of Computational and Applied Mathematics, 2014, 267: 218-227. |
| [9] |
CHEN X, YANG J, SUN L. A Nonconvex Low-rank Tensor Completion Model for Spatiotemporal Traffic Data Imputation[J]. Transportation Research Part C: Emerging Technologies, 2020, 117: 102673. |
| [10] |
XIE Y, GU S, LIU Y, et al. Weighted Schatten p-norm Minimization for Image Denoising and Background Subtraction[J]. IEEE Transactions on Image Processing, 2016, 25(10): 4842-4857. |
| [11] |
CHEN X, HE Z, SUN L. A Bayesian Tensor Decomposition Approach for Spatiotemporal Traffic Data Imputation[J]. Transportation Research Part C: Emerging Technologies, 2019, 98: 73-84. |
| [12] |
CHEN X, HE Z, CHEN Y, et al. Missing Traffic Data Imputation and Pattern Discovery with a Bayesian Augmented Tensor Factorization Model[J]. Transportation Research Part C: Emerging Technologies, 2019, 104: 66-77. |
| [13] |
HU C, RAI P, CHEN C, et al. Scalable Bayesian Non-negative Tensor Factorization for Massive Count Data[C]//Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Porto: Springer, 2015: 53-70.
|
| [14] |
RAI P, HU C, HARDING M, et al. Scalable Probabilistic Tensor Factorization for Binary and Count Data[C]//IJCAI'15: Proceedings of the 24th International Conference on Artificial Intelligence. Buenos Aires: AAAI Press, 2015: 3770-3776.
|
| [15] |
ZHANG T, ZHANG D, YAN H, et al. A New Method of Data Missing Estimation with FNN-based Tensor Heterogeneous Ensemble Learning for Internet of Vehicle[J]. Neurocomputing, 2020, 420: 98-110. |
| [16] |
TAN H, FENG G, FENG J, et al. A Tensor-based Method for Missing Traffic Data Completion[J]. Transportation Research Part C: Emerging Technologies, 2013, 28: 15-27. |
| [17] |
GOULART J H D M, KIBANGOU A Y, FAVIER G. Traffic Data Imputation via Tensor Completion Based on Soft Thresholding of Tucker Core[J]. Transportation Research Part C: Emerging Technologies, 2017, 85: 348-362. |
| [18] |
TAN H, WU Y, SHEN B, et al. Short-term Traffic Prediction Based on Dynamic Tensor Completion[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(8): 2123-2133. |
| [19] |
DUAN H, XIAO X, LONG J, et al. Tensor Alternating Least Squares Grey Model and Its Application to Short-term Traffic Flows[J]. Applied Soft Computing, 2020, 89: 106145. |
| [20] |
NIE F, HUANG H, DING C. Low-rank Matrix Recovery via Efficient Schatten p-norm Minimization[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Toronto: AAAI Press, 2012.
|
| [21] |
HU Y, ZHANG D, YE J, et al. Fast and Accurate Matrix Completion via Truncated Nuclear Norm Regularization[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 35(9): 2117-2130. |
| [22] |
LIU J, MUSIALSKI P, WONKA P, et al. Tensor Completion for Estimating Missing Values in Visual Data[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 35(1): 208-220. |
| [23] |
MIRSKY L. A Trace Inequality of John von Neumann[J]. Monatshefte Für Mathematik, 1975, 79(4): 303-306. |
| [24] |
BERGSTRA J, YAMINS D, COX D D. Making a Science of Model Search: Hyperparameter Optimization in Hundreds of Dimensions for Vision Architectures[C]//30th International Conference on Machine Learning. Atlanta: JMLR, 2013: 115-123.
|
 2021, Vol. 38
2021, Vol. 38
