扩展功能
文章信息
- 高宏伟
- GAO Hong-wei
- 大跨度市政通道开挖近接轨道交通隧道变形特性分析
- Analysis on Deformation Characteristics of Excavating Long-span Municipal Underpass Adjacent to Metro Tunnel
- 公路交通科技, 2021, 38(12): 81-90
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(12): 81-90
- 10.3969/j.issn.1002-0268.2021.12.010
-
文章历史
- 收稿日期: 2021-03-22
随着我国城市化进程的不断推进,交通压力迅速增大,城市轨道交通凭借其高效载客及节省地面空间等优势成为解决交通问题的有效途径。城市交通的发展逐渐呈现立体化发展模式,在有限的城市空间内,市政通道与轨道交通工程不可避免存在相互影响,周边地块的开发亦对城市轨道交通工程存在一定的影响。因此,采用合理的施工或加固方法确保既有轨道交通隧道的安全稳定和规划线路的实施具有重要的工程意义。
在基坑开挖卸载作用下,邻近既有轨道交通隧道会发生纵向不均匀变形、管片开裂、错台、渗漏等一系列病害,严重威胁轨道交通运营安全。基于宁波轨道交通1号线,Chen等[1]研究了敏感软土中临近大开挖对既有轨道交通隧道的影响,发现邻近开挖引起的左线隧道位移较大,并且出现了可见的裂缝和渗漏。Chang等[2]报道了台北捷运轨道交通某区间盾构隧道由于紧邻高层建筑基坑施工导致隧道管片发生严重损害,影响列车运营。受盾构下穿影响,北京轨道交通某区间隧道累计沉降23 mm,并产生大量新增裂缝及多处渗水[3]。英国Heathrow机场快线站厅隧道下穿引起既有Piccadilly线隧道最大沉降达63 mm,3 a后沉降发展至80 mm,并出现大量裂缝[4]。上海轨道交通2号线受盾构近接的影响,隧道总隆起量达到10.5 mm[5]。类似工程灾害在国内其他已运营轨道交通的城市也时常发生,各大城市也相继出台了轨道交通保护条例,旨在确保轨道交通运营安全。
针对市政通道建设及周边地块开发等项目所进行的基坑开挖工程对邻近轨道交通的影响这一研究课题,国内外学者通过理论分析[6-8]、数值分析[9-11]和模型试验[12-13]等方法进行了大量的研究。利用搁置于Pasternak地基上的Euler-Bernoulli梁来模拟既有隧道并借助于Mindlin解,程康等[14]提出了计算既有隧道在上覆基坑卸荷影响下形变响应的简化计算法。康成等[15]通过引入非线性Pasternak地基模型考虑隧道-地基的非线性相互作用,推导得到基坑卸载下盾构隧道纵向变形控制的微分方程。陈郁等[16]采用Winkler地基模型推导了基坑开挖卸荷引起隧道隆起变形的定量计算方法。
以西安科技八路市政通道近接轨道交通已建成6号线及未建8号线工程为例,建立三维有限元模型,分析近接通道及轨道交通6号线隧道的结构变形。在与工程实测数据进行比对后,进一步研究规划轨道交通8号线的可实施性,提出具体方案措施。
1 工程概况轨道交通6号线1期工程已基本完成建设,其向北为大里程方向,隧道为双连拱暗挖断面,采用浅埋暗挖法施工,底板埋深17.33~27.41 m,即将通车运营。轨道交通8号线区间同样采用浅埋暗挖法施工,尚未建设。科技八路规划为城市快速路,道路范围内设置隧道1座,总长度为4 200 m,主线暗埋段全长3 680 m,东、西侧敞口段各长260 m。隧道呈东西走向沿科技八路下穿唐延路,在唐延路与科技八路交叉口和南北走向的轨道交通6号、8号线区间隧道段相交,相交处市政通道结构形式为单层双跨矩形隧道,断面宽20 m,高6.5 m,结构顶板覆土约0.8 m。
根据地勘资料,工程区域地层从上到下依次为杂填土、黄土、中砂、古土壤、粉质黏土等。地下水位位于通道结构以下,自身施工时不需要降水,但轨道交通6号线隧道施工时需要降水。为防止后续通道结构施工期间地下水位上浮导致轨道交通6号线隧道随之上浮变形,在市政通道近接轨道交通6号线隧道处应保证在通道施工前和施工期间仍维持降水,保证地下水位低于轨道交通6号线隧道底板不小于1 m。
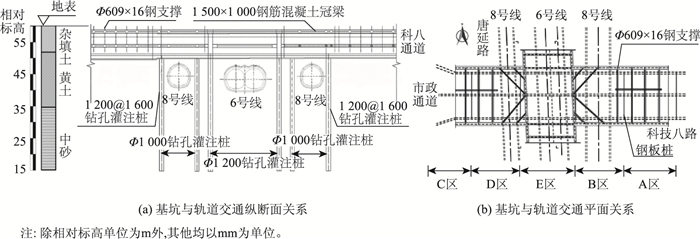
市政通道近接轨道交通段采用明挖施工,基坑与轨道交通的位置关系见图 1。其采用的支护形式见表 1。
|
| 图 1 通道、基坑与轨道交通关系 Fig. 1 Relationship between underpass foundation pit and subway |
| |
| 区段 | E区 | D, B区 | A, C区 |
| 位置 | 近接轨道交通6号线隧道 | 近接轨道交通8号线隧道 | 轨道交通8号线两侧隧道 |
| 基坑深度 | 8 m | 8 m | 8 m |
| 支护形式 | 围护桩(1 200@1 600钻孔桩) | 钢板桩(Ⅳ小齿口拉森) | 围护桩(1 200@1 600钻孔桩) |
| 混凝土内支撑(2个竖向支撑+4个水平支撑) | 钢管内支撑(2个竖向支撑,直径609 mm,壁厚16 mm) | 钢支撑(2竖向支撑,Φ609×16) | |
| 其他 | 南北向放坡开挖 | — | — |
2 主要技术问题及轨道交通隧道控制标准
在基坑卸载作用下,位于基坑下方的隧道会产生向上隆起变形,而一旦该位移或内力超过限值,可能会产生裂缝、沉降等结构损坏,严重危及轨道交通营运安全。针对市政通道近接轨道交通结构的工程特性,大面积开挖可能会引起的技术问题包括:
(1) 引起轨道交通6号线既有结构(轨道)上浮变形较大或不均匀变形较大。
(2) 市政通道建设属于卸荷作用,轨道交通结构的抗浮稳定性需满足要求。
(3) 考虑规划轨道交通8号线可实施性问题。
依据轨道交通6号线现状调查及有关规范要求,结合该地区多个工程实例分析结果,确定轨道交通6号线隧道结构变形控制指标,如表 2所示。
| 项目 | 限值 | |
| 水平位移 | ≤20 mm | |
| 竖向位移 | ≤20 mm | |
| 径向收敛 | < 20 mm | |
| 变形曲率半径 | > 15 000 m | |
| 变形相对曲率 | < 1/2 500 | |
| 结构外壁附加荷载 | < 20 kPa | |
| 隧道振动速度 | < 2.5 cm/s | |
| 结构裂缝宽度 | 迎水面 | < 0.2 mm |
| 背水面 | < 0.3 mm | |
3 有限元模型 3.1 模型建立
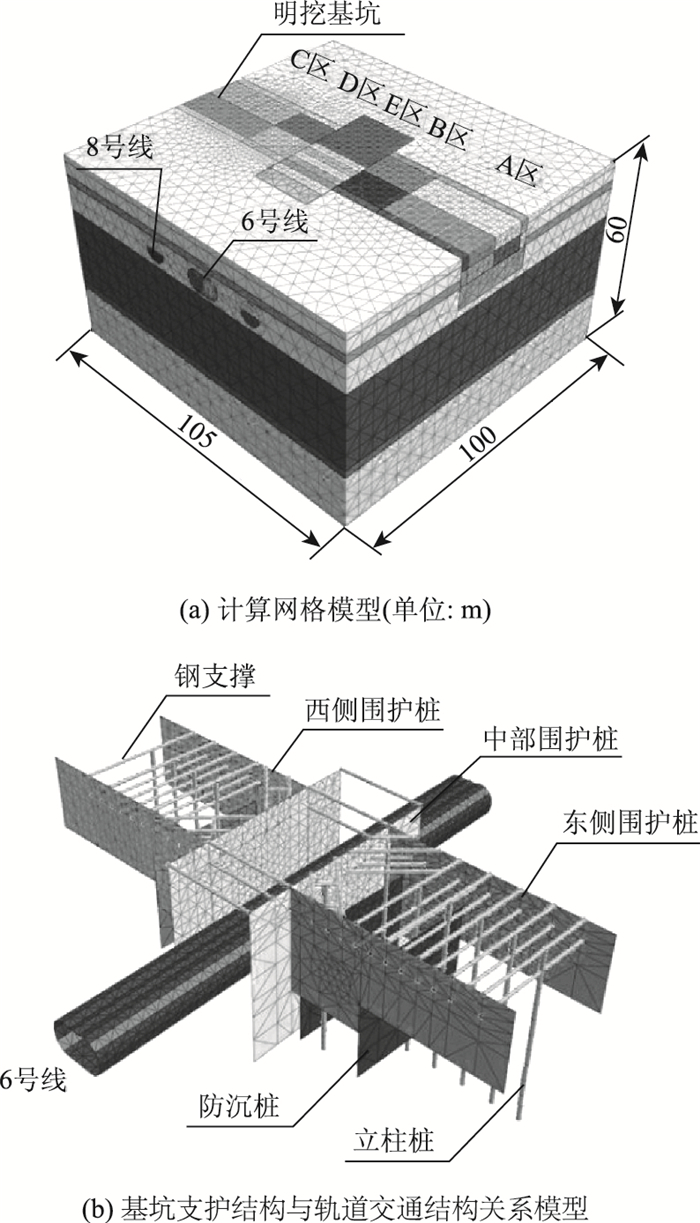
根据开挖市政通道基坑与轨道交通隧道的位置关系,结合本工程的特点、土层地质条件,采用MIDAS/GTS对开挖科技八路市政通道近接6号线及8号线引起的变形进行数值模拟分析。根据工程经验,模型宽度方向按照超出基坑深度不小于3倍来确定,最终模型长、宽、高分别为100, 105, 60 m。共包含5层土,各层深度分别为6,11.3,23.6,2.4,16.7 m。模型所有参数设定及取值皆根据工程现场构造及土层实际情况选取,有限元模型及基坑支护与轨道交通关系见图 2,土层物理力学参数见表 3。
|
| 图 2 计算网格模型和基坑支护结构与轨道交通结构关系模型 Fig. 2 Models of computational grid and relationship between pit supporting structure and subway structure |
| |
| 地层名称 | 重度/(kN·m-3) | 弹性模量/MPa | 泊松比 | 黏聚力/kPa | 内摩擦角/(°) |
| 杂填土 | 20 | 15 | 0.2 | 30 | 40 |
| 黄土 | 16 | 23.2 | 0.3 | 25 | 16.5 |
| 中砂 | 20.1 | 55 | 0.4 | 0 | 30 |
| 古土壤 | 18 | 30.2 | 0.25 | 0 | 35 |
| 粉质黏土 | 19 | 27.6 | 0.3 | 30 | 21 |
3.2 基本假定
土体采用修正Mohr-Coulomb弹塑性本构模型,结构体均采用线弹性本构模型。隧道衬砌、围护桩、支撑、钢板桩等满足弹性变形特性。所有材料均为均质、连续、各项同性体。其中钢支撑和立柱桩采用采用植入式梁单元,冠梁采用梁单元,墙面板、围护桩和隧道初支及二衬采用板单元模拟,其他以三维实体单元模拟,并对土体进行钝化来模拟基坑开挖[17-18]。模型中通过析取土体板单元来模拟盾构管片,由于基坑开挖前轨道交通已经降水,因此不考虑降水的影响。初始应力只考虑土体及结构物的自重应力。各构造物的基本物理力学参数如表 4所示。
| 名称 | 重度/(kN·m-3) | 弹性模量/MPa | 泊松比 |
| 初支 | 23.0 | 1×104 | 0.25 |
| 二衬 | 25.0 | 3.45×104 | 0.2 |
| 钢支撑 | 78.5 | 2.1×105 | 0.2 |
| 立柱桩 | 23.0 | 1×104 | 0.25 |
| 围护桩 | 5.0 | 3.0×104 | 0.2 |
| 加固区 | 20.0 | 1.2×102 | 0.3 |
3.3 施工模拟
为探索市政通道开挖对已建成6号线的影响,该模拟过程严格遵循实际开挖顺序,将整个施工范围分为A,B,C,D,E这5个区块,如图 2所示。模拟过程如下。
(1) 整体开挖顺序为:首先开挖A,C区段,其次为B,D区段,最后开挖6号线上方E区段。
(2) 具体每个区段的开挖顺序为:围护桩及立柱桩施工,基坑开挖,加设第1层钢支撑;继续开挖,加设第2层钢支撑,底板浇注;拆除第2层钢支撑,通道结构施工;拆除第1层钢支撑,基坑回填等。
(3) E区段开挖:将E区段模拟分成7节按照南北向进行开挖,以减少通道开挖对已建成6号线的影响,每节按照施工循环开挖。
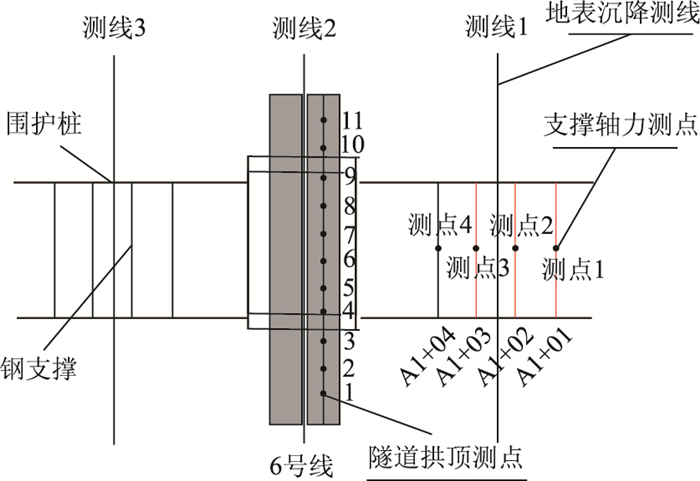
4 计算结果及分析 4.1 基坑开挖对轨道交通6号线影响分析 4.1.1 测点布设图 3为数值模拟过程中分别对支撑轴力、地表沉降及隧道拱顶沉降测点的布设。其中,支撑轴力布设在A区的第1层支撑的中心处点;地表沉降的监测分别位于A,C,E区段上方;拱顶沉降监测点位于6号线左线隧道拱顶上方,均匀分布11个测点。
|
| 图 3 测点布设 Fig. 3 Layout of measuring points |
| |
4.1.2 基坑开挖结构影响分析
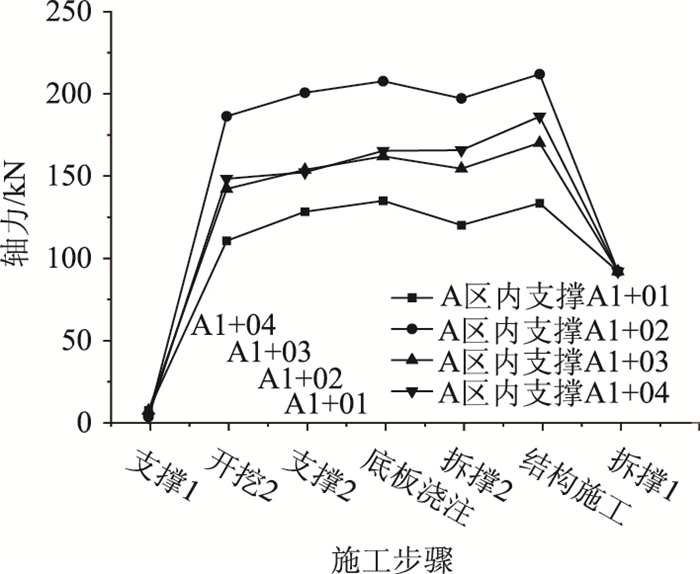
图 4为基坑开挖过程中A区所加设的第1层支撑的轴力变化,提取4个支撑中心处点作为轴力测试点。可以看出,在加设支撑初期轴力迅速增大到150~200 kN左右,随着开挖的推进,该轴力值几乎保持不变。第2个支撑(A1+02)的轴力值在整个开挖阶段都比其他3个支撑大,最大轴力值出现在下方通道结构施工时,达到210 kN。
|
| 图 4 支撑轴力变化 Fig. 4 Variation of support axial force |
| |
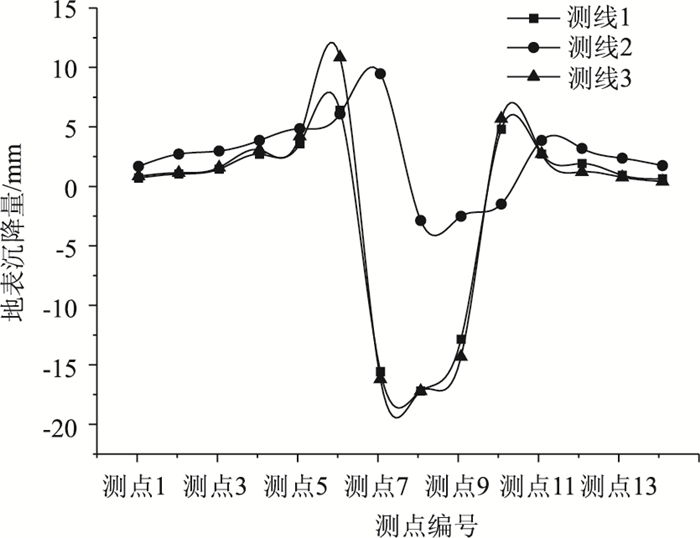
图 5为分别选取地表 3条测线的沉降值,其中3条测线沿Y轴方向,分别经过A,C,E区的中段,且3条测线上均匀分布13个测点。可以看出,经过A,C区的测线1和测线3整体沉降与隆起的波动较大,并且在基坑开挖位置出现较大沉降,最大沉降值达到19.7 mm,最大隆起值为13 mm。途径E区的测线2整体沉降隆起波动较小,这主要是由于考虑E区下部6号线运营采取的多阶段开挖与回填带来的影响较小。整体看来,3条测线值皆是在基坑位置处出现沉降,在基坑量测出现隆起。
|
| 图 5 地表沉降 Fig. 5 Surface settlement |
| |
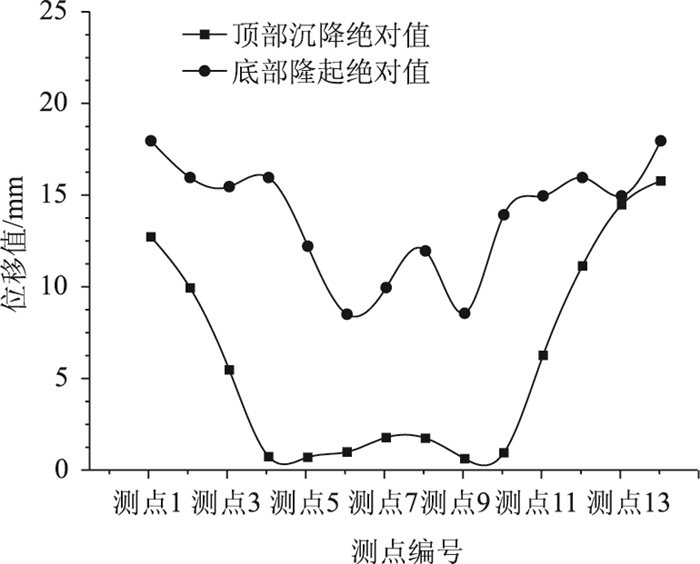
图 6为通道施工完成后顶部沉降与底部隆起沿通道纵向的变化规律。13个测点均匀分布在通道拱顶及拱底中心位置。可以看出,通道底部隆起绝对值在各个测点皆大于顶部沉降值。顶部与底部沉降值与隆起值沿通道纵向呈现凹形分布,其中在E区2种值皆较小,在A,C区沉降及隆起值较大,底部最大隆起值达到18.2 mm,顶部最大沉降值为16 mm。
|
| 图 6 通道底部与顶板变形值 Fig. 6 Deformations of underpass bottom and roof |
| |
4.1.3 轨道交通6号线隧道结构变形分析
(1) 结构竖向变形
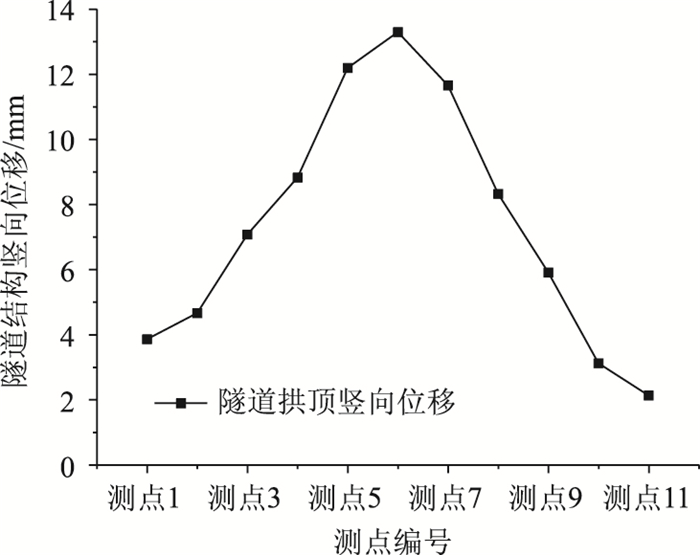
图 7为通道施工完毕后6号线拱顶竖向位移的分布规律。提取隧道方向(Y轴)拱顶位置处均匀分布的11个测点绘制在图中。可以看出,竖向位移沿隧道纵向方向呈现凸形分布,最大竖向位移出现在中部区域,即基坑开挖的正下方。由于基坑的卸载作用,隧道出现较大的竖向位移,最大位移达到13.3 mm,满足控制标准20 mm限制的要求。随着距离基坑的距离不断增大,其竖向位移也不断减小。
|
| 图 7 通道施工完毕时的竖向位移 Fig. 7 Vertical displacement when underpass construction is completed |
| |
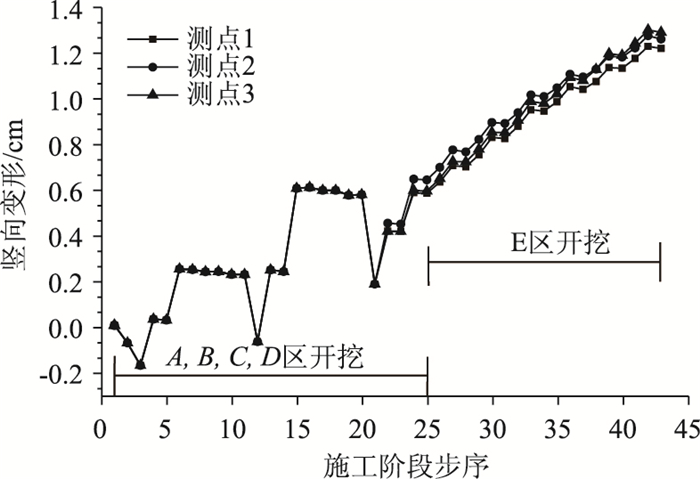
图 8为6号线轨道交通拱顶3个测点随着开挖的推进所产生的竖向变形变化规律。3个测点皆位于6号线中间部位,即通道正下方,其中测点B对应于图 7中的测点5,施工区域A,C沿Y轴向位于B点左右,在图 7中没有对应点。可以看出,各分区基坑开挖过程下,轨道交通6号线隧道结构的竖向隆起变形逐步增大。开挖各分区结构施工和覆土回填时,轨道交通6号线隧道结构的竖向隆起变形显著减小,其中第1波段隆起值出现大幅度减小,这主要是由于A,C区段覆土回填,使上部荷载增大所造成的,同样的第2波段隆起值也出现较大幅度的减小是由于B,D区段覆土回填造成的。
|
| 图 8 典型节点竖向位移曲线 Fig. 8 Curves of vertical displacement of typical nodes |
| |
在A,B,C,D区进行开挖与回填时隧道的隆起变化波动较大,在E区开挖时,竖向隆起变形虽然逐步增大,但该施工阶段增大变化率明显小于前几个区段的大范围分块开挖方案,这主要是由于在该区段采取分节段开挖,扰动较小。
(2) 结构水平变形
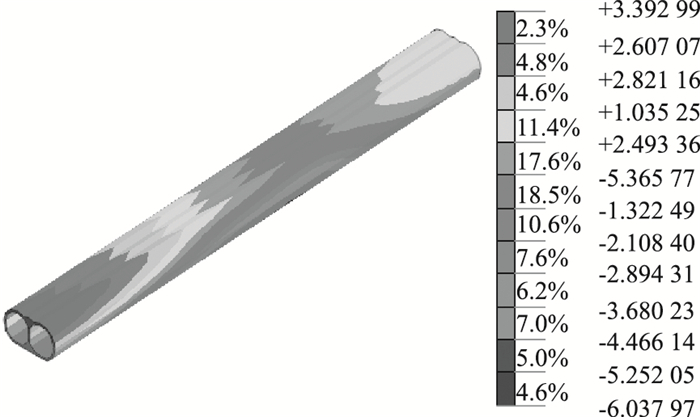
在市政通道施工过程中,轨道交通6号线区间隧道的水平变形较小,结构施工完成后隧道结构的水平变形如图 9所示。6号线隧道2段水平位移和中部水平位移方向相反,且隧道结构的最大水平变形出现在6号线中部,最大为0.61 mm,远远低于控制标准20 mm限制的要求。
|
| 图 9 通道施工完毕时的水平位移云图(单位: ×10-4 m) Fig. 9 Nephogrm of horizontal displacement when underpass construction is completed (unit: ×10-4 m) |
| |
4.1.4 隧道及轨道结构几何形态变化分析
(1) 隧道净空收敛
根据数值计算结果可知,隧道结构最大水平净空收敛为0.3 mm,最大竖向净空收敛为0.5 mm,满足控制标准20 mm限制的要求。
(2) 相对曲率半径
根据数值计算结果可知,隧道结构最大相对曲率半径为[(8.9-8.5)2+5 0002]/[2×(8.9-8.5)]/1 000=31 250 m>15 000 m。
(3) 相对曲率
隧道钢轨所在长度范围内(10 m)最大差异变形为1.4 mm,其相对变曲=1.4/10 000≤1/2 500,满足控制指标。
(4) 轨道横向高差(< 4 mm)
根据计算分析结果,施工导致的区间隧道最大轨道横向高差为0.2 mm,满足要求。
(5) 轨向高差(< 4 mm)
根据计算分析结果,施工导致的区间隧道最大轨道纵向高差为1.2 mm,满足要求。
(6) 轨间距变形(>-4 mm,< 6 mm)
根据计算分析结果,施工导致的区间隧道最大轨间距变形为0.16 mm,满足要求。
4.1.5 工程技术措施根据计算分析结果,结合现场实际情况,为确保轨道交通结构安全,提出以下技术措施。
(1) 对近接轨道交通6号线隧道部分采取注浆加固,竖向加固范围为:隧道正上方为地面以下2 m至轨道交通隧道上方0.8 m处,隧道两侧为地面以下2 m至隧道底板下3 m处;平面范围为隧道外侧1.0 m至围护桩的土体进行压密注浆加固。
(2) 在6号线上方采用门式抗浮结构(底板与工程桩形成门式状的整体)来降低坑底隆起。
(3) 在通道底板上采用钢板堆载压重,堆载值为50 kN/m2。
(4) 在开挖时遵循“分块限时开挖”,把底板分成每3 m 1条的板带进行施工,减小基坑的开挖尺寸,且减少基坑的暴露时间。
(5) 通道施工期间维持降水,防止轨道交通6号线隧道施工完成后因停止降水致使地下水位上升导致隧道上浮。
4.2 区间隧道可实施性分析 4.2.1 市政通道预处理措施针对8号线本市政通道做如下考虑。
(1) 市政通道建设设计方案需避免基坑支护结构及主体结构与规划轨道交通8号线隧道空间冲突,为后续轨道交通8号线区间隧道施工预留一定施工空间。
(2) 市政通道建设与轨道交通8号线区间隧道的竖向净距最小为1.2 m,距离较小。为保证后序轨道交通隧道下穿施工安全,设计时在轨道交通8号线隧道两侧设置防沉桩,以保证在通道下部土体被扰动的情况下仍可保持结构稳定。
(3) 市政通道建设时,对轨道交通8号线下穿区域采用旋喷桩加固,以提高下穿区域的土体强度和自稳性,从而保证轨道交通隧道下穿施工安全和变形可控。
4.2.2 隧道施工对通道结构影响分析(1) 计算模型
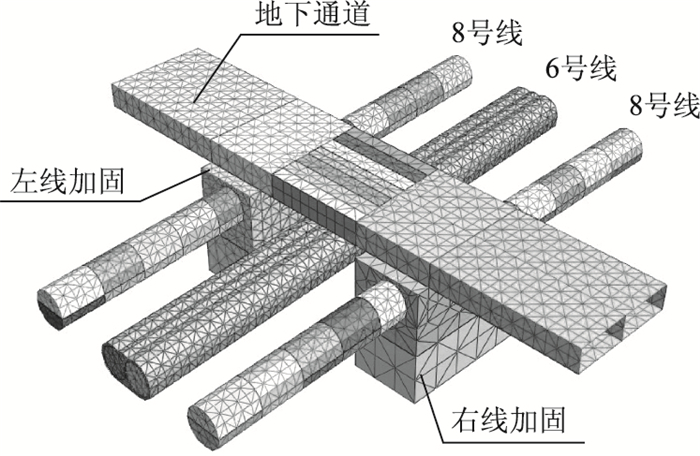
仍采用上节模型,轨道交通8号线、6号线与市政通道的位置关系如图 10所示。
|
| 图 10 隧道结构与通道结构 Fig. 10 Tunnel structure and underpass tunnel structure |
| |
在原有模型基础上开展8号线的暗挖施工模拟,开挖采用2台阶施工方法。当开挖10 m长度的上台阶土体时,通过设置荷载释放系数来模拟土体累积弹性能的释放,以避免由于开挖产生的不平衡内力一次性加载到开挖阶段上。采用按照40%,30%,30%的比例加载到不同施工阶段,分次逐步降低,最终完全释放的方法来模拟开挖。
进行喷射混凝土形成初支,激活与开挖土体相对应的喷射混凝土单元。由于喷射混凝土刚施作时刚度较小,但随着时间的推移,材料硬化后其刚度会明显提高,为模拟这一过程,分别生成软喷和硬喷属性,在下一阶段钝化软喷、激活硬喷。
(2) 通道结构竖向变形
轨道交通8号线隧道施工期间通道结构的竖向变形逐步增大,在隧道施工完成后竖向变形达到最大,为8.8 mm,如图 11所示。

|
| 图 11 8号线隧道施工完成时通道结构竖向变形云图(单位: mm) Fig. 11 Nephogrm of vertical deformation of underpass structure when Line 8 tunnel construction is completed (unit: mm) |
| |
(3) 通道结构水平变形
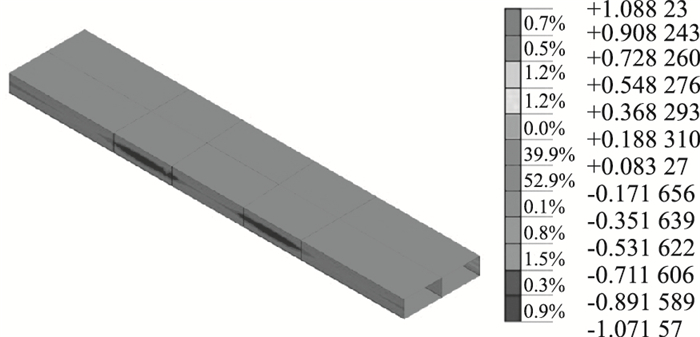
轨道交通8号线隧道施工期间通道结构的水平变形较小,在隧道掌子面到达通道结构侧墙下方时结构的水平变形达到最大,为1.1 mm,如图 12所示。
|
| 图 12 8号线隧道施工完成时通道结构最大水平变形云图(单位: mm) Fig. 12 Nephogrm of maximum horizontal deformation of underpass structure when Line 8 tunnel construction is completed (unit: mm) |
| |
(4) 结构及变形缝差异变形分析
对各个施工阶段下通道结构的竖向差异沉降和变形缝差异沉降进行计算分析。经计算,通道结构最大差异沉降为:(8.7-6.0)/7 500=0.36‰;变形缝最大差异沉降为7.1-6.0=1.1 mm。
故整个通道结构在轨道交通区间隧道施工期间的最大差异沉降为0.36‰,变形缝最大差异沉降为1.1 mm,如图 13所示。

|
| 图 13 通道结构差异变形云图(单位: m) Fig. 13 Nephogrm of differential deformation of underpass structure (unit: m) |
| |
通过对后序轨道交通8号线区间隧道施工时通道结构的变形进行预计算分析,采取基底加固和设置防沉桩措施后,后续轨道交通8号线隧道结构施工导致的通道结构变形可控,满足控制标准的要求。
|
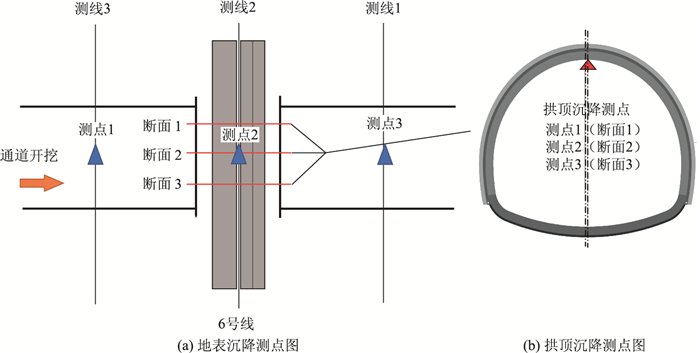
| 图 14 工程现场监测点布设 Fig. 14 Layout of site monitoring points |
| |
5 实测结果
为及时控制由于上部通道基坑开挖引起下部隧道拱顶沉降及水平位移的影响,在工程现场基于监控量测规范在隧道及地表布置测点。隧道的每个断面监测点的布置在拱顶及拱腰的位置,分别监测拱顶沉降及隧道水平收敛,选取通道与6号线交叉处的3个断面做进一步分析。地表沉降共设置3条测线,分别位于左右通道的中部位置及6号线的正上方,地表沉降测点的布设和数值模拟数据点的提取一致,如图 15所示。
|
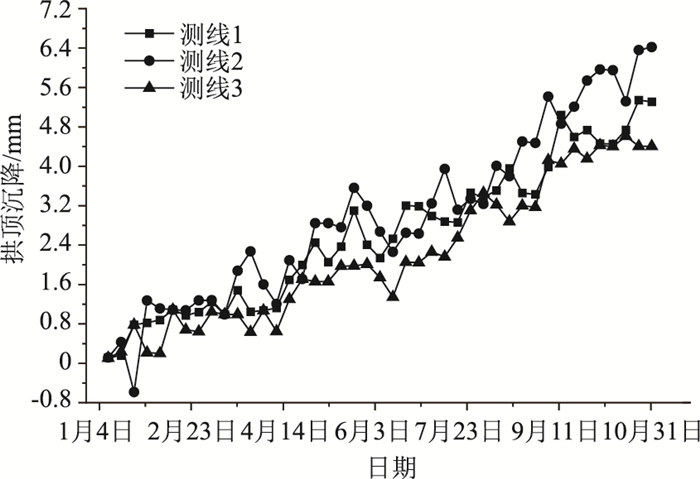
| 图 15 拱顶沉降监测数据 Fig. 15 Monitoring data of vault settlement |
| |
整个监测周期长达10个月,本节所用监测数据均为该段时间内选取的代表性数据。图 16为断面1,2,3中3个测点的时间-变形曲线。由图 16可知,随着通道开挖工序的进一步推进,3条测线的拱顶位移皆逐渐增大,其中断面2所对应的沉降值较断面1和断面3大,说明6号线中部位置所受影响较大。数值模拟中的施工阶段步序35(10 mm)对应于实测中9月11日(5.5 mm),二者存在一定偏差。与模拟数据相比,监测值较小,经过分析,原因为:数值模拟过程中只考虑了开挖步序而未考虑施工时间效应的影响,且模拟施工过程中不能根据监测数据对施工步序进行调整。而实际施工过程存在时间效应的影响,并且根据监测数据对开挖步骤和开挖范围进行调整,充分利用了信息化反馈施工,使现场变形得到有效的控制。经整体比对,数值模拟和实测数据整体变化趋势一致,且差异处在允许范围内,这也在一定程度上验证了数值模型的正确性。
|
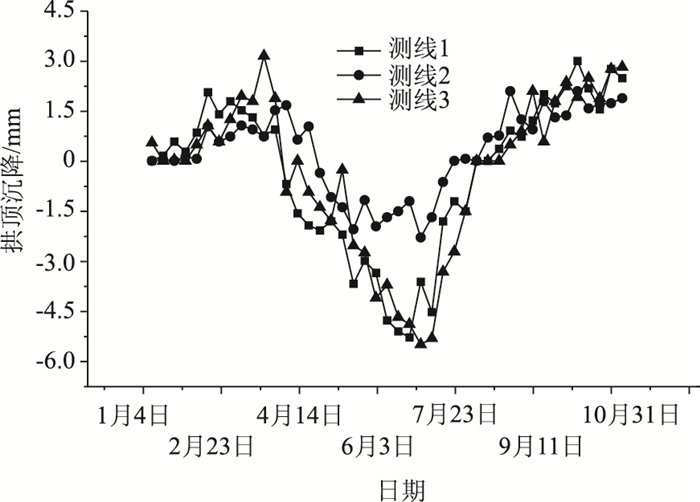
| 图 16 地表沉降监测数据 Fig. 16 Monitoring data of surface subsidence |
| |
图 16为测线1, 2, 3中3个测点的时间-变形曲线。由该曲线可知,随着工程的不断推进,3条测线的变化规律一致,都呈现先隆起后沉降然后在逐渐恢复及隆起的趋势。相比测线2的变化,测线1和测线3的整体变化幅度较大,最大隆起值约为3.1 mm,最大沉降值约为5.81 mm,符合工程安全标准。其中测线2整体沉降变化较小,结合工程实际,该测线所对应监测区域通道采用分小段进行开挖,减小了对该区域的土体扰动所造成的变化。同时结合数值模拟结果可以看出,在沉降监测方面,二者在整体变化规律有较好的吻合性。
工程实际整个建设过程长达1 a时间,本研究数据时段长达10个月。在整个施工过程中,各工序沉降值均在控制范围内,6号线始终处于安全受控状态,实际监测数据变化规律和数值模拟结果有较好的吻合性,进一步验证了数值模型的正确性。
6 结论(1) 市政通道基坑开挖上穿既有6号线,采用分区段分层开挖,结合围护桩及钢板桩,并对轨道交通线路上方区段进行分块放坡开挖的方法,有效减小了其对轨道交通的影响,提供了一种基坑上穿既有线路的成功方法。
(2) 市政通道基坑开挖引起的地表变形最大值出现在基坑附近。通道底面在开挖后出现隆起,顶部出现沉降,通道中间部位位移变化较小,该阶段6号线隆起变化率较小。
(3) 对于规划下穿市政通道的轨道交通隧道,提前采用在下穿轨道交通隧道两侧设置防沉桩、下部采用旋喷桩加固等方法, 可有效保证规划轨道交通隧道下穿施工安全,使其具有可实施性。
| [1] |
CHEN R, MENG F, LI Z, et al. Investigation of Response of Metro Tunnels due to Adjacent Large Excavation and Protective Measures in Soft Soils[J]. Tunnelling and Underground Space Technology, 2016, 58: 224-235. |
| [2] |
CHANG C T, SUN C W, DUANN S W, et al. Response of a Taipei Rapid Transit System (TRTS) Tunnel to Adjacent Excavation[J]. Tunnelling and Underground Space Technology, 2001, 16(3): 151-158. |
| [3] |
王岩. 某盾构隧道下穿既有盾构隧道变形超限原因解析及控制研究[D]. 北京: 北京交通大学, 2015. WANG Yan. Analysis and Control of Deformation of a Shield Tunnel under an Existing Shield Tunnel[D]. Beijing: Beijing Jiaotong University, 2015. |
| [4] |
COOPER M L, CHAPMAN D N, ROGERS C D F, et al. Movements in the Piccadilly Line Tunnels due to the Heathrow Express Construction[J]. Géotechnique, 2002, 52(4): 243-257. |
| [5] |
黄德中, 马险峰, 王俊淞, 等. 软土地区盾构上穿越既有隧道的离心模拟研究[J]. 岩土工程学报, 2012, 34(3): 520-527. HUANG De-zhong, MA Xian-feng, WANG Jun-song, et al. Centrifuge Modelling of Effects of Shield Tunnels on Existing Tunnels in Soft Clay[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(3): 520-527. |
| [6] |
ZHANG Z, HUANG M, WANG W. Evaluation of Deformation Response for Adjacent Tunnels due to Soil Unloading in Excavation Engineering[J]. Tunnelling and Underground Space Technology, 2013, 38: 244-253. |
| [7] |
张强. 开挖卸荷下既有轨道交通隧道的竖向变形及其控制研究[D]. 北京: 北京交通大学, 2012. ZHANG Qiang. Study on Vertical Deformation and Control of Existing Rail Transit Tunnel under Excavation and Unloading[D]. Beijing: Beijing Jiaotong University, 2012. |
| [8] |
ZHANG J F, CHEN J J, WANG J H, et al. Prediction of Tunnel Displacement Induced by Adjacent Excavation in Soft Soil[J]. Tunnelling and Underground Space Technology, 2013, 36: 24-33. |
| [9] |
NG C, HUA S S, LEI G H, et al. Ability of Three Different Soil Constitutive Models to Predict a Tunnel's Response to Basement Excavation[J]. Canadian Geotechnical Journal, 2015, 52(11): 1685-1698. |
| [10] |
郑刚, 邓旭, 刘畅, 等. 不同围护结构变形模式对坑外深层土体位移场影响的对比分析[J]. 岩土工程学报, 2014, 36(2): 273-285. ZHENG Gang, DENG Xu, LIU Chang, et al. Comparative Analysis of Influences of Different Deformation Modes of Retaining Structures on Displacement Field of Deep Soils Outside Excavations[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(2): 273-285. |
| [11] |
SHI J, NG C, CHEN Y. Three-dimensional Numerical Parametric Study of the Influence of Basement Excavation on Existing Tunnel[J]. Computers and Geotechnics, 2015, 63: 146-158. |
| [12] |
HUANG X, HUANG H, ZHANG D. Centrifuge Modelling of Deep Excavation over Existing Tunnels[J]. Geotechnical Engineering, 2014, 167(1): 3-18. |
| [13] |
NG C, SHI J, HONG Y. Three-dimensional Centrifuge Modelling of Basement Excavation Effects on an Existing Tunnel in Dry Sand[J]. Canadian Geotechnical Journal, 2013, 50(8): 874-888. |
| [14] |
程康, 徐日庆, 应宏伟, 等. 既有隧道在上覆基坑卸荷下的形变响应简化算法[J]. 岩石力学与工程学报, 2020, 39(3): 637-648. CHENG Kang, XU Ri-qing, YING Hong-wei, et al. Simplified Method for Evaluating Deformation Responses of Existing Tunnels due to Overlying Basement Excavation[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(3): 637-648. |
| [15] |
康成, 叶超, 梁荣柱. 基坑开挖诱发下卧盾构隧道纵向非线性变形研究[J]. 岩石力学与工程学报, 2020, 39(11): 2341-2350. KANG Cheng, YE Chao, LIANG Rong-zhu. Nonlinear Longitudinal Deformation of Underlying Shield Tunnels Induced by Foundation Excavation[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(11): 2341-2350. |
| [16] |
陈郁, 李永盛. 基坑开挖卸荷引起下卧隧道隆起的计算方法[J]. 地下空间与工程学报, 2005, 1(1): 91-94. CHEN Yu, LI Yong-sheng. Calculation of Tunnel Heaving due to Unloading of Pit Excavation[J]. Chinese Journal of Underground Space and Engineering, 2005, 1(1): 91-94. |
| [17] |
周泽林, 陈寿根, 李岩松. 近距离双孔并行盾构隧道地层位移预测及分布规律研究[J]. 公路交通科技, 2015, 32(6): 109-117. ZHOU Ze-lin, CHEN Shou-gen, LI Yan-song. Research on Predicting and Distribution of Stratum Displacement of Double-tube Parallel Shield Tunnel[J]. ournal of Highway and Transportation Research and Development, 2015, 32(6): 109-117. |
| [18] |
谢立广, 杨群. 关于隧道结构的安全推演及寿命预测[J]. 公路交通科技, 2021, 38(7): 107-113. XIE Li-guang, YANG Qun. Safety Deduction and Life Prediction of Tunnel Structure[J]. Journal of Highway and Transportation Research and Development, 2021, 38(7): 107-113. |
 2021, Vol. 38
2021, Vol. 38
