扩展功能
文章信息
- 涂兵, 刘来辉, 邓年春, 江建文, 李颢旭
- TU Bing, LIU Lai-hui, DENG Nian-chun, JIANG Jian-wen, LI Hao-xu
- 基于遗传算法的大跨钢管混凝土桁式拱肋多目标优化
- Multi-objective Optimization of Long-span CFST Trussed Arch Rib Based on Genetic Algorithm
- 公路交通科技, 2021, 38(12): 56-63, 72
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(12): 56-63, 72
- 10.3969/j.issn.1002-0268.2021.12.007
-
文章历史
- 收稿日期: 2020-10-26
钢管混凝土拱桥具有受力合理、施工方便、刚度大等诸多优点,是近年来发展较快的桥型之一[1-2]。随着钢管混凝土拱桥在我国公路和铁路工程中的不断推广应用,其经济性也日益受到人们的广泛关注。然而,现阶段钢管混凝土拱桥的设计主要参考已有同类工程的经验,拟定的结构尺寸通常并非最优尺寸,未能充分发挥钢管混凝土组合结构的优势,造价也往往偏高[3]。特别是对于作为钢管混凝土拱桥最主要受力构件的拱肋,其截面由钢材和混凝土2种材料组成,且随着拱桥跨度的增大,拱肋截面的构型趋于复杂,由此导致设计变量众多,传统基于经验和试错的设计方法更是难以精确获取最合理的拱肋截面设计参数组合。因此,亟需将结构优化理论引入钢管混凝土拱桥的拱肋截面设计中,以提高设计效率以及设计方案的合理性。
目前,钢管混凝土组合结构截面优化的方法主要有数学规划法、优化准则法和智能优化方法3类[4]。文献[5-6]以造价最低为目标,分别应用序列二次规划算法和约束非线性规划算法对简支钢- 混凝土组合梁进行了截面参数优化。文献[7-8]基于满应力准则,建立了钢管混凝土拱桥拱肋截面的单目标优化模型,并借助有限元程序进行了求解。文献[9]则利用粒子群算法对满应力优化理论进行改进,用于钢管混凝土拱桥哑铃型拱肋的优化,得到了使得钢管总重量最小的拱肋截面参数。文献[10-11]将遗传算法引入钢管混凝土框架柱的截面优化,显著提高了结构的经济性。可以看出,当前阶段钢-混凝土组合结构的截面优化绝大部分都是以造价(或材料用量)最低为目标的单目标优化,对于这类问题,以上3类优化方法均不难求出最优解,但相较而言,以遗传算法为代表的智能优化方法的适用性更强,计算效率更高。
值得注意的是,以造价为单目标的结构优化虽然能显著降低成本,但优化后的截面参数也通常使得结构各项性能指标偏低,对实际工程设计的参考价值受到限制。与之相比,多目标优化可以在数学上实现成本、结构性能等多个相互冲突目标的最优协调,获得一系列非劣解,进而为工程决策者和设计者提供更多的选择[12]。在结构多目标优化领域,由于算法自身的并行性特点恰好与多目标优化问题的多解特征相吻合,遗传算法等进化算法占据主导地位[13-14]。目前,遗传算法已被成功应用于复合材料结构[15-19]、高层建筑[20]、混凝土梁桥[21-22]等工程结构的多目标优化,取得了良好的效果,但鲜见该方法在钢管混凝土拱桥多目标优化中的相关研究报道。
基于此,本研究选取当前应用最广泛的多目标优化遗传算法NSGA-Ⅱ[23](Non-dominated Sorting Genetic Algorithm Ⅱ,带精英策略的非支配排序遗传算法),探究遗传算法在钢管混凝土拱肋截面多目标设计优化中的可行性。首先,以造价最低和面内抗弯刚度最大为双重优化目标,建立大跨钢管混凝土拱桥桁式拱肋截面的通用性优化模型;然后,利用NSGA-Ⅱ算法对优化模型进行求解,得到造价与抗弯刚度的Pareto最优前沿(Pareto-optimal front),以期为结构设计提供参考。之所以选取面内抗弯刚度最大作为另一个优化目标是考虑到随着钢管混凝土拱桥跨径的不断增大,面内稳定性逐渐成为控制结构设计的主要指标,而截面抗弯刚度是决定拱肋面内稳定性能的最主要因素之一。
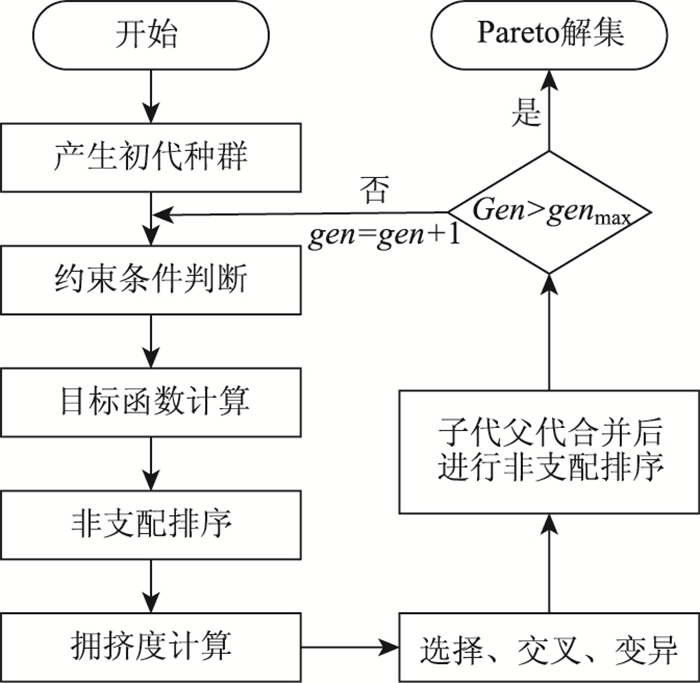
1 NSGA-Ⅱ多目标优化遗传算法 1.1 NSGA-Ⅱ算法简述遗传算法(Genetic Algorithm,GA)是一种通过模拟自然进化过程搜索数学模型最优解的方法。NSGA-Ⅱ是基于Pareto最优概念的遗传算法,该算法既继承了经典遗传算法在全局搜索方面的优点,同时也提出了精英策略、快速非支配排序、拥挤比较算子等策略来提高最优解的收敛性、精确性和均匀性,具体如下[23]:
(1) 带精英机制的策略
提出将父代种群和子代种群合并,然后剔除被支配的子代个体之后继续进行迭代操作,防止优秀基因的流失,从而提高优化结果的准确性。
(2) 快速非支配排序
根据相互支配逻辑关系对种群进行支配等级分类。将所有的非支配解作为第1前沿面,等级为1;然后将剩余个体中的非支配解作为第2前沿面,等级为2,以此类推,加快了算法速度。
(3) 保留多样性
采用拥挤比较的方法替代共享函数方法,通过密度估计和利用拥挤比较算子计算拥挤距离,量化个体所在空间位置的拥挤程度,并将其作为该种群中个体之间的比较准则,解决了经典遗传算法容易局部收敛的问题,使解集能均匀地分散到整个目标空间。
NSGA-Ⅱ优化算法最终给出的解称为Pareto最优解,其定义为:
考察2个决策向量a,b ∈ X,a帕累托占优(Pareto Dominate),记为a > b,当且仅当:
{∀i∈ {1, 2, …, n} fi (a)≤fi (b) }∧ {∃j∈ {1, 2, …, n} fj (a)≤fj (b)}。
如果在整个参数空间内不存在任何决策向量帕累托占优某个决策向量,则称该决策向量即是Pareto最优解。所有Pareto最优解组成了帕累托最优解集合(Pareto Optimal Set),也称为Pareto前沿(Pareto Front)。
1.2 NSGA-Ⅱ算法流程2 4管桁式钢管混凝土拱肋截面优化数学模型 2.1 设计变量
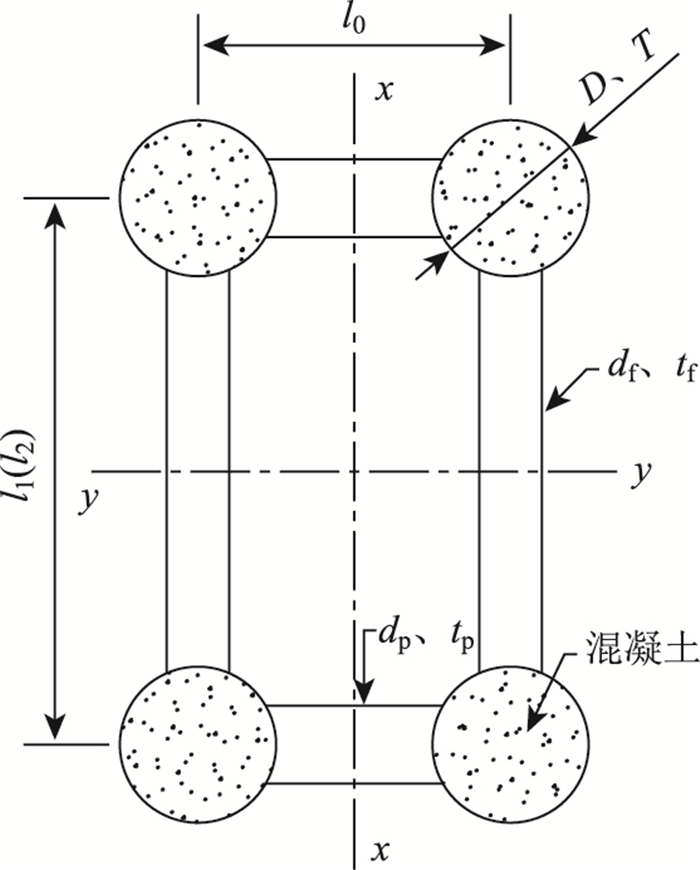
本研究以图 2所示的大跨钢管混凝土拱桥最常用的4管桁式变截面拱肋作为优化对象,将其主管、平联和腹杆3种杆件的外径、壁厚以及拱顶和拱脚的桁高作为优化变量。此外,考虑到钢管混凝土拱肋平联长度的设置通常还受到桥面宽度、非机动车道、人行道等因素影响,暂不考虑将平联长度作为变量,用常量l0表示。
|
| 图 2 4管桁式钢管混凝土拱肋截面参数设置 Fig. 2 Parameter setting for 4-tube trussed CFST arch rib section |
| |
2.2 目标函数
优化目标有:(1)拱肋总体造价最低;(2)拱肋截面面内抗弯刚度最大。
本研究选择以单侧拱肋单位长度的平均造价W为第一个目标函数,W主要包括主管的钢管和混凝土的造价、平联的钢管造价以及腹杆的钢管造价。其中,单位长度单根主管的钢管造价为:
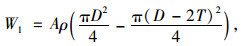
|
(1) |
式中,A为每吨钢管造价;ρ为钢材的密度;D和T分别为主管的外径和壁厚。
单位长度单根主管管内混凝土的造价为:
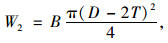
|
(2) |
式中B为每立方米混凝土造价。
单位长度拱肋腹杆W3和平联的钢管平均造价W4可表示为:
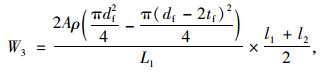
|
(3) |
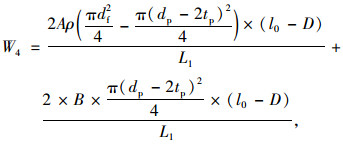
|
(4) |
式中, df和tf分别为腹杆的外径和壁厚;dp和tp分别为平联的外径和壁厚;L1为柱肢间的节间距离;l0为平联长度;l1为拱脚腹杆长度,l2为拱顶腹杆长度。
总造价函数其表达式为:
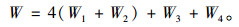
|
(5) |
另一个目标函数截面抗弯刚度F的近似表达式为[24]:
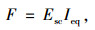
|
(6) |
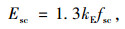
|
(7) |
式中,Esc为钢管混凝土的弹性模量,kE为轴压弹性模量换算系数; fsc为钢管混凝土的抗压强度,kE和fsc的取值见文献[24];Ieq为等效截面惯性矩,可由式(8)~ (9)计算得到。
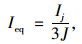
|
(8) |
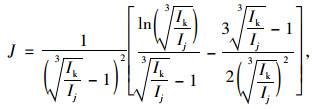
|
(9) |
式中, J为计算参数;Ij,Ik分别为变截面组合主拱拱顶、拱脚组合截面惯性矩。
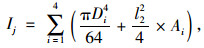
|
(10) |
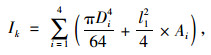
|
(11) |
式中,Di为第i根主管的外径;Ai为第i根钢管混凝土的截面面积。
2.3 约束条件作为钢管混凝土拱桥最主要的受力构件,拱肋需满足构造和强度等基本要求,这些要求构成了优化模型的约束条件。
(1) 构造要求
① 根据《公路钢管混凝土拱桥设计规范》(JTG/T D65-06—2015)[25],管节点及连接件抗疲劳构造应满足:
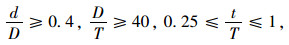
|
(12) |
式中,d和t分别为支管(包括横联和腹杆)的外径和壁厚。
② 细长空管杆件长度与钢管直径之比不应大于40,即[25]:
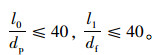
|
(13) |
③ 钢管混凝土钢管的外径尺寸要求不宜小于300 mm,也不宜大于1 500 mm, 且主拱主管壁厚不应小于10 mm,即[25]:
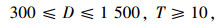
|
(14) |
④ 根据《钢结构设计标准》 (GB 50017—2017)[26],压弯构件允许长细比[λ]≤150,有:
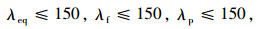
|
(15) |
式中,λeq,λf,λf分别主拱肋等效截面长细比、腹杆的长细比、平联的长细比;λeq根据式(16)~ (17)确定[25]:
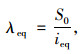
|
(16) |
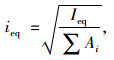
|
(17) |
式中, S0为主拱等效计算长度,对于无铰拱取0.36S,S为拱轴线长度;ieq为主拱等效截面回转半径。
⑤ 对受压为主的钢管混凝土构件,圆形截面的外径与壁厚之比应满足[25]:
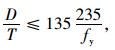
|
(18) |
式中fy为主管钢材屈服强度。
(2) 强度要求
桁式拱肋整体截面偏心受压承载力约束条件为[25]:
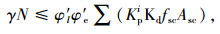
|
(19) |
式中,γ为桥梁重要性系数;N为1/4跨径处拱肋的轴力设计值;φ′ l为长细比折减系数;φ′e为弯矩折减系数;Kpi为钢管初应力折减系数;Kd为混凝土脱空折减系数,具体计算公式参见文献[25];fsc为钢管混凝土组合轴心抗压强度设计值;Asc为钢管混凝土组合截面面积。
拱肋单管压弯承载能力约束条件为[25]:
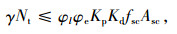
|
(20) |
式中,Nt为单管轴力设计值;φl为组合构件长细比折减系数;φe为组合构件弯矩折减系数;kp为钢管初应力折减系数。
腹杆受拉或受压强度要求[25]:
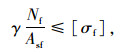
|
(21) |
式中,Nf为腹杆的轴拉力或轴压力设计值;Asf为腹杆的钢截面面积;[σf]为腹杆的钢材强度设计值。
2.4 管桁式变截面拱肋的优化设计模型为:
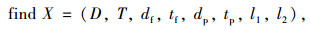
|
(22) |
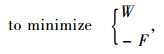
|
(23) |
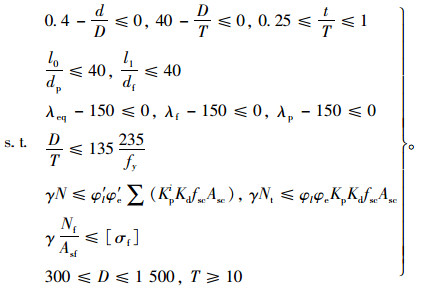
|
(24) |
某特大桥位于广西平南县西江上游,其原设计情况如下:
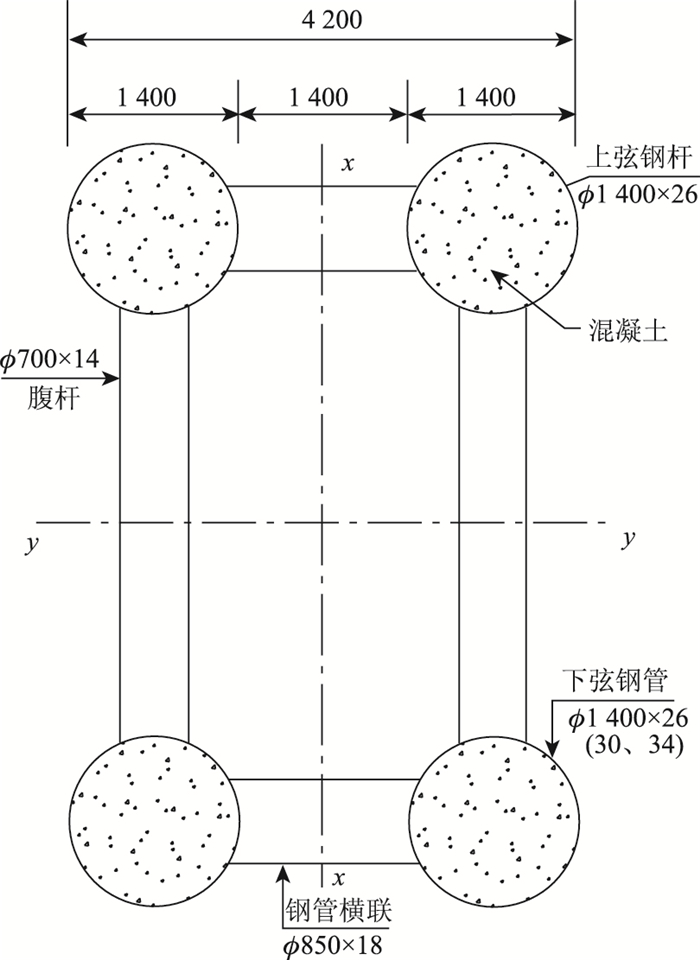
主桥采用主跨575 m(计算跨径560 m)的中承式钢管混凝土拱桥,跨径居全世界拱桥之首,主拱采用悬链线无铰拱,计算矢跨比为1/4,拱轴系数为1.5。单侧拱肋采用4管桁式截面,弦杆直径为1.4 m,管内灌注C70自密实混凝土。弦杆之间通过ϕ850 mm横联钢管和两根ϕ700 mm竖向腹杆钢管连接,单侧拱肋截面如图 3所示。
|
| 图 3 原设计普通横隔处单侧拱肋截面示意图(单位:mm) Fig. 3 Schematic diagram of the single-sided arch rib cross-section at original designed common diaphragm (unit: mm) |
| |
主拱主管采用Q420qD高强钢,其余杆件均采用Q345C钢材。桥道梁为钢格子梁上设置厚15 cm(含8 mm钢底板)C40钢纤维混凝土的钢-混组合结构,吊杆采用整束挤压成型的钢绞线成品索,南北两岸桥台均为重力式抗推力结构。主拱桁和桥道梁节段均采用缆索吊运、斜拉扣挂安装。
3.2 拱肋截面尺寸多目标优化首先,根据第2节程序建立平南三桥拱肋截面尺寸的多目标优化模型,其中,钢材和核心C70混凝土单价分别按4 500元/t和600元/m3计算。另外,综合考虑结构安全性、施工水平和原设计的情况后,确定各尺寸变量的取值范围,设置各变量的约束条件,具体见表 1。
| 变量 | 名称 | 下限值/mm | 上限值/mm |
| D | 主管直径 | 1 000 | 1 400 |
| T | 主管壁厚 | 20 | 40 |
| df | 腹杆直径 | 500 | 800 |
| tf | 腹杆壁厚 | 10 | 20 |
| dp | 平联直径 | 500 | 900 |
| tp | 平联壁厚 | 10 | 20 |
| l1 | 拱脚腹杆长度 | 10 000 | 17 000 |
| l2 | 拱顶腹杆长度 | 6 000 | 8 500 |
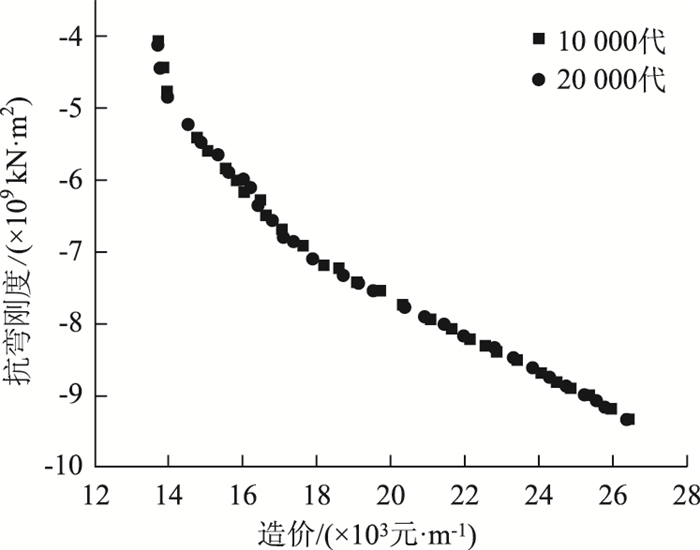
利用NSGA-Ⅱ算法对该优化模型进行求解。根据已有研究[27],算法的参数设置为:种群大小为100,变异系数取0.001,交叉概率为0.3。分别取进化代数10 000和20 000进行计算,得到10 000代和20 000代的优化结果Pareto前沿,如图 4所示。可以看出,10 000代与20 000代的Pareto前沿基本一致,因此可认为就本研究算例而言,10 000代的Pareto解集已经是收敛的。
|
| 图 4 10 000代与20 000代Pareto前沿对比 Fig. 4 Comparison of 10 000-generation and 20 000-generation Pareto fronts |
| |
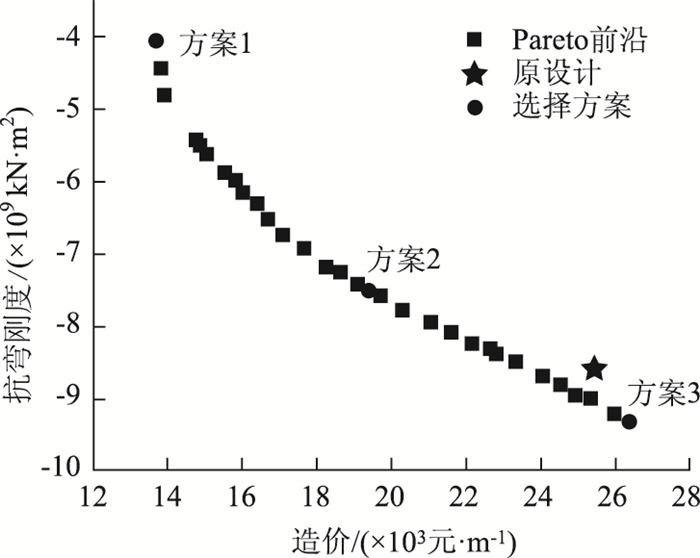
取10 000代的Pareto前沿作进一步分析,如图 5所示,根据多目标优化理论,该Pareto前沿上的每一点都代表了一个Pareto最优解。首先,将原设计方案在图 5中标识出来,可以看出,原设计方案点在Pareto前沿线的右上方,表明就本研究的2个优化目标而言,原设计方案并非最优化(合理)方案,存在优化的空间。在Pareto解集中选择出3个代表性点即3个Pareto最优解进行分析,见图 5中的1、2、3点。这3个点分别代表了造价最低的方案(方案1)、刚度(结构性能)最大的方案(方案3)和中间方案(方案2),相应的主拱截面参数见表 2。可知,与原方案相比,方案1的单位长度造价降低46.2%,方案3的抗弯刚度增大8.8%,表明2个优化目标的改善幅度均较大,优化效果较明显。
|
| 图 5 10 000代Pareto前沿 Fig. 5 10 000-generation Pareto front |
| |
| 变量 | 名称 | 优化前/mm | 优化后/mm | ||
| 方案1 | 方案2 | 方案3 | |||
| D | 主管直径 | 1 400 | 1 200 | 1 400 | 1 400 |
| T | 主管壁厚 | 26,30,34 | 20 | 23 | 35 |
| df | 腹杆直径 | 700 | 500 | 500 | 500 |
| tf | 腹杆壁厚 | 14 | 10 | 10 | 10 |
| αp | 平联直径 | 850 | 500 | 530 | 500 |
| tp | 平联壁厚 | 18 | 10 | 10 | 10 |
| l2 | 拱脚腹杆长度 | 17 000 | 13 340 | 17 000 | 17 000 |
| l2 | 拱顶腹杆长度 | 8 500 | 7 996 | 8 500 | 8 500 |
| 单位长度造价/千元 | 25.45 | 13.70 | 19.35 | 26.36 | |
| 抗弯刚度/(×109 kN·m2) | 8.56 | 4.06 | 7.52 | 9.31 | |
从多目标优化理论的角度来看,Pareto前沿上的所有点都可以被认为是最优的方案,实际设计时还应根据结构实际情况、业主需求和偏好等其他因素在Pareto最优解中进行选择,最终确定设计方案。对于所分析的大桥跨径位居世界拱桥之首,技术难度很大,且位于重要的交通枢纽,预测未来的交通量会比较大,因此其安全系数不宜太小,同时兼顾到桥梁的经济性,本研究推荐选择造价适中、刚度较大的优化组合,即优化方案2,并对其进行后续的结构受力性能分析。方案2这种位于Pareto前沿中间位置的方案也是大部分多目标优化设计最终方案的主要选择。从表 2可以看出,相比于原设计方案,优化方案2的拱肋截面面内抗弯刚度有所减小(减小12.1%),同时,其造价大幅度降低至原方案的76.0%。
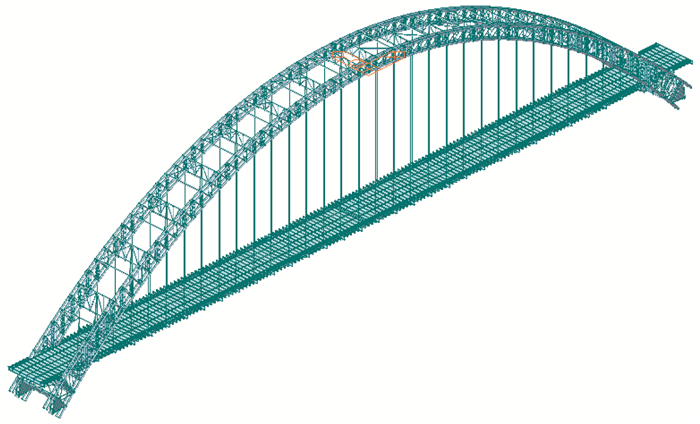
3.3 优化前后结构性能对比为说明选取拱肋截面面内抗弯刚度作为优化目标的合理性并验证优化结果的可行性,利用MIDAS/Civil有限元软件建立全桥三维杆系计算模型,以主拱竖向刚度和面内稳定性为评价标准,对优化方案2和原设计方案进行对比分析。有限元模型中,拱肋的每根主管均选用钢管混凝土组合截面梁单元进行模拟,并利用施工阶段联合截面方法模拟拱肋的两阶段成型历程,用只受拉的桁架单元建立吊杆,桥面钢格子梁和行车道板分别采用梁单元和板单元。拱脚处设置固结约束,桥面端横梁中间采用双向支座,端横梁两边采用单向支座,桥面格子梁与拱肋肋间横梁和立柱横梁之间均采用弹性连接,桥面格子梁与行车道板为共节点连接。汽车荷载等级为公路-Ⅰ级,按双向4车道布载,汽车荷载的横向和纵向折减系数分别取0.67和0.96[28],人群荷载按设计要求取2.5 kN/m2。有限元模型见图 6。
|
| 图 6 平南三桥MIDAS/Civil全桥计算模型 Fig. 6 MIDAS/Civil calculation model of Pingnan Third Bridge |
| |
3.3.1 优化方案主拱承载能力验算
拱桥的设计荷载包括自重、汽车和人群活载、温度荷载、风荷载和混凝土收缩徐变等,根据《公路桥涵设计通用规范》(JTG D60—2015),取基本组合=1.2×恒载+1.4×汽车荷载+0.6×1.4× [人群荷载+升(降)温30 ℃]+0.6×1.1×风荷载对拱肋整体和单管承载能力进行验算[28]。在基本组合下, 主拱整体桁式截面和单肢的最大轴力设计值分别为-154 445 kN和-51 605 kN,对应的弯矩设计值分别为-80 496 kN·m和-1 080 kN·m,代入式(19)、(20)进行验算,结果均满足承载能力要求。
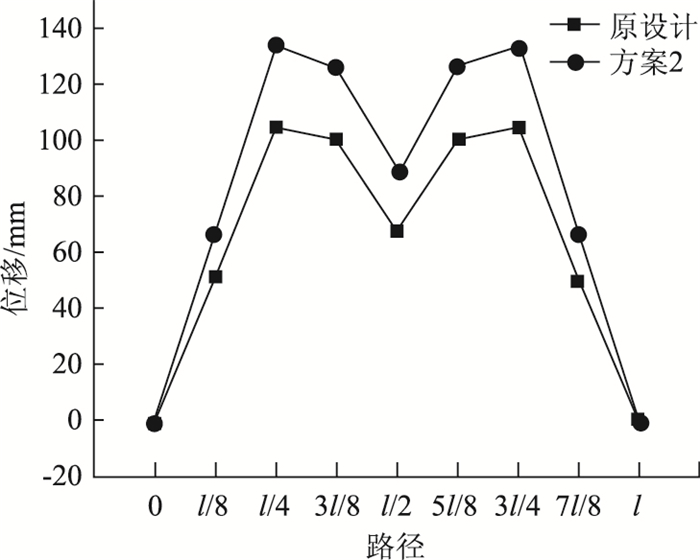
3.3.2 优化前后成桥状态主拱竖向挠度对比根据所建立的全桥计算模型,计算主拱在车道荷载(不及冲击力)作用下的最大竖向挠度(正负挠度绝对值之和)。选择拱肋0,l/8,l/4,3l/8,l/2,5l/8,3l/4,7l/8,l共9个控制点绘制全桥竖向挠度曲线,如图 7所示。可以看出,在车道荷载作用下,方案2的竖向挠度比原设计方案大,这是因为方案2的截面面内抗弯刚度相比原设计方案有所减小(减小约12.1%)。其中,在车道荷载作用下,方案2的拱肋最大竖向挠度(l/4截面)为134 mm,比原设计大29 mm(约增大27.6%),但仍远小于拱肋的最大容许位移l/1 000 (560 mm),满足《公路钢管混凝土拱桥设计规范》 (JTG/T D65-06—2015)[25]的要求。
|
| 图 7 车道荷载(不计冲击力)作用下拱肋正负竖向挠度之和 Fig. 7 Sum of positive and negative vertical deflections of arch rib under vehicle load (excluding impact force) |
| |
3.3.3 成桥状态稳定性分析
根据弹性稳定理论,结构考虑几何初始刚度矩阵下的弹性稳定平衡方程为[3]:
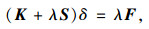
|
(25) |
式中, K为结构整体弹性刚度矩阵;S为几何刚度矩阵,与结构的应力水平相关;δ为荷载F作用下的位移;λ为弹性稳定特征值。
通过所建立的有限元模型分别对优化前后的结构在以下2种工况下进行使用阶段线弹性稳定性分析:工况1:恒载+风荷载+4车道荷载(集中力在跨中);工况2:恒载+风荷载+4车道荷载(集中力在l/4处)。分析时偏安全地将自重恒载和所有活荷载均视为可变荷载,即计算几何刚度时同时考虑恒载和活荷载引起的应力。分析结果表明,对于优化前、后的结构以及2种荷载工况,一阶整体弹性失稳模态均为面外反对称屈曲,且前12阶失稳模态均为面外失稳,第13阶首次出现面内失稳。得到成桥状态一阶屈曲对应的弹性稳定特征值和首次出现面内整体失稳模态对应的弹性稳定特征值见表 3。可以看出,优化组合2的两类弹性稳定特征值(一阶失稳和首次出现面内失稳)相对优化前均略有下降,但均大于4.0,同样满足规范要求[25]。
| 设计方案 | 工况1 | 工况2 | |||
| 一阶失稳模态(面外失稳) | 首阶面内失稳模态 | 一阶失稳模态(面外失稳) | 首阶面内失稳模态 | ||
| 优化前 | 5.458 | 9.949 | 5.468 | 9.971 | |
| 优化后 | 4.424 | 8.059 | 4.432 | 8.077 | |
4 结论
(1) 提出同时以造价和截面面内抗弯刚度作为优化目标的4管桁式钢管混凝土拱肋多目标优化模型,相较于传统以造价为单目标的优化模型更加科学、合理,可得到一系列Pareto最优解供设计者和决策者选择。
(2) NSGA-Ⅱ遗传算法应用于4管桁式钢管混凝土拱肋的多目标优化时可快速、准确地得到优化解集,是该类组合结构多目标优化问题的一种高效求解手段。
(3) 截面面内抗弯刚度与结构整体竖向刚度以及面内稳定性相关性强,选择该参数作为表征桁式钢管混凝土拱肋结构性能的优化目标具有一定的合理性。
(4) 分析算例优化后结构的面内稳定性和刚度满足规范要求,同时造价大幅度降低,优化效果良好。
| [1] |
陈宝春, 刘君平. 世界拱桥建设与技术发展综述[J]. 交通运输工程学报, 2020, 20(1): 27-41. CHEN Bao-chun, LIU Jun-ping. Review of Construction and Technology Development of Arch Bridges in the World[J]. Journal of Transportation Engineering, 2020, 20(1): 27-41. |
| [2] |
郑皆连. 大跨径拱桥的发展及展望[J]. 中国公路, 2017(13): 40-42. ZHENG Jie-lian. Development and Prospect of Long-span Arch Bridge[J]. China Highway, 2017(13): 40-42. |
| [3] |
陈宝春. 钢管混凝土拱桥[M]. 3版. 北京: 人民交通出版社, 2016. CHEN Bao-chun. Concrete Filled Steel Tubular Arch Bridge[M]. 3rd ed. Beijing: China Communications Press, 2016. |
| [4] |
王石刚, 陈新度, 余俊. 组合结构优化设计及其应用[J]. 中国机械工程, 1993, 21(2): 18-20, 64. WANG Shi-gang, CHEN Xin-du, YU Jun. Combined-structural Optimal Design and Application[J]. China Mechanical Engineering, 1993, 21(2): 18-20, 64. |
| [5] |
刘齐茂, 李微, 李暾, 等. 钢-混凝土组合梁的截面优化设计[J]. 兰州理工大学学报, 2006(3): 115-118. LIU Qi-mao, LI Wei, LI Tun, et al. Optimization Design of Cross-section of Steel-concrete Composite Beams[J]. Journal of Lanzhou University of Technology, 2006(3): 115-118. |
| [6] |
张静. 工字钢-混凝土组合梁桥截面设计参数优化研究[D]. 西安: 长安大学, 2007. ZHANG Jing. Optimization of Sectional Design Parameters of I-steel-concrete Composite Girder Bridge[D]. Xi'an: Chang'an University, 2007. |
| [7] |
黄泽权. 大跨度多肢钢管混凝土拱桥主拱构造优化研究[D]. 重庆: 重庆交通大学, 2009. HUANG Ze-quan. Study on Structural Optimization of Main Arch of Long-span Multi-limb Concrete-filled Steel Tube Arch Bridge[D]. Chongqing: Chongqing Jiaotong University, 2009. |
| [8] |
刘桂林. 大跨钢管混凝土刚架系杆拱桥主拱优化设计[D]. 长沙: 中南大学, 2009. LIU Gui-lin. Optimization Design of Main Arch of Long-span Concrete-filled Steel Tubular Rigid Frame Tied Arch Bridge[D]. Changsha: Central South University, 2009. |
| [9] |
李剑桥. 基于粒子群算法大跨径上承式钢管混凝土拱桥优化分析[D]. 西安: 长安大学, 2017. LI Jian-qiao. Optimization Analysis of Long-span Deck Concrete-filled Steel Tubular Arch Bridge Based on Particle Swarm Optimization[D]. Xi'an: Chang'an University, 2017. |
| [10] |
肖国涛. 基于遗传算法的钢管混凝土框架结构优化研究[D]. 武汉: 华中科技大学, 2005. XIAO Guo-tao. Research on Optimization of CFST Frame Structure Based on Genetic Algorithm[D]. Wuhan: Huazhong University of Science and Technology, 2005. |
| [11] |
袁朝阳, 吴成国, 张宇亮, 等. 基于加速遗传算法的方钢管混凝土柱优化模型[J]. 华北水利水电大学学报: 自然科学版, 2016, 37(2): 57-61. YUAN Chao-yang, WU Cheng-guo, ZHANG Yu-liang, et al. The Optimization Model of Concrete-filled Square Steel Tubular Columns Based on Accelerating Genetic Algorithm[J]. Journal of North China University of Water Resources and Hydropower: Natural Science Edition, 2016, 37(2): 57-61. |
| [12] |
MARLER R T, ARORA J S. Survey of Multi-objective Optimization Methods for Engineering[J]. Structural & Multidiplinary Optimization, 2004, 26(6): 369-395. |
| [13] |
LAGAROS N D, PAPADRAKAKIS M, KOKOSSALAKIS G. Structural Optimization Using Evolutionary Algorithms[J]. Computers & Structures, 2002, 80: 571-589. |
| [14] |
COELLO C A. Evolutionary Multi-objective Optimization: a Historical View of the Field[J]. IEEE Computational Intelligence Magazine, 2006, 1(1): 28-36. |
| [15] |
WALKER M, SMITH R E. A Technique for the Multi-objective Optimization of Laminated Composite Structures Using Genetic Algorithms and Finite Element Analysis[J]. Composite Structures, 2003, 62(1): 123-128. |
| [16] |
PELLETIER J L, VEL S S. Multi-objective Optimization of Fiber Reinforced Composite Laminates for Strength, Stiffness and Minimal Mass[J]. Computers & Structures, 2006, 84: 2065-2080. |
| [17] |
ALMEIDA F S, AWRUCH A M. Design Optimization of Composite Laminated Structures Using Genetic Algorithms and Finite Element Analysis[J]. Composite Structures, 2009, 88(3): 443-454. |
| [18] |
PARK C H, SAOUAB A, BREARD J, et al. An Integrated Optimization for the Weight, the Structural Performance and the Cost of Composite Structures[J]. Composites Science & Technology, 2009, 69(7/8): 1101-1107. |
| [19] |
DE MUNCK M, DE SUTTER S, VERBRUGGEN S, et al. Multi-objective Weight and Cost Optimization of Hybrid Composite-concrete Beams[J]. Composite Structures, 2015, 134: 369-377. |
| [20] |
ASADI E, DA SILVA M G, ANTUNES C H, et al. Multi-objective Optimization for Building Retrofit: A Model Using Genetic Algorithm and Artificial Neural Network and an Application[J]. Energy and Buildings, 2014, 81: 444-456. |
| [21] |
FURUTA H, KAMEDA T, NAKAHARA K, et al. Optimal Bridge Maintenance Planning Using Improved Multi-objective Genetic Algorithm[J]. Structure and Infrastructure Engineering, 2006, 2(1): 33-41. |
| [22] |
OKASHA N M, FRANGOPOL D M. Lifetime-oriented Multi-objective Optimization of Structural Maintenance Considering System Reliability, Redundancy and Life-cycle Cost Using GA[J]. Structural Safety, 2009, 31(6): 460-474. |
| [23] |
DEB K, PRATAP A, AGARWAL S, et al. A Fast and Elitist Multi-objective Genetic Algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. |
| [24] |
GB 50936—2014, 钢管混凝土结构技术规程[S]. GB 50936—2014, Technical Code for Concrete Filled Steel Tubular Structures[S]. |
| [25] |
JTG/T D65-06—2015, 公路钢管混凝土拱桥设计规范[S]. JTG/T D65-06—2015, Specifications for Design of Highway Concrete-filled Steel Tubular Ach Bridges[S]. |
| [26] |
GB 50017—2017, 钢结构设计标准[S]. GB 50017—2017, Standard for Design of Steel Structures[S]. |
| [27] |
李琳, 聂臻, 沙林秀. 基于NSGA2的钻进参数多目标优化[J]. 石油机械, 2013, 41(3): 55-57, 71. LI Lin, NIE Zhen, SHA Lin-xiu. NSGA2-based Multi-objective Optimization of Drilling Parameters[J]. China Petroleum Machinery, 2013, 41(3): 55-57, 71. |
| [28] |
JTG D60—2015, 公路桥涵设计通用规范[S]. JTG D60—2015, General Specifications for Design of Highway Bridges and Culverts[S]. |
 2021, Vol. 38
2021, Vol. 38