扩展功能
文章信息
- 张艳, 王淑云
- ZHANG Yan, WANG Shu-yun
- 控制力影响定价的生鲜品供应链优化模型
- An Optimal Model of Fresh Product Supply Chain with Influence of Control Power on Pricing
- 公路交通科技, 2021, 38(11): 150-158
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(11): 150-158
- 10.3969/j.issn.1002-0268.2021.11.018
-
文章历史
- 收稿日期: 2020-10-13
2. 烟台大学 经济管理学院, 山东 烟台 264005;
3. 山东外事职业大学 管理学院, 山东 威海 264504
2. School of Economics and Management, Yantai University, Yantai Shandong 264005, China;
3. School of Management, Shandong Vocational University of Foreign Affairs, Weihai Shandong 264504, China
供应链管理的核心是合作与协调,成员企业通过建立战略伙伴关系进行长期的合作。然而供应链成员企业拥有的渠道资源不同,会导致渠道权力失衡,供应链关系中的合作或斗争都是供应链成员权力平衡或失衡的一种表现。供应链管理实践中,绝大多数企业希望通过自身拥有的控制力,对供应链及成员企业施加影响,关于控制权的争夺一直是供应链成员间普遍存在的问题,如2004年3月的国美电器和格力空调之战,2010年11月的康师傅和家乐福的价格之争等。以上例子充分说明,供应链中权力占优一方会对另一方的运作管理(如定价决策、库存决策、渠道管理等)加以影响和控制,而由此产生的后果则是在一定程度上损害了权力弱势一方的利益,进而对合作绩效带来一定的负面影响[1],严重时甚至会破坏供应链合作关系。由此可见,供应链控制力在不同成员之间的合理分配对供应链合作的可持续性具有较大影响,供应链权力管理尤为重要。
权力是一个企业影响另一个企业决策与行动的能力[2],供应链控制力是供应链成员主导供应链决策的权力[3-4]。在仅考虑一个供应商和一个零售商的二级供应链中,如果零售商的控制力比供应商大,供应商会有一个被动的供应策略,则零售商主导供应链;如果供应商的控制力比零售商大,零售商会有一个被动的订购策略,则供应商主导供应链;如果双方的控制力是相等的,则供应链由二者共同主导,是一种权力均衡的合作状态[5]。因此,控制力在供应链成员之间的配置结构决定了供应链的权力结构。现有研究主要集中在渠道领导(权力)及权力结构如何影响定价和供应链绩效,大都基于传统的Stackelberg博弈,主导者被认为拥有供应链的绝对控制权(控制力为1),而追随者则没有任何控制权(控制力为0)[6-8],事实上,追随者在供应链中的控制力较低,并不是绝对没有。Kirilenko[9]认为,控制力是一个0~1之间的连续变量,Liu等[4, 10]将0~1之间的供应链控制力作为内生变量,通过数学建模发现,对于Stackelberg博弈,供应链主导方的控制力并非越大越好,存在最优控制力水平使得系统绩效最大。
针对生鲜品供应链系统定价的研究成果,亦是基于传统的Stackelberg模型,认为供应链成员权力的大小仅仅决定供应链决策次序,权力占优一方作为“领导者”优先决策,权力劣势一方作为“追随者”后作决策,领导者通过预测追随者的反应做出最有利于自己的决策[11-12]。Coughlan[13]指出权力的概念包括2个层面的含义,一是直接控制,一个权力成员可以决定另一个成员的决策变量,如转售价格维持,上游制造商决定本应由零售商决定的零售价格;另一种是间接控制,认为权力表现在决策的先后顺序上,先动者具有更高的市场权力,并且比后动者能获得更多的收益。本研究同时考虑控制的2层含义,将控制力视为价格的函数,从分散决策和集中决策、以及有无控制力影响的角度,构建控制力影响价格的生鲜品供应链优化模型,分析生鲜品供应链中是否存在最优控制力配置、控制力对生鲜品供应链定价及其绩效有何影响,以期为生鲜品供应链的优化决策提供借鉴。
1 问题描述和研究假设供应链成员企业拥有的供应链资源不同,导致他们的权力有很大差异,亦导致他们在供应链上的竞争能力和控制能力上存在差异。拥有较大控制力的一方在供应链关系中占据主导地位,其会通过权力作用影响其他供应链成员的决策,如定价决策等[14],同时也会发生一定的控制成本。具有强大渠道优势的零售商在向供应商采购时可以凭借其渠道控制力决定采购价格,从而达到降低成本、低价销售从而获取更多利润的目的,如国美—格力价格之争;制造商也可以通过“最低定价”、“维持转售价格”等要求零售商以一定的价格进行销售,从而实现制造商对其商品售价的控制,如处于供应商主导地位的苹果公司凭借其强大的品牌优势和技术水平影响零售商的定价策略,在其产品未上市之前就预先公布了产品价格。本研究考虑由1个供应商S和1个零售商R组成的二级生鲜品供应链,供应商具有供应链绝对控制力,不仅控制批发价格,也控制或建议零售价格(烟台地区新鲜熟食肉制品的生产企业——喜旺食品有限公司即是如此),博弈过程中,供应商为领导者,零售商为追随者。将价格视为供应链主导成员控制力的函数,主导成员控制力为0.5~1之间的连续变量,供应商对生鲜品进行基础保鲜,零售商根据消费者对产品新鲜度的偏好再进行必要的保鲜投入。研究基于以下假设:
假设1:生鲜品市场需求受价格p和保鲜努力e的共同影响[15],采用加法形式的需求函数,令市场需求q=a-bp+re,其中,a为基本市场需求;
假设2:供应商以批发价w将产品销售给零售商,并可以控制产品价格。令零售价格p=w+ηx,其中,η为控制力价格影响系数,x为供应商系统控制力水平,u=1-x为零售商系统控制力水平,0.5 < x < 1;
假设3:供应链权力占优一方为追求自身效益最大化,会损害其他合作伙伴的利益,从而导致供应链冲突加剧,合作风险加大。当供应链成员企业拥有的控制权力增加时,争夺权力的争斗将更加激烈,产生的权力控制成本也就更大,权力控制成本的边际变化率随控制力的增加而增加,参考Iossa和Martimort[16]以及Greco[17]的假设,将供应商控制力成本函数表示为c(x)=1/2βx2,零售商控制力成本函数则为c(x)=1/2β(1-x)2;
假设4:零售商进行产品保鲜,会发生相应的保鲜投资成本,保鲜努力水平e越高,付出的保鲜成本越高,采用Chambers等[18]中的成本表示法,将零售商保鲜投入成本函数表示为c(e)=1/2ke2;
假设5:决策过程中,供应商和零售商完全理性,信息对称,剩余产品残值为零,不考虑缺货情况。
模型中的其他相关参数及其含义参见表 1。
| 参数符号 | 含义 |
| b | 消费者价格敏感系数,且b>0 |
| c | 供应商的固定生产成本 |
| r | 保鲜努力水平对市场需求的影响系数,且r>0 |
| β | 供应商和零售商的控制力成本系数,且β>0 |
| k | 零售商保鲜投入成本系数,且k>0 |
| πri, πsi, πi | 表示不同决策模型下零售商、供应商、供应链系统的利润(其中i=1, 2, 3, 4) |
| xi*, ei*, wi*, pi*, qi* |
表示不同决策模型下的最优控制力水平、最优保鲜努力水平、最优批发价、最优零售价格和最优销售量(其中i=1, 2, 3, 4) |
| πri*, πsi*, πi* | 表示不同决策模型下零售商、供应商、供应链系统的最优利润(其中i=1, 2, 3, 4) |
2 模型构建与求解
本研究分别构建控制力影响产品零售价格并影响决策顺序、价格和保鲜努力共同影响市场需求,以及不考虑控制力对零售价格的影响、仅是价格和保鲜努力共同影响市场需求的二级生鲜品供应链决策模型,旨在就分散决策和集中决策下,分析控制力的有无对二级生鲜品供应链系统利润及节点企业优化决策的影响、生鲜品供应链的最优控制力配置,以期为生鲜品供应链的运作管理提供理论指导。
2.1 考虑控制力的供应商主导的Stackelberg决策供应商主导的Stackelberg决策下,供应商决定批发价格w和控制力水平x,零售商决定保鲜努力水平e,供应商的控制力水平x在0.5~1之间取值,博弈过程中,供应商为领导者,零售商为追随者。此种模式下,
供应商的利润函数为:
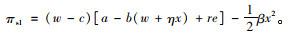
|
(1) |
零售商的利润函数为:
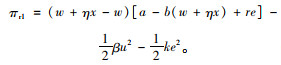
|
(2) |
由于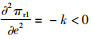
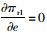
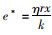
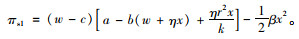
|
(3) |
式(3)关于x和w的二阶海赛矩阵:
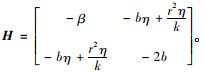
|
(4) |
可证,当2bβk2-η2(r2-bk)2>0时,H为负定矩阵,存在唯一的(x*,w*)使得πs1最大。对式(3)分别求解关于x和w的一阶偏导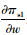
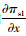
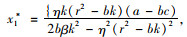
|
(5) |
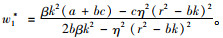
|
(6) |
进一步求解,考虑控制力的供应商主导的Stackelberg优化决策如下:
最优保鲜努力水平:
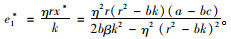
|
(7) |
最优零售价格:
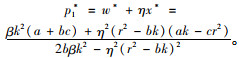
|
(8) |
市场最优需求量:
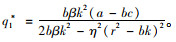
|
(9) |
零售商最优利润:
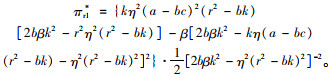
|
(10) |
供应商最优利润:
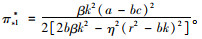
|
(11) |
供应链整体最优利润
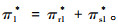
|
本部分构建一个不含控制力决策变量x的模型,自然不考虑控制力水平x产生的控制力成本,其他条件和模型1一致。则:
供应商的利润函数为:
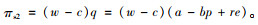
|
(12) |
零售商的利润函数为:
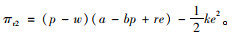
|
(13) |
为方便求解,假设p=w+m,m为零售商单位产品利润,将p=w+m代入式(12)和(13)中,运用逆序求解法,先对零售商利润πr2求关于e的一阶偏导,求解得出e的最优值,然后代入πs2中,求解w和m的最优值。
πr2关于e的二阶偏导为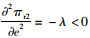
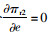
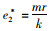
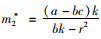
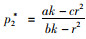
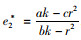
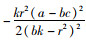
集中决策下,供应链双方以系统利润最大化为决策依据,零售价格仍受控制力水平的影响,设一方对系统的控制力水平为x,则p=w+ηx,相应的控制成本1/2βx2,供应链系统利润函数为:
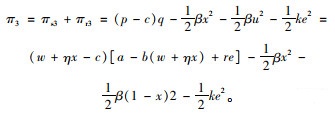
|
(14) |
对式(14)分别求解关于x,e和w的一阶偏导和二阶偏导,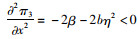
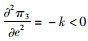
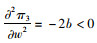
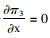
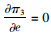
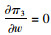
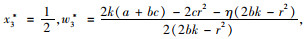
|
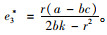
|
进而求得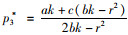
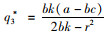
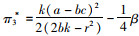
本部分构建一个不含控制力x变量的集中决策模型,模型中也不考虑由控制力水平x产生的控制力成本,其他条件和模型3一致。
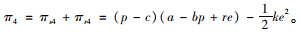
|
(15) |
可证当2bk-r2>0时,式(15)关于p和e的二阶海赛矩阵为负定矩阵,存在唯一的(p*,e*)使得π4最大。对式(15)分别求解关于p和e的一阶偏导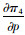
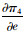
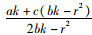
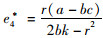
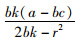
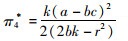
对比分析上述4个模型,可以得到以下命题:
命题1:生鲜品二级供应链中,控制力是客观存在的,且Stackelberg决策模式下存在最优控制力配置水平使得供应商和零售商利润最大。
模型2所示传统Stackelberg博弈模型,没有引入控制力因素,求解得出最优批发价格等于成本,供应商赚取的利润为0,零售商赚取的利润为负值,显然与实际生产运作不符;相反,模型1中,考虑控制力对系统决策的影响,满足2bβk2-η2(r2-bk)2>0时,存在最优控制力水平、批发价格、零售价格以及最优利润水平,从而证明控制力应当作为一个决策变量纳入供应链决策模型中。命题1得证。
命题2:集中决策下,控制力因素不影响系统最优定价及保鲜努力水平,当供应商和零售商的控制力水平分别为1/2时,集中决策更易实施。
集中决策模式下,虽然不存在谁主导谁从属的问题,但仍存在系统整体定价与运营控制问题,即控制风险成本客观存在,考虑控制力及其成本更符合实际情况。由模型3和模型4可知,π3*=π4*-1/4β,恰好说明考虑控制力因素的集中决策系统利润等于不考虑控制力因素下的系统利润减去控制力成本;另外p3*=p4*,e3*=e4*,说明供应链控制力因素对系统最优定价和最优保鲜努力水平不会产生影响。集中决策以系统利润最大化为目的开展合作决策,不能保证对所有成员企业都是有利的,因此为保证供应链一体化策略的顺利开展,供应链双方需达到一个理想的控制力配置状态,模型3说明当供应商和零售商的控制力水平分别为1/2时,系统利润水平最大,也就说明该情况下集中决策的开展具有较强的可行性。命题2可证。
命题3:满足2βk>η2(r2-bk)时,有e3*>e1*,q3*>q1*。
证明:
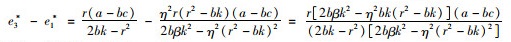
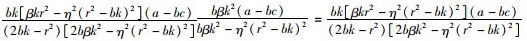
βkr2>2βk(r2-bk)>η2(r2-bk)2,因此q3*-q1*>0成立。命题3可证。
命题3说明满足一定条件时,集中决策下零售商的保鲜努力水平和市场需求量大于分散决策下的保鲜努力水平和市场需求量,这符合生鲜品销售特点。针对生鲜品的销售,产品新鲜度越大,销量会越大。集中决策下,供应链双方以系统利润最大化为目标进行决策,共同承担保鲜成本,而分散决策下,供应链双方以自身利润最大化为目标独立进行决策,此时只有零售商承担保鲜成本,零售商在维持其利润的前提下,会在一定程度上减少保鲜投入,因此,即使供应商能够控制供应链并影响零售商的保鲜努力水平,集中决策下的保鲜努力水平和销量也会比分散决策大。另外,考虑价格和利润最优解的复杂性,用命题4对不同决策下最优价格水平进行分析,系统利润对比则以算例分析予以说明。
命题4:满足2bβk2-η2(r2-bk)2>0和2bk-r2>0条件时,有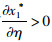
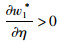
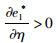
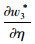
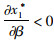
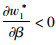
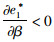
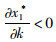
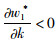
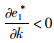
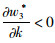
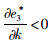
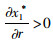
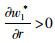
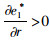
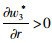
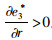
对于生鲜品而言,由于其易腐特质,产品新鲜度和价格是消费者最为关注的2个因素,本研究将价格视为控制力的函数,因此,我们重点考虑与新鲜度和控制力有关的参数变化对决策变量的影响。命题4说明,分散决策下最优控制力水平、批发价格和保鲜努力水平随控制力价格影响系数和消费者生鲜度敏感系数的增加而增大,随控制力成本系数和保鲜努力投入成本系数的增加而减小。与分散决策不同的是,集中决策下最优控制力水平是固定值1/2,不受各参数影响;系统价格(批发价)随控制力价格影响系数的增加而减小,与控制力成本系数无关;最优保鲜努力水平仅与消费者生鲜度敏感系数和保鲜努力投入成本系数有关,与控制力因素无关。我们对模型1和模型3中的各决策变量分别求关于参数η,β,k,r的一阶导数,可得上述结果,证明过程略。
由命题4,我们还可以得出一个有意思的结论,即分散决策下的最优批发价格与集中决策下的最优批发价格(因为控制力水平是固定值,在零售价格一定的情况下,我们可以求出最优批发价格,这里仅用于数值比较分析)没有确定的大小关系,由于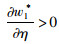
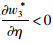
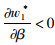
为验证模型有效性,我们以烟台某食品有限公司销售的熟食产品为例,对其实际销售数据进行调查,通过Matlab软件进行算例仿真,利用数值分析探讨变量之间的关系,以及参数η,β,k,r的变化对系统最优决策及利润的影响。烟台某食品有限公司是一家主要从事肉制品加工及销售的企业,采用国际连锁直营的销售模式,通过“形象统一、价格统一、考核统一、服务统一”的销售理念,在省内外设立了1 000多家专卖连锁店,其品牌形象日益深入民心。作为生鲜熟食产品的供应商,该公司对其产品进行源头控制,对其下游分销商、零售网点制订统一的销售价格,而零售商在进行售卖时需要对熟食产品进行保鲜,并进行一定的保鲜投入,这与前述理论模型中的假设一致。相关参数赋值见表 2。
| 参数 | a/件 | b | η/(元·件-1) | β | r | k | c/(元·件-1) |
| 赋值 | 700 | 25 | 8 | 124 | 47 | 80 | 20 |
4.1 Stackelberg决策和集中决策的绩效比较
| x* | e* | w*/(元·件-1) | p*/(元·件-1) | q*/件 | πs*/元 | πr*/元 | π*/元 | |
| 分散决策(模型1) | 0.725 | 3.409 | 24.303 | 30.106 | 107.579 | 430.317 | 154.716 | 585.033 |
| 集中决策(模型3) | 0.5 | 5.248 | 24.933 | 28.934 | 223.339 | — | — | 862.356 |
由表 3可知,考虑控制力的供应商主导的分散决策下,最优控制力水平为0.725,符合假设条件0.5 < x < 1。集中决策下最优保鲜努力水平为5.24、最优销量223.339,远大于分散决策下的最优值3.409和107.597,命题3得证。另外数据显示,分散决策下供应商利润430.317大于零售商利润154.716,说明控制力强势一方的利润水平大于弱势一方的利润水平;π3*远大于π1*,说明一体化决策比分散决策更有利,这与理论分析结果一致。
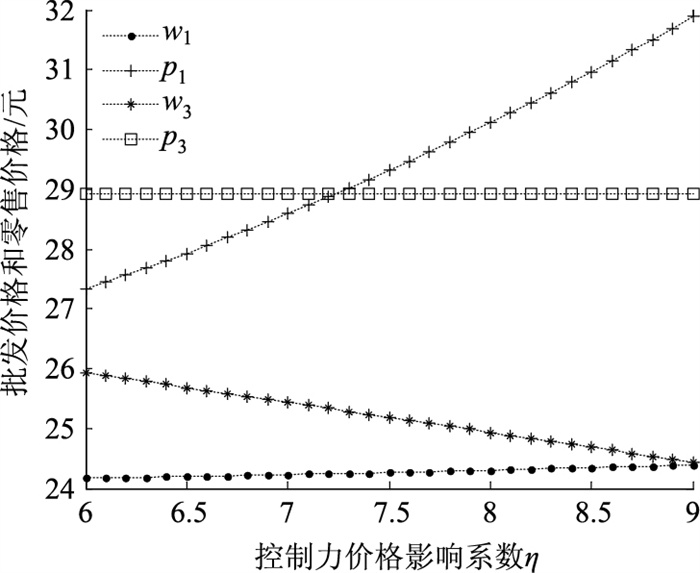
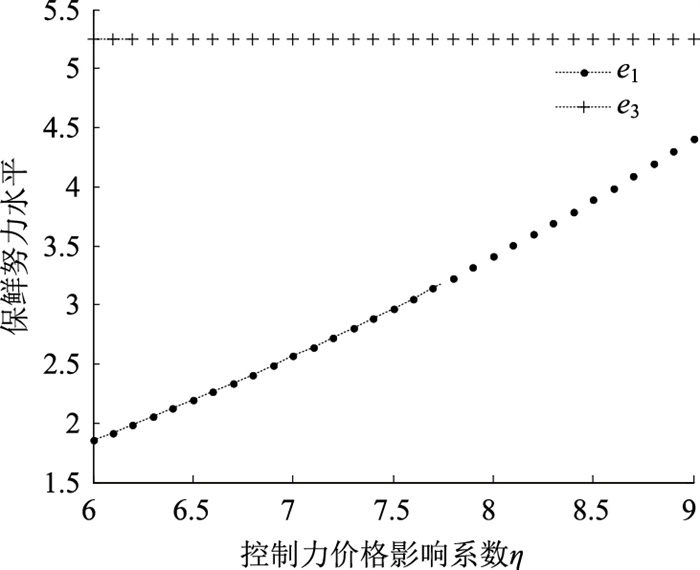
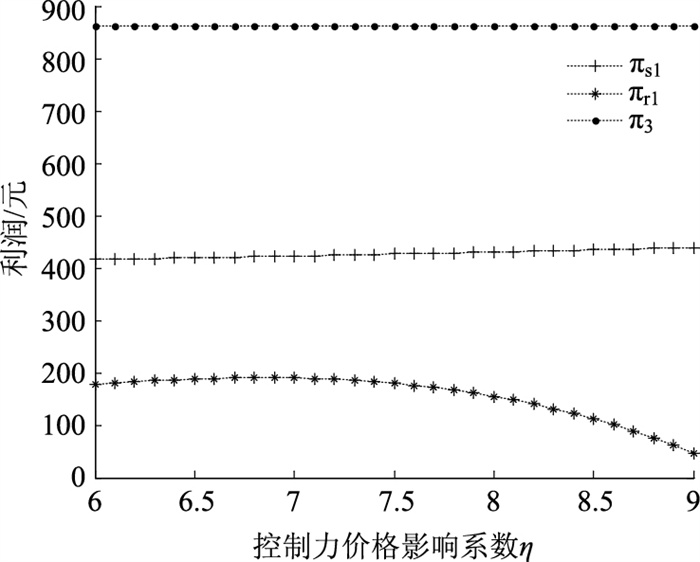
4.2 控制力价格影响系数(η)对最优决策及利润的影响显然,供应商主导的分散决策下,随着控制力价格影响系数的增大,最优批发价格w1和最优零售价格p1会随之增大(如图 1所示),控制力价格影响系数达到一个阈值(如图 1所示p1和p3的交叉点)时,会出现p3* < p1*,此时一体化决策比分散决策更有优势。为保证产品能够顺利销售,供应商利用其强大的控制力,让零售商投入更多的保鲜努力,表现为图 2中最优保鲜努力水平e1也逐渐增加。最终供应商获取可观的利润水平,而零售商则会因为投入大量的保鲜努力成本利润水平则不断下降,表现为图 3中πs1的轻微增加和πr1的急剧减少。实务中,供应商如果拥有绝对的产品优势、良好的品牌形象以及较强的市场占有率,控制力价格影响系数也就越大,更易获取较高的利润,如某公司的生鲜熟食销售都是统一定价,控制销售渠道,从而控制利润水平。但是如果供应商控制力太高的话,零售商利润水平会受到不利影响,保鲜投入和获取的利润水平达不到平衡,供应链双方之间的合作便会消失。因此,供应商的控制力水平会根据其产品特性保持在一个合适的水平上,以保障合作顺利进行。命题1和命题4可证。
|
| 图 1 η对价格的影响 Fig. 1 Influence of ηon price |
| |
|
| 图 2 η对保鲜努力水平的影响 Fig. 2 Influence of η on freshness-keeping effort level |
| |
|
| 图 3 η对利润的影响 Fig. 3 Influence of η on profit |
| |
集中决策下,不管控制力价格影响系数如何变化,最优保鲜努力水平始终不变,且远大于分散决策下的最优水平(由图 2可知),说明一体化决策下,较高的保鲜努力水平也可以带来较高的市场销量,进而产生较高的利润。命题3和命题4得证。
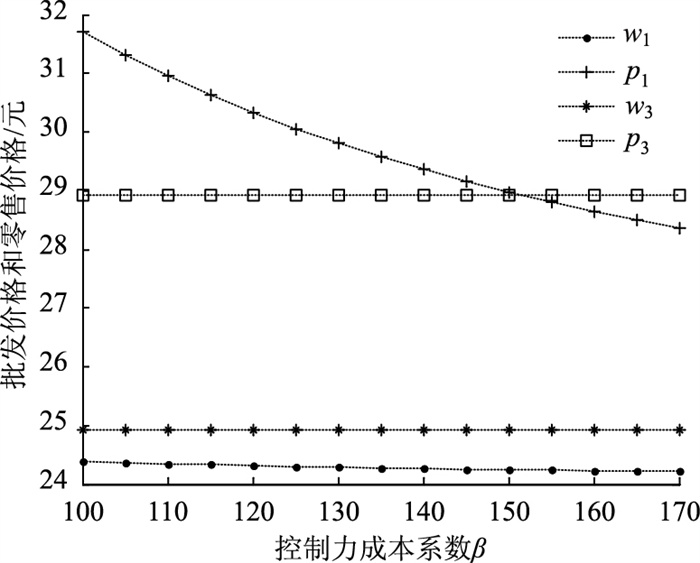
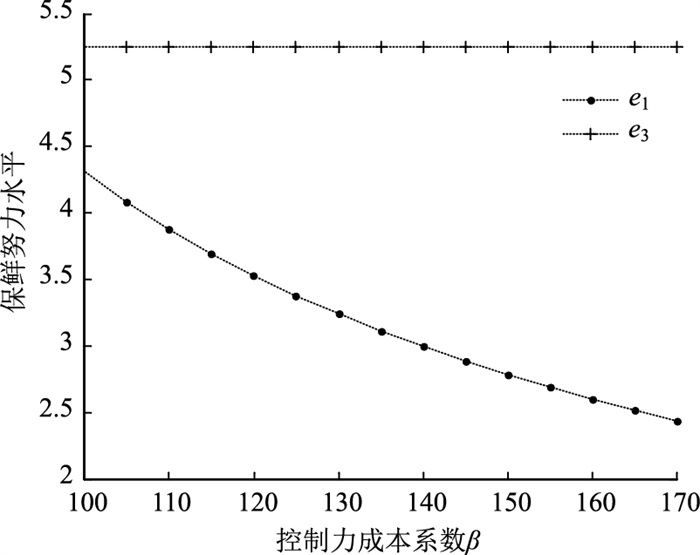
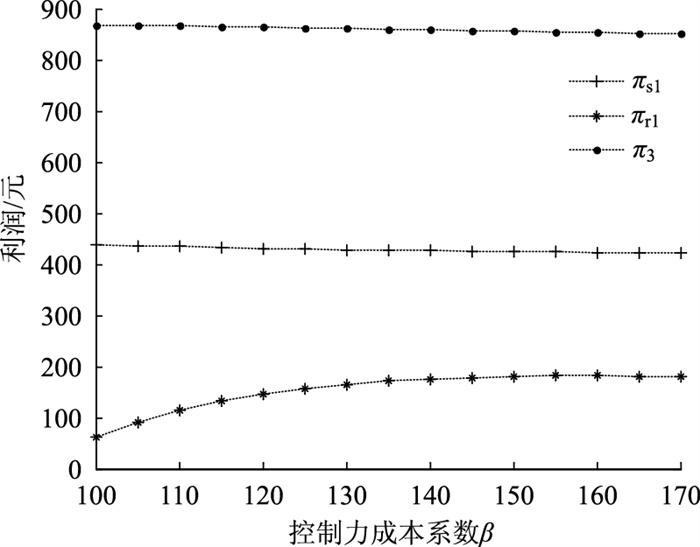
4.3 控制力成本系数(β)对最优决策及利润的影响供应商主导的分散决策下,随着控制力成本系数的增大,控制成本随之增大,供应商争夺供应链控制力的意愿随之减弱,控制力水平随之降低,供应商控制价格的能力下降,因此会出现图 4所示最优零售价格随β的增加而下降的趋势,且控制成本系数达到一个阈值(如图 4所示p1和p3的交叉点)之前,一直会有p3* < p1*,说明此时一体化决策比分散决策更有优势。随着供应商的控制力减弱,零售商控制力增强,零售商为保证自己利润最大化,会减少保鲜投入,因此会出现图 5所示保鲜努力水平逐渐下降的趋势,零售商的利润会随β的增加而增加,如图 6所示。因此,实务中,供应商应考虑控制力成本因素,避免出现一味追求控制力而导致利润下降的情形,也间接说明了供应商主导的分散决策下,会存在最优控制力水平使得双方实现最优合作,供应链系统出现平衡,命题1可证。
|
| 图 4 β对价格的影响 Fig. 4 Influence of β on price |
| |
|
| 图 5 β对保鲜努力水平的影响 Fig. 5 Influence of β on freshness-keeping effort level |
| |
|
| 图 6 β对利润的影响 Fig. 6 Influence of β on profit |
| |
集中决策下,不存在谁主导谁从属的问题,但仍存在系统整体定价与运营控制问题,如图 4~6可知,控制力成本系数通过影响控制成本而影响系统利润水平,对系统最优保鲜努力水平及最优定价水平不产生影响,命题2和命题4得证。
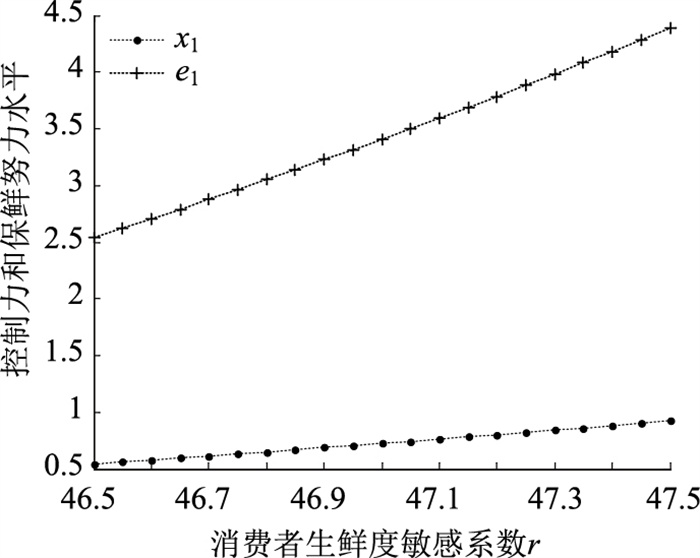
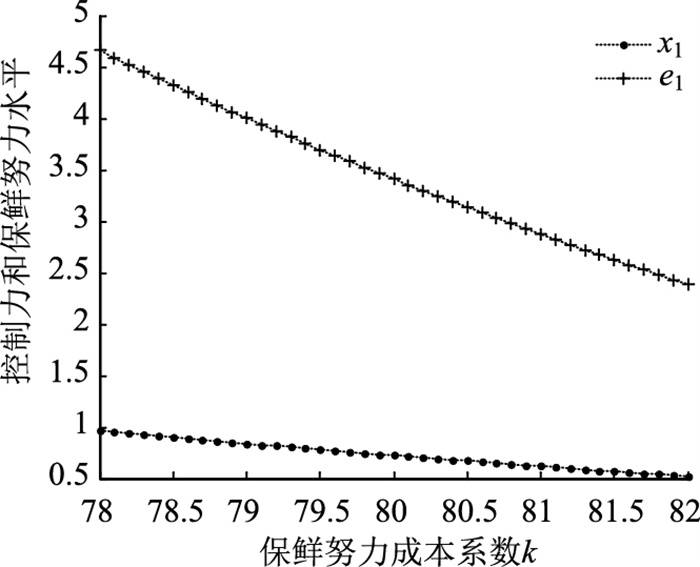
4.4 消费者生鲜度敏感系数(r)和保鲜努力投入成本系数(k)对最优决策的影响消费者生鲜度敏感系数体现了产品新鲜度对消费者需求的影响,r越大,消费者对生鲜品新鲜度的要求也就越高,供应商主导的分散决策下,为满足客户需求,会提高自身对供应链的控制能力,并要求零售商提高保鲜努力水平,如图 7所示,最优控制力水平和保鲜努力水平会随r的增大而增大。因此,针对消费者生鲜度比较敏感的产品,供应商应尽可能提升自己的控制能力,以增强产品的新鲜度水平,进而提升销量和利润水平。另一方面,由图 8可知,最优控制水平和保鲜努力水平会随保鲜努力投入成本系数的增大而减少,这是因为当保鲜努力投入成本系数增大时,零售商需承担的保鲜努力成本的增加幅度就越大,导致其利润水平大幅降低,因此零售商保鲜投入的意愿会大大下降,为保证合作的顺利开展,供应商会降低对系统价格的控制能力,从而保证足够多的市场销量。命题4可证。
|
| 图 7 r对控制力和保鲜努力水平的影响 Fig. 7 Influence of ron control power and freshness-keeping effort level |
| |
|
| 图 8 k对控制力和保鲜努力水平的影响 Fig. 8 Influence of kon control power and freshness-keeping effort level |
| |
5 结论
控制力争夺一直是供应链成员企业之间普遍存在的问题,并最终会导致供应链的不稳定,因此设计合理的权力配置便成为供应链运作管理中较为重要的问题。本研究构建了控制力影响产品价格的生鲜品供应链优化模型,研究发现,考虑控制力因素更符合生鲜品供应链实际运作情况。对生鲜品供应链运作管理的启发在于:(1)供应商应该清楚地认识到控制力在供应链合作中的作用,根据产品的特性以及控制力成本大小考虑和零售商的合作,合理确定对权力的掌控,而不是盲目的争夺控制权。(2)对消费者生鲜度比较敏感的产品,供应商应尽可能提升自己的控制能力,以增强产品的新鲜度水平,进而提升销量和利润水平。(3)一体化决策下,供应链双方权力相等,即都为1/2时,更有助于合作的开展;一般情况下集中决策的零售价格会低于分散决策下的零售价格,而考虑控制力因素时,当控制力价格影响系数和控制力成本系数达到一个阈值时,会有p3* < p1*,一体化决策才更易开展。本研究针对的是确定性市场需求、市场需求与保鲜努力水平呈线性变化的二级生鲜品供应链优化决策,可作为后续研究复杂生鲜品供应链网络权力影响机制的基础,为进一步探索供应链关系提供了一个新的视角。
| [1] |
RYU S, PARK J E, MIN S. Factors of Determining Long-term Orientation in Inter Firm Relationships[J]. Journal of Business Research, 2007, 60(12): 1225-1233. |
| [2] |
EMERSON R M. Power-dependence Relations[J]. American Sociological Review, 1962, 27(1): 31-41. |
| [3] |
MEEHAN J, WRIGHT G H. Power Priorities: A Buyer-Seller Comparison of Areas of Influence[J]. Purchasing and Supply Management, 2011, 17(1): 32-41. |
| [4] |
LIU W, WANG S, ZHU D. The More Supply Chain Control Power, the Better?A Comparison among Four Kinds of Cooperation Models[J]. Mathematical Problems in Engineering, 2015(9): 44-51. |
| [5] |
DEMIRKAN H, CHENG H K. The Risk and Information Sharing of Application Services Supply Chain[J]. European Journal of Operational Research, 2008, 187(3): 765-784. |
| [6] |
CHOI T M, LI Y, XU L. Channel Leadership, Performance and Coordination in Closed Loop Supply Chains[J]. International Journal of Production Economics, 2013, 146(1): 371-380. |
| [7] |
王淑云, 马文秀. 基于保鲜努力的生鲜农产品库存和协调优化[J]. 公路交通科技, 2019, 36(6): 125-134. WANG Shu-yun, MA Wen-xiu. Fresh Agricultural Products Inventory and Coordinative Optimization Based on Fresh Keeping Effort[J]. Journal of Highway and Transportation Research and Development, 2019, 36(6): 125-134. |
| [8] |
冯颖, 张炎治. 不同权力结构下TPL服务增值的供应链决策与效率评价[J]. 中国管理科学, 2018, 26(10): 164-175. FENG Ying, ZHANG Yan-zhi. Decision Making and Efficiency Evaluation in A Supply Chain with TPL's Value-added Services under Different Power Structures[J]. Chinese Journal of Management Science, 2018, 26(10): 164-175. |
| [9] |
KIRILENKO A A. Valuation and Control in Venture Finance[J]. The Journal of Finance, 2001, 56(2): 23. |
| [10] |
LIU W, WANG S, CHEN L. The Role of Control Power Allocation in Service Supply Chains: Model Analysis and Empirical Examination[J]. Journal of Purchasing & Supply Management, 2017(23): 176-190. |
| [11] |
王淑云, 范晓晴, 马雪丽, 等. 考虑商品新鲜度与量变损耗的三级冷链库存优化模型[J]. 系统管理学报, 2020, 29(2): 409-416. WANG Shu-yun, FAN Xiao-qing, MA Xue-li, et al. A Three-stage Cold Chain Inventory Optimization Model Considering Freshness and Quantity Loss of Goods[J]. Journal of Systems & Management, 2020, 29(2): 409-416. |
| [12] |
杨磊, 肖小翠, 张智勇. 需求依赖努力水平的生鲜农产品供应链最优定价策略[J]. 系统管理学报, 2017, 26(1): 142-153. YANG Lei, XIAO Xiao-cui, ZHANG Zhi-yong. Optimal Pricing Policies of Fresh Agricultural Product Supply Chain with Effort Level Dependent Demand[J]. Journal of Systems & Management, 2017, 26(1): 142-153. |
| [13] |
COUGHLAN A T, ANDERSON E, STERN L W, et al. Marketing Channels[M]. Upper Saddle River: Prentice-Hall, 2006.
|
| [14] |
MUNSON C L, ROSENBLATT M J, ROSENBLATT Z. The Use and Abuse of Power in Supply Chains[J]. Business Horizons, 1999, 42(1): 55-65. |
| [15] |
王淑云, 姜樱梅, 王宪杰. 冷链库存优化与定价研究[M]. 北京: 经济科学出版社, 2018. WANG Shu-yun, JIANG Ying-mei, WANG Xian-jie. Research on Cold Chain Inventory Optimization and Pricing[M]. Beijing: Economic Science Press, 2018. |
| [16] |
IOSSA E, MARTIMORT D. The Simple Microeconomics of Public-private Partnerships[J]. Journal of Public Economic Theory, 2015, 17(1): 4-48. |
| [17] |
GRECO L. Imperfect Bundling in Public-private Partnerships[J]. Journal of Public Economic Theory, 2015, 17(1): 136-146. |
| [18] |
CHAMBERS C, KOUVELIS P, SEMPLE J. Quality-based Competition, Profitability, and Variable Costs[J]. Management Science, 2006, 52(12): 1884-1895. |
 2021, Vol. 38
2021, Vol. 38
