扩展功能
文章信息
- 王博文, 王景升, 朱茵, 王统一, 张泽有
- WANG Bo-wen, WANG Jing-sheng, ZHU Yin, WANG Tong-yi, ZHANG Ze-you
- 基于ARMA-SVR的短时交通流量预测模型研究
- Study on Short-term Traffic Volume Prediction Model Based on ARMA-SVR
- 公路交通科技, 2021, 38(11): 126-133
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(11): 126-133
- 10.3969/j.issn.1002-0268.2021.11.015
-
文章历史
- 收稿日期: 2021-03-15
2. 山东科技大学 电气信息学院, 山东 济南 250000
2. School of Electrical Information, Shandong University of Science and Technology, Jinan Shandong 250000, China
交通流量预测是智能交通系统(Intelligent Traffic System, ITS)的重要组成部分,准确的交通流量预测模型可以辅助交通信号配时、拥堵疏导等任务,是智能交通领域研究的热点问题。
早期的交通流预测任务通常采用传统统计模型,通过使用线性模型挖掘交通流序列中存在的线性关系[1-3]。如EMAMI等[4]研发了一种卡尔曼滤波器对交通流进行了有效的预测,为短期交通流量预测提供了一种低成本手段。KUMAR等[5]提出季节性自回归移动平均(Autoregressive Integrated Moving Average, ARIMA)模型,利用历史数据和实时数据对早晚高峰时段的交通流量进行短期预测,得到了良好的预测效果。但是,随着居民出行需求的提高,交通流所具备的非线性特征愈发明显,许多机器学习的算法,如支持向量机,及深度学习算法,如等及长短时记忆(Long Short-Term Memory, LSTM)、卷积神经网络(Convolutional Neural Network, CNN)、图神经网络(Graph Neural Networks, GNN)及其改进算法,被应用于短时交通流预测[6-18],这类模型多为非线性模型,以期望充分挖掘交通流序列的非线性关系。邹宗民等[19]使用粒子群算法对支持向量回归(Support Vector Regression, SVR)进行参数寻优,并将优化后的模型用于交通流预测任务中。相较于传统统计算法,提高了模型的预测准确性,相较于深度学习算法,SVR在小样本交通流序列预测中表现较好。温惠英等[20]引入双长短期记忆网络,将基准模型拆分为两个方向,并通过试验证明了模型对于非线性交通流数据具备良好的预测和泛化能力。李磊等[21]提出一种CNN和LSTM的结合方法,有效提取了交通流的时空特征,并通过大量试验证明了非线性模型对于交通流序列的预测情况较为良好。GUO等[22]构建一种基于注意力机制的时空图卷积网络,对交通流序列进行了准确的预测。单一的传统统计模型或浅层机器学习模型不能够同时挖掘交通流序列中存在的线性及非线性关系。基于深度学习的模型,尤其是基于GNN及其改进算法的模型,对于试验样本为大样本量的依赖性较高,数据计算成本高,并且时间复杂度相较于传统统计模型及浅层机器学习算法高。短时交通流预测任务作为辅助ITS进行决策的关键工作,需要预测模型对道路情况进行快速、准确的判断,对于预测实时性的要求极高。
因此,为解决小样本、快速短时交通流预测问题,并充分挖掘交通流序列中存在线性与非线性关系,本研究将对于线性数据具备良好拟合效果,并且时间复杂度较低的自回归滑动平均(Auto Regressive Moving Average,ARMA)模型与对于非线性、小样本数据的处理具有计算准确率高、时间复杂度低等优势的SVR模型进行组合,达到提高交通流预测模型预测准确率及降低模型时间复杂度的目的。
1 交通流预测方法 1.1 理论模型 1.1.1 ARMA模型ARMA模型是目前应用最广的线性平稳时间序列预测模型,模型的形式为:
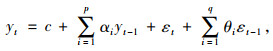
|
(1) |
式中,yt为被预测变量;yt-1为与被预测变量相关的滞后阶;c为常数;εt为白噪声序列,服从均值为0的正态分布;αi为自相关系数(i=1, 2,…, p);θi为移动平均系数(i=1, 2,…, q);p,q分别为自回归、移动平均过程中的滞后阶数。
参数p,q的选择决定了ARMA模型的拟合效果。当样本量n固定时,使赤池信息准则(Akaike Information Criterion,AIC)达到最小值的(p,q)即为最佳参数组合,AIC的计算公式为:
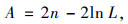
|
(2) |
式中,n为样本个数;L为似然函数。
1.1.2 SVR模型SVR是将支持向量机(Support Vector Machine,SVM)应用于回归问题,目的在于建立一个最优的超平面,使训练样本距离最优超平面的误差最小,此时模型达到最佳拟合效果。
对于非线性数据集(i=1, 2,…,m),xi, yi分别为输入和输出。把样本从低维空间映射到高维空间,超平面公式表示为:
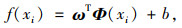
|
(3) |
式中,ω为超平面的法向量;Ф(xi)为xi映射到高维空间后的特征向量;b为位移项。
模型的训练过程即参数ω,b的寻优过程,最终得到一组参数ω,b使f(xi)最接近yi,将问题转化为凸二次规划问题,表示为:
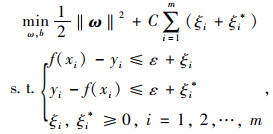
|
(4) |
式中,C为惩罚项,C用于平衡结构风险和经验风险,即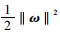
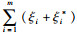
使用拉格朗日乘子法计算得到:
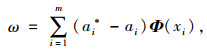
|
(5) |
式中ai,ai*为拉格朗日对偶问题的解。
使用核函数代替线性方程中的线性项可以使原来的线性算法非线性化,即能做非线性回归,此时引进核函数达到了提升维度的目的,也可以有效地控制过拟合。不同的核函数会对SVR的性能产生影响。径向基核函数(RBF)的抗干扰能力及适应能力较强,表示为:

|
(6) |
式中,K(X,X′)为满足Mercer条件的核函数;γ为核参数,决定映射样本在特征空间的分布;X为输入样本构成的特征向量;X′为RBF核函数的中心。
计算得到SVR回归模型为:

|
(7) |
RBF的参数C(惩罚项)和g(核函数方差)的选取对于模型的结果存在较大影响。
1.2 两种组合预测方法 1.2.1 ARMA-SVR加权组合模型CRITIC法是一种比熵权法和标准离差法更好的客观权重赋权法,它基于评价指标的对比强度和指标之间的冲突性来综合衡量指标的客观权重。
假设有n个待评价样本,p项评价指标,形成原始指标数据矩阵:
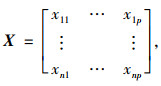
|
(8) |
式中xij为第i个样本的第j项评价指标的值。
指标的对比强度以标准差的形式来表现:
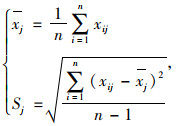
|
(9) |
式中,xj为第j项指标的均值;Sj为第j项指标的标准差。
在CRITIC法中使用标准差来表示各指标的内取值的差异波动情况,标准差越大表示该指标的数值差异越大,越能反映出更多的信息,该指标本身的评价强度也就越强,应该给该指标分配更多的权重。
指标的冲突性用相关系数进行表示:
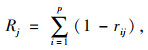
|
(10) |
式中rij为评价指标i和j之间的相关系数。
使用相关系数来表示指标间的相关性,与其他指标的相关性越强,则该指标就与其他指标的冲突性越小,反映出相同的信息越多,所能体现的评价内容就越有重复之处,一定程度上也就削弱了该指标的评价强度,应该减少对该指标分配的权重。
第j个评价指标所包含的信息量Cj表示为:
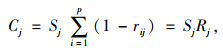
|
(11) |
所以第j个指标的客观权重Wj为:
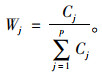
|
(12) |
ARMA-SVR加权组合模型原理如图 1所示。

|
| 图 1 ARMA-SVR加权组合模型的建模流程 Fig. 1 Modeling process of ARMA-SVR weighted composite model |
| |
(1) 使用ARMA模型对样本进行建模,得到预测结果PARMA。
(2) 使用SVR模型对样本进行建模,得到预测结果PSVR。
(3) 使用CRITIC赋权法对ARMA与SVR模型的预测结果进行客观赋权,分别得到权重WARMA和WSVR。
(5) 将ARMA模型预测结果PARMA与SVR模型预测结果PSVR进行加权相加,得到ARMA-SVR加权组合模型的预测结果表示为:
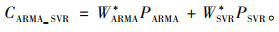
|
(13) |
交通流存在线性和非线性的特性,而ARMA和SVR模型分别对线性模型和非线性模型的处理上具备优势,理论上将两个模型的优势相结合,能够达到提高模型效果的目的。假设时间序可视为线性自相关部分与非线性残差相结合的结果,表示为:
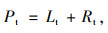
|
(14) |
式中,Lt为线性自相关部分;Rt为非线性残差。
ARMA-SVR残差优化组合模型原理如图 2所示。

|
| 图 2 ARMA-SVR残差优化组合模型的建模流程 Fig. 2 Modeling process of ARMA-SVR residual optimization composite model |
| |
由图 2得,ARMA-SVR残差优化组合模型的基本原理为:
(1) 使用ARMA模型对样本的线性部分进行建模,得到预测结果ARMA,进而得出残差序列R。
(2) 以特定的输入步长对残差序列进行重构。
(3) 将重构后的残差序列R*作为SVR模型的输入。
(4) 使用SVR模型对残差序列的非线性部分进行建模,得到残差序列预测结果。
(5) 将残差序列预测结果与ARMA模型预测结果相加,得到ARMA-SVR残差优化组合模型的预测结果。
1.3 评价指标回归模型中,常用均方误差(Mean Absolute Error,MAE)、平均绝对误差(Mean Squared Error,MSE)、均方根误差(Root Mean Squard Error,RMSE)作为模型的评价指标,本研究使用MAE和RMSE作为评价指标,模型的MAE和RMSE越小,预测效果越好。
2 实例验证 2.1 数据来源本试验采用内蒙古包头市某路段2020年9月的地磁交通流量数据,每组数据的单次采样时间间隔为5 min,包括单向所有车道的交通流量总和,样本总量为8 640。
2.2 数据分析与预处理将数据分别处理为以5,10,15 min为时间间隔的数据。3个样本集的样本数量分别为8 640个, 4 320个,2 880个。将3个样本集分别按照8∶2的比例划分训练集与测试集。处理后的交通流量变化趋势如图 3所示。

|
| 图 3 不同样本时间间隔下的交通流量的变化趋势 Fig. 3 Variation trends of traffic volume at different sample time intervals |
| |
2.3 模型建立 2.3.1 ARMA模型
平稳性及白噪声检验。对样本进行平稳性检验及白噪声检验详见表 1。
| 样本的时间间隔/min | 平稳性检验 | 白噪声检验 | ||||||
| t统计量 | 置信度 | P值 | LB统计量 | P值 | ||||
| 1% | 5% | 10% | ||||||
| 5 | -9.45 | -3.43 | -2.86 | -2.57 | 4.65E-16 | 6 135.459 | 0 | |
| 10 | -11.44 | -3.43 | -2.86 | -2.57 | 6.11E-21 | 3 245.015 | 0 | |
| 15 | -11.79 | -3.43 | -2.86 | -2.57 | 1.00E-21 | 2 323.877 | 0 | |
| 注:LB统计量为白噪声检验的检验统计量。 | ||||||||
由表 2得,平稳性检验的t统计量值小于1%,5%,10%这3个水平的值,且P值小于0。白噪声检验的P值小于0,所以3个样本集均为平稳非白噪声序列。
| 样本的时间间隔/min | 参数 | 回归系数 | 标准误差 | t统计量 | 显著性 |
| 5 | 常量 | 71.36 | 5.07 | 14.07 | 0.00 |
| α1 | 0.84 | 0.06 | 14.68 | 0.00 | |
| α2 | 0.61 | 0.07 | 8.76 | 0.00 | |
| α3 | -0.74 | 0.06 | -12.30 | 0.00 | |
| α4 | 0.27 | 0.02 | 16.13 | 0.00 | |
| θ1 | -0.42 | 0.06 | -7.26 | 0.00 | |
| θ2 | -0.73 | 0.06 | -12.93 | 0.00 | |
| θ3 | 0.50 | 0.04 | 12.03 | 0.00 | |
| 10 | 常量 | 142.74 | 10.17 | 14.04 | 0.00 |
| α1 | 0.56 | 0.06 | 9.11 | 0.00 | |
| α2 | -0.52 | 0.08 | -6.72 | 0.00 | |
| α3 | 0.88 | 0.05 | 18.80 | 0.00 | |
| α4 | 0.17 | 0.02 | 14.13 | 0.00 | |
| θ1 | -0.15 | 0.06 | -2.36 | 0.02 | |
| θ2 | 0.73 | 0.06 | 11.64 | 0.00 | |
| θ3 | -0.38 | 0.04 | -10.78 | 0.00 | |
| 15 | 常量 | 215.08 | 4.78 | 45.04 | 0.00 |
| α1 | 0.66 | 0.04 | 15.06 | 0.00 | |
| α2 | 1.27 | 0.04 | 31.62 | 0.00 | |
| α3 | -0.67 | 0.04 | -15.30 | 0.00 | |
| α4 | -0.28 | 0.04 | -6.91 | 0.00 | |
| θ1 | -0.12 | 0.05 | -2.66 | 0.01 | |
| θ2 | -0.97 | 0.01 | -178.56 | 0.00 | |
| θ3 | 0.15 | 0.04 | 3.32 | 0.00 | |
| 注:αi为ARMA模型的自相关系数(i=1, 2,…, p);θi为ARMA模型的移动平均系数(i=1, 2,…, q)。 | |||||
ARMA模型参数确定。多次试验得到,当样本的时间间隔分别为5,10,15 min时p=4,q=3,AIC值达到最小,最佳参数组合为(4,3)。
对3个ARMA模型的参数进行显著性检验,详见表 2。由表 2可得,3个模型均满足显著性小于0.05,说明参数的取值具备合理性。上述建模流程得到ARMA模型预测结果。
2.3.2 SVR模型数据归一化。使用SVR模型之前,将数据做归一化操作,以此提高模型的收敛速度和预测能力。本研究采用Rescaling,即Min-Max归一化,将交通流量数据归一化至[0, 1]区间,表示为:
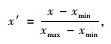
|
(9) |
式中,x′为归一化后的交通流量数据;x为原始交通流量数据;xmin为样本的最小值;xmax为样本的最大值。
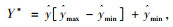
|
(10) |
式中,Y*为反归一化后的交通流量预测值;ŷ为模型输出的交通流量预测值。ŷmax为模型输出的交通流量预测值的最大值;ŷmin为模型输出的交通流量预测值的最小值。
本研究中SVR模型的建立均基于sklearn机器学习库,模型的参数为默认值。使用训练好的SVR模型对测试集进行预测,对SVR预测结果进行反归一化后,上述建模流程得到SVR模型预测结果。
2.3.3 ARMA-SVR加权组合预测模型在模型相互补偿的过程中,需要确定各个模型输出结果的权重,使用CRITIC权重法对ARMA和SVR预测的交通流量进行融合。模型的权重详见表 3。
| 采样时间间隔/min | WARMA | WSVR |
| 5 | 0.510 | 0.490 |
| 10 | 0.497 | 0.503 |
| 15 | 0.477 | 0.523 |
将ARMA模型预测结果与SVR模型预测结果进行加权组合,得到ARMA-SVR加权组合预测模型的预测结果。
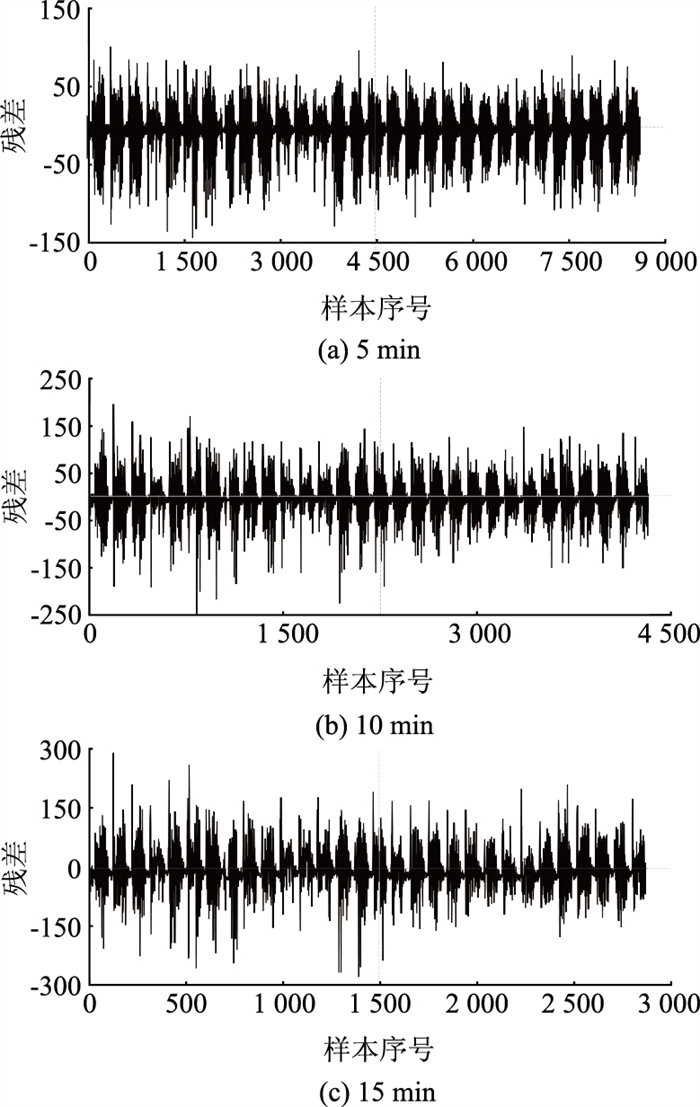
2.3.4 ARMA-SVR残差优化组合模型ARMA模型得到的残差如图 4所示。
|
| 图 4 不同样本时间间隔下ARMA模型得到的残差 Fig. 4 Residues obtained by ARMA model at different sample time intervals |
| |
首先对通过ARMA模型得到残差进行归一化处理,将残差值规约在[0, 1]。然后按照8∶2的比例划分训练集与测试集。最后使用SVR对重构后的残差序列进行预测。
使用SVR模型以2个时间步长读取训练集的残差序列进行训练,然后使用训练好的ARMA-SVR残差优化组合模型对测试集进行预测。对残差预测结果进行反归一化后,将SVR模型残差预测结果与ARMA模型预测结果相加,得到ARMA-SVR残差优化组合模型的预测结果。
2.4 模型评价为验证ARMA-SVR残差优化组合模型的优越性,将ARMA模型、SVR模型、长短期记忆网络(Long Short-Term Memory, LSTM)模型、人工神经网络(Artificial Neural Networks, ANN)模型及ARMA-SVR加权组合模型作为对照组进行模型评价。
LSTM和ANN模型的建立均基于Keras深度学习网络框架,激活函数均为线性整流函数Relu,损失函数为MSE,优化器为Adam,默认神经网络隐层数设置为1,神经元数量为8,通过compile方法完成学习过程的配置,训练的迭代次数为100,当监测到loss停止改进时,结束训练。
使用Min-Max归一化,将交通流量数据归一化至[0, 1]区间,分别使用训练好的LSTM和ANN模型以t-1及t时刻的交通流量值预测t+1时刻的交通流量值。
不同模型在样本的时间间隔分别为5,10,15 min时对于测试集的拟合评价结果详见表 4。
| 模型 | RMSE | MAE | |||||
| 5 min | 10 min | 15 min | 5 min | 10 min | 15 min | ||
| ARMA | 23.726 | 40.094 | 54.547 | 4.058 | 5.410 | 6.386 | |
| SVR | 26.103 | 43.178 | 55.343 | 4.367 | 5.555 | 6.468 | |
| ANN | 28.625 | 46.532 | 59.586 | 4.779 | 5.877 | 6.743 | |
| LSTM | 26.351 | 43.651 | 58.499 | 4.398 | 5.785 | 6.741 | |
| ARMA-SVR(CRITIC) | 23.681 | 40.948 | 54.754 | 4.056 | 5.539 | 6.411 | |
| ARMA-SVR(Residual) | 23.303 | 39.469 | 54.005 | 3.977 | 5.331 | 6.332 | |
由表 4得,在预测准确率方面,对于小样本数据,相较于传统统计模型及机器学习模型,深度学习模型的预测准确率较低。当采样间隔为5 min时,ARMA-SVR加权组合模型的RMSE,MAE值均低于ARMA,SVR,LSTM,ANN的单一模型,模型拟合效果较4个单一模型好。在不同的采样时间间隔下,ARMA-SVR残差优化组合预测模型的预测准确率和稳定性较其他模型均有所提升,RMSE降低约0.378~7.063,MAE降低约0.054~0.802,可以为不同采样时间间隔下交通流量预测提供方法参考。除此之外,通过大量试验得到,在时间复杂度方面,ARMA和SVR的两种组合模型的时间复杂度及设备的配置远远低于深度学习模型ANN及LSTM。相关研究人员可将模型的预测结果用于ITS的短期决策任务中,如交叉口的信号配时。
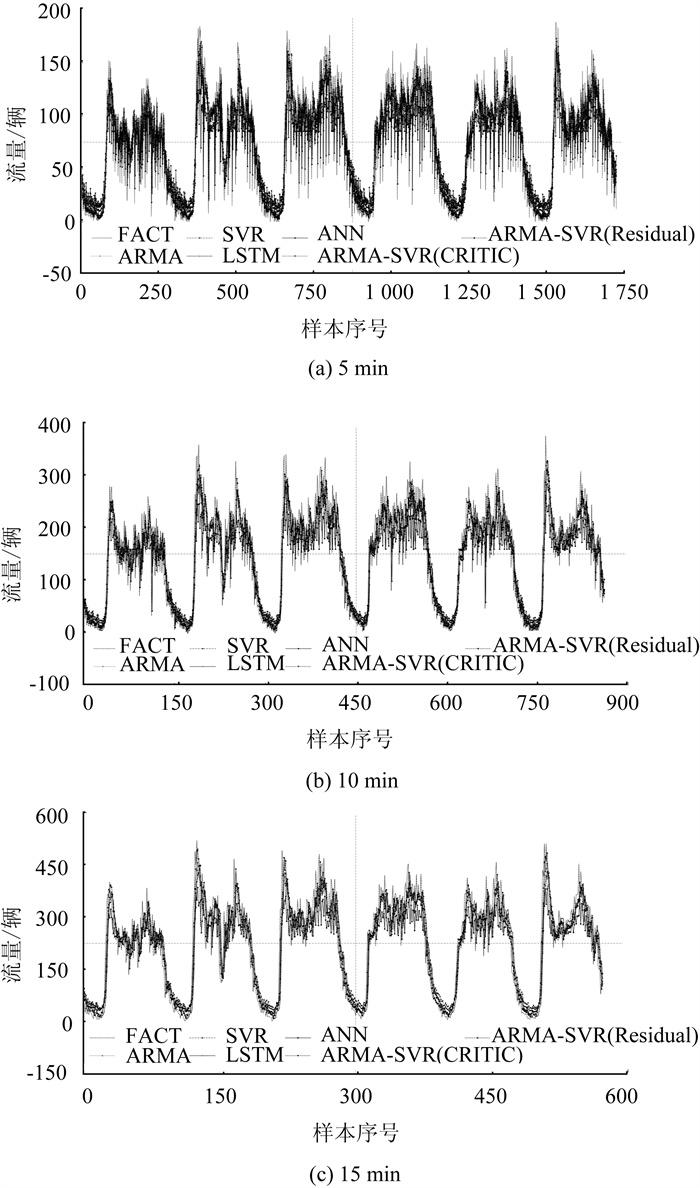
不同模型在样本的时间间隔分别为5,10,15 min时,在测试集上的拟合情况如图 5所示。
|
| 图 5 不同时间间隔下交通流量预测模型在测试集上的拟合情况 Fig. 5 Fitting condition of traffic volume prediction model on test set at different time intervals |
| |
3 结论
本研究将对于线性数据具备良好拟合效果的ARMA模型与对于非线性数据处理具有优势的SVR模型进行组合,充分挖掘了交通流序列中的线性及非线性关系,提高了模型预测的准确率。并通过试验证明,对比ARMA,SVR,LSTM,ANN及ARMA-SVR加权组合预测模型,ARMA-SVR残差优化组合模型在小样本的短时交通流预测任务中表现出预测精度高、计算速度快及数据计算成本低的优势。并且在样本的时间间隔分别为5,10,15 min时ARMA-SVR残差优化组合模型均能较好地反映交通流量序列中的线性及非线性关系,可以满足基于不同样本时间间隔的交通流流量预测的需要,将该模型应用于支持ITS的决策需求,可以提升ITS决策速度及精确度,同时能够降低ITS决策系统的建设成本。因为交通流序列往往受多因素的影响,本研究未考虑多因素对预测目标的影响,之后的研究可以通过扩展数据获取的范围,将速度、占有率、天气状况、能见度及事故信息等因素纳入预测模型。
| [1] |
刘潭秋, 孙湘海, 钟翔. 基于三制度SETAR模型的短期交通流预测[J]. 公路交通科技, 2010, 27(10): 122-127, 142. LIU Tan-qiu, SUN Xiang-hai, ZHONG Xiang. Short-term Traffic Flow Forecasting Based on a Three-regime SETAR Model[J]. Journal of Highway and Transportation Research and Development, 2010, 27(10): 122-127, 142. |
| [2] |
盛慧, 王炜, 胡晓健. 基于改进型CTM模型的道路交通量预测[J]. 公路交通科技, 2009, 26(增1): 49-52. SHENG Hui, WANG Wei, HU Xiao-jian. Traffic Volume Forecast Based on Improved Cell Transmission Model[J]. Journal of Highway and Transportation Research and Development, 2009, 26(S1): 49-52. |
| [3] |
孙占全, 潘景山, 张赞军, 等. 基于主成分分析与支持向量机结合的交通流预测[J]. 公路交通科技, 2009, 26(5): 127-131. SUN Zhan-quan, PAN Jing-shan, ZHANG Zan-jun, et al. Traffic Flow Forecast Based on Combining Principal Component Analysis with Support Vector Machine[J]. Journal of Highway and Transportation Research and Development, 2009, 26(5): 127-131. |
| [4] |
EMAMI A, SARVI M, BAGLOEE S A. Using Kalman Filter Algorithm for Short-term Traffic Flow Prediction in a Connected Vehicle Environment[J]. Journal of Modern Transportation, 2019, 27(3): 222-232. |
| [5] |
KUMAR S V, VANAJAKSHI L. Short-term Traffic Flow Prediction Using Seasonal ARIMA Model with Limited Input Data[J]. European Transport Research Review, 2015, 7(3): 1-9. |
| [6] |
韩志聪, 樊彦国, 吴会胜, 等. 基于GA-SVR模型的短期交通流量预测方法研究[J]. 公路交通科技, 2017, 34(1): 130-136. HAN Zhi-cong, FAN Yan-guo, WU Hui-sheng, et al. Study on Methods of Short-time Traffic Volume Forecasting Based on GA-SVR Model[J]. Journal of Highway and Transportation Research and Development, 2017, 34(1): 130-136. |
| [7] |
马秋芳. 改进PSO优化的BP神经网络短时交通流预测[J]. 计算机仿真, 2019, 36(4): 94-98, 323. MA Qiu-fang. BP Neural Network Short-term Traffic Flow Prediction Based on Improved Particle Swarm Optimization[J]. Computer Simulation, 2019, 36(4): 94-98, 323. |
| [8] |
吴晋武, 张海峰, 冉旭东. 基于数据约减和支持向量机的非参数回归短时交通流预测算法[J]. 公路交通科技, 2020, 37(7): 129-134. WU Jin-wu, ZHANG Hai-feng, RAN Xu-dong. Nonparametric Regressive Short-term Traffic Flow Forecast Algorithm Based on Data Reduction and SVM[J]. Journal of Highway and Transportation Research and Development, 2020, 37(7): 129-134. |
| [9] |
JIANG W W, ZHANG L. Geospatial Data to Images: A Deep-learning Framework for Traffic Forecasting[J]. Tsinghua Science and Technology, 2019, 24(1): 52-64. |
| [10] |
万玉龙, 李新春, 周红标. 基于WPD-PSO-ESN的短期交通流预测[J]. 公路交通科技, 2019, 36(8): 144-151. WAN Yu-long, LI Xin-chun, ZHOU Hong-biao. Prediction of Short-term Traffic Flow Based on WPD-PSO-ESN[J]. Journal of Highway and Transportation Research and Development, 2019, 36(8): 144-151. |
| [11] |
张逸飞, 付玉慧. 基于ARIMA-BP神经网络的船舶交通事故预测[J]. 上海海事大学学报, 2020, 41(3): 47-52. ZHANG Yi-fei, FU Yu-hui. Prediction of Ship Traffic Accidents Based on ARIMA-BP Neural Network[J]. Journal of Shanghai Maritime University, 2020, 41(3): 47-52. |
| [12] |
CHAN K Y, DILLON T S, SINGH J, et al. Neural-network-based Models for Short-term Traffic Flow Forecasting Using a Hybrid Exponential Smoothing and Levenberg-Marquardt Algorithm[J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(2): 644-654. |
| [13] |
HUANG W H, SONG G J, HONG H K, et al. Deep Architecture for Traffic Flow Prediction: Deep Belief Networks With Multitask Learning[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(5): 2191-2201. |
| [14] |
WANG X X, XU L H, CHEN K X. Data-driven Short-term Forecasting for Urban Road Network Traffic Based on Data Processing and LSTM-RNN[J]. Arabian Journal for Science and Engineering, 2019, 44(4): 3043-3060. |
| [15] |
熊亭, 戚湧, 张伟斌. 基于DCGRU-RF模型的路网短时交通流预测[J]. 计算机科学, 2020, 47(5): 84-89. XIONG Ting, QI Yong, ZHANG Wei-bin. Short-term Traffic Flow Prediction Based on DCGRU-RF Model for Road Network[J]. Computer Science, 2020, 47(5): 84-89. |
| [16] |
朱征宇, 刘琳, 崔明. 一种结合SVM与卡尔曼滤波的短时交通流预测模型[J]. 计算机科学, 2013, 40(10): 248-251, 278. ZHU Zheng-yu, LIU Lin, CUI Ming. Short-term Traffic Flow Forecasting Model Combining SVM and Kalman Filtering[J]. Computer Science, 2013, 40(10): 248-251, 278. |
| [17] |
LOPEZ-GARCIA P, ONIEVA E, OSABA E, et al. A Hybrid Method for Short-term Traffic Congestion Forecasting Using Genetic Algorithms and Cross Entropy[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(2): 557-569. |
| [18] |
刘钊, 杜威, 闫冬梅, 等. 基于K近邻算法和支持向量回归组合的短时交通流预测[J]. 公路交通科技, 2017, 34(5): 122-128, 158. LIU Zhao, DU Wei, YAN Dong-mei, et al. Short-term Traffic Flow Forecast Based on Combination of K Nearest Neighbor Algorithm and Support Vector Regression[J]. Journal of Highway and Transportation Research and Development, 2017, 34(5): 122-128, 158. |
| [19] |
邹宗民, 郝龙, 李全杰, 等. 基于粒子群优化-支持向量回归的高速公路短时交通流预测[J]. 科学技术与工程, 2021, 21(12): 5118-5123. ZOU Zong-min, HAO Long, LI Quan-jie, et al. Short-term Traffic Flow Prediction of Expressway Based on Particle Swarm Optimization-Support Vector Regression[J]. Science Technology and Engineering, 2021, 21(12): 5118-5123. |
| [20] |
温惠英, 张东冉. 基于Bi-LSTM模型的高速公路交通量预测[J]. 公路工程, 2019, 44(6): 51-56. WEN Hui-ying, ZHANG Dong-ran. Highway Traffic Volume Prediction Based on Bi-LSTM Model[J]. Highway Engineering, 2019, 44(6): 51-56. |
| [21] |
李磊, 张青苗, 赵军辉, 等. 基于改进CNN-LSTM组合模型的分时段短时交通流预测[J]. 应用科学学报, 2021, 39(2): 185-198. LI Lei, ZHANG Qing-miao, ZHAO Jun-hui, et al. Short-Term Traffic Flow Prediction Method of Different Periods Based on Improved CNN-LSTM[J]. Journal of Applied Sciences, 2021, 39(2): 185-198. |
| [22] |
GUO S, LIN Y, FENG N, et al. Attention Based Spatial-temporal Graph Convolutional Networks for Traffic Flow Forecasting[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Atlanta: AAAI Press, 2019, 33(1): 922-929.
|
 2021, Vol. 38
2021, Vol. 38
