扩展功能
文章信息
- 尉浩浩, 张元海
- WEI Hao-hao, ZHANG Yuan-hai
- 变截面三跨连续箱梁桥活载作用下的约束扭转分析
- Analysis on Restrained Torsion of 3-span Continuous Box Girder Bridge with Variable Section under Live Load
- 公路交通科技, 2021, 38(11): 68-76
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(11): 68-76
- 10.3969/j.issn.1002-0268.2021.11.009
-
文章历史
- 收稿日期: 2020-10-26
约束扭转作为箱梁理论的重要组成部分,国内外学者对其做了大量研究[1-7]。箱梁在偏载作用下发生约束扭转时,不仅会因弯曲而产生弯曲应力,还会因扭转而产生翘曲应力[8-10]。为分析箱梁在偏载作用下的约束扭转效应,文献[11]通过实际桥梁的有限元模型,研究了影响波形钢腹板组合箱梁抗扭性能的因素,并指出扭转正应力最大值的出现位置。文献[12]通过有限元法和解析法的对比分析,研究了箱梁在活载作用下发生约束扭转时翘曲应力的大小和变化规律。以上文献对约束扭转引起的翘曲应力进行了探讨和分析,但未对偏载引起的应力放大效果做出具体分析和总结。为给桥梁设计提供直接有效的理论依据,文献[13]以波形钢腹板三跨连续箱梁桥为实例,通过理论计算、有限元数值分析和模型试验,分析了偏载系数的影响因素及变化规律。文献[14]采用实体有限元模型,用偏载系数和剪滞系数讨论了偏载效应和剪滞效应。文献[15]在推导弯曲、约束扭转和畸变单元刚度矩阵的基础上编写了用于箱梁分析的计算程序,通过程序计算与试验分析得到了较为精确的偏载系数。目前,在桥梁设计中,考虑偏载对应力的放大效应时仍采用经验系数,一般认为因约束扭转引起的翘曲正应力与弯曲正应力的比值在15%左右,而这种近似的处理方法仍值得商榷,因此对具体的变截面连续箱梁桥的约束扭转效应仍需做进一步的研究。
本研究引入应力放大系数表征偏载对正应力的放大效应,并自编程序YSNZ分析了变截面三跨连续箱梁桥在偏心车道荷载作用下的约束扭转效应。
1 约束扭转控制微分方程及初参数解根据乌曼斯基第二理论,对薄壁箱梁约束扭转变形问题,关于扭转角θ(z)的控制微分方程[16]为:
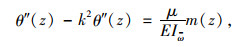
|
(1) |
式中,k为约束扭转弯扭特性系数;μ为截面约束系数;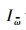
式(1)对应的齐次微分方程的初参数解为:
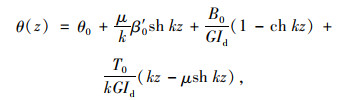
|
(2) |
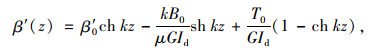
|
(3) |
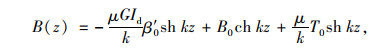
|
(4) |
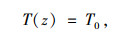
|
(5) |
式中,β′(z)为广义翘曲位移;T(z)为扭矩;B(z)为翘曲双力矩;G为剪切模量;Id为抗扭惯性矩; θ0,β0,T0和B0为4个初参数,分别表示z=0时的扭转角、广义翘曲位移、扭矩和翘曲双力矩。
式(2)~式(5)只适用于跨间无外荷载作用的情况,当箱梁跨间作用外荷载时需增加相应荷载项,当跨间满布均布扭矩荷载mt时有:
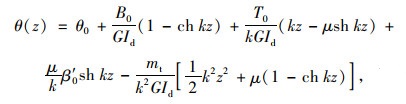
|
(6) |
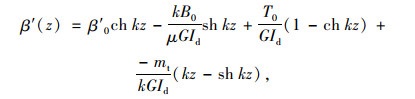
|
(7) |
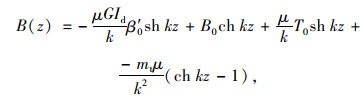
|
(8) |
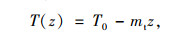
|
(9) |
确定4个初参数所需的边界条件如下:
自由端:T=0,B=0;简支端:θ=0,B=0;固定端:θ=0,β′=0。
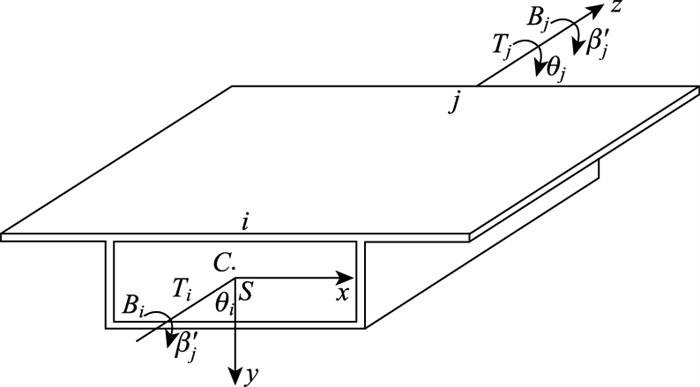
2 单元刚度矩阵及等效结点荷载列阵以箱梁约束扭转时的扭转角和广义翘曲位移为结点位移,根据约束扭转控制微分方程的初参数解推导箱梁单元刚度矩阵和等效节点荷载列阵。箱梁单元如图 1所示,图中S为箱梁截面的扭转中心,C为截面形心,在扭心坐标系下分析约束扭转效应,在形心坐标系下分析竖向挠曲,本研究此处对约束扭转效应的分析以扭转中心为坐标原点。引入局部坐标系下的节点位移列阵δ=[θi βi′ θj βj′]T和单元节点力列阵F=[Ti Bi Tj Bj]T。
|
| 图 1 箱梁单元 Fig. 1 Box girder element |
| |
根据有限元理论,单元平衡方程为
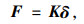
|
(10) |
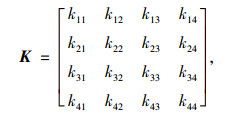
|
(11) |
式中,K为单元刚度矩阵;kij(i=1,2,3,4;j=1,2,3,4)的物理意义表示结构在第j列对应的梁端位移分量为1(其余梁端位移分量均为0)时,所引起的i行对应的梁端力分量的数值。
记z=0为i端,z=l为j端。令θi=1,βi′=θj=βj′=0,即只有在i端发生单位扭转角,其余节点位移为0,根据式(2)~式(5)有:
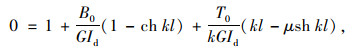
|
(12) |
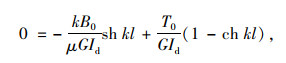
|
(13) |
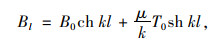
|
(14) |
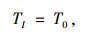
|
(15) |
将式(12)、式(13)联立解得:

|
(16) |
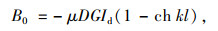
|
(17) |
式中,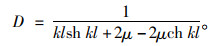
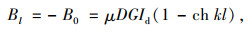
|
(18) |
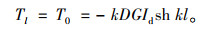
|
(19) |
根据kij的物理意义可知,式(16)~式(19)所求出的T0,B0,Tl,Bl依次代表单元刚度矩阵中第1列4个元素,而微分方程中待求量的方向与单元刚度矩阵方向不完全一致,单元刚度矩阵中第1列和第2列的系数均需变换正负号。故有:
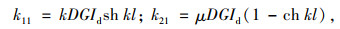
|
(20) |
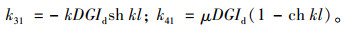
|
(21) |
同理,按上述步骤先后令βi′=1,θj=1,βj′=1,根据其边界条件可求得单元刚度矩阵全部系数,将系数组集后得到对称的4×4阶单元刚度矩阵。下面列出矩阵下三角的其余元素为:
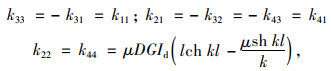
|
(22) |
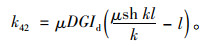
|
(23) |
当梁单元间作用均布扭矩荷载时,由对称性有:
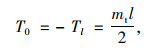
|
(24) |
令式(6)、式(8)中c=0,z=l,根据边界条件有θ0=β0′=θl=βl′=0,联立两式解得:
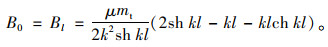
|
(25) |
根据式(20)、式(21)求得的值均为内力,而等效节点荷载为外荷载,故等效节点荷载列阵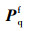
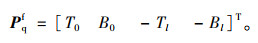
|
(26) |
在对箱梁空间效应的分析中,为简化问题常将箱梁上作用的偏心荷载分解为相互独立的对称荷载和反对称荷载(扭矩荷载)。对称荷载作用下,箱梁发生竖向挠曲,按梁的弯曲理论求解,反对称荷载作用下,箱梁发生扭转,按箱梁扭转理论求解,然后将两者计算结果叠加。
在形心坐标系Cxyz下分析箱梁的竖向挠曲,由箱梁弯曲理论得弯曲正应力σm的表达式为:
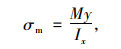
|
(27) |
式中,M为计算截面的弯矩;y为应力计算点到截面中性轴的距离;Ix为截面对x轴的惯性矩。
在扭心坐标系Sxyz下分析箱梁的约束扭转,由箱梁约束扭转理论得约束扭转翘曲正应力σω的表达式为:
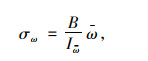
|
(28) |
式中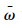
根据力的独立作用原理,将对称荷载引起的弯曲正应力和扭矩荷载引起的翘曲正应力按照叠加原理叠加,可得两者的应力和。为表示约束扭转效应对应力的放大效果,此处引入弯曲应力、翘曲应力之和与弯曲应力的比值作为应力放大系数η,其计算表达式为:
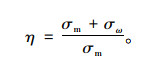
|
(29) |
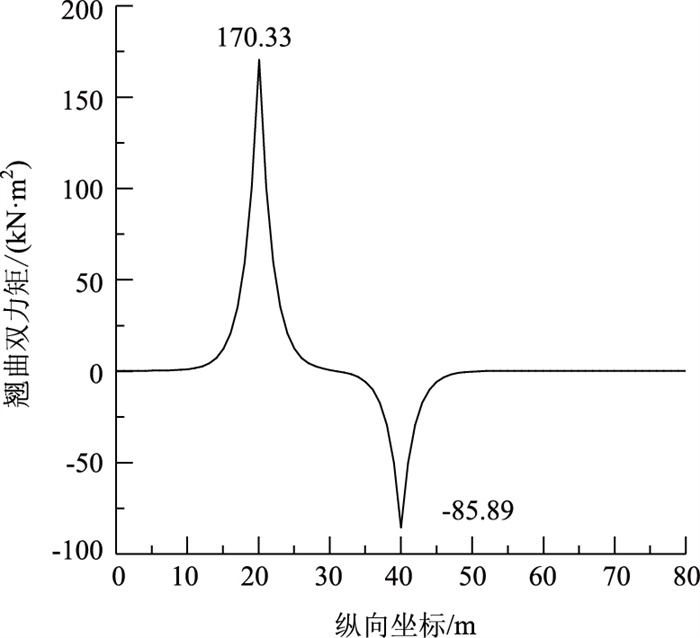
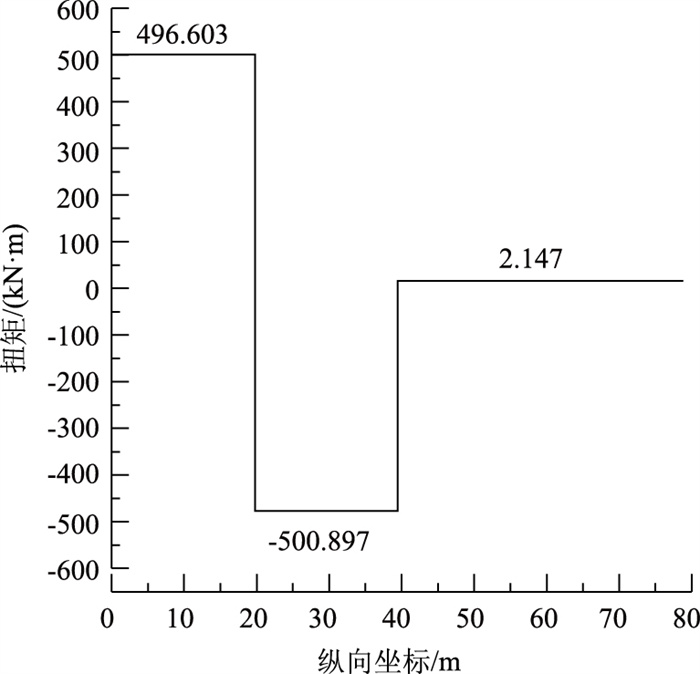
本研究参考有限元程序FRAME2[17],利用Fortran语言编写用于分析变截面连续箱梁桥约束扭转效应的程序YSNZ,用所编程序对文献[16]第78页算例所给的两跨连续箱梁桥的内力进行计算,将双力矩和扭矩的计算结果汇总整理为图 2和图 3。
|
| 图 2 双力矩曲线 Fig. 2 Curve of bi-moment |
| |
|
| 图 3 扭矩曲线 Fig. 3 Curve of torque |
| |
将图 2、图 3与文献[16]所给双力矩图、扭矩图对比可知本研究值与文献[16]第84页图 3-23所给值完全一致,验证了程序的正确性。
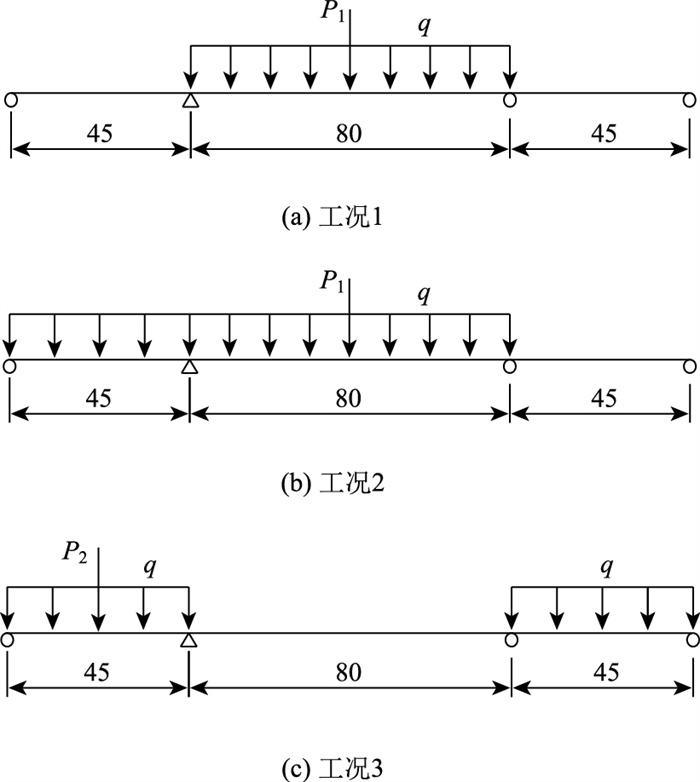
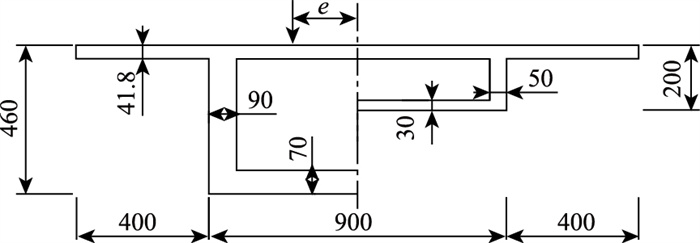
5 工程实例分析以京杭古运河大桥为算例,该桥是一座跨径布置为(45+80+45) m的变截面三跨连续箱梁桥。桥宽35 m,沿中央分隔带对称布置,桥中间设置宽度为1.0 m的中央分隔带,桥两侧设置宽度为0.5 m的外护栏,内侧设置宽度为1.0 m的内护栏。行车道为宽15.5 m的单向车道,根据规范[18]设置为4条车道。箱梁根部梁高4.6 m,跨中梁高2.0 m,顶板宽为17.0 m,底板宽为9.0 m,翼缘板悬臂长为4.0 m,其中主梁高度从距墩中心1.75 m处到跨中合龙段呈二次抛物线分布。工况1为在中跨布置偏心距为e的集中荷载P1和均布荷载q,P1作用在中跨跨中位置,此布载方式会使中跨跨中正弯矩达到最大。工况2为在中跨跨中布置偏心距为e的集中荷载P1,在一边跨和中跨布置偏心距为e的均布荷载q,此布载方式会使中支点处负弯矩达到最大。工况3为在左边跨跨中布置偏心距为e的集中荷载P2,在两边跨布置偏心距为e的均布荷载q,此布载方式会使边跨跨中正弯矩达到最大。计算简图及荷载布置见图 4,截面尺寸见图 5。弹性模量E=34 GPa,剪切模量G=14.45 GPa,车道荷载为公路I级。
|
| 图 4 立面及布载示意图(单位:m) Fig. 4 Schematic diagram of elevation and layout of loads (unit: m) |
| |
|
| 图 5 中支点和中跨跨中处横截面图(单位:cm) Fig. 5 Cross-section of middle support and middle of central span(unit: cm) |
| |
箱梁在偏载作用下发生空间效应时,截面上的正应力主要由弯曲正应力和翘曲正应力组成,根据文献[15]和经验系数可知,弯曲正应力在总的正应力中占比较大,故本研究的算例桥按照使该桥弯曲效应最显著的布载方式布载,即按照4车道布载,同时这也是与实际情况最相符的布载方式,计算得偏心距e=1.95 m。根据规范[18]的相关规定,桥面布置多车道荷载时需考虑横向车道布载系数(4车道为0.67),折减后集中荷载P1=964.8 kN,P2=938 kN,均布荷载q=28.14 kN/m。
用程序分析前,需先将箱梁桥划分为若干个箱梁单元,每个单元两端各对应一个节点,每个节点对应一个截面,取单元两端节点对应的两个截面几何特征值的平均数为该单元几何特征值,然后将节点、单元、约束及荷载等信息按一定规则编辑成输入文件。
输入文件中单元的几何信息由单元几何特征值体现,将单元组集成结构时认为将各等截面单元对应截面的扭心置于结构的轴线上,并以扭心位置为该截面对应的节点位置。由程序计算可得每个单元的内力及位移,然后将第n个单元i端值与第n-1个单元j端值相反数的平均值作为第n个单元i端值,将第n个单元j端值与第n+1个单元i端值相反数的平均值作为第n个单元j端值。计算结果的精确度由划分的单元数决定,对于同一模型,划分的单元越小,结果越精确。本研究在分析时将全桥划分为132个单元,由此可得节点与其对应的截面各133个,相同尺寸的截面为一种截面类型,共有32种截面类型。
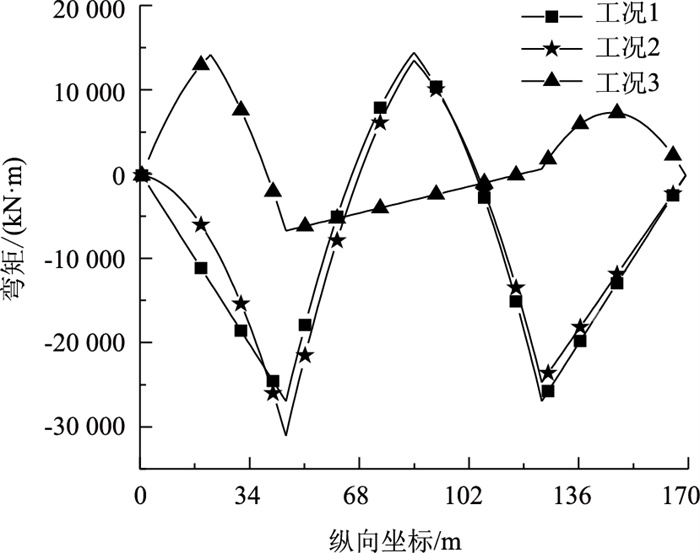
利用FRAME2程序可计算各截面的剪力和弯矩。图 6为3种工况下的弯矩分布图。
|
| 图 6 弯矩曲线 Fig. 6 Curves of bending moment |
| |
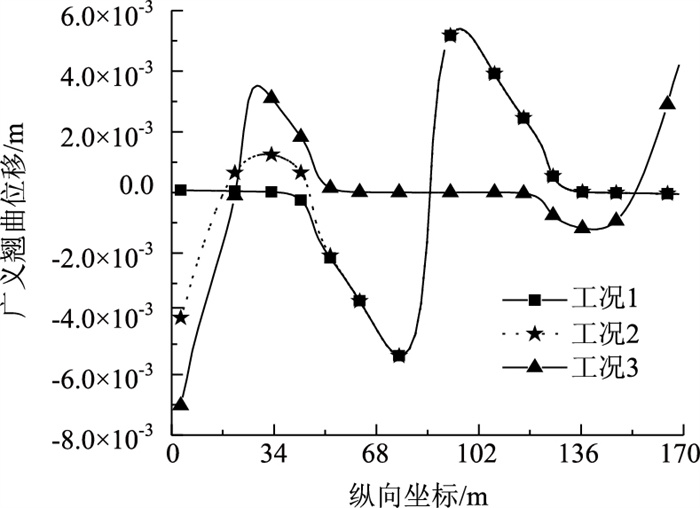
利用YSNZ程序可计算各截面扭转角、广义翘曲位移、总扭矩和翘曲双力矩。图 7为3种工况下的广义翘曲位移图。从图 7可以看出,广义翘曲位移主要分布在偏心活载作用的桥跨内;在工况1或工况2下,广义翘曲位移均在纵向坐标为75 m处达到峰值。
|
| 图 7 广义翘曲位移曲线 Fig. 7 Curves of generalized warping displacement |
| |
将广义翘曲位移代入式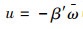
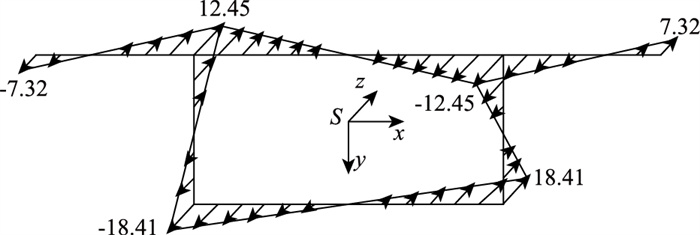
|
| 图 8 纵向坐标75 m处的截面翘曲位移图(单位:mm) Fig. 8 Section warping displacement at longitudinal coordinate of 75 m (unit: mm) |
| |
图 9为3种工况下的双力矩分布图。从图 9可以看出,翘曲双力矩具有从峰值点向两侧快速衰减的规律,在3种工况下翘曲双力矩均在中支点截面和集中荷载作用截面出现极值,这说明支座约束和集中荷载会对双力矩产生较大的影响。
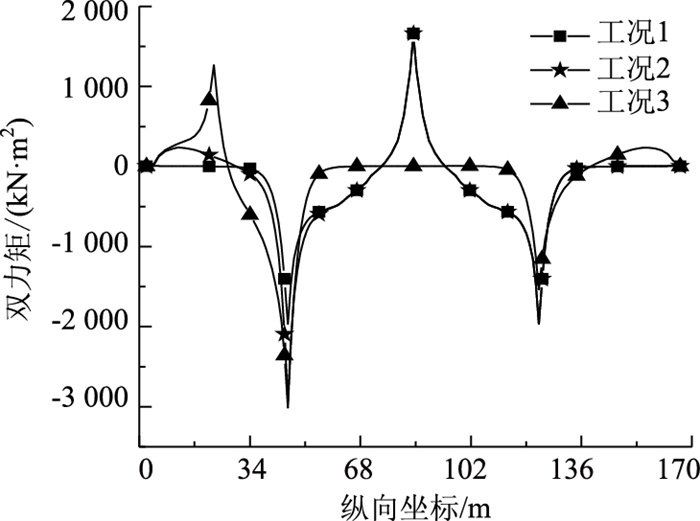
|
| 图 9 双力矩曲线 Fig. 9 Curves of bi-moment |
| |
利用式(23)和式(24)可分别计算截面上各点弯曲正应力和翘曲正应力。因篇幅所限,本研究仅给出工况1下的弯曲正应力图以及工况1和工况2下的翘曲正应力图。图 10为工况1下截面上计算点的弯曲正应力分布图。
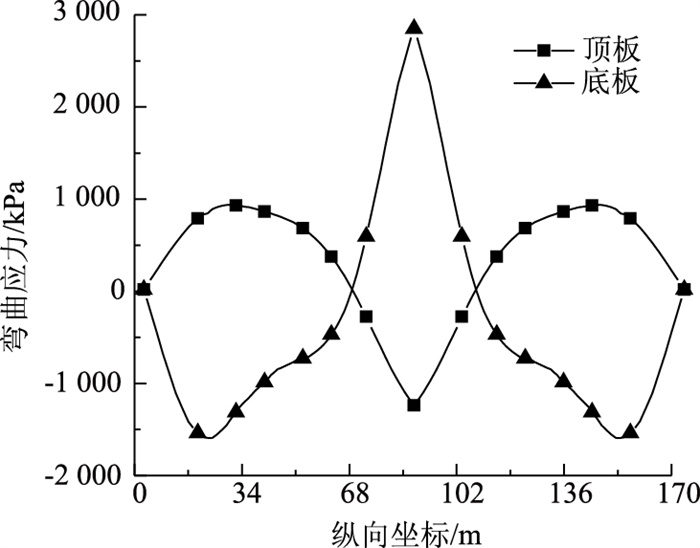
|
| 图 10 弯曲正应力曲线(工况1) Fig. 10 Curves of bending normal stress (case 1) |
| |
图 11为2种工况下截面上计算点的翘曲正应力分布图。从图 11可以看出,翘曲正应力除了具有上述翘曲双力矩的所有分布规律外,在不同工下,翘曲正应力的极值均出现在集中荷载作用截面,最大正值出现在底板与腹板的交点处,最大负值出现在顶板与腹板的交点处。
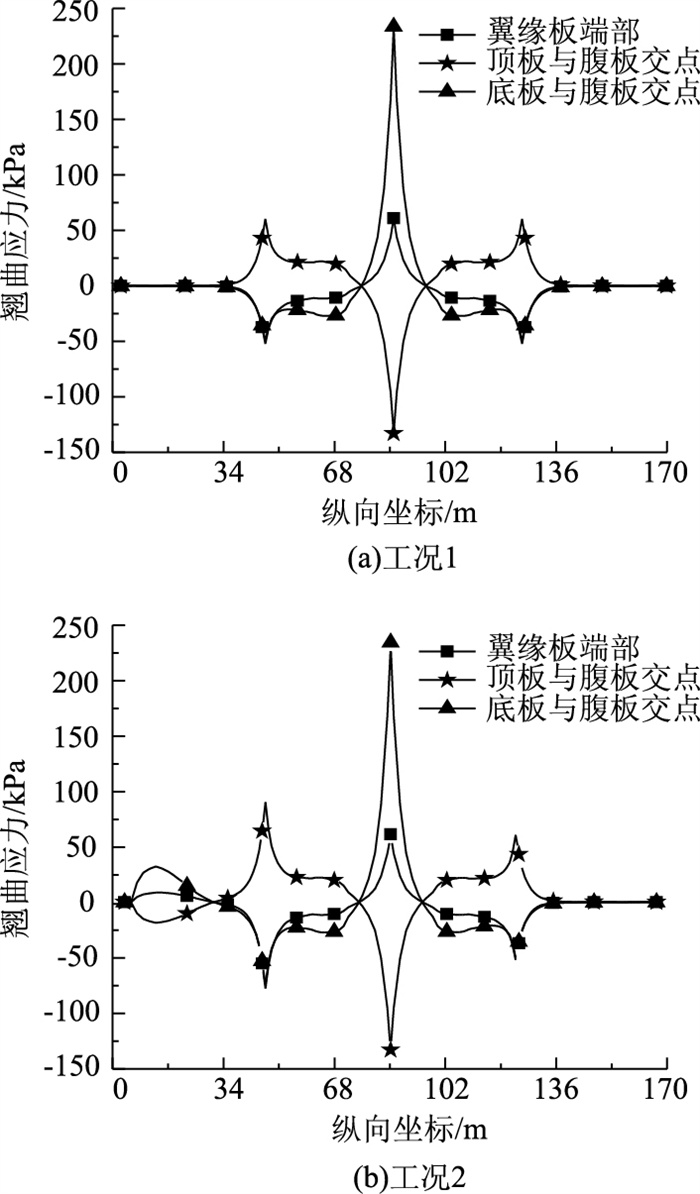
|
| 图 11 翘曲正应力曲线 Fig. 11 Curves of warping normal stress |
| |
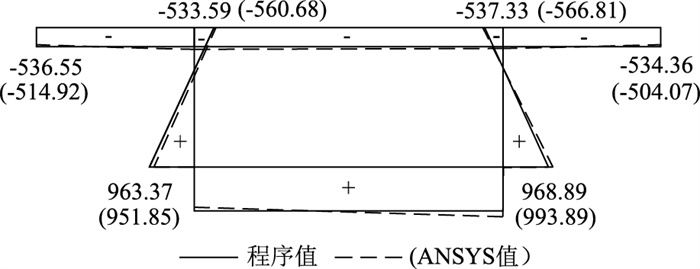
利用ANSYS有限元软件,对工况1下的京杭古运河大桥采用空间块体单元建立模型并进行分析,将ANSYS有限元软件与本研究程序的应力计算结果进行对比。图 12为根据计算结果绘制的纵向坐标为75 m处的截面正应力图。从图 12可以看出,本研究程序计算结果与ANSYS有限元软件计算结果相差不大,截面上同一点处两者的差值不超过该点程序计算结果的5.7%;此外从图 12中可以看出,程序计算的应力在箱梁截面上为直线分布,而ANSYS有限元软件计算出的应力为曲线分布。
|
| 图 12 纵向坐标75 m处的截面正应力图(单位: kPa) Fig. 12 Normal stresses of section at longitudinal coordinate of 75 m (unit: kPa) |
| |
一般在分析偏载作用对箱梁应力的放大效应时,先选取若干控制截面,然后以控制截面作为参考进行活载内力增大系数的取值。表 1列出了4个控制截面(边跨跨中、中支点、中跨1/4和中跨跨中)分别在3种工况下的应力放大系数(横截面上的最大值)。从表 1可以看出,应力放大系数分布在1.0~1.407之间,与文献13, 16]的相关计算结果接近,这也再次验证了本研究计算方法的可靠性。
| 截面位置 | 应力放大系数 | ||
| 工况1 | 工况2 | 工况3 | |
| 边跨跨中 | 1.000 | 1.012 | 1.056 |
| 中支点 | 1.104 | 1.135 | 1.407 |
| 中跨1/4 | 1.224 | 1.132 | 1.000 |
| 中跨跨中 | 1.126 | 1.134 | 1.000 |
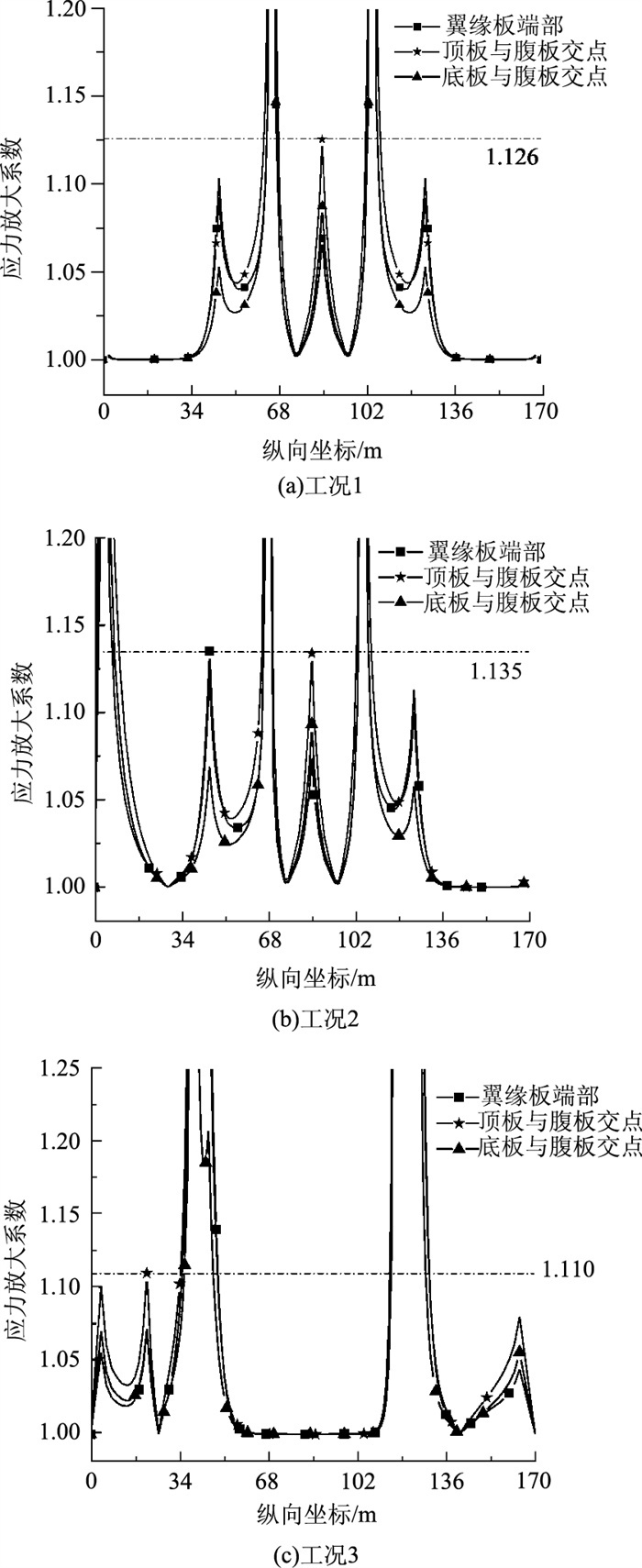
为清楚地看出应力放大系数的分布规律,图 13示出了3种工况下截面上计算点的应力放大系数分布图。从图 13可以看出,变截面三跨连续箱梁桥在偏载作用下发生约束扭转时,应力放大系数的极值点出现在翘曲正应力的极值点所在截面,最大值出现在弯曲正应力极值点所在截面。
|
| 图 13 应力放大系数分布曲线(主跨80m) Fig. 13 Distribution curves of stress amplification factors (80 m mainspan) |
| |
从图 13(a)可以看出,在工况1下,应力放大系数主要分布在1.0~1.126之间,在中跨跨中截面的顶板与腹板交点为1.126。但也可看出,在纵向坐标为63~67 m和103~107 m的区域内,应力放大系数大于1.126,在这些区域内的截面上,弯曲正应力的绝对值均小于中跨跨中截面底板与腹板交点处弯曲正应力值的8.7%。从图 13(b)可以看出,在工况2下,应力放大系数主要分布在1.0~1.135之间,在中支点截面的翼缘板端部为1.135,在纵向坐标为2~8, 67~69和103~108 m的区域内,应力放大系数大于1.135,在这些区域内的截面上,弯曲正应力的绝对值均小于中跨跨中截面底板与腹板交点处弯曲正应力值的9.2%。从图 13(c)可以看出,在工况3下,应力放大系数主要分布在1.0~1.110之间,在边跨跨中截面的顶板与腹板的交点为1.110,在纵向坐标为34~49 m和114~131 m的区域内,应力放大系数大于1.110,在这些区域内的截面上,弯曲正应力值的绝对值均小于左边跨跨中截面底板与腹板交点处弯曲正应力值的11.5%。
对于弯曲正应力值较小的截面上的计算点,在考虑了对应的应力放大系数后其应力值仍不大,对桥梁的结构安全性无影响。对本研究算例桥,舍去弯曲正应力值小于该工况下弯曲正应力最大值的11.5%的区域即可使应力放大系数的取值合理。相反,若是在应力放大系数取值时考虑弯曲正应力值较小的点,就会造成应力放大系数取值偏大的问题。
分析表 1和图 13可以看出,由表 1所得到的应力放大系数最大值远大于由图 13所到的结果,这是由于在表 1的分析中未对弯曲应力值较小的区域进行分析并做合理取舍,而这也解释了一些文献中活载内力增大系数取值偏大的原因。显然,根据图 13所得到的结论更为合理,对于京杭古运河大桥,应力放大系数分布在1.0~1.135之间。
本研究再对跨径布置为(75+120+75) m的预应力混凝土连续箱梁桥进行分析,因篇幅所限,此处不再详细给出工程概况及截面尺寸。工况1为中跨满布均布偏心荷载q,中跨跨中布置偏心集中荷载P。工况2为第1个边跨和中跨满布均布荷载q,中跨跨中布置集中荷载P。其中q=42.997 5 kN/m,P=842.4 kN。
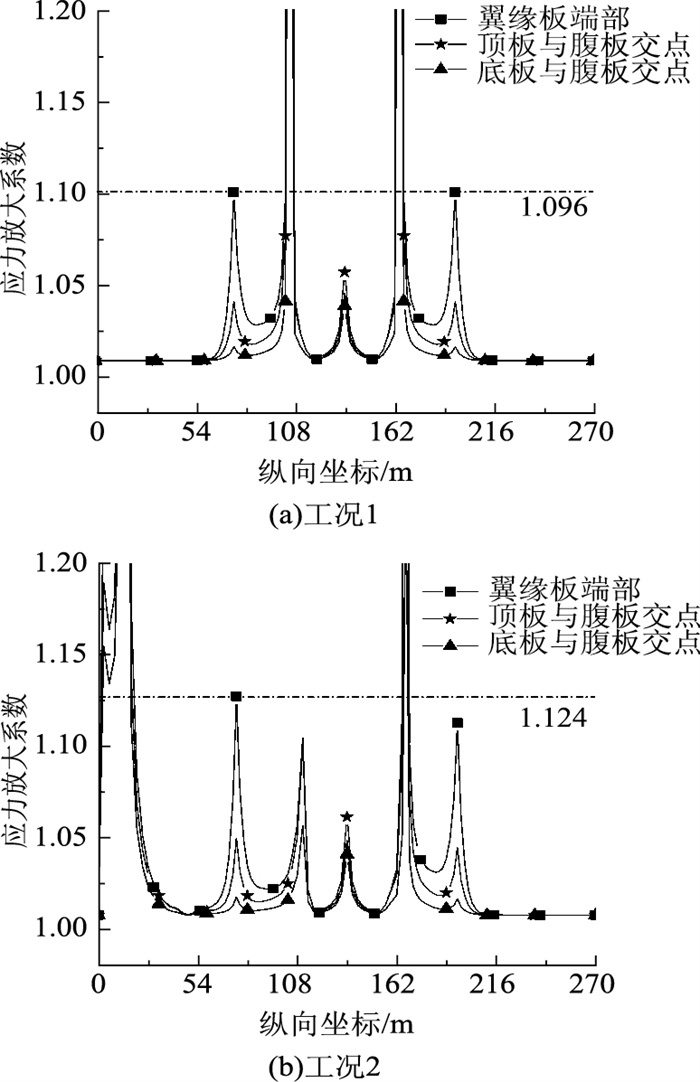
分析该三跨连续箱梁桥的约束扭转效应,其翘曲双力矩、广义翘曲位移、截面翘曲变形、翘曲正应力和应力放大系数的分布规律与主跨为80 m的变截面三跨连续箱梁桥相同。图 14为该桥在2种工况下的应力放大系数分布图。从图 14可以看出,应力放大系数在工况1下分布在1.0~1.096,在工况2下分布在1.0~1.124。
|
| 图 14 应力放大系数分布曲线(主跨120 m) Fig. 14 Distribution curves of stress amplification factors (120 m mainspan) |
| |
6 结论
(1) 翘曲双力矩和翘曲应力都具有从峰值点向两侧快速衰减的规律,都会在支座约束和集中荷载作用位置出现极值。翘曲正应力的峰值出现在集中荷载作用截面。
(2) 变截面三跨连续箱梁桥在偏载作用下发生约束扭转时,应力放大系数的极值点出现在翘曲应力的极值点所在截面,峰值点出现在弯曲应力极值点所在的截面。
(3) 在利用内力增大系数法分析约束扭转效应对弯曲正应力的放大效应时,为避免内力增大系数取值偏大,不宜考虑弯曲正应力值较小的区域,建议选取弯曲正应力极值点所在截面为控制截面。
(4) 对于本研究计算的2座变截面三跨连续箱梁桥,不同工况下的应力放大系数均小于1.135。
(5) 变截面三跨连续箱梁桥在偏心荷载作用下发生约束扭转时,翘曲变形主要分布在偏心活载作用的桥跨内。
| [1] |
MOON J, LIM N H, LEE H E. Moment Gradient Correction Factor and Inelastic Flexural-torsional Buckling of I-girder with Corrugated Steel Webs[J]. Thin-Walled Structures, 2013, 62: 18-27. |
| [2] |
SHEN K J, WAN S, MO Y L, et al. A Softened Membrane Model for Prestressed Concrete Composite Box Girders with Corrugated Steel Webs under Pure Torsion[J]. Advances in Structural Engineering, 2019, 22(2): 384-401. |
| [3] |
施成, 蔺鹏臻. 铁路双线箱梁的约束扭转效应研究[J]. 铁道科学与工程学报, 2018, 15(1): 110-117. SHI Cheng, LIN Peng-zhen. Restrained Torsion Effect Research of Double Track Railway Box Girder[J]. Journal of Railway Science and Engineering, 2018, 15(1): 110-117. |
| [4] |
PROKIĆ A, MANDIĆ R, VOJNIĆ-PURČAR M. Influence of Bimoment on the Torsional and Flexural-torsional Elastic Stability of Thin-walled Beams[J]. Thin-Walled Structures, 2015, 89: 25-30. |
| [5] |
ZHU L, WANG J J, LI M J, et al. Finite Beam Element with 22 DOF for Curved Composite Box Girders Considering Torsion, Distortion, and Biaxial Slip[J]. Archive of Civil and Mechanical Engineering, 2020, 20(4): 1928-1939. |
| [6] |
文颖, 陈泽林. 基于协调翘曲场的开闭口混合薄壁截面杆件约束扭转一维有限元分析[J]. 工程力学, 2020, 37(9): 38-49. WEN Ying, CHEN Ze-lin. One-dimensional Finite Element Analysis of Warping Torsion for Thin-walled Members with Open-closed Cross Sections Based on Compatible Warping Field[J]. Engineering Mechanics, 2020, 37(9): 38-49. |
| [7] |
龚耀清, 罗亚南. 单箱双室不等壁厚箱梁受弯与约束受扭的有限节线法分析[J]. 长安大学学报: 自然科学版, 2018, 38(1): 59-66. GONG Yao-qing, LUO Ya-nan. Analysis on Single-box Double-cells Unequal-wall-thickness Girder due to Bending and Restrained Torsion by Finite Nodal-line Method[J]. Journal of Chang'an University: Natural Science Edition, 2018, 38(1): 59-66. |
| [8] |
LI L F, ZHOU C, WANG L H. Distortion Analysis of Non-prismatic Composite Box Girders with Corrugated Steel Webs[J]. Journal of Constructional Steel Research, 2018, 147: 74-86. |
| [9] |
ARICI M, GRANATA M F, OLIVA M. Influence of Secondary Torsion on Curved Steel Girder Bridges with Box and I-girder Cross-sections[J]. KSCE Journal of Civil Engineering, 2015, 19(7): 2157-2171. |
| [10] |
邓文琴, 毛泽亮, 刘朵, 等. 单箱三室波形钢腹板悬臂梁扭转与畸变分析及试验研究[J]. 建筑结构学报, 2020, 41(2): 173-181. DENG Wen-qin, MAO Ze-liang, LIU Duo, et al. Analysis and Experimental Study on Torsion and Distortion of Single Box Three-cell Cantilever Girder with Corrugated Steel Webs[J]. Journal of Building Structures, 2020, 41(2): 173-181. |
| [11] |
唐杨, 唐卫国, 田俊国. 大跨度变截面波形钢腹板组合箱梁抗扭性能研究[J]. 结构工程师, 2020, 36(2): 51-59. TANG Yang, TANG Wei-guo, TIAN Jun-guo. Research on Torsion Resistance of Long Span Composite Box Girder with Variable Cross Section and Corrugated Steel Webs[J]. Structural Engineers, 2020, 36(2): 51-59. |
| [12] |
马俊军, 蔺鹏臻. 时速250 km/h铁路双线箱梁的扭转效应研究[J]. 铁道科学与工程学报, 2018, 15(10): 2463-2470. MA Jun-jun, LIN Peng-zhen. Restrained Torsion Effect of Double Track Railway Box Girders with Speed of 250 km/h[J]. Journal of Railway Science and Engineering, 2018, 15(10): 2463-2470. |
| [13] |
陈水生, 彭武, 桂水荣, 等. 单箱双室波形钢腹板pc组合箱梁桥偏载系数研究[J]. 公路工程, 2017, 42(5): 42-46. CHEN Shui-sheng, PENG Wu, GUI Shui-rong, et al. Research on Partial Load Coefficient of pc Multi-cell Single-box Composite Box Girder with Corrugated Steel Webs[J]. Highway Engineering, 2017, 42(5): 42-46. |
| [14] |
董爱平, 郭增伟, 李龙景. 混凝土宽箱梁汽车偏载效应分析[J]. 土木工程与管理学报, 2018, 35(6): 117-122, 156. DONG Ai-ping, GUO Zeng-wei, LI Long-jing. Study on Eccentric Load Effect of Wide-flange Concrete Box-girder under Offset Loaded Vehicles[J]. Journal of Civil Engineering and Management, 2018, 35(6): 117-122, 156. |
| [15] |
钟新谷, 赵超, 舒小娟, 等. 预应力混凝土箱梁桥偏载系数的数值分析与试验[J]. 湖南科技大学学报: 自然科学版, 2018, 33(4): 40-48. ZHONG Xin-gu, ZHAO Chao, SHU Xiao-juan, et al. Numerical Analysis and Experimental Study on Eccentric Load Coefficient of Prestressed Concrete Box Girder[J]. Journal of Hunan University of Science & Technology: Natural Science Edition, 2018, 33(4): 40-48. |
| [16] |
郭金琼, 房贞政, 郑振. 箱形梁设计理论[M]. 2版. 北京: 人民交通出版社, 2008: 78-84. GUO Jin-qiong, FANG Zhen-zheng, ZHENG Zhen. Design Theory of Box Girder[M]. 2nd ed. Beijing: China Communications Press, 2008: 78-84. |
| [17] |
吴鸿庆, 任侠. 结构有限元分析[M]. 北京: 中国铁道出版社, 2000. WU Hong-qing, REN Xia. Structural Finite Element Analysis[M]. Beijing: China Railway Publishing House, 2000. |
| [18] |
JTG D60—2015, 公路桥涵设计通用规范[S]. JTG D60—2015, General Specifications for Design of Highway Bridges and Culverts[S]. |
 2021, Vol. 38
2021, Vol. 38
