扩展功能
文章信息
- 吴桐, 唐亮, 周志祥
- WU Tong, TANG Liang, ZHOU Zhi-xiang
- 基于曲率模态面积差方比的桥梁结构损伤识别
- Identifying Damage of Bridge Structure Based on Curvature Mode Area Difference Square Ratio
- 公路交通科技, 2021, 38(11): 59-67
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(11): 59-67
- 10.3969/j.issn.1002-0268.2021.11.008
-
文章历史
- 收稿日期: 2020-12-17
2. 深圳大学 土木与交通工程学院, 广东 深圳 518060
2. School of Civil and Transportation Engineering, Shenzhen University, Shenzhen Guangdong 518060, China
桥梁在运营中极易受到来自外部环境和桥梁自身结构和材料老化等不利因素带来的影响,使其无法达到设计预期寿命。如果没有及时检测到这些结构中的损伤,则可能导致损伤加剧,甚至发生灾难性的后果。因此,结构健康监测(Structural Health Monitoring, SHM)对于保证桥梁结构在其使用寿命中的安全至关重要[1-2]。
目前对桥梁的损伤识别方法大致可以分为3类:(1) 基于动力参数的损伤识别方法: 如振型、频率等[3-4];(2) 基于静力参数的损伤识别方法,如挠度、应变等[5-8];(3) 基于动-静力参数的综合方法。在基于动力参数的方法中,振动系统的特性可以用固有频率、振型、阻尼等参数来描述。结构发生损伤将会引起自振特性改变,因此可以通过模态分析所得到的模态参数的改变来判断结构是否损伤并对损伤定位。
在利用曲率模态进行损伤识别方面,国内外学者已经进行了大量研究。Pandey等[9]人提出用曲率模态进行损伤识别的方法,并采用中心差分近似法,由位移模态计算曲率模态。Wahab等[10]人采用曲率模态法对一个实桥进行了损伤识别,研究了模态曲率变化在预应力混凝土桥梁损伤检测中的应用。郑明刚等[11]人将曲率模态用于桥梁状态监测,结果表明,曲率模态对结构损伤较为敏感,能够反映桥梁的局部状态变化,可以用来检测损伤位置及损伤程度,且高阶的曲率模态对结构损伤的敏感性要优于低阶的曲率模态。Chen等[11]人研究了一种适用于桥梁和连续梁的基于曲率模态的损伤识别方法,通过计算二维框架,比较了不同模态、不同损伤程度和不同测点数目对损伤识别的影响。胡业平等[13]人在分析绝对曲率差用于损伤定位的理论依据基础上,以悬臂梁有限元模型为例,结合工程实际,研究了绝对曲率差曲线的特点及其损伤定位效果。韩西等[14]人将曲率模态的损伤识别方法推广到二维结构,提出了基于高斯曲率模态的损伤识别方法,综合考虑二维结构的加速度振型曲面在纵向和横向上的弯曲程度,通过计算结构损伤前后加速度振型的高斯曲率差来判断结构损伤的位置。刘义伦等[15]人针对在利用曲率模态识别桥梁损伤过程中遇到的一些问题,提出了曲率振型规范化处理方法,并对曲率零点处的变化量计算作了特殊处理,以避免此处引起的损伤识别干扰。贺文宇等[16]人提出了一种基于间接法识别的桥梁损伤定位指标,利用希尔伯特变换从移动车辆响应中提取出高分辨率的损伤桥梁振型,采用区域振型曲率替代传统的振型曲率,综合损伤前后的区域振型曲率定义损伤定位指标。Rong等[17]人提出了一种基于曲率振型和频率扰动的结构损伤识别方法,根据结构在未损伤和损伤状态下曲率模态形状的差异,建立了损伤方程。
上述研究均表明动态参数中曲率模态包含有关刚度降低和相应损伤的信息[18-19]。以往的损伤识别方法中计算曲率模态通常有两种方法: (1)对离散点位移模态进行2阶差分,近似求得曲率模态;(2) 直接测量结构的应变模态,再根据应变与曲率的关系求曲率模态。
本研究提出一种用曲率模态面积差方比来进行损伤识别的方法,将损伤前后的曲率模态曲线所包围的面积作为损伤识别参数AD。
1 结构损伤定位的模态曲率面积差方法模态曲率法的实现流程[9]是:首先分析、测量得到结构的位移模态,再通过对位移模态求2阶差分获得曲率模态参数。由结构力学可知,结构损伤的本质是局部刚度减小,导致位移模态发生变化,对应的曲率会产生突变,这就是用曲率模态参数进行损伤定位最基本原理。基于模态曲率参数可以推导出多种损伤定位参数,模态曲率面积差方比就是本研究所采用的参数。
1.1 模态曲率的理论推导以简支梁为例,其自由振动微分方程为[20]:
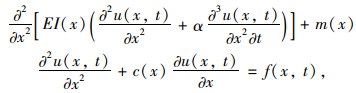
|
(1) |
式中,u (x, t)为t时刻x处的竖向振动位移; EI为截面抗弯刚度; α为刚度比例系数; m(x)为单位长度质量; c(x)为x处的阻尼,若c (x)≠0,假定该梁采用比例阻尼系统。
由模态分析理论可知,式(1)的解可以表示为各阶模态的叠加形式:
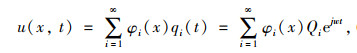
|
(2) |
式中,φi(x)为位移模态; qi (t)为模态坐标; Qi为复数。无限自由度体系位移模态振型具有正交性:

|
(3) |
式中,Ωi和mi分别为第i阶模态频率和模态质量。
根据材料力学中弹性梁弯曲变形曲线曲率与位移的关系,对于任意截面x处,梁弯曲振动曲线曲率的函数为:
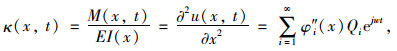
|
(4) |
式中,φi″(x)为梁的第i阶曲率模态,与位移模态一一对应; κ(x)为截面x处的曲率。
由式(4)可知,当结构中出现损伤时,会导致局部刚度降低,结构的曲率模态随结构刚度变化而单调变化,并且曲率模态与位移模态一一对应,所以曲率模态是结构位置坐标的单调函数,因此曲率模态可以作为结构损伤识别参数。
1.2 曲率模态面积差方比方法概述当桥梁结构中出现损伤时,其动态特性会随之变化,结构位移模态会随之改变,其曲率也会发生突变,结构的动力试验或者长期健康监测系统可以捕捉到这些信息。通过研究位移模态及其1,2阶导数之间的关系,引入了曲率模态面积差方比参数来进行损伤识别。
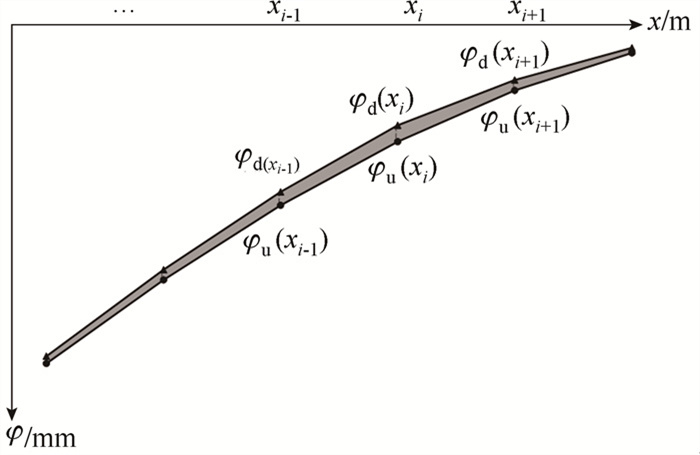
假设如图 1所示长度为L的简支梁,将其纵向等分为n个长度为a的单元,单元编号从左至右依次为1#~n#。假设第i个单元发生损伤,通过计算可以得到各节点损伤前后的位移模态、转角模态和曲率模态,分别如图 2~4所示。可以看出,损伤前后的各参数曲线之间包围着微小面积,该面积也被分为n个单元,分别为A1~An。则第i个单元的曲率面积差方比参数定义为第i个单元面积的平方与所有单元面积平方和的比值:

|
| 图 1 简支梁基本图示 Fig. 1 Basic diagram of a simply supported beam |
| |
|
| 图 2 损伤前后位移模态曲线 Fig. 2 Deformation modal curves before and after damage |
| |
|
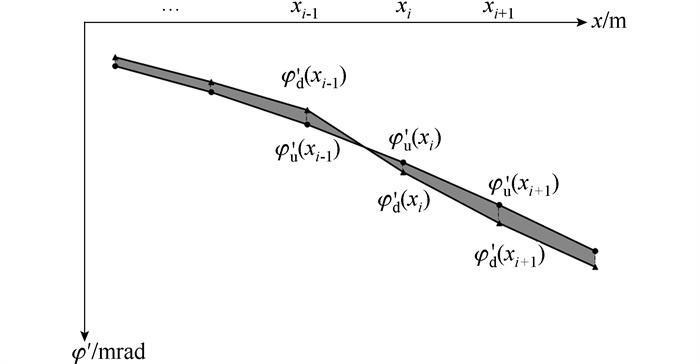
| 图 3 损伤前后转角模态曲线 Fig. 3 Rotation angle modal curves before and after damage |
| |
|
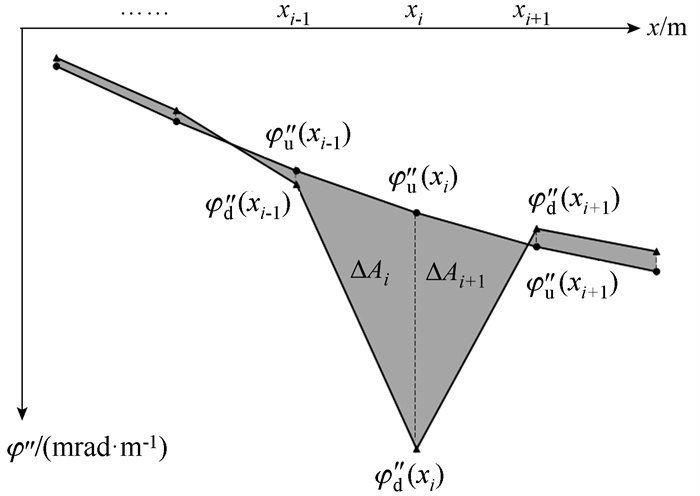
| 图 4 损伤前后曲率模态曲线 Fig. 4 Curvature modal curves before and after damage |
| |
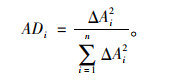
|
(5) |
式中,ADi为第i个单元的面积差方比参数;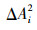
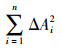
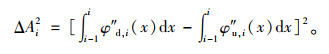
|
(6) |
因为曲率模态是由转角模态求1阶导数而得,所以有:
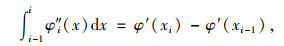
|
(7) |
将上式代入可得:
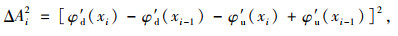
|
(8) |
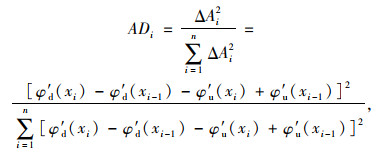
|
(9) |
式中,φd′(xi)为损伤工况下xi位置处的转角模态;φu′(xi)为未损伤工况下xi位置处的转角模态; φd′(xi)为损伤工况下xi位置处的曲率模态; φu′(xi)表示未损伤工况下xi位置处的曲率模态。
从式(9)可以看出,ADi可以直接由转角模态值计算而得,设该梁的第r阶位移模态为:φr(x)= {φr (x1), φr (x2), …, φr (xn+1)}T,因此这n+1个节点的转角模态值和曲率模态值可以根据位移模态的中心差分公式求得:
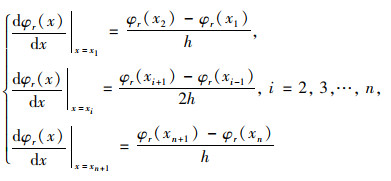
|
(10) |
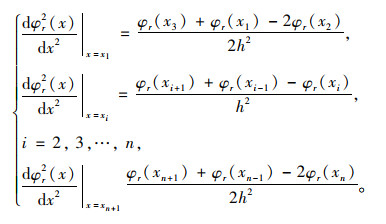
|
(11) |
以往利用曲率模态差的损伤识别方法中,为了计算曲率模态,通常有两种方法:(1)对离散点位移模态进行2阶差分,近似求得曲率模态;(2)直接测量结构的应变模态,再根据应变与曲率的关系求曲率模态。与以上两种方法不同的是,本研究得到离散点的位移模态之后,进行一次差分求得转角模态,再根据式(9)直接计算出损伤前后的曲率模态面积差,来识别结构损伤。这样做的优势在于只需要对位移模态进行1阶差分,相比由2阶差分求模态曲率,可减少误差的传递和放大。
2 简支梁适用性试验研究 2.1 简支梁模型桥试验为研究所提出曲率模态面积差方比法的适用性,我们在结构形式最简单的简支梁模型上进行了探索性试验。试验所用简支梁模型跨径为5.0 m,横向由5片Q235空心矩形钢箱梁焊接而成,从左至右依次编号为1#~5#梁。每片梁高20 mm,宽40 mm,壁厚1 mm。梁的表面两边缘布置两条槽型钢条,并将钢条与梁固定起来。在梁下等间距布置7个低频压电式竖向加速度传感器,传感器从左至右依次编号为1#~7#测点,其型号为1A202E,频响范围0.2~1 500 Hz,灵敏度为100 mV/m·s-2,采样频率设置为500 Hz,配合动态采集仪进行加速度信号采集。模型传感器布置如图 5所示,图 6为试验现场照片。

|
| 图 5 模型简支梁桥传感器布置图(单位:mm) Fig. 5 Layout of sensors on simply supported beam (unit: mm) |
| |

|
| 图 6 模型简支梁桥照片 Fig. 6 Photo of simply supported beam model |
| |
通过力锤敲击模型桥跨中,利用强迫激励法测定模型桥的振动响应,再对结构响应进行模态分析识别结构的自振频率、振型和阻尼特性。将采集未损伤工况下模型桥的振动响应作为损伤识别基准数据。人工切割简支梁跨径5/16位置1#~3#梁底板与腹板,其中底板横向贯通,腹板切至高度一半,以模拟结构损伤,采集结构的振动响应,作为结构损伤后的数据。
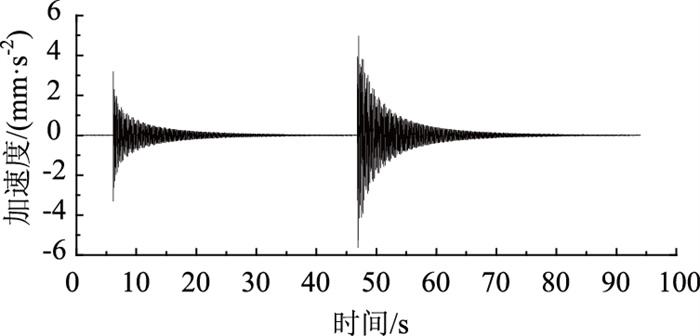
2.2 简支梁模型损伤定位通过对结构响应数据进行模态分析,得到了各工况的模态特征,图 7为3#测点实测加速度时程曲线,图 8为3#测点的频谱曲线。图 9为损伤前后简支梁各阶位移模态。
|
| 图 7 损伤后3#测点加速度时程曲线 Fig. 7 Acceleration time history curves of measuring point 3 after damage |
| |
|
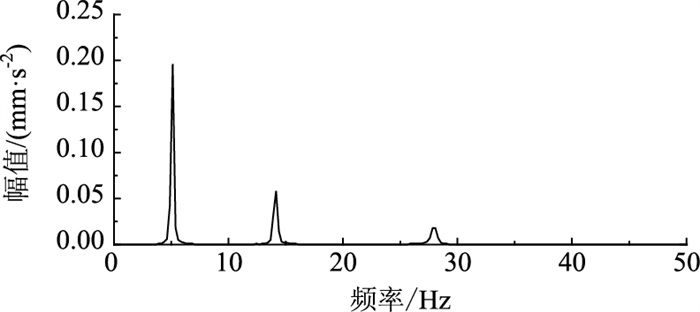
| 图 8 损伤后3#测点频谱 Fig. 8 Spectrums of measuring point 3 after damage |
| |
|
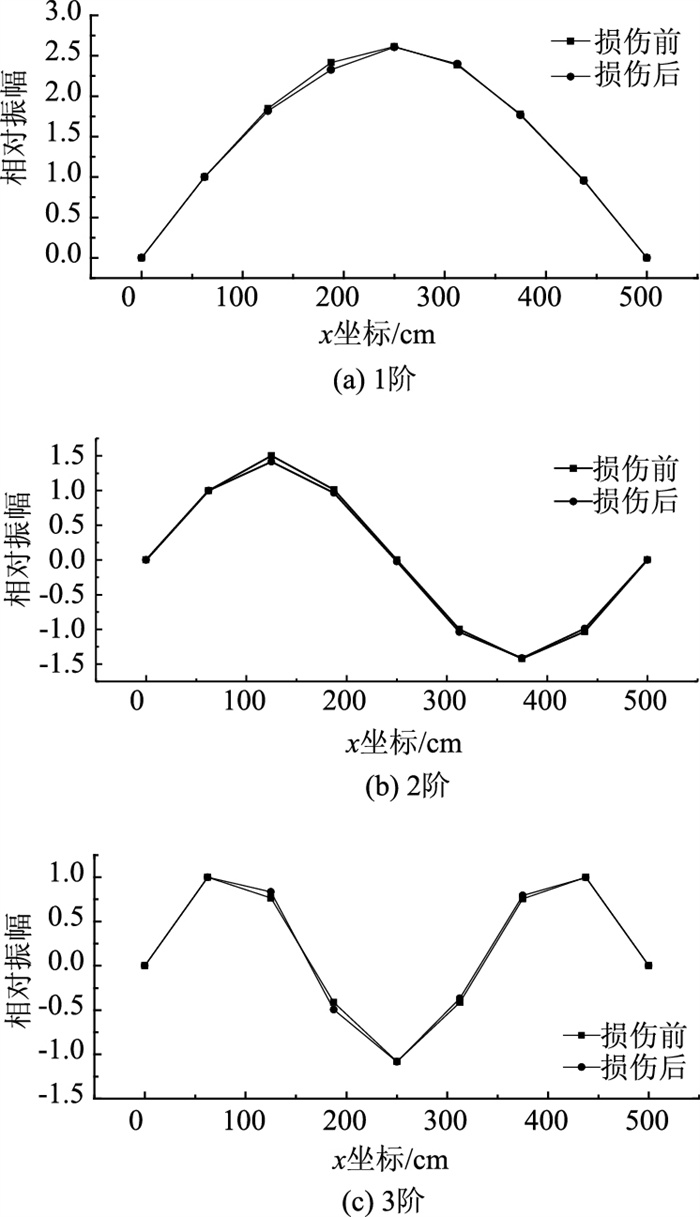
| 图 9 损伤前后位移模态 Fig. 9 Displacement modes before and after damage |
| |
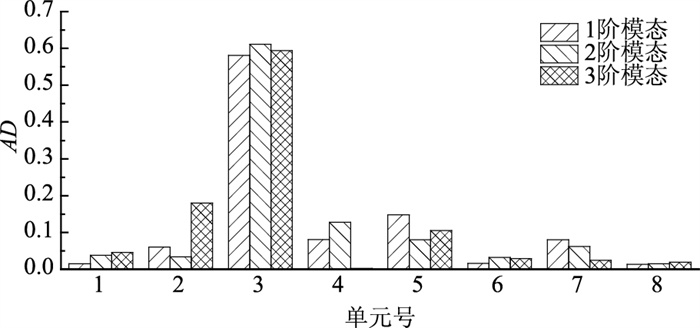
根据式(10)求得各测点的转角模态值后,代入式(9)可直接求得1~8#单元的ADi值,将各单元AD值绘制成柱状图如图 10所示。由于损伤位于5L/16处,即3#单元损伤,从图 10中可以看出,3#单元的ADi值达0.6左右,明显大于其他单元,表明ADi值准确定位了结构损伤位置。
|
| 图 10 简支梁各单元AD值 Fig. 10 AD values of each element of simply supported beam |
| |
3 复杂桥型应用试验 3.1 自锚式悬索桥模型试验概况
桃花峪黄河大桥是河南省境内连接郑州市荥阳市和焦作市武陟县的过河通道,为目前世界上跨度最大的自锚式悬索桥。将所提出曲率模态面积差方比方法用于桃花峪黄河公路悬索桥1/30缩尺模型桥的损伤识别。模型桥跨径为(5.333 5+13.533+5.333 5) m=24.200 m,桥面宽为1.2 m。两个边跨分别设置10对吊索,中跨设置29对吊索,各吊索之间的距离为0.45 m,主塔两侧吊索之间为0.933 m,边吊索与梁端距离为0.817 m。北索塔总高为3.87 m,南索塔总高为3.96 m。模型加劲梁每450 mm设置1道厚2 mm的横隔板,横隔板与钢箱梁焊接连接。各主要部件的材料为:加劲梁和横隔板采用Q345D钢材,主缆选用16根直径为3 mm的钢丝,截面面积为117.78 mm2,吊索选用1根直径为4 mm细钢丝。主塔采用Q345D钢材,横系梁选用4 mm厚钢材,塔柱选用3 mm厚钢材。主塔底部通过5 mm厚加劲板与锚固于地面的5 mm底钢板连接。加劲板分别与主塔及底钢板焊接连接。底钢板通过4颗Φ50螺栓锚固于地面上。
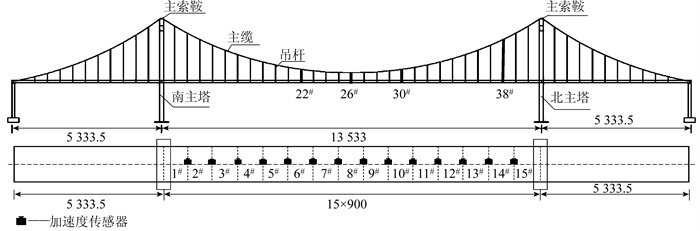
3.2 损伤工况及数据采集为了采集主跨的模态,在模型桥主跨桥面沿桥梁纵向等间距布置了14个竖向压电式加速度传感器,从南主塔往北主塔方向依次编号为1#~14#。传感器采用压电式加速度传感器1A202E,频响范围为0.2~1 500 Hz,灵敏度为100 mV/ (m·s-2),配合坚固型数据采集分析系统进行数据采集。加速度传感器将模型桥主跨沿梁长度方向等分为15个单元,传感器布置及单元编号如图 11所示。吊杆为悬索桥主要传力构件,将主梁所受荷载传递到主缆,若吊杆发生损伤,会造成结构局部刚度降低。试验时,通过释放单根或多根吊杆拉力的方式来模拟损伤,释放拉力后即认为该吊杆为损伤吊杆。各工况的具体信息如表 1所示。
|
| 图 11 模型桥桥型及传感器布置(单位:mm) Fig. 11 Model bridge type and layout of sensors (unit: mm) |
| |
| 工况编号 | 损伤吊杆号 | 损伤单元号 |
| 1 | 无 | 无 |
| 2 | 22# | 6# |
| 3 | 22#, 30# | 6#, 10# |
| 4 | 22#, 26#, 30# | 6#, 8#, 10# |
| 5 | 22#, 26#, 30#, 38# | 6#, 8#, 10#, 14# |
通过人工在模型索桥主跨跨中单次跳跃,利用强迫激励法测定模型桥的振动响应,再对结构响应进行模态分析识别结构的自振频率、振型和阻尼特性。采样频率fs为200 Hz,单次分析采用5次强迫激励后的自由衰减信号,单工况采集20组数据进行分析。
首先,采集未损伤工况下模型桥的振动响应作为损伤识别的对比基准数据。然后,将编号相同的一对吊杆拉力完全释放,即该对吊杆不承受荷载时采集结构的振动响应,作为结构损伤后的数据。由于吊杆索力释放后结构状态发生变化,若再对该吊杆施加索力,结构状态相比于未释放前也发生了改变,因此,不对已释放索力的吊杆做任何处理,即工况2~5损伤吊杆数量依次增加,分别为1~4对。
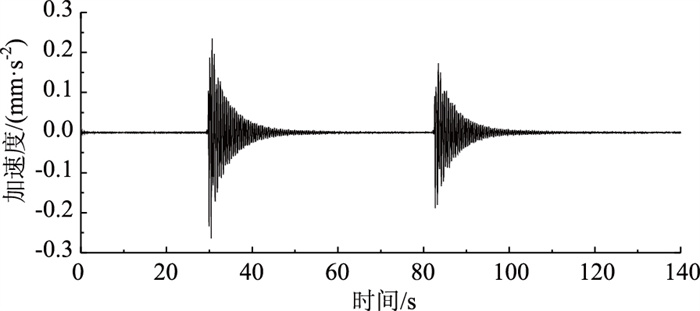
3.3 悬索模型桥损伤识别 3.3.1 模态识别结果通过对结构响应数据进行模态分析,得到了各工况的模态特征,取第1组测试数据作为示例,图 12为1#测点单组实测加速度时程曲线,图 13为1#测点单组频谱曲线,表 2为工况1~5单组前4阶模态频率和阻尼比。从表 2可以看出,当模型桥发生损伤后,其前2阶频率较损伤前几乎不变,第3阶和第4阶频率较损伤前有所降低,且损伤吊杆数量越多,即结构刚度降低程度越高,频率越低,表明结构刚度损伤会造成自振频率降低,且对高阶频率的影响大于对低阶频率的影响,而刚度损伤对结构阻尼比几乎没有影响。
|
| 图 12 1#测点单组加速度时程曲线 Fig. 12 Single group of acceleration time history curves of measuring point 1 |
| |
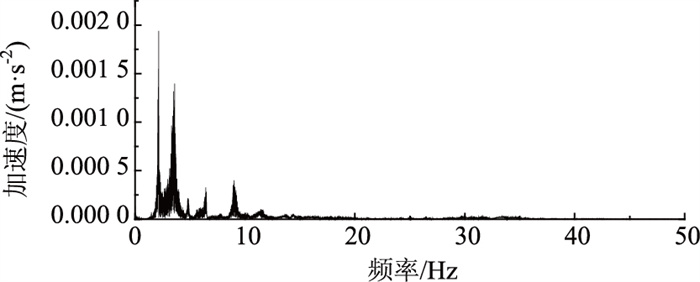
|
| 图 13 1#测点单组频谱曲线 Fig. 13 Single group of spectra curves of measuring point 1 |
| |
| 模态号 | 1 | 2 | 3 | 4 | |||||||
| 工况编号 | 频率/Hz | 阻尼比/% | 频率/Hz | 阻尼比/% | 频率/Hz | 阻尼比/% | 频率/Hz | 阻尼比/% | |||
| 1 | 2.148 | 2.395 | 3.564 | 4.419 | 4.834 | 1.780 | 6.493 | 2.130 | |||
| 2 | 2.148 | 2.300 | 3.516 | 4.590 | 4.834 | 1.740 | 6.445 | 1.211 | |||
| 3 | 2.148 | 2.411 | 3.467 | 4.600 | 4.785 | 1.850 | 6.396 | 1.491 | |||
| 4 | 2.148 | 2.495 | 3.564 | 4.659 | 4.761 | 1.847 | 6.348 | 1.426 | |||
| 5 | 2.148 | 2.197 | 3.316 | 4.671 | 4.737 | 1.701 | 6.324 | 1.084 | |||
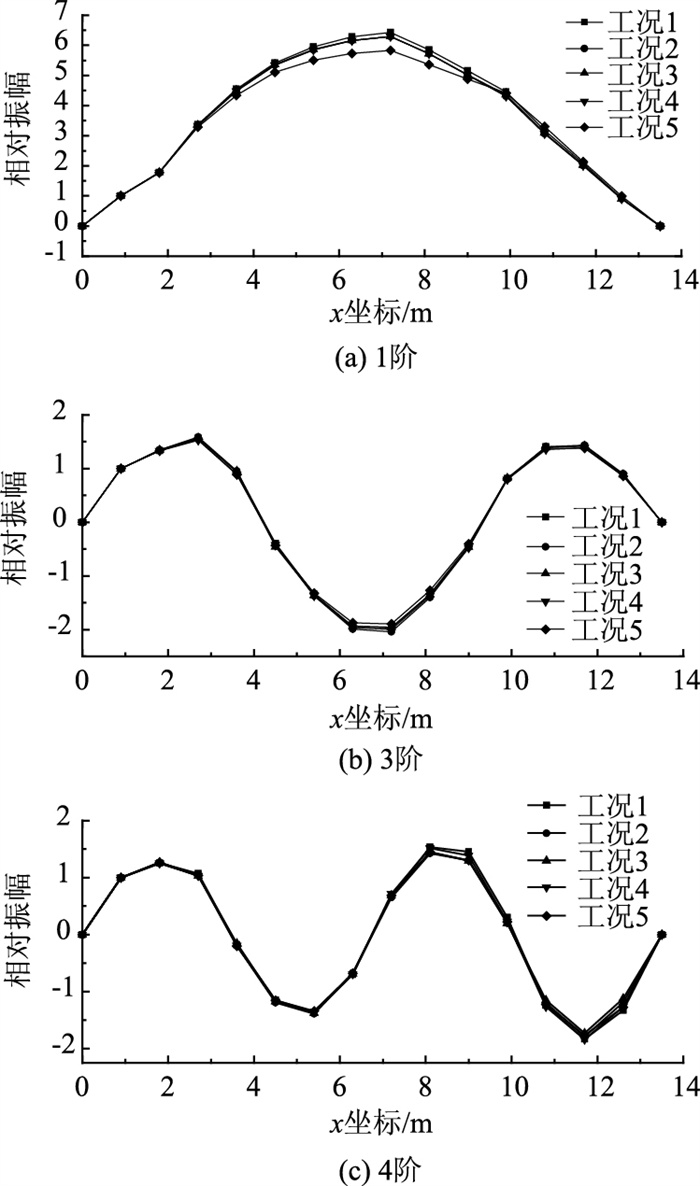
以1#测点为参考点,将其余测点的振幅进行归一化,图 14(a)~(c)分别为模型桥各工况下第1,3,4阶位移模态图。从图中可以看出,相比于未损伤工况(工况1),损伤后结构的位移模态幅值有所降低,且位移模态峰值点的相对其他点降低更多。表明损伤会造成位移模态的改变,但无法通过位移模态直接定位结构损伤。
|
| 图 14 各工况单组位移模态 Fig. 14 Single group of displacement modes under different conditions |
| |
3.3.2 模型桥损伤定位
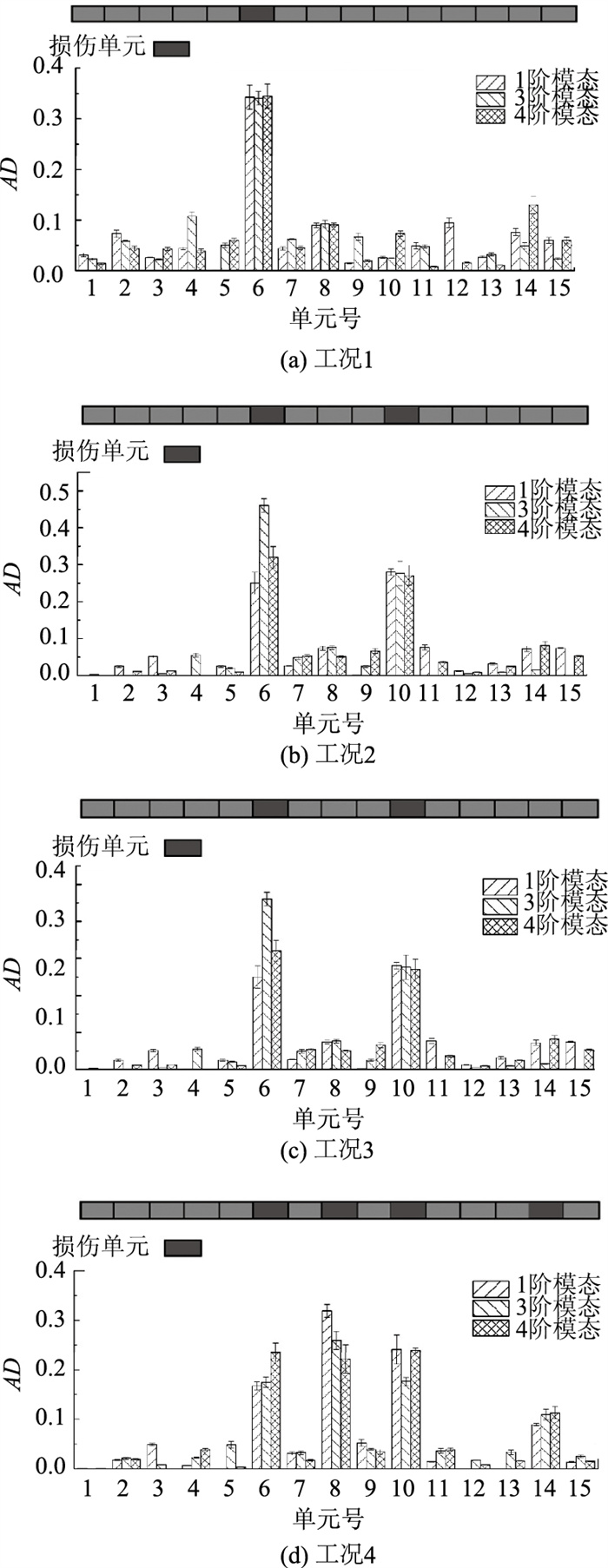
根据式(10)求得各测点的转角模态值后,代入式(9)可直接求得1#~15#单元的ADi值。将20组测试数据各单元AD值平均值绘制成柱状图,标准差作为误差棒值绘制图 15(a)~(d)。在图 15(a)中各阶模态下6#单元的AD值约为0.34,明显大于其他单元;在图 15(b)中,各阶模态下6#单元的AD值约为0.30,10#单元的AD值约为0.30,明显大于其他单元;在图 15(c)中,各阶模态下6#单元的AD值约为0.20,10#单元的AD值约为0.25,8#单元的AD值约为0.35,明显大于其他单元;在图 15 (d)中,各阶模态下6#单元的AD值约为0.20,10#单元的AD值约为0.20,8#单元的AD值约为0.25,14#单元的AD值约为0.15,明显大于其他单元,表明ADi值较准确定位了结构损伤位置。
|
| 图 15 工况2-5各单元AD值 Fig. 15 AD values of each element under different conditions |
| |
同时,由于第4阶位移模态的节点位于8#单元,从图 15(c)和图 15(d)还可以看出,在第4阶下,8#单元的AD值相比第1, 3阶模态小。但仍明显大于未损伤单元。
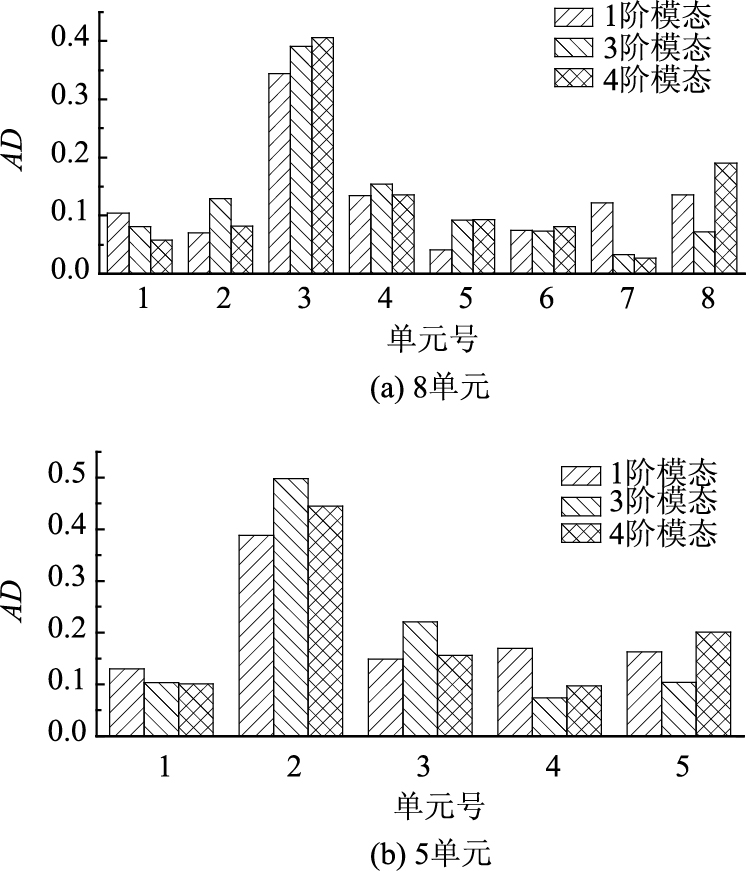
3.3.3 测点数量对识别结果的影响在前面的分析中,悬索桥计算单元长度为90 cm,单元长度与梁长的比值为1/15,测点总数量为14。原则上,计算单元长度越短,即测点的密度越大,损伤位置的识别越准确。本节通过改变测点的密度,来分析单元长度改变对识别效果的影响。
将测点数量减少至原数量的一半,即仅使用奇数号测点的加速度响应进行分析,单元数量减少为8个,单元长度为180 cm;再间隔抽取传感器减少至4个,单元数量减少至5个,单元长度为270 cm。
图 16(a)和图 16(b)分别为8个单元和5个单元的AD值分布图。
|
| 图 16 不同单元数量AD值分布 Fig. 16 Distribution of AD values for different element numbers |
| |
可以看到,无论是单元长度的大小,即测点布置的疏密,损伤带来的AD值增大总能在其范围内的测点体现出来,即使测点数量很少,也能定位损伤单元。当然,测点密度越大,损伤位置的识别也越准确。
4 结论本研究根据位移模态、转角模态和曲率模态三者之间的关系,提出了一种使用损伤前后曲率模态面积差方比来定位结构损伤的方法,并利用实验室简支梁和悬索桥缩尺模型对该方法的有效性进行了验证。得到如下结论:
(1) 损伤单元的AD值远大于未损伤单元,能够准确定位结构中不同位置和数量的局部刚度损伤。
(2) 本研究方法对离散点的位移模态仅进行一次差分计算,由转角模态值直接计算出损伤前后的曲率模态面积差方比,与以往利用曲率模态差的损伤识别方法相比,减少了由于二次差分所带来的误差传递和放大。
| [1] |
PHARES B M, WASHER G A, ROLANDER D D, et al. Routine Highway Bridge Inspection Condition Documentation Accuracy and Reliability[J]. Journal of Bridge Engineering, 2004, 9(4): 403-413. |
| [2] |
李爱群, 丁幼亮, 王浩, 等. 桥梁健康监测海量数据分析与评估: "结构健康监测"研究进展[J]. 中国科学: 技术科学, 2012, 42(8): 972-984. LI Ai-qun, DING You-liang, WANG Hao, et al. Analysis and Assessment of Bridge Health Monitoring Mass Data: Progress in Research/Development of "Structural Health Monitoring"[J]. Scientia Sinica (Technologica), 2012, 42(8): 972-984. |
| [3] |
WICKRAMASINGHE W, THAMBIRATNAM D P, CHAN T H T, et al. Vibration Characteristics and Damage Detection in a Suspension Bridge[J]. Journal of Sound and Vibration, 2016, 375: 254-274. |
| [4] |
SHIH H W, THAMBIRATNAM D P, CHAN T H T. Damage Detection in Slab-on-girder Bridges Using Vibration Characteristics[J]. Structural Control and Health Monitoring, 2013, 20(10): 1271-1290. |
| [5] |
LE N T, THAMBIRATNAM D P, NGUYEN A, et al. A New Method for Locating and Quantifying Damage in Beams from Static Deflection Changes[J]. Engineering Structures, 2019, 180: 779-792. |
| [6] |
CHEN Z, CAI Q, ZHU S. Damage Quantification of Beam Structures Using Reflection Influence Lines[J]. Structural Control and Health Monitoring, 2018, 25(11): 2242. |
| [7] |
HE W, REN W, ZHU S. Damage Detection of Beam Structures Using Quasi-static Moving Load Induced Displacement Response[J]. Engineering Structures, 2017, 145: 70-82. |
| [8] |
杨书仁, 丁松. 基于应变比的桥梁损伤识别与评估方法[J]. 公路交通科技, 2021, 38(1): 87-96, 111. YANG Shu-ren, DING Song. A Method for Bridge Damage Identification and Evaluation Based on Strain Ratio[J]. Journal of Highway and Transportation Research and Development, 2021, 38(1): 87-96, 111. |
| [9] |
PANDEK A K, BISWAS M, SAMMAN M M. Damage Detection from Changes in Curvature Mode Shapes[J]. Journal of Sound and Vibration, 1991, 145(2): 321-332. |
| [10] |
WAHAB M M A, ROECK G D. Damage Detection in Bridges Using Modal Curvature: Application to a Real Damage Scenario[J]. Journal of Sound and Vibration, 1999, 226(2): 217-235. |
| [11] |
郑明刚, 刘天雄, 朱继梅, 等. 曲率模态在桥梁状态监测中的应用[J]. 振动与冲击, 2000, 19(2): 81-82. ZHENG Ming-gang, LIU Tian-xiong, ZHU Ji-mei, et al. Bridge Diagnosis Using Curvature Mode Shapes[J]. Journal of Vibration and Shock, 2000, 19(2): 81-82. |
| [12] |
陈江, 熊峰. 基于曲率模态振型的损伤识别方法研究[J]. 武汉理工大学学报, 2007, 29(增1): 57-63. CHEN Jiang, XIONG Feng. Curvature Mode Shapes-based Damage Identification Method[J]. Journal of Wuhan University of Technology, 2007, 29(3): 99-102. |
| [13] |
胡业平, 张成海, 屠义强. 基于曲率模态的结构损伤定位[J]. 解放军理工大学学报: 自然科学版, 2009, 10(增1): 57-63. HU Ye-ping, ZHANG Cheng-hai, TU Yi-qiang. Curvature Mode-based Structure Damage Localization[J]. Journal of PLA University of Science and Technology: Natural Science Edition, 2009, 10(S1): 57-63. |
| [14] |
韩西, 李庆达, 钟厉, 等. 基于高斯曲率模态差的T梁结构二维损伤识别研究[J]. 重庆交通大学学报: 自然科学版, 2012, 31(4): 747-750. HAN Xi, LI Qing-da, ZHONG Li, et al. Study on Two-dimensional Damage Identification of T-beam Based on Gaussian Curvature Mode Difference[J]. Journal of Chongqing Jiaotong University: Natural Science Edition, 2012, 31(4): 747-750. |
| [15] |
刘义伦, 时圣鹏, 廖伟. 利用曲率模态识别桥梁损伤的研究[J]. 振动与冲击, 2011, 30(8): 77-81, 96. LIU Yi-lun, SHI Sheng-peng, LIAO Wei. Bridge Damage Identification Using Curvature Mode Shapes[J]. Journal of Vibration and Shock, 2011, 30(8): 77-81, 96. |
| [16] |
贺文宇, 何健, 任伟新. 基于间接法识别的桥梁振型的损伤定位方法[J]. 振动与冲击, 2018, 37(24): 13-17. HE Wen-yu, HE Jian, REN Wei-xin. A Damage Localization Method Based on Indirectly Identified Mode Shapes[J]. Journal of Vibration and Shock, 2018, 37(24): 13-17. |
| [17] |
HE R, ZHU Y, HE W, et al. Structural Damage Recognition Based on Perturbations of Curvature Mode Shape and Frequency[J]. Journal of Solid Mechanics, 2018, 31(6): 794-803. |
| [18] |
SIM S H, SPENCER B F, J r, ZHANG M, et al. Automated Decentralized Modal Analysis Using Smart Sensors[J]. Structural Control Health Monitoring, 2010, 17(8): 872-894. |
| [19] |
HOSKERE V, PARK J W, YOON H, et al. Vision-based Modal Survey of Civil Infrastructure Using Unmanned Aerial Vehicles[J]. Journal of Structural Engineering, 2019, 145(7): 04019062. |
| [20] |
包世华. 结构动力学[M]. 武汉: 武汉理工大学出版社, 2003. BAO Shi-hua. Structural Dynamics[M]. Wuhan: Wuhan University of Technology Press, 2003. |
 2021, Vol. 38
2021, Vol. 38
