扩展功能
文章信息
- 曾加东, 李明水, 张志田, 李少鹏, 李志国
- ZENG Jia-dong, LI Ming-shui, ZHANG Zhi-tian, LI Shao-peng, LI Zhi-guo
- 斜风作用下桥塔对大跨度斜拉桥主梁静风荷载特性的影响
- Influence of Pylon on Static Wind Load Characteristics of Main Girder of Long-span Cable-stayed Bridge under Action of Oblique Wind
- 公路交通科技, 2021, 38(11): 52-58
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(11): 52-58
- 10.3969/j.issn.1002-0268.2021.11.007
-
文章历史
- 收稿日期: 2020-10-09
2. 西南交通大学 风工程四川省重点实验室, 四川 成都 610031;
3. 重庆大学 土木工程学院, 重庆 400045
2. Key Laboratory of Wind Engineering of Sichuan Province, Southwest Jiaotong University, Chengdu Sichuan 610031, China;
3. School of Civil Engineering, Chongqing University, Chongqing 400045, China
大跨度桥梁桥址处的实际风向常与桥轴线成一定偏角,而其静风失稳临界风速也以较大概率出现在斜风工况[1-2]。同时,当自然风流经高耸的桥塔后形成特征紊流,将加剧对主梁流场的干扰[3]。但已有研究较少有综合考虑斜风-桥塔联合作用引起的干扰效应,一般斜风作用研究主要针对主梁整体静力风荷载和风振响应评估,而桥塔干扰研究则侧重于塔区局部风环境的变化[4]。因此,目前仍缺乏对斜风-桥塔联合作用的深入认识,现行研究的不足可能导致分析理论与实际情况不符,得到偏不安全的结果,有必要采用有效的研究方法开展深入分析。
已有研究指出,斜风对大跨度桥梁的静风稳定性、桥面行车安全性更不利,且抖振响应最大值常出现在斜风工况下,斜风作用成为影响大跨度桥梁抗风性能分析的重要因素[5]。为评估斜风对大跨度桥梁风振响应的影响,常用的分析方法主要有平均风速正交分解法[6]和斜气动片条法[7]。Tanaka和Davenport[8]为计算斜风下大跨度桥梁抖振响应,提出了斜风分解法,但该方法可能会低估斜拉桥施工态响应。谢霁明[7]通过引入风速和相对尺度等参数来近似评估斜风下的抖振响应,提升了已有理论的应用范围。Kimura[9]和Scanlan[10]采用类似方法,通过引入不同气动参数进一步完善斜风分析理论。朱乐东[11]基于一系列试验研究,采用风速坐标系和平均风向下的斜气动片条假设来解决斜风下大跨度桥梁的抖振问题。通过研发的试验模型和测量系统来获取计算所需的气动力参数,并指出斜拉桥抖振通常发生在5°~30°的风偏角下。刘小兵等[12]开发了一种获取斜风下主梁静力风荷载的试验系统,其结果指出传统的斜风分解法在计算大跨度斜拉桥静风荷载时存在偏差,且该系统无法考虑桥塔对主梁风环境的干扰。
桥塔是大跨度桥梁中的高耸结构,其较大的几何尺寸将显著改变塔区流场特性,产生突变大风,给施工期安全、行车风环境、桥面附属结构和主梁局部气动力准确评估带来严重影响。李永乐[13]、郑史雄[14]和李小珍等[15]采用CFD数值模拟和风洞试验方法,研究了桥塔遮挡效应对列车气动参数和行车安全性的影响,结果表明桥塔的遮挡效应十分显著,可能导致列车气动参数发生突变。LI等[4]基于测力试验得到了桥塔干扰下三分力系数结果,对斜风分解法的有效性进行了分析,并基于试验结果分析了对桥梁抖振响应计算精度的影响。袁达平[16]采用数值模拟和桥塔-主梁局部刚性模型风洞试验,对塔区局部风环境开展研究,深入分析了桥塔的风速放大和尾流脉动特性,指出桥面不同高度风速受影响程度存在差别。
从上述分析可知,虽然已有大量学者对斜风和桥塔干扰开展了大量卓有成效的研究,但在斜风-桥塔联合干扰效应对主梁静风荷载特性影响方面仍缺乏足够的认识,尚未完全掌握气动力特性沿轴向的非均匀变化。特别在某些斜风工况下,不考虑桥塔的干扰,将导致低估静风荷载和施工期抖振响应的可能,得到偏不安全的结果。因此,有必要根据大跨度桥梁的结构特点,设计一套能综合考虑斜风和桥塔干扰作用的测力模型系统,并结合数值计算和理论分析,得到全流场风速、风压信息,研究斜风-桥塔联合作用对主梁绕流状态和静力风荷载特性的影响。
针对以上问题,本研究采用测力试验、数值模拟和理论分析相结合的研究方法,设计了一套能考虑斜风-桥塔联合干扰效应的测力系统,以获取不同位置处主梁的绕流特性和三分力系数结果。在此基础上,基于CFD数值计算得到主梁的流场信息,分析气动力沿轴向变化的气动机理,并与风洞试验、斜风分解法计算结果进行对比,量化分析斜风下桥塔对塔区局部风环境和主梁静风荷载特性的影响,可为类似桥梁的静风荷载评估、抖振响应分析及施工阶段和塔区行车安全性研究提供一定的参考。
1 试验简介 1.1 工程背景该桥为主跨730 m的半漂浮体系双塔斜拉桥,跨径布置为:4×57.5 m + 730 m + 4×57.5 m。主梁断面为混合箱梁断面,主跨为钢箱梁,边跨为混凝土。桥塔为钻石型,塔高为248 m。本桥的主梁布置、主跨箱梁断面和桥塔如图 1所示。

|
| 图 1 大跨度桥梁的布置(单位:m) Fig. 1 Layout of long-span bridge (unit: m) |
| |
1.2 模型试验
试验分成两个部分,首先开展节段模型测力试验,获取三分力系数,安装在风洞中的节段模型如图 2所示。节段模型缩尺比为1∶ 50,模型长2.1 m。为验证雷诺数效应的影响[17],本次试验测试了3种风速下的结果,得到的三分力系数差别较小。节段模型结果表明,在试验风速范围内雷诺数效应的影响较小,结合《桥梁风洞试验指南》[18]中雷诺数效应的规定,本研究暂不讨论其对测力试验的影响。节段模型静力系数将作为参照,对比分析斜风-桥塔对主梁静力系数的干扰。

|
| 图 2 节段模型试验 Fig. 2 Segment model test |
| |
通过设计的气动刚性模型测力系统,测取斜风-桥塔工况下的主梁静力系数,安装在风洞中的试验模型如图 3所示。气动刚性模型与气弹模型概念类似,但不同之处在于主梁刚度很大,主要目的是控制自激力对测力系统的影响,并通过高精度天平测得主梁节段上的气动力系数。与节段模型相比,气动刚性模型的适用性更好:一是能有效模拟桥塔的干扰效应;另外,还可以较为精确地测量任意位置处主梁节段的气动力。考虑到主梁高度固定,并便于与节段模型试验结果对比,气动刚性模型试验将在均匀流中开展。

|
| 图 3 气动刚性模型风洞试验 Fig. 3 Aerodynamic rigid model wind tunnel test |
| |
气动刚性模型的缩尺比为1∶ 100,悬臂端长1.4 m,设置5段测力梁段,梁端间隔不超过4 mm,以避免端部效应的影响,梁段编号如图 4所示。模型另一边是与测力段对称的假模型。主梁为刚度很大的矩形刚性芯梁,以提高测力系统的基频,远离风荷载频率,保证测力系统的固有频率不低于20 Hz。测力天平安装在图 4所示测力梁段的芯梁中间位置。天平底座通过螺栓固定在钢芯梁侧面,测力梁段安装于天平顶部,并保证连接刚度,测力天平及测力系统安装方式见图 5。桥塔与气弹模型一致,底座固定在风洞底部的转盘,通过计算机控制刚性模型与转盘同步转动。为进一步增强主梁刚度,在梁端设置2组带滑轮支架,可方便地调整风偏角。

|
| 图 4 主梁节段编号及风偏角定义 Fig. 4 Number of main girder segments and definition of wind inclined angle |
| |

|
| 图 5 测力天平及安装方式 Fig. 5 Force measuring balance and installation way |
| |
定义当来流与主梁轴线垂直时风偏角β=0°,顺时针旋转为正,风偏角工况β∈ [-90°, 90°]。通过调整桥塔底座角度改变来流风攻角,试验风攻角α为-1.5°, 0°和+1.5°。本研究主要侧重讨论阻力和升力系数的变化,并按如下公式计算:
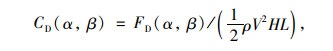
|
(1) |
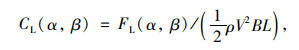
|
(2) |
式中,CD (α, β),CL (α, β)分别为阻力系数和升力系数; L,B和H为梁段的长、宽和高; FD(α, β),FL (α, β为天平测得的阻力和升力。
1.3 数值模型采用与风洞试验相同的缩尺比建立数值模型,所有数值模拟均基于CFD计算软件Fluent开展。根据模拟精度和计算效率要求,合理确定计算域尺寸、模型位置和网格尺寸等。将计算域高度设置为塔高的8~16倍,即上游到主梁截面中心、宽度和高度为塔高8倍,下游为16倍,如图 6所示。

|
| 图 6 数值模型计算域 Fig. 6 Computational domain of numerical model |
| |
流场采用分块结构化网格,贴体最小网格厚度为0.5 mm,采用壁面函数考虑粘性影响,网格单元数约为218万。经网格无关性检查,确保计算Re数下的最大Y+不超过30,以保证较好的网格质量,塔-梁细部网格划分如图 7所示。此外,将计算域前方设定为速度入口,后方为压力出口,模型表面为无滑移边界条件。

|
| 图 7 塔-梁细部网格划分 Fig. 7 Pylon-girder detailed meshing |
| |
采用定常2阶格式,湍流强度取0.5%,入口风速与试验风速一致。采用有限体积法进行方程的离散求解,网格离散格式为2阶中心差分,压力和速度耦合采用SIMPLE算法,对流项使用2阶迎风差分。数学模型采用雷诺时均的N-S方程,湍流模型根据相关三维RANS计算研究成果,选用标准RANSk-ε湍流模型,能满足捕捉紊流场流动信息和气动力特性的要求[17]。经过三维计算的时间步无关检查,确定无量纲时间步长为Δt=0.061。定义风速系数ψ=Umean/Uin,其中Umean为测点处提取的平均风速。
2 试验结果与讨论 2.1 主梁绕流特性提取塔-梁周围的流线图,可定性的分析塔-梁对局部流场的干扰作用,如图 8、图 9所示。从图可知,桥塔对主梁局部风环境的干扰效应显著,形成遮挡和压缩,流经桥塔两侧后风速被放大,导致局部风环境的脉动性增强,形成了复杂的特征紊流,最终导致主梁静力风荷载分布特性的改变。

|
| 图 8 桥塔流场干扰效应 Fig. 8 Flow field interference effect of pylon |
| |
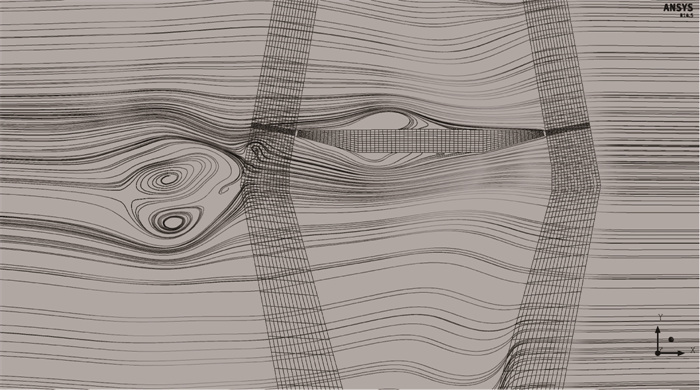
|
| 图 9 塔-梁流场迹线图(10°风偏角) Fig. 9 Pylon-girder flow field trace diagram (10° wind inclined angle) |
| |
分别在主梁中轴线下方5 m、桥面上1.5 m和5 m处设置观测点提取平均风速,其分布如图 10所示。
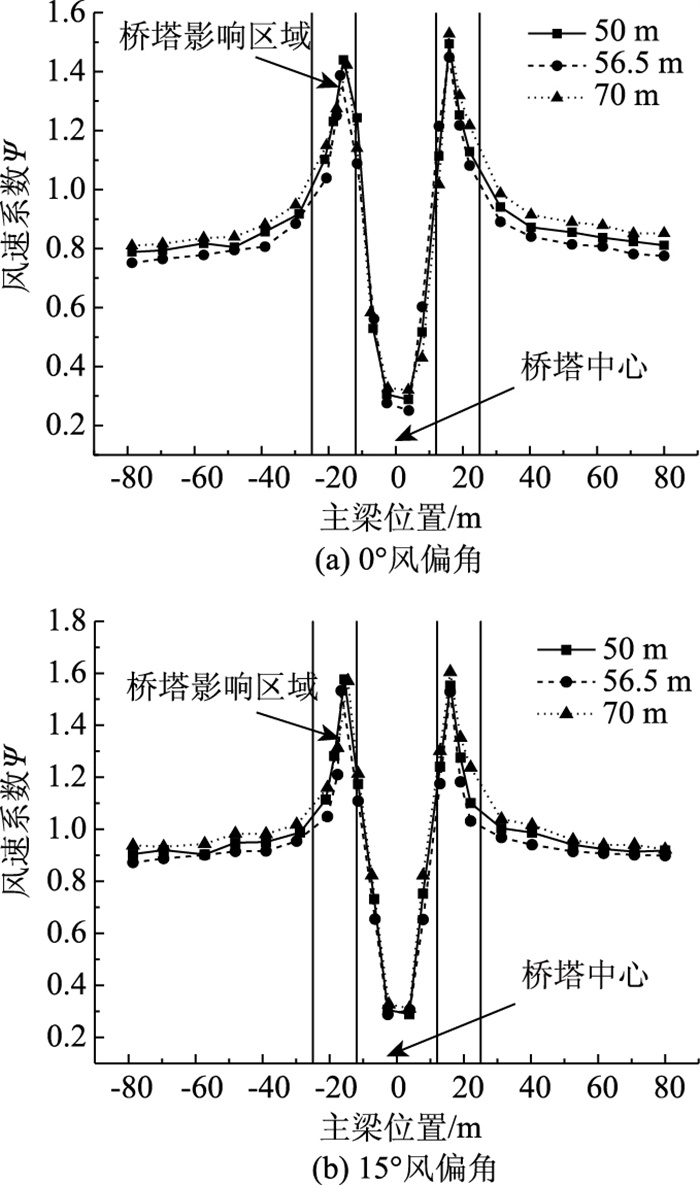
|
| 图 10 主梁轴向平均风速分布 Fig. 10 Distribution of mean wind speeds in axial direction of main girder |
| |
斜风-桥塔联合干扰使塔区风场分布变得更加复杂,特别在10°~30°风偏角范围时,干扰效应更加强烈,风速放大系数最大可达1.62。经统计分析,发现各计算工况下桥塔两侧约有25 m的区域受扰显著,其风速系数基本超过1.2。若将其定义为桥塔干扰区间,其长度约为塔高的1/5,在进行抗风分析时应引起重点关注。基于上述分析,可知斜风下桥塔干扰效应变得更加强烈,主梁风速波动更为显著,是导致主梁静风荷载沿轴向非均匀分布的流场因素。此外,还应注意风速突变对大跨度桥梁施工安全、行车安全和桥面附属设施造成不利影响的可能。
随着离塔间距增加,风速系数逐渐减小,桥塔干扰效应减弱,并在超过50 m后,干扰效应基本消失。与已有文献相比[11-18],本研究的桥塔类型和主梁截面虽然有一定的特殊性,但受扰流场的分布规律基本一致。
2.2 主梁静风荷载特性斜风-桥塔联合干扰效应对主梁流场存在显著影响,是大跨度桥梁静风荷载精确评估中不可忽视的问题。在桥梁抖振计算时,一般采用斜风分解法考虑斜风效应,若不考虑斜风-桥塔的联合干扰,可能导致理论计算结果与实际情况不符。其中,斜风分解法的表达式如下:
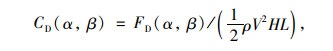
|
(3) |
式中,CXi (α, β)为风偏角β和风攻角α时的三分力系数; Ci (α, 0)为节段模型值; i表示升力和阻力。
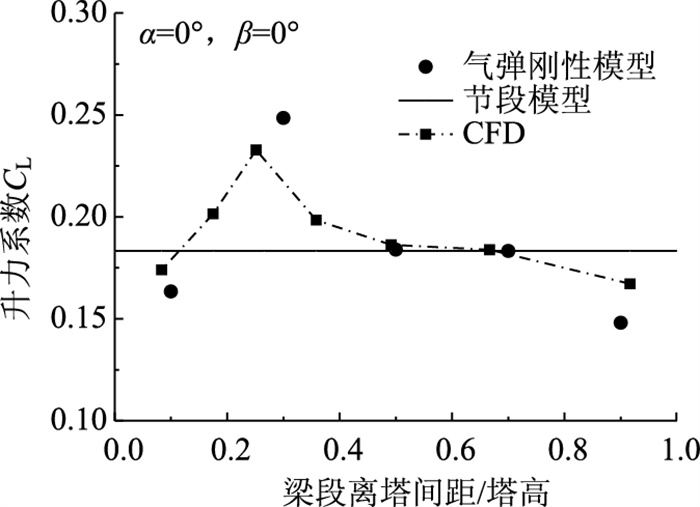
为探明斜风-桥塔联合作用对主梁三分力系数的影响,本研究将通过节段模型、气动刚性模型和CFD数值计算的对比分析进行描述。图 11以0°风偏角下的0°攻角升力系数为例,给出3种研究方法的对比情况。
|
| 图 11 升力系数对比(0°风偏角) Fig. 11 Comparison of lift coefficients (0° wind inclined angle) |
| |
由图可知,刚性模型的1#梁段升力系数值低于节段模型,这是由桥塔遮挡引起。在距离桥塔约20 m时(2#梁段),刚性模型升力系数达到峰值,其测量值显著大于节段模型,偏大幅度约为30%,该区域内的气动力放大效应十分明显。还应注意的是,5#梁段偏离幅度较大,可能是端部效应的影响。同时,数值模拟结果与试验值的分布规律吻合较好,基本能够反映出斜风-桥塔的联合干扰作用。
随着间距增大,升力系数结果逐渐回归节段模型。当间距超过50 m后,三者的结果已较为接近,说明桥塔干扰效应逐渐减弱,这与流场分布规律一致。
图 12给出了刚性模型在不同风偏角下的阻力和升力系数测量结果。为量化说明试验值与斜风分析理论的关系,同时给出由公式(3)计算得到的理论值。

|
| 图 12 斜风-桥塔联合作用下的静力系数分布 Fig. 12 Distribution of static coefficients under combined action of inclined wind-pylon |
| |
对于阻力系数(图 12(a)),同一风向角下沿主梁轴向的分布与图 10的分布趋势一致,阻力系数最大值出现在3#梁段。在斜风工况下,除靠近桥塔的1#梁段变化规律与节段模型一致外,其他梁段的最大值均出现在15°~30°的风偏角范围内。根据斜风分解法,若完全采用节段模型结果可能存在低估主梁静力风荷载的情况,如15°来流下的3#梁段,偏小幅度达10.6%。斜风下升力系数变化更加复杂(图 12(b)),若不考虑桥塔的干扰效应会导致更大偏差。同样,在15°~30°的风向角范围内,各梁段的升力系数取较大值,特别是2#梁段,其最大偏差接近40%(2#梁段,β=15°)。因此,斜风-桥塔联合干扰效应的影响不可忽视,主梁局部位置静风荷载将在其作用下出现较大幅度增大,可能出现偏不安全的情况。
3 总论本研究基于模型测力试验、数值模拟和理论分析的方法,研究了斜风-桥塔联合作用对主梁的流场参数和静风荷载特性的影响,并讨论斜风分解法在该情况下的适用性和可能引起的偏差,得到以下结论:
(1) 斜风-桥塔联合作用对主梁流场的干扰更为强烈,桥塔两侧受扰区域长度约为H/5;
(2) 斜风-桥塔联合作用对大跨度桥梁的静力风荷载特性存在不可忽视的影响,可能导致主梁局部位置气动力增大的不利情况;
(3) 在桥塔影响区域内,斜风分解法计算结果相对主梁实际受力偏小;
(4) 本研究仅针对特定气动外形的桥塔—主梁刚性模型,在其他桥梁结构中的适用性还有待进一步研究。
| [1] |
BIETRY J, DELAUNAY D, CONTI E. Comparison of Full-scale Measurement and Computation of Wind Effects on A Cable-stayed Bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 57(2/3): 225-235. |
| [2] |
XU Y L, ZHU L D, WONG K Y, et al. Field Measurement Results of Tsing Ma Suspension Bridge Uring Typhoon Victor[J]. Structural Engineering and Mechanics, 2000, 10(6): 545-559. |
| [3] |
苏洋, 李鹏, 胡朋, 等. 施工态下塔吊对钢桥塔涡激振动影响的风洞试验[J]. 公路交通科技, 2020, 37(9): 67-72, 89. SU Yang, LI Peng, HU Peng, et al. Wind Tunnel Test on Influence of Tower Crane on Vortex-induced Vibration of Steel Bridge Pylon at Construction Stage[J]. Journal of Highway and Transportation Research and Development, 2020, 37(9): 67-72, 89. |
| [4] |
LI S P, LI M S, ZENG J D, et al. Aerostatic Load on the Deck of Cable-stayed Bridge in Erection Stage under Skew Wind[J]. Wind & Structures, 2016, 22(1): 43-63. |
| [5] |
刘焕举, 韩万水, 丁晓婷, 等. 斜风作用下风-车-桥非线性分析系统建立[J]. 中国公路学报, 2018, 31(7): 110-118. LIU Huan-ju, HAN Wan-shui, DING Xiao-ting, et al. A Nonlinear Analysis System for Wind-vehicle-bridge under Skew Wind[J]. China Journal of Highway and Transport, 2018, 31(7): 110-118. |
| [6] |
王浩, 李爱群. 斜风作用下大跨度桥梁抖振响应时域分析(I): 分析方法[J]. 土木工程学报, 2009, 42(10): 74-80. WANG Hao, LI Ai-qun. Time-domain Analysis on Buffeting Response of Long Span Bridges under Oblique Winds (Ⅰ): Analysis Methods[J]. China Civil Engineering Journal, 2009, 42(10): 74-80. |
| [7] |
XIE J, TANAKA H, WARDLAW R L, et al. Buffeting Analysis of Long Span Bridges to Turbulent Wind with Yaw Angle[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1991, 37(1): 65-77. |
| [8] |
TANAKA H, DAVENPORT A G. Response of Taut Strip Models to Turbulent Wind[J]. Journal of the Engineering Mechanics Division, 1982, 108(1): 33-49. |
| [9] |
KIMURA K, TANAKA H. Bridge Buffeting due to Wind with Yaw Angles[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 42(1/2/3): 1309-1320. |
| [10] |
SCANLAN R H. Bridge Buffeting by Skew Winds in Erection Stages[J]. Journal of Engineering Mechanics, 1993, 119(2): 251-269. |
| [11] |
ZHU L D, XU Y L, ZHNAG F, et al. Tsing Ma Bridge Deck under Skew Winds—Part 1: Aerodynamic Coefficients[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(7): 781-805. |
| [12] |
刘小兵, 陈政清, 刘志文. 斜风下大跨度桥梁主梁三分力系数试验研究[J]. 湖南大学学报: 自然科学版, 2008, 35(9): 10-14. LIU Xiao-bing, CHEN Zheng-qing, LIU Zhi-wen. Experimental Study on the Aerodynamic Coefficients of Long Span Bridge Deck under Skew Winds[J]. Journal of Hunan University: Natural Science Edition, 2008, 35(9): 10-14. |
| [13] |
李永乐, 陈宁, 蔡宪棠, 等. 桥塔遮风效应对风-车-桥耦合振动的影响[J]. 西南交通大学学报, 2010, 45(6): 875-881, 887. LI Yong-le, CHEN Ning, CAI Xian-tang, et al. Wake Effect of Bridge Tower on Coupling Vibration of Wind-vehicle-bridge System[J]. Journal of Southwest Jiaotong University, 2010, 45(6): 875-881, 887. |
| [14] |
郑史雄, 袁达平, 张向旭, 等. 大跨桥梁桥塔遮风效应对列车气动参数的影响研究[J]. 桥梁建设, 2016, 43(3): 63-68. ZHENG Shi-xiong, YUAN Da-ping, ZHANG Xiang-xu, et al. Study of Influences of Wind Shielding Effect of Pylon of Long Span Bridge on Aerodynamic Parameters of Trains[J]. Bridge Construction, 2016, 43(6): 63-68. |
| [15] |
李小珍, 唐庆, 吴金峰, 等. 桥塔遮风效应对移动列车气动参数及行车安全的影响[J]. 中国公路学报, 2019, 32(10): 191-199. LI Xiao-zhen, TANG Qing, WU Jin-feng, et al. Influence of the Bridge Tower Shielding Effect on Aerodynamic Parameters and Running Safety of Moving Train[J]. China Journal of Highway and Transport, 2019, 32(10): 191-199. |
| [16] |
袁达平, 郑史雄, 洪成晶, 等. 大跨公铁两用斜拉桥塔区风环境[J]. 哈尔滨工业大学学报, 2018, 50(9): 19-24. YUAN Da-ping, ZHENG Shi-xiong, HONG Cheng-jing, et al. Wind Environment around the Tower of Long Span Railway-highway Combined Cable-stayed Bridge[J]. Journal of Harbin Institute of Technology, 2018, 50(9): 19-24. |
| [17] |
祝志文, 袁涛, 陈魏. 扁平箱梁气动特性CFD模拟的维数对比研究[J]. 铁道科学与工程学报, 2016, 13(8): 1555-1562. ZHU Zhi-wen, YUAN Tao, CHEN Wei. Comparative Investigation on Prediction of Aerodynamic Characteristics of Steel Flat Box Girders by CFD with Different Simulation Dimension[J]. Journal of Railway Science and Engineering, 2016, 13(8): 1555-1562. |
| [18] |
葛耀君, 赵林, 张志田, 等. 桥梁风洞试验指南[M]. 北京: 人民交通出版社, 2018. GE Yao-jun, ZHAO Lin, ZHANG Zhi-tian, et al. Guidelines for Wing Tunnel Testing of Bridge[M]. Beijing: China Communications Press, 2018. |
 2021, Vol. 38
2021, Vol. 38
