扩展功能
文章信息
- 邓世磊, 万旭升, 路建国, 李双洋, 晏忠瑞
- DENG Shi-lei, WAN Xu-sheng, LU Jian-guo, LI Shuang-yang, YAN Zhong-rui
- 粉质黏土未冻水含量预测模型及参数变化规律研究
- Study on Prediction Model of Unfrozen Water Content in Silty Clay and Parameter Variation Rule
- 公路交通科技, 2021, 38(11): 28-36
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(11): 28-36
- 10.3969/j.issn.1002-0268.2021.11.004
-
文章历史
- 收稿日期: 2020-11-26
2. 中国科学院西北生态环境资源研究院 冻土工程国家重点实验室, 甘肃 兰州 730000
2. State Key Laboratory of Frozen Soil Engineering, CAS Northwest Institute of Eco-environment and Resources, Lanzhou Gansu 730000, China
我国是世界上的第3冻土国,多年冻土面积约占国土面积的22.3%,主要分布于西部的青藏高原和东北的大小兴安岭等地[1]。冻土是一种特殊性质的土,主要由土颗粒和冰、液态水和气体等对温度极其敏感的成分组成,它在结构、物理和化学性质上与一般土种均有较大差异。在土体冻结之后,并非所有液态水都会转换成冰,土体中始终保留着部分液态水,称之为未冻水[2]。在多年冻土地区施工时,应充分考虑温度变化对地基的影响[3]。在四季交替变化过程中温度会不断变化,所引起的冻土中未冻水含量的变化会对土壤的力学性质产生巨大的影响。从而对当地的建筑、交通工程及基础造成诸多安全问题,如房屋塌陷、路面隆起和下沉、地基承载力和稳定性明显变化等。所以,未冻水含量是冻土相关研究的关键指标,其随温度变化规律在数值模拟中发挥重要作用。
近年来,随着测量手段和信息技术的发展,未冻水含量的测试方法也变得多种多样,测试结果越精确,得出的结论更具有科学性。未冻水测量常用方法有量热法、脉冲核磁共振法(NMR)、频域反射法(FDR)、频域传播法(FDT)及其衍生的多种测量手段[4],其原理是不同液态水含量对应不同的信号值,可通过不同温度下的信号值建立未冻水含量与温度的关系。在大量未冻水含量试验基础上,Anderson等[5]基于试验数据提出了描述未冻水含量随温度变化的幂函数模型。徐敩祖等[6]在此模型基础上,提出了采用一点法和二点法来预测未冻水含量的方法。Sheng等[7]考虑未冻水含量指数函数变化规律,建立了土的冻胀预测模型。冷毅飞等[8]测试了俄石油管道工程沿线大量土样的未冻水含量,并用此模型进行拟合,得到了良好的效果。
土体的基本物理参数及特征研究为未冻水含量预测提供了新的思路。Dall’Amico等[9]结合土水特征曲线和土体冻结曲线,建立了未冻水含量和温度的关系式。Topp等[10]建立了一个用介电常数计算土中未冻水含量的三次多项式,并用试验值确定了常数项的取值。之后,Liu等[11]在试验数据的基础上提出了一种利用土壤表观介电常数和初始盐浓度来计算土壤未冻水含量的经验方法。万旭升等[12]基于理想成冰模型,推导出了利用土壤孔隙比计算土中未冻水含量的计算公式,并引入有效应力原理,建立了负温下未冻水含量和温度的关系式。李顺群等[13]基于比热随负温的变化过程和潜热的宏观表现形式,建立了未冻水含量的反演算法。张翻等[14]根据Johansen导热系数计算式,反演得到了不同温度下细粒土的未冻水含量计算公式。Chai等[15]提出了粉质黏土中考虑冰点的未冻水含量物理计算模型,并计算了土中体积水、毛细水和结合水的冰点。Mu等[16]考虑了毛细作用和吸附作用,提出了此模型参数化的计算方法。自然界中冻土的压力环境复杂,基于此,Zhou等[17]建立了不同压力下的未冻水含量计算模型。
综上所述,已有未冻水含量模型种类繁多,但是在未冻水含量计算时,大多需要借助仪器设备测量土体的物理参数,且模型中参数随土的初始物理状态变化较大,变化规律没有统一表述,模型参数难以确定。故本研究选择3种典型的模型进行研究,通过对粉质黏土的大量试验数据进行拟合,研究模型参数变化规律,并讨论模型的计算精度。最后,给出各模型使用的建议温度范围。
1 经典未冻水含量模型 1.1 Anderson和Tice模型Anderson和Tice根据未冻水含量随温度变化的关系,建立了一个幂函数模型来计算未冻水含量,计算公式如下:
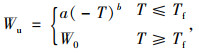
|
(1) |
式中,Wu为质量未冻水含量;W0为初始质量含水率;a和b为模型参数,无实际物理意义;T为土壤温度,Tf为土壤冻结温度,无其他因素影响时,一般认为Tf=0 ℃。由于幂函数的数学特性,温度接近冰点时出现奇异值。
1.2 Michalowski模型Michalowski考虑了土的残余水含量,并根据试验数据提出了以下未冻水含量计算模型:
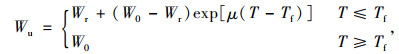
|
(2) |
式中,Wr为低温下的残余质量未冻水含量;μ为模型参数。该模型与幂函数模型相比,解决了当温度靠近冻结温度时未冻水含量出现无限大的问题。
1.3 Dall’Amico模型Dall’Amico在土水特征曲线的基础上,考虑土体冻结特征,结合Clapeyron方程,给出了低温下的未冻水含量计算模型:
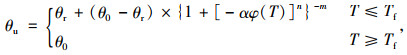
|
(3) |
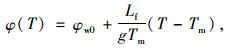
|
(4) |
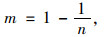
|
(5) |
式中,θu为体积未冻水含量;θ0为初始体积含水率;θr为残余体积未冻水含量;φ(T)为不同温度下的土壤基质势;φw0为总含水率(液体和冰)相对应的基质势(当土为饱和土时φw0=0);Lf为熔化潜热(333.7 kJ/kg);Tm为大气压下水的融化温度(273.15 K);g为重力加速度(9.81 m/s2);α,n,m均为模型参数。在本研究的计算中,将土体近似于饱和状态,且不考虑冻结温度的影响。
为了将单位统一化,将所有试验数据的含水率均转化为体积含水率,质量含水率与体积含水率的转换关系为:

|
(6) |
式中,θ为体积含水率;W为质量含水率;ρd为土的干密度;ρw为水的密度。
2 研究方法 2.1 粉质黏土基本物理参数为了让分析结果更具有科学性,排除个别特殊数据组对结果产生影响,本研究采集了不同区域的粉质黏土试验数据进行拟合研究[4, 12-13, 15, 18-23]。组别前面的字母代表不同的文献来源,后面的数字为数据的组内编号。其中A,B,C,D各为1组数据,H组内为2组数据,F组内为3组数据,其余的E,G,I,J组内各为5组数据,共29组试验数据。其中,E组数据的初始含水率使用土壤水分仪测量,其他数据组采用烘干法测量,干密度均采用环刀法测量。不同区域的粉质黏土的矿物成分、液塑限和颗粒级配会有所差异。本研究中引用的粉质黏土的液塑限和粒径分布如表 1所示。
| 组别 | 液塑限 | 粒径分布/mm | |||||||
| 粉质黏土塑限 | 液限 | 塑性指数 | 10~1 | 1~ 0.1 | 0.1~ 0.01 | 0.01~ 0.001 | 0.001~ 0.0001 | ||
| A | — | — | — | — | — | — | — | — | |
| B | 12.5 | 23.4 | 10.9 | 0 | 0.9 | 7.6 | 55.4 | 36.1 | |
| C | 18.4 | 29.7 | 11.3 | — | — | — | — | — | |
| D | — | — | — | — | — | — | — | — | |
| E | — | — | 10~12 | — | — | — | — | — | |
| F | 18.6 | 36.70 | 17.94 | 0 | 1.73 | 46.80 | 46.80 | 9.35 | |
| G | — | — | — | 0 | 5.24 | 64.80 | 19.72 | 10.24 | |
| H | — | — | — | — | — | — | — | — | |
| I | 12.5 | 23.4 | 10.9 | 0 | 0.9 | 7.6 | 55.4 | 36.1 | |
| J | 17.44 | 31.87 | 14.43 | 0 | 20.44 | 57.82 | 18.12 | 3.62 | |
| 注:“—”表示引文中未提及。 | |||||||||
从表 1的数据可知,本研究选取的粉质黏土塑限位于12.5~18.6之间,液限位于23.40~36.70之间,塑性指数位于10.9~17.94之间,变化范围较小。从粒径分布可以看出,粉质黏土的粒径主要集中在0.1~0.001 mm之间,颗粒级配较为均匀。
2.2 数据拟合及误差分析为了分析模型的精度,绘出试验数据的T-θu散点图,采用origin软件中的非线性拟合的方法,将以上试验数据组分别用3种模型进行拟合,确定各模型参数的取值。并引入均方根误差(RMSE)和均差(AD)作为模型精度的评价手段,均方根误差将直接反映模型的整体预测效果,而均差将反映模型是否会过低或过高地预测未冻水含量。均方根误差和均值的计算公式为:
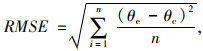
|
(7) |
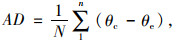
|
(8) |
式中,n为每组数据中数据点数;θe为试验所测得的体积未冻水含量;θc为未冻水含量模型计算所得的体积未冻水含量。
3 结果与分析 3.1 模型边界条件参考各参数的取值,且取Tf=0 ℃,在计算过程中,当温度接近0 ℃(冻结温度)时,各模型的边界条件如下:
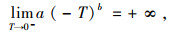
|
(9) |
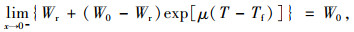
|
(10) |
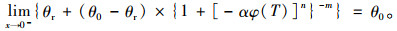
|
(11) |
从各模型的边界条件可以看出,当温度趋近于0 ℃时,Anderson和Tice模型的预测值接近无限大,而Michalowski模型和Dall’Amico模型的值为土样的初始含水率。所以在计算均方根误差和均差时,去除了0 ℃的函数值。Michalowski模型和Dall’Amico模型规避了Anderson和Tice模型在温度接近0 ℃时值出现无限大的现象。
3.2 模型参数对冻结曲线影响本研究选择I-1数据样本进行模型参数对温度-未冻水含量曲线影响分析,探究模型参数变化时对3种模型拟合曲线的影响。I-1土壤样本初始体积含水率25.43%,干密度1 560 kg/m3,冻结温度Tf=0 ℃。在I-1组数据中,模型参数a=15.600,b=-0.537,μ=0.518,α=0.009,n=2.6,m=0.615。改变各模型参数的数值,观察T-θu曲线形态的变化。
通过改变3种模型中参数的数值,可以对比出在拟合过程中各参数对拟合曲线形态的影响。从图 1(a)中可以看出,在Anderson和Tice模型中,当a值不变时,b值变化对冻结初始阶段(T>-2 ℃)无明显影响,对后段冻结阶段(T < -2 ℃)曲线形态产生影响,b值减小时后段冻结曲线整体下移,b值增大使后段冻结曲线整体上移;当b值不变时,a值会影响曲线的整体上下移动,a值增大会让曲线整体上移,减小时整体下移。从图 1(b)中可以看出,在Michalowski模型中,参数μ的变化会引起曲线下凹部分上下移动,μ值增大时冻结曲线下凹部分下移,减小时下凹部分上移。从图 1(c)可以看出,在Dall’Amico模型中,参数α,n,m对冻结曲线有类似的影响,其值变化时曲线下凹部分发生变化,当α值不变时,n值增大会使曲线下凹部分上移,减小时下移;相反,当n,m值不变时,α值增大使冻结曲线下凹部分下移,减小时上移。

|
| 图 1 参数变化对各模型曲线的影响 Fig. 1 Influence of parameter change on each model curve |
| |
3.3 模型精度分析
通过对试验数据的拟合,可以得出各数据组的参数取值。不同模型都有不同的拟合特点和效果,为了对比3种模型的计算精度和拟合效果,计算出在各数据组下的RMSE和AD值。画出了均方根误差的柱状图(图 2)和均差的散点图(图 4),比较和分析3种模型的预测准确性。

|
| 图 2 RMSE柱状分布图 Fig. 2 Columnar distribution of RMSE |
| |
从图 2中可看出,Anderson和Tice模型的均方根误差计算值明显低于其他2种预测模型。为了让结果更清晰化,计算了29组数据的RMSE的平均值,结果如表 2所示。
| 模型 | Anderson和Tice模型 | Michalowski模型 | Dall’Amico模型 |
| RESM平均值 | 0.874 | 1.676 | 1.356 |
从表 2中可以看出,Anderson和Tice模型的RMSE均值为0.874%,显著低于Michalowski模型的1.676%和Dall’Amico模型的1.356%。综上所述,Anderson和Tice模型的整体预测效果优于其他2种模型,且其计算精度已经非常高,计算数值在实际数值上下浮动仅为0.874%,而Dall’Amico模型略微优于Michalowski模型。
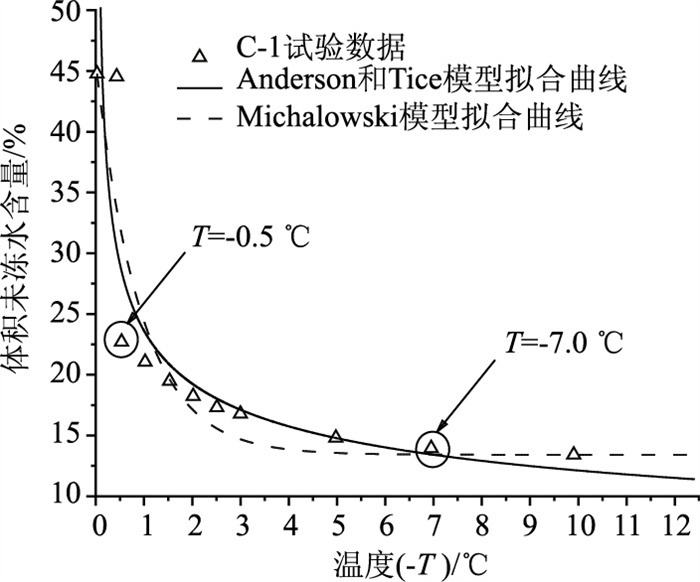
通过原始数据的拟合曲线(图 3)可以发现,C-1组数据的RMSE值明显高于其他数据组,在该土样中在冻结温度附近大量水分冻结,在-0.5 ℃时未冻水含量发生骤降,在-7 ℃时冻结基本完成[14]。冻结温度附近水分快速冻结及冻结过早完成导致拟合效果较差,数据组的RMSE值偏高。
|
| 图 3 C-1组数据拟合曲线 Fig. 3 Data fitting curves of C-1 |
| |
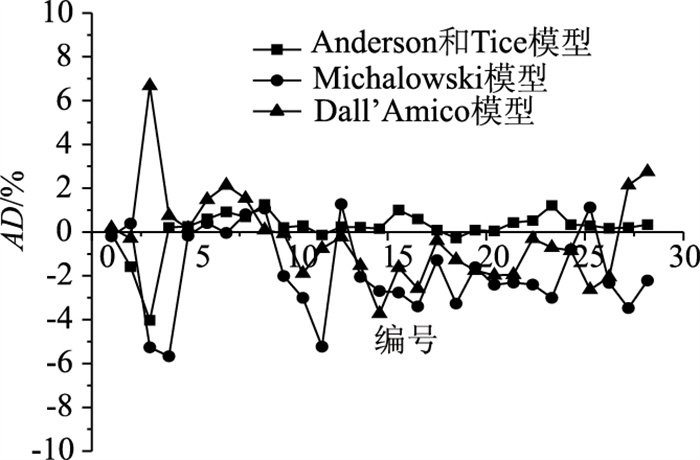
从AD散点分布图(图 4)可以看出,在Anderson和Tice模型中,AD负值仅出现7个,其余22个均为正值,说明Anderson和Tice模型会高估土中的未冻水含量;而在Michalowski模型和Dall’Amico模型中,AD计算值的负值个数分别为23个和20个,直观地表明了Michalowski模型和Dall’Amico模型在实际使用中会低估土体的未冻水含量。从图 4中折线的形态可以看出,Anderson和Tice模型的AD值在0点附近仅有微小的波动,整体预测效果优于Michalowski模型和Dall’Amico模型。相比之下,Michalowski模型和Dall’Amico模型在0点处起伏较大,估值误差较大。
|
| 图 4 AD散点分布图 Fig. 4 Scattergram of AD |
| |
3.4 模型的整体预测效果评价
通过对3种模型进行粉质黏土数据的拟合分析,得出了3组模型在不同数据组内的参数取值,并计算了均方根误差和均差, 对拟合结果进行了分析评价。最后计算结果一致表明,Anderson和Tice模型的计算精度明显高于Dall’Amico模型和Michalowski模型,在使用过程中会高估土中的未冻水含量,而Dall’Amico模型计算精度略微优于Michalowski模型,且二者都会低估未冻水含量。
4 模型参数变化规律在拟合过程中,Anderson和Tice模型未冻水含量预测模型具有形式简单、拟合方便和应用范围广泛等优点,自从提出以来,被广大学者推崇使用。Michalowski模型只有1个拟合参数μ,相较于其他2个模型拟合更为简单。Dall’Amico模型虽然有3个拟合参数,但是m和n相关,且其拟合参数的变化较小,易于确定。
4.1 模型参数的取值范围在未冻水含量计算模型中,参数影响函数曲线的形态,确定了冻结过程中未冻水含量随温度变化的关系。但是随着粉质黏土的初始含水率、干密度、颗粒级配和孔隙比的变化,模型参数的值也会改变。将上述29组T-θu试验数据进行汇总,在数据点集集中区域的上下方分别确定不同模型中的上下边界,求出上下界曲线的模型参数。与实际拟合得出的参数取值进行对比,并计算参数取值范围的涵盖率(涵盖率为位于上下边界取值区间内的数据组数与总数据组数的百分比),结果如表 3所示。
| 曲线 | Anderson和Tice模型 | Michalowski模型 | Dall’Amico模型 | |||||
| a | b | μ | α | n | m | |||
| 上边界 | 45 | -0.65 | 0.208 | 0.002 5 | 2.8 | 0.64 | ||
| 下边界 | 7 | -0.185 | 1.200 | 0.012 0 | 2.0 | 0.50 | ||
| 涵盖率/% | 100 | 96.6 | 96.6 | 79.3 | 82.6 | 82.6 | ||
从表 3可以看出,在Anderson和Tice模型中,模型参数a的取值范围为7~45,b的取值范围为-0.185~-0.65,在29组数据中,参数拟合取值中a最大值为43.589,最小值为7.520。b最大值为-0.185,最小值为-0.733,除了b的最小值外,其他数据均介于上下边界的b值之间,参数a取值涵盖率为100%,参数b的涵盖率为96.6%。在Michalowski模型中,拟合参数μ的取值范围为0.208~1.200,除D-1组的参数取值2.934外,其他数据样本取值均位于取值范围之内,参数μ取值涵盖率为96.6%。在Dall’Amico模型中,参数α取值范围为0.002 5~0.012,参数n为2.0~2.8(参数m与n具有一致性),参数α有6组数据取值位于范围之外,除E组的5组数据外,参数n的取值全位于范围之内,参数α的取值涵盖率为79.3%,n和m的涵盖率为82.6%。从各模型参数的取值涵盖率可以看出,由上下边界确定的参数取值范围都具有较佳的指导意义。
4.2 初始含水率对模型参数的影响在不同地区的粉质黏土中,含水率有着明显的差异,所以,探究模型参数取值与初始含水率的关系尤为重要。下面选取6组来自同一篇文章的数据进行对比分析,保证基本物理性质相同,排除其他干扰因素的影响,分析初始含水率对参数取值的影响。
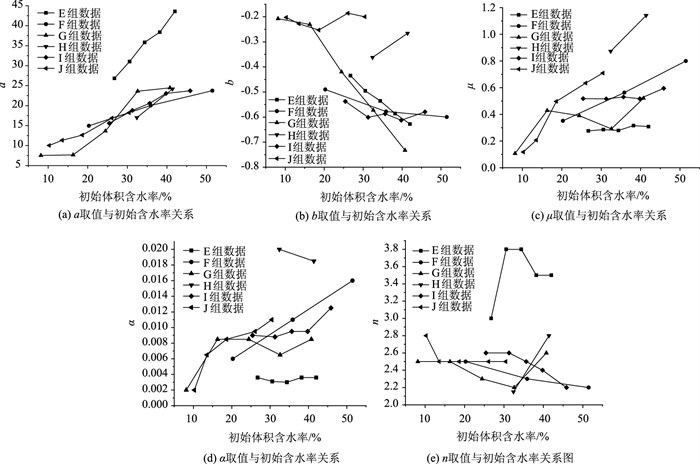
从图 5(a)~(b)可以看出,在Anderson和Tice模型中,在E,F,G组土样数据内,随着初始含水率增加,参数a的值也在增加,b值减小。在H组的2组土样数据内,随着初始含水率的增加,参数a的值增大,b值增大。在I组和J组土样数据内,随着初始含水率的增加,参数a在增大,但是b值没有出现固定增大或减小的现象,其值出现波动的现象。从图 5(c)可以看出,在Michalowski模型中,除了J组数据中随着初始含水率的增大出现了μ取值减小外,其他5组数据均出现μ取值随着初始含水率增大而增大的现象。而图 5(d)~(e)反映出在Dall’Amico模型中,参数α和n的取值与初始含水率的关系规律性较差,整体上,α的取值随初始含水率增大而出现减小的趋势,n的取值随着初始含水率的增大而出现减小的趋势,但二者都有反常的增大和减小。由此可以总结出,在相同的土体中,初始含水率的增大会直接导致a值的增大,μ值有增大的趋势,但是对b,α,n,m的取值没有固定的影响,b,α,n,m值的变化可能还与土的冻结过程紧密相关。
|
| 图 5 参数取值与初始含水率关系 Fig. 5 Relationship between parameter value and initial water content |
| |
5 讨论
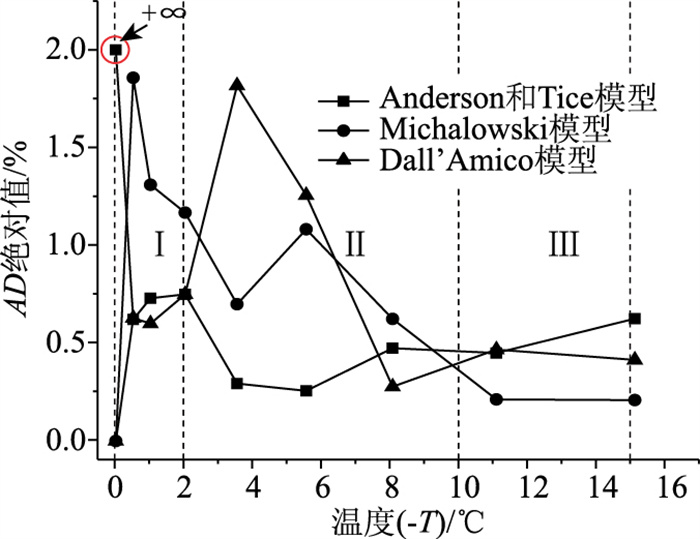
以上分析表明,Anderson和Tice模型计算精度较高,但在冻结温度附近不收敛,而Michalowski模型和Dall’Amico模型在冻结温度处的计算值为初始含水率,且在冻结结束阶段计算值更接近残余水含量。根据3个模型的计算误差,现拟将3个模型根据最佳温度适用范围,分温度区段结合使用。以未冻水含量测试温度点一致的F组和I组试验数据为例,对比各模型在各温度点的计算值与实际值的差值,绘出AD绝对值分布图,如图 6所示。
|
| 图 6 AD绝对值分布 Fig. 6 Distribution of absolute values of AD |
| |
根据差值的分布的特点,将0~-15 ℃温度区间从-2 ℃和-10 ℃分成3个阶段,依次为剧烈相变阶段、主要冻结阶段和冻结稳定阶段。从图 6中可以看出,Dall’Amico模型在0~-2 ℃剧烈相变阶段的计算精度较高;Anderson和Tice模型在主要冻结阶段,即-2~-10 ℃的计算值更接近实际值;而Michalowski模型在冻结稳定阶段精度高于其他2个模型。基于此,现将3个模型根据以上温度区间的计算特性,把土中未冻水含量计算分成3个区段,提出未冻水含量分段计算公式:
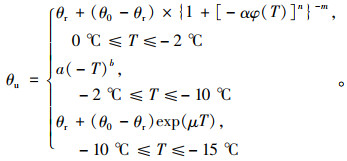
|
(12) |
为了验证式(12)的可行性,现用F组与I组的数据进行计算精度校核,对比3个经典未冻水含量模型和式(12)的RMSE值,计算结果如表 4所示。
| 模型 | Anderson和Tice模型 | Michalowski模型 | Dall’Amico模型 | 式(12) |
| RESM平均值 | 0.654 | 1.140 | 1.013 | 0.572 |
从表 4的F组和I组数据的RMSE计算结果来看,在3个模型中,Anderson和Tice模型计算精度较高,RMSE值仅为0.654%,拟合效果较佳,其他2个模型分别为1.140%和1.013%。在使用式(12)对土中的未冻水含量进行分段预测之后,整体的RMSE计算平均值降至0.572%,整体预测效果优于其他3个模型。由此可以得出,式(12)结合了3个模型的优点,能更好地模拟土中未冻水含量随温度的变化。
土的液塑限、颗粒级配等会影响未冻水含量变化。已有研究表明,塑性指数对土体冻结特征曲线过冷阶段无明显影响;塑性指数的增大会减缓土中水分冻结的速率,使冻结阶段曲线变得平缓, 对冻结完成阶段未冻水含量几乎无影响[24]。土中孔径影响未冻水含量的变化,未冻水含量改变随着孔径减小而减小,土中孔径大小与颗粒级配密切相关,颗粒越小,孔径越小,水分冻结愈发困难[6]。然而,土中未冻水含量模型参数与土体基本物理量之间还未建立具体关系,大部分参数物理意义不明确,故在后期研究中要考虑土的物理参数建立新的未冻水含量预测模型。
6 结论本研究对已有粉质黏土试验数据进行拟合分析,通过计算模型的均方根误差RMSE和均差AD,对Anderson和Tice提出的幂函数模型、Michalowski考虑初始含水率和残余水含量的指数函数模型,Dall’Amico结合Clapeyron方程提出的未冻水含量预测模型进行评价,归纳了模型参数的取值范围,讨论了参数取值和初始含水率的关系。结论如下:
(1) 对于特定土而言,Anderson和Tice模型具有较高的预测精度,但是在冰点处出现奇异值,误差较大,且随初始含水率变化,预测值离散性较大。Dall’Amico模型整体性较好,可较好地反映不同初始含水率变化规律,而Michalowski模型模拟效果相比较差。Anderson和Tice模型会高估土中未冻水含量,Michalowski模型和Dall’Amico模型会低估未冻水含量。
(2) Anderson和Tice模型中,参数a取值范围变化最大,为5~45,反映了模型随土的不同初始物理状态波动较大;Michalowski模型中,参数μ取值范围为0.208~1.200;Dall’Amico模型中,参数α变化最小,取值范围为0.0025~0.012,n为2.0~2.8,反映出模型稳定性较好。土的初始含水率的增大会引起参数a和μ的值增大,对b,α,n,m值没有明确的影响。
(3) 基于各模型的计算特性建立的分段计算公式结合了三者的优点,剧烈相变阶段使用Dall’Amico模型计算,主要冻结阶段和稳定冻结阶段分别使用Anderson和Tice模型和Michalowsk模型,可较好地预测土中的未冻水含量。
| [1] |
周幼吾, 郭东信, 邱国庆, 等. 中国冻土[M]. 北京: 科学出版社, 2000. ZHOU You-wu, GUO Dong-xin, QIU Guo-qing. Geocryology in China[M]. Beijing: Science Press, 2000. |
| [2] |
覃英宏, 张建明, 郑波, 等. 基于连续介质热力学的冻土中未冻水含量与温度的关系[J]. 青岛大学学报: 工程技术版, 2008, 13(1): 77-82. QIN Ying-hong, ZHANG Jian-ming, ZHENG Bo, et al. The Relationship between Unfrozen Water Content and Temperature Based on Continuum Thermodynamics[J]. Journal of Qingdao University: Engineering & Technology Edition, 2008, 13(1): 77-82. |
| [3] |
汪水银. 多年冻土地区填方路基温度场分布特征[J]. 公路交通科技, 2018, 35(3): 28-35. WANG Shui-yin. Temperature Field Distribution Characteristics of Filled Roadbed in Permafrost Region[J]. Journal of Highway and Transportation Research and Development, 2018, 35(3): 28-35. |
| [4] |
路建国, 张明义, 张熙胤, 等. 冻融过程中未冻水含量及冻结温度的试验研究[J]. 岩石力学与工程学报, 2017, 36(7): 1803-1812. LU Jian-guo, ZHANG Ming-yi, ZHANG Xi-yin, et al. Experimental Study on the Unfrozen Water Content and the Freezing Temperature during Freezing and Thawing Processes[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(7): 1803-1812. |
| [5] |
ANDERSON D, TICE A R. Predicting Unfrozen Water Contents in Frozen Soils from Surface Area Measurements[J]. Highway Research Record, 1972, 393: 12-18. |
| [6] |
徐敩祖, 奥利奋特J L, 泰斯A R. 土水势、未冻水含量和温度[J]. 冰川冻土, 1985, 7(1): 1-12. XU Xiao-zu, OLIPHANT J L, TICE A R. Soil-water Potential and Unfrozen Water Content and Temperature[J]. Journal of Glaciology and Geocryology, 1985, 7(1): 1-12. |
| [7] |
SHENG D, AXELSSON K, KNUTSSON S. Frost Heave due to Ice Lens Formation in Freezing Soils 2. Field Application[J]. Hydrology Research, 1995, 26(2): 147-168. |
| [8] |
冷毅飞, 张喜发, 杨凤学, 等. 冻土未冻水含量的量热法试验研究[J]. 岩土力学, 2010, 31(12): 3758-3764. LENG Yi-fei, ZHANG Xi-fa, YANG Feng-xue, et al. Experimental Research on Unfrozen Water Content of Frozen Soils by Calorimetry[J]. Rock and Soil Mechanics, 2010, 31(12): 3758-3764. |
| [9] |
DALL'AMICO M, ENDRIZZI S, GRUBER S, et al. A Robust and Energy-conserving Model of Freezing Variably-Saturated Soil[J]. The Cryosphere, 2014, 5(2): 469-484. |
| [10] |
TOPP G, DAVIS J, ANNAN A. Electromagnetic Determination of Soil Water Content Measurements in Coaxial Transmission[J]. Water Resources Research, 1980, 16(3): 574-582. |
| [11] |
LIU J, YANG P, YANG Z. Electrical Properties of Frozen Saline Clay and Their Relationship with Unfrozen Water Content[J]. Cold Regions Science and Technology, 2020, 178: 1-9. |
| [12] |
万旭升, 赖远明, 张明义, 等. 土中未冻水含量与温度关系研究[J]. 铁道学报, 2018, 40(1): 123-129. WAN Xu-sheng, LAI Yuan-ming, ZHANG Ming-yi, et al. Research on Relationship between Unfrozen Water Content in Soil and Temperature[J]. Journal of the China Railway Society, 2018, 40(1): 123-129. |
| [13] |
李顺群, 杨文喜, 王杏杏, 等. 基于冻土比热的未冻水含量反演算法[J]. 山东农业大学学报: 自然科学版, 2018, 49(5): 841-846. LI Shun-qun, YANG Wen-xi, WANG Xing-xing, et al. Inversion Algorithm of Unfrozen Water Content Based on Specific Heat of Frozen Soil[J]. Journal of Shandong Agricultural University: Natural Science Edition, 2018, 49(5): 841-846. |
| [14] |
张翻, 李顺群, 夏锦红, 等. 基于热参数和土水势变化的冻土冻结势研究[J]. 工业建筑, 2019(7): 97-101, 82. ZHANG Fan, LI Shun-qun, XIA Jin-hong, et al. Freezing Potential Analysis of Frozen Soil Based on Thermal Parameters and Soil-water Potential Variation[J]. Industrial Construction, 2019(7): 97-101, 82. |
| [15] |
CHAI M, ZHANG J, ZHANG H, et al. A Method for Calculating Unfrozen Water Content of Silty Clay with Consideration of Freezing Point[J]. Applied Clay Science, 2018, 161: 474-481. |
| [16] |
MU Q Y, NG C, ZHOU C, et al. A New Model for Capturing Void Ratio-dependent Unfrozen Water Characteristics Curves[J]. Computers and Geotechnics, 2018, 101: 95-99. |
| [17] |
ZHOU J, WEI C, LAI Y, et al. Application of the Generalized Clapeyron Equation to Freezing Point Depression and Unfrozen Water Content[J]. Water Resources Research, 2018, 55(11): 9412-9431. |
| [18] |
陈之祥, 李顺群, 夏锦红, 等. 基于未冻水含量的冻土热参数计算分析[J]. 岩土力学, 2017, 38(增2): 67-74. CHEN Zhi-xiang, LI Shun-qun, XIA Jin-hong, et al. Calculation of Frozen Soil Thermal Parameters Considering Unfrozen Water Content[J]. Rock and Soil Mechanics, 2017, 38(S2): 841-846. |
| [19] |
刘宏伟, 张喜发, 冷毅飞. 冻土未冻水影响因素试验分析[J]. 北方交通, 2010(3): 22-24. LIU Hong-wei, ZHANG Xi-fa, LENG Yi-fei. Testing Analysis on Influencing Factors of Unfrozen Water of Frozen Earth[J]. Northern Communications, 2010(3): 22-24. |
| [20] |
于司杭. 基于近红外光谱技术的冻土未冻水含量研究[D]. 哈尔滨: 东北林业大学, 2016. YU Si-hang, Research on Unfrozen Water Content of Frozen Soil Based on Near Infrared Spectroscopy[D]. Harbin: Northeast Forestry University, 2016. |
| [21] |
LU J, PEI W, ZHANG X, et al. Evaluation of Calculation Models for the Unfrozen Water Content of Freezing Soils[J]. Journal of Hydrology, 2019, 575: 976-985. |
| [22] |
TANG L, WANG K, JIN L, et al. A Resistivity Model for Testing Unfrozen Water Content of Frozen Soil[J]. Cold Regions Science and Technology, 2018, 153: 55-63. |
| [23] |
WEN Z, MA W, FENG W, et al. Experimental Study on Unfrozen Water Content and Soil Matric Potential of Qinghai-Tibetan Silty Clay[J]. Environmental Earth Sciences, 2012, 66: 1467-1476. |
| [24] |
KONG L, WANG Y, SUN W, et al. Influence of Plasticity on Unfrozen Water Content of Frozen Soils as Determined by Nuclear Magnetic Resonance[J]. Cold Regions Science and Technology, 2020, 172: 102993. |
 2021, Vol. 38
2021, Vol. 38
