扩展功能
文章信息
- 谭波, 杨涛
- TAN Bo, YANG Tao
- 大粒径级配碎石在循环旋转轴压下的变形规律分析
- Analysis on Deformation Rule of Large-size Graded Crushed Stone under Cyclic Rotary Axial Compression
- 公路交通科技, 2021, 38(11): 19-27
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(11): 19-27
- 10.3969/j.issn.1002-0268.2021.11.003
-
文章历史
- 收稿日期: 2020-10-26
2. 广西建筑新能源与节能重点实验室, 广西 桂林 541004
2. Guangxi Key Laboratory of New Energy and Building Energy Saving, Guilin Guangxi 541004, China
在道路建设工程中,级配碎石主要被应用于底基层和垫层,属于典型的弹塑性颗粒材料[1-2]。大粒径级配碎石通常指公称最大粒径在25~63 mm的碎石混合料[3],在我国道路工程建设中经常使用在旧路改造和垫层中,已有学者研究证明其较常规粒径级配碎石具有更好的承载能力和力学性能[4-5]。但对大粒径级配碎石混合料在长期反复荷载作用下累积变形的相关研究却鲜有报道,而大粒径级配碎石混合料的累积变形作用对道路结构的长期稳定性非常重要。
为研究级配碎石在长期反复荷载作用下的变形规律,国内外学者通过引入安定性理论对其进行了相应的研究。Werkmester[6-7]通过三轴试验对粒料类材料施加重复荷载并对其进行安定性分析,发现粒料类材料在不同荷载下变形规律差异较大,根据其变形规律可将试件划分为3个安定性状态。张吉庆[8]使用MTS试验仪对级配碎石进行安定性测试,发现其结构安定性行为与施加荷载大小有密切的关系,荷载越大结构变形越大,试件越容易达到破坏状态。研究表明结构安定极限荷载随材料屈服应力的增大基本呈线性增长,粒料类材料在循环荷载作用下,试件整体结构的安定性行为与围压、动应力幅值和细颗粒含量紧密相关[9-10]。以往关于级配碎石在重复荷载下的安定性行为研究,大多使用三轴试验仪或MTS试验仪,对常规粒径级配碎石试件施加重复荷载,通过对试件的变形规律进行分析然后判断其安定性状态,而对大粒径级配碎石在循环旋转轴压重复荷载下的安定性行为研究却十分缺乏。
本研究在应用安定性理论及相应测试方法的基础上,提出旋转轴压下大粒径级配碎石安定性测试方法,根据逐级填充法[11]和i法[12]设计出6组级配碎石,对其开展安定性测试,揭示大粒径级配碎石级配参数变化与安定性之间的规律,并结合6组级配碎石的CBR值结果与安定性的关系,提出大粒径级配碎石的优化设计方法。
1 安定性理论 1.1 安定性原理安定性理论(Shakedown理论)最初用于研究具有明显弹塑性行为的金属体在温度和荷载场耦合作用下的变形特性[8],后由Sharp等[13]引入到对路面材料结构的研究中来。通过众多学者的研究和总结,认为材料或结构一般有3个安定性行为和2个临界荷载,即:弹性安定、塑性蠕变、塑性增量累积破坏和安定临界荷载、破坏临界荷载[7]。
通常认为路面材料或者结构承受的应力低于某值时,随着重复荷载次数的增加,其应变增加速率会越来越小,应变趋于收敛。此时的应力大小一般被称为安定临界荷载,它指材料达到弹性安定状态时加载应力的门槛值,在小于等于该荷载的重复作用下,其结构产生的响应均为弹性响应,最终产生的塑性变形趋于稳定值,不会出现塑性的无限积累而最后产生结构破坏,在低于该应力等级下试件的安定性行为被称为安定状态。当路面材料承受的应力大于某值时,安定状态被打破,应变率没有减小的迹象甚至增大,应变快速累积,此时的应力值被称为破坏临界荷载,路面材料或结构所承受的应力大于该荷载时会被破坏,此时的试件则处于塑性增量累积破坏状态。当荷载大于安定临界荷载小于破坏临界荷载时,试件处于塑性蠕变状态。
级配碎石混合料具有明显的骨架结构特征,在受到反复荷载时会有明显的累积变形行为。在实际工程中,道路受到过大重复荷载时会产生累积变形,变形量累积过大时其内部结构会被破坏,出现脱空情况,然后使得道路基层和面层产生开裂进而影响道路结构的整体稳定性。因此,研究大粒径级配碎石混合料的安定性,需要分析它的安定临界荷载和破坏临界荷载值的大小和变形规律,并通过分析临界荷载、变形规律和碎石级配类型之间的关系,提出适合于大粒径碎石级配的优化设计方法。
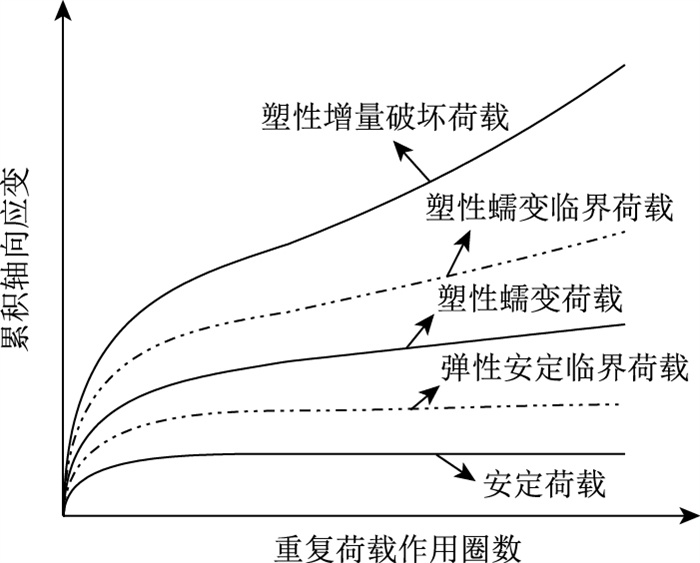
1.2 安定性测试及行为评价前人在研究粒料类材料结构安定性时主要的测试方法有2种:重复荷载三轴试验和MTS试验仪测试。2种方法都可进行重复荷载的三轴试验,而MTS试验仪还可进行重复荷载单轴试验。基于以上2种方法,国内外研究人员取得了大量科研成果,文献[5]将循环重复荷载下的粒料类材料试件的状态分为3种:弹性安定、塑性蠕变、塑性破坏,并以此为依据绘制了安定行为曲线,见图 1。
|
| 图 1 粒料材料在循环荷载作用下的变形行为[6] Fig. 1 Deformation behaviors of granular materials under cyclic load |
| |
Dawson[14-15]对级配碎石材料进行室内三轴试验,发现粒料类材料由于没有黏结料,在车轮荷载下只能承受压应力而不能承受拉应力,所以粒料类材料的安定行为主要分为3个阶段:塑性安定、塑性蠕变破坏、塑性变形积累增量破坏。
Werkmester以重复荷载三轴试验为基础,经过大量研究分析后,总结出了粒料类材料在重复荷载下评价安定行为的标准。该标准以重复荷载次数3 000~5 000次累积轴向应变Δε为基础,计算两荷载次数间累积轴向应变的变化速率,然后以该速率的大小评价试样处于何种状态。具体评价标准如下:
Δε5 000-Δε3 000≤4.5×10-5,材料处于弹性安定状态(Range A);4.5×10-5 < Δε5 000-Δε3 000≤4.5×10-4,材料处于塑性蠕变状态(Range B); Δε5 000-Δε3 000>4.5×10-4,材料处于塑性增量破坏状态(Range C)。
近年来,Chen等[16]在该标准的基础上提出了改进,并通过使用其他学者的研究数据进行验证,最后证明了其方法的合理性。该标准以Yin[17]提出的描述粒料类材料蠕变公式(式(1))为理论基础。
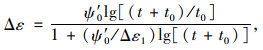
|
(1) |
式中,Δε为累积蠕变应变;t为土样产生蠕变过程中受到的重复荷载次数;Ψ′0,t0,Δε1为常量参数。
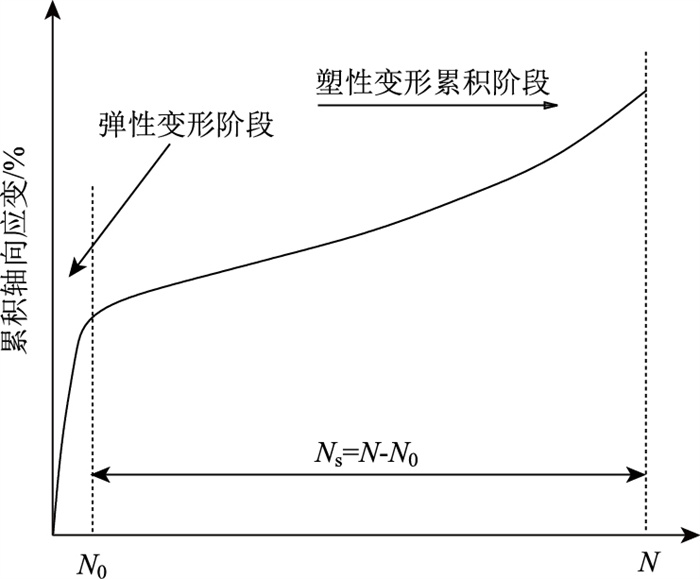
以式(1)为基础,将循环旋转轴压荷载作用圈数Ns和N0(见图 2)替换式(1)中的t和t0,为方便计算, 将式(1)中的常量参数更换为ns和ms,得到式(2):
|
| 图 2 循环旋转轴压圈数选取节点[22] Fig. 2 Selected points of cycles under cyclic rotary axial compression |
| |
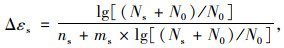
|
(2) |
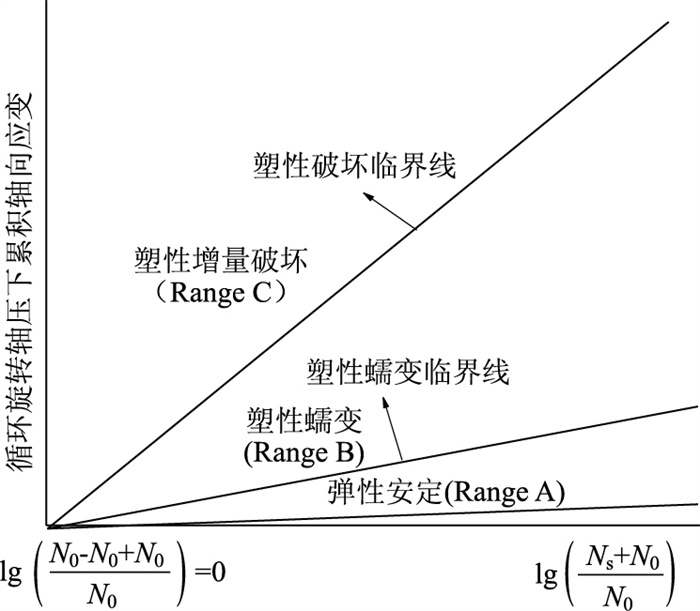
式中,Δεs为试样在旋转轴压重复荷载作用下的累积轴向应变;1/ms为N趋于无穷时试样的累积轴向应变;1/ns为应变曲线的斜率(见图 2);N0为试样开始产生塑性变形时的旋转轴压作用圈数;Ns为试样处于塑性变形积累阶段时的旋转轴压作用圈数。
图 2中N为试样受到旋转轴压重复荷载的总圈数,且Ns=N-N0。因此可得到式(3)。1/ns的大小即可表示累积轴向应变变化的快慢速度,可用来较好地判断循环旋转轴压下粒料类材料的安定性行为。
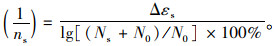
|
(3) |
以试样变形阶段的旋转轴压作用圈数Ns+N0与N0比值的对数做为横坐标,试样累积塑性应变值作为纵坐标绘制其变形曲线,即可绘制出图 3。
|
| 图 3 累积轴向应变与旋转圈数关系[16] Fig. 3 Relationship between accumulated axial strain and rotary cycles |
| |
因为式(3)在推导过程没有将材料性质作为主要考虑的对象,主要考虑颗粒类材料在重复荷载作用下的累积变形规律,而大粒径级配碎石混合料具有明显的颗粒类材料特征,因此式(3)适用于分析大粒径级配碎石混合料。结合式(3)可知试样累积应变等于应变曲线斜率乘以横坐标的值,即:
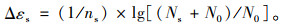
|
(4) |
Chen[16]通过对以往研究人员的研究数据进行总结分析,最后给出了关于1/ns值与安定性行为的具体数值关系,即:
1/ns≤0.1,试件处于弹性安定状态。
0.1 < 1/ns≤0.434,试件处于塑性蠕变状态。
0.434 < 1/ns,试件处于塑性增量破坏状态。
本研究以该方法为基础,提出基于循环旋转轴压下级配碎石混合料试件安定性行为的评价标准。
2 试验加载方式此次研究采用旋转施压的方式实现剪切应力和轴向压力耦合作用机制,并使用道路材料振动旋转压实仪,对成型级配碎石试件实现循环旋转轴压。该仪器具体性能参数如下。振动频率:3 000次/min;振幅:0.6 mm;旋转速率:5 r/min;施加压力:100~700 kPa(可自由控制)。该仪器具有振动、旋转和压实功能,不仅可实现多种不同道路材料成型方式,还可观测试样在整个试验过程中的轴向压实位移变化。
道路材料振动旋转压实仪能在试验过程中自动识别压头端载荷大小,因此在设定荷载大小后,仪器可自动根据实际荷载大小进行自动调整以保证荷载稳定在设定荷载范围。
循环旋转轴压加载方式与三轴试验和MTS试验仪施加重复荷载时其作用机制存在较大区别,主要在于旋转轴压加载方式通过施加轴压和试样旋转同时进行的方式,可以较好地实现轴压和剪切应力耦合作用,因此,研究循环旋转轴压下级配碎石的变形规律,可为今后大粒径级配碎石道路基层在重复荷载下的变形分析提供一些参考和借鉴。
3 原材料及制样 3.1 原材料(1) 细骨料:采用路用粒径4.75 mm以下的花岗岩碎石颗粒。
(2) 粗骨料:采用路用花岗岩碎石,粒径范围在4.75~53 mm之间。碎石材料性质如表 1所示。
| 集料/ mm |
压碎 值/% |
表观密度/ (g·cm-3) |
表干密度/ (g·cm-3) |
毛体积 相对密度 |
吸水 率/% |
针片状 含量/% |
| 19~53 | 21.57 | 2.729 | 2.672 | 2.646 | 1.24 | 7.30 |
| 9.5~19 | 14.08 | 2.753 | 2.691 | 2.662 | 1.32 | 6.58 |
| 4.75~9.5 | — | 2.735 | 2.702 | 2.684 | 0.70 | 6.89 |
| 0~4.75 | — | 2.720 | 2.705 | 2.694 | 0.92 | — |
| 规范要求 | ≤28 | 实测数据 | 实测数据 | 实测数据 | 实测数据 | ≤15 |
(3) 水:日常饮用水。
3.2 制样方式此次研究碎石混合料使用的成型制样仪器为道路材料振动旋转压实仪。经过前期对道路材料振动旋转压实仪进行制样方式研究,总结出具体制样试验步骤:(1)按级配称取5 kg碎石混合料,压实前预留200 g细集料作撒粉用。(2)将4 800 g碎石混合料按最佳含水率加水,搅拌均匀后使用保鲜膜密封养护12 h。(3)将养护好的碎石混合料分为2份分2层压实,每层压实4 min。(4)将预留的200 g细料均匀洒在碎石混合料表层,并喷最佳含水率的水,压实4 min。(5)将压实完毕的碎石混合料静置1 d,然后进行各项力学性能测试。
3.3 试件制作试验用大粒径级配碎石混合料取自广西某高速公路施工点。其中表 2中SJJP开头的5个级配类型是通过设计出来的理论级配,使用的级配设计方法为:运用逐级填充法设计3档粗骨料比例,用i法设计细集料组成比例,最后将不同比例粗骨料与细集料混合料混合,共选出5组设计级配进行研究。为对比分析大粒径级配碎石与常规粒径级配碎石安定性行为的差异性,根据规范[18]推荐级配范围选用中值级配GFJP-1进行对比试验。
| 级配 编号 |
通过下列筛孔(mm)的质量百分率/% | |||||||||
| 53 | 37.5 | 31.5 | 26.5 | 19 | 9.5 | 4.75 | 1.18 | 0.6 | 0.075 | |
| SJJP-1 | 100 | 97.05 | 92.87 | 73.57 | 51.93 | 48.00 | 28.92 | 14.13 | 9.98 | 3.43 |
| SJJP-2 | 100 | 96.89 | 92.47 | 72.12 | 49.29 | 44.96 | 22.35 | 9.41 | 6.18 | 1.70 |
| SJJP-3 | 100 | 97.15 | 93.11 | 74.48 | 53.58 | 49.62 | 28.92 | 14.13 | 9.98 | 3.43 |
| SJJP-4 | 100 | 97.47 | 93.87 | 77.30 | 58.71 | 55.19 | 36.77 | 20.63 | 15.59 | 6.58 |
| SJJP-5 | 100 | 97.15 | 93.10 | 74.23 | 52.09 | 47.98 | 28.92 | 14.13 | 9.98 | 3.43 |
| GFJP-1 | 100 | 100 | 100 | 95.00 | 82.50 | 55.00 | 38.00 | 22.50 | 16.50 | 5.00 |
研究表明,含水率对于级配碎石的压实密度、应力、应变都有影响,因此大粒径级配碎石混合料试样制作时采用最优含水率,最优含水率为4.1%。具体的制样过程采用3.2节中建议的制样方式。试样筒尺寸内径150 mm,高230 mm。
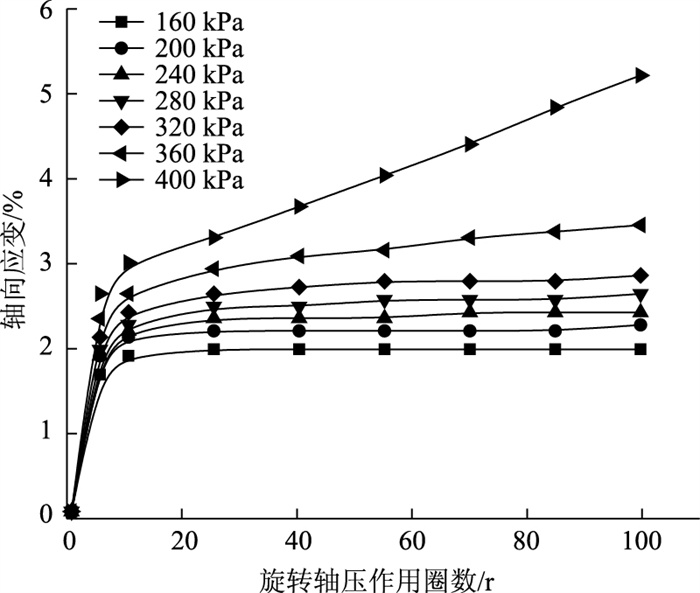
4 试验结果分析 4.1 安定性分析(以SJJP-5为例)对SJJP-5级配大粒径碎石混合料施加不同荷载等级的100圈循环旋转轴压重复荷载,其累积轴向应变与作用圈数的关系见图 4。根据式(3)计算SJJP-5大粒径碎石混合料试件的安定行为评价参数1/ns,其中初始作用圈数N0取10,累积作用圈数N取100,绘制1/ns与不同荷载的关系图,并用1.2节中的1/ns值大小的评价标准判断SJJP-5试件在不同荷载等级下的安定行为状态,具体分析见图 11。
|
| 图 4 不同荷载下级配碎石累积轴向应变 Fig. 4 Accumulated axial strains of graded crushed stone under different loads |
| |
根据图 4试验结果发现,SJJP-5级配碎石试件在不同荷载等级循环旋转轴压下,其变形规律差异很大。荷载为160 kPa和200 kPa时,试件经过弹性变形阶段后,累积轴向应变不再增加,基本上处于弹性安定状态;荷载为240,280,320 kPa时,试件先是经过弹性变形阶段的应变快速累积阶段,然后随着旋转圈数的增加累积应变有一点增加,累积轴向应变变化速率很小;荷载达到360 kPa时,试件在经过弹性变形阶段后,其累积轴向应变依然在以较快的速度增加;当荷载达到400 kPa时,累积轴向应变变化速率则变得非常高,因此可判断试件在400 kPa荷载旋转轴压下整个试件的骨架结构已经被破坏,此时属于明显的塑性增量破坏状态。
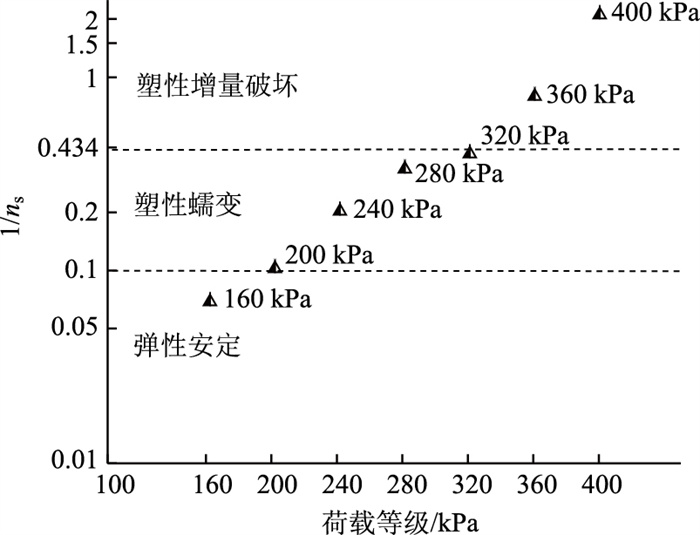
根据图 5的试验结果可分析出SJJP-5级配碎石试件在不同荷载等级下的安定行为。当荷载低于200 kPa时,试件基本上处于弹性安定状态,当荷载达到200 kPa时,其1/ns值已经超过了0.1,根据1.2中的评价标准,说明SJJP-5试件的安定临界荷载在200 kPa附近且高于200 kPa。荷载等级在200~320 kPa间时,SJJP-5试件处于塑性蠕变状态,当荷载达到320 kPa时,其1/ns值已较接近0.434,根据1.2中的评价标准,说明SJJP-5试件的破坏临界荷载就在320 kPa附近且低于320 kPa。
|
| 图 5 级配碎石试件安定行为划分 Fig. 5 Classification of shakedown behaviors of graded crushed stone specimens |
| |
当荷载大于320 kPa时,SJJP-5试件在循环旋转轴压下的累积轴向应变快速增加,且没有趋于收敛的迹象,该现象说明此时试件内部的骨架结构已遭受到严重的破坏且碎石颗粒有了错移情况。若该现象出现在道路实际工程中,表面道路结构已经处于失稳状态,因此实际工程中需要避免达到破坏临界荷载。
4.2 级配对安定行为的影响为分析不同级配碎石试件在不同等级荷载下的安定性行为和临界荷载差异,对6组级配类型大粒径碎石混合料进行循环旋转轴压测试,每组级配类型每个荷载测试等级下的试样为3个,此次研究一共测试了126个试样的变形数据。在进行不同等级荷载下的循环旋转轴压测试后,计算其1/ns均值并评价各自的安定行为状态,具体数据见表 3。
| 级配编号 | CBR/% | 不同荷载下1/ns值及安定行为状态 | 安定临界 荷载/kPa |
破坏临界 荷载/kPa |
||||||||||
| 200 kPa | 状态 | 280 kPa | 状态 | 320 kPa | 状态 | 360 kPa | 状态 | |||||||
| SJJP-1 | 312 | 0.073 | 弹性安定 | 0.367 | 塑性蠕变 | 0.367 | 蠕变 | 0.806 | 塑性破坏 | 207.35 | 326.10 | |||
| SJJP-2 | 317 | 0.074 | 0.369 | 0.443 | 破坏 | 0.813 | 207.03 | 315.14 | ||||||
| SJJP-3 | 324 | 0.073 | 0.291 | 0.364 | 塑性 | 0.727 | 215.00 | 327.71 | ||||||
| SJJP-4 | 321 | 0.073 | 塑性蠕变 | 0.220 | 0.367 | 蠕变 | 0.806 | 214.59 | 326.10 | |||||
| SJJP-5 | 293 | 0.107 | 0.356 | 0.427 | 破坏 | 0.854 | 192.63 | 320.66 | ||||||
| GFJP-1 | 251 | 0.149 | 0.298 | 0.447 | 0.819 | 174.55 | 316.51 | |||||||
表 3中临界荷载根据其测试压强与安定性行为参数1/ns值使用插值法计算得出,具体计算公式见式(4)和式(5)。
表 3中临界荷载根据其测试压强与安定性行为参数1/ns值然后使用插值法计算得出,具体计算公式为:
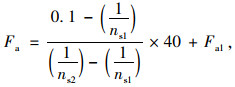
|
(5) |
式中,Fa为安定临界荷载;1/ns1为试件安定行为参数1/ns小于0.1但最接近0.1时的值;1/ns2为试件1/ns大于0.1但最接近0.1时的值;Fa1为1/ns1值对应的试验荷载值。
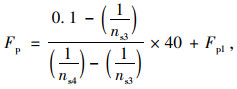
|
(6) |
式中,Fp为破坏临界荷载;1/ns3为试件安定行为参数1/ns小于0.434但最接近0.434时的值;1/ns4为试件1/ns大于0.434但最接近0.434时的值;Fp1为1/ns3值对应的试验荷载值。
4.2.1 级配类型影响根据表 3的试验结果发现,级配类型不同的碎石试件的安定性状态、安定临界荷载和破坏临界荷载差异很大。大粒径碎石SJJP-3试件安定临界荷载高达215 kPa,而常规粒径碎石GFJP-1试件仅为174.55 kPa,二者相差较大的原因是常规粒径碎石试件比大粒径碎石混合料试件的抗变形和承载能力更弱,导致其在相同等级荷载下更容易发生变形,因此常规粒径碎石试件更容易发生塑性蠕变。
表 3试验结果表明,6组级配碎石试件的破坏临界荷载相差不大,差异最大的2组试件其差值也未超过4%,原因是在较大的荷载下各碎石试件密实度达到了顶峰且相差不大,同一材料在密实度相差不大的情况下其抗破坏能力没有太大区别。
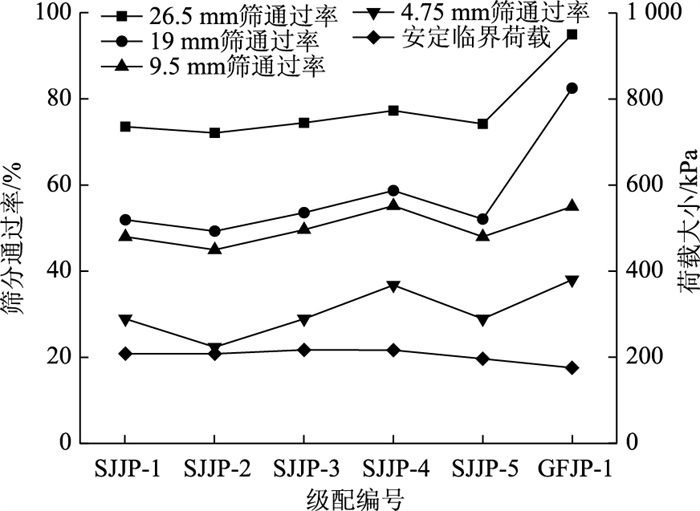
4.2.2 级配参数影响为深入分析6组级配各级配参数对其安定性行为和临界荷载的影响,绘制了几个重要筛孔的筛分通过率与其累积轴向应变、安定临界荷载及破坏临界荷载间的关系,见图 6和图 7。
|
| 图 6 级配参数与安定临界荷载关系 Fig. 6 Relationships between gradation parameters and critical shakedown load |
| |
|
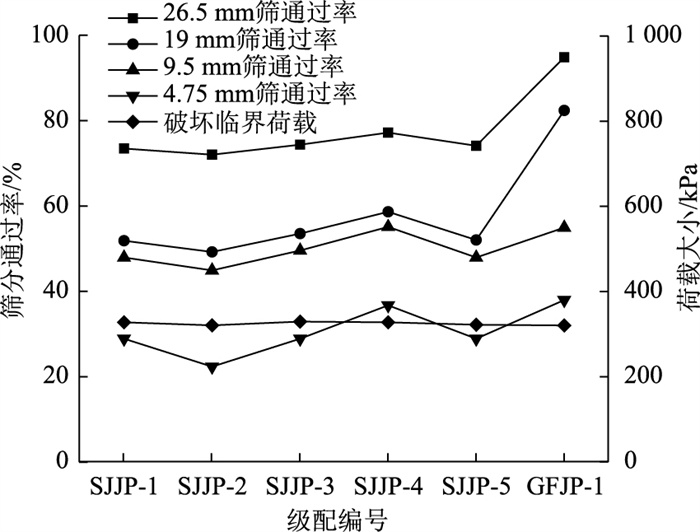
| 图 7 级配参数与破坏临界荷载关系 Fig. 7 Relationships between gradation parameters and critical failure load |
| |
从图 6可发现,安定临界荷载与26.5 mm筛通过率关系最大,当26.5 mm筛通过率增大时,其安定临界荷载就会下降。该现象说明,在粒径大的碎石含量更少时,试件的骨架结构性能就会减弱而导致试件的整体结构抗变形和承载能力减弱。在5组设计级配中,其安定临界荷载与4.75 mm筛通过率呈现出较强的关系,随着4.75 mm筛通过率的增大,试件的安定临界荷载也在增大,这表明试件中较细颗粒的碎石含量越多其密实程度越高,由此导致其抗变形能力和承载能力就会更强。
综上分析,可发现级配碎石试件的安定临界荷载不仅与大粒径碎石含量有关,也与细颗粒碎石含量有关,因此在设计大粒径级配碎石混合料试件时,既要考虑其大颗粒碎石的含量以增强其骨架结构性能,也要考虑其密实程度。图 7中呈现的各级配试件的破坏临界荷载变化并不大,但结合表 3中的数据发现SJJP-3和SJJP-4的破坏临界荷载最大。
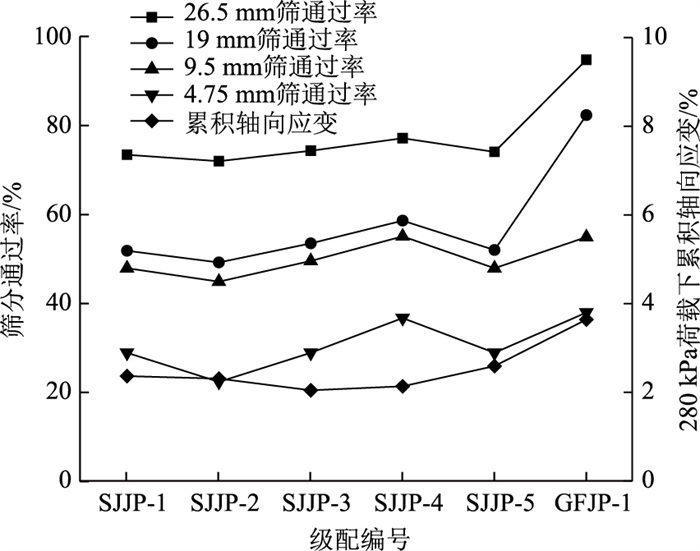
从图 8可发现,试件的累积轴向应变与筛分通过率呈现的关系为:当26.5 mm筛通过率大幅度增大时,其累积轴向应变也会大幅度增加,说明大粒径碎石含量越低试件抗变形能力越弱。而在5组设计级配碎石混合料试件中,这一规律并不是很满足,原因是5组设计级配试件中粒径大于26.5 mm的碎石含量相当,而随着其细颗粒碎石含量的增加,其密实程度得到了提升,试件的整体抗变形能力与承载能力也得到了增强。因此,级配碎石试件的抗变形能力和承载能力与其骨架结构性能和密实程度都存在关系,这也证明了图 6和图 7的分析结论。
|
| 图 8 级配参数与280 kPa荷载下的累积轴向应变关系 Fig. 8 Relationships between gradation parameters and accumulated axial strain under 280 kPa load |
| |
4.2.3 CBR值与累积轴向应变的关系
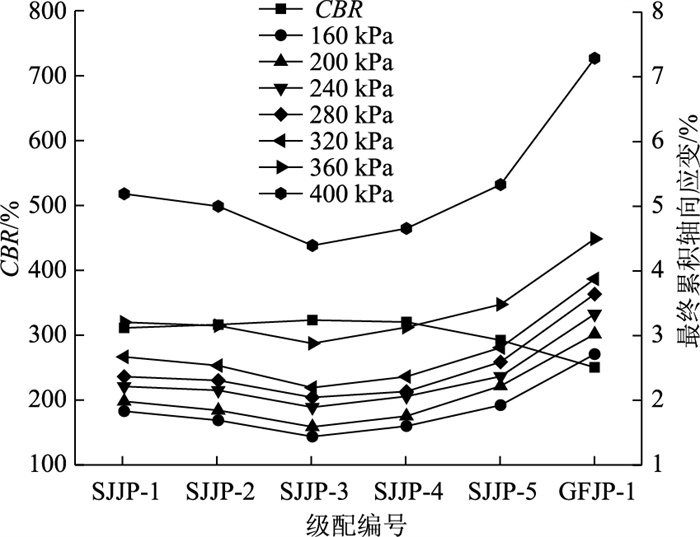
CBR值是描述级配碎石混合料承载能力和抗变形能力的一个重要参数,CBR值越大表示碎石试件的骨架结构性能越强,其承载能力和抗变形能力也越强。参照《公路土工试验规程》(JTG 3430—2020)[18]进行CBR试验,测试6组级配碎石试件的CBR值,结果见表 3。根据结果可发现,CBR值越大的试件其安定临界荷载也越大,表明碎石混合料的骨架结构性能越强, 其抗变形和承载能力也越强。为分析CBR值与各级配累积轴向应变的关系,绘制CBR值与不同等级荷载100圈作用圈数后的累计轴向应变的关系曲线,见图 9。
|
| 图 9 六组级配CBR与不同荷载下的累积轴向应变关系曲线 Fig. 9 Relationships between CBR values and accumulated Vaxial strain of 6 groups of graded crushed stone under different loads |
| |
图 9表明,级配碎石试件CBR值越大其累积轴向应变越小,说明级配碎石混合料试件的骨架结构性能越强, 其抗变形和承载能力也越强,该结果也证明了前述CBR值与临界荷载关系的合理性。其中SJJP-3和SJJP-4试件的CBR值在6组级配中最大,其累积轴向应变也比其他级配试件更小,因此从CBR和累计轴向应变角度可说明SJJP-3和SJJP-4级配碎石试件的性能较其他几组级配更加良好。
根据对各级配碎石试件的CBR值、累计轴向应变、级配参数和临界荷载的综合分析,发现大粒径碎石混合料在大粒径碎石含量恰当的基础上,密实度更高的试件力学性能更强,推荐大粒径碎石的级配范围应控制在SJJP-3和SJJP-4之间。
5 结论(1) 通过对前人关于粒料类材料安定性研究进行总结,提出了一种适用于评价循环旋转轴压下大粒径级配碎石试件安定性行为的方法。
(2) 大粒径级配碎石试件在循环旋转轴压下,其累积轴向应变随着荷载的提升而增加,且累积轴向应变增加的速率随着荷载等级的提升快速增大。大粒径级配碎石试件较常规粒径级配碎石试件具有更强的骨架结构性能,更优的安定性、抗变形和承载能力。
(3) 在本次试验中,大粒径级配碎石试件安定临界荷载最低为192.63 kPa,最高为215 kPa,均明显高于常规粒径碎石试件的174.55 kPa,因此常规粒径级配碎石试件更容易发生塑性蠕变。
(4) 试件的累积轴向应变、安定临界荷载和破坏临界荷载与级配参数间的关系表明,试件的抗变形能力和承载能力与其骨架结构性能和密实程度均存在密切关系,级配碎石试件在恰当的大粒径碎石含量以及较高的密实程度下具有更优的性能表现。
(5) 随着CBR值的增大,试件的轴向累积应变减小,表明试件的变形与其骨架结构性能有着密切的关系。综合分析安定临界荷载、破坏临界荷载、CBR值、累积轴向应变和级配参数之间的关系,最后推荐最佳级配设计范围在SJJP-3和SJJP-4之间。
| [1] |
王文真, 申爱琴, 郭寅川, 等. 基于图像分析的粗集料形状特征参数及分布规律[J]. 公路交通科技, 2020, 37(1): 25-31. WANG Wen-zhen, SHEN Ai-qin, GUO Yin-chuan, et al. Shape Feature Parameters and Distribution Rule of Coarse Aggregate Based on Image Analysis[J]. Journal of Highway and Transportation Research and Development, 2020, 37(1): 25-31. |
| [2] |
涂慕溪, 严二虎, 陈礼彪, 等. 基于性能的级配碎石混合料设计指标[J]. 公路交通科技, 2019, 36(9): 31-36. TU Mu-xi, YAN Er-hu, CHEN Li-biao, et al. Performance-based Design Indicators for Graded Macadam Mixture[J]. Journal of Highway and Transportation Research and Development, 2019, 36(9): 31-36. |
| [3] |
WANG J. Analysis the Control Techniques of Reflection Crack on Asphalt Overlay of Old Cement Concrete Pavement[J]. Applied Mechanics and Materials, 2012, 204/205/206/207/208: 1945-1948. |
| [4] |
张俊文, 王海龙, 陈绍杰. 大粒径破碎岩石承压变形特性[J]. 煤炭学报, 2018, 43(4): 1000-1007. ZHANG Jun-wen, WANG Hai-long, CHEN Shao-jie, et al. Bearing Deformation Characteristics of Large-size Broken Rock[J]. Journal of China Coal Society, 2018, 43(4): 1000-1007. |
| [5] |
付其林, 魏建国, 周兴壮. 开级配大粒径沥青碎石低温性能评价[J]. 建筑材料学报, 2020, 23(4): 896-903. FU Qi-lin, WEI Jian-guo, ZHOU Xing-zhuang. Evaluation of Low Temperature Performance of Open-graded Large Stone Asphalt Mixes[J]. Journal of Building Materials, 2020, 23(4): 896-903. |
| [6] |
WERKMESTER S. Shakedown Analysis of Unbound Granular Materials Using Accelerated Pavement Test Result Form New Zealand's CAPTIF Facility[C]//GeoShanghai International Conference 2006. Shanghai: [s. n. ], 2006.
|
| [7] |
WERKMEISTER S. Permanent Deformation Behaviour of Unbound Granular Materials in Pavement Constructions[D]. Dresden: University of Technology, 2003.
|
| [8] |
张吉庆. 路用粒料类材料安定行为及路面结构安定性分析研究[D]. 广州: 华南理工大学, 2012. ZHANG Ji-qing. Study on Shakedown Behavior of Granular Material Used in Pavement and Shakedown Analysis of Pavement Structures[D]. Guangzhou: South China University of Technology, 2012. |
| [9] |
庄妍, 王康宇. 基于Von-Mises屈服准则的结构安定性研究[J]. 地下空间与工程学报, 2016, 12(增1): 170-191. ZHUANG Yan, WANG Kang-yu. Shakedown Analysis of Structures Obeying Von-mises Criterion[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(S1): 170-191. |
| [10] |
蒋应军, 陈浙江, 李寿伟. 级配碎石塑性变形特性及其安定行为的数值模拟[J]. 同济大学学报: 自然科学版, 2015, 43(6): 872-876. JIANG Ying-jun, CHEN Zhe-jiang, LI Shou-wei, et al. Plastic Deformation Characteristics and Numerical Simulation of Shakedown Behavior of Graded Broken Stone[J]. Journal of Tongji University: Natural Science, 2015, 43(6): 872-876. |
| [11] |
陈忠达, 袁万杰, 高春海. 多级嵌挤密实级配设计方法研究[J]. 中国公路学报, 2006, 19(1): 32-37. CHEN Zhong-da, YUAN Wan-jie, GAO Chun-hai. Research on Design Method of Multilevel Dense Built-in Gradation[J]. China Journal of Highway and Transport, 2006, 19(1): 32-37. |
| [12] |
林绣贤. 沥青混凝土合理集料组成的计算公式[J]. 华东公路, 2003(1): 82-84. LIN Xiu-xian. The Calculating Formula of Aggregate Composition of Rational Bituminous and Concrete[J]. East China Highway, 2003(1): 82-84. |
| [13] |
SHARP R W, BOOKER J R. Shakedown of Pavements under Moving Surface Loads[J]. Journal of Transportation Engineering, 1984, 110(1): 1-14. |
| [14] |
WERKMEISTER S, DAWSON A R, WELLNER F. Permanent Deformation Behavior of Granular Materials and the Shakedown Concept[J]. Transportation Research Record, 2001, 1757: 75-81. |
| [15] |
DAWSON A R, MUNDY M J, HUHTALA M. European Research into Granular Material for Pavement Bases and Subbases[J]. Transportation Research Record, 2000, 1721: 91-99. |
| [16] |
CHEN W B, FENG W Q, YIN J H, et al. Characterization of Permanent Axial Strain of Granular Materials Subjected to Cyclic Loading Based on Shakedown Theory[J]. Construction and Building Materials, 2019, 198: 751-761. |
| [17] |
YIN J H. Non-linear Creep of Soils in Oedometer Tests[J]. Geotechnique, 1999, 49(5): 699-707. |
| [18] |
JTG 3430—2020, 公路土工试验规程[S]. JTG 3430—2020, Test Methods of Soils for Highway Engineering[S]. |
 2021, Vol. 38
2021, Vol. 38
