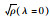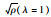扩展功能
文章信息
- 周辰雨, 周猛, 余强, 赵轩, 张硕
- ZHOU Chen-yu, ZHOU Meng, YU Qiang, ZHAO Xuan, ZHANG Shuo
- 基于T-S模糊方法的车辆主动悬架多目标控制研究
- Study on Multi-objective Control of Vehicle Active Suspension Based on T-S Fuzzy Method
- 公路交通科技, 2021, 38(10): 144-152
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(10): 144-152
- 10.3969/j.issn.1002-0268.2021.10.019
-
文章历史
- 收稿日期: 2021-02-24
主动悬架可以根据行驶路面不同,有效保证车辆的平顺性和操纵稳定性,是当前智能车辆、悬架领域研究的热点。目前所采用的主动悬架控制算法控制目标经过设定后便不能根据路面情况进行调整,控制效率受到了限制。对此,不同学者提出了不同控制策略,同时获得较小的车身加速度和悬架挠度[1],其中最优控制是实现这一目标的有效方法之一[2-4]。虽然该算法在长时间的发展中逐渐成熟,但对于主动悬架控制不同性能目标而言,根据不同路面干扰输入设计控制器参数从而提升控制器效率问题,依然是研究的重要方向[5]。与此同时,众多学者引入了几种新颖的最优控制方案[6-7],来解决此类主动悬架控制器效率下降、算法保守的不足[8]。例如,自适应动态规划中局部系统动态知识或无模型算法的应用[9]。但是,这使得稳定性分析变得困难,需要基于模型的控制来促进主动悬架的稳定性分析[10]。
另外,电液主动悬架因其较高的比功率是乘用车和重型商用车辆中最有效的作动器之一[11],对电液作动器内环控制也需要精确的模型作为基础,非线性和相关参数的不确定性是主动控制策略设计中必不可少的考虑因素[12-14]。在建模阶段,为了简化控制设计,对模型精度影响不大的非线性条件通常被假定为常数或被忽略,造成控制器设计误差。为了克服这个问题,反演控制、滑模控制等控制策略被逐渐应用于主动悬架中[15-16]。反演控制由于其较好的鲁棒性和渐近稳定性得到了广泛的应用,是基于李雅普诺夫稳定性分析的有效方法[17],但是当迭代步骤的数量较大时,其性能急剧下降,导致微分爆炸的发生。而滑模控制可以获得良好的鲁棒性和系统瞬态性能[18],但在处理延迟问题时引起的系统颤振降低了系统稳定性[19]。
除了系统的控制稳定性,车辆的侧倾稳定性是主动悬架需要保证的另一个主要性能。为了提升车辆抗侧翻能力,采用主动防倾杆和直线作动器的主动悬架有效地降低了车辆在危险工况下发生侧翻的概率,其中采用直线作动器的主动悬架由于其作用更加直接受到了研究者的广泛关注。在当前的主动悬架防侧倾控制中,通常采用LTR阈值控制方法,该方法检测到车辆侧倾角超过阈值时,进行相应的防侧倾控制。该类控制方法的一个主要不足是其无法将侧倾阈值和车辆平顺性等相关性能控制相融合,也无法在该参数效应下分析系统的稳定性[20]。
本研究采用Takagi-Sugeno(T-S)模糊控制方法,将加速度、悬架动挠度等控制目标进行模糊融合,并采用自适应鲁棒控制对外环期望力进行跟踪。通过采用T-S模糊控制方法将稳定性分析和性能优化不等式组进行融合,在较小路面激励下采用较大的加速度权重系数并在较大路面激励下采用较大的悬架动挠度权重系数。同时通过对悬架动挠度的优化,抑制车辆转向工况中车身过度侧倾,避免悬架过度拉伸、压缩的危险工况。建立SIMULINK®及CARSIM®联合模型,对本研究提出的控制策略进行仿真试验,通过不同路面输入及转向工况,验证算法的准确性。
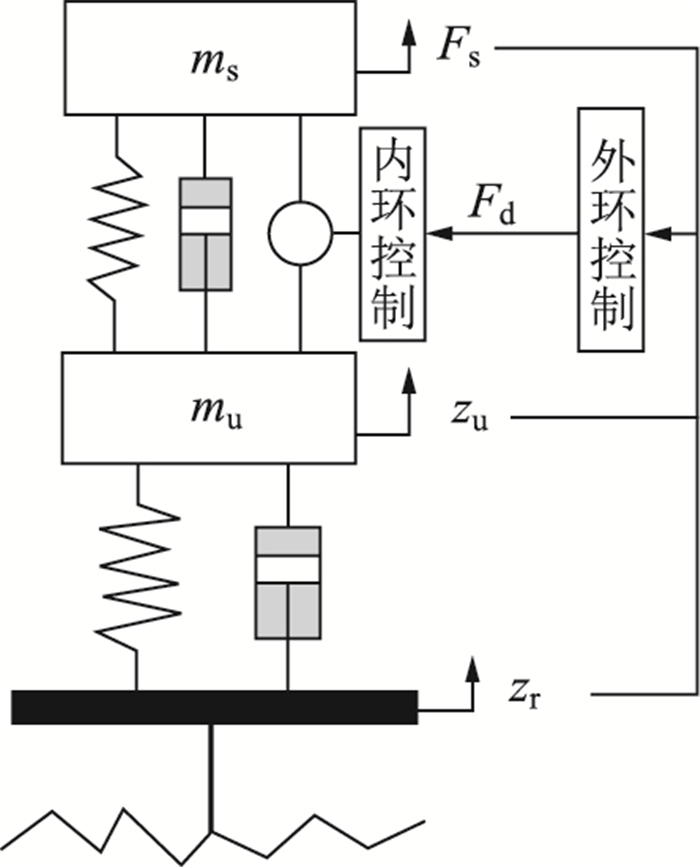
1 基于T-S模糊的主动悬架建模方法二自由度悬架模型如图 1所示,图中ms和mu分别表示簧载质量和非簧载质量;zs和zu分别表示其位移;ks和cs分别为悬架刚度和阻尼;Fd为簧上质量与簧下质量之间的电液作动器的期望输出力;zr为路面输入激励;kt为车轮刚度。该物理模型可以通过以下状态方程(1)进行描述:
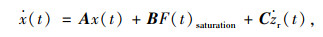
|
(1) |
|
| 图 1 四分之一汽车主动悬架模型 Fig. 1 Active suspension model of 1/4 vehicle |
| |
式中, 状态变量x(t)= [x1, x2, x3, x4]T= [zs-zu, 
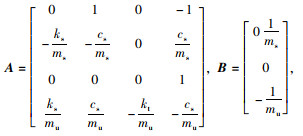


|
(2) |
式中,Fmax及Fmin为输入力的界限, 分别代表上限和下限,是执行器实际产生的力。为了根据不同的路面输入调节控制目标,引入目标矩阵:
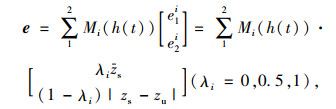
|
(3) |
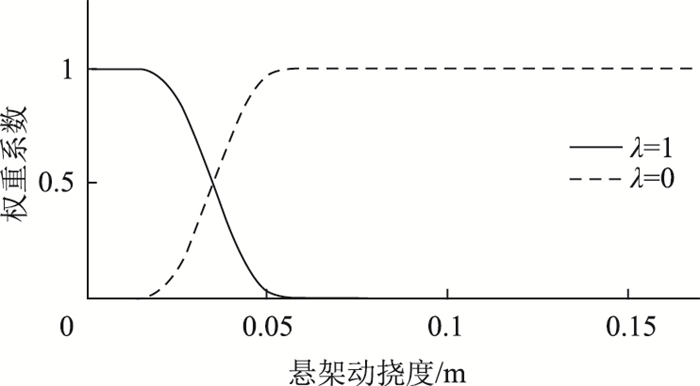
式中,h (t)是时域中悬架挠度;ei为局部性能输出矩阵;λi表示上述性能权重系数,用于描述式(3)中的不同模糊函数;Mi (h (t))>0是隶属度函数且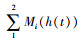
|
| 图 2 模糊隶属度函数 Fig. 2 Fuzzy membership function |
| |
当主动悬架性能矩阵满足要求时,该静态反馈作动器的求解问题可以转化为一个线性矩阵不等式组的求解问题,该线性矩阵不等式组可以表示为:
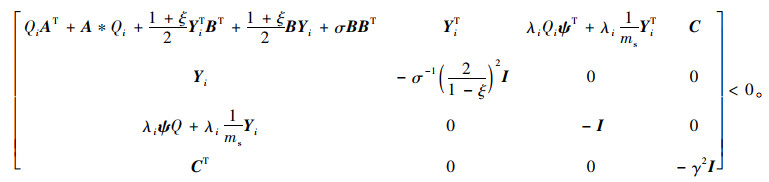
|
(4) |

|
(5) |
式中,*表示对称矩阵块;I用于描述和对称矩阵Pi同维度的单位矩阵,Pi>0表示该矩阵为正定矩阵,且Qi= Pi-1,T表示矩阵的转置,Yi= KiQi是与反馈系数Ki相关的中间矩阵,σ>0,γ>0,δ为性能指标参数,同时引入性能矩阵φ = [1 0 0 0]及ψ = [-ks/ms -cs/ms 0 cs/ms],悬架动挠度和车身加速度可以表示为zs-zu= (1-λi)φx,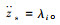
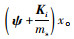
证明:引入Lyapunov函数V (x(t))= xT(t)·Pix (t),对其进行求导可以得到:
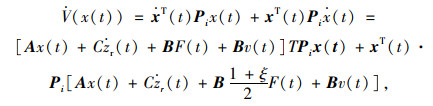
|
(6) |
式中,v (t)=F (t)saturation- (1+ξ)F (t)/2,根据饱和作动器输出力相关引理[19],可以得到:
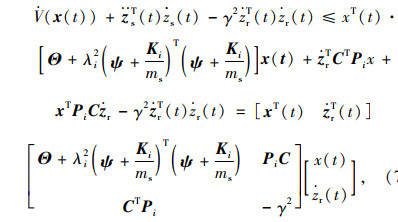
|
(7) |
其中,
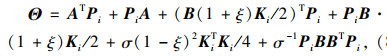
|
(8) |
当且仅当:
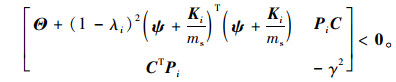
|
(9) |
系统在零干扰下渐近稳定。对上式前后同乘以矩阵diag (Qi I)及其转置矩阵,并采用Schur补对其进行表述,可得性能矩阵不等式。对方程左方进行积分,可以得到积分耗散不等式:
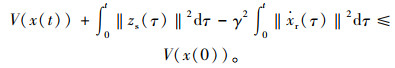
|
令不等式右侧V (x (0))=0并且假设路面干扰输入上界为



|
其中eigen (·)是矩阵的特征值,为了保证悬架簧载质量和非簧载质量相对运动处于一定范围内,对其进行不等式限制如下:
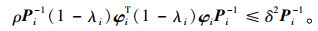
|
(10) |
同样采用舒尔补对上述不等式进行转述,可以得到其不等式表达如式(5)所示。将该控制器反馈增益的求解转化为线性矩阵不等式的求解,通过Ki= YiQi-1得到最终反馈增益。此处选择MATLAB®LMI工具箱对线性矩阵不等式进行求解,提升了不等式的求解效率。当且仅当该悬架加速度鲁棒性能矩阵、悬架动挠度矩阵组成的不等式组有解,且参数γ和ρ最小化时,使用PDC方法可得主动悬架作动器期望控制力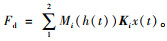
由于非线性不确定性通常包含在求解跟踪力的内环当中,因此当车辆参数发生变化时,很难保证跟踪的准确性。本研究采用自适应鲁棒控制(ARC)求解内环跟踪力,常规模型可以表示为:
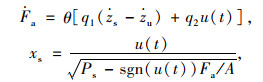
|
(11) |
式中,q1和q2为已知参数;q1为与作动器活塞两侧面积相关的结构参数;q2为与通流截面相关的结构参数;θ为液压系统未知参数;Ps为系统流体压力;Fa为施加在执行器活塞上的力; A为活塞面积; xs为阀芯位移。对于自适应鲁棒控制,力由两项组成[13],即自适应项ua和鲁棒项us。
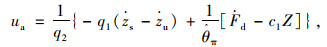
|
(12) |
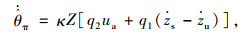
|
(13) |
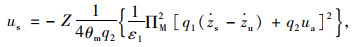
|
(14) |
式中,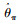
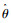
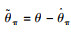
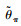
本研究采用SIMULINK®及CARSIM®联合仿真方法,通过正弦波路面输入、随机波路面输入对该控制策略的平顺性进行对比研究,控制结构框图如图 3所示。同时通过设定避障工况,对被动悬架和主动悬架在高速行驶下转向盘突然转向时侧倾稳定性进行对比研究。为了验证自适应鲁棒控制对不确定参数改变后性能控制的鲁棒性,通过调节车辆参数,对力的跟踪效果进行了研究分析。车辆结构参数如表 1所示,表中各参数含义如前文所示。表 2为模糊鲁棒控制器参数,在实际应用中,选定的ρ, γ2值越大,悬架动挠度越小,通过反复调节对比,最终确定该参数具体值。
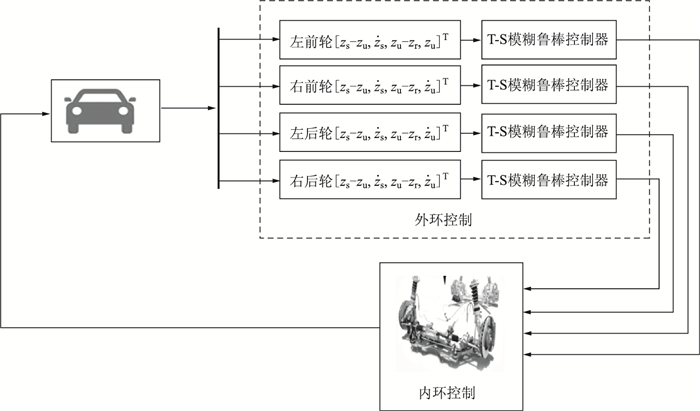
|
| 图 3 控制结构框图 Fig. 3 Block diagram of control structure |
| |
| 参数 | 参数值 | 参数 | 参数值 | |
| ks/(N·m-1) | 16 000 | q1/m4 | 1.70×10-6 m | |
| ms/kg | 300 | q2/(m5·s-1·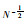 |
1.86×10-6 | |
| mu/kg | 60 | θ/(N·m-4) | 3.79×1011 | |
| cs/(N·s·m-1) | 1 000 | θm/(N·m-4) | 2.25×1011 | |
| kt/(N·m-1) | 190 000 | θM/(N·m-4) | 5.28×1011 |
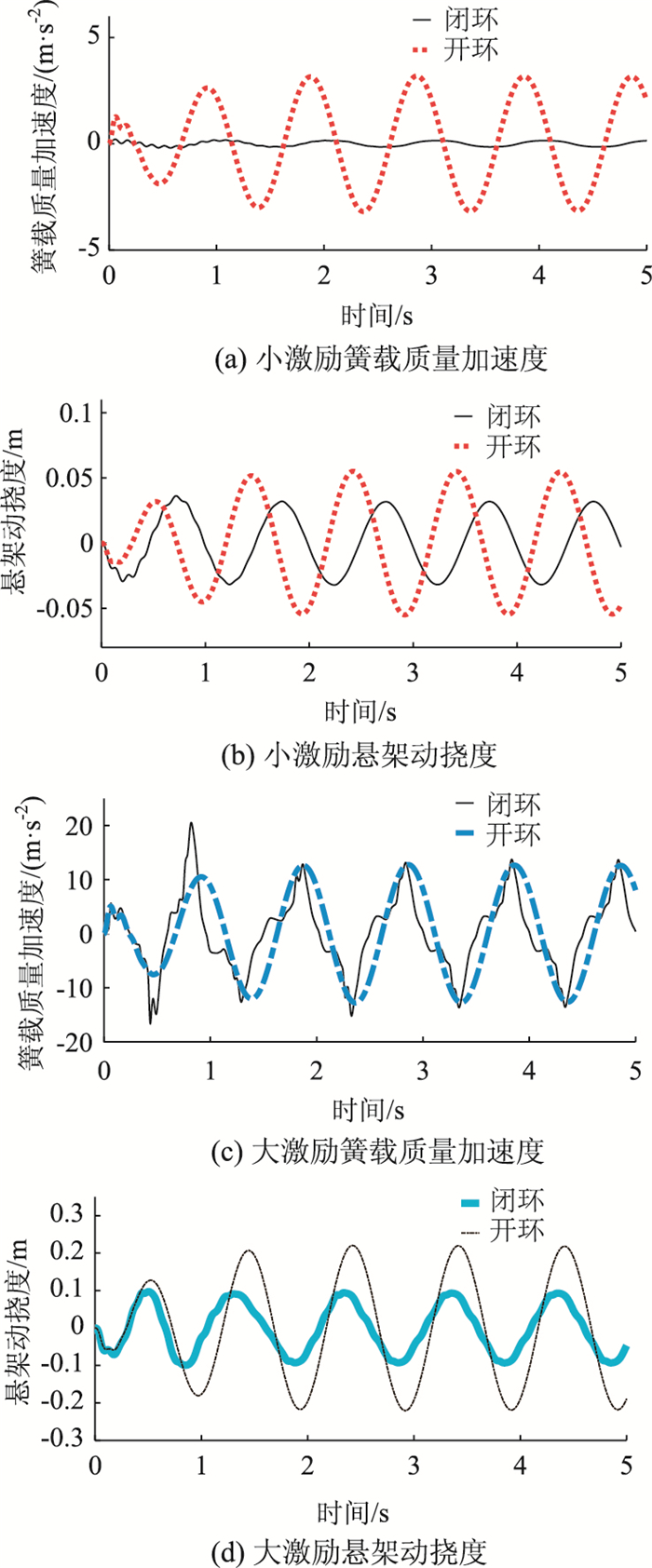
正弦输入和随机输入是当前常见的2种车辆平顺性验证试验方法,首先设计路面为1 Hz正弦波输入,为了验证控制器对不同路面下控制目标的转移效果,本研究对正弦波幅值分别设置为0.03 m及0.12 m,对其加速度、悬架动挠度与被动悬架进行对比,其结果如图 4所示。
|
| 图 4 不同正弦激励的悬架响应 Fig. 4 Suspension responses under different sinusoidal excitations |
| |
由结果可见,基于T-S Fuzzy的鲁棒控制可以在小激励下保证车辆拥有较小的车身加速度,与被动悬架相比其加速度峰值降低了70%以上,悬架动挠度峰值降低了20%以上。当路面激励逐渐增大为大激励时,该控制策略可以将控制目标转移并限制悬架动挠度,防止其撞击限位块。由图 4中对比可以看出,在该大激励下,簧载质量加速度较被动悬架相比,虽在试验初始阶段有所增加,但是其悬架动挠度峰值下降了15%以上,最大程度地降低了悬架动挠度,防止其冲击限位块。通过仿真结果也可以看出,该控制策略对控制目标的转移是有效的。表 3中也对加速度均方根值进行了计算,可以看出不论在大激励还是小激励情况下,其加速度均方根值均下降18%以上。
| 试验组别 | 随机输入被动悬架 | 随机输入主动悬架 | 正弦大激励主动悬架/ 被动悬架 | 正弦小激励主动悬架/ 被动悬架 |
| RMS/(m·s-2) | 0.160 1 | 0.153 7 | 6.857 5/ 8.387 6 | 0.113 2/ 2.099 7 |
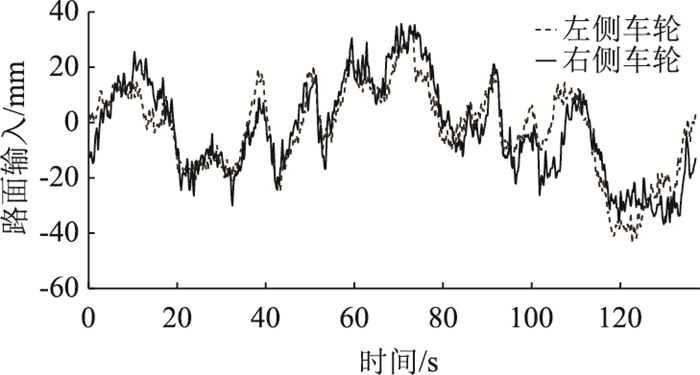
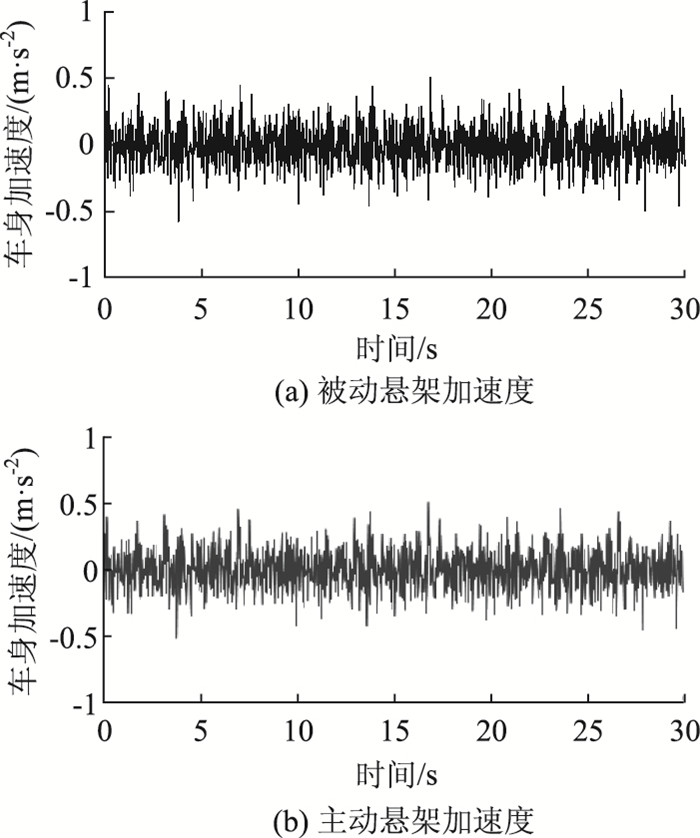
为了进一步验证算法的有效性,采用CARSIM®与SIMULINK®联合仿真,在模型构建中,单个车轮处均采用本研究所提出的T-S Fuzzy鲁棒控制策略,选择随机激励并采集车辆质心加速度验证本研究所提出算法的有效性。图 5为左右两侧车轮路面随机输入谱,被动悬架和主动悬架对比结果如图 6、图 7所示。可以看出,采用该策略的主动悬架在前轴与后轴处对悬架动挠度都有一定衰减效果,特别是车辆后轴,悬架动挠度峰值可降低近20%,前轴对悬架动挠度的抑制并没有后轴明显。这主要是由于后轴的悬架动挠度较大,已经处于模糊隶属度函数中控制目标转移区间内,控制目标发生了转移,从而有效地降低了悬架的动挠度。对车辆质心加速度对比可以看出,车辆质心加速度峰值接近,但是根据表 3所述的加速度均方根值可见,采用该主动控制策略的加速度均方根值下降了4%,起到了振动的衰减效果。
|
| 图 5 不同随机激励悬架响应 Fig. 5 Suspension responses under different random excitations |
| |
|
| 图 6 随机输入整车加速度响应 Fig. 6 Acceleration response of vehicle under random input |
| |

|
| 图 7 随机输入整车悬架动挠度响应 Fig. 7 Dynamic deflection responses of vehicle suspension under random input |
| |
由此可以看出,基于T-S Fuzzy的主动悬架鲁棒控制可以在正弦输入及随机输入道路情况下根据路面激励,转换控制目标,获得良好的减振效果。
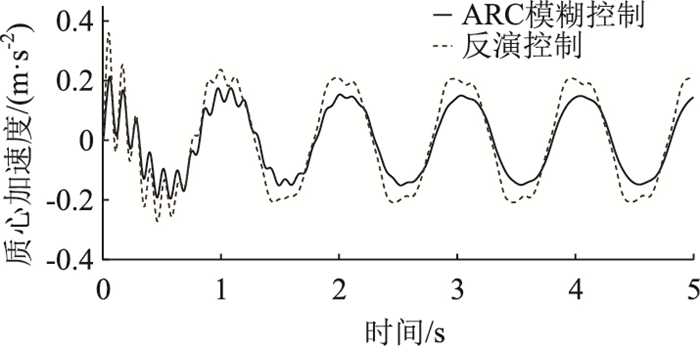
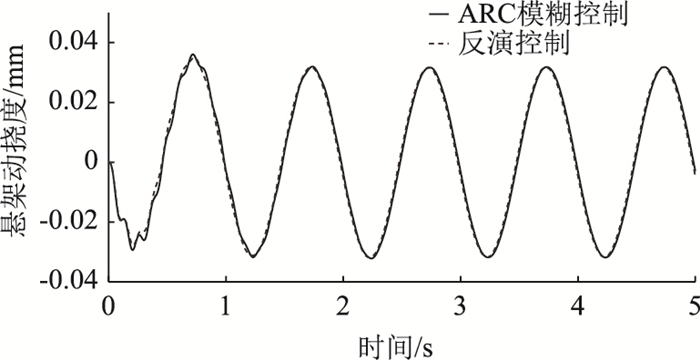
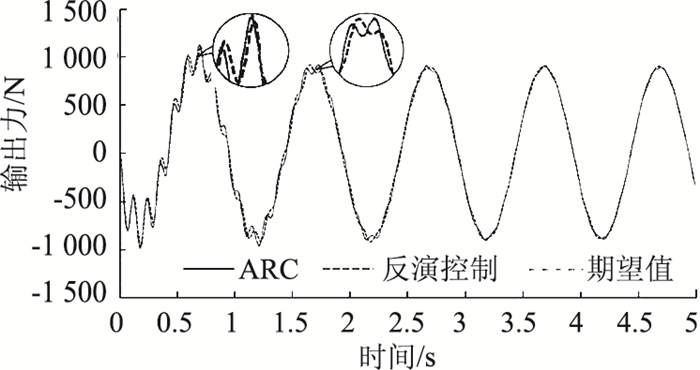
为了验证该控制器在系统参数发生变化时的鲁棒性,本研究将车辆参数θ改变为3.0×1011 N/m4,此时液压缸的体积常数变大,并分析该自适应鲁棒控制的控制性能,其结果如图 8、图 9所示。可以看出,与传统的反演控制主动悬架相比,自适应鲁棒控制在处理非线性不确定性方面效果良好,尽管参数θ发生变化,通过所提出的控制方法可以有效地保持系统控制性能,特别在较大路面输入下,此类参数不确定性通常较为常见。图 10表明了不同控制算法对期望力的跟踪效果,可以明显看出本研究所采用的自适应鲁棒控制跟踪效果优于对比组反演控制,放大曲线的细节可以看出其输出力与期望输出力基本一致。
|
| 图 8 簧载质量加速度响应 Fig. 8 Acceleration response of sprung mass |
| |
|
| 图 9 悬架动挠度响应 Fig. 9 Dynamic deflection responses of suspension |
| |
|
| 图 10 期望力跟踪性能 Fig. 10 Tracking property of expected force |
| |
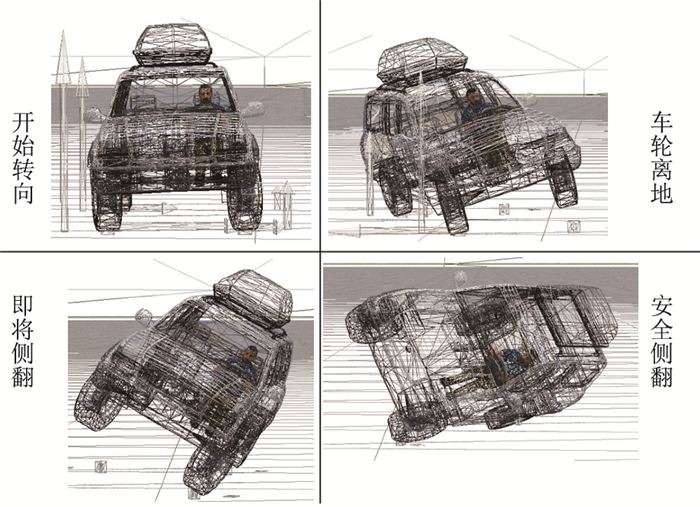
由于本控制策略对悬架动行程进行了限制,因此,为进一步验证该控制策略在车辆极端高速转向工况下对车辆侧翻的抑制能力,研究选取大角度瞬时转向如图 11所示,在0.5 s内,转向盘转角急剧增大至240°,之后立刻回转至相反方向。仿真采用SIMULINK®及CARSIM®联合仿真的方法,SIMULINK®搭建双环控制器模型,为CARSIM®中的高质心SUV车辆动力学模型提供作动器控制力,通过仿真结果可以看出,被动悬架在极端输入下,在3 s时已经完全失去了控制,其侧倾角突增;在4 s时完全侧翻,其全阶段车辆状态如图 12所示,侧倾角和质心侧偏角响应如图 13、14所示。当采用T-S Fuzzy鲁棒主动控制时,车辆首先向左转向,侧倾角逐渐增大,左右两侧悬架动挠度逐渐增大并开始发生控制目标转移,保证悬架整体对车辆强有力支撑作用;之后随着转向盘突然变向,悬架的拉伸与支撑作用左右互换,此时控制目标依然控制悬架动挠度,侧倾角不再反向增大,车辆未发生侧翻。由质心侧偏角对比可以看出,在发生侧翻前,主动悬架与被动悬架质心侧偏角都发生了较大的变化,随着被动悬架发生侧翻,其质心侧偏角在侧翻前突增,而主动悬架由于垂向力的控制,同时也增加了车辆的横向稳定性,质心侧偏角逐渐减小,最终随车速降低为零。
|
| 图 11 转向盘转角输入 Fig. 11 Steering wheel input |
| |
|
| 图 12 车辆侧翻状态历程 Fig. 12 History of vehicle rollover states |
| |
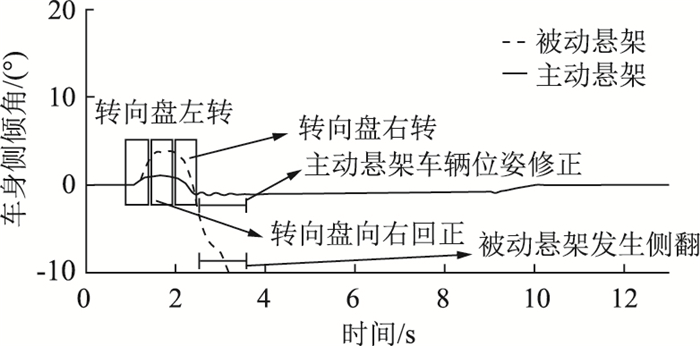
|
| 图 13 侧倾角响应 Fig. 13 Roll angle response |
| |
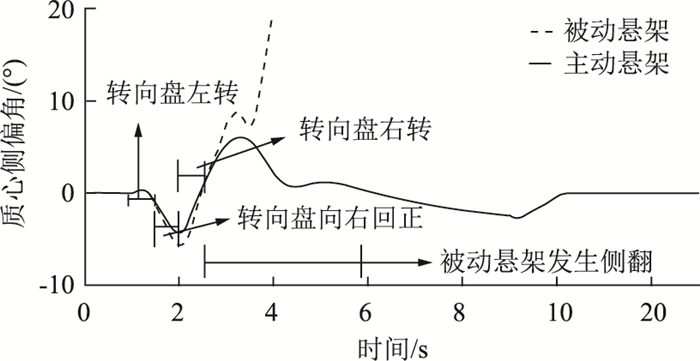
|
| 图 14 质心侧偏角响应 Fig. 14 Sideslip angle response of center of mass |
| |
4 结论
(1) 采用基于T-S模糊建模方法所构建的自适应鲁棒控制可以根据路面输入工况对控制目标进行有效的转换,当路面输入较小时,以车辆平顺性为调节目标,降低悬架质心加速度。当路面输入较大时,控制目标转移至限制悬架动挠度,从而降低悬架撞击限位块概率,最终提升车辆平顺性。仿真结果表明,在小激励下,其加速度峰值可以降低70%以上,在大激励下动挠度峰值相比被动悬架降低了15%以上。
(2) 通过内环控制对外环期望力的跟踪效果对比可见,本研究所提出的自适应鲁棒控制器可以在参数发生变化时,有效的保证期望力的跟踪效果,与反演控制相比,此控制策略的力跟踪效果更佳。
(3) 由于T-S Fuzzy鲁棒控制对悬架的拉伸、压缩量进行约束,因此当车辆发生大角度侧倾时,可以提升在车辆危险工况下对车身的支撑效果。采用转向盘瞬时大转角避障模拟工况可以看出,基于T-S Fuzzy的自适应鲁棒控制可以降低车辆侧倾角60%以上,防止车辆发生侧翻,提升车辆在危险工况下的行驶安全性。尽管如此,在本研究中,对喷嘴挡板、弹簧的非线性和其他一些未知参数仍采用忽略的方式进行简化,将在以后工作中进行改进提升。
| [1] |
MIN X, LI Y, TONG S, et al. Adaptive Fuzzy Output Feedback Inverse Optimal Control for Vehicle Active Suspension Systems[J]. Neurocomputing, 2020, 403(1): 257-267. |
| [2] |
SUN W, GAO H, YAO B. Adaptive Robust Vibration Control of Full-car Active Suspensions with Electrohydraulic Actuators[J]. IEEE Transactions on Control Systems Technology, 2013, 21(6): 2417-2422. |
| [3] |
MENG J, CHEN Q, HE R. Research on Optimal Control for the Vehicle Suspension Based on the Simulated Annealing Algorithm[J]. Journal of Applied Mathematics, 2014(5): 1-5. |
| [4] |
MRAZHUA J, TISSSIR E H, OUAHI M. Fuzzy Fault-tolerant H∞ Control Approach for Nonlinear Active Suspension Systems with Actuator Failure[J]. Procedia Computer Science, 2019, 148: 465-474. |
| [5] |
D'AMATO F J, VIASSOLS D E. Fuzzy Control for Active Suspensions[J]. Mechatronics, 2000, 10(8): 897-920. |
| [6] |
NKOMO L I, DOVE A, NGWAKO M T, et al. Heaviside Based Optimal Control for Ride Comfort and Actuation Energy Optimization in Half-car Suspension Systems[J]. IFAC-Papers on Line, 2017, 50(2): 259-264. |
| [7] |
LONG G, DING F, ZHANG N, et al. Regenerative Active Suspension System with Residual Energy for In-wheel Motor Driven Electric Vehicle[J]. Applied Energy, 2020, 260(1): 114180-114198. |
| [8] |
陶伟, 刘志强, 陈世斌, 等. 基于模糊控制的轮式装载机驾驶室悬架减振设计[J]. 公路交通科技, 2020, 37(11): 118-129. TAO Wei, LIU Zhi-qiang, CHEN Shi-bin, et al. Design of Suspension Damping for Wheel Loader Cab Based on Fuzzy Control[J]. Journal of Highway and Transportation Research and Development, 2020, 37(11): 118-129. |
| [9] |
JIANG Y, JIANG Z. Computational Adaptive Optimal Control for Continuous-Time Linear Systems with Completely Unknown Dynamics[J]. Automatica, 2012, 48(10): 2769-2704. |
| [10] |
余曼, 周辰雨, 魏朗, 等. 基于T-S模糊模型的车辆电液悬架系统H∞控制[J]. 中国公路学报, 2018, 31(8): 205-217. YU Man, ZHOU Chen-yu, WEI Lang, et al. Takagi-Sugeno Fuzzy-model-based Automobile Electrohydraulic Active Suspension H-infinity Control[J]. China Journal of Highway and Transport, 2018, 31(8): 205-217. |
| [11] |
ZOU J, GUO X, ABDELKAREEM, et al. Modelling and Ride Analysis of a Hydraulic Interconnected Suspension Based on the Hydraulic Energy Regenerative Shock Absorbers[J]. Mechanical Systems and Signal Processing, 2019, 127(1): 345-369. |
| [12] |
SUN W, PAN H, ZHANG Y, et al. Multi-objective Control for Uncertain Nonlinear Active Suspension Systems[J]. Mechatronics, 2014, 24(4): 318-327. |
| [13] |
CHANTRANUWATHANA S, PENG H. Adaptive Robust Force Control for Vehicle Active Suspensions[J]. International Journal of Adaptive Control & Signal Processing, 2004, 18(2): 83-102. |
| [14] |
WANG Q, ZHAO Y, XU H, et al. Adaptive Backstepping Control with Grey Signal Predictor for Nonlinear Active Suspension System Matching Mechanical Elastic Wheel[J]. Mechanical Systems and Signal Processing, 2019, 131(1): 97-111. |
| [15] |
秦武, 朱钢, 上官文斌, 等. 具有扰动观测器的汽车主动悬架滑模控制[J]. 振动工程学报, 2020, 33(1): 158-167. QIN Wu, ZHU Gang, SHANGGUAN Wen-bin, et al. Sliding Mode Control with Disturbance Observer for Active Suspension[J]. Journal of Vibration Engineering, 2020, 33(1): 158-167. |
| [16] |
寇发荣, 许家楠, 刘大鹏, 等. 电动静液压主动悬架双滑模控制研究[J]. 中国机械工程, 2019, 30(5): 542-548, 553. KOU Fa-rong, XU Jia-nan, LIU Da-peng, et al. Study on Dual Sliding Mode Control of EHA Active Suspensions[J]. China Mechanical Engineering, 2019, 30(5): 542-548, 553. |
| [17] |
李雅琦, 李伟, 陈应鹏, 等. 基于RBF的主动悬架反演滑模控制策略研究[J]. 机电工程, 2020, 37(4): 425-428. LI Ya-qi, LI Wei, CHEN Ying-peng, et al. Active Suspension Inversion Sliding Mode Control Strategy Based on RBF[J]. Journal of Mechanical & Electrical Engineering, 2020, 37(4): 425-428. |
| [18] |
DUAN M, JIA J, ITO T. Fast Terminal Sliding Mode Control Based on Speed and Disturbance Estimation for an Active Suspension Gravity Compensation System[J]. Mechanism and Machine Theory, 2021, 155(1): 104073. |
| [19] |
DU H, ZHANG N. Fuzzy Control for Nonlinear Uncertain Electrohydraulic Active Suspensions with Input Constraint[J]. IEEE Transactions on Fuzzy Systems, 2009, 17(2): 343-356. |
| [20] |
田顺, 魏朗, 刘晶郁, 等. 全速度多工况下客车横向转移率预测研究[J]. 中国安全科学学报, 2016, 26(11): 127-132. TIAN Shun, WEI Lang, LIU Jing-yu, et al. Study on Prediction of Bus Lateral Transfer Ratio Considering both Whole Speed Range and Muti-conditions[J]. China Safety Science Journal, 2016, 26(11): 127-132. |
 2021, Vol. 38
2021, Vol. 38