扩展功能
文章信息
- 孙然然, 张静萱, 朱广宇
- SUN Ran-ran, ZHANG Jing-xuan, ZHU Guang-yu
- 基于SVM的危险交通流状态实时识别模型
- A Real-time Recognition Model of Dangerous Traffic Flow State Based on SVM
- 公路交通科技, 2021, 38(10): 120-128
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(10): 120-128
- 10.3969/j.issn.1002-0268.2021.10.016
-
文章历史
- 收稿日期: 2020-08-18
2. 北京交通大学 综合交通运输大数据应用技术交通运输行业重点实验室, 北京 100044;
3. 国家铁路局规划与标准研究院, 北京 100055
2. Key Laboratory of Big Data Application Technologies for Comprehensive Transport of Transport Industry, Beijing Jiaotong University, Beijing 100044, China;
3. Planning and Standard Research Institute of National Railway Administration, Beijing 100055, China
实时高效的对道路交通状况进行识别,有助于降低交通事故的发生率,保障交通系统的运营安全。交通事故是各种事件在特定的动态交通系统中互为因果、综合作用的结果[1],往往呈现为多种形态,主要包括突发型、渐进型、混合型等。事故发生的前期通常会表现出某些交通运营状况的渐变或突变[2],不同程度地体现在交通流参数上。因此,通过实时监测道路交通流参数的变化情况,可有效对易引发交通事故的危险交通流状态进行识别,及时预判潜在的交通事故,为相关管理部门制订相应的管控措施提供依据,以达到减少交通事故的目的[3]。
早期对交通流状态的研究,侧重于交通事故检测与交通拥堵判别,主要有California算法[4]、静态判别McMaster算法[5]、基于数理统计的平滑算法[6]等。上述经典算法主要通过辨识道路断面交通流量、地点车速、交通密度等交通参数变化的单一方法对交通流进行分析与处理,快速判定是否有交通事故及交通拥挤发生,且算法检测效率低,误报率高。后期,国内外先进交通流检测设备的涌现,为交通事故预测与异常交通状态辨识的研究提供了便利,可通过监测实时交通流数据来研究交通流运行状态,常见的有基于视频数据处理的异常交通流状态识别技术[7-10]。例如:方晓莹等[7]运用数字图像处理技术获取交通参数的变化情况,进而对各时刻的异常交通状态检测并根据各参数的变化趋势预测异常交通状态。林震等[11]分析交通事故与车速偏差量之间具有显著的相关性,以车速指标的不稳定性来表征异常交通运行状态,构建基于贝叶斯理论的交通事故最小风险预测模型,及时准确地评估异常交通流状态。徐铖铖等[12]分析高速公路交通流数据与事故数据,构建交通安全实时评价指标体系,运用Fisher判别分析方法,构造关于实时交通流参数的线性判别函数,根据判别函数值判断实时交通流状态。
随着计算机技术以及智能交通运输体系的发展,人工智能算法在道路异常交通流状态研究中逐渐占主导地位,神经网络、模糊算法和支持向量机等被广泛应用[13-20]。姜桂艳等[13]利用高速公路流量和车道占有率两项指标,基于神经网络构建了一种适用于高速公路的具有3级报警制度的交通事件自动检测系统,结果表明其检测率与检测时间均优于传统算法。向怀坤等[14]提取反映交通流特性的路段车辆占有率和车辆运行速度特征,构建基于粒子群(PSO)算法优化的BP神经网络模型,结果显示PSO神经网络算法提高了交通事件的检测效率。神经网络具有检测率高的特点,但在训练过程中对样本的需求量比较大。由于交通流状态是不断变化的,杨奎河等[15]改善以往单一检测方式,融合多种检测数据,建立基于模糊聚类的交通流状态识别,试验表明, 该方法能更加准确地识别交通流状态,有助于判别路段危险交通状况。模糊算法基于规则将一些难以量化的参数模糊处理,应用具有局限性。在众多人工智能算法中,支持向量机模型凭借其良好的学习能力与泛化能力以及在小样本、高维非线性样本下也可获得最优解而被广泛用于道路交通事故风险预测问题[16-20]。Yuan等[18]分别采用不同非线性核函数的两个支持向量机模型对道路交通事故进行检测,试验结果表明,在分类率、检测时间方面,支持向量机优于多层前向神经网络和概率神经网络模型。周洲等[19]根据高速公路交通流的特点,设计了基于不同核函数的SVM模型用于有无交通事件发生的检测,结果表明,合适的SVM模型和核函数可提高检测率,缩短检测时间。后期,游锦明等[20]基于支持向量机模型实时检测高速公路上的不良交通流状态,为提高支持向量机分类器性能,首先运用主成分分析法对交通流参数进行分析处理,网格遍历法优化模型中的惩罚参数C和核函数参数γ。
上述研究均表明交通事故风险往往与交通流运行中某些实时状态参数(如交通流,车速等)存在显著关系,即危险的交通流状态易诱发交通事故,交通事故的发生也常伴随着危险交通流状态的存在。因此,危险交通流状态的实时识别可转化为分类问题,故选用上述分类性能良好的支持向量机模型作为交通流状态识别模型。针对参数分析不全面以及算法识别效率低等问题,本研究对基于支持向量机的危险交通流状态识别算法进一步优化研究。主要研究内容如下:(1)数据预处理;(2)提取交通事故发生的相关前兆特征变量,并通过相关性选择算法(Relevance Selection Algorithm,RSA)对特征变量降维处理;(3)提出基于改进网格搜索算法的支持向量机模型对危险交通流状态进行识别,应用于某市快速路的事故数据进行案例分析。
1 数据预处理本研究的对象为某市快速路的某个路段,危险交通流的判别以该路段交通事故发生前的交通运行参数为依据。提取2015年6月11日—2015年11月11日的事故数据与事故发生前上游(a1、a2)、下游(a3、a4)各两个检测器的交通流数据(流量F、速度V和时间占有率U)。数据集划分为事故发生的“案例组”和未发生事故的“对照组”,比例为1∶ 1,为保证试验结果的准确性,两组数据选取规则为:无重大天气变化情况下,所选地点、时间段均相同,仅日期不同。
Pande等[21]指出:交通流状态的识别以5 min的时间长度集计较佳。此外,危险交通流状态的识别需具备一定的超前性,故选取事故发生前T1 (5~10 min)和T2 (10~15 min)两个时间片段进行研究。因此,一个事故点包含8条(4个检测器×2个时间段)数据记录,事故发生的前兆特征变量可初定为24个,如表 1所示。其中F (a1, T1)代表a1检测器所检测的交通事故发生前T1时间段的交通流量。原始数据因检测器突发故障等因素,会存在数据不完整、数据异常错误等,需要对数据进一步清洗,最终经过数据提取与预处理,得到案例组和对照组样本各123个,记为数据集A,部分数据如表 2所示。每个样本有24个特征变量和1个类别标签(“1”记为危险状态,“0”记为正常状态)。
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 前兆特征变量 | F(a1, T2) | F(a1, T1) | F(a2, T2) | F(a2, T1) | F(a3, T2) | F(a3_T1) | F(a4_T2) | F(a4_T1) |
| 序号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 前兆特征变量 | U(a1, T2) | U(a1, T1) | U(a2, T2) | U(a2, T1) | U(a3, T2) | U(a3, T1) | U(a4, T2) | U(a4, T1) |
| 序号 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 前兆特征变量 | V(a1, T2) | V(a1, T1) | V(a2, T2) | V(a2, T1) | V(a3, T2) | V(a3, T1) | V(a4, T2) | V(a4, T1) |
| 数据集A | 1 | 2 | … | 245 | 246 |
| F(a1, T1) | 133.5 | 149.5 | … | 129.5 | 134 |
| F(a1, T2) | 135 | 155 | … | 143.5 | 125.5 |
| F(a2, T2) | 142 | 110.5 | … | 132.5 | 129.5 |
| … | … | … | … | … | … |
| 类别标签 | 1 | 1 | … | 0 | 0 |
2 交通事故前兆特征变量降维
由于特征变量的量纲不一致, 首先对其进行归一化处理。为降低模型的计算复杂度、提高分类器性能,本研究构造了一种相关性选择算法(Relevance Selection Algorithm,RSA)首先对路段上事故发生的前兆特征变量进行降维处理。
(1) 特征变量与类别间相关性
记D (i)值表示第i个特征变量与类别的相关性,D (i)值越大,表示特征变量与类别强相关,反之,为弱相关或不相关。
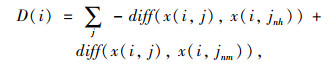
|
(1) |
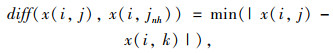
|
(2) |
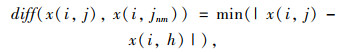
|
(3) |
式中, x(i, j)为所有样本的第j个样本在特征变量i上的取值;x (i, jnh)为与x (i, j)同类别的最近邻;x (i, jnm)为与x(i, j)非同类别的最近邻;diff (x(i, j), x (i, jnh))为x (i, j)与同类别最近邻在特征变量i上的距离;diff (x (i, j), x (i, jnm))为x(i, j)与非同类别的最近邻在特征变量i上的距离。
(2) 特征变量间冗余性
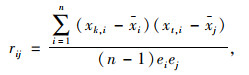
|
(4) |
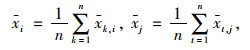
|
(5) |
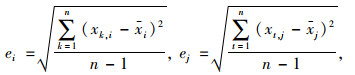
|
(6) |
式中,rij为第i个特征变量与第j个特征变量的相关系数。当两个特征变量之间的相关性越高,所含重复信息越多时,rij绝对值越大。当两个特征变量无相关性时,rij=0;交通事故前兆特征变量之间相关系数绝对值矩阵R表示如下:
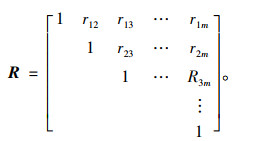
|
(7) |
(3) 特征变量降维算法
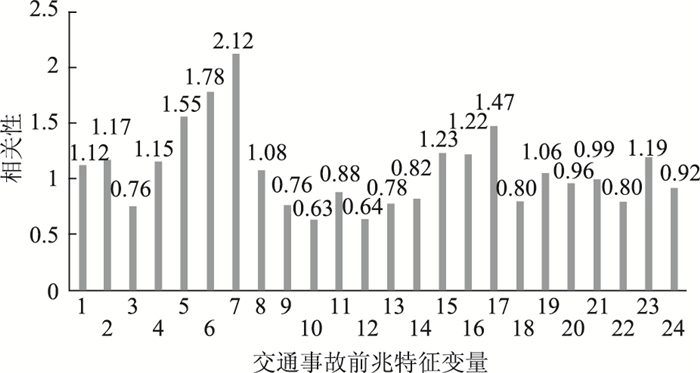
特征变量与类别间的相关性以及各特征变量之间的相关性计算部分结果如图 1、表 3所示。为保证特征变量选取的合理性,最终设计特征变量提取算法如图 2所示。
|
| 图 1 交通事故前兆特征变量与类别相关性 Fig. 1 Correlation between traffic accident precursor characteristic variable and category |
| |
| 特征变量 | F(a1, T2) | F(a1, T1) | … | V(a4, T1) |
| F(a1, T2) | 1 | 0.867 99 | … | 0.283 89 |
| F(a1, T1) | 0.867 99 | 1 | … | 0.322 44 |
| F(a2, T2) | 0.564 68 | 0.614 56 | … | 0.262 95 |
| … | … | … | … | … |
| V(a4, T2) | 0.315 04 | 0.319 49 | … | 0.926 13 |
| V(a4, T1) | 0.283 89 | 0.322 44 | … | 1 |

|
| 图 2 特征变量提取算法 Fig. 2 Feature variable extraction algorithm |
| |
根据上述特征变量提取方案,最终得到包含4个特征变量(F (a3, T2),F (a3, T1),F (a4, T2),F (a4, T1)) 的数据集B。将数据集A、B分为两部分:60%训练集和40%测试集,训练集和测试集包含的“案例组”及“对照组”的样本比例1∶ 1。
3 基于SVM的危险交通流状态识别模型 3.1 基于SVM的危险交通流状态识别支持向量机(Support Vector Machine,SVM)在模式分类问题上, 具有的良好的泛化性能,其主要思想是将输入变量X通过特定的非线性映射算法映射到一个高维特征空间Z,在Z中构造最优分类超平面。
(1) 最优超平面
给定训练数据集:
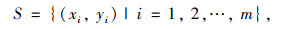
|
(8) |
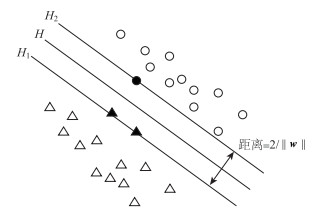
式中,xi∈Rn为第i个样本的特征变量;yi∈n为第i个样本的标签且yi∈ {±1},m为样本规模。SVM目的是寻找一个超平面H将yi以最优的方式区分出来,即不仅可以将标签为1和-1分开,同时还能使分开的数据点距离H最远,如图 3所示,H为最优超平面。超平面可表示为:
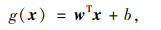
|
(9) |
|
| 图 3 最优超平面图 Fig. 3 Diagram of optimal hyperplane |
| |
式中,x为输入向量;w为权值向量;b为常量参数。
对于yi∈ {±1}的样本点,到超平面的几何间隔为:
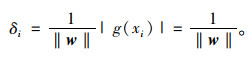
|
(10) |
即H1和H2的距离为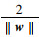
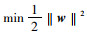
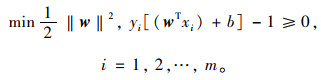
|
(11) |
(2) 惩罚变量
由于两类数据标签有可能存在线性不可分割的情况,进而影响支持向量机分类超平面的形成。因此模型引入惩罚项{ξi}i=1m和惩罚因子C。即上述问题表示为:给定训练样本{ (xi, yi)}i=1m,寻找权值向量w和参数b,使得:
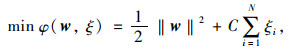
|
(12) |
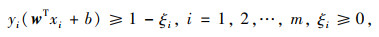
|
(13) |
式中C为用户选定的正参数。引入拉格朗日函数,此问题表示为:
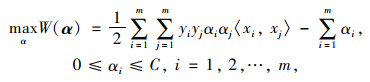
|
(14) |
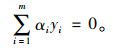
|
(15) |
求解得α = (α1, α2, …, αm)T,超平面进一步表示为:
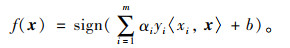
|
(16) |
(3) 核函数
核函数的选择是影响支持向量机模型性能的关键因素,核函数可将线性不可分的数据映射到一个高维的特征空间内,使得数据在该特征空间内是可分的。常用的径向基核函数可将样本映射到一个更高维的空间,参数少且数值计算相对简单。
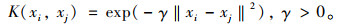
|
(17) |
因此,本研究选用基于径向基核函数的支持向量机模型作为交通流状态识别分类模型,其决策函数为:
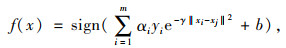
|
(18) |
式中,xi,yi,αi,b为模型优化求解得到的参数;模型求解中惩罚系数C值与核函数中参数γ值影响训练模型的分类性能。传统网格搜索法搜索时间较长,本研究首先在大区域范围内确定小区域,进一步采用较小的步长搜索,首先对数据集B进行训练与测试,实现过程和结果如下。
① 参数寻优。输入数据集B中的训练集,K折交叉验证中K=5,设定a=1%,当网格搜索的参数C,γ的取值所对应的危险交通流状态的识别准确率与前一次的准确率之差比a大,则减小步长,缩小搜索范围。反之,终止搜索。C, γ初始搜索范围:C∈ [2-10, 210],γ∈ [2-10, 210],步长为1。初次SVM参数寻优结果如图 4所示。

|
| 图 4 初次参数寻优结果 Fig. 4 Initial parameter optimization result |
| |
图 4中X,Y,Z轴分别表示γ,C的寻优范围以及危险交通流状态的准确率。得出最优值C=8,γ=0.5,准确率为77.702 7%,寻优时间为2.609 4 s。根据图 4,显然可得,当识别准确率较高时,γ∈ [2-3, 2-2],C∈ [22, 23],即C, γ在该范围内进一步搜索,步长减小为0.1,参数寻优结果如图 5所示。
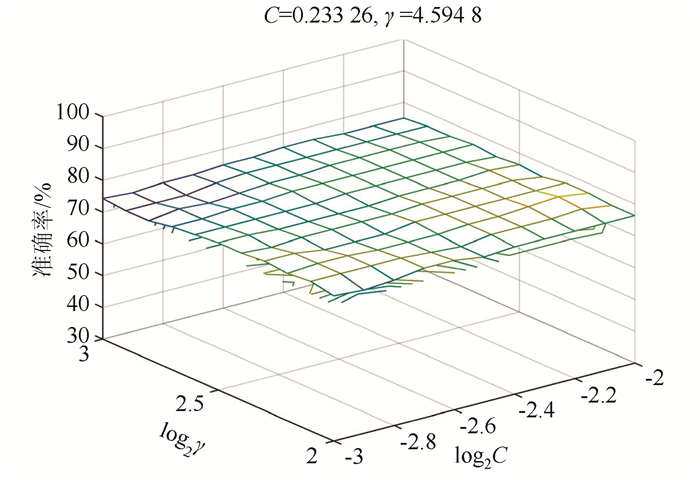
|
| 图 5 参数寻优结果 Fig. 5 Parameter optimization result |
| |
根据图 5,得出支持向量机模型惩罚参数最优为0.233 3,核函数参数最优值为4.594 8,交通流状态的识别准确率达78.378 4%。优化过的网格搜索算法在整个参数寻优过程中共花费时间3.4 s。两次寻优准确率差为0.68% < 1%。因此,选取参数C=0.233 3,γ=4.594 8。与传统的网格搜索算法参数寻优对比结果如表 4所示,显然,改进的网格搜索法所需时间更短。
| 传统网格搜索法 | 改进网格搜索法 | |||
| 搜索时间/s | 准确率/% | 搜索时间/s | 准确率/% | |
| 196 | 78.378 4 | 3.4 | 78.378 4 | |
② 支持向量机训练。采用C=0.233 3,γ=4.594 8训练支持向量机,具体结果如图 6所示。
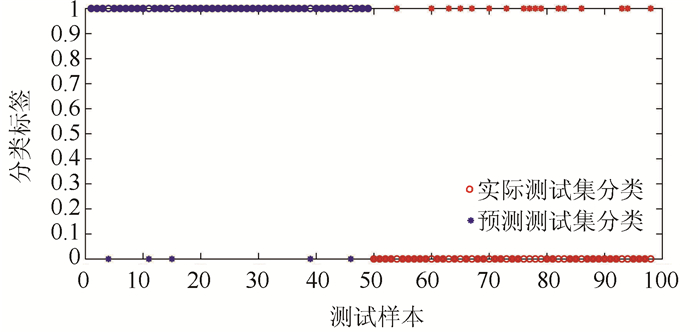
|
| 图 6 数据集B训练效果图 Fig. 6 Training effect diagram of dataset B |
| |
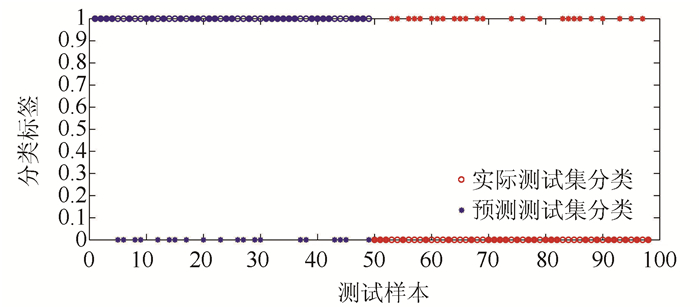
选用以数据集A训练好的SVM应用于A数据集中的测试集,分类结果如图 7所示。
|
| 图 7 测试集分类结果图 Fig. 7 Test set classification result diagram |
| |
图 6中圆圈代表 98个测试样本的实际类别,“*”为模型分类结果。“*”与圆圈重合代表分类正确,反之错误。从图 6中,我们可以得出“*”与圆圈重合的样本有91个,即分类准确率达77.55%。案例组的分类正确率达89.8%,对照组样本分类正确率达65.3%。此外,案例组样本错误分类的数量少于对照组样本分类错误的数量。
从图 7中,我们可以得出“*”与圆圈重合的样本仅有45个,即分类准确率只有54.1%。案例组的分类正确率达59.2%,对照组样本分类正确率达49%。显然,案例组的分类正确率与对照组样本分类正确率均比较低。因此,通过特征变量降维后的数据集B的危险交通流状态识别准确率高于数据集A。
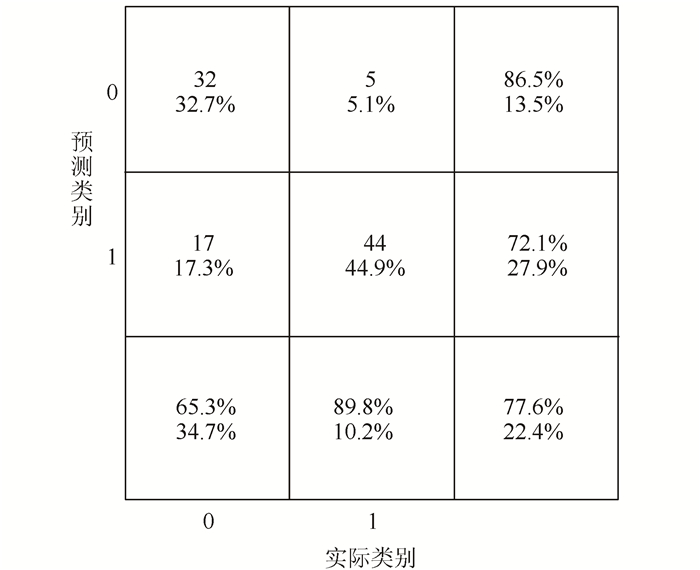
③ 分类效果评价。数据集B交通流状态识别的混淆矩阵如图 8所示。
|
| 图 8 混淆矩阵 Fig. 8 Confusion matrix |
| |
图 8混淆矩阵中行表示案例样本与对照样本测试集预测分类标签,列表示案例样本与对照样本测试集的实际类别。从图 8可知,危险交通流状态的分类正确率为89.8%;此外,案例所研究的123起事故中有因驾驶员操作不当或入口频繁变换车道引起,因此排除道路、驾驶员等偶发性因素,本研究所构建的支持向量机模型对危险交通流状态的识别准确率较高。值得注意的是,该模型易把安全交通流状态判别为危险交通流状态。但由于在日常的危险交通流状态监测过程中,我们更注重危险交通流状态的发生。因此,本研究所构建的危险交通流状态识别模型具有良好适用性。
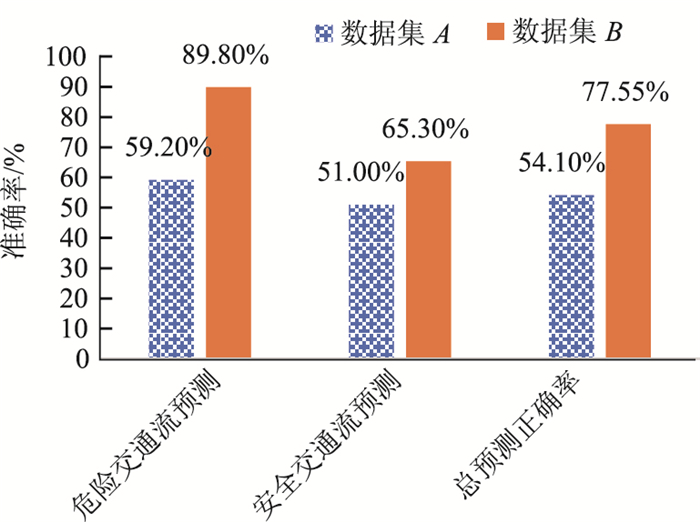
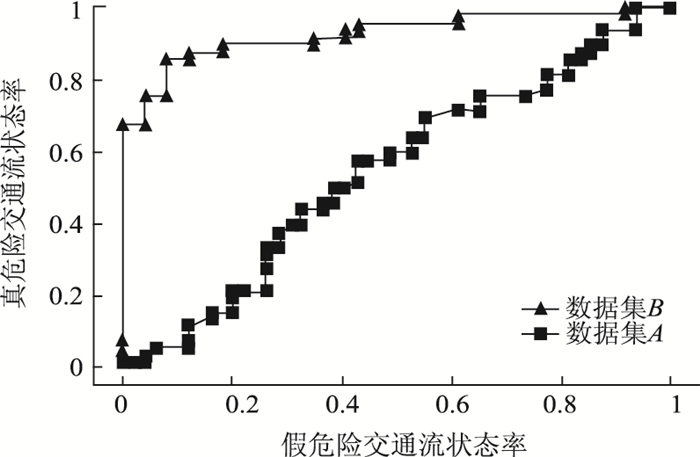
3.2 结果对比分析 3.2.1 RSA算法合理性验证为了验证RSA算法的合理性,选用数据集A来训练和测试支持向量机。数据集A, B的交通流状态识别结果对比如图 9所示。算法测试结果的ROC曲线如图 10所示。
|
| 图 9 数据集A, B的交通流状态识别对比 Fig. 9 Comparison of traffic flow state recognition between data set A and data set B |
| |
|
| 图 10 ROC曲线 Fig. 10 ROC curves |
| |
从图 9可知,不论是正常交通流状态还是危险交通流状态,数据集B的分类精度均高于数据集A。从图 10数据集B的ROC曲线与数据集A的ROC曲线对比可知,数据集B的曲线更接近Y=1。此外,ROC曲线与Y=0以及X=1所围的面积为AUC值,面积越大,表明分类器的性能有所提高。由图 10可知,数据集B的AUC值较大,因此本研究提出的RSA算法可以提高分类器的分类精度及性能。
3.2.2 不同算法结果对比分析为了验证本研究所构建模型的适用性,本研究选取常用的K近邻算法和BP神经网络算法应用于前兆特征变量降维后的数据集B,具体对比情况如下:
(1) K-近邻算法
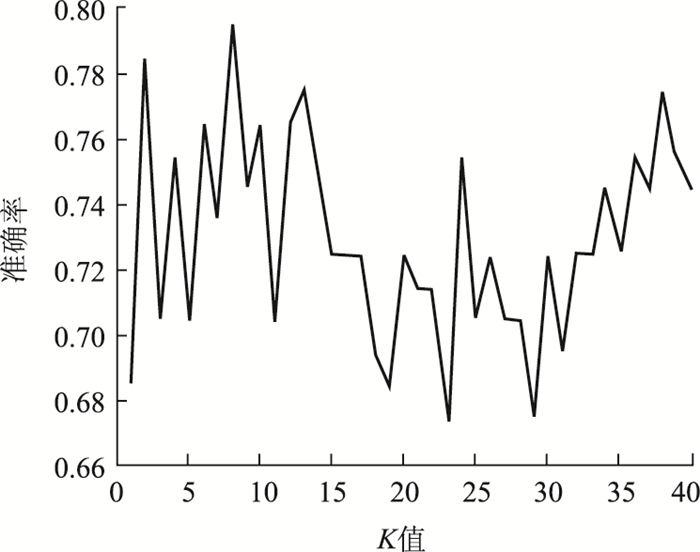
K-近邻算法中两样本间的距离计算常采用欧式距离度量方法。取K∈ (1, 40),样本分类准确率结果如图 11所示,显然,最佳K值为8,分类总正确率为79.59%。
|
| 图 11 不同K值算法准确率 Fig. 11 Accuracy rates of algorithm with different K values |
| |
(2) BP神经网络算法
本研究BP神经网络的构建过程中,分输入层、隐含层、输出层3层,激励函数选择Sigmoid函数。通过梯度下降法来调整输入层各节点与隐含层各节点之间的连接权重以及阈值,使误差沿梯度方向下降。隐含层节点与输出层节点之间的连接权重与阈值处理方法同上。迭代次数1 000次, 期望误差为10-6,学习速率0.01,试验结果如图 12所示。图 12中,分类正确率较高的曲线为训练样本。从图 12可以明显看出,当隐含层的节点数取15时,数据集B中训练样本的交通流状态分类总正确率为84.69%,测试样本交通流状态分类总正确率达73.40%。3种方法的识别结果对比如图 13所示。

|
| 图 12 测试样本分类准确率 Fig. 12 Classification accuracy of test samples |
| |
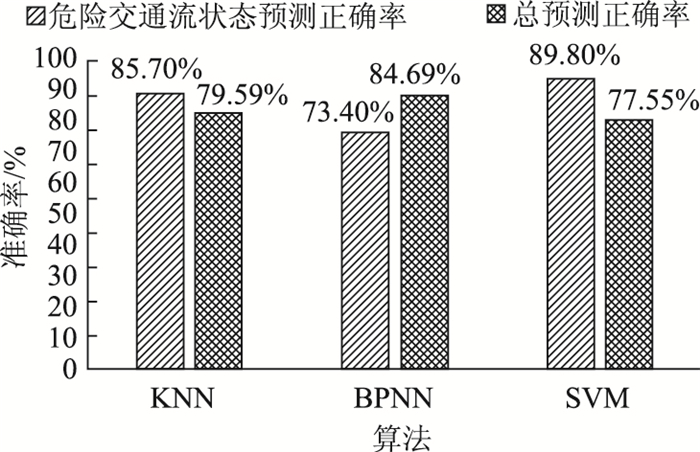
|
| 图 13 交通流状态识别结果对比 Fig. 13 Comparison of traffic flow state recognition results |
| |
由图 13可知,SVM算法对于危险交通流状态识别准确率高于KNN算法和BP神经网络算法,KNN和BP神经网络算法容易将危险状态判断为安全状态,导致较多的潜在危险交通流状态无法检测准确,即基于SVM的危险交通流状态识别算法优于KNN算法和BP神经网络算法,可为道路交通管理部门提供可靠的决策支持。
4 结论本研究提出了基于支持向量机的危险交通流状态检测方法。采用事故所对应的交通流状态作为危险交通流状态进行研究,根据交通流特性,提取与交通事故发生相关的24个前兆特征变量,并通过相关性选择算法实现降维,最终保留4个特征变量。结合支持向量机模型实现了对危险交通流状态的检测识别,精度高于KNN算法和BPNN算法。此外,改进后的网格搜索算法,使得惩罚参数C和核函数参数γ寻优效率提高了98.3%,极大减少了搜索时间。因此,本研究可以有效地对危险交通流状态进行实时识别,为交通管理部门保障城市快速路的正常运营提供决策依据。
| [1] |
高洪涛, 刘凯, 李红启. 加强交通运输安全生产管理的对策探讨[J]. 北京交通大学学报: 社会科学版, 2005, 4(4): 47-50. GAO Hong-tao, LIU Kai, LI Hong-qi. Measures to Promote the Safety Management of Traffic and Transportation[J]. Journal of Beijing Jiaotong University: Social Sciences Edition, 2005, 4(4): 47-50. |
| [2] |
江永生. 基于交通流因素的城市道路交通事故分析预测研究[D]. 西安: 西安建筑科技大学, 2009. JIANG Yong-sheng. Study of Urban Road Traffic Accidents Analysis and Forecast Based on Traffic Flow Factors[D]. Xi'an: Xi'an University of Architecture and Technology, 2009. |
| [3] |
GOLOB T F, RECKER W W. Relationships among Urban Freeway Accidents, Traffic Flow, Weather, and Lighting Conditions[J]. Journal of Transportation Engineering, 2003, 129(4): 342-353. |
| [4] |
楚杨杰, 陈春红, 刘昭, 等. 道路交通拥堵自动检测的改进加州算法及仿真[J]. 数学杂志, 2012, 32(4): 740-744. CHU Yang-jie, CHEN Chun-hong, LIU Zhao, et al. Road Traffic Congestion Automatic Detection of Improvement of the Algorithm of California and the simulation[J]. Journal of Mathematics, 2012, 32(4): 740-744. |
| [5] |
PERSAUD B N, HALL F L, HALL L M. Congestion Identification Aspects of the McMaster Incident Detection Algorithm[J]. Transportation Research Record, 1990, 1287: 167-175. |
| [6] |
杨兆升, 王爽, 马道松. 基础交通信息融合方法综述[J]. 公路交通科技, 2006, 23(3): 111-116. YANG Zhao-sheng, WANG Shuang, MA Dao-song. Review of Basic Traffic Data Fusion Methods[J]. Journal of Highway and Transportation Research and Development, 2006, 23(3): 111-116. |
| [7] |
方晓莹, 王小君. 基于视频的智能交通异常检测系统[J]. 微型机与应用, 2010, 29(6): 35-38. FANG Xiao-ying, WANG Xiao-jun. A Traffic Abnormity Detection Algorithm Based on Vision in the ITS[J]. Microcomputer & Its Applications, 2010, 29(6): 35-38. |
| [8] |
方晓莹, 黄林伟, 刘富强. ITS中基于视频的交通异常情况检测[J]. 计算机工程与应用, 2006, 36: 212-215. FANG Xiao-ying, HUANG Lin-wei, LIU Fu-qiang. Traffic Abnormity Detection Algorithm Based on Vision in ITS[J]. Computer Engineering and Applications, 2006, 36: 212-215. |
| [9] |
张新, 常云涛, 郭佳宁, 等. 基于视频投影法的交通拥挤实时检测算法[J]. 合肥工业大学学报: 自然科学版, 2013, 36(3): 319-323. ZHANG Xin, CHANG Yun-tao, GUO Jia-ning, et al. Video-based Projecting Algorithm for Real-time Traffic Congestion Detection[J]. Journal of Hefei University of Technology: Natural Science Edition, 2013, 36(3): 319-323. |
| [10] |
廖律超, 蒋新华, 邹复民, 等. 基于交通视频的交通拥堵状态自动识别方法[J]. 公路交通科技, 2014, 31(1): 110-117. LIAO Lü-chao, JIANG Xin-hua, ZOU Fu-min, et al. An Automatic Recognition Approach for Traffic Congestion States Based on Traffic Video[J]. Journal of Highway and Transportation Research and Development, 2014, 31(1): 110-117. |
| [11] |
林震, 杨浩. 基于车速的交通事故贝叶斯预测[J]. 中国安全科学学报, 2003, 13(2): 34-36. LIN Zhen, YANG Hao. Bayesian Prediction of Traffic Accident Based on Vehicle Speed[J]. China Safety Science Journal, 2003, 13(2): 34-36. |
| [12] |
徐铖铖, 刘攀, 王炜, 等. 基于判别分析的高速公路交通安全实时评价指标[J]. 东南大学学报: 自然科学版, 2012, 42(3): 555-559. XU Cheng-cheng, LIU Pan, WANG Wei, et al. Discriminant Analysis Based Method to Develop Real-time Crash Indicator for Evaluating Freeway Safety[J]. Journal of Southeast University: Natural Science Edition, 2012, 42(3): 555-559. |
| [13] |
姜桂艳, 温慧敏, 杨兆升. 高速公路交通事件自动检测系统与算法设计[J]. 交通运输工程学报, 2001, 1(1): 77-81. JIANG Gui-yang, WEN Hui-min, YANG Zhao-sheng. Design of Freeway Automatic Incident Detection System and Algorithm[J]. Journal of Traffic and Transportation Engineering, 2001, 1(1): 77-81. |
| [14] |
向怀坤, 李伟龙, 谢秉磊. 粒子群优化神经网络的交通事件检测算法研究[J]. 计算机测量与控制, 2016, 24(2): 171-174. XIANG Huai-kun, LI Wei-long, XIE Bing-lei. Research on Traffic Incident Detection Algorithm Based on Particle Swarm Optimizer Neural Network[J]. Computer Measurement & Control, 2016, 24(2): 171-174. |
| [15] |
杨奎河, 张行, 王晓东. 基于多源数据融合的交通流状态识别研究[J]. 信息通信, 2019, 7: 14-15. YANG Kui-he, ZHANG Xing, WANG Xiao-dong. Traffic Flow State Recognition Based on Multi-source Data Fusion[J]. Information & Communications, 2019, 7: 14-15. |
| [16] |
林浩, 李雷孝, 王慧. 支持向量机在智能交通系统中的研究应用综述[J]. 计算机科学与探索, 2020, 14(6): 901-917. LIN Hao, LI Lei-xiao, WANG Hui. Survey on Research and Application of Support Vector Machines in Intelligent Transportation System[J]. Journal of Frontiers of Computer Science and Technology, 2020, 14(6): 901-917. |
| [17] |
CHEN S, WANG W, VAN ZUYLEN H. Construct Support Vector Machine Ensemble to Detect Traffic Incident[J]. Expert Systems with Applications, 2009, 36(8): 10976-10986. |
| [18] |
YUAN F, CHEU R L. Incident Detection Using Support Vector Machines[J]. Transportation Research Part C: Emerging Technologies, 2003, 11(3): 309-328. |
| [19] |
周洲, 周林英, 张立成, 等. 基于支持向量机的高速公路事件检测算法研究[J]. 西安工业大学学报, 2014, 34(9): 726-731. ZHOU Zhou, ZHOU Lin-ying, ZHANG Li-cheng, et al. Algorithm for Freeway Incident Detection Based on SVM Classification[J]. Journal of Xi'an Technological University, 2014, 34(9): 726-731. |
| [20] |
游锦明, 方守恩, 唐棠, 等. 不良交通流状态实时监测支持向量机模型算法研究[J]. 交通运输系统工程与信息, 2018, 18(4): 83-87, 95. YOU Jin-ming, FANG Shou-en, TANG Tang, et al. A Support Vector Machine Approach on Real-time Hazardous Traffic State Detection[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 18(4): 83-87, 95. |
| [21] |
PANDE A, ABDEL-ATY M, LIANG H. Spatiotemporal Variation of Risk Preceding Crashes on Freeways[J]. Transportation Research Record, 2005, 1908(1): 26-36. |
 2021, Vol. 38
2021, Vol. 38
