扩展功能
文章信息
- 王依兰, 陈新, 徐永能
- WANG Yi-lan, CHEN Xin, XU Yong-neng
- 高速公路路径标识站选址优化模型与算法研究
- Study on Model and Algorithm of Optimal Location of Expressway Path Identification Station
- 公路交通科技, 2021, 38(10): 114-119
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(10): 114-119
- 10.3969/j.issn.1002-0268.2021.10.015
-
文章历史
- 收稿日期: 2020-08-27
近年来高速公路不断建设发展,高速公路网结构变得错综复杂。随着省界收费站的拆除和联网收费工作的推进,高速公路结算路网越来越庞大,环状路网、嵌套环路等情况越来越多,相同的起终点(即OD点)有多条不同的路径可以选择,这就导致路径多义性问题产生[1]。路径多义性成为高速通行费用合理拆分的阻碍,进而影响高速公路的整体效能和服务水平的提高。为保证高速公路通行费用的合理拆分,确保道路投资者与使用者利益,车辆路径识别成为现阶段高速公路联网收费的关键问题,而车辆的路径信息识别,标识站的合理选址布局是其中关键的一环。标识站选址优化研究不仅能实现对车辆路径信息的精准识别,有利于道路投资者和使用者对通行费用无异议,同时有助于节省标识站的投资建设成本,以提高标识站的实用性和经济性。
早期高速公路车辆路径识别方法主要采取概率识别方法,如最短路径法、抽样调查法、布瑞尔分配法等[2-3]。随着高速公路的迅猛发展,基于概率的路径识别方案已不能满足道路投资者和使用者的利益。为实现高速公路通行费用公平、合理拆分,车辆精准路径识别是其关键。目前,高速公路多义性路径精准识别技术主要包括卫星导航(GPS、北斗)[4]、射频识别(RFID)技术(433 MHz射频技术、5.8 GHz专用短程通信[5-6]等)、车牌识别[7]、车辆电子标识[8]等方法。这些方法实现的基础是依托于高速公路网中多义性的路段设置标识站,通过标识站与车辆之间信息的交互,达到识别车辆信息的目的。
标识站的设置主要是为了标记车辆在高速公路中的路径行驶信息并及时上传至高速公路收费站,从而使车辆在到达收费站后,收费系统能及时准确的还原车辆实际行驶的路径,从而确定车辆的通行费用,并为通行费用的拆分提供依据。因此标识站的选址受多种因素的影响,如路段流量、建设成本、标识站识别可靠度和环境等。丛浩哲等[9]提出了基于深度优先搜索算法的标识站选址和数量的确定。但该方法容易造成缺栈或者堆栈的情况。高洁等[10]提出了基于支撑树理论的大型路网的标识站选址算法,但该方法仅对单一的封闭环状路网进行了分析,对于嵌套路网的布局可能会造成重要路段标识站数量不足或冗余的现象。蒋贵川等[11]分析了冗余标识站布局与系统整体可靠性之间关系的研究,提出了简单重复布局是标识站数量最小的布局理念,但并未考虑标识站的影响因素。曲建华等[12]采用最小生成树理论对河南高速公路标识站设置进行研究。苏晓明等[13]提出了基于概率模型的标识站设置方法,并提出了多阶段多候选的标识站选址方法。孙荣[14]通过遗传算法确定标识站的最优布局,并为提高系统的可靠性,提出了分布式布局和简单重复布局的方法。王握等[15]分析了标识站选址的影响因素与选址条件,采用关联矩阵算法优化了高速公路标识站选址模型。
目前有关标识站选址布局的相关文献中,并没有考虑复杂的收费路网,且在最优标识站的数量下,标识站的选址布局存在方案并不唯一,存在布局方案的优化问题。标识站的选址应在以标识站设置数量最小的前提下,达到车辆实际行驶路线的无模糊性,同时标识站的选址应以检测多义性路段车流量最小为目标,降低标识站工作负荷。
因此,在已有研究的基础上,同时考虑到车流量和路段权值对标识站选址的影响,本研究采用生成树理论确定高速公路标识站的数量和选址位置,由于生成树的不唯一性,导致余边集的组成也存在多种可能,因此标识站位置选址方案并不唯一。通过以多义性路段权值最小和车流量最大为优化目标,构建了标识站选址优化模型。同时考虑到蚁群算法在路径搜索问题中具有很大的优势,因此本研究利用蚁群算法求解模型。
1 高速公路标识站选址问题分析 1.1 生成树理论高速公路车辆的实际行驶路径可以根据高速公路的出入口和标识站的信息确定。根据图论中树的特点,在树中路径不具有环路,路段和路径具有唯一性,只要把图变成树,便可消除存在歧义的路径。
因此高速公路网可以抽象为连通图G= (V, E),其中V(G)为连通图G中节点集合,V(G)= {V1, V2, …, Vn};E(G)为连通图G中路段集合,E(G)= {E1, E2, …, Em},若边ek的顶点为i和j,则记ek= (i, j);用n(G)为节点的个数,m(G) 为边的数量。高速公路网中标识站数量问题可以转化为求解连通图中标识站的问题。对于大型高速路网中,标识站数量的确定可以结合图论相关知识分析。
根据图论中生成树的相关原理。余边集:连通图G,若T为连通图G的一棵生成树,RG为生成树的余边集,m(RG)为余边集RG中所含边的数量,且m(RG)=m(G)-n(G)+1[16]。
定理1:对高速公路网G= (V, E)中的车辆进行精准路径识别,标识站的位置应设置在余边集RG上,且标识站的最佳数量为余边集边的数量m(RG)。
给定图 1的连通图G,它的生成树的边数为n(G)-1,节点数为n,标识站设立在余边集上,即:生成树的边数m(T)=5-1=4,标识站的数量为m(RG)=6-4=2,布设(非最优标识站的布设)在图G的余边集上。
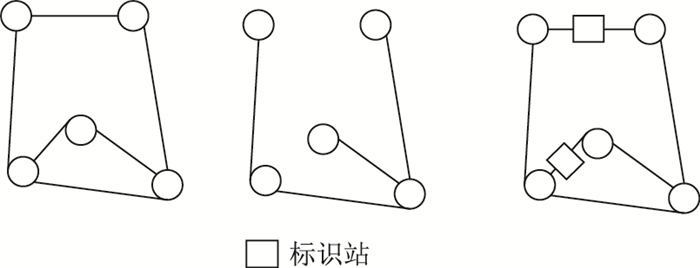
|
| 图 1 图G及生成树T和标识站布设示意图 Fig. 1 Schematic diagram of layouts of figure G, spanning tree T and identification station |
| |
1.2 模型假设
在采用图论生成树理论对标识站数量问题进行分析后,确定来标识站的设置数量及标识站的布设方案,结合数学建模中的优化理论,即可建立高速公路标识站的优化布局模型,但因标识站的设置需考虑到多种因素的影响,模型建立及求解过程相对复杂,为简化其问题分析,需要在模型建立之处做出模型假设。
(1) 高速公路的交通路网为互通立交,即V(G)表示为高速公路与高速公路之间的交点集合。
(2) E(G)为路网连通图G中的路段,设E1 (G)为有标识站的路段;E2 (G)为未设标识站的路段,则E1 (G)∪E2 (G)=E(G)且E1 (G)∩E2 (G)=Ø。
(3) 标识站的设置仅考虑其时间因素和路段车流量因素。
1.3 标识站优化布设模型建立标识站的优化布设问题可以转化为求大型高速公路路网G中最小生成树和对应余边集的求解问题。标识站优化布设模型的数学描述为:通过针对标识站设置主要影响因素之间不同权重比寻找最小目标函数,求解出路网G上的最小生成树,结合定理1确定标识站的最优布设。
根据研究内容,模型的目标函数如下:
(1) 目标函数:
道路运行速度的特征值可以体现车辆在道路上的整体运行概况[17],由
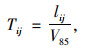
|
(1) |
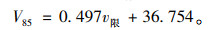
|
(2) |
则求解最少时间的出行者路径选择可转化为求解最小路段里程的目标函数。

|
(3) |
在保证路网车辆路径全覆盖的原则下,为减少标识站识别车辆路径信息的工作量,同时也可预防标识站出现故障时,不能识别行驶路径的车辆数较小,建立基于车流量因素的目标函数如下:
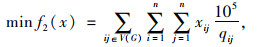
|
(4) |
式中,Tij为边(i, j)路段的行驶时间;V85为道路运行速度的特征指标;v限为高速公路的限制速度;xij为生成树(i, j)的边;lij为节点i到节点j之间路段的里程;qij为节点i到节点j之间路段上的车流量。
为得到模型的最终优化目标,引入权重系数ω1和ω2,且ω1+ω2=1,则模型的最终优化目标函数为:
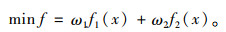
|
(5) |
(2) 约束条件
① 所求解应满足树的要求,约束条件为:
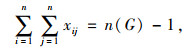
|
(6) |
式中,xij满足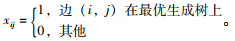
② 生成树中应不产生任何子回路,约束条件为:
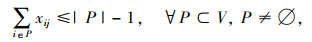
|
(7) |
式中,|P|为集合P中所含图G的节点个数。
③ 路段上标识站的设置数量应小于等于余边集边的数量,约束条件表示为:
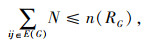
|
(8) |
式中N为标识站的数量。
④ 路网G中应包含所有生成树的边,约束条件表示为:
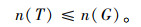
|
(9) |
⑤ 路网G中应含有所有生成树的节点,约束条件表示为:
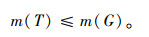
|
(10) |
为提高搜索效率,本研究采用的蚁群算法(Ant System, AS)来求解标识站的选址优化问题[17-19],并根据模型特点对信息素的更新做出相适应的改进。模型求解过程如下:
(1) 参数信息初始化。设置蚂蚁数目m, 信息素系数α, 期望启发系数β, 信息素挥发系数ρ, Nc为循环次数。
(2) 状态转移概率函数
在求解过程中,t时刻蚂蚁k从节点Vi依据状态概率pijk转移到Vi+1,状态转移概率函数定义式为:
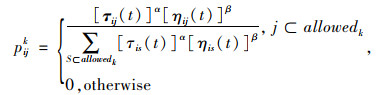
|
(11) |
式中,allowedk为蚂蚁满足目标函数要求且未访问的节点;ηij为启发函数,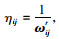
(3) 信息素更新策略
在搜索最优路径时,当m个蚂蚁在移动的过程中,每条边都留下了信息素。设Δτij为m个蚂蚁完成一次搜索后边(i, j)上信息素增量,则路径eij上信息素含量在边(i, j)刻按照如下进行更新调整:
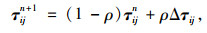
|
(12) |
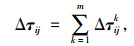
|
(13) |
式中,(1-ρ)为信息素残留系数,且0<ρ<1;初始时刻Δrij=0;Δijk为当前次循环中蚂蚁k在边(i, j)上留下的单位长度轨迹信息素数量。
根据Δijk运算过程的不同,Δijk按照以下3种定义形式:
① Ant-Cycle模型
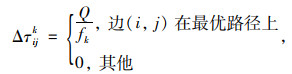
|
(14) |
② Ant-Density模型
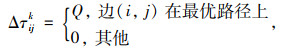
|
(15) |
③ Ant-Quantity模型
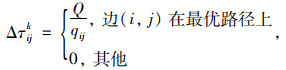
|
(16) |
式中,Q为单个蚂蚁所留轨迹强度常数;fk为第k个蚂蚁在当前循环中所得目标函数的值;qij为边(i, j)上的车流量。
(4) 每个蚂蚁依次进行Ncmax次循环后,便可得到问题的一个最优解。
高速公路标识站选址优化问题算法流程图如图 2所示。
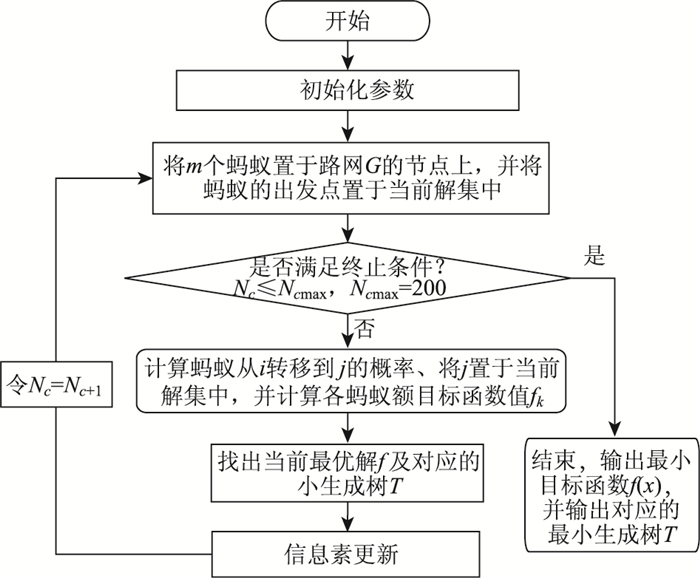
|
| 图 2 高速公路标识站选址优化问题算法流程图 Fig. 2 Flowchart of algorithm of optimal location of expressway path identification station |
| |
3 算法验证
假设路网A,其中m(A)=11,n(G) =16, V= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, E= {e1, e2, …e16, e1, e2, … e15}, 路网A如图 3所示,其对应关系,各路段的里程及流量如表 1所示。
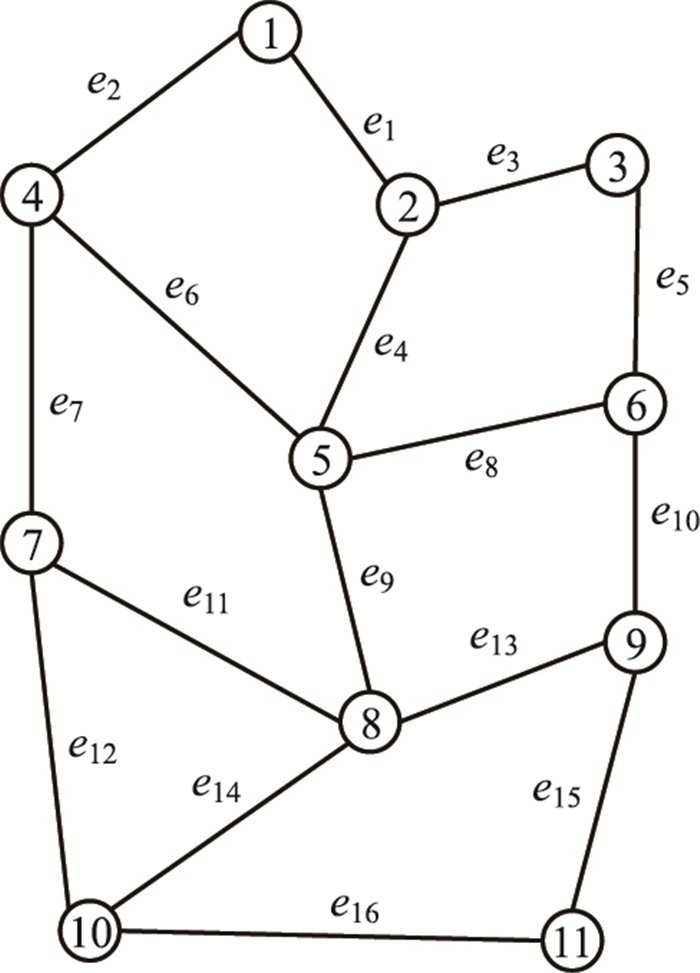
|
| 图 3 算例路网A Fig. 3 An example of road network A |
| |
| 路段编号 | e1 | e2 | e3 | e4 | e5 | e6 | e7 | e8 |
| 路段里程/km | 26 | 28 | 55 | 32 | 69 | 30 | 100 | 50 |
| 车流量/veh | 6 320 | 4 590 | 5 300 | 6 400 | 3 200 | 4 700 | 3 900 | 8 000 |
| 路段编号 | e9 | e10 | e11 | e12 | e13 | e14 | e15 | e16 |
| 路段里程/km | 105 | 72 | 15.6 | 62 | 112 | 52 | 104 | 110 |
| 车流量/veh | 2 600 | 4 300 | 6 200 | 5 000 | 3 200 | 5 500 | 4 300 | 1 900 |
取参数K=50,α=1,β=5,ρ=0.1,Nc=0,Ncmax=200。针对不同ω1和ω2,在满足约束条件,对上述模型在MATLAB中进行优化计算,得到最优解。计算结果如表 2所示。
| 序号 | ω1 | ω2 | min f(x) | T={x, j}∈E(G) |
| 1 | 0.5 | 0.5 | 383.154 | 3-2-1-4-5-6-9-11-10-8-7 |
| 2 | 0.3 | 0.7 | 319.375 | 3-2-1-4-5-6-9-8-7-10-11 |
| 3 | 0.7 | 0.3 | 446.932 | 3-2-1-4-5-8-7-10-11-9-6 |
根据所得的最优解,图G最小生成树路径以及标识站的分布如表 3所示。
| 序号 | 图G的最小生成树T | 标识站的最优选址 |
| 1 | 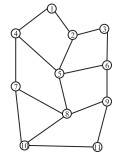 |
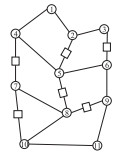 |
| 2 | 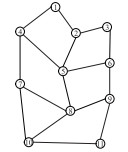 |
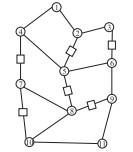 |
| 3 | 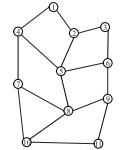 |
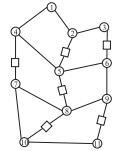 |
影响标识站的因素有很多,本研究重点讨论的基于出行时间的路径选择对标识站选址的影响和基于标识站最少识别车辆数标识站影响因素,通过分配不同的权重比,得出不同权重比下标识站的最优选址。
根据上述模型在MATLAB求解之下得到最小目标函数,迭代次数如图 4所示。该算法在进行到50次时,目标函数迭代到了最优值,具有快速寻优能力。其次在进行多目标优化时,根据所选择权值的不同,所得到的最优解也是不同的。
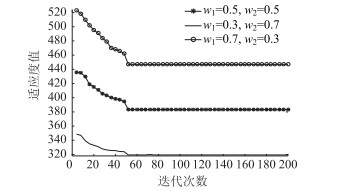
|
| 图 4 适应度进化曲线 Fig. 4 Fitness evolution curve |
| |
4 结论
本研究通过采用基于生成树-蚁群算法对高速公路标识站选址问题进行分析研究,得到优化后路网中标识站的选址分布,同时通过对比标识站影响因素之间的不同占比,得出不同影响因素的占比不同,标识站的选址也是不同的。模型具有较强的通用性,能满足通行费用精确拆分的实际需要。然而,本研究未考虑标识站建设成本、老化、损坏及识别精度等其他因素对标识站选址影响的问题,下一步的研究中将加以考虑。
| [1] |
钟永恒. 高速公路联网收费多义性路径问题及解决方案研究[D]. 广州: 华南理工大学, 2011. ZHONG Yong-heng. Research on Ambiguity Path Problem and Solution of Expressway Network Tolling[D]. Guangzhou: South China University of Technology, 2011. |
| [2] |
孙文波. 高速公路联网收费多路径通行费拆分研究[D]. 天津: 天津大学, 2014. SUN Wen-bo. Study on Splitting of Multi-path Tolls by Expressway Interconnection Charging[D]. Tianjin: Tianjin University, 2014. |
| [3] |
陈洪星, 孙洋. 改进的布瑞尔交通分配模型在高速公路路径识别问题中的应用[J]. 交通与运输, 2008, 24(2): 37-40. CHEN Hong-xing, SUN Yang. The Use of Improved Burell's Traffic Probability Allotting Model in the Routes Distinguish of Expressway[J]. Traffic and Transportation, 2008, 24(2): 37-40. |
| [4] |
赵超杰. 基于GPS技术的高速公路收费系统精确路径识别研究[D]. 西安: 长安大学, 2015. ZHAO Chao-jie. Research on Accurate Path Identification of Expressway Toll Collection System Based on GPS Technology[D]. Xi'an: Chang'an University, 2015. |
| [5] |
韩豪. 基于5.8G专用短程通信技术的高速公路多义性路径识别系统设计[D]. 西安: 长安大学. 2017. HAN Hao. Design of Expressway Polysemant Path Identification System Based on 5.8G Dedicated Short-range Communication Technology[D]. Xi'an: Chang'an University, 2017. |
| [6] |
MELLO-SAMPAYO F D. Competing-destinations Gravity Model: An Application to the Geographic Distribution of FDI[J]. Applied Economics, 2009, 41(17): 2237-2253. |
| [7] |
杨佳莉. 基于车牌识别的高速公路网多路径精确识别研究[D]. 西安: 长安大学, 2014. YANG Jia-li. Research on Multi-path Accurate Recognition of Expressway Network Based on License Plate Recognition[D]. Xi'an: Chang'an University, 2014. |
| [8] |
顾席光, 胡家彬, 钱彬, 等. 汽车电子标识在智能交通中的应用与研究[J]. 公路交通科技, 2017, 34(增2): 110-117. GU Xi-guang, HU Jia-bin, QIAN Bin, et al. Application and Study on Electronic Identification of Motor Vehicles in Intelligent Transport[J]. Journal of Highway and Transportation Research and Development, 2017, 34(S2): 110-117. |
| [9] |
丛浩哲, 姜杰. 基于支撑树法的高速公路多路径识别问题研究[J]. 交通与运输, 2007, 23(1): 85-88. CONG Hao-zhe, JIANG Jie. Study of Expressway Multi-path Recognition Problem Based on Spanning Tree[J]. Traffic and Transportation, 2007, 23(1): 85-88. |
| [10] |
高洁, 施其洲. 高速公路标识站选址模型与算法研究[J]. 公路交通科技, 2008, 25(1): 139-141, 145. GAO Jie, SHI Qi-zhou. Study on Positioning Model and Algorithm of Identifier of Expressway[J]. Journal of Highway and Transportation Research and Development, 2008, 25(1): 139-141, 145. |
| [11] |
蒋贵川, 易术, 林莉. 路径二义性判别问题中的标识站设置研究[J]. 公路, 2011(5): 104-107. JIANG Gui-chuan, YI Shu, LIN Li. Research on Layout of Identifying Stations in Ambiguous Routes Identification[J]. Highway, 2011(5): 104-107. |
| [12] |
曲建华, 崔岩, 徐广印, 等. 基于最小生成树的河南省高速公路多义性路径标识站设置[J]. 河南科学, 2012, 31(5): 640-643. QU Jian-hua, CUI Yan, XU Guang-yin, et al. The Layout of Ambiguity Route Identifying Station in Henan Province Highway Based on Minimum Spanning Tree[J]. Henan Science, 2012, 31(5): 640-643. |
| [13] |
苏晓明, 徐东彬. 基于概率模型的二义性路径识别标识站设置方法[J]. 公路交通科技, 2013, 30(4): 119-123. SU Xiao-ming, XU Dong-bin. A Method of Identification Station Establishment for Ambiguous-path Identification Based on Probability Model[J]. Journal of Highway and Transportation Research and Development, 2013, 30(4): 119-123. |
| [14] |
孙荣. 高速公路多路径标识点选址方法研究[D]. 西安: 长安大学, 2013. SUN Rong. Study on Location Selection Method of Expressway Multi-path Identification Points[D]. Xi'an: Chang'an University, 2013. |
| [15] |
王握, 张晗, 任仲山, 等. 基于关联矩阵的高速公路标识站优化选址模型与算法研究[J]. 交通运输研究, 2015, 40(6): 64-70. WANG Wo, ZHANG Han, REN Zhong-shan, et al. Optimal Locating Model and Algorithm of Identification Station of Expressway Based on Associated Matrix[J]. Transport Research, 2015, 40(6): 64-70. |
| [16] |
邓文华. 数据结构[M]. 2版. 北京: 清华大学出版社, 2007. DENG Wen-hua. Data Structure[M]. 2nd ed. Beijing: Tsinghua University Press, 2007. |
| [17] |
王丽金. 高速公路限速与运行速度的关系研究[D]. 北京: 北京工业大学, 2011. WANG Li-jin. Research on Relationship between Expressway Speed Limit and Operating Speed[D]. Beijing: Beijing University of Technology, 2011. |
| [18] |
王志杰. 蚁群算法的改进及应用[D]. 长沙: 湖南师范大学, 2009. WANG Zhi-jie. Improvement and Application of Ant Colony Algorithm[D]. Changsha: Hunan Normal University, 2009. |
| [19] |
魏欣, 马良, 张惠珍. 多目标度约束最小生成树的蚁群优化算法求解[J]. 数学理论与应用, 2017, 37(1): 81-89. WEI Xin, MA Liang, ZHANG Hui-zhen. An Ant Colony Optimization Algorithm for Multi-criteria Degree-constrained Minimum Spanning Tree[J]. Mathematical Theory and Applications, 2017, 37(1): 81-89. |
 2021, Vol. 38
2021, Vol. 38
