扩展功能
文章信息
- 王健宇, 陆化普, 孙智源, 王天实
- WANG Jian-yu, LU Hua-pu, SUN Zhi-yuan, WANG Tian-shi
- 基于MNL模型的车车碰撞事故严重程度影响因素辨识方法
- A Method for identifying Influencing factors of Severity of Vehicle Crash Based on MNL model
- 公路交通科技, 2021, 38(10): 107-113
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(10): 107-113
- 10.3969/j.issn.1002-0268.2021.10.014
-
文章历史
- 收稿日期: 2020-07-02
2. 北京工业大学 城市交通学院, 北京 100124
2. School of Metropolitan Transportation, Beijing University of Technology, Beijing 100124, China
交通安全问题是全世界共同面对的严峻公共安全挑战。根据世界卫生组织(World Health Organization,WHO)最新全球交通事故统计报告:2016年世界范围内因道路交通事故死亡的总人数超过135万[1],道路交通事故位列全球十大致死原因的第8名,是全球十大致死原因中唯一的非疾病类影响因素[2]。日益增长的道路交通量导致了交通事故的不断增加[3],因此对道路交通安全的研究一直是交通领域紧迫的基础研究课题[4]。
道路交通事故研究的主要目的是降低事故的发生风险和减少事故的危害性[5],事故的频次分析旨在降低事故的发生风险[6],事故的严重程度分析旨在减少事故的危害性[7]。本研究聚焦交通事故严重程度的研究。
事故严重程度的分析方法主要包含离散选择模型和数据挖掘方法。离散选择模型主要用于找寻事故严重程度的显著影响因素,是稳定且使用久远的统计分析模型。离散选择模型主要包含logistic模型和probit模型[8]。Al-Ghamdi采用二项logistic回归模型对9项相关因素(事故位置、事故形态、碰撞方位、事故时间、事故原因、驾驶员国籍、驾照状态、车辆形态、驾驶员年龄)与事故是否致死之间的关系进行分析,最终发现事故发生地点和事故原因是具有最显著相关性的[9]。Celik和Oktay采用多项logistic回归模型对土耳其埃尔祖鲁姆省和卡尔斯省发生的11 771例道路交通事故的影响因素进行分析,发现驾驶员年龄达到65岁及以上、驾龄低、高速路、人行横道是可能导致死亡事故高发的因素[10]。Azimi等(2020)采用有序logistic模型对大型货车倾覆事故的影响因素进行分析,发现粗心驾驶行为和异常驾驶情况是可能导致严重事故高发的因素[11]。参考已有研究,发现logistic模型能够有效地找寻事故严重程度的影响因素。因此,本研究采用Multinomial Logistic Regression(MNL)模型,即多项logistic回归模型,找寻不同严重程度下的显著影响因素。
交通事故严重程度的研究对象主要为交通事故严重程度的影响因素[12]。事故严重程度的影响因素包含人员属性[13]、车辆属性[14]、道路及环境属性[15]、时间属性[16]等。人员属性的影响因素包括:驾驶员年龄[17]、驾龄[18]、性别[19],是否涉及行人[20]等。车辆属性的影响因素包括:碰撞类型[21]、事故责任[22]等。道路及环境属性的影响因素包括:城市分区[23]、道路物理条件[24]、天气[25]等。时间属性的影响因素包括:季节[26]、高峰[27]等。参考已有研究中包含的影响因素,本研究整理形成4大类的影响因素进行研究,分别为过失方人员及车辆因素、受害方人员及车辆因素、时间因素、环境因素。
综上所述,本研究采用MNL模型,对车辆间的交通事故进行分析,辨识影响事故严重程度的主要因素。
1 影响因素的定义与数据描述统计根据沈阳市2015年至2017年的交通事故数据,对两车之间的不同类型事故进行研究,提取对象为碰撞双方具有差异化的责任,即同时包含过失方(全责或主责)和受害方(无责或次责),共提取事故593例。
对593例事故进行标定和结构化处理,将事故严重程度定义为因变量Y,将事故严重程度的影响因素定义为自变量Xk。影响因素Xk共包含19项,可分为4大类:过失方人员及车辆因素、受害方人员及车辆因素、时间因素、环境因素。其中每大类包含的具体因素如下所示:
(1) 过失方人员及车辆因素:车辆类型(X1)、性别(X2)、年龄(X3)、驾龄(X4)、逃逸行为(X5)、碰撞类型(X6);
(2) 受害方人员及车辆因素:车辆类型(X7)、性别(X8)、年龄(X9)、驾龄(X10);
(3) 时间因素:工作日(X11)、季节(X12)、时段(X13)、高峰时刻(X14);
(4) 环境因素:城市分区(X15)、道路横断面位置(X16)、道路物理隔离(X17)、路面状况(X18)、天气(X19)。
表 1所示的结果为车辆间事故严重程度和影响因素不同取值的定义。其中,根据货运、客运车辆的差异性将车辆类型分为小客车、大客车、小货车、大货车和其他等5类,对年龄和驾龄通过合理分组进行分析。
| 事故程度/影响因素 | 定义(各取值在数据集中百分比) |
| 过失方车辆类型(X1) | 1(58.01%)=小客车(低速汽车、微型客车、小型客车);2(9.61%)=小货车(轻型货车);3(3.54%)=大客车(中型客车、大型客车);4(24.28%)=大货车(汽车列车、中型货车、重型货车);5(4.55%)=其他 |
| 过失方性别(X2) | 1(94.60%)=男;2(5.40%)=女 |
| 过失方年龄(X3) | 1(0.51%)=0~18岁;2(74.03%)=19~45岁;3(22.43%)=46~59岁;4(3.04%)≥60岁 |
| 过失方驾龄(X4) | 1(46.21%)=0~6 a;2(35.41%)=7~16 a;3(18.38%)≥16 a |
| 逃逸行为(X5) | 1(8.26%)=是;2(91.74%)=否 |
| 碰撞类型(X6) | 1(10.79%)=正面碰撞;2(44.69%)=侧面碰撞;3(23.95%)=追尾碰撞;4(20.57%)=其他 |
| 受害方车辆类型(X7) | 1(44.52%)=小客车(低速汽车、微型客车、小型客车);2(4.55%)=小货车(轻型货车);3(2.87%)=大客车(中型客车、大型客车);4(22.93%)=大货车(汽车列车、中型货车、重型货车);5(25.13%)=其他 |
| 受害方性别(X8) | 1(94.10%)=男;2(5.90%)=女 |
| 受害方年龄(X9) | 1(0.84%)=0~18岁;2(64.92%)=19~45岁;3(27.49%)=46~59岁;4(6.75%)≥60岁 |
| 受害方驾龄(X10) | 1(45.36%)=0~6 a;2(33.56%)=7~16 a;3(21.08%)≥16 a |
| 工作日(X11) | 1(72.01%)=是;2(27.99%)=否 |
| 季节(X12) | 1(20.40%)=春季(4月、5月);2(31.87%)=夏季(6月、7月、8月);3(12.48%)=秋季(9月;10月);4(35.24%)=冬季(11月、12月、1月、2月、3月) |
| 时段(X13) | 1(15.01%)=0:00—6:00;2(23.78%)=6:00—12:00;3(34.06%)=12:00—18:00;4(27.15%)=18:00—24:00 |
| 高峰时刻(X14) | 1(19.56%)=是(7:00—9:00,17:00—19:00);2(80.44%)=否(剩余时段) |
| 城市分区(X15) | 1(15.85%)=主城区(和平区、沈河区、大东区、皇姑区、铁西区);2(48.23%)=近郊区(苏家屯区、浑南区、沈北新区、于洪区);3(28.16%)=远郊区(辽中区、新民市、康平县、法库县);4(7.76%)=市域高速 |
| 道路横断面位置(X16) | 1(76.39%)=机动车道;2=(16.86%)机非混合车道;3(3.37%)=非机动车道;4(3.37%)=其他 |
| 道路物理隔离(X17) | 1(0.84%)=机非隔离;2(76.05%)=无隔离;3(21.25%)=中心隔离;4(1.85%)=中心隔离及机非隔离 |
| 路面状况(X18) | 1(99.49%)=良好;2(0.51%)=其他 |
| 天气(X19) | 1(88.36%)=晴朗;2(11.64%)=其他 |
2 多项logistic回归模型
本研究以沈阳交通事故为数据来源进行分析,令Y为事故严重程度。依照财产损失、受伤人数和死亡人数的参考值,事故的严重程度被设置为3分类变量。令Y的取值为1,2,3,分别对应仅财产损失、有受伤但无死亡、有死亡这3种事故严重程度的情况,数据中仅财产损失(Y=1)占比12.14%、有受伤但无死亡(Y=2)占比47.55%、有死亡(Y=3)占比40.30%。Xk为K个影响因素的第k项,bjk为影响因素Xk的影响系数,则对j=1,2,3的无分类变量,则可构建2个分类变量的模型,其模型表达式为:
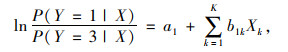
|
(1) |
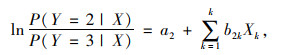
|
(2) |
式中,a1, a2为常数项;α为模型参数,即Logistic回归系数。
对全部J分类中的第j项概率计算表达式为:
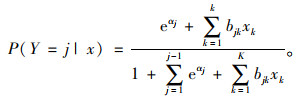
|
(3) |
通过计算,可获得bjk的值,即为各项影响因素的系数,其指数函数Exp (bjk)即为各影响因素的OR值,也称优势比,表示相对于被参考项,该影响因素在此取值情况下可能导致Y发生变化的相对概率。通常显著水平P的临界值设为0.05来筛选显著的影响因素。对建立的模型需进行似然比检验,当P < 0.05时说明模型具有意义。
3 虚拟变量的建立对影响因素Xk需对其中的多分类变量进行处理,引入虚拟变量,使多分类变量转化多个为0-1分类的变量,代入进行计算。通常引入虚拟变量的规则为:对某含有n分类的变量因素Xk,引入n-1个虚拟变量,使得该变量避免多重共线性。以过失方车辆类型(X1)为例建立虚拟变量,共5种取值,分别为1=小客车(低速汽车、微型客车、小型客车);2=小货车(轻型货车);3=大客车(中型客车、大型客车);4=大货车(汽车列车、中型货车、重型货车);5=其他。其中,以1=小客车为参考,引入4个虚拟变量,如表 2所示。
| 过失方车辆类型 (X1) |
虚拟变量 | |||
| X1-1 | X1-2 | X1-3 | X1-4 | |
| 小客车 | 0 | 0 | 0 | 0 |
| 小货车 | 1 | 0 | 0 | 0 |
| 大客车 | 0 | 1 | 0 | 0 |
| 大货车 | 0 | 0 | 1 | 0 |
| 其他 | 0 | 0 | 0 | 1 |
依照上述方法对过失方年龄(X3)、过失方驾龄(X4)、碰撞类型(X6)、受害方车辆类型(X7)、受害方年龄(X9)、受害方驾龄(X10)、季节(X12)、时段(X13)、城市分区(X15)、道路横断面位置(X16)、道路物理隔离(X17)进行数据处理,引入虚拟变量代入计算。
4 MNL模型结果分析MNL模型在加入二元自变量参量和经虚拟变量处理后的自变量参量后,拟合优化,最终模型拟合似然比检验P < 0.05,说明构建模型具有统计学意义,模型分析结果具有可靠性。
令P=0.05为显著性界限值,在全部19项影响因素中,经模型计算可得过失方车辆类型(X1)、过失方年龄(X3)、碰撞类型(X6)、受害方车辆类型(X7)、城市分区(X15)这5项影响因素为显著的影响因素,其对应P值分别为0.004,0.021,0.003,0.000,0.000,Y=1与Y=2情况下的计算结果如表 3和表 4所示。其中,B表示影响因素的对应参数;P为显著值;Wald,即参数B与其标准误平方值的比值,表征对参数B的检验值;OR值为参数B的指数函数,即优势比,表征相对的发生概率倍数。本研究对Y=1和Y=2情况下的OR值进行分析,以Y=3为参照,表征不同场景发生的相对概率。
4.1 仅财产损失事故的计算结果Y=1表示事故严重程度为“仅财产损失”,其显著值P小于0.05处对应自变量的系数有显著统计意义,即对因变量有显著性的影响。OR值表示Y=1“仅财产损失”场景在该参考项下对Y=3“有死亡”场景发生概率相对的可能性倍数。根据表 3所示的结果,正面碰撞(X6=1)、受害方车辆类型为小客车(X7=1)、主城区(X15=1)、近郊区(X15=2)为具有显著意义的参考项,过失方车辆类型(X1)、过失方年龄(X3)的各类取值为无显著意义的参考项。
| 不同取值的影响因素Xk | OR | B | Wald | P |
| 小客车(X1=1) | 3.158 | 1.150 | 1.360 | 0.243 |
| 小货车(X1=2) | 1.255 | 0.227 | 0.040 | 0.842 |
| 大客车(X1=3) | 2.871 | 1.055 | 0.566 | 0.452 |
| 大货车(X1=4) | 1.658 | 0.506 | 0.214 | 0.643 |
| 其他(X1=5) | # | # | # | # |
| 0至18(X3=1) | M | 17.049 | 0.000 | 0.996 |
| 19至45(X3=2) | 1.611 | 0.477 | 0.284 | 0.594 |
| 46至59(X3=3) | 0.731 | -0.313 | 0.120 | 0.729 |
| 60及以上(X3=4) | # | # | # | # |
| 正面碰撞(X6=1) | 0.206 | -1.578 | 4.555 | 0.033* |
| 侧面碰撞(X6=2) | 1.215 | 0.195 | 0.204 | 0.652 |
| 追尾碰撞(X6=3) | 0.774 | -0.256 | 0.228 | 0.633 |
| 其他(X6=4) | # | # | # | # |
| 小客车(X7=1) | 9.986 | 2.301 | 11.760 | 0.001* |
| 小货车(X7=2) | 1.252 | 0.225 | 0.031 | 0.860 |
| 大客车(X7=3) | 1/M | -12.819 | 0.000 | 0.983 |
| 大货车(X7=4) | 1.919 | 0.652 | 0.642 | 0.423 |
| 其他(X7=5) | # | # | # | # |
| 主城区(X15=1) | 35.292 | 3.564 | 9.130 | 0.003* |
| 近郊区(X15=2) | 18.549 | 2.920 | 6.335 | 0.012* |
| 远郊区(X15=3) | 4.258 | 1.449 | 1.361 | 0.243 |
| 市域高速(X15=4) | # | # | # | # |
| 注:“#”表示该影响因素的参照项;“M”表示一个极大数;“*”标记P值小于0.05的项。 | ||||
(1) 碰撞类型(X6)
对于碰撞类型(X6),其取值为1时为具有显著影响的参考项取值(P=0.033),表明“仅财产损失”事故与“有死亡”事故相比,当碰撞事故类型为正面碰撞(X6=1)时,更偏向于出现“仅财产损失”的事故,这种可能性为其他碰撞类型(X6=4)情况的4.854倍。因此对于不同碰撞类型而言,正面碰撞更多出现的是轻微事故。
(2) 受害方车辆类型(X7)
对于受害方车辆类型(X7),其取值为1时为具有显著影响的参考项取值(P=0.001),表明“仅财产损失”事故与“有死亡”事故相比,当受害方车辆类型为小客车(X7=1)时,更偏向出现“仅有财产损失”的事故,这种可能性为其他车辆类型(X7=4)情况的9.986倍。因此,对于不同类型的车辆而言,小客车发生事故类型多为仅有财产损失的轻微事故,相比于小客车,其他类型的车辆更应该关注其产生严重交通事故的可能性。
(3) 城市分区(X15)
对于城市分区(X15),其取值为1和2都具有显著影响的参考项取值(P=0.003和P=0.012),表明“仅财产损失”事故与“有死亡”事故相比,当城市分区分别为主城区(X15=1)和近郊区(X15=2)时,更偏向于出现“仅财产损失”事故,这种可能性分别为市域高速(X15=4)情况的35.292倍、18.549倍。因此,相比于在市域高速出现的交通事故,出现在主城区和近郊区的交通事故都主要为仅有财产损失的轻微事故。王建军等通过统计分析方法发现高速公路发生的事故具有重大、特大事故占比高的特点,部分原因可能为追尾碰撞、气候情况、驾驶员特征及车辆本身特征,需相应找寻预防事故和提高保护措施的方法[28]。对于沈阳市,主城区和近郊区的经济发展水平高于远郊区,基础设施防护水平相对较高,因而更倾向于出现轻微事故。
(4) 对整体显著但对仅财产损失事故不显著
过失方车辆类型(X1)和过失方年龄(X3)这两项影响因素对模型整体为显著的影响因素,但在Y=1情况与Y=3情况的比对分析中未展现其显著性。因而对“仅财产损失”事故和“有死亡”事故相比较的场景,过失方车辆类型(X1)和过失方年龄(X3)并未展现其显著性。
4.2 有受伤但无死亡事故的计算结果Y=2表示事故严重程度为“有受伤但无死亡”,其显著值P小于0.05处对应自变量的系数有显著统计意义,即对因变量有显著性的影响。OR值表示Y=2“有受伤但无死亡”场景在该参考项下对Y=3“有死亡”场景发生概率相对的可能性倍数。根据表 4的结果,过失方年龄为19至45岁(X3=2)、侧面碰撞(X6=2)为具有显著意义的参考项。过失方车辆类型(X1)、受害方车辆类型(X7)、城市分区(X15)的各类取值为无显著意义的参考项。
| 不同取值的影响因素Xk | OR | B | Wald | P |
| 小客车(X1=1) | 1.027 | 0.027 | 0.002 | 0.961 |
| 小货车(X1=2) | 0.315 | -1.155 | 3.214 | 0.073** |
| 大客车(X1=3) | 1.580 | 0.457 | 0.302 | 0.583 |
| 大货车(X1=4) | 0.375 | -0.981 | 2.629 | 0.105 |
| 其他(X1=5) | # | # | # | # |
| 0至18(X3=1) | M | 16.654 | 0.000 | 0.996 |
| 19至45(X3=2) | 6.671 | 1.898 | 7.018 | 0.008* |
| 46至59(X3=3) | 3.282 | 1.188 | 2.795 | 0.095** |
| 60及以上(X3=4) | # | # | # | # |
| 正面碰撞(X6=1) | 0.626 | -0.468 | 1.401 | 0.237 |
| 侧面碰撞(X6=2) | 2.037 | 0.712 | 5.589 | 0.018* |
| 追尾碰撞(X6=3) | 0.939 | -0.063 | 0.032 | 0.858 |
| 其他(X6=4) | # | # | # | # |
| 小客车(X7=1) | 1.670 | 0.513 | 2.206 | 0.137 |
| 小货车(X7=2) | 0.657 | -0.420 | 0.540 | 0.462 |
| 大客车(X7=3) | 1.016 | 0.016 | 0.001 | 0.981 |
| 大货车(X7=4) | 0.564 | -0.573 | 1.680 | 0.195 |
| 其他(X7=5) | # | # | # | # |
| 主城区(X15=1) | 1.215 | 0.195 | 0.136 | 0.712 |
| 近郊区(X15=2) | 2.307 | 0.836 | 2.992 | 0.084** |
| 远郊区(X15=3) | 0.449 | -0.800 | 2.310 | 0.129 |
| 市域高速(X15=4) | # | # | # | # |
| 注:“#”表示该影响因素的参照项;“M”表示一个极大数;“*”标记P值小于0.05的项;“**”标记P值小于0.1的项。 | ||||
(1) 过失方年龄(X3)
对于过失方年龄(X3),其取值为2时为具有显著影响的参考项取值(P=0.008),表明“有受伤但无死亡”事故与“有死亡”事故相比,当过失方年龄为19~45岁(X3=2)时,更偏向出现“有受伤但无死亡”的事故,这种可能性为60岁及以上(X3=4)情况的6.671倍。因此,对于不同年龄的过失方,19~45岁的群体容易出现受伤事故而非死亡事故,一种可能的解释为19~45岁群体精力很旺盛,因而可能在驾驶过程中风格依然较为激进,但由于其身体反应条件和注意力都更加集中,因此,当遇到危险时,通常这一年龄段的驾驶员都可以通过使用果断的措施来避免致命事故的出现。在未来的监管改进中,可对这一年龄段群体进行持续研究,挖掘其出现更容易出现交通事故,但并非出现致死交通事故的根本原因。
(2) 碰撞类型(X6)
对于碰撞类型(X6),其取值为2时为具有显著影响的参考项取值(P=0.018),表明“有受伤但无死亡”事故与“有死亡”事故相比,当碰撞类型为侧面碰撞(X6=2)时,更偏向于出现“有受伤但无死亡”的事故,这种可能性为其他碰撞类型(X6=4)的2.037倍。因此,说明参与交通组织的交通工具中对于侧面碰撞风险的保护做得较好,可有效地降低死亡事故出现的概率,下一步提高方向为车辆提高侧面碰撞的承受能力,进一步将“有死亡”事故转化为“有受伤但无死亡”事故。通过侧面碰撞的分析模型,评价侧面碰撞对乘客胸部、髋关节等部位的损伤,发现当侧面碰撞被限制在一定的低侵入速度时,通过车门自身刚度可显著减轻乘客所受到的伤害[29]。同时,侧面气囊在侧面碰撞时对乘客的保护效果也是至关重要的[30]。以上研究和本节的结论充分说明在汽车工业设计中,通过合理的工艺设计使得车辆在发生侧面碰撞时,有效地降低了致死事件发生的可能性。
(3) 对整体显著但对有受伤但无死亡事故不显著
过失方车辆类型(X1)、受害方车辆类型(X7)和城市分区(X15)这3个影响因素对模型整体为显著的影响因素,但在Y=2情况与Y=3情况的比对分析中未展现其显著性。因而对“有受伤但无死亡”事故和“有死亡”事故相比较的场景,过失方车辆类型(X1)、受害方车辆类型(X7)、城市分区(X15)并未展现其显著性。
过失方车辆类型(X1)在Y=1和Y=2两种情况与Y=3的比对分析中均未展现出显著性,但对模型是显著的影响因素,则可得其为弱影响因素,仅有部分取值贴近影响因素显著性的临界值。
5 结论本研究以沈阳为例,进行了车辆间碰撞事故影响因素的研究。从过失方人员及车辆属性、受害方人员及车辆属性、时间属性、道路及环境属性等4个方面构建了影响因素集合。建立MNL模型识别道路交通安全的显著性影响因素,并根据事故严重程度的不同等级进行了差异性讨论,获得研究结论如下:
(1) 在降低车辆间事故的安全风险时,需要重点考虑过失方车辆类型、过失方年龄、碰撞类型、受害方车辆类型、城市分区等5个因素。
(2) 对仅财产损失事故和有受伤但无死亡事故,影响因素的取值存在差异性。其中对仅财产损失事故,正面碰撞、受害方车辆类型为小客车, 主城区、近郊区是可能的显著影响因素。对有受伤但无死亡事故,过失方年龄为19~45岁, 侧面碰撞是可能的显著影响因素。
(3) 持续提高对驾驶员的教育警示,使用新技术监督驾驶员的行车状态,提升车辆防御侧面碰撞的能力是可能降低事故严重程度的手段。
| [1] |
World Health Organization. Global Status Report on Road Safety[R]. Geneva: World Health Organization, 2019.
|
| [2] |
World Health Organization. Global Status Report on Road Safety 2015[R]. Geneva: World Health Organization, 2016.
|
| [3] |
ABDEL-ATY M A, RADWAN A E. Modeling Traffic Accident Occurrence and Involvement[J]. Accident Analysis and Prevention, 2000, 32(5): 633-642. |
| [4] |
《中国公路学报》编辑部. 2016中国交通工程学术研究综述[J]. 中国公路学报, 2016, 29(6): 1-161. Editorial Office of China Journal of Highway and Transport. Review on China's Traffic Engineering Research Progress: 2016[J]. China Journal of Highway and Transport, 2016, 29(6): 1-161. |
| [5] |
黄合来, 许鹏鹏, 马明, 等. 道路交通安全规划理论研究前沿[J]. 中国公路学报, 2014, 27(9): 90-97, 118. HUANG He-lai, XU Peng-peng, MA Ming, et al. Recent Theoretical Researches on Transportation Safety Planning[J]. China Journal of Highway and Transport, 2014, 27(9): 90-97, 118. |
| [6] |
裴玉龙, 王炜. 道路交通事故成因及预防对策[M]. 北京: 科学出版社, 2004. PEI Yu-long, WANG Wei. Causes of Road Traffic Accidents and Preventive Measures[M]. Beijing: Science Press, 2004. |
| [7] |
CHUNG Y. Injury Severity Analysis in Taxi-pedestrian Crashes: An Application of Reconstructed Crash Data Using a Vehicle Black Box[J]. Accident Analysis and Prevention, 2018, 111: 345-353. |
| [8] |
ZENG Q, GU W H, ZHANG X, et al. Analyzing Freeway Crash Severity Using a Bayesian Spatial Generalized Ordered Logit Model with Conditional Autoregressive Priors[J]. Accident Analysis and Prevention, 2019, 127: 87-95. |
| [9] |
AL-GHAMDI A S. Analysis of Traffic Accidents at Urban Intersections in Riyadh[J]. Accident Analysis and Prevention, 2003, 35(5): 717-724. |
| [10] |
ÇELIK A K, OKTAY E. A Multinomial Logit Analysis of Risk Factors Influencing Road Traffic Injury Severities in the Erzurum and Kars Provinces of Turkey[J]. Accident Analysis and Prevention, 2014, 72: 66-77. |
| [11] |
AZIMI G, RAHIMI A, ASGARI H, et al. Severity Analysis for Large Truck Rollover Crashes Using a Random Parameter Ordered Logit Model[J]. Accident Analysis and Prevention, 2020, 135: 105355. |
| [12] |
李相勇, 张南, 蒋葛夫. 道路交通事故灰色马尔可夫预测模型[J]. 公路交通科技, 2003, 20(4): 98-100, 104. LI Xiang-yong, ZHANG Nan, JIANG Ge-fu. Grey-markov Model for Forecasting Road Accidents[J]. Highway and Transportation Science and Technology, 2003, 20(4): 98-100, 104. |
| [13] |
AL-BDAIRI N S S, HERNANDEZ S. Comparison of Contributing Factors for Injury Severity of Large Truck Drivers in Run-off-road (ROR) Crashes on Rural and Urban Roadways: Accounting for Unobserved Heterogeneity[J]. International Journal of Transportation Science and Technology, 2020, 9(2): 116-127. |
| [14] |
AHMED M M, FRANKE R, KSAIBATI K, et al. Effects of Truck Traffic on Crash Injury Severity on Rural Highways in Wyoming Using Bayesian Binary Logit Models[J]. Accident Analysis and Prevention, 2018, 117: 106-113. |
| [15] |
WANG Y G, PRATO C G. Determinants of Injury Severity for Truck Crashes on Mountain Expressways in China: A Case-study with a Partial Proportional Odds Model[J]. Safety Science, 2019, 117: 100-107. |
| [16] |
OSMAN M, PALETI R, MISHRA S. Analysis of Passenger-car Crash Injury Severity in Different Work Zone Configurations[J]. Accident Analysis and Prevention, 2018, 111: 161-172. |
| [17] |
WU Q, ZHANG G H, ZHU X Y, et al. Analysis of Driver Injury Severity in Single-vehicle Crashes on Rural and Urban Roadways[J]. Accident Analysis and Prevention, 2016, 94: 35-45. |
| [18] |
MISKINIS P, VALUNTAITE V. Mathematical Simulation of the Correlation between the Frequency of Road Traffic Accidents and Driving Experience[J]. Transport, 2010, 25(3): 237-243. |
| [19] |
KIM J K, ULFARSSON G F, KIM S, et al. Driver-injury Severity in Single-vehicle Crashes in California: A Mixed Logit Analysis of Heterogeneity due to Age and Gender[J]. Accident Analysis and Prevention, 2013, 50: 1073-1081. |
| [20] |
BEHNOOD A, MANNERING F L. An Empirical Assessment of the Effects of Economic Recessions on Pedestrian-injury Crashes Using Mixed and Latent-class Models[J]. Analytic Methods in Accident Research, 2016, 12: 1-17. |
| [21] |
马壮林, 邵春福, 李霞. 基于Logistic模型的公路隧道交通事故严重程度的影响因素[J]. 吉林大学学报: 工学版, 2010, 40(2): 423-426. MA Zhuang-lin, SHAO Chun-fu, LI Xia. Analysis of Factors Affecting Accident Severity in Highway Tunnels Based on Logistic Model[J]. Journal of Jilin University: Engineering and Technology Edition, 2010, 40(2): 423-426. |
| [22] |
ISLAM S, JONES S L, DYE D. Comprehensive Analysis of Single- and Multi-vehicle Large Truck at-fault Crashes on Rural and Urban Roadways in Alabama[J]. Accident Analysis and Prevention, 2014, 67: 148-158. |
| [23] |
WANG J Y, LU H P, SUN Z Y, et al. Exploring Factors Influencing Injury Severity of Vehicle At-fault Accidents: A Comparative Analysis of Passenger and Freight Vehicles[J]. International Journal of Environmental Research and Public Health, 2020, 17(4): 1146. |
| [24] |
SZE N N, WONG S C. Diagnostic Analysis of the Logistic Model for Pedestrian Injury Severity in Traffic Crashes[J]. Accident Analysis and Prevention, 2007, 39(6): 1267-1278. |
| [25] |
CHENG W, GILL G, SAKRANI T, et al. Predicting Motorcycle Crash Injury Severity Using Weather Data and Alternative Bayesian Multivariate Crash Frequency Models[J]. Accident Analysis and Prevention, 2017, 108: 172-180. |
| [26] |
ZHAI X Q, HUANG H L, SZE N N, et al. Diagnostic Analysis of the Effects of Weather Condition on Pedestrian Crash Severity[J]. Accident Analysis and Prevention, 2019, 122: 318-324. |
| [27] |
朱建安, 戴帅, 朱新宇. 电动自行车交通事故特征与安全改善对策[J]. 城市交通, 2018, 16(3): 15-20. ZHU Jian-an, DAI Shuai, ZHU Xin-yu. Characteristics of Electric Bike Accidents and Safety Enhancement Strategies[J]. Urban Transport of China, 2018, 16(3): 15-20. |
| [28] |
王建军, 王军锋, 毕明涛. 区域公路交通事故及高速公路交通事故特征[J]. 长安大学学报: 自然科学版, 2005, 25(3): 66-69. WANG Jian-jun, WANG Jun-feng, BI Ming-tao. Characteristics of Traffic Accidents on Highway and Expressway[J]. Journal of Chang'an University: Natural Science Edition, 2005, 25(3): 66-69. |
| [29] |
GIERCZYCKA D, CRONIN D. Influence of the Chest Compression Measurement Method on Assessment of Restraint Performance in Side-impact Crash Scenarios[J]. Journal of Biomechanics, 2018, 75: 53-57. |
| [30] |
HWANG E, HU J W, REED M P. Validating Diverse Human Body Models against Side Impact Tests with Post-mortem Human Subjects[J]. Journal of Biomechanics, 2020, 98: 109444. |
 2021, Vol. 38
2021, Vol. 38
