扩展功能
文章信息
- 杜晓雷, 葛华
- DU Xiao-lei, GE Hua
- 无黏结预应力桥墩桥梁结构耐震时程分析
- Endurance Time Analysis on Bridge with Unbonded Prestressed Piers
- 公路交通科技, 2021, 38(10): 82-91, 99
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(10): 82-91, 99
- 10.3969/j.issn.1002-0268.2021.10.011
-
文章历史
- 收稿日期: 2020-07-09
2. 四川电力设计咨询有限责任公司, 四川 成都 610041
2. PowerChina Sichuan Electric Power Engineering Co., Ltd., Chengdu Sichuan 610041, China
现行国内外桥梁抗震设计规范主要采用延性抗震设计的理念[1-3],其允许墩柱进入塑性,形成塑性铰而延长结构周期,耗散地震能量。但此理念使墩柱塑性铰区域在强震时发生严重损伤,产生较大的塑性不可恢复变形,震后需花费大量人力物力来修复或拆除。为了减小桥梁结构震后的残余位移,保证其震后使用功能,国内外学者对具有自复位能力的桥梁体系进行了大量探索研究[4-7]。目前实现桥梁自复位能力主要有两种途径:利用地震中桥梁下部结构的摇摆,通过自重来提供自复位力,达到减小震后残余位移的目标[4];或在墩身中安装预应力钢筋或钢绞线,通过施加的预应力来提供自复位的能力,从而控制和减小桥墩震后残余位移[7]。利用摇摆特性虽在一定条件下能减小结构残余变形,但其抗倾覆能力和耗能能力均较差,且在摇摆面会发生滑移和碰撞现象,导致柱脚混凝土局部压碎[8],因此往往还需在墩身中施加无黏结预应力来实现自复位的目标。
20世纪90年代初,美国开展预制抗震结构体系(PRESS)研究计划,并率先进行了无黏结预应力筋提供结构自复位能力的研究[9]。随后,Sakai等[10-11]提出在普通钢筋混凝土墩柱中设置无黏结预应力钢筋,利用无黏结预应力为结构提供弹性恢复力,而墩底的普通钢筋提供滞回耗能;并通过一系列振动台试验证实了这种新型体系除能增大结构的屈后刚度外,还能同时减小结构的最大和残余位移。此外,通过Chandara[12]等人研究发现无黏结预应力的引入还能增大墩柱的延性能力。近年来,我国学者对此新体系也开展了大量研究。孙治国等[13]通过拟静力试验探究了此体系中预应力筋布置形式、预应力大小以及预应力筋与普通钢筋相对用量等参数对结构耗能能力和破坏过程的影响;发现配置无黏结预应力的钢筋混凝土墩柱与普通钢筋混凝土桥墩破坏过程和形式相似,均是墩底一定高度内保护层混凝土剥落,核心混凝土破坏;此外,不同预应力布置形式和预应力大小易对结构抗震性能产生影响。针对这种混合体系桥墩,刘笑显等[7, 14]也通过拟静力试验探究预应力大小对墩柱抗震性能的影响,并提出一种新的自复位能力评价指标;其同样发现混凝土墩身底部区域易发生破坏,且墩柱抗震性能受预应力布置形式和大小影响。由此可见,地震下预应力普通钢筋混凝土墩柱需避免墩底混凝土损伤,且需精确地分析出预应力对其抗震性能影响,为此类桥墩抗震设计提供数据支撑。考虑到钢管能有效约束混凝土,提高其强度、塑性和韧性[15-16],学者们提出预应力钢管混凝土桥墩结构[17-18],并研究发现结合预应力技术和钢管混凝土桥墩体系能增大结构的极限位移且保证结构小损伤[11]。此方法虽能提高桥墩抗震性能,缓解墩柱塑性铰区域损伤,但进一步加大了结构的复杂性。
为高效获取复杂结构体系的地震响应,伊朗学者提出了类似于动力Pushover分析的耐震时程法(ETM),并已被证实可用于多种结构的抗震评估和分析[19-22]。针对此方法在桥梁结构中的应用,郭安薪等[23]首次将其用于梁式桥地震碰撞响应分析;随后,沈禹等[22]研究了考虑行波效应的大跨度桥梁碰撞响应耐震分析,扩展了此方式在桥梁地震碰撞响应适用性的范围。此外,针对耐震时程法在高墩刚构桥[24]和考虑冲刷效应影响[25]的适用性也已被证实,但此方法还未被用于自复位桥墩桥梁结构的抗震分析中。预应力钢管混凝土自复位桥墩体系复杂,受预应力大小和地震动特性影响大,因此有必要进行耐震时程法对此类桥墩桥梁结构的适用性研究。
本研究首先阐述了耐震时程法的理念, 并基于桥梁抗震规范反应谱合成的3条耐震时程曲线,进行此方法在预应力钢管混凝土自复位桥墩桥梁结构抗震分析的适用性研究;最后,采用耐震时程法进行了桥墩的无黏结预应力对桥梁结构地震响应影响的研究。
1 耐震时程法耐震时程分析(ETA)是一种新型结构动力评估方法,其理念是对结构输入幅值随时间不断增大的人工合成地震动进行动力时程分析[19]。本质是将动力分析和Pushover分析相结合,通过地震动持时与幅值正相关的特点来简化运算量。因此,只需通过一次动力分析便能得到目标结构在不同地震动强度下的响应。此方法还可通过不同结构达到性能目标时,所需经受的时间长短来判断结构抗震性能的优劣,结构所能经受时间越长,表明结构的抗震性能越好,这也是“耐震”一词的含义。
合成高质量的耐震加速度曲线是ETA方法能否准确捕捉到结构响应的关键。依照新一代耐震时程曲线的合成准则[19-20],其在某一时间段t内的加速度反应谱SaT (T, t)和位移反应谱SuT (T, t)均与该时间段t成线性关系,即满足式(1)和式(2)。
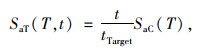
|
(1) |
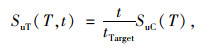
|
(2) |
式中, SaT (T, t)和SuT (T, t)分别是0至t时刻的耐震加速度反应谱和位移反应谱;T是结构的一阶周期;SaC (T)和SuC (T)是目标加速度反应谱和目标位移谱,一般为规范中反应谱;tTarget是用于缩放耐震加速度曲线的目标时间,其含义是0至tTarget时刻的耐震加速度反应谱SaT (T, t)和位移反应谱SuT (T, t)分别与目标加速度反应谱SaC (T)和目标位移谱SuC (T)相吻合。
考虑到在不同时间段均需满足式(1)和式(2)存在很大难度,因此我们采用无约束变量优化法将式(1)和(2)转化为式(3)进行迭代优化:
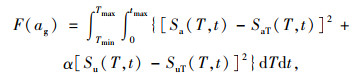
|
(3) |
式中, ag是优化合成的耐震时程曲线,其为目标方程优化到最小值时所得出的加速度时程;Tmax和Tmin分别是优化过程中,目标反应谱考虑的最大和最小周期;tmax是合成耐震加速度的持续时间;Sa (T, t)和Su (T, t)分别是0至t时段内,T周期结构的耐震加速度谱值和耐震位移谱值;α则是位移反应谱的权重系数,因加速度反应谱和位移反应谱密切相关,可选任意一个作为迭代响应参数,本研究取加速度反应谱为目标谱,即α=0。
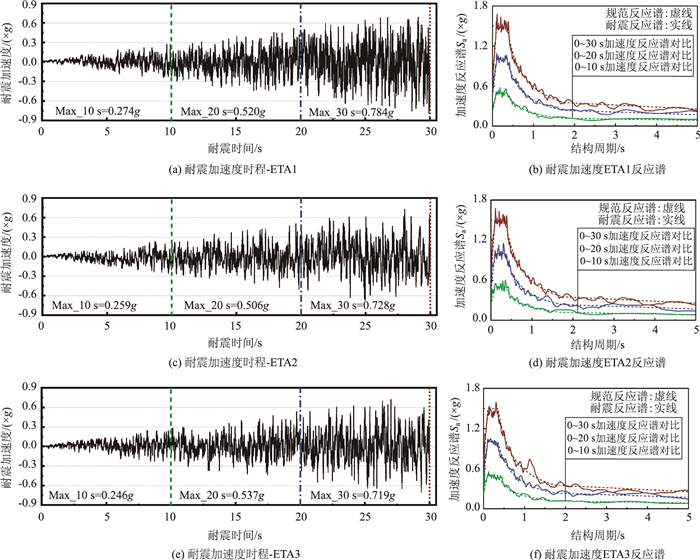
基于我国《城市桥梁抗震设计规范》(CJJ 166—2011) 中设计加速度反应谱公式(5.2.1-1)和(5.2.1-2)[2]合成了3条持时为30 s的ETA时程曲线(命名为ETA1, ETA2和ETA3),如图 1所示。考虑到本文研究对象的一阶周期和场地特征,规范加速度反应谱平台段和特征周期分别取为0.5g和0.35 s。目标时间tTarget在本研究中取为10 s,从图中可以看出3条耐震时程曲线的峰值加速度均随时间的增长在不断增大,如对于耐震曲线ETA1,在3个时间段内的加速度峰值分别为0.274g,0.520g和0.784g,与耐震时程法的基本理念一致。此外,图 1还给出3条耐震时程曲线分别在0~10 s,20 s和30 s时间段内的耐震加速度反应谱,可以发现合成的3条耐震时程曲线,其在3个时间段内的耐震加速度谱与目标规范反应谱均能很好地吻合,表明生成的3条耐震曲线满足合成准则。虽然3条耐震曲线均能符合耐震时程法的基本理念,理论上采用一条耐震时程曲线便可满足分析要求,但从图 1中发现各条耐震曲线的峰值加速度和反应谱存在一定差异,为提高耐震时程法的分析精度,本研究采用3条耐震时程曲线分析的均值作为此方法预测结构的响应值[22]。
|
| 图 1 耐震时程曲线及其不同耐震时间下的加速度反应谱 Fig. 1 Endurance time curves and their acceleration response spectra with different durations |
| |
2 桥梁分析模型 2.1 桥梁工程概况
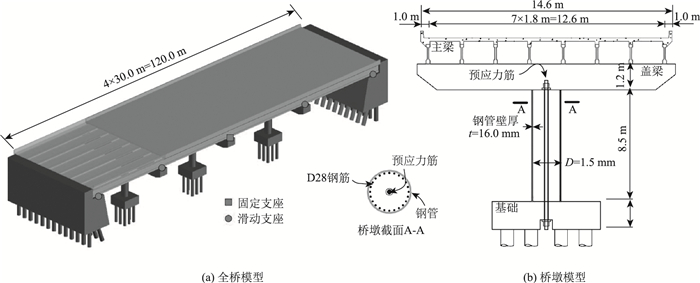
本研究选取采用圆形预应力钢管混凝土桥墩的四跨连续梁桥为原型,如图 2(a)所示[26]。考虑到未有此桥梁的实测数据,因此本研究选用的桥梁模型仅作为研究的计算示例。全桥跨径布置为4×30.0 m,上部结构由8个纵向工字型肋梁和宽14.6 m的桥面板组成,双向车道,每延米质量为14.5 t,截面面积为5.4 m2,左右侧通过纵向活动盆式支座支撑于桥台处。下部结构如图 2(b)所示,由直径1.5 m的圆形钢管混凝土单墩和盖梁组成,桥墩和盖梁高分别为8.5 m和1.2 m,钢管壁厚为16 mm;墩身和盖梁均采用C40混凝土浇注,钢管采用Q345钢材;墩身主筋配置32根直径28 mm的HRB400钢筋,配筋率为1.12%,如图 2中截面A-A所示;墩身中预应力筋采用螺纹钢筋,预应力配筋率为0.5%,屈服强度和抗拉强度分别为1 080 MPa和1 230 MPa[27],初始张拉力为5 695.8 kN,对应的轴压比为8%。纵桥向中间墩设置固定盆式橡胶支座,其余墩顶处设置纵向活动盆式支座;横桥向各墩顶和承台处均为固结,如图 2(a)所示。
|
| 图 2 预应力钢管混凝土墩桥梁示意图 Fig. 2 Schematic diagram of bridge with prestressed CFST piers |
| |
2.2 桥梁有限元模型
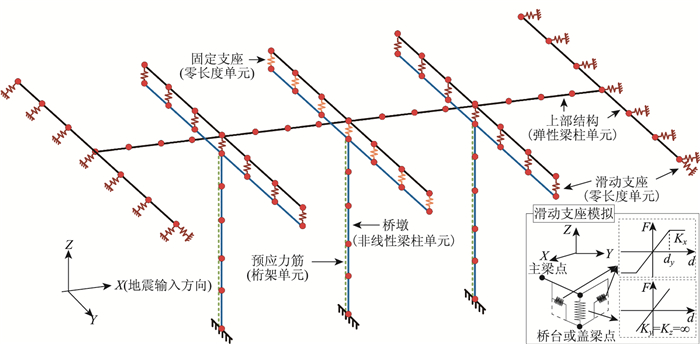
基于OpenSees分析软件建立了全桥三维有限元模型,如图 3所示,其中x轴方向为桥梁纵向。有限元模型中每一跨上部结构纵横向分别划分为5个和7个单元节点,依据主梁每延米质量计算出每个单元的质量,并以集中质量的形式赋予在每个节点上;考虑到上部结构在地震时不易损坏,因此采用弹性梁柱(elastic Beam-Column)单元模拟,每一单元赋予轴向刚度和两个方向抗弯和抗扭刚度。主梁与盖梁处支座采用零长度(zero Length)单元模拟,对于固定支座,采用大刚度的方式提供水平侧向刚度;对于活动盆式支座,如图 3右下角所示,其横向同样采用大刚度方式保证固结,纵向则采用双线性理想弹塑性材料进行模拟,其中临界摩擦力Fy采用式(4)描述:
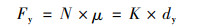
|
(4) |
|
| 图 3 桥梁三维有限元模型图 Fig. 3 Three-dimensional FE model of bridge |
| |
式中,初始滑动位移dy取2 mm;K为支座的初始刚度;N为支座的恒载竖向反力;μ为滑动摩擦系数,考虑支座为聚四氟乙烯和不锈钢之间滑动,取为0.02;为确保固定支座和滑动支座在地震下不出现脱空现象,竖向刚度取为无穷大。此外,因桥址地质条件好,土质较硬,所以未考虑承台和桥台下的桩-土相互作用,而将墩底和承台底保持固结。
桥梁的桥墩为预应力钢管混凝土结构,如图 3所示,采用并联钢管混凝土墩柱和预应力筋对其进行模拟。预应力筋采用桁架(Truss)单元模型,但须保证其在地震下一直处于弹性。此外,本研究采用添加初始应变的方式给预应力筋提供初始张拉力。因钢管混凝土墩柱在地震时易进入非线性,因此将墩柱截面分成核心混凝土、纵向钢筋和钢管3部分,采用基于力的非线性梁柱(Force-based Beam-Column)纤维单元进行模拟,其中每个单元取5个高斯积分点。钢管和钢筋的本构均采用考虑钢材同向和随动强化以及包辛格效应的Steel02材料;而核心混凝土本构采用韩林海提出的应力-应变关系,如式(5)所示[15]:
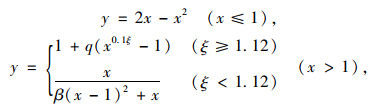
|
(5) |
式中,x=ε/ε0;y=σ/σ0;ε和σ分别为钢管内混凝土的应变和应力;ε0和σ0分别为钢管内混凝土的峰值应变和峰值应力;β和q是与材料性能和截面尺寸有关的系数,详见文献[15];ξ为约束效应系数,表达式为:
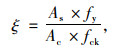
|
(6) |
式中,As和Ac分别是钢管和核心混凝土的截面面积;fy是钢材的屈服强度;fck是混凝土轴心抗压强度标准值。
对建立的桥梁有限元模型进行模态分析,得到墩柱施加无黏结预应力时,桥梁纵向一阶周期为0.95 s,横向一阶周期为0.24 s;墩柱不考虑无黏结预应力时的纵横向一阶周期分别为0.99 s和0.30 s,可见桥墩中无黏结预应力的引入可增大结构刚度。但无黏结预应力筋的引入并未对桥梁的一二阶模态产生影响,均分别是纵向振动和横向振动。此外,由于本研究仅考虑纵向地震响应,因此地震动仅沿纵桥向(x方向)输入。
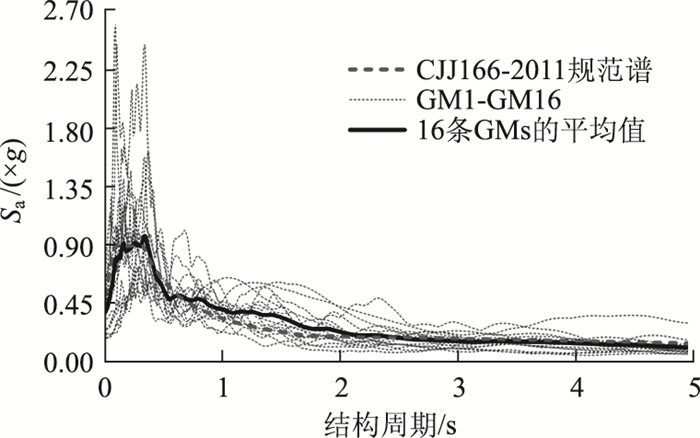
3 耐震时程法适应性分析 3.1 地震动挑选采用与增量动力分析(IDA)结果对比,进行耐震时程法对预应力钢管混凝土桥墩桥梁结构地震响应捕捉的适用性分析。IDA分析虽同样表征结构工程需求参数与地震动强度的关系,但此方法需选择多条地震动,进行大量地震动调幅运算才能得到IDA曲线[28]。因此,首先以合成耐震曲线的桥梁抗震设计规范反应谱为基础,在PEER-NGA地震数据库中选择16条天然地震动用于IDA分析,挑选的地震动详细信息见表 1。挑选的原则是16条天然地震动分别调幅后的加速度反应谱均值与规范反应谱曲线吻合较好。图 4为16条调幅后的天然地震动反应谱及其均值与规范反应谱曲线的对比图,可以发现天然地震动反应谱均值与规范谱在0~5 s周期范围内均能较好地吻合。
| 地震名称 | 震级 | 站台 | 峰值加速度/(×g) | 调幅系数 |
| Borreg0.194 2 | 6.50 | El Centro Array #9 | 0.066 | 6.81 |
| Kern County, 1952 | 7.36 | LA-Hollywood Stor FF | 0.042 | 4.53 |
| Kern County, 1952 | 7.36 | Taft Lincoln School | 0.159 | 2.66 |
| Northern Calif-03, 1954 | 6.50 | Ferndale City Hall | 0.163 | 1.55 |
| Parkfield, 1966 | 6.19 | Cholame-Shandon Array #12 | 0.060 | 6.84 |
| Borrego Mtn, 1968 | 6.63 | El Centro Array #9 | 0.133 | 2.53 |
| Borrego Mtn, 1968 | 6.63 | San onofre-So Cal-Edison | 0.041 | 10.75 |
| San Fernando, 1971 | 6.61 | 2516 Via Tejon PV | 0.026 | 9.63 |
| San Fernando, 1971 | 6.61 | Carbon Canyon Dam | 0.071 | 9.38 |
| San Fernando, 1971 | 6.61 | LA-Hollywood Stor FF | 0.225 | 1.61 |
| San Fernando, 1971 | 6.61 | LB-Terminal Island | 0.029 | 6.53 |
| San Fernando, 1971 | 6.61 | Pacoima Dam (upper left abut) | 1.219 | 0.53 |
| San Fernando, 1971 | 6.61 | Port Hueneme | 0.027 | 6.93 |
| San Fernando, 1971 | 6.61 | Santa Felita Dam (Outlet) | 0.155 | 3.52 |
| San Fernando, 1971 | 6.61 | UCSB-Fluid Mech Lab | 0.017 | 12.56 |
| San Fernando, 1971 | 6.61 | Whittier Narrows Dam | 0.101 | 4.68 |
|
| 图 4 选取的地震动反应谱及其均值与规范反应谱对比 Fig. 4 Response spectra of selected earthquakes and comparison of their means with code spectra |
| |
3.2 适用性结果分析
本研究采用16条地震动IDA分析曲线的均值作为参照进行耐震时程法的适用性分析。此外,需通过式(7)建立起耐震时程法中耐震时间t与IDA分析中谱加速度值Sa (T)的关系:
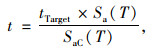
|
(7) |
式中Sa (T)为IDA分析中单条地震动调幅后反应谱值。
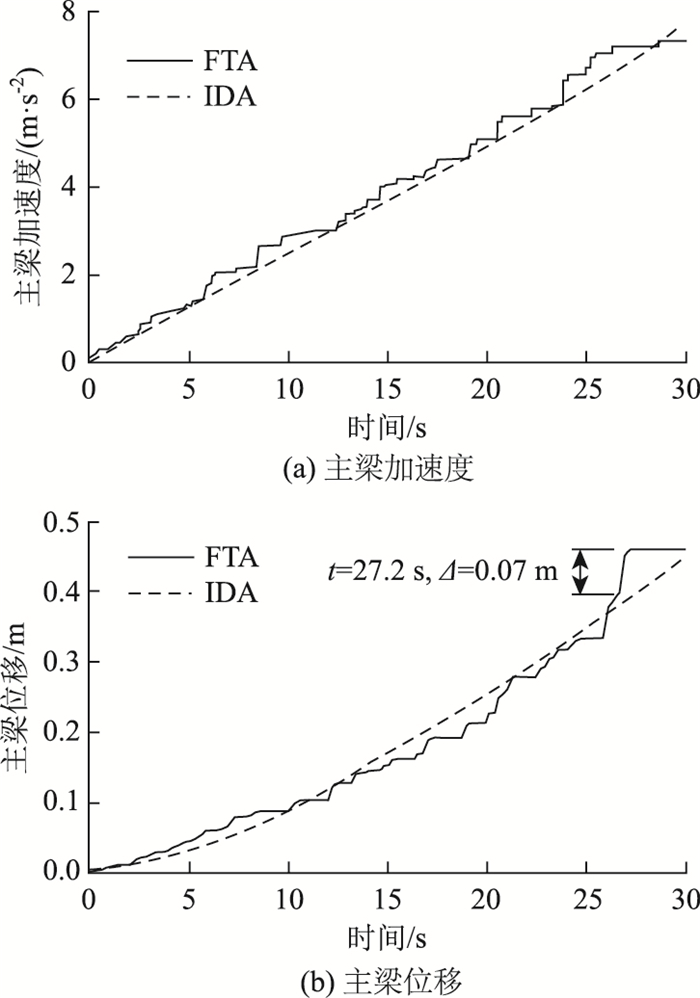
图 5给出了IDA和ETA分析下桥梁主梁加速度和位移响应值的对比图。从图中可以看出与IDA平滑的曲线不同,ETA分析因其方法统计的离散性而使曲线呈锯齿状,但两种方法得到的结构响应均随着时间(谱加速度值)增大而增加。此外,对比图 5中ETA和IDA曲线,发现不论是主梁的加速度还是位移,二者的响应值均能很好地吻合。在图 5(a)中,虽然两种分析下主梁加速度在10,20 s和30 s时的误差分别为12.9%,4.5%和4.4%,但考虑到ETA分析只进行了3次运算,且曲线为锯齿状,因此这些分析误差在可接受范围内。对于主梁位移,如图 5(b)所示,ETA同样能够很好地预测其响应值。虽在大震时,ETA预测的位移值较IDA分析的值大,在27.2 s时达到0.07 m(误差17.6%),但考虑到大震下结构进入强非线性,此误差可接受。因此,可以表明耐震时程法可以很好地预测出预应力钢管混凝土桥墩桥梁地震下的主梁响应。
|
| 图 5 IDA和ETA方法下主梁响应对比 Fig. 5 Comparison of responses of main girder between IDA and ETA |
| |
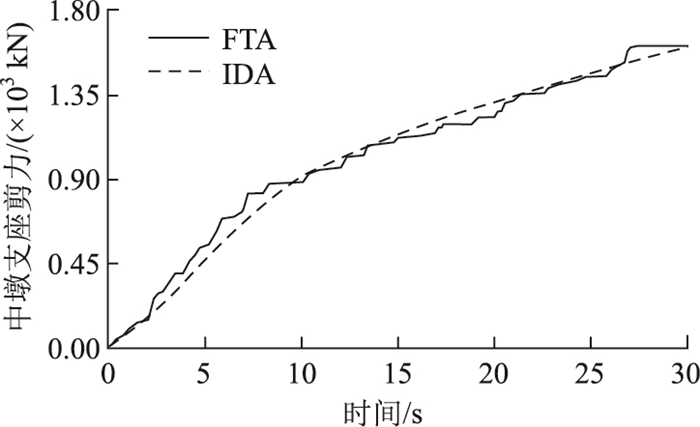
基于数据分析,图 6给出了中墩顶固定支座剪力在IDA和ETA分析下的对比曲线。可以发现耐震时程法同样可以很好地捕捉到支座剪力;在30 s时,IDA和ETA分析下的固定支座剪力分别为1 609.3 kN和1 597.9 kN,二者数值几乎一致。此外,左右桥墩顶采用了滑动支座,在较小耐震时间下便发生滑动,因此本研究并未给出滑动支座的剪力时程图,但IDA和ETA分析出滑动支座开始发生滑动的时间分别为0.31 s和0.25 s,表明ETA分析同样能够捕捉到滑动支座发生滑动的时间。因此表明耐震时程法可以用于支座响应分析。
|
| 图 6 IDA和ETA方法下中墩支座剪力对比 Fig. 6 Comparison of shear forces of bearing in middle pier between IDA and ETA |
| |
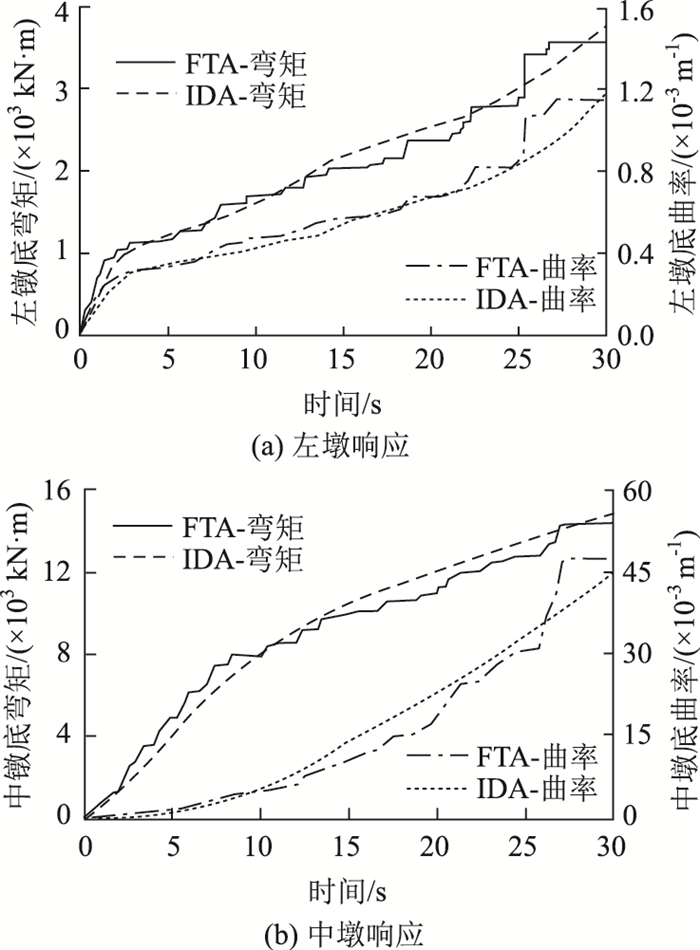
因整个桥梁为中心对称结构,左右墩的地震响应几乎一致,因此本研究仅列出左边墩和中间墩的地震响应。图 7(a)和(b)分别给出了左桥墩和中间桥墩墩底弯矩和曲率在两种方法下的响应对比图。对比左边墩和中间墩响应值可以发现,因为左侧墩顶的滑动支座发生滑动后,主梁惯性力几乎由中墩顶的固定支座传递到墩底,因此中墩的地震响应远大于左右边墩的响应。如图 7(a)所示,左墩底的弯矩和曲率随耐震时间的增长趋势几乎一致,这是因为滑动支座的隔震作用,导致左墩身受上部质量影响小,整个墩身几乎处于线性;而中墩底两种方法的弯矩和曲率曲线随时间增长的差异性较大,如图 7(b)所示,这是因为中墩承受了大部分上部质量的惯性力,墩身进入强非线性,导致大震下的弯矩增长趋势放缓,而曲率响应增长速率变大。此外,从图中可以发现两种方法预测墩底弯矩和曲率曲线基本重合,表明耐震时程法能够很好地反映出16条IDA分析的结果。两种方法在耐震时间为15 s时,左墩底弯矩和曲率的误差分别为4.3%和6.9%,而中墩底的弯矩和曲率的误差分别为5.9%和21.5%,可见墩身进入强非线性后两种方法的误差增大,但考虑到耐震加速度和真实地震动存在的差异,这些误差均可接受。此外,当耐震时间进一步增大,两种方法预测中墩底响应的误差有减小趋势。因此,可以采用耐震时程法进行预应力钢管混凝土桥墩抗震性能评估。
|
| 图 7 IDA和ETA方法下桥墩响应对比 Fig. 7 Comparison of responses of bridge piers between IDA and ETA |
| |
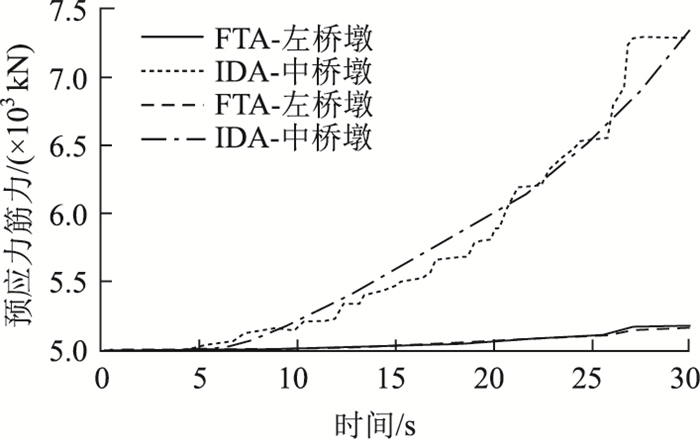
图 8分别给出了IDA和ETA分下左墩和中墩预应力筋的力随着耐震时间的对比曲线,可以发现两种方法下的预应力大小随地震强度的增大而增大,且因中墩顶设置了固定支座,使其预应力增长幅度较两侧边墩的预应力大。对于左墩的预应力,因墩身未进入强非线性,因此两种方法下的曲线几乎重合;而中墩的预应力值,当耐震时间在10 s至20 s时,ETA方法低估了响应,最大误差为3.8%,但25 s后又出现高估预应力值的现象,这是由于结构进入强非线性,导致两种方法分析的误差增大。但考虑到ETA分析是一种简化且快捷的抗震分析方法,此误差是可接受的。因此,耐震时程法可以用于预测预应力墩柱进入强非线性后,预应力值的大小。
|
| 图 8 IDA和ETA方法下预应力筋力对比 Fig. 8 Comparison of forces of prestressed bars between IDA and ETA |
| |
4 预应力影响的耐震时程分析
基于上述ETA适用性分析可知,其可用于分析预应力钢管混凝土自复位桥墩桥梁的地震响应。因此,本节进行此方法下墩柱内是否考虑预应力对桥梁地震响应影响的分析。为更好地表明墩柱内预应力引入对结构响应的影响,定义了结构响应的无量纲系数β,其计算公式如下:
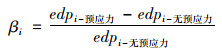
|
(8) |
式中,edpi-预应力和edpi-无预应力分别为钢管混凝土桥墩中考虑预应力和不考虑预应力下第i个工程需求参数。本节分析中不考虑预应力的工况是将第2节的桥梁模型去除无黏结预应力单元和初始张拉力。
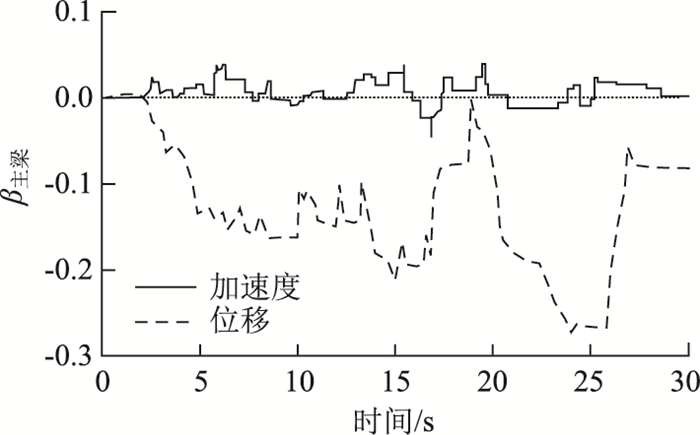
图 9列出了ETA分析下主梁加速度和位移的β曲线图。从图中可以看出,ETA结果的锯齿状曲线导致其β值曲线也存在锯齿,但预应力筋对主梁响应的影响依旧可通过β曲线的变化趋势清晰的表达出。自复位预应力筋的引入对主梁加速度的影响很小,只在0.05范围内波动;但其对主梁位移的响应较大且复杂,在耐震时间3 s前,有无预应力筋对主梁位移几乎不产生影响,但当耐震时间超过3 s后,随着耐震时间的增长,预应力可明显减小主梁位移,在25 s左右减小幅度达到最大值26.7%,如图 9短虚线所示,这是因为预应力的引入增大了墩柱刚度,减小了主梁位移。但需注意在耐震区间 [18, 20] s和 [27, 30] s时,预应力对主梁位移的限制出现不敏感现象,这可能是因为合成的耐震时程曲线的频谱缺失了此区间内的结构振动频率。
|
| 图 9 主梁响应的β曲线 Fig. 9 β curves of response of main girder |
| |
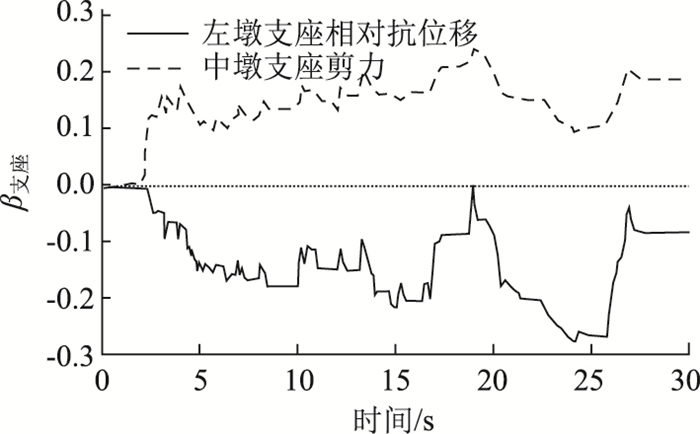
图 10给出了耐震时程分析下,预应力对左墩顶支座纵向相对位移(即支座变形)和中墩顶支座纵向剪力的影响。对比图 9和图 10可以发现,预应力对滑动支座相对位移的影响与对主梁位移影响相似,即都在耐震时间大于3 s后出现预应力限制位移值的现象。但预应力的出现会导致中墩支座剪力增大,如图 10所示,当耐震时间达到3 s时,支座剪力突然增大到不考虑预应力筋响应的1.12倍左右,且此增长幅度几乎不随耐震时间的继续增大而发生较大改变,在[0.9, 1.2]范围内波动。
|
| 图 10 支座响应的β曲线 Fig. 10 β curves of response of bearing |
| |
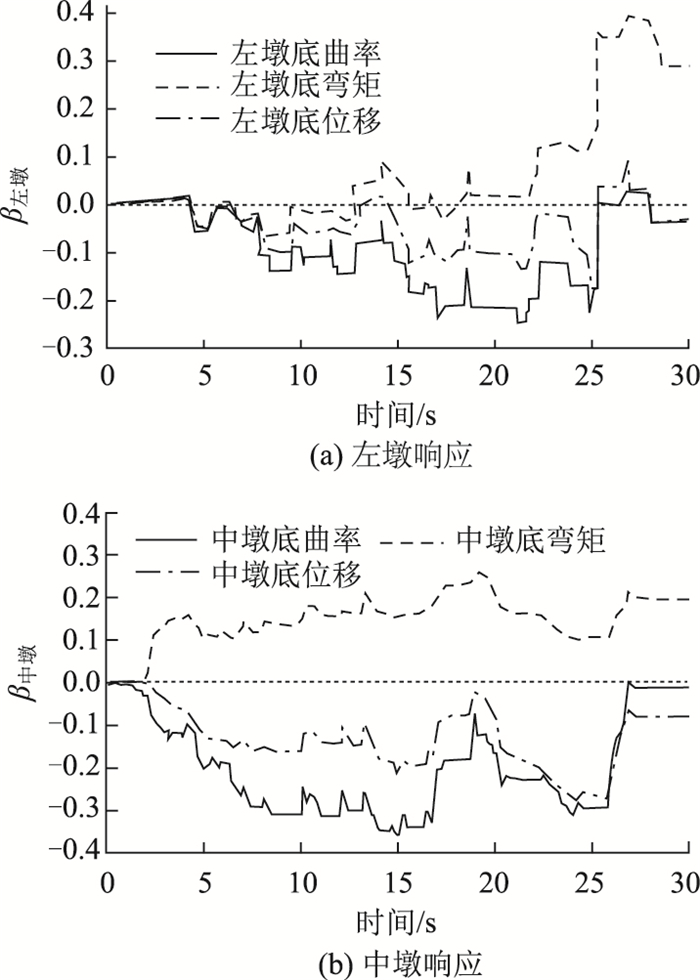
图 11给出了左侧桥墩和中间桥墩底部曲率、弯矩和顶部位移随耐震时间增长的预应力影响β曲线图。从图 11(a)中可以看出,左墩底弯矩的预应力影响β值在22 s前,即Sa (T) ≤ 0.43g时,在[-0.1 0.1]范围内波动,表明此时预应力的引入对左墩底弯矩影响较小;但当耐震时间大于22 s后,β值迅速增长,在27 s左右时达到最大正值40%,可见在大震下,预应力的引入会增大左墩墩底弯矩。对于左墩底曲率,当耐震时间小于4 s,预应力对其影响可忽略不计,但当耐震时间继续增大后,预应力减小左墩底曲率的趋势愈发明显,且在22 s左右达到最低负值24.6%;而当耐震时间超过27 s后,有无预应力筋对于左墩底曲率影响有限。中墩底因为在大震下进入非线性,因此其β曲线与左墩底存在一定差异,但总体趋势为预应力的引入在耐震时间大于2 s后,会增大墩底弯矩,但减小墩底曲率。这是因为预应力会增大墩身刚度,周期减小,导致其变形减小,即墩底曲率减小,但与加速度有关的惯性力增大,从而增加墩底弯矩。此外,大震时,预应力筋对于墩底曲率几乎不产生影响的现象同样在中间墩底处出现。两桥墩顶部位移响应的β曲线随耐震时间的变化趋势均与各自墩底曲率β曲线相似,但β值更小,这是因为墩顶位移本质上是由墩底曲率变形和墩身变形叠加引起,但考虑到是钢管混凝土墩柱自身变形小,因此墩底曲率引起的变形对墩顶位移起主要作用,从而使顶部位移和底部曲率的β曲线变化趋势相似。
|
| 图 11 桥墩响应的β曲线 Fig. 11 β curves of responses of bridge piers |
| |
为研究钢管混凝土墩柱中引入预应力对结构自复位能力的响应,表 2列出了3条耐震时程曲线输入下,有无预应力时主梁的残余位移以及其均值。表中可以看出钢管混凝土墩柱中加入无黏结预应力筋均减小了3条ETA输入下的主梁残余位移,在无预应力时的平均残余位移为5.72 cm,而加入8%轴压比的预应力后,平均残余位移减小为1.40 cm,减小幅度达到75.5%。因此,墩柱中加入预应力可显著增大钢管混凝土桥墩桥梁的自复位能力,保证其震后残余位移与变形较小。
| 地震 | 位移/cm | 减小幅度/% | |
| 不考虑预应力筋 | 考虑预应力筋 | ||
| ETA1 | 3.54 | 0.87 | 75.4 |
| ETA2 | 9.74 | 1.96 | 79.9 |
| ETA3 | 3.87 | 1.36 | 56.3 |
| 平均值 | 5.72 | 1.40 | 75.5 |
5 结论
本研究在验证耐震时程法能高效预测出预应力钢管混凝土桥墩桥梁结构地震响应基础上,进行了墩柱中引入预应力对结构地震响应的影响分析,得到以下主要研究结论:
(1) 通过与16条IDA分析结果对比验证,耐震时程法在桥梁结构中的适用性范围得到扩展,可用于分析预应力钢管混凝土桥墩桥梁等自复位结构的内力、预应力大小以及残余位移等地震响应。
(2) 墩柱中引入预应力可减小主梁位移,但固定支座剪力增大;此外,当耐震时间t在区间[18, 20] s和 [27, 30] s下,即对应于结构谱加速度Sa (T)在[0.35g, 0.39g]和[0.53g, 0.59g]时,钢管混凝土墩柱是否采用无黏结预应力对桥梁上部结构的影响较小。
(3) 预应力对下部结构变形和内力的影响与墩柱中的支座形式有关:对于顶部是滑动支座的桥墩,当耐震时间小于22 s,即Sa (T)≤0.43g时,预应力会增大墩底内力,而墩底曲率几乎不受影响。但当耐震时间继续增大时,预应力的引入对桥墩地震响应有利,在不增大内力的同时减小墩底曲率。对于顶部是固定支座的桥墩,预应力总体上会减小墩柱的变形,但增大其内力。
(4) 在墩柱中引入无黏结预应力增大结构刚度,减小结构周期,同时能显著增大结构的自复位能力,减小结构的残余位移和变形。但其对结构地震响应的影响与地震动强度有关,因为在进行此类桥梁抗震设计时需重点考虑设计场地的地震动强度。
(5) ETA分析只需3次运算便能得到预应力对自复位钢管混凝土桥墩桥梁结构地震响应的影响,这为快速分析出不同预应力大小对自复位桥梁结构的影响提供了潜在可能。
| [1] |
AASHTO-2015, Guide Specification for LRFD Seismic Bridge Design[S].
|
| [2] |
CJJ 166-2011, 城市桥梁抗震设计规范[S]. CJJ 166-2011, Code for Seismic Design of Urban Bridges[S]. |
| [3] |
JTG/T B02-01-2008, 公路桥梁抗震设计细则[S]. JTG/T B02-01-2008, Guidelines for Seismic Design of Highway Bridges[S]. |
| [4] |
DU X L, ZHOU Y L, HAN Q, et al. Shaking Table Tests of a Single-Span Freestanding Rocking Bridge for Seismic Resilience and Isolation[J]. Advances in Structural Engineering, 2019, 22(15): 3222-3233. |
| [5] |
杜修力, 周雨龙, 韩强, 等. 摇摆桥墩的研究综述[J]. 地震工程与工程振动, 2018, 38(5): 1-11. DU Xiu-li, ZHOU Yu-long, HAN Qiang, et al. State-of-the-art on Rocking Piers[J]. Earthquake Engineering and Engineering Dynamics, 2018, 38(5): 1-11. |
| [6] |
李建中, 管仲国. 桥梁抗震设计理论发展: 从结构抗震减震到震后可恢复设计[J]. 中国公路学报, 2017, 30(12): 1-9. LI Jian-zhong, GUAN Zhong-guo. Research Progress on Bridge Seismic Design: Target from Seismic Alleviation to Post-earthquake Structural Resilience[J]. China Journal of Highway and Transport, 2017, 30(12): 1-9. |
| [7] |
LIU X, LI J, TSANG H H, et al. Experimental Evaluation of Seismic Performance of Unbonded Prestressed Reinforced Concrete Column[J]. Engineering Structures, 2019, 208: 109913. |
| [8] |
张于晔. 装配式桥墩抗震性能的提升方法研究进展[J]. 公路交通科技, 2017, 34(4): 72-79. ZHANG Yu-ye. Research Progress of Methods for Improving Seismic Performance of Prefabricated Bridge Piers[J]. Journal of Highway and Transportation Research and Development, 2017, 34(4): 72-79. |
| [9] |
NAKAKI S D, STANTON J F, SRITHARAN S. An Overview of the PRESSS Five-Story Precast Test Building[J]. PCI Journal, 1999, 44(2): 26-39. |
| [10] |
SAKAI J, MAHIN S A. Analytical Investigations of New Methods for Reducing Residual Displacements of Reinforced Concrete Bridge Columns, PEER 2004/02[R]. San Francisco: Pacific Earthquake Engineering Research Center, 2004.
|
| [11] |
SAKAI J, JEONG H, MAHIN S. Reinforced Concrete Bridge Columns That Re-center Following Earthquakes[C]//Proceedings of the 8th U. S. National Conference on Earthquake Engineering. San Francisco: Curran Associates, Inc., 2006.
|
| [12] |
CHANDARA K, CHANG-SU S, SUNG-JUN P. Seismic Performance of Prefabricated Bridge Columns with Combination of Continuous Mild Reinforcements and Partially Unbonded Tendons[J]. Smart Structures and Systems, 2016, 17(4): 541-557. |
| [13] |
SUN Z, WANG D, BI K, et al. Experimental and Numerical Investigations on the Seismic Behavior of Bridge Piers with Vertical Unbonded Prestressing Strands[J]. Bulletin of Earthquake Engineering, 2016, 14: 501-527. |
| [14] |
刘笑显. 地震作用下无粘结预应力钢筋混凝土桥墩的自复位性能研究[D]. 上海: 同济大学, 2018. LIU Xiao-xian. Study on Self-centering Capacity of Unbonded Prestressed Reinforced Concrete Bridge Columns Subjected to Earthquake Ground Motions[D]. Shanghai: Tongji University, 2018. |
| [15] |
韩林海. 钢管混凝土结构-理论与实践[M]. 3版. 北京: 科学出版社, 2016. HAN Lin-hai. Concrete Filled Steel Tubular Structures: Theory and Practice[M]. 3rd ed. Beijing: Science Press, 2016. |
| [16] |
黄育凡, 吴庆雄, 袁辉辉, 等. 地震作用下钢管混凝土组合桁梁-格构墩轻型桥梁行车安全性分析[J]. 公路交通科技, 2018, 35(11): 77-86. HUANG Yu-fan, WU Qing-xiong, YUAN Hui-hui, et al. Analysis on Running Safety on Lightweight Bridge with CFST Composite Truss Girder and Lattice Piers under Earthquakes[J]. Journal of Highway and Transportation Research and Development, 2018, 35(11): 77-86. |
| [17] |
李宁, 张双城, 李忠献, 等. 预制拼装钢管混凝土自复位桥墩变形分析模型及验证[J]. 工程力学, 2020, 37(4): 135-143. LI Ning, ZHANG Shuang-cheng, LI Zhong-xian, et al. Deformation Analysis Model and Validation for Precast Segmental Concrete Filled Steel Tube Self-centering Bridge Column[J]. Engineering Mechanics, 2020, 37(4): 135-143. |
| [18] |
LI C, HAO H, BI K. Seismic Performance of Precast Concrete-filled Circular Tube Segmental Column under Biaxial Lateral Cyclic Loadings[J]. Bulletin of Earthquake Engineering, 2019, 17: 271-296. |
| [19] |
ESTEKANCHI H E, MASHAYEKHI M, VIFAI H, et al. A State-of-knowledge Review on the Endurance Time Method[J]. Structures, 2020, 27: 2288-2299. |
| [20] |
白久林, 欧进萍. 基于耐震时程法的钢筋混凝土框架结构抗震性能评估[J]. 工程力学, 2016, 33(10): 86-96. BAI Jiu-lin, OU Jin-ping. Seismic Performance Evaluation of Reinforced Concrete Frame Structures Using the Endurance Time Method[J]. Engineering Mechanics, 2016, 33(10): 86-96. |
| [21] |
徐强, 徐舒桐, 陈健云, 等. 基于耐震时程法的重力坝失效概率密度演化分析[J]. 工程科学与技术, 2019, 51(2): 28-37. XU Qiang, XU Shu-tong, CHEN Jian-yun, et al. Failure Probability Density Evolution Analysis of Gravity Dam Based on ETA Method[J]. Advanced Engineering Sciences, 2019, 51(2): 28-37. |
| [22] |
沈禹, 谈华顺, 王献挚, 等. 考虑行波效应的大跨度矮塔斜拉桥耐震时程分析[J]. 工程力学, 2020, 37(3): 131-141, 148. SHEN Yu, TAN Hua-shun, WANG Xian-zhi, et al. Application of the Endurance Time Method to Seismic-induced Pounding Analysis for Long-span Extradosed Cable-stayed Bridges Considering Wave Passage Effects[J]. Engineering Mechanics, 2020, 37(3): 131-141, 148. |
| [23] |
GUO A, SHEN Y, BAI J, et al. Application of the Endurance Time Method to the Seismic Analysis and Evaluation of Highway Bridges Considering Pounding Effects[J]. Engineering Structures, 2017, 131: 220-230. |
| [24] |
郝朝伟, 陈彦江, 何浩祥, 等. 耐震时程法在高墩刚构桥抗震分析中的应用[J]. 防灾减灾工程学报, 2017, 37(2): 215-221. HAO Chao-wei, CHEN Yan-jiang, HE Hao-xiang, et al. The Endurance Time Method in the Seismic Analysis of the Continual Rigid-bridge with High Piers[J]. Journal of Disaster Prevention and Mitigation Engineering, 2017, 37(2): 215-221. |
| [25] |
HE H, WEI K, ZHANG J, et al. Application of Endurance Time Method to Seismic Fragility Evaluation of Highway Bridges Considering Scour Effect[J]. Soil Dynamics and Earthquake Engineering, 2020, 136: 106243. |
| [26] |
万尚辉. 预应力钢管混凝土自复位桥墩抗震性能研究[D]. 上海: 同济大学, 2017. WANG Shang-hui. Research on Seismic Performance of Prestressed Concrete-filled Steel Tubular Self-centering Columns[D]. Shanghai: Tongji University, 2017. |
| [27] |
GB/T 20065-2006, 预应力混凝土用螺纹钢筋[S]. GB/T 20065-2006, Screw-thread Steel Bars for the Prestressing of Concrete[S]. |
| [28] |
VAMVATSIKOS D, CORNELL C A. Applied Incremental Dynamic Analysis[J]. Earthquake Spectra, 2004, 20(2): 523-553. |
 2021, Vol. 38
2021, Vol. 38
