扩展功能
文章信息
- 王志华, 陈猇, 王振, 李文虎, 张汁
- WANG Zhi-hua, CHEN Xiao, WANG Zhen, LI Wen-hu, ZHANG Zhi
- 典型桥墩局部冲刷深度公式在不同水文地质区的适用性
- Applicability of Typical Formulas of Local Scour Depth at Bridge Pier in Different Hydrogeological Regions
- 公路交通科技, 2021, 38(10): 72-81
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(10): 72-81
- 10.3969/j.issn.1002-0268.2021.10.010
-
文章历史
- 收稿日期: 2021-05-07
2. 北京交通大学 土木建筑工程学院, 北京 100044
2. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China
基础局部冲刷是造成桥梁垮塌的主要原因。桥墩局部冲刷最大(平衡)深度与下部结构几何特征、水流和泥沙特性密切相关。随着对桥梁基础冲刷规律研究的不断深入和工程实践的蓬勃发展,国内外学者提出了许多关于桥墩局部冲刷深度的计算公式,世界各国也以规范或标准形式对桥墩局部冲刷深度计算方法给出具体规定[1-3]。然而,由于局部冲刷机理的复杂性和工程建设环境的多样性,现有计算公式在准确性和普适性方面还存在较大不足,因此,对已有局部冲刷深度计算公式进行对比是指导具体工程选择合适设计方法的重要途径。
同提出桥墩局部冲刷深度计算公式一样,国内外研究人员对不同公式开展对比性研究也具有久远历史。Jones[4]在1984年将已有冲刷深度预测公式利用模型实验和有限的现场观测数据进行对比,发现这些公式均可包络所有测试数据,即对于工程设计而言总是安全的;Johnson[5]在1995年使用收集到的大量原型观测数据对当时使用最广泛的7个冲刷深度计算公式进行对比,发现部分公式的预测结果在许多情况下是不安全的,而个别公式的预测结果则过于保守;Sheppard等[6]收集整理了半个多世纪以来提出的多个冲刷计算方法,利用实桥数据进行对比分析,并在融合Sheppard & Miller [7]公式和Melville[8]公式的基础上提出了桥梁平衡冲刷深度计算的新公式(简称S/M式);Qi等[9]基于模型实验和实桥冲刷数据对中国规范65-1修正式、65-2式、美国HEC-18式以及Melville式等进行了比较评估,分析了主要变量对公式预测结果的影响规律;祝志文等[10]结合实例计算对中美桥墩局部冲刷公式进行了评估;雷婷等[11]对美国HEC-18公式、包尔达柯夫计算方法、中国规范65-1修正式、65-2式、王亚玲公式等进行了对比分析,并比较了公式计算结果的差异。然而,现有对比研究对实测数据的运用比较笼统,缺乏针对不同水流、泥沙及结构参数条件下各公式适用性的具体分析,研究结果对于特殊水文地质地区(如我国柴达木盆地地区)的桥梁建设难以提供针对性指导。
本研究针对我国西部干旱地区桥梁大量建设的需求,选择中、美、俄3大世界桥梁强国设计规范推荐的桥墩局部冲刷深度计算公式,采用水流、泥沙及桥墩参数分组分析的方法,对各公式在不同参数条件下的预测性能进行评估,并结合柴达木盆地地区工程实例进行分析,以期为不同水文地质地区桥墩局部冲刷设计方法的选择提供依据。
1 局部冲刷深度计算公式与数据 1.1 桥墩局部冲刷深度计算公式我国现行《铁路工程水文勘测设计规范(TB 10017—99)》及《公路工程水文勘测设计规范(JTG C30—2015)》均推荐65-1修正式用以计算非黏性土桥墩局部冲刷深度。
65-1修正式:
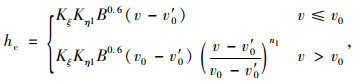
|
(1) |
式中, hc为桥墩局部冲刷深度;Kξ为墩形系数;Kη1=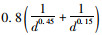
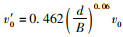
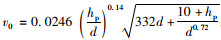
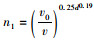
我国《公路工程水文勘察设计规范》(JTG C30—2015)中同时推荐了65-2式用以计算非黏性土桥墩局部冲刷深度。
65-2式:
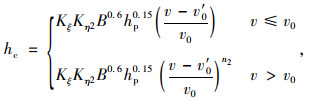
|
(2) |
式中, 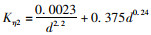
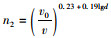
美国运输部联邦公路管理局最新发布的水利工程通告(HEC-18)第5版中沿用了基于科罗拉多州立大学成果持续改进的公式(简称HEC-18式)计算非黏性土桥墩局部冲刷深度。
HEC-18式:
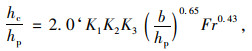
|
(3) |
式中, K1为墩形修正系数;K2为水流攻角修正系数;K3为河床条件系数;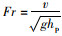
在第5版水利工程通告中,美国联邦公路管理局同时推荐了融合Sheppard & Miller公式和Melville公式优点的S/M公式计算桥墩局部冲刷深度。
S/M式:
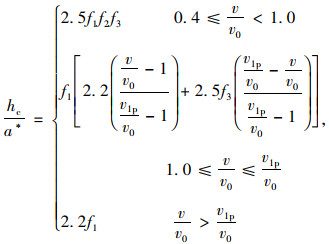
|
(4) |
式中, a*为桥墩有效直径;ν0为起动流速;ν1p为动床冲刷峰值流速;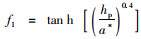
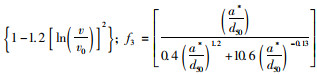
20世纪50年代,我国从苏联整体引进了桥渡设计学科,因此,两国桥墩局部冲刷计算公式具有显著承启关系。俄罗斯现行《桥渡与路堤构筑规范(SP 32-102-95)》规范中推荐了计算非黏性土河床桥墩局部冲刷深度的公式(简称俄罗斯公式)。
俄罗斯公式:
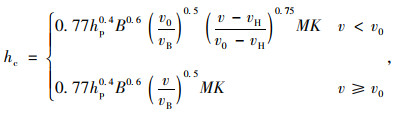
|
(5) |
式中, 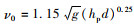
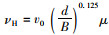
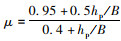
本研究收集了国内外现有关于桥墩局部冲刷的工程实例数据共计507例,这些数据主要来源于公开发表的学术论文,包括Zhuravljov[12], Froehlich[13], Gao[14], Mueller & Wagner[15]等。所收集的工程数据覆盖了不同结构类型、尺寸及较大范围的水流、泥沙条件,其中泥沙粒径范围为0.1~150 mm,墩宽范围为0.2~13 m,墩前水深范围为0.11~18.8 m,水流行近流速范围为0.27~4.7 m/s,冲刷深度范围为0.15~7.8 m。对影响桥墩局部冲刷深度的主要无量纲量的分析表明,墩前水深与墩宽之比(简称相对水深)范围为0.04~7.75,覆盖了窄墩和宽墩两种类型;墩前行近流速与泥沙起动流速之比(简称相对流速)范围为0.55~6.89, 包含清水冲刷与动床冲刷两种工况;墩宽与泥沙粒径之比(简称相对粒径)范围为8.47~52 941.18,包含细沙和粗沙两种条件。本研究基于以上数据对各国规范公式在不同参数条件下的适用性进行对比。
1.3 数据分析方法为了分析每个局部冲刷深度计算公式在不同工况条件下的预测性能,将实测工程数据按水流、泥沙及桥墩参数进行分组。对于每个实测数据和计算公式,利用已知的水流、泥沙和结构参数可计算平衡冲刷深度hc,再根据对应的实测冲刷深度hm按式(6)得到公式计算值的相对误差。此外分别按式(7)和式(8)统计每组工况条件下各计算公式相对误差的均值和方差,得到每个冲刷深度计算公式在该工况条件下的平均偏差μm和表示误差离散程度的均方误差σm,为定量评价公式预测性能提供依据。
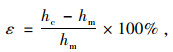
|
(6) |
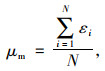
|
(7) |
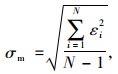
|
(8) |
式中,ε为局部冲刷深度计算公式的相对误差;N为各工况条件下的实测数据量。
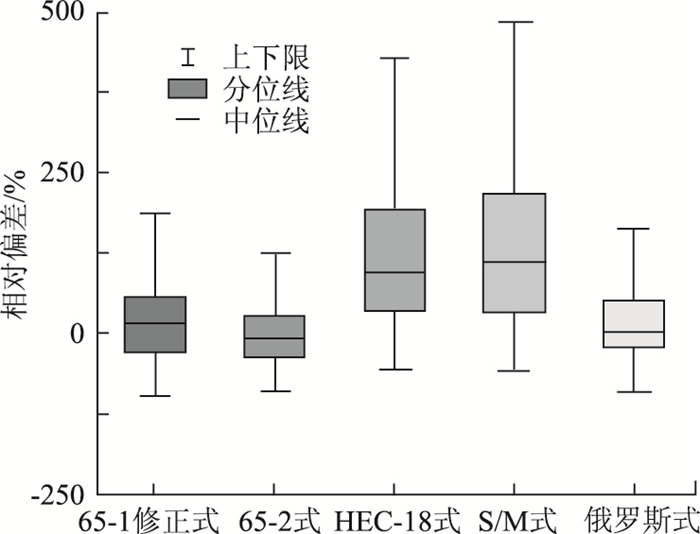
2 桥墩局部冲刷深度计算公式性能对比 2.1 基于全体数据的预测性能分析以收集到的全部507组工程数据为样本,统计各公式冲刷深度计算结果的相对误差的分布情况,并以箱线图展示在图 1。图中结果表明,当不区分水流、泥沙及结构条件时,中国和俄罗斯规范公式的平均偏差较小且误差分布更为集中,而美国规范公式计算结果明显正偏且误差离散程度较大,表明其计算结果偏安全且在不同工况条件下的预测精度差异较大,上述规律与祝志文、雷婷等[10-11]已有的研究结果相符合。各国公式性能的差异主要与其推导方法有关,中国和俄罗斯公式主要基于工程实测数据拟合而来,因而与工程实测数据吻合良好;相反,美国规范公式尽管量纲和谐,但主要基于冲刷平衡条件下的模型试验数据拟合建立,且公式参数拟合时采用了所有数据外包络线的保守做法,因此计算结果比实测冲刷深度大。
|
| 图 1 全体算例误差箱线图 Fig. 1 Error boxplot of all examples |
| |
2.2 不同粒径条件下的预测性能对比
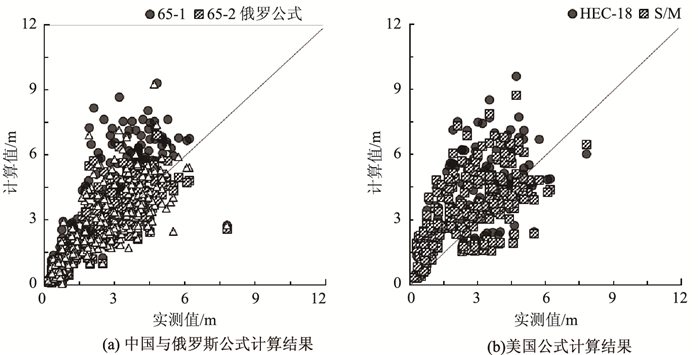
床沙粒径是反映局部冲刷时河床抗冲能力的主要变量,在不同地区和河段往往具有不同的大小。本研究参照水利与土木工程中常用的泥沙粒径分类方法,将收集到的507组工程数据按泥沙粒径分为沙粒、砾石、卵石3组,其中沙粒的粒径范围为0.1~2 mm,砾石粒径范围为2~20 mm,卵石粒径范围为20~150 mm。图 2~4分别展示了沙粒、砾石、卵石条件下各局部冲刷深度计算公式计算值与实测值,进一步统计各公式在不同粒径条件下的平均偏差和均方误差,结果见表 1。
|
| 图 2 沙粒组各局部冲刷深度计算结果对比 Fig. 2 Comparison of calculation results of laeal scour depths of sand grain group |
| |
|
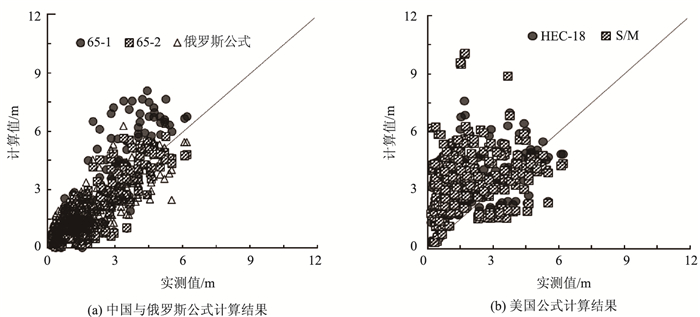
| 图 3 水深为1~5 m组各局部冲刷深度计算结果对比 Fig. 3 Comparison of calculation results of local scour depths of group with water depth of 1-5 m |
| |
|
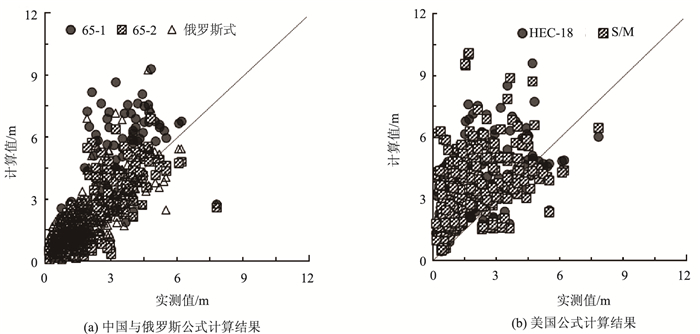
| 图 4 相对水深为0.2~1.4组各局部冲刷深度计算结果对比 Fig. 4 Comparison of calculation results of loeal scour depths of group with relative water depth of 0.2-1.4 |
| |
| d/mm | 65-1 | 65-2 | 俄罗斯式 | HEC-18 | S/M | |||||||||
| μm/% | σm/% | μm/% | σm/% | μm/% | σm/% | μm/% | σm/% | μm/% | σm/% | |||||
| 0.1~2 | 49.31 | 81.45 | 6.64 | 47.82 | 16.85 | 57.92 | 74.42 | 121.13 | 68.61 | 123.58 | ||||
| 2~20 | 12.11 | 72.74 | 13.50 | 71.83 | 22.02 | 77.20 | 163.20 | 229.85 | 199.34 | 273.48 | ||||
| 20~150 | -1.09 | 67.37 | 0.34 | 67.45 | 42.02 | 102.29 | 270.36 | 381.77 | 343.11 | 499.65 | ||||
由表 1中各列数据可知,俄罗斯公式、美国HEC-18式及S/M公式计算结果的平均偏差与均方误差均随粒径增大而变大,中国65-1修正式的平均偏差及均方误差均随粒径增大而变小,中国65-2式的平均偏差和均方误差随粒径无趋势性变化。上述规律表明,大多数桥墩局部冲刷公式的预测性能均受泥沙粒径影响。当床沙为沙粒时,由图 2及表 1第1行数据可知,各公式间的计算精度差异不显著,中国65-2式及俄罗斯公式预测性能相对较好,中国65-1修正式、美国HEC-18式及S/M公式的计算结果相对更偏保守且离散性更大。当床沙为砾石时,由砾石条件下各局部冲刷计算公式计算值与实测值结果对比及表 1第2行数据可知,中国65-1修正式、65-2式及俄罗斯公式表现较好且预测性能基本一致。当床沙为卵石时,结合卵石条件下各局部冲刷深度计算公式计算值与实测值结果对比和表 1第3行数据可知,中国65-1修正式及65-2式的预测值普遍小于实测值,这对于工程的安全性是不利的;俄罗斯公式则具有偏保守的相对较好的预测性能。根据砾石、卵石3种条件下各局部冲刷深度计算公式计算值与实测值结果对比可知,美国HEC-18及S/M公式在床沙为砾石及卵石时的计算值均显著大于实测值,尽管可以确保工程设计绝对安全,但会降低桥梁建设的经济性。
2.3 不同水深条件下的预测性能对比在天然河流中,水深是反映桥位河段河流等级的重要变量,中小型河流的水深通常小于大江大河,因而也具有显著的地域特征。本研究将收集到的工程数据按水深分别小于1,1~5和大于5 m分为3组,分析各个公式在不同水深条件下的预测性能。图 3展示了具有代表性的水深为1~5 m条件下各局部冲刷深度计算公式计算值与实测值(水深小于1和大于5 m各局部冲刷深度计算公式计算值与实测值结果对比图由于篇幅受限未给出),进一步统计各公式在不同水深条件下的平均偏差和均方误差,结果见表 2。
| hp/m | 65-1 | 65-2 | 俄罗斯公式 | HEC-18 | S/M | |||||||||
| μm/% | σm/% | μm/% | σm/% | μm/% | μm/% | σm/% | μm/% | σm/% | μm/% | |||||
| < 1 | 32.78 | 70.96 | 2.62 | 59.75 | 12.98 | 53.90 | 143.60 | 196.33 | 138.33 | 188.02 | ||||
| 1~5 | 18.90 | 73.88 | 2.94 | 59.83 | 21.81 | 80.03 | 155.21 | 272.80 | 197.05 | 357.25 | ||||
| >5 | 52.27 | 89.60 | 23.91 | 57.04 | 54.53 | 89.89 | 129.62 | 175.35 | 132.12 | 205.71 | ||||
根据表 2各列数据可知,除俄罗斯公式的平均偏差与均方误差随水深增大而变大外,其余公式的计算精度随水深无趋势性变化。当水深小于1 m时,由表 2第1行数据及水深小于1 m组计算结果可知,尽管中国65-2式及俄罗斯公式的平均偏差为正,但上述公式在冲刷深度较大时的计算值容易小于实测值,对于工程设计是不安全的;相反,美国HEC-18式及S/M式的计算值则较为保守和离散;比较而言,中国65-1修正式更适合用于此水深条件下的工程设计。当水深介于1~5 m时,中国65-1修正式、65-2式及俄罗斯公式的计算值与实测值均吻合较好,美国HEC-18式及S/M式的计算值则过于保守和离散;当水深大于5 m时,根据水深大于5 m组计算结果可知各国公式的计算值均较为保守,但中国65-1修正式、65-2式及俄罗斯公式计算值的离散程度小于美国HEC-18公式与S/M公式。
2.4 不同相对水深条件下性能对比相对水深hp/B即墩前水深hp与墩宽B的比值,是影响局部冲刷深度的关键无量纲量之一。Melville[9]的研究表明,相对水深较小时,局部冲刷深度与墩宽无关,与水深呈线性正相关关系,此时为宽墩工况;相对水深较大时,冲刷深度与水深无关,与墩宽呈线性正相关关系,称为窄墩工况;相对水深介于宽墩和窄墩之间时,冲刷深度同时受墩宽和水深影响,称为过渡墩工况。关于宽墩和窄墩的划分界限,不同学者有不同的结论,本研究根据Ettema等[16]的建议取相对水深等于0.2和1.4分别作为宽墩和窄墩的界限,并将收集到的所有工程数据按相对水深划分为hp/B≤0.2,0.2 < hp/B < 1.4和hp/B≥1.4共3组工况进行分析。图 4展示了具有代表性的相对水深为0.2~1.4条件下各局部冲刷深度计算公式计算值与实测值(相对水深小于0.2和大于1.4条件下各局部冲刷深度计算公式计算值与实测值计算结果对比图由于篇幅受限未给出),进一步统计各公式在不同相对水深条件下的平均偏差和均方误差,结果见表 3。
| hp/B | 65-1 | 65-2 | 俄罗斯式 | HEC-18 | S/M | |||||||||
| μm/% | σm/% | μm/% | σm/% | μm/% | μm/% | σm/% | μm/% | σm/% | μm/% | |||||
| < 0.2 | 106.85 | 124.67 | 45.87 | 69.03 | 66.97 | 83.24 | 262.26 | 303.11 | 242.09 | 296.59 | ||||
| 0.2~1.4 | 30.68 | 81.66 | 9.54 | 64.68 | 24.40 | 80.72 | 160.41 | 269.30 | 191.19 | 341.74 | ||||
| >1.4 | 12.21 | 54.90 | -4.53 | 45.29 | 22.18 | 67.47 | 113.23 | 174.61 | 131.85 | 219.27 | ||||
根据表 3可知,所有5个公式的平均偏差及均分误差均随着相对水深的增大而减小,表明公式预测性能受相对水深影响且在宽墩时性能相对较差。由相对水深小于0.2组计算结果对比可知,实际工程中满足宽墩条件的案例相对较少,表 3第1行数据表明,中国65-2式及俄罗斯公式的计算精度在宽墩时较好,中国65-1修正式、美国HEC-18式和S/M式的计算值则较为保守,且美国HEC-18式和S/M式的计算误差过于离散。在过渡墩条件下,由图 4及表 3第2行数据可知,中国65-1修正式、65-2式及俄罗斯公式的计算精度均较好。窄墩条件下,相对水深大于1.4组的计算结果对比及表 3第3行数据表明,中国65-2式计算结果偏负,用于工程设计时已不安全,中国65-1修正式和俄罗斯公式具有相似的预测性能,美国HEC-18式和S/M公式的计算结果相对较保守和离散。不同相对水深条件下各局部冲刷深度计算公式计算值与实测值。
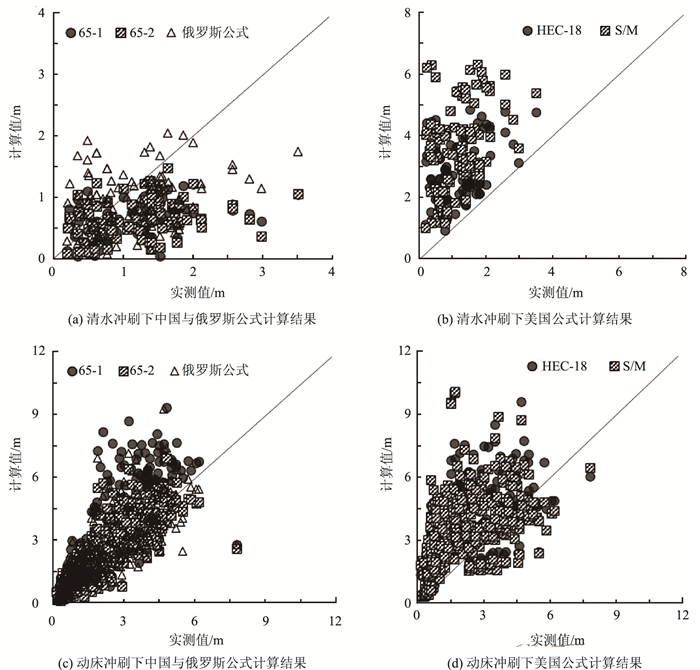
2.5 不同相对流速条件下性能对比本研究定义相对流速为墩前行近流速ν与床沙起动流速ν0之比,在桥梁基础冲刷过程中,相对流速小于和大于1时分别称为清水冲刷与动床冲刷。本节将所有实测工况划分为清水冲刷和动床冲刷两种工况进行分析。图 5展示了清水冲刷和动床冲刷条件下各局部冲刷深度计算公式计算值与实测值,进一步统计各公式在不同相对流速条件下的平均偏差和均方误差,结果见表 4。
|
| 图 5 不同相对流速条件下各局部冲刷深度计算结果对比 Fig. 5 Comparison of calculation results of local scour depths under different relative flow velocity conditions |
| |
| ν/ν0 | 65-1 | 65-2 | 俄罗斯式 | HEC-18 | S/M | |||||||||
| μm/% | σm/% | μm/% | σm/% | μm/% | μm/% | σm/% | μm/% | σm/% | μm/% | |||||
| < 1 | -30.03 | 68.14 | -27.90 | 67.43 | 14.70 | 101.58 | 242.67 | 398.93 | 342.94 | 544.67 | ||||
| >1 | 41.92 | 77.67 | 14.92 | 56.99 | 27.64 | 68.90 | 124.16 | 184.54 | 130.07 | 204.65 | ||||
由图 5(a)和5(b)及表 4第1行数据可知,在清水冲刷条件下,中国65-1修正式和65-2式计算结果的平均偏差为负,用于工程设计时偏危险;俄罗斯公式的平均偏差尽管大于0,但其计算值在冲刷深度较大时基本均小于实测值,因而也不建议用于指导工程设计;另一方面,美国HEC-18式及S/M公式的计算值则过于保守和离散。上述结果表明清水冲刷条件下的局部冲刷深度预测公式还需要进一步研究。动床冲刷条件下,由图 5(c)和5(d)及表 4第2行数据可知,中国65-1修正式、65-2式及俄罗斯公式计算精度基本一致,且这些公式在不同冲刷深度条件下的预测性能较为稳定;美国HEC-18式及S/M式的平均偏差尽管显著大于零,但其保守性主要体现在冲刷深度较小时,且这两个公式的计算值离散性较大。
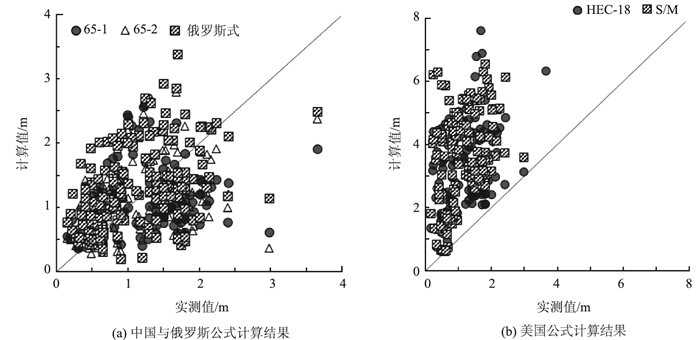
2.6 不同相对粒径条件下性能对比相对粒径通常定义为墩宽B与床沙粒径d之比,是影响桥墩局部冲刷深度的3个主要无量纲量之一。Melville等[9]的早期试验结果表明,当非黏性沙的相对粒径小于25~50时,局部冲刷深度随粒径增大而减小,而相对粒径大于50时的局部冲刷深度与粒径无关。Sheppard等[17]增加更多试验资料后发现局部冲刷深度在相对粒径大于40~50后随粒径变大而增加。Lee和Sturm[18]进一步补充试验数据后发现,冲刷深度随粒径增大的情况主要发生在相对粒径为25~400时,相对粒径大于400时泥沙粒径对平衡冲刷深度的影响已可以忽略。基于以上分析,本研究根据相对粒径将所有实测数据划分为小于25、25~400和大于400这3组进行分析。图 6展示了具有代表性的相对粒径为25~400条件下各局部冲刷深度计算公式计算值与实测值(相对粒径小于25和大于400条件下各局部冲刷深度计算公式计算值与实测值计算结果对比图由于篇幅受限未给出),进一步统计各公式在不同相对粒径条件下的平均偏差和均方误差,结果见表 5。
|
| 图 6 相对粒径为25~400组各局部冲刷深度计算结果对比图 Fig. 6 Comparison of calculation results of local scour depths of group with relative particle size of 25-400 |
| |
| B/d | 65-1 | 65-2 | 俄罗斯公式 | HEC-18 | S/M | |||||||||
| μm/% | σm/% | μm/% | σm/% | μm/% | μm/% | σm/% | μm/% | σm/% | μm/% | |||||
| < 25 | -40.99 | 59.70 | -35.61 | 65.62 | 18.05 | 85.16 | 210.53 | 264.47 | 281.64 | 348.38 | ||||
| 25~400 | 20.28 | 76.29 | 20.01 | 74.23 | 39.91 | 99.41 | 241.84 | 362.76 | 295.21 | 463.70 | ||||
| >400 | 46.16 | 78.76 | 7.14 | 47.06 | 17.62 | 57.11 | 79.88 | 123.60 | 78.55 | 130.71 | ||||
由表 5可知,除中国65-1式平均偏差及均方误差随相对粒径增大而变大,其余公式的平均偏差和均分误差均随着相对粒径先增大后减小,而表明已有公式对于相对粒径介于25~400范围内的冲刷深度影响机理考虑不充分。当相对粒径小于25时,中国65-1修正式及65-2式的平均偏差为负,俄罗斯公式尽管平均偏差为正,但根据相对粒径小于25组中国和俄罗斯公式计算结果对比可知其计算值在冲深较大时明显小于实测值,因此,上述3个公式应用于工程设计是不安全的;相反,根据表 5第1行数据和相对粒径小于25组美国公式计算结果对比可知,美国HEC-18公式及S/M公式在该工况下的计算值则过于保守。当相对粒径介于25~400之间时,由表 5第2行数据和图 6可知,中国65-1修正式、65-2式及俄罗斯公式的平均偏差和均方误差较为合理,而美国HEC-18式及S/M式的计算结果则过于保守和离散。当相对粒径大于400时,由表 5第3行数据和相对粒径大于400组公式计算结果对比可知,此时5个公式的预测性能相差不大,均可用于指导工程设计,但美国HEC-18式及S/M式计算结果的离散程度相对更大。
3 已有公式在柴达木盆地的适用性柴达木盆地地形四周高、中间低,周围山区及山前冲积平原区地貌以荒漠为主,气候干旱、全年降雨少但时空集中,区域内河流多为发源于山区的间歇性流水中小河流,河床坡度较大,汛期洪水以陡涨陡落且含沙量较大的山洪为主,河床沉积物中盐渍土分布较为广泛。盆地内公路及铁路主要沿山前区等高线修建,线路跨越河流的桥梁以中小跨度梁桥为主,桥墩在高含沙山洪的作用下产生冲刷,近年来已多次发生桥梁水毁事故。为了科学指导柴达木山前区特殊环境下的公路桥梁设计,本研究进一步收集了该地区典型桥梁的桥墩局部冲刷数据,评估已有桥墩局部冲刷设计方法在本地区的适用性。
3.1 实桥资料获取在柴达木盆地拖拉海河新老桥开展了水流、泥沙、桥墩及冲刷资料勘测。拉托海新桥为2×20 m简支梁桥,老桥为5×8 m简支梁桥,新老桥平行布置,桥墩相互不遮挡;新老桥均采用双柱式圆形桥墩,单桩基础的直径分别为1.4 m和1 m;桥址处覆盖层深厚,对河床质的取样分析表明,泥沙中值粒径为0.63 mm;桥位河段河流顺直,水流与桥轴线基本正交,河床实测比降为1.8%,由于勘测时河流无水,根据现场洪痕位置得知洪水水深为0.7 m,根据相似河流的糙率取值按谢奇公式计算出墩前行近流速为1.98 m/s;根据桥位河段河床地形分析,基础一般冲刷已发展充分,墩周局部冲刷坑明显且无明显回淤现象,实测新老桥典型桥墩的局部冲刷深度分别为0.45 m和0.3 m。根据上述实测资料,拖拉海河桥的相对水深分别为0.5和0.7,相对流速为5.66,相对粒径分别为2 222和1 587,桥墩局部冲刷属于过渡墩条件下的动床冲刷。
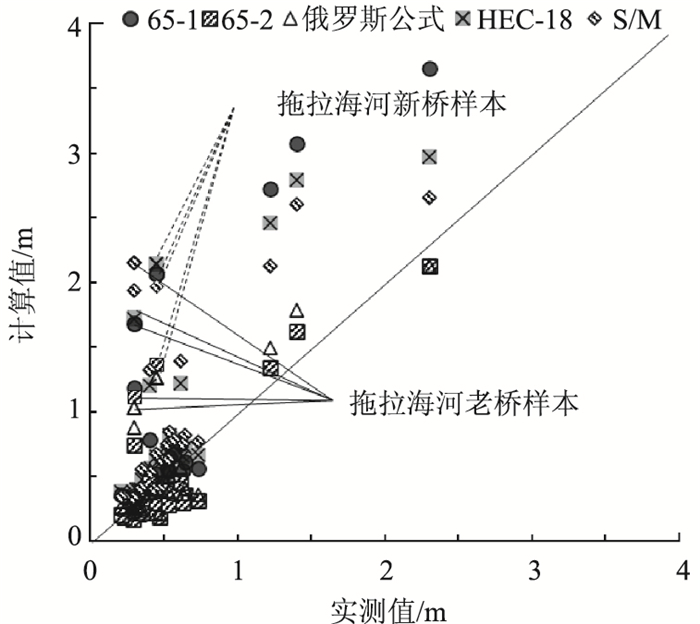
3.2 公式适用性评价根据实测水流、泥沙及桥墩数据,利用中国65-1修正式、65-2式、俄罗斯公式、美国HEC-18式及S/M式分别计算局部冲刷深度,对应的计算值与实测值如图 7所示。为了分析柴达木盆地地区桥墩局部冲刷规律与其他地区的异同,从收集到的507组数据中选取同时满足水深小于1 m,泥沙粒径小于2 mm且流速小于2.5 m/s的相似工况数据26组,这些工况对应的局部冲刷深度计算值与实测值也点绘于图 7进行对照分析。
|
| 图 7 类同工况条件下冲刷深度计算结果对比 Fig. 7 Comparison of calculation results of scour depth under similar working conditions |
| |
图 7表明,对于柴达木盆地及其他相似水沙条件地区的桥墩局部冲刷深度,中国65-2式及俄罗斯式的计算值与实测值最为接近,美国HEC-18式及S/M公式的计算值显著大于实测值,中国65-1修正式的计算值介于上述4个公式之间。与其他具有相似水沙条件的桥梁相比,各公式计算出的拉托海河新老桥局部冲刷深度均明显偏小,表明该桥在相同水沙条件下的实际冲刷深度小于其他地区的桥梁,这可能与本地区河道水流多为季节性山洪及河床含盐量高有关。其中,陡涨陡落的山洪历时较短,使桥墩局部冲刷深度不能充分发展;盐渍土干河床表面坚硬,洪水发生时需要先溶解河床再产生冲刷,进一步缩短了有效冲刷时长。根据前文分析结果,尽管中国65-2修正式及俄罗斯公式在床沙为沙粒、过渡墩、相对粒径大于400的动床冲刷条件下具有最好的计算精度,但在水深小于1 m时计算结果会略微不安全。而在实际冲刷深度偏小的柴达木盆地地区,中国65-2修正式及俄罗斯公式在低水深条件下计算值偏小的问题将不复存在,可以作为指导本地区桥梁局部冲刷深度设计的最优方法,而中国65-1修正式及美国公式应用于本地区将过于保守。
4 结论本研究利用广泛收集的实际桥梁局部冲刷数据,对中国65-1修正式、65-2式、俄罗斯规范公式及美国HEC-18式和S/M式在不同水流、泥沙及桥墩条件下的预测性能进行分析,并初步讨论了这些公式在柴达木盆地的适用性,得到了以下主要结论:
(1) 局部冲刷深度计算公式的预测性能受部分水流、泥沙及桥墩参数的影响。大多数公式的预测性能随床沙粒径及相对水深趋势性变化,同时,现有公式在清水冲刷和过渡墩条件下的预测性能均相对较差。
(2) 从确保工程安全的角度,中俄局部冲刷深度计算公式均存在不适用工况。中国65-1修正式、65-2式及俄罗斯公式均不适用的工况包括清水冲刷及床沙相对粒径小于25,中国65-2式及俄罗斯公式的不适用工况还包括水深小于1 m,此外,中国65-1修正式在床沙为卵石时的计算值也偏小。
(3) 除床沙为沙粒、水深小于1 m或大于5 m、相对粒径大于400、动床冲刷、相对水深大于1.4等工况外,美国HEC-18式和S/M式的计算值平均误差大于150%且方差大于200%,应用于实际工程将不经济和存在较大不确定性。
(4) 柴达木盆地地区桥梁的局部冲刷深度整体小于其他相似水沙条件下的桥梁,最合适依据中国65-2式进行桥墩局部冲刷深度的设计。
| [1] |
TB 10017-99, 铁路工程水文勘测设计规范[S]. TB 10017-99, Code for Survey and Design on Hydrology of Railway Engineering[S]. |
| [2] |
JTG C30-2015, 公路工程水文勘测设计规范[S]. JTG C30-2015, Hydrological Specifications for Survey and Design of Highway Engineering[S]. |
| [3] |
ARNESON L A, ZEVENBERGEN L W, LAGASSE P F, et al. Evaluating Scour at Bridges[R]. 5th ed. Washington, D.C. : US National Highway Institute, 2012.
|
| [4] |
JONES J S. Comparison of Prediction Equations for Bridge Pier and Abutment Scour[J]. Transportation Research Record, 1984, 950: 202-209. |
| [5] |
JOHNSON P A. Comparison of Pier-scour Equations Using Field Data[J]. Journal of Hydraulic Engineering, 1995, 121(8): 626-629. |
| [6] |
SHEPPARD D M, MELVILLE B, DEMIR H. Evaluation of Existing Equations for Local Scour at Bridge Piers[J]. Journal of Hydraulic Engineering, 2014, 140(1): 14-23. |
| [7] |
SHEPPARD D M, MILLER W, J r. Live-bed Local Pier Scour Experiments[J]. Journal of Hydraulic Engineering, 2006, 132(7): 635-642. |
| [8] |
MELVILLE B W. Pier and Abutment Scour: Integrated Approach[J]. Journal of Hydraulic Engineering, 1997, 123(2): 125-136. |
| [9] |
QI M L, LI J Z, CHEN Q G. Comparison of Existing Equations for Local Scour at Bridge Piers: Parameter Influence and Validation[J]. Natural Hazards, 2016, 82(3): 2089-2105. |
| [10] |
祝志文, 喻鹏. 中美规范桥墩局部冲刷深度计算的比较研究[J]. 中国公路学报, 2016, 29(1): 36-43. ZHU Zhi-wen, YU Peng. Comparative Study between Chinese Code and US Code on Calculation of Local Scour Depth around Bridge Piers[J]. China Journal of Highway and Transport, 2016, 29(1): 36-43. |
| [11] |
雷婷, 任建民, 陶虎, 等. 桥墩基础局部冲刷计算方法的对比研究[J]. 泥沙研究, 2020, 45(5): 61-68. LEI Ting, REN Jian-min, TAO Hu, et al. Review on Calculation Methods for Local Scour of Pier Foundations[J]. Journal of Sediment Research, 2020, 45(5): 61-68. |
| [12] |
ZHURAVLJOV M M. New Method for Estimation of Local Scour due to Bridge Piers and Its Substantiation[M]. Moscow: Ministry of Transport Construction, 1978.
|
| [13] |
FROEHLICH D C. Analysis of Onsite Measurements of Scour at Piers[C]//Hydraulic Engineering: Proceedings of the 1988 National Conference on Hydraulic Engineering. New York: ASCE, 1988: 534-539.
|
| [14] |
GAO D, POSADA G, NORDIN C F. Pier Scour Equations Used in China[R]. New York: ASCE, 1993: 1031-1036.
|
| [15] |
MUELLER D S, WAGNER C R. Field Observations and Evaluations of Streambed Scour at Bridges[R]. McLean: Federal Highway Administration, 2005.
|
| [16] |
ETTEMA R, CONSTANTINESCU G, MELVILLE B W. Flow-field Complexity and Design Estimation of Pier-scour Depth: Sixty Years Since Laursen and Toch[J]. Journal of Hydraulic Engineering, 2017, 143(9): 03117006. |
| [17] |
SHEPPARD D M, ODEH M, GLASSER T. Large Scale Clear-water Local Pier Scour Experiments[J]. Journal of Hydraulic Engineering, 2004, 130(10): 957-963. |
| [18] |
LEE S O, STURM T W. Effect of Sediment Size Scaling on Physical Modeling of Bridge Pier Scour[J]. Journal of Hydraulic Engineering, 2009, 135(10): 793-802. |
 2021, Vol. 38
2021, Vol. 38
