扩展功能
文章信息
- 侯宁, 王修山
- HOU Ning, WANG Xiu-shan
- 考虑结构损伤的在役混凝土桥梁有限元模型修正方法
- A Method for Updating FE Model of In-service Concrete Bridge Considering Structural Damage
- 公路交通科技, 2021, 38(10): 64-71
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(10): 64-71
- 10.3969/j.issn.1002-0268.2021.10.009
-
文章历史
- 收稿日期: 2020-12-23
2. 浙江理工大学 建筑工程学院, 浙江 杭州 310018
2. School of Civil Engineering and Architecture, Zhejiang Sci-Tech University, Hangzhou Zhejiang 310018, China
高精度的有限元模型可以准确地反映出桥梁结构的受力状态,在桥梁工程设计、施工以及管养阶段均可以发挥重要的作用[1-4]。对于采用现场浇注方法施工的混凝土桥梁,其受到环境、施工水平、材料性能的影响更为显著,因此有必要对混凝土桥梁的有限元模型进行修正,提高其有限元计算结果的可靠性。
目前常用的桥梁有限元模型修正方法包括矩阵型修正法和参数型修正法[4-8]。参数修正法可以与有限元模型进行有机结合,通过有限元模型计算结果与桥梁工程实测数据的对比来对理论模型进行不断的修正,因此得到了较为广泛的应用[9-15]。本研究所采用的响应面法也属于参数型修正法的范畴。
响应面法通过将根据试验设计方法及参数范围生成的参数样本代入有限元模型进行计算,并根据计算结果来得到响应面方程。该响应面方程是根据有限元结果对于待拟合参数和目标函数关系的近似表达式[16-17]。而有限元模拟方法的准确确定则依靠试验结果来进行检验。因此得到的响应面函数还应进行二次验证和修正[18]。
对于达到一定服役期限的桥梁,其材料的力学性能会出现不同程度的劣化,同时混凝土桥梁的结构参数也会随着裂缝的增多以及耐久性的降低而有所改变。在桥梁的养护过程中通常会定期对其进行荷载试验。本研究提出了一种能够基于桥梁荷载试验结果来对桥梁有限元模型进行修正的方法,该方法修正的数据来源于实桥试验。该方法最大限度地利用了桥梁荷载试验结果,依据既有试验数据反推出在役桥梁的重要结构参数,并在有限元模型的进行实时修正。该方法具有精度高,模型修正简单的特点,具有较好的工程推广应用价值。
采用该有限元修正的方法的意义在于:桥梁结构参数并不是始终不变的。比如混凝土的弹模也会随着龄期的增长而有所提高,在役桥梁混凝土结构产生病害时其对应的弹模也可能会有一定程度的折减。而在桥梁完工投入运营之后再测定桥梁的材料或者结构参数较为困难,采用本研究方法则可以通过桥梁荷载试验来反推桥梁当前状况下的参数状态,实现对桥梁结构的精确模拟。因此本研究方法不仅适用于新建桥梁,也可对长期运营的桥梁的结构状态进行反推和模拟。
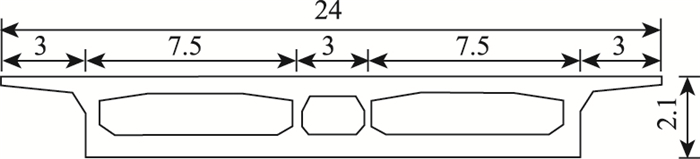
1 工程概况及实桥试验 1.1 工程概况研究的工程背景为1座部分预应力的混凝土斜拉桥。斜拉桥为塔墩梁固结体系。斜拉桥全长为76 m,跨径为(46+30) m。桥梁结构的立面示意图和主梁的横断面示意图分别如图 1和图 2所示。桥塔采用混凝土结构,桥塔向小跨侧倾斜58°,以此来平衡桥塔结构的自重,桥塔竖向高度为25.25 m。作为部分预应力斜拉桥,其斜拉索索力主要用于平衡桥塔自重以及承载桥梁活荷载的作用。该斜拉桥的混凝土主梁为双向4车道布置,梁体宽度为24 m,主梁高度为2.1 m,并且在索塔结合段处进行了局部的加强处理,并设计了倒角以避免应力集中现象。混凝土桥梁的桥塔采用C45标号的现浇混凝土结构,主梁则采用了更高标号的C50混凝土。

|
| 图 1 依托工程立面图(单位: m) Fig. 1 Elevation view of supporting project (unit: m) |
| |
|
| 图 2 依托工程主梁横断面尺寸(单位: m) Fig. 2 Cross-section dimensions of main girder of supporting project (unit: m) |
| |
1.2 初始有限元模型
桥梁荷载试验着重对桥梁的整体力学性能进行分析,因此通常采用Midas Civil来建立全桥有限元杆系计算模型。其中混凝土主梁和桥塔均采用了梁单元进行模拟。混凝土主梁的梁单元根据实际的混凝土箱室布置沿纵向划分为了3列,每个箱室沿纵向均为1列梁单元。考虑箱型的总体力学性能,在横桥向箱梁单元之间采用了无容重,但与混凝土弹模相同的虚拟单元进行横向连接。这样一来,纵横向混凝土梁单元所形成的梁格体系便可以较好地模拟宽箱梁在荷载作用下纵桥向以及横桥向的力学性能。混凝土桥塔以受压为主,因此直接采用梁单元按照桥塔实际线型建立。斜拉索则采用仅受拉的桁架单元模拟,忽略其抗弯性能。斜拉索在桥塔端和主梁端的锚固区域均采用刚臂耦合及共节点的方式进行连接。斜拉索的索力则根据现场桥梁实测结果进行施加。车辆荷载根据实测加载车轴重采用节点荷载进行模拟。
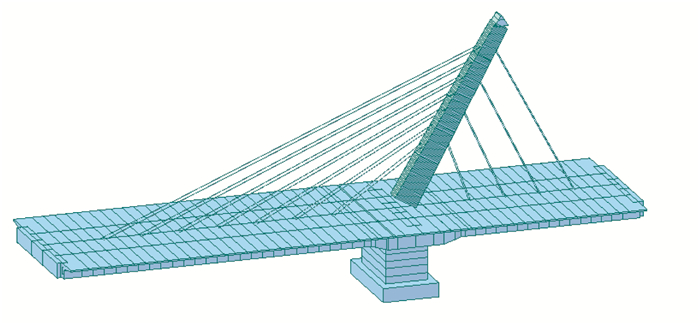
主塔C50混凝土弹模按34 500 MPa记取,主梁C45混凝土弹模按33 000 MPa计取,主塔及主梁混凝土容重均按2 500 kg/m3取值,拉索初始弹模按206 000 MPa计取。全桥模型共计833个节点,44个桁架单元模拟斜拉索,1 028个梁单元及不考虑容重的虚拟梁单元模拟混凝土桥塔和主梁。最终建立的初始有限元模型如图 3所示。
|
| 图 3 有限元模型 Fig. 3 FE model |
| |
1.3 实桥试验
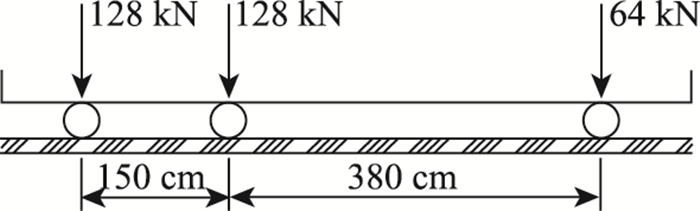
在研究的依托工程竣工后,开展实桥荷载试验。加载参数如图 4所示,实桥试验加载照片如图 5所示,试验中测得的加载车参数见表 1。
|
| 图 4 加载车轴重及轴距示意图 Fig. 4 Schematic diagram of loaded axle load and wheelbase |
| |

|
| 图 5 实桥加载照片 Fig. 5 Loads photo of real bridge |
| |
| 编号 | 轴重/kN | 总重/kN | |
| 前轴 | 后轴 | ||
| 1 | 63.8 | 255.9 | 319.7 |
| 2 | 64.3 | 255.9 | 320.2 |
| 3 | 64.4 | 256.1 | 320.5 |
| 4 | 64.2 | 255.6 | 319.8 |
| 5 | 63.6 | 255.8 | 319.4 |
| 6 | 64.2 | 255.8 | 320 |
| 7 | 63.9 | 256.1 | 320 |
| 8 | 63.7 | 255.7 | 319.4 |
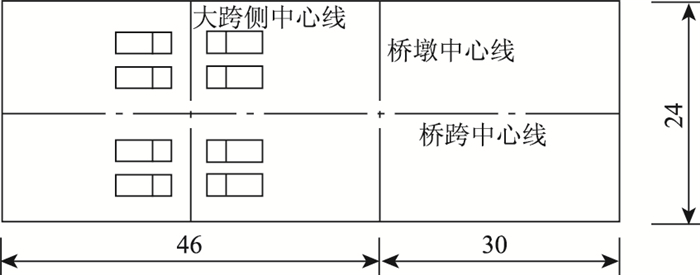
在正式试验前进行预加载。正式加载阶段,在每一级加载中,当加载车到达桥面指定位置后持荷2~3 min,然后待实测应变、挠度数据稳定后进行数据的采集工作,接着再进行下一级加载工作。实桥试验一共进行了7个工况的加载,本研究选取大跨最大正弯矩工况的实测数据来对有限元模型进行修正,该工况的加载车辆布置在大跨侧的中跨跨中位置,如图 6所示。
|
| 图 6 加载车布置(单位: m) Fig. 6 Layout of loading vehicles(unit: m) |
| |
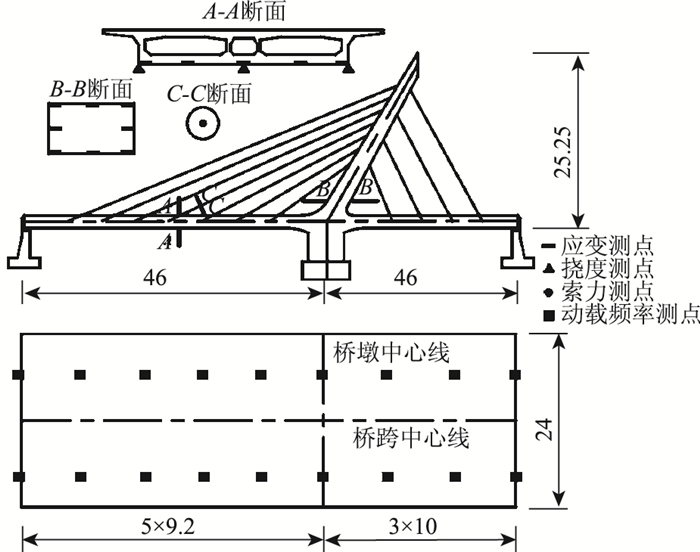
依托工程荷载试验大跨最大正弯矩工况中用于有限元模型修正的测点布置如图 7所示。其中在大跨侧跨中主梁A-A截面的底板等间距布置了5个应变测点以及3个挠度测点,应变片粘贴方向为顺桥向,主塔根部B-B截面则沿主塔径向均匀布置了8个应变片,应变片粘贴方向为主塔轴向。在恒载索力最大的N4号索靠近主梁的C-C截面上布置了索力测点,用于测量桥梁竖向振动基频的动载测点则均布于两个行车道的中心线处。总共布设应变测点13个,挠度测点3个,动载测点18个。荷载试验的挠度采用百分表进行测量,应变则采用应变片进行测量,采用TDS-520进行数据的汇总和收集,采用东华仪器DS5950动态数据采集仪对桥梁的基频进行测量。
|
| 图 7 测点布置(单位: m) Fig. 7 Layout of measuring points(unit: m) |
| |
2 考虑施工误差的有限元模型修正 2.1 目标函数与修正参数的选取
采用有限元修正方法所得到的参数修正结果不唯一,且随着选取的参数不同而变化,但其所得到最满足约束条件的参数值通常非常接近。因此在进行有限元模型修正时应选取敏感性程度较高的参数,适当忽略影响较小的参数,来进行修正便可实现较高的精度。
研究依托工程桥梁的混凝土主梁和主塔均采用现场浇注的方式进行施工,斜拉索则采用钢绞线进行现场张拉,考虑到实桥施工中可能存在一定施工误差,研究选取主梁混凝土弹性模量、桥塔混凝土弹性模量、斜拉索弹性模量、主梁梁高4个结构参数以及荷载试验中的加载车辆荷载这1个试验参数作为模型的待修正参数。
混凝土施工的振捣、养护等流程均可能对弹性模量造成不同程度的影响,混凝土结构施工常常对强度控制较为严格而对弹性模量较少关注。因此,现浇混凝土结构弹性模量的离散性一般较大。本研究依托工程的主梁混凝土与桥塔混凝土均选取C50,但由于其浇注、振捣方式不同,且主梁混凝土施工时扰动较大,因此模型中主梁混凝土和桥塔混凝土的初值均取34 500 MPa,主梁混凝土的变化幅度取±20%,主塔混凝土变化幅度取10%。斜拉索采用钢绞线,其在工厂进行加工制作,材料离散性较小,因此斜拉索弹性模量初值按20 600 MPa计取,弹性模量变化范围按±5%计取。依托工程桥梁在设计阶段采用保守的方法忽略了桥面铺装以及附属设置对结构抗力的贡献,但在桥梁实际的运营过程中其仍然承担了一部分桥梁所受到的竖向荷载,对于桥面栏杆等附属设施,考虑到有限元建模方便,按照抗弯刚度等效的原则将其一并折算到桥面铺装的厚度参数之中去。此外在实际施工过程中对于桥面标高的控制也存在一定的施工误差,因此主梁梁高的初值按设计值210 mm取值,参数变化范围取±3%。另一方面,采用加载车对依托工程进行加载试验时,首先采用地磅对加载车进行称重,其测量结果可能存在约2%偏差;在进行实桥加载试验时,靠近加载位置的杆件内力对加载车大小的影响敏感度较高。因此,引入加载参数修正加载车测量误差,综合考虑后确定车辆荷载初值取理论值320 kN,参数变化幅度为±2%。最后得到的待修正的结构参数及其变化范围如表 2所示。
| 参数 | 待修正结构参数 | 修正范围/% | 水平 | ||
| 低水平 | 初始值 | 高水平 | |||
| A | 主梁混凝土弹模/MPa | ±20 | 27 600 | 34 500 | 41 400 |
| B | 桥塔混凝土弹模/MPa | ±10 | 31 050 | 34 500 | 37 950 |
| C | 斜拉索弹模/MPa | ±5 | 19 570 | 20 600 | 21 630 |
| D | 主梁梁高/cm | ±3 | 203.7 | 210 | 216.3 |
| E | 加载车荷载/kN | ±5 | 304 | 320 | 336 |
对于桥梁有限元模型修正应全面考虑桥型的各项特征,目标函数的选取应尽量覆盖到依托工程桥梁的各项竖向承重构件(主梁、桥塔、斜拉索)的受力状态。本研究根据实桥荷载试验结果来对初始有限元模型进行修正,因此本研究选取了主梁大跨侧跨中挠度R1和应力R2,桥塔塔底应力R3,索力最大的N4号索索力R4以及桥梁基频即第一阶竖向振动频率R5 5个目标函数如表 3所示。
| 目标函数 | 含义 |
| R1/mm | 主梁大跨侧跨中挠度 |
| R2/MPa | 主梁大跨侧跨中底板应力 |
| R3/MPa | 主塔塔底应力 |
| R4/kN | N4索索力 |
| R5/Hz | 结构基频 |
上述目标函数中测试截面的应力及挠度实测值均由测试断面上的应变测点及挠度的均值计算得到(测试断面如图 7所示),桥梁基频则根据桥梁脉动试验加速度时程曲线提取得到。提取与实际测点布设位置对应的单元应力均值可以得到有限元模型的计算值。上述5个目标函数充分覆盖了现场荷载试验的结果,包含桥梁结构的静、动力指标,且对主梁、桥塔以及斜拉索的力学性能均进行了考察,从而能够全面、准确地反映依托工程的结构特点和力力学性能。
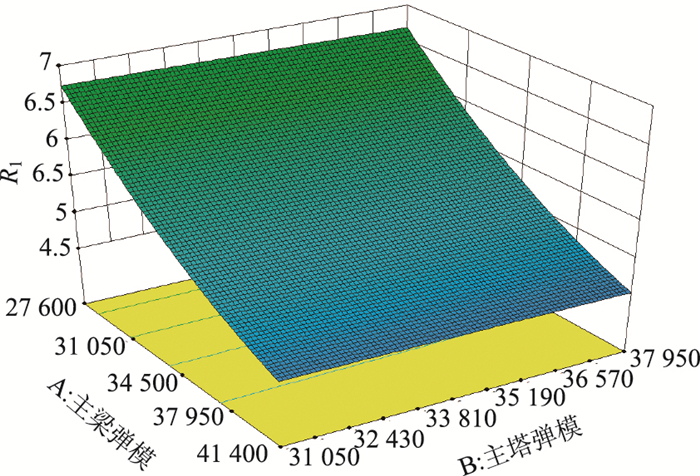
2.2 试验设计及响应面拟合在选定待修正参数以及目标函数后,采用中心复合设计方法来对待修正参数在其变化范围内进行参数组合。5参数2水平的中心复合设计共计可生成包含43组参数组合的样本集。将43组不同的参数组合分别导入初始桥梁有限元模型进行计算,并分别提取对应的目标函数值R1~R5,其结果汇总如表 4所示。限于篇幅,仅列出了5个目标函数针对A,B两个参数的响应面R1和R3结果如图 8、图 9所示。
| 待修正参数 | A | B | C | D | E |
| 取值范围/MPa | 18 089~ 50 911 |
26 294~ 42 705 |
18 150~ 23 049 |
195.02~ 224.98 |
281.95~ 358.05 |
| 目标函数 | R1 | R2 | R3 | R4 | R5 |
| 计算结果/MPa | 3.8~ 9.69 |
13.9~ 20.6 |
5.3~ 8.32 |
32.96~ 82.77 |
2.2~ 3.52 |
|
| 图 8 R1的响应面(单位: MPa) Fig. 8 Response surface for R1(unit: MPa) |
| |

|
| 图 9 R3的响应面(单位: MPa) Fig. 9 Response surface for R3(unit: MPa) |
| |
2.3 拟合精度检验
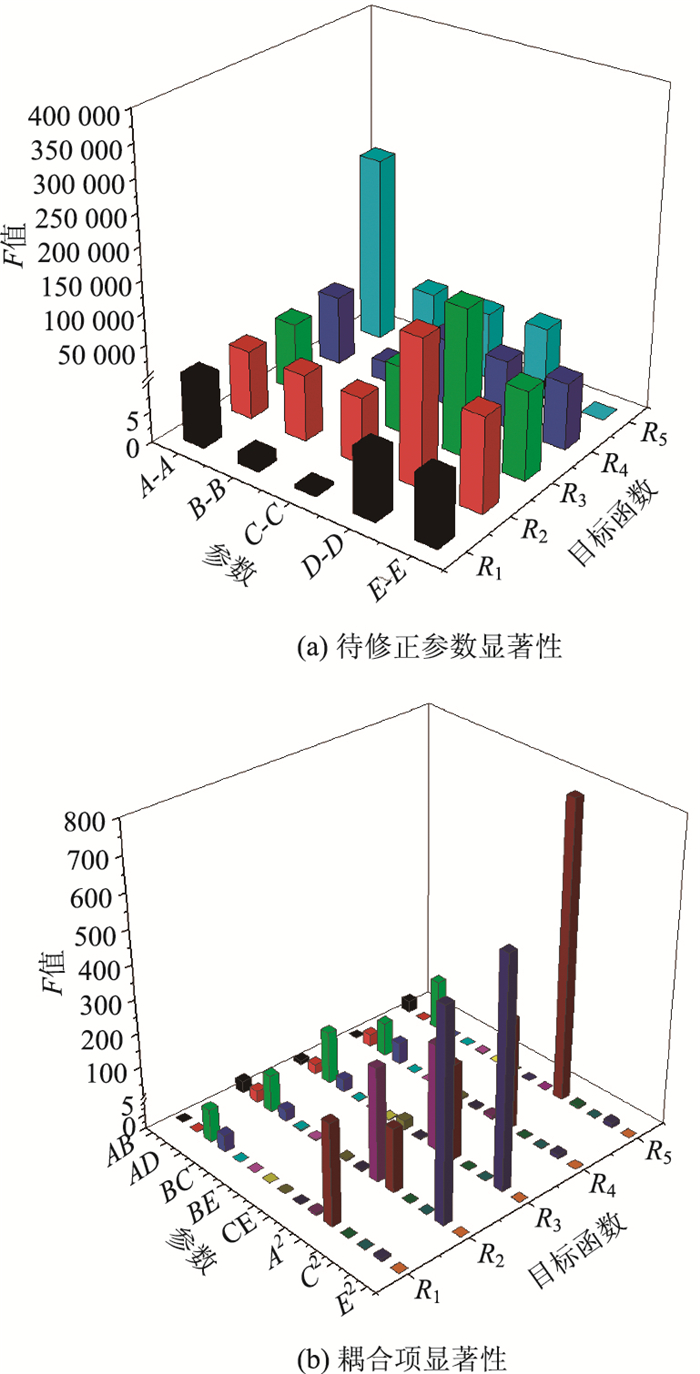
待拟合的响应面方程中不仅包括待修正的参数A~E,还包括它们之间的耦合项。在给出响应面方程之前,还应对不同参数项的显著性进行检验,本研究拟采用F检验法进行检验。取显著性水平为0.01,已知n=5,m=50则F1-α(m-1, n-m)=5.1。因此当参数项的F值大于5.1时,可认为其对目标函数的显著性较大。当按照二次多项式构造目标函数时,各个参数及其耦合项的显著性如图 10所示。
|
| 图 10 参数显著性检验 Fig. 10 Parameter significance test |
| |
由图 10可得A,B,C,D,E参数对R1~R5这5个目标函数大部分都具有较好的显著性,但其中斜拉索弹模(参数C)对主梁跨中截面应力(R1)以及加载车荷载(参数E)对结构基频(R5)的显著性水平较低,在响应面方程中予以舍去,这也与实际结构的受力特性相符,表明了响应面可以较为准确地表达出结构力学特性。同理,一些参数的耦合项及平方项的F值较小,没有显著性,如AB,AC,BE等参数耦合项,以及B2,C2,D2等平方项均对目标函数R1的显著性较低,此处舍去这些值。因此经过简化的二次多项式拟合的响应面方程仍具有较高的拟合精度,为不完全二次多项式,最终得到的拟合结果见式(1)~(5):
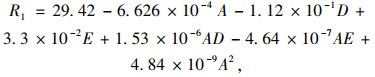
|
(1) |

|
(2) |
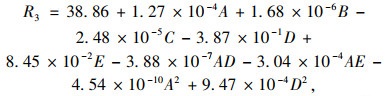
|
(3) |
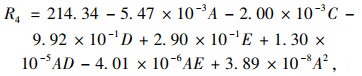
|
(4) |

|
(5) |
对拟合后的二次多项式进行R2拟合精度检验,检验结果见表 5。
| 目标函数 | R2 |
| R1 | 0.995 4 |
| R2 | 0.999 8 |
| R3 | 0.999 8 |
| R4 | 0.995 3 |
| R5 | 0.999 7 |
由表 5可以看出:5个目标函数的决定系数R2值均超过了0.995,可以得出响应面方程的结果与有限元模型的计算结果基本吻合,即构建的响应面模型能较为准确地反映待修正参数与目标函数的关系。
2.4 模型修正根据实桥试验的结果,对初始有限元模型的参数修正,参数修正结果如表 6所示。
| 编号 | 待修正参数 | 初始值 | 修正值 | 修正幅度/% |
| A | 主梁混凝土弹模/MPa | 34 500 | 34 932 | 1.25 |
| B | 桥塔混凝土弹模/MPa | 34 500 | 32 852 | -4.78 |
| C | 斜拉索弹模/MPa | 20 600 | 21 182 | 2.83 |
| D | 主梁梁高/cm | 210 | 212.82 | 1.34 |
| E | 加载车荷载/kN | 320 | 316.41 | -1.12 |
由表 6可得修正后主梁混凝土弹模较初始值有了小幅提高(1.25%),修正后的主梁弹模为34 932 MPa,这说明主梁混凝土施工质量较好。桥塔混凝土弹模则较初始值降低了4.78%,修正后的弹模为32 852 MPa,这可能是由于现浇主塔混凝土时振捣不到位导致的,倾斜的混凝土主塔在施工时也可能出现部分部位不密实或在主塔边角处存在较小程度的脱空。经过修正后的斜拉索弹模为21 182 MPa,在其合理的弹模变化范围之内。本研究依托工程桥梁跨径较小(76 m),采用了部分斜拉桥的设计理念,即斜拉索以承担活载为主。斜拉索的材料为钢绞线,与预应力钢束的材料相同,其功能类似于体外预应力。因此由于其跨径较小,故垂度效应不明显,而预应力钢绞线斜拉索的弹模及截面面积均存在一定离散性,故修正后的弹模增大仍处于合理范围。经过修正的主梁梁高较设计值(210 mm)提高了2.82 cm,修正幅度为1.34%。这是由于桥梁有限元模型建模时并未考虑桥面铺装及护栏等附属设施,但在实际工程中其又对桥梁竖向抗弯刚度具有一定的贡献,因此这些结构对依托工程力学性能的影响均被折算在主梁梁高的参数之内。根据实际的桥梁荷载试验情况,在加载车的轴重称重通常采用地磅进行,存在一定测量误差。此外加载车在桥面上的最终加载位置也会存在一定误差,由于荷载试验通常按照影响线加载的模型进行加载,因此本研究将加载车称重的测量误差和实际加载位置的定位误差统一按照加载车的轴重误差进行修正,其修正结果较好地排除了由于外加荷载的误差带来对桥梁力学性能分析的影响。
上述分析表明经过修正之后的参数具有较高精度,同时也与依托工程现场施工的实际情况吻合良好,故采用修正后参数建立的桥梁有限元模型可以良好地反映出依托工程的力学特性。
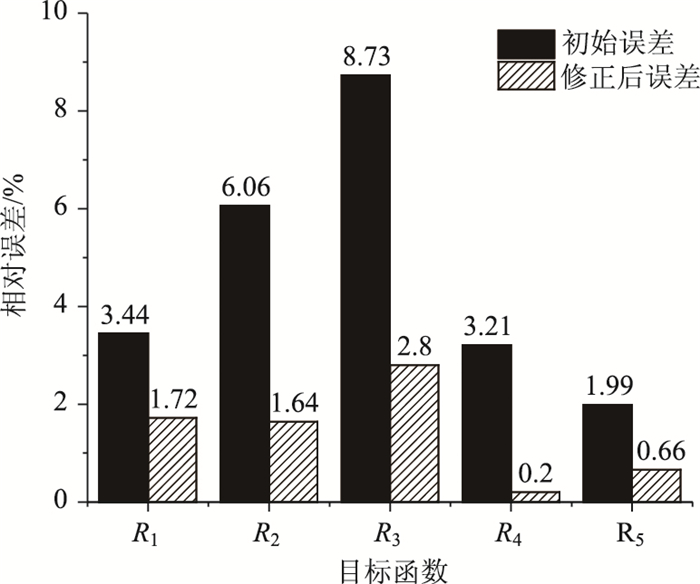
将修正后的参数代入初始有限元模型进行,通过模型计算得到的目标函数值与实测结果见表 7,目标函数修正结果对比如图 11所示。由表 7可知,修正后的有限元模型计算得到的目标函数值更加吻合, 最大相对误差在3%以内,说明构建的响应面模型可以较好地反映特征值与设计参数的关系。
| 目标函数 | 实测值 | 初始模型计算值 | 修正后 | 初始偏差/% | 修正后偏差/% |
| R1 | 5.23 | 5.41 | 5.14 | 3.44 | 1.72 |
| R2 | 15.84 | 16.80 | 16.1 | 6.06 | 1.64 |
| R3 | 6.07 | 6.60 | 6.24 | 8.73 | 2.80 |
| R4 | 45.71 | 47.18 | 45.622 | 3.21 | 0.20 |
| R5 | 3.01 | 2.95 | 2.99 | 1.99 | 0.66 |
|
| 图 11 目标函数修正结果对比 Fig. 11 Comparison of updating results of objective function |
| |
由图 11可以得出,初始有限元模型修正前的计算结果与荷载试验实测结果的误差超过8%,其余目标函数值也存在较大误差。而修正后的有限元模型进行的计算结果中,各项目标函数值与试验实测结果的误差均大幅下降,误差值降为0.20%~2.8%,研究结果表明,经过修正的有限元模型具备更高的精度。
3 结论根据依托工程桥梁结构特点,选取了主梁弹模、主塔弹模、斜拉索弹模、主梁梁高4个结构参数以及加载车荷载1个试验参数。结合荷载试验选取了主梁大跨侧跨中挠度、应力,主塔塔底应力,N4索索力以及结构基频为5个覆盖了桥梁静、动力力学性能指标的目标函数,建立了初始有限元模型,通过响应面法对该模型进行了修正,最终得到如下结论:
(1) 基于荷载试验结果,通过显著性分析后发现,经过简化的不完全二次多项式作为响应面方程时,可以较为准确地拟合待修正参数与结构静、动力响应之间的函数关系,且拟合精度较高。
(2) 目标函数计算值与实测值的最大相对误差由模型修正前的8.73%降低至2.80%,模型修正后的参数与依托工程的实际施工状况相符,静、动力响应也与实测值高度吻合。修正后的全桥有限元模型具有高精度的特点。
(3) 桥梁结构及材料参数在服役期间处于动态变化过程(如材料劣化)。而在桥梁完工投入运营之后再测定桥梁的材料或者结构参数较为困难,采用本研究方法则可以通过桥梁荷载试验来反推桥梁当前状况下的参数状态,实现对桥梁结构的精确模拟。因此本研究方法不仅适用于新建桥梁, 也可对长期运营的桥梁的结构状态进行反推和模拟。
| [1] |
聂建国, 周萌, 姬同庚, 等. 基于多尺度模型的自锚式钢箱梁悬索桥主缆锚固区受力性能研究[J]. 土木工程学报, 2014, 47(6): 57-69. NIE Jian-guo, ZHOU Meng, JI Tong-geng, et al. Study on Behaviors of Cable Anchorage Zone of Self-anchored Suspension Bridges with Steel Box Girders Based on Multi-scale Modeling Method[J]. China Civil Engineering Journal, 2014, 47(6): 57-69. |
| [2] |
李立峰, 李辉辉, 徐开铎, 等. 基于均匀设计响应面法的桥梁地震易损性分析[J]. 公路交通科技, 2017, 34(11): 100-109. LI Li-feng, LI Hui-hui, XU Kai-duo, et al. Analysis on Bridge Seismic Fragility Based on Uniform Design Response Surface Method[J]. Journal of Highway and Transportation Research and Development, 2017, 34(11): 100-109. |
| [3] |
WANG F, XU Y, SUN B, et al. Updating Multiscale Model of a Long-span Cable-stayed Bridge[J]. Journal of Bridge Engineering, 2018, 23(3): 4017148. |
| [4] |
李兆霞, 王滢, 吴佰建, 等. 桥梁结构劣化与损伤过程的多尺度分析方法及其应用[J]. 固体力学学报, 2010, 31(6): 731-756. LI Zhao-xia, WANG Ying, WU Mo-jian, et al. Multi-scale Modeling and Analyses on Structural Deterioration and Damage in Long-span Bridges and Its Application[J]. Chinese Journal of Solid Mechanics, 2010, 31(6): 731-756. |
| [5] |
宗周红, 高铭霖, 夏樟华. 基于健康监测的连续刚构桥有限元模型确认(Ⅰ): 基于响应面法的有限元模型修正[J]. 土木工程学报, 2011, 44(2): 90-98. ZONG Zhou-hong, GAO Ming-lin, XIA Zhang-hua. Finite Element Model Validation of the Continuous Rigid Frame Bridge Based on Structural Health Monitoring Part Ⅰ: FE Model Updating Based on the Response Surface Method[J]. China Civil Engineering Journal, 2011, 44(2): 90-98. |
| [6] |
YANG J, GUO X, OUYANG H, et al. A Kriging Model Based Finite Element Model Updating Method for Damage Detection[J]. Applied Sciences, 2017, 10(7): 1039. |
| [7] |
MALVEIRO J, RIBEIRO D, SOUSA C, et al. Model Updating of a Dynamic Model of a Composite Steel-concrete Railway Viaduct Based on Experimental Tests[J]. Engineering Structures, 2018, 164: 40-52. |
| [8] |
韩建平, 骆勇鹏. 基于响应面的刚构-连续组合梁桥有限元模型静动力修正[J]. 公路交通科技, 2013, 30(11): 53-61. HAN Jian-ping, LUO Yong-peng. Response Surface Based Finite Element Model Updating for a Rigid Frame Continuous Composite Girder Bridge Using Static and Dynamic Test Data[J]. Journal of Highway and Transportation Research and Development, 2013, 30(11): 53-61. |
| [9] |
梁鹏, 李斌, 王秀兰, 等. 基于桥梁健康监测的有限元模型修正研究现状与发展趋势[J]. 长安大学学报: 自然科学版, 2014, 34(4): 52-61. LIANG Peng, LI Bin, WANG Xiu-lan, et al. Present Research Status and Development Trend of Finite Element Model Updating Based on Bridge Health Monitoring[J]. Journal of Chang'an University: Natural Science Edition, 2014, 34(4): 52-61. |
| [10] |
马印平, 刘永健, 龙辛, 等. 钢管混凝土组合桁梁受弯承载力简化计算方法研究[J]. 建筑结构学报, 2020, 41(5): 76-84. MA Yin-ping, LIU Yong-jian, LONG Xin, et al. Simplfied Calculation Method for Flexural Strength of CFST Composite Truss Girder[J]. Journal of Building Structures, 2020, 41(5): 76-84. |
| [11] |
陈力波, 黄才贵, 谷音. 基于改进响应面法的公路简支梁桥地震易损性分析[J]. 工程力学, 2018, 35(4): 208-218. CHEN Li-bo, HUANG Cai-gui, GU Yin. Seismic Vulnerability Analysis of Simply Supported Highway Bridges Based on an Improved Response Surface Method[J]. Engineering Mechanics, 2018, 35(4): 208-218. |
| [12] |
方志, 张国刚, 唐盛华, 等. 混凝土斜拉桥动力有限元建模与模型修正[J]. 中国公路学报, 2013, 26(3): 77-85. FANG Zhi, ZHANG Guo-gang, TANG Sheng-hua, et al. Finite Element Modeling and Model Updating of Concrete Cable-stayed Bridge[J]. China Journal of Highway and Transport, 2013, 26(3): 77-85. |
| [13] |
张亮亮, 张伟, 张康. 响应面法在高墩大跨连续刚构桥长期变形预测中的应用[J]. 公路交通科技, 2014, 31(1): 77-81. ZHANG Liang-liang, ZHANG Wei, ZHANG Kang. Application of Response Surface Method in Predicting Long-term Deflection of Long-span Rigid Frame Bridge with High-rise Piers[J]. Journal of Highway and Transportation Research and Development, 2014, 31(1): 77-81. |
| [14] |
DENG L, CAI C S. Bridge Model Updating Using Response Surface Method and Genetic Algorithm[J]. Journal of Bridge Engineering, 2010, 5(15): 553-564. |
| [15] |
马印平, 刘永健, 刘江. 基于响应面法的钢管混凝土组合桁梁桥多尺度有限元模型修正[J]. 中国公路学报, 2019, 32(11): 51-61. MA Yin-ping, LIU Yong-jian, LIU Jiang. Multi-scale Finite Element Model Updating of CFST Composite Truss Bridge Based on Response Surface Method[J]. China Journal of Highway and Transport, 2019, 32(11): 51-61. |
| [16] |
ZHU Q, XU Y L, XIAO X. Multiscale Modeling and Model Updating of a Cable-stayed Bridge. I: Modeling and Influence Line Analysis[J]. Journal of Bridge Engineering, 2015, 20(10): 4014112. |
| [17] |
万利军, 单炜, 姜华. 基于响应面法的桥梁动力学有限元模型修正[J]. 公路交通科技, 2014, 31(8): 96-101. WAN Li-jun, SHAN Wei, JIANG Hua. Modification of Finite Element Model of Bridge Dynamics Based on Response Surface Method[J]. Journal of Highway and Transportation Research and Development, 2014, 31(8): 96-101. |
| [18] |
代汉超, 石雪飞, 阮欣. 基于改进响应面的桥梁抗弯刚度修正[J]. 中南大学学报: 自然科学版, 2014, 45(7): 2387-2393. DAI Han-chao, SHI Xue-fei, RUAN Xin. Bending Stiffness Updating of Bridge Structures Based on Improved Response-surface Method[J]. Journal of Central South University: Science and Technology Edition, 2014, 45(7): 2387-2393. |
 2021, Vol. 38
2021, Vol. 38
