扩展功能
文章信息
- 钟伟斌, 曹骏驹, 张江洪, 王贵山, 李赞勇
- ZHONG Wei-bin, CAO Jun-ju, ZHANG Jiang-hong, WANG Gui-shan, LI Zan-yong
- 互通式立交主线同侧相邻入口最小间距研究
- Study on Minimum Distance between Adjacent Entrances on Same Side of Mainline of Interchange
- 公路交通科技, 2021, 38(9): 148-158
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(9): 148-158
- 10.3969/j.issn.1002-0268.2021.09.019
-
文章历史
- 收稿日期: 2021-04-25
2. 江苏省交通工程建设局, 江苏 南京 210001;
3. 中交第一公路勘察设计研究院有限公司, 陕西 西安 710075
2. Jiangsu Traffic Engineering Construction Bureau, Nanjing Jiangsu 210001, China;
3. CCCC First Highway Consultants Co., Ltd., Xi'an Shaanxi 710075, China
随着高速公路里程规模的不断扩大和路网密集程度的逐步增加,互通式立交(以下简称互通)的数量也不断增加,其设置条件越来越复杂,互通出入口路段的安全问题也日益凸显出来。高速公路同侧相邻入口间距,是指相邻入口匝道的合流鼻之间的距离。是互通设计中存在的许多亟待解决的问题中的一个重要方面。由于前后匝道车辆的汇入、合流,使得连续合流段交通流变得复杂,不仅提高了拥堵现象发生率,影响道路的通行能力,更为严重时将导致车辆尾随、碰撞等交通事故。
国外一些标准规范规定了同侧相邻入口间距,美国AASHTO《A Policy on Geometric Design of Highways and Streets》(以下简称《绿皮书》)[1]规定了互通范围内相邻匝道端部间距,认为高速公路主线上同侧相邻入口最小间距为300 m。日本在匝道组合形式与间距方面的研究成果主要体现在《日本公路技术标准的解说与运用》[2]中,该标准对互通范围内相邻匝道间距做出了相应规定,且给出了较为完整的计算过程,也对匝道连接段之间的距离进行了规定,其参考了《绿皮书》中对驾驶人辨认标志时间、反应时间及汽车换道所需时间,总计为5~10 s,认为连续出口或连续入口间距的取值还要考虑变速车道及标志设置的距离。国外关于互通同侧相邻入口之间的距离研究得很少,主要侧重于对互通各组成部分与车辆行为的研究。Pilko、Bared等通过分析加利福尼亚州和华盛顿州的事故数据,建立了事故频率与互通间距的回归模型[3]。Mahmoud等[4]通过驾驶模拟器,对不同工作区域、不同交通密度和不同标志设置情况下的驾驶人合流行为进行分析。Sun等人提出换道行为的新规则,对主线和匝道两种不同上游到达率情况下入口匝道瓶颈的交通量进行了讨论,分析了入口匝道瓶颈合流比例与换道概率和合流段长度的关系[5]。
我国《公路路线设计规范》(JTG-D20—2017版)(以下简称《路线规范》)[6]和《公路立体交叉设计细则》(JTG D21—2014)(以下简称《立交细则》)[7]均对互通主线同侧相邻匝道入口做了相应的规定。然而,目前关于高速公路同侧相邻入口最小间距的规定,均未考虑上游匝道设计速度及匝道形式的影响。上游匝道设计速度不同,车辆由匝道汇入主线的加速距离也不同,而上游匝道形式不同将影响上游加速车道长度,这都将直接影响连续入口之间的间距。从理论分析层面而言,相邻匝道之间的距离由变速车道及其渐变段长度、基本段长度和识别交通标志的距离3部分构成,国内众多学者以此为出发点研究相邻出、入口之间的间距。吴江[8]建立了不设辅助车道与设置辅助车道两种情况下同侧相邻出入口最小间距计算模型,提出同侧相邻出入口最小间距建议值;高建平[9]通过对匝道分流最小间距影响因素进行,从车辆换道行为角度进行考虑,建立匝道连续分流点间距模型,得出最小间距推荐值。王灵利等[10]通过分析驾驶人认读标志的特点、高速公路车头时距的分布规律以及换道模型特征,建立主线同侧连续出口最小间距模型。潘兵宏、谢君平通过分析高速公路匝道间距影响因素,界定了匝道功能区,进而确定匝道入口间距的设置方法[11-12]。汤振农[13]通过分析匝道出、入口间距影响因素,并对互通组合模式及间距进行了调查研究,得出匝道出、入口最小间距。韩敏等[14]对城市道路入口与相邻交叉口影响范围内的交通特性进行了研究,确定了城市道路的相邻交叉口间距和位置。邵阳等[15]对主线连续出入口间车辆的运行特性展开研究,得到4种主线连续出入口组合形式下的匝道出入口间距值。魏代梅[16]通过分析匝道的组合形式,得出了城市快速路连续出入口最小间距计算模型及推荐值。蒋飞[17]通过分析匝道连续出入口的形式、影响因素以及交通车辆运行特性,建立了互通式立交连续出相邻入口的最小间距计算模型。
综上,美国对互通匝道相邻入口间距研究较早,但取值是依靠工程经验,与我国实际情况并不完全符合。日本较早提出了相邻入口间距计算模型,且在规范中有较为完整的计算过程。与国外相比,国内的多数研究主要集中在高速公路互通分、合流端之间的距离,出、入口关键技术指标上,且大多学者较多地利用理论分析方法研究匝道出入口最小间距,研究理论尚属探索阶段,缺乏对现有互通的系统性统计分析和相关专题研究。我国高速公路修建起步较晚,在高速公路分合流端间距主要技术指标多是基于我国国情,并参考国外标准和相关研究制定的,有值得肯定的地方,也有需改进的地方。因此,从宏观和微观的交通流角度研究主线同侧匝道入口间距成为尚待解决的问题。
因此,需在总结分析互通出入口设计指标与行车安全性之间关系的基础上,对主线同侧相邻匝道入口最小间距进行深入研究,以便更好地指导设计工作,降低连续入口路段交通安全事故风险。本研究将以驾驶心理学原理和驾驶人对标志的响应特性为基础,将主线同侧相邻匝道入口最小间距分为合流车辆加速段距离、合流车辆等待段距离、三角渐变段距离,在确定了合流鼻初速度、合流点末速度、平均加速度、平均等待时间等关键参数之后,建立满足安全性和舒适性要求的主线同侧相邻匝道入口最小间距计算模型,并提出相应的建议值。
1 主线同侧连续合流设计形式 1.1 主线同侧连续合流设计形式当主线同侧相邻的两个匝道入口因条件限制,导致设置距离较近时,上下游入口的交通流会相互产生干扰。若相邻入口之间距离过短,上游驶入车辆未能在到达下游入口时换道进入主线内侧车道,则会在下游入口的主线外侧车道形成交通流屏障,这将造成上游驶入车辆因下游驶入车辆的突然换道而强制减速或停车,或者下游驶入车辆因上游驶入车辆的阻碍难以汇入主线,在入口匝道中形成排队。无论哪种情况都将降低高速公路入口区域的通行效率和安全水平。因此需要将距离较近的相邻入口匝道之间的设计进行统一安排,且应控制对二者之间的最小距离,避免发生上述通行能力或者安全水平降低的情况。
《立交细则》中为保证合流区的车道数平衡,上游入口匝道的车道数分别为单车道和双车道时(图 1),其设计形式因辅助车道的设置而不同。此外,将上下游入口匝道连接部鼻端之间的距离界定为连续合流鼻端间距,即主线同侧相邻入口间距,并给出最小间距规定值。
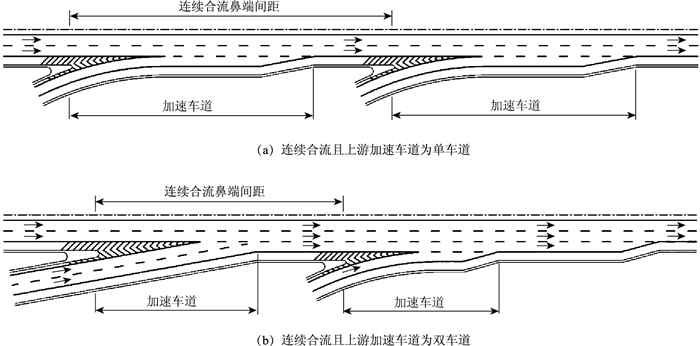
|
| 图 1 主线侧连续合流连接部设计 Fig. 1 Design of continuous merging connection on same side of mainline |
| |
1.2 连续合流设计形式对间距的影响分析
(1) 上游入口匝道为单车道
当上游入口匝道的车道数为单车道时,上下游的加速车道均设置在主线直行车道外侧。上游加速车道在到达下游入口鼻端前结束,在主线外侧增加的变速车道已经通过渐变段合并进主线,主线恢复基本车道数。上游匝道上驶入车辆经过鼻点后,首先通过加速段,将自身速度提高至接近主线运行速度;然后保持该速度继续在变速车道内行驶,等待主线外侧车道上出现可插入间隙后,向左换道驶入主线;进入主线后,车辆如果不继续换道进入内侧车道,将以主线运行速度行驶在外侧车道,并时刻观察下游匝道入口的车辆情况,以免与下游驶入车辆发生碰撞。此时间距的影响主要考虑上游加速车道的长度和下游入口匝道的合流安全视距。
(2) 上游入口匝道为双车道匝道
当上游入口匝道为双车道匝道时,应设置辅助车道应连接上游出口和下游出口,以保证入口车道数的平衡。此时下游入口加速车道设置在上游辅助车道外侧,因此下游合流区需要通过两次渐变分别减少下游加速车道和上游辅助车道增加的车道数。在这种情况下,若上游汇入交通量较大,一部分车辆通过加速车道直接汇入主线基本车道,而剩余车辆则可通过加速车道直接进入上游辅助车道,等待可插入间隙后换道进入主线基本车道。到达下游入口鼻端时,若还没有成功换道的车辆依然可以行驶在上游辅助车道上,而此时下游驶入车辆虽然行驶在最外侧的下游加速车道上,但随时有可能进行突然换道与上游在辅助车道上直行的车辆发生碰撞。这种运行状况与上游单车道匝道极为相似,均为通过上游减速段后,行驶在辅助车道上的车辆同样需要在到达下游入口前时刻观察驶入车辆状况。区别在于上游单车道匝道时多出一次换道行为。因此,无论上游是单车道还是双车道,相邻入口间距都主要考虑上游加速车道的长度和下游入口匝道合流安全视距。
2 相邻入口最小间距计算模型与参数分析 2.1 最小间距计算模型根据上节连续入口间的车辆运行特征分析,驶入车辆通过上游鼻点后先后经历加速阶段、等待插入阶段和换道阶段进入主线车道,随后观察下游出口的驶入状况来操作车辆,确保合流安全视距。与《立交细则》中连续合流鼻端间距不同的是,本研究的主线同侧相邻匝道入口间距的结束位置不是下游入口匝道鼻段,而是下游匝道与主线相接的合流点,这是因为下游驶入车辆只有在驶过分流点后,才被允许向主线变换车道,这时才会存在与主线最外侧车道车辆发生碰撞的风险。因此我们将主线同侧相邻匝道入口间距L分为两大部分,即上游驶入车辆成功汇入主线所需最小长度Lm和驾驶人观察下游入口车辆运行状况的合流安全视距Ls(图 2)。

|
| 图 2 高速公路相邻入口最小间距组成示意图 Fig. 2 Schematic diagram of composition of minimum distance between adjacent entrances of expressway |
| |
其计算式如下:
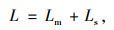
|
(1) |
式中,L为主线同侧相邻匝道入口间距;Lm为上游驶入车辆成功汇入主线所需最小长度;Ls为驾驶人观察下游入口车辆运行状况的最小安全视距。
2.2 汇入主线所需最小长度Lm立交入口加速车道包括加速段、辅助车道和渐变段,而车辆进入主线需经过加速、等待、变道3个阶段。在车辆实际行驶过程中,上述3个阶段并非与加速车道3部分相互对应,而是一个连续的过程。当按规范选取的加速车道总长度大于3个阶段所需的总长度时能够满足需求,但当计算得到的所需长度大于规范取值时,应按实际所需的长度进行考虑。因此在计算车辆汇入主线所需最小长度时并未直接选用《规范》对于加速车道长度的规定值,而是采取实测断面数据结合车辆动力学分析进行计算,考虑车辆进入主线时实际所需的长度。与规范相比,在计算汇入主线所需最小长度时测量了特征断面实际通过速度,以及加速过程中车辆动力学性能,并决定采用所需加速距离较长的大货车进行计算。另外,计算车辆等待变道距离时的车头时距采用二阶埃尔朗分布,计算变道距离时考虑驾驶人舒适性分析。
相邻入口匝道之间的间距首先应满足上游驶入车辆的合流需要,即汇入主线所需最小长度Lm。因此其最小长度应能保证入口车辆完成加速、等待和换道的过程。因此汇入主线所需最小长度Lm进一步划分为车辆加速所需长度、等待可插入间隙长度和换道所需长度,用式(2)计算。
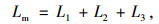
|
(2) |
式中,L1为车辆加速所需距离;L2为等待可插入间隙使车辆行驶的距离;L3表示换道所需距离。
2.2.1 车辆加速所需距离L1车辆加速所需距离指车辆从运行速度较低的匝道中驶出,通过加速段逐渐提高自身速度至高速主线运行速度50%~70%所经过的距离。对于加速段车辆运行特征和长度计算方法,有关学者已开展了大量研究。其中被普遍接受的理论为驶入车辆在加速段内以平均加速度完成自身速度从鼻点初速度提高至最低合流速度,计算如式(3)所示。
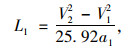
|
(3) |
式中,L1为上游驶入车辆加速所需长度;V1为车辆通过合流鼻时的速度;V2为驶入车辆能够进行合流的最低速度,即加速结束时的末速度;a1为车辆平均加速度。
对于式中各参数的取值,本研究将利用实测数据回归值与数据统计值进行选取,以此来计算各阶段所需长度,各参数研究如下。
(1) 车辆通过合流鼻时的速度V1
对于车辆通过合流鼻时的速度美国和日本已开展大量研究,并在其规范中提出了计算加速段长度时所采用的合流鼻平均初速度。而我国驾驶人驾驶习惯和车辆性能与美国日本并非完全相同,若直接参考国外取值,计算结果可能不适用于我国道路环境。根据相关研究,影响车辆通过合流鼻速度的因素较多,如连接处的线形指标、视距和交通量等。合流区线形指标良好,视距充足,交通量较低均会导致车辆通过鼻端速度较高,反之将导致车速较低。因此应该调查我国道路环境下的分流鼻通过的速度。
本研究通过现场观测来研究加速车道特征断面的车辆运行速度特性,根据大量数据统计来确定分流鼻断面车辆的通过速度。本次调查地点分布在沪宁、沈大、连霍和京港澳高速公路,调查地点均为8车道的多车道高速公路。调查主线均按车道分车型限速,第1车道为小型车道,限速120 km/h;第2车道为中小型车道,限速120 km/h;第3车道为大中型车道,限速100 km/h;第4车道为大型车道,限速100 km/h。
调查地点高速公路入口段平纵线形指标良好,路面状况良好,视野条件良好,利于数据测量。测量采用雷达测速仪进行,置信度水平取95%,车速观测值允许误差为2 km/h,计算得到调查样本量最小值为384辆。调查时间选择在道路无拥堵,交通流处于自由流状态的时段进行。
实测10处高速公路单车道加速车道合流鼻点的车辆速度,其中3处为枢纽互通入口,匝道设计速度为60 km/h;7处为一般互通入口,匝道设计速度为40 km/h,调查结果如表 1所示。
| 互通类型 | 测量点 | 匝道设计速度 | 小型车平均速度 | 大型车平均速度 | 所有车辆平均速度 |
| 枢纽互通 | 无锡枢纽 | 60 | 66 | 55 | 63 |
| 正仪枢纽 | 74 | 63 | 71 | ||
| 绣江枢纽 | 77 | 62 | 68 | ||
| 苏州 | 40 | 55 | 46 | 54 | |
| 横山 | 56 | 52 | 55 | ||
| 达道湾 | 55 | 49 | 52 | ||
| 金州 | 63 | 44 | 53 | ||
| 柳林 | 47 | 39 | 44 | ||
| 许昌 | 48 | 42 | 46 |
根据表 1统计结果结合调查情况,可以看出:小型车通过合流鼻点的平均速度高于大型车;小型车和大型车通过合流鼻点的平均速度存在大于匝道设计速度的情况;所有车辆的平均速度均大于匝道的设计速度。因此,从运行安全角度考虑,车辆通过合流鼻点的平均速度取匝道设计速度或低于匝道设计速度,能够保证一定的安全余量。参考美国和日本对于合流鼻通过速度的规定,结合本次调查情况,本研究建议合流鼻通过速度选取值如表 2所示。
| 匝道设计速度 | 80 | 70 | 60 | 50 | 40 | 30 | 25 |
| 美国合流鼻通过速度 | 70 | 63 | 51 | 42 | 35 | 28 | 23 |
| 日本合流鼻通过速度 | 80 | 70 | 60 | 50 | 40 | 30 | 25 |
| 本研究建议合流鼻通过速度 | 65 | 60 | 55 | 50 | 40 | 35 | 30 |
(2) 加速结束时的末速度V2
加速结束时的末速度指车辆在加速段末尾所能达到的平均行驶速度,其大小与加速段长短、驾驶人习惯、车辆性能和主线设计速度有关。加速结束时的末速度同样也是驶入车辆能够进行合流的最低速度。车辆驶出加速段后,将以该速度继续行驶在加速车道上,等待可插入间隙进行换道,完成合流过程。若加速结束时的末速度过低,车辆直接换道进入主线可能会因速差过大,存在车辆追尾的风险;而继续在加速车道进行加速,可能导致车辆没有足够的长度寻找机会进行换道,引发拥堵。国内外一些学者认为匝道与主线之间的速差不宜超过20 km/h。同样,美国和日本设计规范中也提出了加速段结束的末速度选取值。根据调查,我国部分高速公路入口加速段结束区域的车辆速度如表 3所示。
| 互通类型 | 测量点 | 匝道设计速度 | 主线设计速度 | 小型车平均速度 | 大型车平均速度 | 平均速度 |
| 枢纽互通 | 无锡枢纽 | 60 | 120 | 87 | 71 | 73 |
| 正仪枢纽 | 94 | 72 | 91 | |||
| 绣江枢纽 | 102 | 77 | 80 | |||
| 一般互通 | 苏州 | 40 | 120 | 74 | 58 | 72 |
| 横山 | 73 | 63 | 68 | |||
| 达道湾 | 80 | 65 | 78 | |||
| 金州 | 82 | 67 | 78 | |||
| 柳林 | 72 | 61 | 69 | |||
| 许昌 | 81 | 69 | 78 |
从表 3中可以看出,小型车的合流点末速度均高于大型车,小型车的合流点末速度大部分介于日本规定的70 km/h和美国规定的88 km/h之间;而大型车的合流点末速度达不到美国规定的88 km/h,且大部分情况下略低于日本规定的70 km/h。为了车辆运行安全,合流点末速度的取值应在本次调查结果的基础上,在合理范围内尽量将末速度取高值,降低因加速段末速度不够引发的互通入口追尾事故。除主线设计速度120 km/h情况以外,借鉴美国和日本对于100 km/h和80 km/h下的末速度规定值,以及有关合流点末速度的研究成果[18],综合确定合流点末速度V2,结果如表 4所示。
| 主线设计速度 | 120 | 100 | 80 |
| 美国合流点末速度 | 88 | 77 | 63 |
| 日本合流点末速度 | 70 | 65 | 63 |
| 小型车末速度建议值 | 80 | 75 | 65 |
| 大型车末速度建议值 | 68 | 65 | 63 |
(3) 车辆平均加速度a1
车辆平均加速度主要与车辆自身性能和驾驶人操作习惯有关,不同品牌车辆的加速性能差异较大,此外还与车辆行驶的道路环境有关。有研究指出,车辆的加速性能可以用加速到100 km/h的所需时长来衡量,将该时长称作加速时间。其测量条件为驾驶经验丰富的驾驶人将性能良好的车辆以最快速度从最低档提升至最高档,并将车辆速度升至100 km/h所需时间。通过调查,我国小型车的加速性能差异较大,最优加速性能与最差相差一倍以上,加速度在1.75~3.64 m/s2之间。但是此类加速度尽在车辆、人员、道路环境全部理想的条件下才会出现。而实际的驾驶环境是十分复杂的,驾驶人在加速过程中不会将车辆加速踏板踩至最大限度从而发挥车辆全部加速性能,同时车辆也受到路面和空气等的各种阻力。因此结合实际条件和安全方面的考虑,小型车选择《路线规范》中提到的能够使乘客感觉舒适的加速度1.0 m/s2来计算。
大型车体积大、重量大,因此产生的空气阻力和路面摩阻力不能忽视,日本研究提出在平坦路段上大型车的加速度可以按式(4)计算。从式(4)中可以看出,车辆加速度计算公式考虑了车辆自身的输出功率、自重。
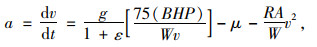
|
(4) |
式中,a为车辆加速度;v为车辆行驶速度;t为时间;g为重力加速度;ε为加速阻力比;BHP为有效输出功率;W为车重系数;μ为滚动摩擦系数;R为空气阻力系数);A为汽车迎风面积,即正面投影面积。
参考式(4)计算方法,以我国东风EQ140作为代表车型,计算大型车在道路环境中的加速度。根据上述分析,同时考虑车辆的驱动力、空气阻力、路面摩阻力、自重阻力和惯性阻力,结合汽车牵引力方程构建如式(5)的计算公式。
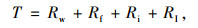
|
(5) |
式中,T为车辆驱动力;Rw为空气阻力;Rf为路面摩阻力;Ri为自重阻力;RI为惯性阻力。对式(4)中每一部分单独计算并回代进式(5),得到式(6)。
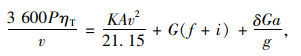
|
(6) |
式中,P为发动机功率,取值为99.3 kW;ηT为传动系统的机械效率,取值为0.9;v为车辆运行速度;K为空气阻力系数,取值为0.9;A取4.185 m2;G为车辆自重,根据调查取91 135 N;f为路面摩阻系数,取值0.01;i为道路纵坡度,平坦路段可不考虑该项;δ为惯性力系数,取值1.07;g取值9.81 m/s2。
将各参数对应取值代入式(6),计算得到大型车加速度a(表 5)。
| 车辆速度/(km·h-1) | 80 | 70 | 60 | 50 | 40 | 35 | 30 |
| 日本加速度取值/(m·s-2) | 0.190 | 0.280 | 0.360 | 0.470 | 0.620 | 0.730 | 0.910 |
| 加速度建议值/(m·s-2) | 0.198 | 0.282 | 0.383 | 0.510 | 0.689 | 0.811 | 0.971 |
通过这种计算模型得到的加速度值与日本规范中采用的加速度值较为接近。对比表 4和表 5,可以发现大型车的加速度小于小型车的加速度,导致大型车所需加速距离会更长,因此计算加速长度主要考虑大型车加速所需要的长度,加速度a1从表 5中选取。
2.2.2 等待可插入间隙距离L2上游驶入车辆通过加速段后,一部分车辆可以直接换道进入主线完成合流,而另一部分车辆则需要继续在加速车道行驶一段时间,等待主线外侧车道的可插入间隙,然后换道进入主线。不同车辆的等待时间不同,其时间长短取决于道路环境和驾驶人操作习惯。若加速车道提供的长度不足,车辆在加速车道末端强制换道或停车等待,会降低合流区通行效率,增大事故风险。因此应该计算大多数车辆在加速车道中所需的等待可插入间隙长度,保证车辆能安全合流。等待可插入间隙长度的计算公式如下。
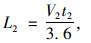
|
(7) |
式中,L2为车辆等待可插入间隙行驶的距离;V2为车辆行驶速度;t2为平均等待时间。
平均等待时间指车辆通过加速段后,等待左侧车道可插入间隙所用的平均时间。可插入间隙表示主线最外侧车道相邻前后车的车头时距满足外侧车辆换道插入的情况。因此计算平均等待时间即可转换为计算主线外侧车道出现相邻前后车的车头时距大于一特定值的平均时间。已有大量研究表明车辆在不同车道和不同路段中车头时距服从不同的分布,其中最主要的两类分布为负指数分布和埃尔朗分布。研究表明合流区主线交通流一般服从二阶埃尔朗分布[11],其概率密度函数如式(8)所示。
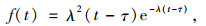
|
(8) |
式中,f(t)为车头时距t服从的概率密度函数;t为车头时距;τ为车头时距最小值,取1.2 s;e为自然常数;λ为车辆平均到达率,λ=Q/3 600;Q为三级服务水平下单车道最大通行能力。则任意两辆相邻车辆车头时距h大于t的概率可以为为式(9):
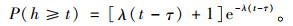
|
(9) |
假设驶入车辆在接受可插入车头时距前,拒绝了i个不可插入车头时距,其概率可表示为式(10):
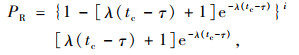
|
(10) |
式中,tc为可插入临界间隙,根据相关研究可插入车头时距一般为3~4 s,取3.5 s。则平均拒绝的车头时距个数可表示为式(11):
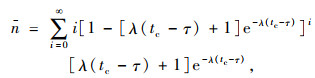
|
(11) |
式(11)绝对收敛于:
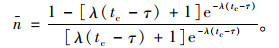
|
(12) |
而拒绝的i个车头时距的平均时长h可用式(13)计算。
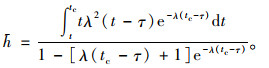
|
(13) |
因此等待可插入间隙所用时长t2可通过拒绝不可插入间隙平均次数乘以每次拒绝所用的平均时长进行计算(式14)。
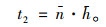
|
(14) |
根据上述公式计算得到等待可插入间隙的平均时间,结果如表 6所示。
2.2.3 汇入主线换道距离L3
换道为计算最小间距,应充分利用加速车道长度和渐变段长度。因此在本研究中认为车辆在加速车道末尾获得可插入间隙并准备换道。随后整个换道过程发生在加速车道的渐变段,即利用渐变段长度进行车道变换。日本在其设计规范中提出,车辆横移一条车道所需的时间为3~4 s,并基于该时间计算了加速车道渐变段最小长度。我国在《路线规范》编制时借鉴了这一结果。根据现有研究结论,车辆在横移换道时为保证舒适性,一般以1 m/s的速度匀速横移。在这里认为车辆横移3.5 m,将换道横移时间取为3.5 s。因此,驶入车辆换道所需的长度可以通过下式计算。
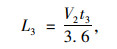
|
(15) |
式中,V2为车辆通过加速段后的末速度;t3为车辆换道所需的时长,取3.5 s。
2.3 最小安全合流视距当上游匝道内的驶入车辆从渐变段换道进入主线最外侧车道后,就完成了整个合流过程。在车辆进入主线后,驾驶人将观察到主线外侧的入口提示标志,引导驾驶人视线寻找下游高速公路入口。出于安全考虑,驾驶人在获得下游出口位置信息后,将采取两种操作措施:如果观察到相邻内侧车道有可插入间隙,一般首选将车辆换道至内侧车道,离开最外侧车道避免与下游驶入交通流相互产生干扰;而当内侧车道交通量过大,不具备换道条件时,驾驶人会降低速度至下游驶入车辆合流速度,以保证安全。因此,上游加速车道渐变段终点至下游合流点必须具备足够的视距,该距离需要保证驾驶人在识别到下游合流点后有足够的长度采取必要的安全措施。
因此如式(1)所示,上下游鼻点之间的距离除了需要满足车辆成功合流所需距离外,还应该满足上游车辆与下游汇入车辆安全合流视距的要求。若安全合流视距过小,驾驶人没有足够的时间操作车辆避让下游合流车辆,易引发交通事故。根据前文分析驾驶人在看见下游合流车辆后的操作特征,可将安全合流距离分为两个阶段:识别决策阶段、向内换道阶段或原车道减速阶段,与此对应的距离分别为识别决策距离、换道距离和减速距离,则最小安全合流视距可用式(16)进行计算。下面将对这3个阶段进行分析,最后得到最小安全合流视距。
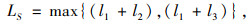
|
(16) |
式中,LS为最小安全合流视距;l1为识别决策长度;l2为换道所需长度;l3为减速所需长度。
2.3.1 合流前识别决策距离车辆驶入主线后,将观察到前方入口提示标志,此时驾驶人将寻找前方入口位置,并观察下游合流区车辆行驶状况,并调整操作决策。此过程为识别决策距离。识别决策时间包括判断时间,驾驶人转头观察时间和驾驶准备时间。相对于停车视距的计算模型,比反应时间多了转头观察时间,此过程中汽车的行驶距离为:
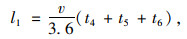
|
(17) |
式中,l1为驾驶人识别决策距离;v为车辆行驶速度,考虑最不利条件选取主线运行速度;t4为识别判断时间,根据实测数据取为1.5 s;t5为驾驶人转头观察时间,取0.5 s;t6为驾驶准备时间,取0.5 s。
2.3.2 合流前换道距离根据上文换道所需长度的分析,此处车辆换道距离计算与式(15)相似,但参数取值不同。变道时认为车辆以主线运行速度匀速行驶,换道横向距离为3.75 m,则换道所需时间取为3.75 s。同时,换道时车辆速度取高速公路主线车辆行驶速度。因此该过程中车辆换道所需长度可用下式计算。
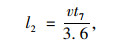
|
(18) |
式中,l2为车辆换道所需长度;v为主线车辆运行速度;t7为车辆换道所用时间,取3.75 s。
综上,主线最外侧车道行驶的车辆若选择向内换道决策,在到达下游合流鼻点前所需的最小距离计算结果如表 7所示。
| 主线设计速度/(km·h-1) | 120 | 100 | 80 |
| 反应距离l1/m | 83 | 69 | 56 |
| 换道距离l2/m | 100 | 83 | 67 |
| 安全合流视距l/m | 183 | 152 | 123 |
2.3.3 合流前减速距离
当内侧车道不具备换道条件时,驾驶人会继续在外侧车道上行驶,并采取减速策略,降低车辆速度至下游驶入车辆合流速度,宜避免与下游汇入车辆碰撞。研究表明驾驶人操作车辆减速时一般服从3阶段制动模型,即驾驶人从确定减速至踩下减速踏板的第1阶段、踩下减速踏板后车辆制动力匀速上升的第2阶段和车辆制动力达到极限进行匀减速的第3阶段。为简化计算模型,将制动3阶段等价转换为两阶段计算,即无制动力阶段和匀速制动阶段,因此车辆减速所需距离用式(19)计算。
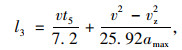
|
(19) |
式中,l3为车辆减速所需长度;t5为无制动阶段持续时间,调查表明此过程一般为0.2 ~0.9 s,取0.5 s;为保证足够的安全余量,考虑最不利情况,即下游驶入车辆以匝道设计速度直接汇入主线,因此减速结束时的速度vz采用匝道设计速度;amax表示制动减速度,根据《绿皮书》的相关研究,90%驾驶人在潮湿路面上所采用的减速度一般为3.4 m/s2,本研究选取该值计算。将参数相应取值代入式(19)计算,结果如表 8所示(取为整5 m)。
| 主线设计速度/(km·h-1) | 不同匝道设计速度(km·h-1)下安全合流视距/m | ||||||
| 80 | 70 | 60 | 50 | 40 | 35 | 30 | |
| 120 | 185 | 200 | 215 | 230 | 240 | 245 | 245 |
| 100 | 120 | 135 | 150 | 165 | 175 | 180 | 180 |
| 80 | — | 80 | 95 | 105 | 120 | 125 | 125 |
比较表 7和表 8中两种驾驶行为所需要的安全合流视距,从安全行车的角度上考虑,,采用较充裕的合流视野范围,有助于驾驶人有足够时间选择换道行驶或减速行驶,避免汇流处的碰撞及挤撞事故,须推荐两者中的较大值,如式(16)所示。因此最小安全视距取值如表 9所示。
| 主线设计速度/(km·h-1) | 不同匝道设计速度(km·h-1)下安全合流视距/m | ||||||
| 80 | 70 | 60 | 50 | 40 | 35 | 30 | |
| 120 | 185 | 200 | 215 | 230 | 240 | 245 | 245 |
| 100 | 155 | 155 | 155 | 165 | 175 | 180 | 180 |
| 80 | — | 125 | 125 | 125 | 125 | 125 | 125 |
2.4 主线同侧相邻入口匝道最小间距推荐值
综上所述,通过计算上游驶入车辆成功汇入主线所需最小长度和驾驶人观察下游入口车辆运行状况并保证安全的最小安全合流视距,通过式(1)计算得到主线同侧相邻入口最小间距(表 10,取为整5 m)。
| 主线设计速度/(km·h-1) | 《路线规范》规定值/m | 各匝道设计速度(km·h-1)下最小间距/m | ||||||||
| 一般值 | 最小值 | 80 | 70 | 60 | 50 | 40 | 35 | 30 | ||
| 120 | 400 | 350 | 370 | 460 | 560 | 620 | 640 | 655 | 660 | |
| 100 | 350 | 300 | — | 355 | 425 | 460 | 520 | 540 | 545 | |
| 80 | 310 | 260 | — | 285 | 340 | 380 | 430 | 445 | 450 | |
从表 10可以看出,当匝道设计速度不同时所需的相邻入口最小间距并不相同,且主线与匝道的速差越大,所需的最小间距越长。而在《路线规范》中主线同侧相邻入口匝道最小间距取值仅与主线设计速度有关,未考虑不同匝道设计速度的情况。此外,规范规定的最小值在任意设计情况下均小于本研究计算得到的推荐值,而规范规定的一般值也仅能满足匝道设计速度80 km/h和70 km/h的小部分情况。在匝道设计速度低于70 km/h的各种设计条件下,《规范》规定值无法满足上游车辆所需的最小合流视距。
3 工程实例分析为验证上述计算结果的合理性,以西安市绕城高速灞桥立交为设计依托,研究该立交内相邻入口之间的交通运行状况。为分析不同间距对通行效率与交通安全的影响,选用交通仿真软件VISSIM对该立交进行仿真。由于本次仿真目的是对比不同间距下的通行效率和交通安全性,因此控制仿真交通量和车型比例固定。仿真模型主要参数为:主线双车道,设计速度120 km/h;环圈匝道单车道,设计速度40 km/h;直连式匝道单车道,设计速度40 km/h;主线直行交通量与合流交通量均按不超过3级服务水平的最大服务交通量选取,且合流后主线不超过3级服务水平,即主线2 055 pcu/h,环圈匝道623 pcu/h,直连式匝道623 pcu/h。
构建VISSIM仿真模型如图 3所示。在设计模型时,将相邻入口匝道之间的间距作为变量,构建了4种不同间距长度的模型,分别为:间距655 m(原始模型)、间距470 m(规范规定400 m+合流鼻至合流点70 m)、间距640 m(表 10推荐值)、间距520 m(中间值)。路网构建完成后,在模型中标定车辆驾驶行为,输入交通量参数,设置加速范围,确定输出数据并进行仿真。将仿真数据输入SSAM交通安全评估软件,得到仿真过程中发生的交通事故次数,以此作为安全性评价的依据。仿真结果如图 4、图 5所示。
|
| 图 3 VISSIM仿真模型示意图 Fig. 3 Schematic diagram of VISSIM simulation model |
| |
|
| 图 4 交通量与延误仿真结果 Fig. 4 Traffic volume and delay simulation result |
| |
|
| 图 5 安全性评价结果 Fig. 5 Safety evaluation result |
| |
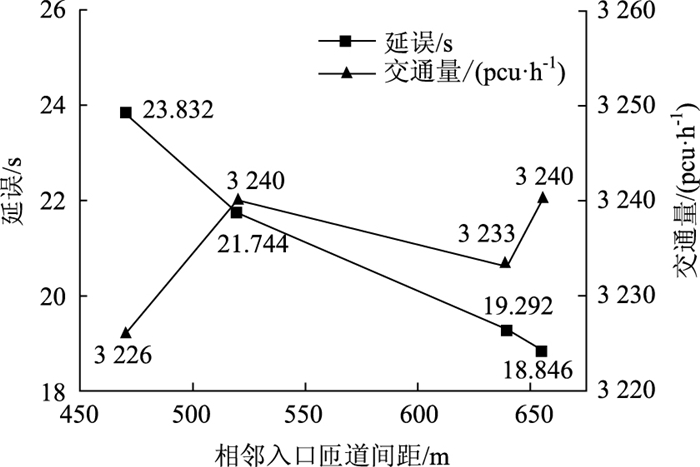
图 4为交通量与延误随相邻入口匝道间距的变化结果,从中可以看出延误与相邻入口匝道间距呈正相关,增加匝道之间的间距后延误降低明显;而交通量没有与间距表现出明显的相关性,但根据本次仿真结果,当相邻匝道间距选用《路线规范》规定的400 m时,路段的通行效率最低。
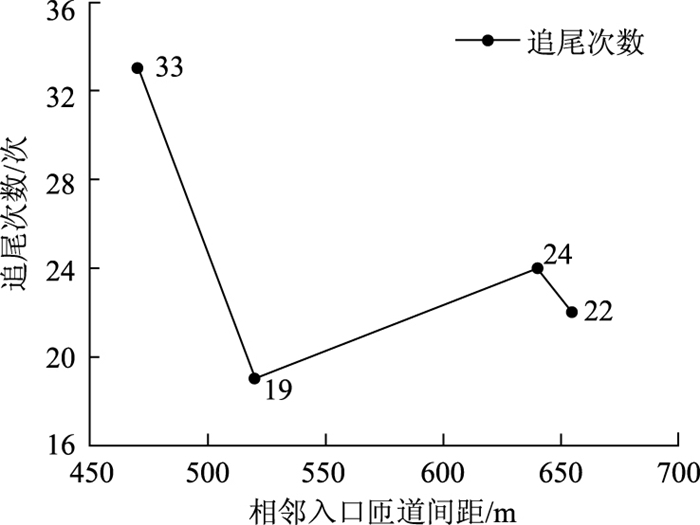
图 5为SSAM处理得到的仿真过程中追尾次数与相邻入口匝道间距的关系图,由于仿真时随机种子的偶然性,本次仿真结果中事故数的变化趋势未表现出与匝道间距之间的负相关性,但从整体趋势上看,通过增加相邻入口匝道间距对减少路段事故发生次数具有一定的积极作用。另外,当间距采用表 10推荐值时,追尾事故发生次数相比《路线规范》取值有明显减少。
4 结论为提高互通式立交主线同侧连续相邻入口路段的交通安全,本研究在界定主线同侧相邻匝道入口间距的基础上,通过分析上游驶入车辆在通过相邻入口的运行特征建立了互通式立交主线同侧相邻入口的最小间距计算模型。模型中考虑了上游驶入车辆成功汇入主线所需的最小距离和在通过下游入口前所需的安全合流视距。并基于实测数据,对计算模型中的特征参数进行分析讨论,从行车安全交通计算得到了基于主线和上游匝道设计速度的高速公路同侧相邻入口最小间距指标建议值。本研究主要结论如下:
(1) 基于高速公路主线同侧相邻匝道入口间驶入车辆的运行特征,考虑上游驶入车辆决策选择与安全需要,建立了同侧相邻入口最小间距计算模型。
(2) 考虑驾驶人的操作规律,从识别决策距离、换道距离或减速距离3个方面,组合并建立了两种最小安全视距模型,计算得到了不同设计速度下的安全视距值。
(3) 综合上游驶入车辆成功汇入主线所需最小长度和最小安全视距,从行车安全角度,提出基于主线设计速度和匝道设计速度的高速公路同侧相邻入口最小间距指标建议值。
(4) 根据西安市灞桥立交工程实例,构建VISSIM仿真模型,并采用SSAM软件对仿真结果进行安全性分析,结果表明相邻入口匝道间距采用本研究推荐值与《路线规范》规定值相比,路段延误更低,追尾事故数发生更少,提高了路段的通行效率和安全性。
研究中未考虑匝道内的大型车比例以及主线大型车比例对匝道车辆汇入主线的影响,还需对此做进一步研究。
| [1] |
AASHTO. A Policy on Geometric Design of Freeway and Street[M]. Washington, D.C.: AASHTO.
|
| [2] |
日本道路协会. 日本公路技术标准的解说与运用[M]. 北京: 人民交通出版社, 1980. Japanese Road Association. Explanation and Application of Japanese Highway Technical Standards[M]. Beijing: China Communications Press, 1980. |
| [3] |
BARED J G, EDARA P K, KIM T. Safety Impact of Interchange Spacing on Urban Freeways[C]//Transportation Research Board 85th Annual Meeting. Washington, D.C.: TRB, 2006.
|
| [4] |
SHAKOURI M, IKUMA L H, AGHAZADEH F, et al. Drivers' Merging Behavior Data in Highway Work Zones[J]. Data in Brief, 2016, 6: 829-832. |
| [5] |
SUN J, LI Z P, SUN J. Study on Traffic Characteristics for a Typical Expressway On-ramp Bottleneck Considering Various Merging Behaviors[J]. Physica A: Statistical Mechanics & Its Applications, 2015, 440: 57-67. |
| [6] |
JTG D20-2017, 公路路线设计规范[S]. JTG D20-2017, Design Specifications for Highway Alignment[S]. |
| [7] |
JTG/T D21-2014, 公路立体交叉设计细则[S]. JTG/T D21-2014, Guidelines for Design of Highway Grade-separated Intersections[S]. |
| [8] |
吴江. 高速公路互通式立体交叉设计中的连续出口和入口间距设计[J]. 公路工程, 2018, 43(4): 242-247. WU Jiang. Design of Continuous Exit and Entrance Distance in Interchange Design of Interworking Freeway[J]. Highway Engineering, 2018, 43(4): 242-247. |
| [9] |
高建平, 廖丽. 互通式立交匝道连续分流点最小间距研究[J]. 重庆交通大学学报: 自然科学版, 2014, 33(2): 103-107. GAO Jian-ping, LIAO Li. Minimum Spacing between Successive Exits Terminals in Interchange Ramps[J]. Journal of Chongqing Jiaotong University: Natural Science Edition, 2014, 33(2): 103-107. |
| [10] |
王灵利, 李新伟, 潘兵宏, 等. 高速公路主线侧连续出口最小间距研究[J]. 铁道科学与工程学报, 2016, 13(4): 626-631. WANG Ling-li, LI Xin-wei, PAN Bing-hong, et al. Study on Minimum Distance of the Highway Line-side Continuous Export[J]. Journal of Railway Science and Engineering, 2016, 13(4): 626-631. |
| [11] |
潘兵宏, 余小龙. 高速公路主线同侧连续入口最小间距研究[J]. 公路, 2017, 62(6): 1-7. PAN Bing-hong, YU Xiao-long. Research on Minimum Distance of the Continuous Entrance on Highway Mainline at the Same Side[J]. Highway, 2017, 62(6): 1-7. |
| [12] |
谢君平. 高速公路出口匝道上游段类型划分及最小间距研究[D]. 南京: 东南大学, 2010. XIE Jun-ping. Study on Type Division and Minimum Spacing of Upstream Section of Expressway Off-ramp[D]. Nanjing: Southeast University, 2010. |
| [13] |
汤振农. 高速公路匝道出入口最小间距研究[D]. 南京: 东南大学, 2010. TANG Zhen-nong. Research on Minimum Distance between Ramp Entrances and Exits of Expressway[D]. Nanjing: Southeast University, 2010. |
| [14] |
韩敏, 沈巍. 城市快速公路无控接入口与相邻大型信号路口接入间距分析[J]. 贵州大学学报: 自然科学版, 2017, 34(4): 115-118. HAN Min, SHEN Wei. Analysis of the Distance between Uncontrolled Access and Adjacent Signal Intersection on the Urban Freeway[J]. Journal of Guizhou University: Natural Science Edition, 2017, 34(4): 115-118. |
| [15] |
邵阳, 潘兵宏, 王云泽. 高速公路互通式立交连续出口和入口间距研究[J]. 铁道科学与工程学报, 2016, 13(8): 1642-1651. SHAO Yang, PAN Bing-hong, WANG Yun-ze. Study on Adjacent Exit and Entrance Distance of Freeway interchanges[J]. Journal of Railway Science and Engineering, 2016, 13(8): 1642-1651. |
| [16] |
魏代梅. 城市快速路进出口匝道组合类型和间距对组合区平均速度的影响分析[D]. 上海: 上海交通大学, 2013. WEI Dai-mei. Analysis on Influence of Combination Type and Spacing of Urban Expressway Ramp on Average Speed of Combination Area[D]. Shanghai: Shanghai Jiaotong University, 2013. |
| [17] |
蒋飞. 互通式交叉匝道连续出入口最小间距研究[D]. 西安: 长安大学, 2018. JIANG Fei. Research on Minimum Spacing of Ramp Successive Exit and Entrance of Interchange[D]. Xi'an: Chang'an University, 2018. |
| [18] |
倪旭. 客货分离高速公路互通式立交变速车道设计指标研究[D]. 西安: 长安大学, 2019. NI Xu. Study on Design Indexes of Speed Change Lanes of Interchange on Expressway with Separation between Passenger Cars and Trucks[D]. Xi'an: Chang'an University, 2019. |
 2021, Vol. 38
2021, Vol. 38
