扩展功能
文章信息
- 李涛, 方志森, 吴善根, 潘兵宏, 柳银芳
- LI Tao, FANG Zhi-sen, WU Shan-gen, PAN Bing-hong, LIU Yin-fang
- 高速公路主线同侧相邻单车道入口与出口最小间距研究
- Study on Minimum Distance between Entrance and Exit of Adjacent Single Lanes on Expressway Mainline at Same Side
- 公路交通科技, 2021, 38(9): 141-147
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(9): 141-147
- 10.3969/j.issn.1002-0268.2021.09.018
-
文章历史
- 收稿日期: 2021-04-26
2. 长安大学 公路学院, 陕西 西安 710001
2. School of Highway, Chang'an University, Xi'an Shaanxi 710064, China
随着高速公路里程规模的不断扩大和路网密集程度的逐步增加,互通式立交的数量也不断增加,也出现了主线同侧相邻入口和出口。主线同侧相邻入口和出口之间的路段(定义为主线合分流区)上交通流存在交织运行的情况,交织段内车流运行较复杂,存在交通冲突,对交通安全影响较大。设计中为避免交织区对主线直行车流的影响,一般采用设置集散车道的方式(集散车道是指为隔离交织区、减少主线出入口数量而设置于主线外侧与主线隔离的附加道路),此时相邻入口和出口路段均位于集散车道上,称为匝道合分流区。本研究主要探讨不设置集散车道的情况,即主线合分流区。主线合分流区的最小间距对该区域的通行能力和交通安全影响较大。《公路立体交叉设计细则》(JTG D21—2014)(以下简称《立交细则》)[1]中以辅助车道长度(辅助车道是为出入主线车辆调整车速、车距、变换车道或为平衡车道等而平行设置于主线直行车道外侧的附加车道,与主线直行车道之间不设置隔离设施)来标定主线合分流区的最小间距,并给出了最小长度固定值(10.6.3条),当入出口匝道均为单车道时,均应以平行式与主线相接,辅助车道宜由分流鼻端开始渐变结束,渐变率不应大于1/40。但《立交细则》中并没有考虑匝道设计速度,也没有区分入口车道数和出口车道数,且条文说明中也未解释最小长度来源或依据,因此修订的《公路路线设计规范》(JTG-D20—2017)(以下简称《路线规范》)[2]未采纳《立交细则》的意见,在11.5.5条中对此依然未作规定。可见仍需要对主线合分流区的最小间距深入研究。
通过文献收集可分析发现,国内外目前对高速公路主线同侧相邻单车道入口与出口(以下简称“同侧入出口”)最小间距的研究较少。与之相关的影响因素的研究主要有:国外,Dabbour等[3]提出了一种基于驾驶人实际行为和车辆加速能力确定高速公路互通式立交(以下简称互通)加速车道长度的新方法。Fatema等[4]基于合流过程中驾驶人加速行为和考虑可插入间隙设计加速车道长度。Calvi等[5]通过对90名被试人员在驾驶模拟器上的速度和轨迹数据,分析了加速车道与减速车道的驾驶性能。Evans 等[6]通过综合利用概率论与马尔科夫链,研究了因合流操作失败而不得不选择停车的概率,并总结了驾驶人在接近合流路段时的车流特性。Bokare等[7]利用GPS等现代工具,研究各种车辆类型的加速与减速行为,以得到加、减速车道的计算模型。Bared等[8]基于加州3条高速公路的碰撞事故数据,建立了碰撞频率与高速公路互通立交间距的回归模型。Iwasaki等[9]通过对互通范围内各项间距与交通事故之间内在联系的探究,回归了交通事故率与出、入口匝道间距之间的关系。国内相关的研究主要包括驾驶人对标志的响应特性、车辆换道与可插入间隙等。张伯明[10]通过测定认读时间确定了最小认读距离。王慧然等[11]指出传统换道模型的缺点,提出了基于行车安全边界的换道控制方法,并通过仿真试验验证了其合理性。赵晓翠[12]对出口路段不同断面与交通量情况的车头时距作了假设检验,并验证了其分布。还有利用调查数据分析研究互通范围内出、入口路段及交织区的交通流特性等,如吴兵等[13]通过分析入口匝道通行能力主要制约因素,结合互通连接部交通特性,建立了匝道通行能力计算模型。此外还有对互通立交间距方面研究,如李爱增等[14]分析了互通间距的构成要素,结合概率论和微分方法、动力学理论及驾驶心理学等建立了互通最小立交间距模型。
综上所述,主线分合流区的交通流特性是近年来的研究热点,且多数学者通过实测调查得到主线分合流区车辆的运行规律,并以此为基础建立了互通范围内各部分之间间距的计算模型。但目前已有研究中对主线同侧入出口间距方面的研究较少。本研究探讨的主线同侧入出口是指在较近距离内的主线同侧出现匝道先合流,随后又有匝道分流的形式。本研究参考国内外关于交通流方面的成熟理论,采用相关数据调查资料,分析主线同侧入出口间距的影响因素,并考虑标志前置距离和变速车道设置要求,建立主线同侧入出口最小间距的计算模型,并提出间距建议值。
1 主线同侧相邻入口与出口间距界定匝道车道数直接影响着主线合分流的形式。对于双车道匝道,为保证车道平衡,需在合分流区域设置辅助车道。当不设辅助车道时,主线合分流区的设置形式为单入单出式(图 1)。在此仅研究入口和出口均为单车道的合分流形式。
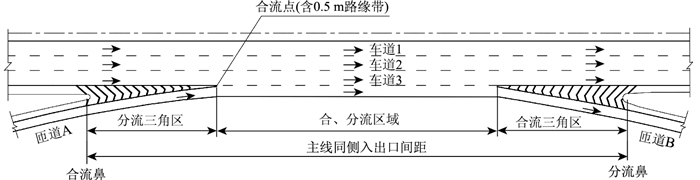
|
| 图 1 主线同侧入出口最小间距示意图(无辅助车道) Fig. 1 Schematic diagram of minimum distance between entrance and exit on same side of mainline (without auxiliary lanes) |
| |
美国绿皮书《A Policy on Geometric Design of Highways and Streets》[15]、我国《城市道路交叉口设计规程》(CJJ152—2010)[16]及《立交细则》中所规定的主线同侧入出口间距均为前后2匝道分合流鼻端之间的距离。综合国内外相关规定,本研究明确主线同侧入出口间距是指入口匝道合流鼻与相邻出口分流鼻对应的主线平面里程之差(图 1)。
2 间距影响因素分析 2.1 主线同侧相邻入口与出口间交通流特点主线同侧相邻单车道入出口范围内交通流具有如下特点。从入口匝道驶入主线的车辆,若不立即在下个出口驶出,为免受下游分流的影响,出于换道需要,通常需不断观察左后方来车情况与前方车辆,寻找可插入间隙或超车机会,以便伺机汇入主线。此时汇入车辆与主线直行车辆形成较大速差,存在换道、加速2种操作,造成“合流影响区”。
同时,将要分流驶出的内侧车道车辆与主线直行车辆并行,首先需从直行交通流中分离出来进入最外侧车道,整个车流也会重新调整交通量的车道分布,此时存在交织段与冲突,导致该路段车辆行驶速度多样、车辆运行轨迹离散、换道频率高、车辆交织严重,交通冲突明显,形成“分流影响区”。
受诸多因素的影响,实际过程中主线合、分流区域的车流运行状态较为复杂。
2.2 主线同侧入出口间距影响因素根据以上对主线同侧入出口路段车流特性的分析可知,主线同侧入出口间距的设计应考虑从物理行车环境上改善交通流运行条件,给驾驶人重新调整车道提供充足的时间和空间,即保证入出口路段一定的车流密度要求,以避免交通拥堵和保证行车安全。这种需求也就成为限制主线同侧入出口间距的一项重要因素。因此,在不设置辅助车道的情况下,高速公路同侧入出口的最小间距与主线和匝道设计速度、路段设计通行能力(或服务水平)等因素有关。
本研究将利用HCM2000中[17]关于匝道之间连接点的分析方法,通过对分合流区交通量的确定及对交通流密度的计算,研究满足一定服务水平的主线同侧入出口最小间距。
3 服务水平与交通量的确定 3.1 服务水平在稳定运行条件下,依据交通流密度将高速公路分、合流路段的服务水平划分为表 1所示的标准。
| 服务水平 | 1级 | 2级 | 3级 | 4级 | 5级 | 6级 |
| 交通流密度/[pcu·(km·ln)-1] | ≤6 | >7~12 | >12~18 | >18~25 | >25~35 | >35 |
3.2 交通量
在高速公路入口路段,上游基本路段和匝道汇入交通量的总和不得大于下游路段通行能力。故下游路段设计通行能力是主要限制因素。为保证主线服务水平不因合流而降低,需对主线上游及匝道交通量予以折减,折减系数与主线和匝道设计通行能力有关。主线与匝道的交通量分别按3级和4级服务水平对应的设计通行能力取值(表 2、表 3)。
| 设计速度/(km·h-1) | 120 | 100 | 80 |
| 设计通行能力/[pcu·(h·ln)-1] | 1 650 | 1 600 | 1 500 |
| 匝道设计速度/(km·h-1) | 80 | 70 | 60 | 50 | 40 | 35 | 30 | |
| 设计通行能力/(pcu·h-1) | 单车道 | 1 500 | 1 400 | 1 300 | 1 200 | 1 000 | 900 | 800 |
| 双车道 | 2 900 | 2 600 | 2 300 | 2 000 | 1 700 | 1 500 | 1 300 | |
在计算时,交通量需转化为高峰小时流率:
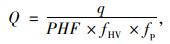
|
(1) |
式中,Q为高峰小时流率;q为小时交通量;PHF为高峰小时系数,取全国平均值0.901;fHV为交通组成修正系数,因上述通行能力系标准小客车当量值,故取1;fp为驾驶员总体特征修正系数,取1。
4 合、分流区车流密度计算本节在上文界定的主线同侧相邻入出口间距基础上,通过分析前后合、分流区交通量、服务水平、车流密度等的影响,建立满足合、分流区交通服务水平的主线同侧入出口最小间距计算模型。具体思路是:从驶入合流影响区及分流影响区范围的主线外侧2条车道的流率预测模型出发,建立起主线流率与合流匝道起点距下游出口的距离和分流匝道起点距上游入口距离之间的函数关系,最后根据合、分流路段的交通流密度临界值与3.2节确定的交通量,反算确定并提出无辅助车道情况下高速公路主线同侧入出口最小间距值。
4.1 合流区合流影响区范围为合流匝道末端上游150 m到下游750 m的范围内,见图 2。
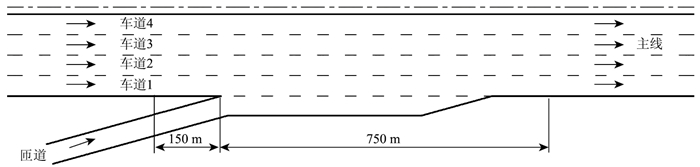
|
| 图 2 入口匝道合流区影响范围示意图 Fig. 2 Schematic diagram of influence scope of on-ramp converging area |
| |
驶入合流影响区范围的主线外侧2条车道的流率预测模型为:
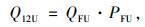
|
(2) |
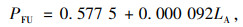
|
(3) |
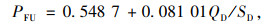
|
(4) |
式中,Q12U为驶入合流影响区的主线流率;QFU为主线合流区上游的总交通流率;PFU为紧邻合流区上游主线外侧2车道的流率占该方向总流率之比;LA为加速车道长度;QD为下游出口交通流率;SD为合流匝道起点距下游出口的距离,见图 3。
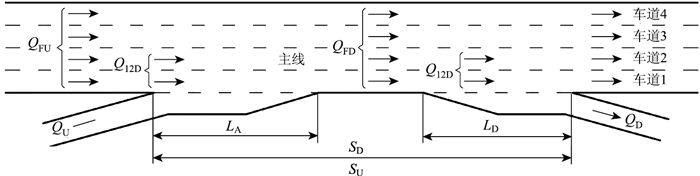
|
| 图 3 合、分流区通行能力的主要影响因素示意图 Fig. 3 Schematic diagram of main influencing factors of capacity of converging and diverging areas |
| |
对于PFU计算式的选择,其判别式为:
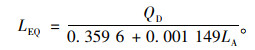
|
(5) |
式中LEQ等效距离,用于判断匝道是否受上下游相邻匝道影响。
若SD>LEQ,选用式(3)计算,否则选用式(4)。受下游分流影响的合流区车流密度KU计算式如下:
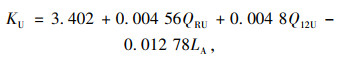
|
(6) |
式中,KU为合流区车流密度;QRU为入口匝道需求流率。
4.2 分流区分流区影响范围为分流匝道始端上游750 m到下游150 m的范围内,见图 4。
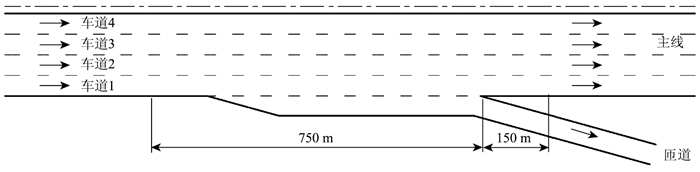
|
| 图 4 出口匝道分流区影响范围示意图 Fig. 4 Schematic diagram of influence range of off-ramp diversion area |
| |
驶入分流影响范围的主线外侧2条车道的流率预测模型为:
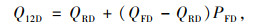
|
(7) |
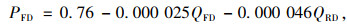
|
(8) |
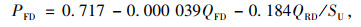
|
(9) |
式中,Q12D为驶入分流影响区范围的主线流率;QRD为出口匝道需求流率;QFD为分流区上游的交通需求;PFD为紧邻分流区上游主线外侧2车道的流率占该方向总流率之比;SU为分流匝道起点距上游入口的距离。
对于PFD计算式的选择,判别式如下:
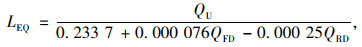
|
(10) |
式中QU为上游入口交通流率。
若SU>LEQ,选用式(8)计算,否则选用式(9)。此时,受到上游合流影响的分流区车流密度KD的计算式为:
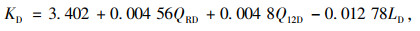
|
(11) |
式中LD为减速车道长度。
5 最小间距计算根据以上各条件,代入相关参数,反算确定满足合、分流区服务水平的主线同侧入出口最小间距(即SD及SU)。取主线合、分流路段3级服务水平下的交通流密度临界值为22 pcu/(km·ln)(此时交通流处于稳定运行状态,无明显阻塞),计算得到表 4的结果。
| 匝道设计速度/(km·h-1) | 主线设计速度/(km·h-1) | 120 | 100 | 80 | |
| 主线同侧入、出口最小间距/m | 80 | 合流临界状态 | 483 | 473 | — |
| 分流临界状态 | 938 | 934 | — | ||
| 70 | 合流临界状态 | 431 | 422 | — | |
| 分流临界状态 | 865 | 861 | — | ||
| 60 | 合流临界状态 | 386 | 377 | 314 | |
| 分流临界状态 | 795 | 792 | 688 | ||
| 50 | 合流临界状态 | 345 | 337 | 283 | |
| 分流临界状态 | 729 | 725 | 635 | ||
| 40 | 合流临界状态 | 275 | 268 | 227 | |
| 分流临界状态 | 602 | 599 | 531 | ||
| 35 | 合流临界状态 | 243 | 237 | 202 | |
| 分流临界状态 | 541 | 538 | 479 | ||
| 30 | 合流临界状态 | 214 | 208 | 178 | |
| 分流临界状态 | 480 | 479 | 428 | ||
据表 4计算结果显示,相同设计速度条件下,分流临界状态对应的间距值均大于合流临界状态对应的间距值,表明满足分流服务水平要比满足合流服务水平所要求的主线同侧入出口最小间距值更大。分流区密度在较大程度上受上游合流交通影响。故主线同侧入出口最小间距主要由分流区密度决定。此时该间距值不仅需满足分流服务水平的要求,还应满足设置变速车道的长度要求(表 5)及出口预告标志的前置距离要求。
| 主线设计速度/(km·h-1) | 分流减速车道长度/m | 合流加速车道长度/m | |||
| 变速段 | 渐变段 | 变速段 | 渐变段 | ||
| 120 | 单车道 | 145 | 100 | 230 | 90 |
| 双车道 | 225 | 90 | 400 | 180 | |
| 100 | 单车道 | 125 | 90 | 200 | 80 |
| 双车道 | 190 | 80 | 350 | 160 | |
| 80 | 单车道 | 110 | 80 | 180 | 70 |
| 双车道 | 170 | 70 | 310 | 150 | |
其中,标志前置距离L1的计算式为:
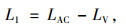
|
(12) |
式中, LAC为标志认读距离与决策距离之和;LV为标志可视距离。
按照式(13)计算得到标志可视距离LV(表 6)。
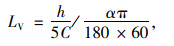
|
(13) |
| 设计速度/(km·h-1) | 120 | 100 | 80 | 70 | 60 | 50 | 40 | 35 | 30 |
| 字高/m | 0.7 | 0.6 | 0.45 | 0.45 | 0.4 | 0.4 | 0.35 | 0.3 | 0.3 |
| 标志可视距离/m | 125 | 107 | 80 | 80 | 72 | 72 | 63 | 54 | 54 |
式中,h为汉字字高;C为汉字与视标的转换常数,取3.073 5[10];α为缪氏视力五分法指出的系数,当双眼裸视力达到对数视力表中的4.9时,α=1.259[18]。
当依据服务水平确定的间距小于变速车道长度和标志前置距离时,应取满足后者所需的间距值作为最终推荐值(取整为5 m,表 8)。
| 主线设计速度/(km·h-1) | 120 | 100 | 80 | |
| 匝道设计速度/(km·h-1) | 80 | 940 | 940 | — |
| 70 | 870 | 860 | — | |
| 60 | 800 | 800 | 690 | |
| 50 | 730 | 730 | 640 | |
| 40 | 610 | 600 | 530 | |
| 35 | 610 | 540 | 480 | |
| 30 | 610 | 530 | 480 | |
分析表 8计算结果,可得到主线同侧入出口最小间距推荐值(以下简称“推荐值”)具有如下一些特点:(1)推荐值的最终取值基本上是由表 4分流临界状态对应值的取整,原因在于,一是满足分流服务水平比满足合流服务水平所要求的间距值更大,二是根据服务水平确定的间距值普遍大于变速车道长度和标志前置距离;(2)推荐值与主线和匝道的设计速度均有关;(3)相同匝道设计速度下,主线设计速度越大,推荐值越大;(4)相同主线设计速度下,匝道设计速度越大,推荐值也越大。原因在于变速车道及分合流路段小客车实际行驶速度会随着设计速度的增大而增大。与《立交细则》、《城市快速路设计规程》(CJJ129—2009)中关于单入单出形式下主线同侧合分流区最小间距的单一规定值(以下简称“规范值”)相比,本研究推荐值考虑了更多的影响因素(如匝道设计速度),且相同主线设计速度下,推荐值普遍小于规范值。这对于设计者灵活地处理实际工程问题更为有利。
6 结论(1) 考虑入口匝道与出口匝道对主线合、分流范围交通流密度的影响,确定了驶入合流或分流影响区域的外侧2车道的交通流率,并建立了满足分、合流区服务水平条件的主线同侧入出口最小间距计算模型,以合、分流路段的交通流密度临界值为限定条件,计算得到了主线同侧入出口最小间距推荐值。
(2) 通过分析驾驶人看到出口预告标志后的识认特征及过程,确定了满足安全舒适所需的相邻匝道入、出口预告标志前置距离计算方法,并提出了标志前置距离。
(3) 不同于规范值,本研究所建立的主线同侧入出口最小间距计算模型具有同主线和匝道设计速度、合分流区交通流密度等均相关的特点。根据计算结果,推荐值直接受分流区的交通流密度影响,应取满足分流服务水平要求所对应的计算值。
| [1] |
JTG/T D21-2014, 公路立体交叉设计细则[S]. JTG/T D21-2014, Guidelines for Design of Highway Grade-separated Intersections[S]. |
| [2] |
JTG B20-2017, 公路路线设计规范[S]. JTG B20-2017, Design Specifications for Highway Alignment[S]. |
| [3] |
DABBOUR E, EASA S M, DABBOUR O. Minimum Lengths of Acceleration Lanes Based on Actual Driver Behavior and Vehicle Capabilities[J]. Journal of Transportation Engineering, Part A: Systems, 2021, 147(3): 04020162. |
| [4] |
FATEMA T, HASSAN Y. Probabilistic Design of Freeway Entrance Speed-change Lanes Considering Acceleration and Gap Acceptance Behavior[J]. Transportation Research Record, 2013, 2348: 30-37. |
| [5] |
CALVI A, D'AMICO F, FERRANTE C, et al. A Driving Simulator Validation Study for Evaluating the Driving Performance on Deceleration and Acceleration Lanes[J]. Advances in Transportation Studies, 2020, 50: 67-80. |
| [6] |
EVANS J L, ELEFTERIADOU L, GAUTAM N. Probability of Breakdown at Freeway Merges Using Markov Chains[J]. Transportation Research Part B: Methodological, 2001, 35(3): 237-254. |
| [7] |
BOKARE P S, MAURYA A K. Acceleration-deceleration Behaviour of Various Vehicle Types[J]. Transportation Research Procedia, 2017, 25: 4737-4753. |
| [8] |
BARED J G, EDARA P K, KIM T. Safety Impact of Interchange Spacing on Urban Freeways[C]//TRB 85th Annual Meeting. Washington, D. C.: TRB, 2006.
|
| [9] |
IWASAKI M, SEKINEI, TAJIMA H. An Analysis of Traffic Accidents at Diverging and Merging Sections on the Metropolitan Expressway[C]//Proceedings of Infrastructure Planning. Tokyo: Japan Society of Civil Engineers, 1992.
|
| [10] |
张伯明. 交通标志汉字视认性的研究[J]. 公路交通科技, 1993, 10(2): 40-46. ZHANG Bo-ming. The Identification of the Chinese Characters in Traffic Signs[J]. Journal of Highway and Transportation Research and Development, 1993, 10(2): 40-46. |
| [11] |
王慧然, 王其东, 陈无畏, 等. 基于车辆行驶安全边界的换道控制[J]. 机械工程学报, 2020, 56(18): 143-153. WANG hui-ran, WANG Qi-dong, CHEN Wu-wei, et al. Lane Change Control Based on Vehicle Driving Safe Boundary[J]. Journal of Mechanical Engineering, 2020, 56(18): 143-153. |
| [12] |
赵晓翠, 杨峰, 邓宝. 高速公路互通立交分流区车头时距分布[J]. 公路交通科技, 2012, 29(2): 136-139. ZHAO Xiao-cui, YANG Feng, DENG Bao. Headway Distribution Characteristics of Diverging Area on Expressway Interchanges[J]. Journal of Highway and Transportation Research and Development, 2012, 29(2): 136-139. |
| [13] |
吴兵, 杨佩昆. 高速道路入口匝道通行能力研究[J]. 同济大学学报, 1999, 27(4): 422-426. WU Bing, YANG Pei-kun. Research into Freeway On-ramp Capacity[J]. Journal of Tongji University, 1999, 27(4): 422-426. |
| [14] |
李爱增, 李文权, 王炜. 城市快速路互通立交最小间距[J]. 公路交通科技, 2008, 25(6): 104-110. LI Ai-zeng, LI Wen-quan, WANG Wei. Minimum Interchange Spacing of Urban Expressway[J]. Journal of Highway and Transportation Research and Development, 2008, 25(6): 104-110. |
| [15] |
AASHTO. A Policy on Geometric Design of Highways and Streets[R]. Washington, D.C.: American Association of State Highway and Transportation Officials, 2018.
|
| [16] |
CJJ 152-2010, 城市道路交叉口设计规程[S]. CJJ 152-2010, Specification for Design of Intersections on Urban Roads[S]. |
| [17] |
Transportation Research Board. Highway Capacity Manual 2000[M]. Washington, D. C.: National Research Council, 2000.
|
| [18] |
GB 7258-2012, 机动车运行安全技术条件[S]. GB 7258-2012, Safety Specifications for Power-driven Vehicles Operating on Roads[S]. |
 2021, Vol. 38
2021, Vol. 38
