扩展功能
文章信息
- 李星, 王科, 林宣财, 李涛, 王佐
- LI Xing, WANG Ke, LIN Xuan-cai, LI Tao, WANG Zuo
- 高速公路内侧车道采用紧急制动停车视距安全风险分析
- Analysis on Safety Risk of Stopping Sight Distance for Emergency Braking in Inner lane of Expressway
- 公路交通科技, 2021, 38(9): 78-84
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(9): 78-84
- 10.3969/j.issn.1002-0268.2021.09.010
-
文章历史
- 收稿日期: 2021-04-25
我国现行《公路路线设计规范》(JTG D20—2017)(以下简称《路线规范》[1])对圆曲线最小半径和停车视距分别进行了规定,因高速公路中间带防撞护栏和防眩设施在圆曲线上遮挡驾驶员视线,造成停车视距所需要的圆曲线最小半径比《路线规范》[1]中规定的圆曲线最小半径大很多。山区高速公路地形条件复杂,为了更好地控制工程造价,早期已建高速公路较多项目平面圆曲线最小半径采用一般值或接近一般值,如果依据《路线规范》[1]规定的停车视距所需要的圆曲线最小半径进行核查,较多路段不符合规范要求。根据山区高速公路内侧车道紧急制动停车视距取值的研究,紧急制动停车视距较规范值小,山区高速公路平面半径较小路段如果采用紧急制动停车视距,究竟有没有安全风险或安全风险究竟多大这一核心问题有必要开展系统的研究。
国内针对停车视距安全风险的研究较少,长安大学杨帆等[2]研究认为通过提高视点目标物高度至0.8 m时,规范规定的停车视距对应的圆曲线最小半径值小于规范中圆曲线最小半径,认为没有必要对中央分隔带护栏进行特殊设计或增加高速公路占地措施。武汉理工大学张航等[3]提出满足高速公路对应安全等级的可靠性要求的停车视距。同济大学吴斌等[4]利用远、近目标点的转向理论,建立更加符合实际驾驶员紧急转向特征的变道模型,能较好地复现驾驶员紧急转向变道行为。范爽等[5-10]以事故资料为依据,全面分析了公路平面设计中各元素之间组合关系的安全性,并提出了基于交通安全的高速公路平面设计指标及其组合。陈雨人[11]建立视距计算模型,并将该模型应用于实际隧道的视距检验。文浩雄等[12]对高速公路中央分隔带弯道路段横净距进行验算,发现不能满足停车视距要求,针对性地提出增大中央分隔带横净距、设置限速标志及减速标线等措施。陈瑾等[13-16]考虑互通式立交出口车辆强制换道现象,提出了基于换道模型的分流区主线圆曲线最小半径。涂文靖等[17-18]结合设计速度、圆曲线半径、横向力系数、超高值及过渡段的关系进行深入研究。
综上,停车视距不足的问题,多数研究仅仅是与规范值的比较。为此,基于国内外对停车视距计算参数取值的研究,提出紧急制动停车视距概念,并研究表明在山区高速公路圆曲线半径较小路段行驶时,驾驶员处于有预期的高警惕性状态,当发现前方有障碍物时所做出停车决策的反应时间要短于一般路段,以此计算紧急制动停车视距。当设计速度为80 km/h时,对应的圆曲线最小半径值与规范中规定的圆曲线最小半径一般值基本一致。所以只要圆曲线半径大于规范中规定的一般值,高速公路中间带不需要特殊设计,但究竟安全风险有没有或安全风险究竟多大,有必要进行深入研究。
1 高速公路内侧车道采用紧急制动停车视距概述 1.1 紧急制动停车视距基本概念(1) 紧急制动停车视距基本概念
车辆在高速公路行驶过程中,为了避免追尾或保证安全换道,驾驶员经常需要制动减速,但一般不需要紧急停车;如果发现前方障碍物是静止的物体时需要紧急停车或换道,最短停车距离取决于驾驶员紧急制动反应时间和最大制动减速度。当驾驶员发现前方障碍物后采取紧急制动所需要的反应时间,与驾驶员年龄、性别、驾驶经验有关系,但与行驶时驾驶员的警惕性程度关系最大。为了保证舒适制动驾驶状态,道路通行条件应满足规范规定的停车视距要求,规范规定的停车视距是理想的停车视距。根据紧急制动反应时间的取值研究,所谓紧急制动停车视距是指:驾驶员处于有预期的或高警惕性驾驶状态时发现前方障碍物所需要的反应时间较无预期的正常驾驶状态短,相应的计算停车视距较规范值小。
(2) 高速公路内侧车道采用紧急制动停车视距合理性分析
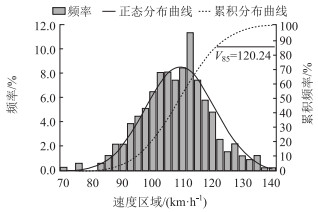
根据高速公路实测运行速度分析,运行速度分布图中V85与高速公路限速基本一致,从图 1可知,设计速度或公路限速为120 km/h时,超过60%车辆行驶速度在110 km/h以下,仅有15%的驾驶员行驶速度达到或超过高速公路限速值,显然行驶速度在110 km/h以上的驾驶员在较小的圆曲线路段上行驶时,驾驶员通常有相当警惕性。高速公路内侧车道作为超车道或快车道,是多车道高速公路限速最高的车道,车辆在内侧车道上行驶,驾驶员需要保持高速行驶的相当警惕性状态;另一方面,从左偏线形停车视距分析,内侧车道行驶条件为最不利位置,车辆在内侧车道保持限制速度高速进入较小圆曲线半径路段时,驾驶员从对道路通行条件的预期考虑,驾驶状态必须保持高警惕性,对行驶速度在110 km/h以下时舒适制动停车视距满足要求。所以,提出高速公路内侧车道采用紧急制动停车视距。
|
| 图 1 高速公路内侧车道运行速度分布 Fig. 1 Speed distribution in inner lane of expressway |
| |
1.2 紧急制动停车视距计算值及推荐值
根据“高速公路内侧车道小客车停车视距合理取值的研究”,小客车紧急制动停车视距和舒适制动停车视距计算值及推荐值如表 1所示。表中计算参数取值:基于路面摩阻力系数的停车视距计算方法,摩阻力系数宜取0.46;基于制动减速度计算方法,制动减速度宜取4.51 m/s2;紧急制动反应时间取1.5 s,舒适制动反应时间取2.5 s。
| 设计速度/(km·h -1) | 120 | 100 | 80 | 60 | |
| 停车视距规范值/m | 210 | 160 | 110 | 75 | |
| 舒适制动停车视距(反应时间2.5 s)/m | 计算值 | 206.5 | 155.0 | 110.3 | 72.5 |
| 推荐值 | 205 | 155 | 110 | 75 | |
| 紧急制动停车视距(反应时间1.5 s)/m | 计算值 | 173.2 | 127.2 | 88.1 | 55.8 |
| 推荐值 | 175 | 130 | 90 | 60 | |
2 山区高速公路内侧车道小客车采用紧急制动停车视距安全风险分析 2.1 紧急制动停车视距小于规范值路段发生概率与危害程度分析 2.1.1 高速公路左侧车道被占发生概率分析
根据调查,高速公路车道内侧车道被占有3种情况:(1)在地质条件复杂区域出现山体滑坡,由于高速公路内侧车道停车视距不利位置在山体的外侧,所以只有当全幅路基的2/3被占时内侧车道才会被占,显然滑坡体较大,中间带防撞护栏和防眩设施可能遮挡不住视线;(2)发生交通事故,事故车辆尚未移除;(3)车辆落物,物体较大。这3类事故都是随机偶发事件,并不完全在圆曲线半径最小或较小的路段,对某一圆曲线路段而言发生概率非常小。
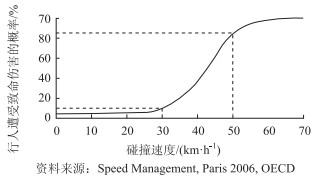
2.1.2 发生事故危害程度分析根据《公路限速标志设计规范》(JTG/T 3381-02—2020)(以下简称《限速规范》)相关研究,行驶速度影响事故所导致伤害的严重程度,当车辆行驶速度超过30 km/h,其所造成的伤害将超过人体的承受能力,但大多数人可以存活;被行驶速度50 km/h的车辆撞击时,大多数人会失去生命,见图 2。假设在高速公路内侧车道发现障碍物,且车辆没有换道机会,以规范规定值为基准,根据紧急制动停车视距与规范值的差值,计算得到相应的碰撞速度,见表 2,不同设计速度可能的碰撞速度均低于20 km/h,显然对车内的人员伤害均非常小,对车辆损坏严重程度较低,高速公路上没有行人,所以,即使出现碰撞事故安全风险较低,可能造成的直接经济损失较小。
|
| 图 2 行人与车辆碰撞遭受致命的可能性 Fig. 2 Possibility of fatal collision between pedestrian and vehicle |
| |
| 设计速度/(km·h -1) | 120 | 100 | 80 | |
| 《路线规范》规定的停车视距/m | 210 | 160 | 110 | |
| 理想停车视距 | 推荐值/m | 205 | 155 | 110 |
| 与规范差值/m | 5 | 5 | 0 | |
| 可能的碰撞速度/(km·h -1) | 2.18 | 2.9 | 0 | |
| 紧急制动停车视距 | 推荐值/m | 175 | 130 | 90 |
| 与规范差值/m | 35 | 30 | 20 | |
| 可能的碰撞速度/(km·h -1) | 17.92 | 18.23 | 16.38 | |
2.2 换道行为的可能性及换道概率分析 2.2.1 换道长度计算模型
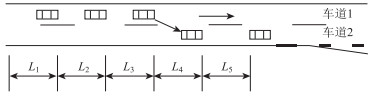
当车辆发现前方有障碍物时,车辆采取紧急停车的同时会考虑换道行为。在内侧车道的车辆要完成变换到外侧车道上,换道过程由发现前方有障碍物时紧急制动反应时间、寻找可插入间隙时间、变换车道时间等3部分组成,如图 3所示。
|
| 图 3 车辆换道过程示意图 Fig. 3 Schematic diagram of vehicle lane changing process |
| |
(1) 紧急制动反应时间及距离L1
① 紧急制动反应时间t1
根据前述,当车辆发现前方有障碍物时车辆采取紧急停车或换道行为的紧急制动反应时间,取1.603 s,即选择信息容量1 bit且为有预期反应时间的值。
② 反应时间前进的距离L1
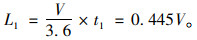
|
(2) |
(2) 等待可插入间隙时前进的距离L2
车辆在准备换道过程中,需要等待相邻车道的可插入间隙时间,在该时间内前进的距离由式(3)计算:
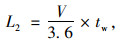
|
(3) |
式中, V为等待可插入间隙过程中车辆的行车速度;tw为平均等待一个可插入间隙的时间,由式(4)计算:
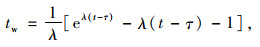
|
(4) |
式中, t为车辆临界间隙,一般取值为4.0 s;λ为单位时间的平均到达率,为直行交通量;τ为车头时距的最小值,一般取值为1.2 s。
(3) 判断可插入间隙时行驶的距离L3
L3为判断可插入间隙是否可以安全插入时纵向行驶距离,由式(5)计算:
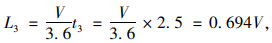
|
(5) |
式中V为判断可插入间隙过程中车辆的运行速度。
(4) 车辆变换一次车道时行驶的距离L4
研究表明,车辆的横移速度为1 m/s,我国车道宽度3.75 m,根据“基于驾驶员视点位置的多车道高速公路最小圆曲线半径研究”,换道横移距离取3.05 m,横移时间t4取值为3.05 s。车辆横移时行驶的距离为L4,由式(6)计算。
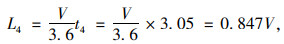
|
(6) |
式中V为变换车道过程中车辆的运行速度。
(5) 车辆换道距离L
综合上述分析,得到车辆完成车道变换所需的距离,由式(7)计算:
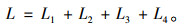
|
(7) |
根据上述换道计算公式计算,正常车辆换道所需要的距离要远大于停车视距,要在停车视距范围内完成换道,其前提条件必须是当驾驶员发现前方有障碍物时能立即进入可插入状态,即换道距离L=L1+L4,同时可考虑障碍物占车道位置情况,本研究紧急制动停车视距是以占半个车道(视点位置)为准进行计算,则L=0.771V。按设计速度为120,100,80,60 km/h计算变换车道所需距离见表 3。
| 设计速度/(km·h -1) | 120 | 100 | 80 | 60 |
| 占半个车道L=0.771 V/m | 92.52 | 77.1 | 61.68 | 46.26 |
| 停车视距规范值/m | 210 | 160 | 110 | 75 |
| 紧急制动停车视距/m | 175 | 130 | 90 | 60 |
从表 3可知,如果障碍物占半个车道(视点位置),在发现障碍物时能立即进入变道情况下,换道长度均短于紧急制动停车视距,具有换道行为的可能性。
2.2.3 换道行为的可行性概率分析车辆在准备换道过程中,需要等待相邻车道的可插入间隙时间,可插入间隙时间计算公式如下:
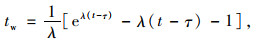
|
(8) |
式中, tw为平均等待一个可插入间隙的时间,由式(4)计算;e为自然常数;t为车辆临界间隙,一般取值为4.0 s;λ为单位时间的平均到达率,为直行交通量;τ为车头时距的最小值,一般取值为1.2 s。
根据可插入间隙时间计算结果,立即进入换道行为的可行性概率,见表 4。不同的设计速度,2级服务水平时换道概率超过65%,最高达79.4%;3级服务水平时换道概率在50%左右,最低为44.2%,最高达69%,显然换道概率较大。
| 设计速度/(km·h -1) | 120 | 100 | 80 | 60 | |
| 换道概率/% | 二级服务水平 | 65.0 | 66.5 | 68.8 | 79.4 |
| 三级服务水平 | 44.2 | 47.1 | 51.4 | 69.0 | |
2.3 基于汽车刹车试验的刹车距离分析
根据许斌等[20]汽车刹车试验得到汽车刹车距离(表 5)可知,在晴天路面干燥状态下,相同的速度在刹车试验结果刹车距离相差较小,车速80 km/h时刹车距离20.18~25.42 m,车速100 km/h时刹车距离26.10~33.43 m。在小雨和中到大雨时,不同的路面类型及不同车型刹车距离相差相对较大;小雨状态下,车速为80 km/h时刹车距离为23.50~29.50 m,相差3.35~4.79 m,车速100 km/h时刹车距离为30.70~37.53 m,相差3.85~4.72 m;在中到大雨状态下,车速为80 km/h时刹车距离25.15~34.03 m,相差4.6~6.88 m,车速100 km/h时刹车距离为34.20~44.11 m,相差6.58~7.19 m。
| 车辆类型 | 车速/ (km· h -1) | 路面类型 | 汽车试验刹车距离/m | 基于减速度的刹车距离计算值/m | |||
| 晴天 | 小雨 | 中到大雨 | |||||
| 大众迈腾 | 80 | PAC路面 | 20.18 | 23.50 | 25.15 | 紧急制动减速度a= 4.51 m/s 2 | 54.75 |
| SMA路面 | 24.30 | 26.85 | 29.75 | ||||
| 100 | PAC路面 | 26.10 | 30.70 | 34.62 | 85.54 | ||
| SMA路面 | 30.23 | 34.55 | 41.20 | ||||
| 别克GL8 | 80 | PAC路面 | 21.59 | 24.71 | 27.15 | 紧急制动减速度a= 4.51 m/s 2 | 54.75 |
| SMA路面 | 25.42 | 29.50 | 34.03 | ||||
| 100 | PAC路面 | 27.33 | 32.81 | 36.92 | 85.54 | ||
| SMA路面 | 33.43 | 37.53 | 44.11 | ||||
该刹车试验是基于两种不同路面结构的试验,路面结构类型不同,试验结果有差别,但相差不大,所以可作为停车视距计算取值时的参考依据。本研究推荐的紧急制动停车视距及理想值,该汽车刹车试验的刹车距离相比较,仍然较小,而且设计速度越高,相差值越大,安全风险越小。
2.4 基于路面横向力系数的高速公路平稳运行圆曲线最小半径分析 2.4.1 横向力系数计算公式圆曲线路段路面横向力系数计算公式如下:
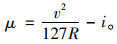
|
(9) |
式中,v为运行速度;R为圆曲线半径;i为超高横坡值;μ为横向力系数。
横向力系数是反应车辆圆曲线上行驶的力学指标,与道路平面圆曲线半径成反比,与运行速度成正比。当将路面与轮胎之间的摩阻系数作为横向力系数时,即可分析计算速度与圆曲线半径之间的关系;当道路圆曲线半径和超高确定,即可分析运行车速与其横向力系数的关系。
2.4.2 基于横向力系数的圆曲线安全性、舒适性判别标准根据现行《路线规范》第7.3.2条文说明:从人的承受能力与舒适感考虑,当μ<0.10时,转弯不感到有曲线的存在,很平稳;当μ=0.15时,转弯感到有曲线的存在,但尚平稳;当μ=0.20时,已感到有曲线的存在,并感到不平稳;当μ=0.35时,感到有曲线的存在,并感到不稳定;当μ>0.40时,转弯非常不稳定,有倾覆的危险。
2.4.3 基于横向力系数安全性判别标准的圆曲线最小半径我国现行《路线规范》对圆曲线最小半径取值计算时,一般值和极限值对应的横向力系数非常小,见表 6,极限值对应的μ=0.10~0.15。不同的横向力系数对应的圆曲线最小半径计算结果如表 7所示。当μ=0.10时,对应的圆曲线最小半径均小于规范规定的一般值;当μ=0.15时,对应的圆曲线最小半径均小于规范规定的极限值。根据《公路限速标志设计规范》(JTG/T 3381-02—2020)条文说明第5.4.2条:“随着车辆性能大幅提升,μ值的冗余性非常充足”,“在圆曲线上的安全稳定性评价,以μ值不大于0.15为限制值较为合适”。因此,根据路面横向力系数计算圆曲线最小半径进行安全性分析,充分表明满足紧急制动停车视距要求的平曲线交通安全风险非常小。
| 设计速度/(km·h -1) | 120 | 100 | 80 | 60 | |
| 《路线规范》规定值 | 横向力系数μ值(极限值) | 0.10 | 0.12 | 0.13 | 0.15 |
| 圆曲线半径一般值(i=7%)/m | 1 000 | 700 | 400 | 200 | |
| 圆曲线半径极限值(i=8%)/m | 650 | 400 | 250 | 125 | |
| 圆曲线最小半径计算值/m | i=-0.15%,μ=0.035 | 5 669 | 3 937 | 2 520 | 1 517 |
| i=7%,μ=0.05~0.06 | 907 | 630 | 403 | 226 | |
| i=8%,μ=0.10 | 630 | 437 | 280 | 157 | |
| i=8%,μ=0.15 | 493 | 342 | 219 | 123 | |
| i=8%,μ=0.20 | 404 | 281 | 180 | 101 | |
| i=8%,μ=0.35 | 264 | 183 | 117 | 66 | |
3 结论
研究主要从高速公路内侧车道被占概率、停车视距不足时可能碰撞速度与风险,以及换道行为的可能性与换道概率等多角度进行了研究。主要结论如下:
(1) 根据调查,高速公路车道内侧车道被占有3种情况,但事故都是随机偶发事件,并不完全在圆曲线半径最小或较小的路段,对某一圆曲线路段发生概率非常小。而且,根据紧急制动停车视距与规范值比较,即使在紧急制动停车视距范围未能将车辆停止,经计算不同的设计速度可能的碰撞速度均低于20 km/h,对车内的人员伤害非常小,对车辆损坏严重程度较低,即使出现碰撞行人事故,安全风险较低,可能造成的直接经济损失小,建议山区高速公路采用紧急制动停车视距作为内侧车道圆曲线最小半径的控制指标。
(2) 正常车辆换道所需要的距离要远大于停车视距,要在停车视距范围内完成换道,其前提条件必须是当驾驶员发现前方有障碍物时能立即进入可插入状态,以此计算结果障碍物占半个车道(视点位置)且在发现障碍物时能立即进入变道行为下,不同设计速度换道长度均短于紧急制动停车视距,具有换道行为的可能性。
(3) 根据可插入间隙时间计算结果,不同的设计速度,2级服务水平时换道概率超过65%,最高达79.4%;3级服务水平时换道概率在50%左右,最低为44.2%,最高达69%,显然换道概率比较高,特别是交通量较小的高速公路。
(4) 根据许斌等[20]汽车刹车试验得到的汽车刹车距离,与基于紧急制动减速度a=4.51 m/s2时计算的设计速度80 km/h刹车距离为54.75 m,设计速度100 km/h时刹车距离为85.54 m相比较,紧急制动停车视距安全冗余度富余较大。
(5) 根据横向力系数对应的圆曲线最小半径计算结果,当μ=0.10时,对应的圆曲线最小半径均小于规范规定的一般值;当μ=0.15时,对应的圆曲线最小半径均小于规范规定的极限值,相比较满足紧急制动停车视距要求的平曲线交通安全风险非常小。
| [1] |
JTG D20-2017, 公路路线设计规范[S]. JTG D20-2017, Design Specifications for Highway Alignment[S]. |
| [2] |
杨帆, 白浩晨, 贺亚龙, 等. 高速公路中央分隔带停车视距评价方法研究[J]. 公路交通科技, 2018, 35(6): 45-51. YANG Fan, BAI Hao-chen, HE Ya-long, et al. Study on Method of Evaluating Stopping Sight Distance of Median Strip in Expressway[J]. Journal of Highway and Transportation Research and Development, 2018, 35(6): 45-51. |
| [3] |
张航, 张肖磊, 吕能超. 高速公路停车视距可靠性设计[J]. 公路交通科技, 2019, 36(4): 44-49, 87. ZHANG Hang, ZHANG Xiao-lei, LÜ Neng-chao. Reliability Design for Stopping Sight Distance of Expressway[J]. Journal of Highway and Transportation Research and Development, 2019, 36(4): 44-49, 87. |
| [4] |
吴斌, 朱西产, 沈剑平. 基于自然驾驶数据的驾驶员紧急转向变道模型[J]. 同济大学学报: 自然科学版, 2019, 47(11): 1618-1629. WU Bin, ZHU Xi-chan, SHEN Jian-ping. Analysis of Driver Emergency Steering Lane Changing Behavior Model Based on Naturalistic Driving Data[J]. Journal of Tongji University: Natural Science Edition, 2019, 47(11): 1618-1629. |
| [5] |
范爽. 高速公路平面线形指标及其组合安全性研究[D]. 西安: 长安大学, 2019. FAN Shuang. Study on Safety of Expressway Horizontal Alignment Index and Its Combination[D]. Xi'an: Chang'an University, 2019. |
| [6] |
路宁. 道路线形与交通事故关系分析[J]. 交通标准化, 2012(4): 120-122. LU Ning. Relationship between Road Alignment and Traffic Accident[J]. Traffic Standardization, 2012(4): 120-122. |
| [7] |
范李, 李刚炎, 陈冉, 等. 基于横向力系数的汽车急转防侧翻车速计算模型与仿真[J]. 农业工程学报, 2016, 32(3): 41-47. FANG Li, LI GANG-yan, CHEN Ran, et al. Speed Calculation Model and Simulation of Rollover Prevention in Condition of Extreme Turn Based on Lateral Force Coefficient[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(3): 41-47. |
| [8] |
程国柱, 程瑞, 徐亮. 基于路侧事故判别的公路平曲线车速限制研究[J]. 交通运输系统工程与信息, 2020, 20(1): 222-227, 240. CHENG Guo-zhu, CHENG Rui, XU Liang. Speed Limit in Curving Sections of Highway Based on Roadside Accidents Discriminant Analysis[J]. Journal of Transportation Systems Engineering and Information Technology, 2020, 20(1): 222-227, 240. |
| [9] |
郭应时, 付锐, 袁伟, 等. 山区公路事故率与平面线形的关系[J]. 交通运输工程学报, 2012, 12(1): 63-71. GUO Ying-shi, FU Rui, YUAN Wei, et al. Relation between Accident Rate and Horizontal Alignment for Mountain Highway[J]. Journal of Traffic and Transportation Engineering, 2012, 12(1): 63-71. |
| [10] |
王浩, 孟祥海, 关志强. 山区高速公路几何线形与事故率关系研究[J]. 公路工程, 2011, 36(4): 89-92. WANG Hao, MENG Xiang-hai, GUAN Zhi-qiang. Research on Relationship between Traffic Accident Rate and Geometric Alignment for Mountainous Freeway[J]. Highway Engineering, 2011, 36(4): 89-92. |
| [11] |
陈雨人, 付云天, 汪凡. 基于支持向量回归的视距计算模型建立和应用[J]. 中国公路学报, 2018, 31(4): 105-113. CHEN Yu-ren, FU Yun-tian, WANG Fan. Establishment and Application of Sight Distance Computing Model Based on Support Vector Regression[J]. China Journal of Highway and Transport, 2018, 31(4): 105-113. |
| [12] |
文浩雄, 钟琨, 刘卓, 等. 高速公路中央分隔带横净距问题及对策[J]. 公路工程, 2013, 38(6): 20-23. WEN Hao-xiong, ZHONG Kun, LIU Zhuo, et al. Lateral Clear Distance Problems and Solutions of Median Divider in Highway[J]. Highway Engineering, 2013, 38(6): 20-23. |
| [13] |
陈瑾. 高速公路互通式立交出口和入口设置相关技术指标研究[D]. 西安: 长安大学, 2016. CHEN Jin. Study on Relative Setting Technical Indicator of Expressway Interchange Entrance and Exit[D]. Xi'an: Chang'an University, 2016. |
| [14] |
尹和山. 高速公路互通式立交路线视距指标研究[J]. 工程与建设, 2017, 31(1): 81-82, 100. YIN He-shan. Research on Sight Distance Index of Highway Interchange Route[J]. Engineering and Construction, 2017, 31(1): 81-82, 100. |
| [15] |
沈强儒, 赵一飞, 杨少伟, 等. 基于识别视距的特殊互通式立交出口区域主线线形指标分析[J]. 安全与环境学报, 2015, 15(3): 89-92. SHEN Qiang-ru, ZHAO Yi-fei, YANG Shao-wei, et al. Analyzing the Mainline Alignment Index of the Special Interchange Exit Based on Recognizing the Distance[J]. Journal of Safety and Environment, 2015, 15(3): 89-92. |
| [16] |
张玥. 基于横向力系数的公路平曲线半径及超高取值方法研究[J]. 中外公路, 2015, 35(2): 5-9. ZHANG Yue. Research on Value Method of Highway Horizontal Curve Radius and Superelevation Based on Transverse Force Coefficient[J]. Journal of China & Foreign Highway, 2015, 35(2): 5-9. |
| [17] |
涂文靖. 曲线超高计算的优化方法及应用[J]. 铁道建筑, 2019, 59(2): 120-125. TU Wen-jing. Optimization Method and Application of Curve Superelevation Calculation[J]. Railway Engineering, 2019, 59(2): 120-125. |
| [18] |
潘兵宏, 周海宇, 刘斌, 等. 基于CarSim仿真的超高过渡起点位置对比研究[J]. 铁道科学与工程学报, 2018, 15(3): 637-644. PAN Bing-hong, ZHOU Hai-yu, LIU Bin, et al. Comparative Study of Superelevation Starting Position Based on Car Simsimulation Model[J]. Journal of Railway Science and Engineering, 2018, 15(3): 637-644. |
| [19] |
FAMBRO D B, FITZPATRICK K, KOPPA R J. Determination of Stopping Sight Distances, NCHRP Report 400[R]. Washington, D.C. : Transportation Research Board, 1997.
|
| [20] |
许斌, 杨志浩, 石鑫, 等. 基于汽车刹车试验的排水沥青路面抗滑性能分析[J]. 公路, 2019(4): 34-41. XU Bin, YANG Zhi-hao, SHI Xin, et al. Skid Resistance Analysis of Porous Asphalt Pavement Based on Automobile Brake Test[J]. Highway, 2019(4): 34-41. |
 2021, Vol. 38
2021, Vol. 38
