扩展功能
文章信息
- 林宣财, 王科, 李涛, 李星
- LIN Xuan-cai, WANG Ke, LI Tao, LI Xing
- 高速公路内侧车道小客车停车视距合理取值的研究
- Study on Stopping Sight Distance of Passenger Cars in Inner Lane of Expressway
- 公路交通科技, 2021, 38(9): 68-77
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(9): 68-77
- 10.3969/j.issn.1002-0268.2021.09.009
-
文章历史
- 收稿日期: 2021-04-25
山区高速公路地形条件复杂,为了更好地控制工程造价,早期已建高速公路较多项目平面圆曲线最小半径采用一般值或接近一般值,如果根据《公路路线设计规范》(JTG D20—2017)(以下简称《路线规范》[1])规定的停车视距对应的圆曲线最小半径进行核查,这些指标都不符合要求。我国规范规定的停车视距值与日本规定值[2-3]相同,比美国规定[4]小,但这些规定都是30多年前的指标,且多车道高速公路内外侧车道停车视距采用统一标准是否合理有待商榷。
国内多数研究者们对不同车道的停车视距进行验算,并针对不满足停车视距的路段提出安全保障措施。陈雨人等[5]基于支持向量机的视距计算模型,并将该模型应用于实际隧道的视距检验。文浩雄等[6]对高速公路中央分隔带弯道路段横净距进行验算,发现不能满足停车视距要求,针对性地提出增大中央分隔带横净距、设置限速标志及减速标线等措施。张玥[7]通过分析横向力系数取值,提出对规范中最小半径值调整的建议, 并提出新的横向力系数与平曲线半径拟合公式,得到不同纵坡下的安全运行临界半径。梁友哲[8]计算了曲线外侧超车道满足视距要求的最小平曲线半径,针对中分带曲线外侧超车视距不足的问题,提出了保障停车视距的措施。邢福东[9]通过分析安全及舒适行驶对半径的需求,提出了不同设计速度下的圆曲线最小半径, 并通过分析停车视距对半径的需求,提出一般路段与隧道路段圆曲线最小半径值。赵永平[10]、王晓楠[11]以及孟云龙[12]等人认为停车视距计算模型的驾驶员视点位置在距离车道左侧边缘线1.2 m处; 驾驶员行驶在隧道路段时,视线容易受隧道侧壁的遮挡,影响行车安全。长安大学周海宇[13]通过数据调查得到, 小客车在第1车道行驶时,视点位置距离左侧行车道边缘线1.6 m,在第2车道行驶时距离右侧车道左边线0.8 m处。长安大学唐力焦[14]在此基础上界定隧道内货车的视点位置,货车在第1车道行驶时,视点位置距离左侧行车道边缘线1.4 m;在第2车道行驶时距离右侧车道左边线1.0 m处。长安大学杨帆[15]等研究认为通过提高视点目标物高度至0.8 m时,规范规定的停车视距对应的圆曲线最小半径值小于规范中圆曲线最小半径,可避免中央分隔带护栏进行特殊设计或增加高速公路占地措施。武汉理工大学张航[16]提出满足高速公路对应安全等级的可靠性要求的停车视距。
国外研究者们对针对曲线路段停车视距计算模型的不足提出改进的建议值。Sarhan和Hassan[17]使用有限元技术软件分析了3维(3D)组合路线中具有路边或中间障碍的水平曲线上的可用停车视距。Xia等人[18]建立了曲线路段停车视距计算模型,将计算值现行规范推荐的停车视距值进行比较,并给出了平曲线停车视距的一般值和极限值。Papadimitriou等人[19]在对若干几何参数的解释性建模方法的基础上,根据停车视距不足的概率和障碍物的高度来修正停车视距值。Bassani等人[20]针对在视距不足时驾驶员通过水平弯道的驾驶行为进行试验研究,发现驾驶员会通过减速或增大横净距来保证行车安全。
综上所述,所谓停车视距不足,多数研究仅仅是按规范规定的停车视距所需要的圆曲线最小半径与实际采用的圆曲线半径进行比较,或与规范中圆曲线最小半径规定值比较,较少从汽车整体性能和高速公路路面摩阻力系数的提高,停车视距富余度越来越大方面考虑,更没有从多车道高速公路不同车道是否应该采用不同的标准考虑。所以有必要分析研究不同车道停车视距及计算参数的合理取值问题,也只有对高速公路内侧车道停车视距规定值或圆曲线最小半径规定值进行修订,才能使停车视距所需要的最小圆曲线半径与规范中圆曲线最小半径规定值相一致。高速公路内侧车道停车视距取值合理性问题,如果没有明确的研究结论,必然造成山区高速公路不得不采用高指标,使工程造价居高不下,本研究基于国内外对停车视距计算参数的大量研究数据,对高速公路内侧车道停车视距及计算参数的合理取值展开较为系统的研究,提出高速公路内侧车道应采用紧急制动停车视距的建议。
1 停车视距对圆曲线最小半径指标运用的影响 1.1 高速公路内侧车道停车视距所需要的圆曲线最小半径我国高速公路中央带均设置防眩设施,小客车在左偏曲线内侧车道行驶时,因受中央带防眩设施的遮挡,存在停车视距不满足规范规定值的要求。根据2009年版《公路路线设计细则》(总校稿)中“高速公路内侧车道几何视距与对应的圆曲线半径”对照表,详见表 1,其中表中内侧车道中心线距护栏以2.5 m为计算基准。停车视距所需要的圆曲线半径较规范中规定的圆曲线最小半径大得较多;设计速度越高,所需要的圆曲线最小半径值越大,设计速度为120 km/h时圆曲线最小半径较一般值增大一倍还多,即由1 000 m变为2 204 m;设计速度为80 km/h时提高了50%,圆曲线最小半径由400 m变为604 m,与极限值相比较,相差更大。
| 设计速度/(km·h-1) | 120 | 100 | 80 | |
| 圆曲线半径-几何视距/m | 一般值 | 1 000~142 | 700~119 | 400~90 |
| 极限值 | 650~114 | 400~90 | 250~71 | |
| 圆曲线半径-停车视距/m | 2 204~210 | 1 279~160 | 604~110 | |
1.2 停车视距对圆曲线最小半径指标运用的影响
圆曲线设计指标如果按停车视距所需要的圆曲线最小半径掌握,显然相当于技术标准中的圆曲线半径规定值提高了,而且提高幅度较大。从2010年之后,受停车视距规定值的影响,山区高速公路较多项目不得不采用高指标,不仅增加桥隧工程规模,造成工程造价大幅度提高,而且有些项目出现大填大挖,造成对自然环境的较大影响,高边坡或深挖路段还可能带来工程安全性问题。
我国圆曲线最小半径极限值与美国、日本等多数国家规定基本一致,美国没有一般值的规定,见表 2。如果以规范中的停车视距对应圆曲线半径值作为控制指标,意味着我国技术标准较美国、日本等国家大得多;如果按美国规定的停车视距反算圆曲线最小半径,所需要的半径值更大,与其圆曲线最小半径规定值相差更大,显然美国圆曲线最小指标不是按照停车视距所需要的最小圆曲线半径确定。根据了解,欧美高速公路较多项目中央带没有设置防眩设施,所以不存在高速公路内侧车道停车视距不足的问题。
| 设计速度/(km·h -1) | 120 | 100 | 80 | |
| 中国 | 圆曲线最小半径一般值/m | 1 000 | 700 | 400 |
| 圆曲线最小半径最小值/m | 650 | 400 | 250 | |
| 停车视距/m | 210 | 160 | 110 | |
| 美国 | 圆曲线最小半径/m | 665 | 395 | 230 |
| 停车视距/m | 250 | 185 | 130 |
1.3 新建高速公路采用辅助措施解决停车视距不足问题的可行性分析
(1) 对中央分隔带进行特殊设计。为了满足停车视距所对应的圆曲线最小半径值要求,当地形条件受限制,平面线形调整困难时,采取辅助措施满足视距要求,如改变中央分隔带型式,把波形护栏改为新泽西护栏,或者将波形护栏向中央分隔带中心移动等。当调整后内侧车道中心距新泽西护栏的距离为3.0 m时,对应设计速度120,100,80 km/h所要求的最小平曲线半径分别为:1 836,1 065,503 m,即对中央分隔带进行特殊设计,最小圆曲线半径也大于现行《路线规范》规定的一般最小值,难以解决根本问题。
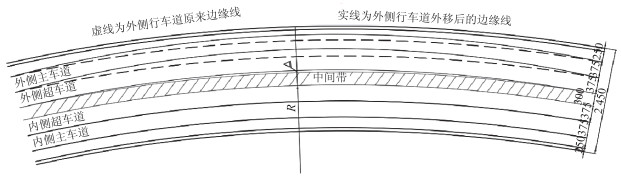
(2) 改变路面标线位置的措施。近几年,一些设计者为了解决规范中不一致的规定问题,提出改变标线位置满足视距要求的设计方案,如设计速度80 km/h的高速公路,平曲线半径小于604 m时,保持中央带防撞护栏及防眩方式不变,将靠中央分隔带的内侧行车道标线外移以增大横净距。由于行车道右侧有2.5 m宽的硬路肩,对圆曲线半径400 m<R<604 m的路段,通过将行车道边缘线及分界线适当外移,以满足横净距要求,见图 1。该设计方案存在安全性问题:①变更后的线形(细实线)已经不是圆曲线,不是圆曲线就不符合规范相关规定要求;②硬路肩宽度大部分被行车道占用,硬路肩宽度就不满足规范要求。
|
| 图 1 基于高速公路内侧车道停车视距的路面标线设计图(单位: cm) Fig. 1 Design drawing of pavement marking based on parking sight distance of inner lane of expressway(unit: cm) |
| |
(3) 考虑我国土地资源紧缺,如果全路段通过加宽中间分隔带宽度解决地形条件受限制路段的停车视距问题,显然不合理,也不经济。
2 既有高速公路停车视距不足路段交通安全性调查2009年版《公路路线设计细则》(总校稿)出来之前,由于设计、审查均没有核查“高速公路内侧车道几何视距与对应所需要的圆曲线半径”之间的关系,所以,山区高速公路圆曲线最小半径都是按规范中规定的圆曲线最小半径一般值控制,即较多项目较多路段圆曲线半径采用接近或等于最小半径一般值。近几年,我国已通车的高速公路限制速度进行了调整,从基于设计速度的高速公路限速调整结果来看,不但没有降低限速,基本上都是“提速”。有些省设计速度不论是100 km/h,还是80 km/h,除了隧道和连续长大纵坡路段外,小客车一律将限速调整为120 km/h;有些省设计速度为80 km/h时小客车限速调整为100 km/h,设计速度为100 km/h时限速调整为120 km/h。提速的高速公路项目中存在较多路段平面指标采用设计速度所对应的最小半径一般值或接近一般值,中间带宽度没有进行特殊设计, 显然,既有高速公路有较多路段停车视距不满足限速调整的要求。但是,根据初步调查,这些路段没有发现交通事故率明显高于其他路段,说明高速公路内侧车道停车视距及计算参数的取值有待商榷。
3 高速公路内侧车道采用紧急制动停车视距的研究 3.1 停车视距概述(1) 停车视距基本概念
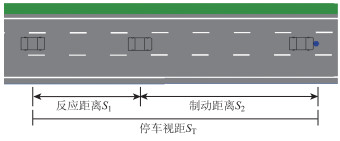
停车视距由驾驶员发现障碍物到采取制动措施期间内(反应时间)的行驶距离和制动过程行驶的减速距离组成的。停车视距计算图式如图 2所示,停车视距的取值主要取决于驾驶员反应时间、车辆的行驶速度及减速度或路面摩阻力系数等参数。
|
| 图 2 停车视距计算图式 Fig. 2 Calculation pattern of parking sight distance |
| |
(2) 停车视距计算方法
① 基于纵向摩阻力的停车视距传统计算方法
基于路面纵向摩阻力系数的停车视距理论计算模型如式(1)[1]所示。
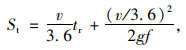
|
(1) |
式中, St为停车视距;v为行驶速度:规范规定设计速度120~80 km/h时为其85%,设计速度60~40 km/h时为其90%,设计速度30~20 km/h时为其100%;tr为驾驶员反应时间;g为重力加速度,取9.8 m/s2,计算小客车停车视距时不考虑纵坡的影响;f为纵向摩阻系数,依车速及路面状况而定,路面为潮湿状态。
由式(1)可知,停车视距的取值主要取决于驾驶员反应时间、车辆的行驶速度及路面纵向摩阻力系数等参数。
② 基于汽车制动减速度的停车视距计算方法
基于汽车制动减速度的停车视距理论计算模型如式(2)[4]所示。
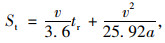
|
(2) |
式中, St为停车视距;v为设计速度或行驶速度;tr为驾驶员反应时间;a为减速度。
3.2 紧急制动停车视距计算参数取值分析 3.2.1 反应时间取值分析(1) 国内相关研究
我国研究人员对反应时间进行了研究,认为反应时间与设计速度、设计控制条件等有关,陈胜营等《公路设计指南》[21]中反应时间设计值如表 3所示。
| 设计车速/(km·h -1) | 110 | 100 | 90 | 80 | 70 | 60 | 50 |
| 理想值/s | 2.5 | 2.5 | 2.5 | 2.4 | 2.3 | 2.2 | 2.1 |
| 最小值/s | 2.0 | 2.0 | 2.0 | 1.9 | 1.8 | 1.7 | 1.6 |
| 极限最小值/s | — | — | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 |
国内相关研究基本上认为反应时间的变化区间是1.5~2.5 s。表中理想反应时间应用于高速公路主车道上,并应尽可能用于其他等级的公路上;极限最短反应时间只能用于驾驶员可望有相当警惕性的区域。根据调查研究,在高速公路圆曲线半径较小路段内侧车道上高速行驶时,驾驶员处于相当警惕性的状态,设计速度为80 km/h时紧急制动反应时间可取1.5 s。
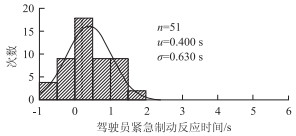
同济大学吴斌等[22]基于中国自然驾驶数据,建立了紧急工况下制动避撞的驾驶员模型,图 3为51例前车慢行或静止的直行追尾危险工况紧急制动反应时间分布图,研究表明:驾驶员的紧急制动反应时间与驾驶工况的紧急长度相关,以碰撞时刻倒数的临界值0.2 s-1作为危险触发阈值,驾驶员的紧急制动反应时间分布均值为0.5 s,标准差为0.63 s,且最大值为2.0 s,一般不超过1.5 s,该研究成果可作为紧急制动反应时间取值的参考依据。图 3中紧急制动反应时间为负的工况表明驾驶员在危险触发阈值前就采取了制动措施。
|
| 图 3 追尾危险场景驾驶员紧急制动反应时间分布及拟合 Fig. 3 Distribution and fitting result of driver's emergency braking response time in scene of rear-end collision |
| |
(2) 国外的研究
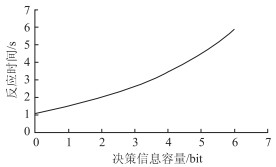
在国外相关研究成果中,以决策的复杂程度,即决策的信息容量来确定驾驶员的反应时间。根据驾驶员对于道路条件是否有了预先的估计,有预期反应时间与决策的信息容量之间的关系见图 4。回归得到式(3)计算。
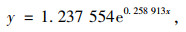
|
(3) |
式中,y为反应时间。x为信息容量,1个bit的信息容量相当于从两个相同概率的反应中选择一个所需的信息处理量,而从3个等概率的选项中决策的信息容量,等于1.5 bit;以此类推,得到信息容量的量化水平。
|
| 图 4 有预期反应时间的模型示意图 Fig. 4 Schematic diagram of model with expected reaction time |
| |
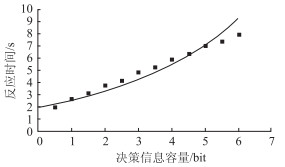
无预期的反应时间,进行同样的分析,得到相关散点图与趋势线,见图 5。回归模型为:
|
| 图 5 无预期反应时间的模型示意图 Fig. 5 Schematic diagram of model without expected reaction time |
| |
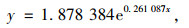
|
(4) |
式中各符号的意义同前。
根据上述模型可计算不同信息容量情况下有、无预期的反应时间见表 4。
| 信息容量/bit | 1.0 | 1.5 | 2.0 |
| 有预期反应时间/s | 1.603 | 1.825 | 2.077 |
| 无预期反应时间/s | 2.439 | 2.779 | 3.166 |
如果选择信息容量1 bit且为无预期反应时间是2.439 s;如果选择信息容量1 bit且为有预期反应时间是1.603 s。与国内相关研究相比较,所谓无预期即为理想行驶状态,有预期就是相当警惕性状态。在山区高速公路圆曲线半径较小路段的内侧车道高速行驶时,符合驾驶员处于相当警惕性的区域,紧急制动反应时间可取1.603 s,理想状态紧急制动反应时间可取2.439 s。
国外除欧洲七国反应时间取2 s外,其余国家驾驶员反应时间大多取2.5 s。根据AASHTO规定,驾驶人识别判断时间1.5 s,作用时间为1.0 s,反应时间取2.5 s。这些反应时间基本上为理想状态的取值。
(3)紧急制动反应时间取值
根据国内相关研究,驾驶员可望有相当警惕性的区域,紧急制动反应时间可取1.5 s;国外相关研究认为如果选择信息容量1 bit且为有预期时反应时间为1.603 s。从国内外的研究成果可以看出,反应时间差别不大。结合我国既有高速公路限速调整(提速)后交通运行平稳考虑,紧急制动反应时间可取1.5 s;理想状态反应时间取2.5 s是国内外研究人员所认可的,即舒适制动反应时间。
3.2.2 路面摩阻力系数根据既有研究成果,路面摩阻力系数一般大于0.5,我国规范对高速公路停车视距计算时摩阻力系数取值范围为0.29~0.31,对低等级公路停车视距计算摩阻力系数为0.38和0.44,见表 5,路面条件较高速公路差,但摩阻力系数取值反而高,说明高速公路摩阻力系数取值偏于安全。国外较多国家摩阻力系数取值高于我国,详见表 6。
| 设计速度/(km·h -1) | 120 | 100 | 80 | 60 | 40 | 30 | 20 |
| 行驶速度/(km·h -1) | 102 | 85 | 68 | 54 | 36 | 30 | 20 |
| 摩阻力系数 | 0.29 | 0.30 | 0.31 | 0.33 | 0.38 | 0.44 | 0.44 |
| 美国(AASHTO,2011 6th Edition) | 德国(RAA,2008) | 澳大利亚(Australia,2009) | |
| 0.35 | 0.38 | 0.26 | 舒适制动 |
| 0.36 | 舒适紧急制动 | ||
| 0.46 | 紧急制动 | ||
我国《路线规范》采用潮湿状态下的道路摩阻系数进行计算,取值明显偏低,与现有路面、车辆性能等匹配度较低。随着车辆性能的提升以及道路条件的发展,原先推荐的道路阻力系数已经不再能准确地反映停车紧急制动的实际情况,综合国内外摩阻力系数取值,并按设计速度计算时,我国高速公路紧急制动摩阻力系数可取0.46。
3.2.3 汽车紧急制动减速度美国绿皮书从2001版开始,运用汽车制动减速度来代替道路摩阻系数计算停车视距,德国、欧盟、澳大利亚也采用制动减速度计算。AASHTO对45名驾驶员进行3 000次制动试验,指出大多数驾驶员在意外发现前方道路有障碍物需停车时所采用的减速度>4.5 m/s2,约90%的驾驶员采用的减速度>3.4 m/s2。调查研究表明大多数的车辆制动系统和多数道路的轮胎与路面摩擦水平都能提供至少3.4 m/s2的减速率。德国对制动减速度的取值为3.7 m/s2,欧盟法律条例规定的制动减速度为5 m/s2,各国平均制动减速度如表 7所示。
| 美国(AASHTO,2011 6th Edition) | 德国(RAA,2008) | 欧盟71/320/ EWG | 澳大利亚(Australia,2009) | |
| 3.40 | 3.70 | 5 | 舒适制动 | 2.55 |
| 舒适紧急制动 | 3.53 | |||
| 紧急制动 | 4.51 | |||
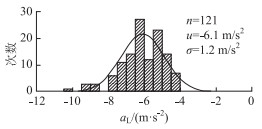
同济大学吴斌等[22]基于中国自然驾驶数据,在紧急制动工况下未发生碰撞,驾驶员的制动过程在其操控能力范围内,大部分最大制动减速度都未达到车辆或路面的极限情况。图 6是121例追尾危险工况下紧急制动避撞最大制动减速度正态分布及拟合图,正态分布均值u=-6.1 m/s2,标准差1.2 m/s2。
|
| 图 6 最大制动减速度分布及拟合 Fig. 6 Distribution and fitting result of maximum braking decelerations |
| |
小客车制动减速度的取值,对停车视距的计算结果影响较大。根据以上相关研究可知,在紧急情况下,小客车的最大减速度一般能达到7.5 m/s2,作为高速公路紧急制动的设计指标,紧急制动减速度取4.51 m/s2,约为最大减速度的60%,不仅留有富余,减速度也不是特别大,给后车保留一定的制动距离,为避免追尾留有空间。基于制动减速度的停车视距计算模型,紧急制动减速度采用4.51 m/s2。
3.3 紧急制动停车视距基本概念车辆在高速公路行驶过程中,为了避免追尾或保证安全换道,驾驶员经常需要制动减速,但一般不需要紧急停车;如果发现前方障碍物是静止的物体时需要紧急停车或换道,最短停车距离取决于驾驶员紧急制动反应时间和最大制动减速度。紧急制动所需要的反应时间与驾驶员年龄、性别、驾驶经验有一定关系,但与驾驶员在行驶时所保持的警惕性程度关系最大。从保证舒适制动驾驶状态考虑,道路通行条件应满足规范规定的停车视距要求,规范规定的停车视距是理想的停车视距。
根据紧急制动反应时间的取值研究,所谓紧急制动停车视距是指:驾驶员处于有预期的或高警惕性驾驶状态时发现前方障碍物所需要的反应时间较无预期的正常驾驶状态短,相应的停车视距计算值较规范值小。
研究表明:当车辆在高速公路内侧车道上以限制速度为基准高速行驶时,驾驶员对道路通行条件有预期,特别是驶入较小的圆曲线路段时,驾驶员保持高警惕性驾驶状态;根据国内外对紧急制动反应时间的研究数据综合分析,紧急制动反应时间可取1.5 s,计算得到的停车视距称为“紧急制动停车视距”,适用于高速公路内侧车道小客车停车视距。在高速公路外侧车道或圆曲线半径较大的路段,多数驾驶员处于无预期的正常驾驶状态;多数国家(包括中国)对无预期的舒适性驾驶状态紧急制动反应时间均取2.5 s,计算得到的停车视距称为“舒适制动停车视距”,其值与规范规定值基本一致,适用于高速公路内侧车道除外的其他车道。
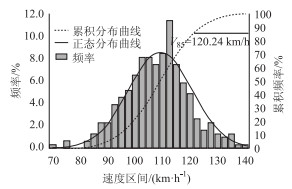
3.4 高速公路内侧车道采用紧急制动停车视距合理性分析根据高速公路实测运行速度分析,运行速度分布图中V85与高速公路限速基本一致,从图 7可知,设计速度或公路限速为120 km/h时,超过60%车辆行驶速度在110 km/h以下,仅有15%的驾驶员行驶速度达到或超过高速公路限速值,显然对行驶速度在110 km/h以上的车辆在较小的圆曲线路段上行驶时,驾驶员通常有相当警惕性。高速公路内侧车道作为超车道或快车道,是多车道高速公路限速最高的车道,车辆在内侧车道上以限制速度为基准高速驶入较小圆曲线半径路段时,特别是驶入左偏线形路段,由于内侧车道停车视距较短,行驶条件最为不利,驾驶员从对道路通行条件的预期考虑,必然处于高警惕性驾驶状态;同时考虑小半径圆曲线路段基本上里程都较短,不存在长时间高警惕性带来疲劳驾驶风险的问题;对行驶速度在110 km/h以下的车辆,舒适制动停车视距基本满足要求,所以,对多车道高速公路提出不同车道采用不同的停车视距标准,高速公路内侧车道采用紧急制动停车视距,高速公路其他车道采用舒适制动停车视距,即规范规定值。
|
| 图 7 高速公路内侧车道运行速度分布 Fig. 7 Speed distribution of driving speeds in inner lane of expressway |
| |
3.5 紧急制动停车视距计算值及推荐值
综上研究,基于路面摩阻力系数的停车视距计算方法,摩阻力系数宜取0.46;基于制动减速度计算方法,制动减速度宜取4.51 m/s2;舒适制动反应时间取2.5 s,紧急制动反应时间取1.5 s。小客车紧急制动停车视距和舒适制动停车视距计算值和推荐值如表 8所示。采用舒适制动反应时间计算的停车视距与我国规范规定值较为一致,计算模型及结果较规范规定值更合理。
| 设计速度/(km·h -1) | 120 | 100 | 80 | 60 | |
| 停车视距规范值/m | 210 | 160 | 110 | 75 | |
| 舒适制动停车视距(反应时间2.5 s)/m | 计算值 | 206.5 | 155.0 | 110.3 | 72.5 |
| 推荐值 | 205 | 155 | 110 | 75 | |
| 紧急制动停车视距(反应时间1.5 s)/m | 计算值 | 173.2 | 127.2 | 88.1 | 55.8 |
| 推荐值 | 175 | 130 | 90 | 60 | |
4 紧急制动停车视距对应的高速公路内侧车道圆曲线最小半径 4.1 基于停车视距的高速公路横净距及圆曲线最小半径计算公式
车辆在圆曲线行驶时,驾驶员的视线主要受道路侧向能提供的最大横净距和圆曲线半径影响,左转曲线和右转曲线道路能提供的横净距差异较大。根据几何关系,计算点满足视距要求圆曲线半径与横净距的关系的计算公式为[23]:
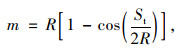
|
(5) |
式中,m为横净距;R为计算行车道中心曲率半径;St为停车视距。
由cos α=1-α2/2!+α4/4!-…+(-1)nα2n/2n!,对式(5)进行近似取代简化时n=2,得停车视距圆曲线半径计算简化公式为:
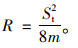
|
(6) |
紧急制动停车视距所需要的圆曲线最小半径计算值及推荐值见表 9(计算过程省略),从表中可知,当设计速度80 km/h时紧急制动停车视距所需要的圆曲线最小半径为390 m,较规范中圆曲线最小半径一般值小10 m。所以推荐内侧车道小客车采用紧急制动停车视距能较好地释义停车视距与规范中圆曲线最小半径规定值之间的关系,即当设计速度为80 km/h时,只要圆曲线半径大于规范中规定的圆曲线半径一般值,高速公路中间带不需要特殊设计。但如果设计速度为100 km/h时或120 km/h时,由于紧急制动停车视距所需要的圆曲线最小半径分别为815 m和1 460 m,分别较规范中圆曲线最小半径一般值700 m和1 000 m大115 m和460 m,在不满足内侧车道小客车紧急制动停车视距要求时,应进行特殊设计或采取限速等措施。
| 设计速度/ (km·h -1) | 停车视距/m | 圆曲线最小半径/m | |||
| 计算值 | 推荐值 | 规范值 | |||
| 120 | 规范值 | 210 | 2 100 | 2 100 | — |
| 舒适制动 | 205 | 2 001 | 2 000 | 1 000 | |
| 紧急制动 | 175 | 1 458 | 1 460 | 650 | |
| 100 | 规范值 | 160 | 1 231 | 1 230 | — |
| 舒适制动 | 155 | 1 155 | 1 155 | 700 | |
| 紧急制动 | 130 | 813 | 815 | 400 | |
| 80 | 规范值 | 110 | 582 | 580 | — |
| 舒适制动 | 110 | 582 | 580 | 400 | |
| 紧急制动 | 90 | 389 | 390 | 250 | |
5 结论
圆曲线最小半径如果按内侧车道停车视距所需要的圆曲线最小半径掌握,显然相当于技术标准中的圆曲线半径规定值提高了,而且提高幅度较大。根据研究,对中央分隔带进行特殊设计时,如果需要增加中间带宽度必然增加较大工程规模;如果采用改变路面标线位置的措施,又会出现行车道轨迹线不符合圆曲线设计要求。结合既有高速公路圆曲线不满足停车视距要求的路段交通运行平稳的现状,有必要研究高速公路不同车道停车视距计算参数的合理取值问题,也只有对高速公路内侧车道停车视距规定值或圆曲线最小半径规定值进行修订,才能使停车视距所需要的最小圆曲线半径与规范中圆曲线最小半径规定值相一致。本文主要研究结论如下:
(1) 根据国内外相关研究:对道路通行条件有无预期或驾驶员是否处于高警惕性驾驶状态,紧急制动反应时间不同。基于已有研究成果基础上,提出多车道高速公路内侧车道停车视距应采用不同的标准。研究表明:当车辆在高速公路内侧车道保持限制速度高速行驶时,驾驶员对道路通行条件是有预期的,特别是驶入较小的圆曲线路段时,驾驶员通常处于高警惕性驾驶状态,这时如果前方发现障碍物所做出紧急制动停车决策的反应时间要短于无预期的舒适性驾驶状态。
(2) 根据国内外大量研究数据综合分析,当驾驶员处于有预期的高警惕性驾驶状态时,紧急制动反应时间可取1.5 s,计算得到的停车视距称为“紧急制动停车视距”,适用于高速公路内侧车道小客车停车视距。在高速公路外侧车道或圆曲线半径较大的路段,多数驾驶员处于无预期的舒适性驾驶状态;多数国家(含中国)对无预期的舒适性驾驶状态紧急制动反应时间均取2.5 s,计算得到的停车视距称为“舒适制动停车视距”,其值与规范规定值基本一致,适用于高速公路内侧车道除外的其他车道。
(3) 紧急制动停车视距较规范规定值小,当设计速度为80 km/h时,紧急制动停车视距所需要的圆曲线最小半径值与现行规范中圆曲线最小半径一般值基本一致;结合既有高速公路圆曲线不满足停车视距要求的路段交通运行平稳的现状,显然高速公路内侧车道小客车采用紧急制动停车视距较为合理。当设计速度为120 km/h或100 km/h时,其紧急制动停车视距所需要的圆曲线最小半径值较现行规范圆曲线最小半径一般值大较多;如果圆曲线路段圆曲线半径不满足紧急制动停车视距要求,应采取特殊设计或限速等安全措施。
(4) 提出的紧急制动停车视距较规范规定值小,应进一步开展高速公路内侧车道采用紧急制动停车视距交通安全风险分析的研究。
| [1] |
JTG D20-2017, 公路路线设计规范[S]. JTG D20-2017, Design Specifications for Highway Alignment[S]. |
| [2] |
日本道路公团. 日本高速公路设计要领[M]. 西安: 陕西旅游出版社, 1991. Japanese Road Corporation. Japanese Expressway Design Essentials[M]. Xi'an: Shaanxi Tourism Publishing House, 1991. |
| [3] |
日本道路协会. 日本公路技术标准的解说与运用[M]. 王治中, 张文魁, 冯理堂, 译. 北京: 人民交通出版社, 1979. Japan Road Association. Explanation and Application of Japanese Highway Technical Standards[M]. WANG Zhi-zhong, ZHANG Wen-kui, FENG Li-tang, translated. Beijing: China Communications Press, 1979. |
| [4] |
AASHTO. Highway Safety Design and Operations Guide[M]. Washington, D. C.: AASHTO, 2011.
|
| [5] |
陈雨人, 付云天, 汪凡. 基于支持向量回归的视距计算模型建立和应用[J]. 中国公路学报, 2018, 31(4): 105-113. CHEN Yu-ren, FU Yun-tian, WANG Fan. Establishment and Application of Sight Distance Computing Model Based on Support Vector Regression[J]. China Journal of Highway and Transport, 2018, 31(4): 105-113. |
| [6] |
文浩雄, 钟琨, 刘卓, 等. 高速公路中央分隔带横净距问题及对策[J]. 公路工程, 2013, 38(6): 20-23. WEN Hao-xiong, ZHONG Kun, LIU Zhuo, et al. Lateral Clear Distance Problems and Solutions of Median Divider in Highway[J]. Highway Engineering, 2013, 38(6): 20-23. |
| [7] |
张玥. 基于横向力系数的公路平曲线半径及超高取值方法研究[J]. 中外公路, 2015, 35(2): 5-9. ZHANG Yue. Research on Method of Determining Radius and Superelevation of Highway Horizontal Curve Based on Lateral Force Coefficient[J]. Journal of China & Foreign Highway, 2015, 35(2): 5-9. |
| [8] |
梁友哲. 高等级公路平曲线外侧超车道停车视距的验算及改善措施[J]. 工程与建设, 2018, 32(4): 520-522, 545. LIANG You-zhe. Checking Calculation and Improvement Measures for Stopping Sight Distance of Overtaking Lane on High-grade Highway[J]. Engineering and Construction, 2018, 32(4): 520-522, 545. |
| [9] |
邢福东. 高等级公路宜采用的平曲线半径分析[J]. 福建交通科技, 2020(5): 48-49. XING Fu-dong. Analysis of Horizontal Curve Radius Suitable for High-grade Highways[J]. Fujian Transportation Science and Technology, 2020(5): 48-49. |
| [10] |
赵永平, 杨少伟, 赵一飞. 高速公路中央分隔带外侧超车道停车视距研究[J]. 公路, 2004, 6(6): 39-42. ZHAO Yong-ping, YAN Shao-wei, ZHAO Yi-fei. Analysis of Passing Lane Stopping Sight Distance Outside Median Divider in Expressway[J]. Highway, 2004, 6(6): 39-42. |
| [11] |
王晓楠, 王云泽, 苗慕楠, 等. 动态停车视距模型研究及应用[J]. 公路, 2015, 60(11): 151-155. WANG Xiao-nan, WANG Yun-ze, MIAO Mu-nan, et al. Study and Application of Dynamic Stopping Sight Distance Model[J]. Highway, 2015, 60(11): 151-155. |
| [12] |
孟云龙. 高速公路曲线路段中央分隔带视距问题及交通安全设施改善措施研究[J]. 公路与汽运, 2017, 180(3): 24-26. MENG Yun-long. Research on Visual Distance Problem of Central Separation Zone in Curved Section of Expressway and Improvement Measures of Traffic Safety Facilities[J]. Highway and Automobile Transportation, 2017, 180(3): 24-26. |
| [13] |
周海宇. 山区高速公路小半径平曲线隧道交通安全保障技术研究[D]. 西安: 长安大学, 2018. ZHOU Hai-yu. Research on Traffic Safety Assurance Technology for Small Radius Flat Curve Tunnel in Mountain Expressway[D]. Xi'an: Chang'an University, 2018. |
| [14] |
唐力焦. 基于高速公路几何线形与路侧安全设施的视线诱导技术研究[D]. 西安: 长安大学, 2019. TANG Li-jiao. Research on Line-of-sight Guidance Technology Based on Expressway Geometry and Roadside Safety Facilities[D]. Xi'an: Chang'an University, 2019. |
| [15] |
杨帆, 白浩晨, 贺亚龙, 等. 高速公路中央分隔带停车视距评价方法研究[J]. 公路交通科技, 2018, 35(6): 45-51. YANG Fan, BAI Hao-chen, HE Ya-long, et al. Study on Method of Evaluating Stopping Sight Distance of Median Strip in Expressway[J]. Highway and Transportation Science and Technology, 2018, 35(6): 45-51. |
| [16] |
张航, 张肖磊, 吕能超. 高速公路停车视距可靠性设计[J]. 公路交通科技, 2019, 36(4): 44-49, 87. ZHANG Hang, ZHANG Xiao-lei, LÜ Neng-chao. Reliability Design for Stopping Sight Distance of Expressway[J]. Journal of Highway and Transportation Research and Development, 2019, 36(4): 44-49, 87. |
| [17] |
HASSAN Y, SAYED T, TABERNERO V. Establishing Practical Approach for Design Consistency Evaluation[J]. Journal of Transportation Engineering, 2001, 127(4): 295-302. |
| [18] |
XIA R X, WU D H, HE J, et al. A New Model of Stopping Sight Distance of Curve Braking Based on Vehicle Dynamics[J]. Discrete Dynamics in Nature and Society, 2016, 20(16): 1-8. |
| [19] |
PAPADIMITRIOU E, MAVROMATIS S, PSARIANOS B. Stopping Sight Distance Adequacy Assessment on Freeways: the Case of Left Horizontal Curves over Crest Vertical Curves[J]. Transportation Letters, 2018, 10(5): 269-279. |
| [20] |
BASSANI M, HAZOOR A, CATANI L. What's Around the Curve? A Driving Simulation Experiment on Compensatory Strategies for Safe Driving along Horizontal Curves with Sight Limitations[J]. Transportation Research Part F: Traffic Psychology and Behaviour, 2019, 66: 273-291. |
| [21] |
陈胜营, 汪亚干, 张剑飞. 公路设计指南[M]. 北京: 人民交通出版社, 2000. CHEN Sheng-ying, WANG Ya-gan, ZHANG Jian-fei. Guide for Highway Design[M]. Beijing: China Communications Press, 2000. |
| [22] |
吴斌, 朱西产, 沈剑平. 基于自然驾驶数据的驾驶员紧急制动行为特征[J]. 同济大学学报: 自然科学版, 2018, 46(11): 1514-1519, 1535. WU Bin, ZHU Xi-chan, SHEN Jian-ping. Driver Emergency Braking Behavior Based on Naturalistic Driving Data[J]. Journal of Tongji University: Natural Science Edition, 2018, 46(11): 1514-1519, 1535. |
| [23] |
杨少伟. 道路勘测设计. 3版[M]. 北京: 人民交通出版社, 2016. YANG Shao-wei. Road Survey and Design. 3th ed[M]. Beijing: China Communications Press, 2016. |
 2021, Vol. 38
2021, Vol. 38
