扩展功能
文章信息
- 白浩晨, 潘兵宏, 张江洪, 林宣财, 王佐
- BAI Hao-chen, PAN Bing-hong, ZHANG Jiang-hong, LIN Xuan-cai, WANG Zuo
- 基于停车视距的高速公路最小圆曲线半径研究
- Study on Minimum Circular Curve Radius of Expressway Based on Stopping Sight Distance
- 公路交通科技, 2021, 38(9): 60-67, 77
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(9): 60-67, 77
- 10.3969/j.issn.1002-0268.2021.09.008
-
文章历史
- 收稿日期: 2021-04-26
2. 长安大学 公路学院, 陕西 西安 710064
2. School of Highway, Chang'an University, Xi'an Shaanxi 710064, China
随着高速公路建设与管理模式的改进,车辆行驶自由度和运行速度相对提高,保障车辆行驶时前方一定距离内的视线通畅变得愈发重要。驾驶人在平曲线路段行驶时,视线易受到车道一侧的护栏、防眩和绿化植物、挖方坡体的阻挡,产生视觉盲区,驾驶人无法及时发现前方异常路况,导致无法及时停车,存在发生交通事故的隐患[1]。据资料统计,我国高速公路平曲线段发生的交通事故占比达到36%,而在山区高速公路更高达77%[2-3]。保障平曲线路段的行车安全,首先应保证停车视距满足要求[4]。JTG D20—2017《公路路线设计规范》 (以下简称《路线规范》)规定各车道参数需满足停车视距要求。
Fambro等人[5]通过分析36个实测点的几何数据及速度数据发现,道路运行速度远高于设计速度,并基于试验数据建立了有限视距条件下曲线大小与运行速度的关系。Sarhan和Hassan[6]使用有限元技术软件分析了3维组合路线中具有路边或中间障碍的平曲线上的有效停车视距。Xia等人[7]建立了停车视距计算模型,给出了平曲线停车视距的一般值和极限值。Papadimitriou等人[8]在对若干几何参数的解释性建模方法的基础上,根据停车视距不足的概率和障碍物的高度来修正停车视距值。Bassani等人[9]针对在视距不足时驾驶人通过弯道的驾驶行为进行试验研究,发现驾驶人会通过减速或增大横净距来保证行车安全。Shirini等人[10]根据道路几何特性建立了竖曲线椭圆方程,并基于椭圆方程计算了夜间视距,研究结果发现与抛物线曲线相反,椭圆曲线的视线距离随着车辆在曲线上的前进而增大。陈雨人等[11]通过分析支持向量机与视距的关系,提出了视距计算模型,为已建隧道工程的视距安全提供保障。文浩雄等[12]对高速公路中央分隔带弯道路段横净距进行验算,发现不能满足停车视距要求。张玥[13]通过分析横向力系数取值,提出对规范中最小半径值调整的建议。梁友哲[14]计算了曲线外侧超车道满足视距要求的最小平曲线半径,针对中分带曲线外侧超车视距不足的问题,提出了保障停车视距的措施。邢福东[15]提出一般路段与隧道路段满足停车视距的圆曲线最小半径值。尹和山等[16]根据匝道类型不同,得到不同车型的横净距和满足停车视距要求匝道圆曲线最小半径值。
综上,国内外对曲线路段停车视距的研究主要聚焦于停车视距计算模型的改进和视距不足时保障措施,鲜有研究者针对平曲线上不同车道视点位置和停车视距进行讨论。《路线规范》[17]在规定圆曲线最小半径时,并没有考虑停车视距的要求,导致部分小半径圆曲线路段内侧车道受中央分隔带影响,停车视距不满足规范要求,右偏曲线的外侧车道的内侧旁边结构物定义视线遮挡引起安全隐患。因此,本研究将基于实测数据,首先研究不同车道、不同车型驾驶人视点位置,然后计算不同路段、不同偏向、不同车道的横净距,最后研究满足现有横净距和停车视距的高速公路圆曲线最小半径,并提出圆曲线最小半径建议值,供设计人员参考,以期提高高速公路圆曲线路段交通安全水平。
1 高速公路停车视距的要求停车视距是在驾驶人观察到障碍并采取制动后,由行驶和减速过程组成的距离。我国《路线规范》[18]中规定停车视距如表 1、表 2所示。
| 设计速度/(km·h -1) | 停车视距/m |
| 120 | 210 |
| 100 | 160 |
| 80 | 110 |
| 60 | 75 |
| 下坡纵坡坡度/% | 不同设计速度/(km·h -1)下的停车视距/m | |||
| 120 | 100 | 80 | 60 | |
| 0 | 245 | 180 | 125 | 85 |
| 3 | 265 | 190 | 130 | 89 |
| 4 | 273 | 195 | 132 | 91 |
| 5 | 200 | 136 | 93 | |
| 6 | 139 | 95 | ||
| 7 | 97 | |||
2 高速公路驾驶人视点位置分析
驾驶人视点横向位置是指在行驶方向上,驾驶人的眼睛距离其所在行车道左侧边线的距离。赵永平[19]、王晓楠[20]、杨帆[21]以及孟云龙[22]等人认为驾驶人视点位置在距离车道左侧边缘线1.2 m处;《路线规范》中指出驾驶人视点位置位于车道宽度的1/2处,即车道中心线。由于规范和现有研究差别较大,因此采用跟车和无人机对多车道高速公路驾驶人视点位置进行调查研究(见图 1)。

|
| 图 1 调查示意图 Fig. 1 Schematic diagram of investigation |
| |
拍摄过程保证无人机位置与车道垂直,已知高速公路行车道宽度为3.75 m,在视频截图中测量得到车道边线以及左侧车身边线至行车道左侧边缘线的距离,通过比例换算,得到实际中左侧车身边线至左侧行车道边线的距离,参照近年来有关领域上一些参数的确定方法[23-24],结合有关统计学原理,确定取85%位的视点横向位置作为驾驶人在车道的横向分布位置(表 3)。本次试验调查了内、中、外侧车道车辆各281,210,208辆,在自由流的状态下,选择在3条不同设计速度、不同横断面类型的高速公路上,采集不同车型在不同车道上的视点位数据,保证了数据的代表性。
| 各车道代表车型 | 样本均值/ m | 85%位视点位置/m | 驾驶人视点位置/m | ||
| 均值 | 85%位 | ||||
| 最内侧车道 | 小客车 | 1 | 0.7 | 1.5 | 1.2 |
| 中间车道 | 小客车 | 1 | 0.6 | 1.5 | 1.1 |
| 中型车 | 0.9 | 0.5 | 1.5 | 1.1 | |
| 货车 | 0.8 | 0.5 | 1.4 | 1.1 | |
| 最外侧车道 | 小客车 | 1 | 0.6 | 1.5 | 1.1 |
| 货车 | 0.6 | 0.9 | 1.2 | 1.5 | |
调查发现不同车型驾驶人车座中心与左车身边缘的距离相差较小,不同车型的车身宽度变化主要体现在两驾驶座的间距上。由于存在中间分隔带,小客车左侧视点位置第1车道大于第2车道。当视点位置运用于停车视距计算时,公路提供横净距与圆曲线半径成反比。考虑驾驶人行车最不利的条件,取第85%位的视点位置作为驾驶人视点横向位置的推荐值。因此,建议最内侧车道小客车驾驶人的视点横向位置取1.2 m,最外侧车道小客车和货车驾驶人的视点横向位置分别为1.1 m和1.5 m,中间车道各种车型的视点横向位置为1.1 m。
3 基于停车视距的圆曲线最小半径 3.1 横净距、停车视距与平曲线半径之间的关系公路曲线路段因挖方边坡、路侧护栏、隧道侧壁、中央分隔带防眩设置等可能遮挡驾驶人视线,使驾驶人无法及时看清道路前方线形和行车道内的各种障碍物,导致没有足够的距离在障碍物前停车,从而增加了行车危险。因此,需要保障有足够的停车视距,而采用满足停车视距的圆曲线半径就是其中有效的手段之一。停车视距是车辆的行驶轨迹线(图 2)。对驾驶员视点轨迹线每隔一定间隔绘出一系列与视线相切的外边缘线称为视距曲线[25]。驾驶人视点轨迹线与视距曲线之间的横向距离称为横净距[23]。横净距范围内应保持视线通畅,无视线遮挡(图 2)。
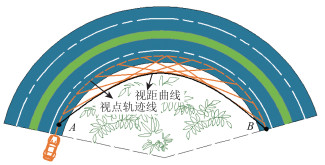
|
| 图 2 平曲线停车视距示意图 Fig. 2 Schematic diagram of horizontal curve stopping sight distance |
| |
横净距采用式(1)[26]计算。
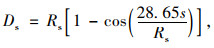
|
(1) |
式中, Ds为横净距;Rs为视点轨迹线的曲线半径;s为小客车或货车停车视距,根据表 1和表 2取值。从图 3中可看出视点所在曲线半径大小决定了驾驶人在曲线路段的最大可视距离。在相同道路条件下,圆曲线半径越小,驾驶人视线受阻程度越大,可视距离越小。当可视距离小于车辆的停车视距时,驾驶人对于紧急情况无法及时处理,容易导致碰撞的交通事故。
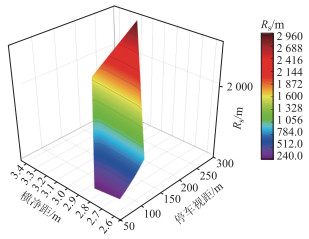
|
| 图 3 横净距、停车视距和平曲线半径关系 Fig. 3 Relationship of horizontal clear distance with stop sight distance and radius of horizontal curve |
| |
3.2 满足停车视距的右偏圆曲线最小半径 3.2.1 右偏填方路段
填方路段路侧一般设有护栏,由于小客车驾驶人视线高度为1.2 m,右偏曲线路侧护栏容易导致最外侧车道的驾驶人视线受阻,故填方路段中检验停车视距的车辆类型仅考虑小客车。右偏曲线的横净距为硬路肩宽度与行车道宽度之和减去驾驶人视点横向位置, 见图 4。
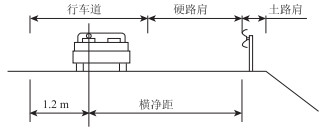
|
| 图 4 填方路段横净距示意图 Fig. 4 Schematic diagram of lateral clear distance of filling section |
| |
填方路段右偏圆曲线视点轨迹线半径计算如图 5所示。
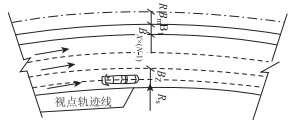
|
| 图 5 填方路段右偏圆曲线视点轨迹线半径计算示意图 Fig. 5 Schematic diagram of calculating radius of right circular curve viewpoint trajectory line of filling section |
| |
视点轨迹线半径计算如式(2)[27]所示。
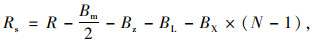
|
(2) |
式中,R为高速公路圆曲线最小半径;Bm为中央分隔带宽度;Bz为驾驶人视点横向位置,取1.2 m;BL为左侧路缘带宽度;BX为行车道宽度;N为车道数。计算右偏曲线填方路段横净距如表 4所示。根据式(1)、(2)和横净距,计算出填方路段最外侧车道满足停车视距的最小圆曲线半径(表 4)。
| 运行速度/ (km·h -1) | 车道宽度/m | 硬路肩宽度/m | 横净距/ m | 圆曲线最小半径/m | 《路线规范》圆曲线半径一般值/m | |||
| 双向4车道 | 双向6车道 | 双向8车道 | 双向10车道 | |||||
| 120 | 3.75 | 3 | 5.65 | 980 | 985 | 990 | 995 | 1 000 |
| 100 | 3.75 | 3 | 5.65 | 572 | 575 | 580 | 584 | 700 |
| 80 | 3.75 | 3 | 5.65 | 275 | 280 | 280 | 285 | 400 |
| 60 | 3.5 | 1.5 | 3.9 | 185 | 190 | 195 | 200 | 200 |
由表 4可知,仅在运行速度为120 km/h时,填方路段右偏圆曲线满足停车视距的最小半径,接近《路线规范》值,在其余运行速度和不同视点位置下均较小于《路线规范》值,即《路线规范》规定的圆曲线半径一般值可满足填方路段右偏曲线停车视距要求。
3.2.2 右偏挖方路段货车驾驶人视点虽然高于路侧护栏但视线仍然会受到挖方边坡的遮挡。基于现有研究成果和实际测量数据,货车的驾驶人视点位置为距离行车道边线1.5 m处(图 6), 小客车的驾驶人视点位置为距离行车道边缘1.1 m处。小客车和货车在最外侧车道的横净距计算如图 7所示。
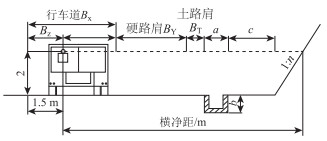
|
| 图 6 挖方路段横净距示意图 Fig. 6 Schematic diagram of lateral clear distance of excavation section |
| |
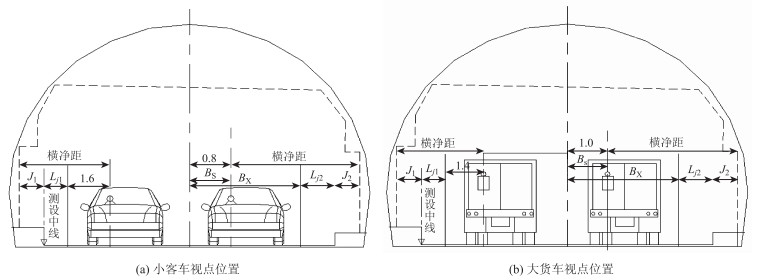
|
| 图 7 隧道路段横净距示意图(单位: m) Fig. 7 Schematic diagram of lateral clear distance of tunnel section(unit: m) |
| |
小客车和货车在最外侧车道的横净距采用式(3)计算[27]:
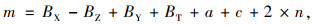
|
(3) |
式中,a为边沟尺寸的宽度;c为碎落台宽度;n为边坡斜率;BY为硬路肩宽度;BT为土路肩宽度。a,c,n这3个参数均采用《路线规范》一般值,即a为0.6 m,c为1.5 m,n为0.75。土路肩宽度为0.75 m,硬路肩和车道宽度见表 4。通过式(3)计算,得到挖方路段的横净距值(表 5)。根据式(2)、(3)和横净距,以双向8车道为例,计算挖方路段满足停车视距的曲线半径,如表 5所示。
| 运行速度/(km·h -1) | 120 | 100 | 80 | 60 | |
| 小客车横净距/m | 10 | 10 | 10 | 8.25 | |
| 货车横净距/m | 9.6 | 9.6 | 9.6 | 7.85 | |
| 小客车最小半径/m | 565 | 340 | 170 | 100 | |
| 不同纵坡坡度(%)满足货车停车视距的最小半径/m | 6 | — | — | 175 | 115 |
| 5 | — | 355 | 175 | 115 | |
| 4 | 680 | 365 | 190 | 115 | |
| 3 | 705 | 380 | 215 | 120 | |
| (-3,3) | 795 | 435 | 215 | 130 | |
| -3 | 925 | 485 | 235 | 140 | |
| -4 | 985 | 465 | 240 | 145 | |
| -5 | — | 535 | 255 | 155 | |
| -6 | — | — | 255 | 155 | |
| 《路线规范》半径一般值/m | 1 000 | 700 | 400 | 200 | |
由表 5可知,挖方路段的右偏曲线,《路线规范》规定的圆曲线最小半径一般值也能满足小客车和货车所需的停车视距。
3.2.3 右偏曲线隧道路段车辆在曲线隧道路段行驶时,驾驶人的视线易受洞壁影响,视线存在不通视情况,不利于安全行车。长安大学周海宇[27]基于试验调查,分析数据获得小客车第1车道视点位置距离左侧行车道边线为1.6 m,第2车道视点位置距离左侧行车道边线为1.6 m。长安大学唐力焦[28]在此基础上界定隧道内货车的视点位置,并以此为基础,确定隧道路段横净距计算示意图,见图 7。
因此隧道路段(右偏曲线)小客车、大货车横净距采用式(4)计算[28]:
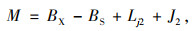
|
(4) |
式中, Lj2为隧道内右侧侧向宽度;J2为检修道宽度;BS为视点位置距离右侧车道左边线距离,小客车取0.8 m,货车取1.0 m。车道宽度BX见表 4。计算得到右偏曲线隧道内小客车和大货车的横净距如表 6所示。在隧道路段,圆曲线半径取视点轨迹线的曲线半径值,因此结合式(2)和表 6中的横净距,可计算出曲线隧道路段满足停车视距的视点轨迹圆曲线最小半径(表 6)。
| 设计速度/(km·h -1) | 60 | 80 | 100 | 120 | |
| 小客车横净距/m | 4.2 | 4.45 | 4.95 | 5.2 | |
| 货车横净距/m | 4 | 4.25 | 4.75 | 5 | |
| 右侧检修道宽度/m | 0.75 | 0.75 | 1 | 1 | |
| 右侧侧向宽度/m | 0.75 | 0.75 | 1 | 1.25 | |
| 满足小客车停车视距最小半径/m | 170 | 340 | 645 | 1 060 | |
| 不同纵坡坡度(%)满足货车停车视距的最小半径/m | 5 | 195 | 370 | 690 | — |
| 4 | 200 | 380 | 715 | 1 280 | |
| 3 | 210 | 400 | 740 | 1 320 | |
| (-3,3) | 225 | 460 | 850 | 1 500 | |
| -3 | 250 | 500 | 950 | 1 755 | |
| -4 | 260 | 515 | 1 000 | 1 865 | |
| -5 | 270 | 545 | 1 050 | — | |
| 《路线规范》最小半径一般值/m | 200 | 400 | 700 | 1 000 | |
由表 6可知:(1)《路线规范》规定的圆曲线最小半径一般值基本能满足小客车停车视距的要求。(2)设计速度小于120 km/h,上坡坡度大于3%时,《路线规范》规定的圆曲线最小半径一般值基本满足隧道路段货车所需的停车视距。(3)不设超高的曲线半径值可满足右偏曲线隧道路段所有情形下停车视距的要求。
3.3 满足停车视距的左偏圆曲线最小半径 3.3.1 左偏一般路段高速公路第1车道限制小客车行驶,驾驶人视点高度为1.2 m,视线易受中央分隔带护栏影响,视线存在不通视情况,因此小客车为最不利的车型。第1车道横净距为C(即侧向安全净宽)值宽度与左侧路缘带宽度、驾驶人视点横向位置之和, 见图 8。
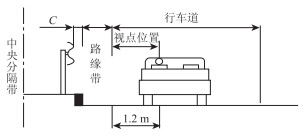
|
| 图 8 第1车道横净距示意图 Fig. 8 Lateral clear distance of the First lane |
| |
一般路段左偏圆曲线视点轨迹线半径计算如图 9所示。
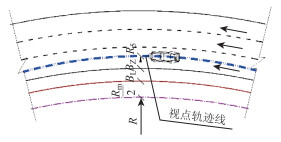
|
| 图 9 一般路段左偏圆曲线视点轨迹线半径计算示意图 Fig. 9 Schematic diagram for calculating radius of left circular curve viewpoint trajectory line of general road section |
| |
左偏曲线第1车道的视点轨迹线半径计算如式(5)[27]所示。
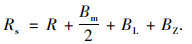
|
(5) |
计算得到左偏曲线一般路段横净距如表 7所示。圆曲线半径取视点轨迹线曲线半径值,采用式(2)和表 7的横净距,计算得到满足停车视距的左偏圆曲线最小半径计算值(见表 7)。
| 运行速度/ (km·h -1) | 左侧路缘带宽度/m | C值/ m | 横净距/m | 圆曲线最小半径/ m | 《路线规范》中圆曲线半径一般值/m |
| 120 | 0.75 | 0.5 | 2.45 | 2 250 | 1 000 |
| 100 | 0.75 | 0.25 | 2.2 | 1 455 | 700 |
| 80 | 0.5 | 0.25 | 1.95 | 775 | 400 |
| 60 | 0.5 | 0.25 | 1.95 | 360 | 200 |
由表 7可看出,当高速公路中央分隔带设置护栏和防眩设施时,基于停车视距的限制,第1车道最小圆曲线半径约为《路线规范》规定值的1.8~2.25倍。因此《路线规范》规定的圆曲线最小半径一般值不能满足左偏曲线路段停车视距的要求。
3.3.2 左偏隧道路段由图 7可知隧道路段(左偏曲线)小客车和大货车的横净距采用式(6)计算[28]:
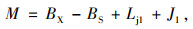
|
(6) |
式中, Lj1为隧道内左侧侧向宽度;J1为左侧检修道宽度;BS为视点位置距离左侧车道左边线距离,小客车取1.6 m,货车取1.4 m。
计算得到隧道路段左偏曲线的横净距(表 8)。圆曲线半径取视点轨迹线的曲线半径值,结合式(2)和表 8的横净距,计算左偏隧道路段满足停车视距的圆曲线最小半径(表 8)。由表 8可知,不设超高的圆曲线半径一般值满足停车视距的要求,而《路线规范》规定的圆曲线半径一般值不满足左偏曲线隧道路段的停车视距要求。
| 设计速度/(km·h -1) | 60 | 80 | 100 | 120 | |
| 货车横净距/m | 2.65 | 2.65 | 2.9 | 3.15 | |
| 小客车横净距/m | 2.85 | 2.85 | 3.1 | 3.35 | |
| 左侧检修道宽度/m | 0.75 | 0.75 | 0.75 | 1 | |
| 左侧侧向宽度/m | 0.5 | 0.5 | 0.75 | 0.75 | |
| 小客车最小半径/m | 245 | 530 | 1 030 | 1 645 | |
| 不同纵坡满足货车停车视距的最小半径/m | 5 | 295 | 612 | 1 130 | — |
| 4 | 300 | 635 | 1 175 | 2 025 | |
| 3 | 315 | 740 | 1 215 | 2 095 | |
| (-3,3) | 340 | 735 | 1 395 | 2 380 | |
| -3 | 375 | 795 | 1 555 | 2 785 | |
| -4 | 390 | 820 | 1 640 | 2 955 | |
| -5 | 410 | 870 | 1 725 | — | |
| 《路线规范》中圆曲线半径一般值/m | 200 | 400 | 700 | 1 000 | |
4 结论
为避免中央分隔带防眩设施和路侧护栏、边坡等限制驾驶人的视线,高速公路平曲线最小半径应满足停车视距要求。采用无人机及图片处理技术,在得到了高速公路不同车道内不同车型驾驶人视点横向位置基础上,考虑不同车型和曲线偏向,分别分析了填方、挖方、隧道这3种路段的横净距。基于《路线规范》停车视距,从安全角度确定了不同路段在曲线偏向不同时,视线受影响的车道与车型。根据停车视距、横净距及圆曲线半径之间的几何关系,提出了不同路段圆曲线左偏与右偏两种情况下满足停车视距的最小圆曲线半径指标建议值。主要结论如下:
(1) 通过实测数据得到驾驶人在不同车道内行驶时视点横向位置,为停车视距对线形指标的影响提供了数据支持。
(2) 右偏圆曲线路段,《路线规范》中规定的圆曲线最小半径一般值能满足对小客车停车视距的要求, 也能满足曲线隧道内纵坡大于3%时货车停车视距的要求,但不满足下坡或纵坡小于等于3%时货车停车视距的要求。对左偏曲线路段,《路线规范》中规定的圆曲线最小半径一般值既不能满足对小客车停车视距的要求, 也不能满足货车停车视距的要求。
(3) 提出了满足停车视距的一般路段和隧道路段右偏和左偏圆曲线半径最小值,为道路设计中圆曲线半径的取值以及公路安全性评价提供了参考价值。
本文的研究成果虽然从满足停车视距角度细化了高速公路圆曲线最小半径的取值范围,但在对高速公路驾驶人视点位置的试验调查中,仅调查西安周边的代表性高速公路,数据不够全面,在以后的研究中需增大数据采集范围,增强研究结论的可信度。另外,需运用工程实例对于本文的研究结论进行检验和修正,完善和丰富本文提出的模型,佐证其研究成果。本研究下一步可将结果进行驾驶模拟试验,配合使用眼动仪采集不同圆曲线半径下的眼动数据,给定评价指标以优化基于停车视距的圆曲线半径值。
| [1] |
WOOD J S, DONNELL E T. Stopping Sight Distance and Horizontal Sight Line Offsets at Horizontal Curves[J]. Transportation Research Record, 2014, 2436: 43-50. |
| [2] |
任园园. 公路弯道路段行车危险区域及驾驶行为模型研究[D]. 长春: 吉林大学, 2011. REN Yuan-yuan. Reserch on Driving Dangerous Area and Driving Behavior Model in Road Curved Section[D]. Changchun: Jilin University, 2011. |
| [3] |
胡圣能. 双车道二级公路平曲线要素与交通安全关系研究[D]. 西安: 长安大学, 2006. HU Sheng-neng. Research on Relationship between Flat Curve Elements and Traffic Safety of Second-class Highway with Two Lanes[D]. Xi'An: Chang'An University, 2006. |
| [4] |
SARHAN M, HASSAN Y. Consideration of Sight Distance in Placement of Concrete Barriers on Horizontal Curves of Roads[J]. Transportation Research Record, 2012, 2301: 9-16. |
| [5] |
FAMBRO D, FITZPATRICK K, RUSSELL C. Operating Speed on Crest Vertical Curves with Limited Stopping Sight Distance[J]. Transportation Research Record, 2000, 1701: 25-31. |
| [6] |
HASSAN Y, SAYED T, TABERNERO V. Establishing Practical Approach for Design Consistency Evaluation[J]. Journal of Transportation Engineering, 2001, 127(4): 295-302. |
| [7] |
XIA R X, WU D H, HE J, et al. A New Model of Stopping Sight Distance of Curve Braking Based on Vehicle Dynamics[J]. Discrete Dynamics in Nature and Society, 2016, 20(16): 1-8. |
| [8] |
PAPADIMITRIOU E, MAVROMATIS S, PSARIANOS B. Stopping Sight Distance Adequacy Assessment on Freeways: the Case of Left Horizontal Curves Over Crest Vertical Curves[J]. Transportation Letters the International Journal of Transportation Research, 2018, 10(5): 269-279. |
| [9] |
BASSANI M, HAZOOR A, CATANI L. What's around the Curve? A Driving Simulation Experiment on Compensatory Strategies for Safe Driving along Horizontal Curves with Sight Limitations[J]. Transportation Research, 2019, 66: 273-291. |
| [10] |
SHIRINI B, KORDANI A A. Proposing an Elliptic Equation for the Symmetrical Sag Vertical Curves Based on Sight Distance in Highway[J]. KSCE Journal of Civil Engineering, 2019, 23(12): 5201-5207. |
| [11] |
陈雨人, 付云天, 汪凡. 基于支持向量回归的视距计算模型建立和应用[J]. 中国公路学报, 2018, 31(4): 105-113. CHEN Yu-ren, FU Yun-tian, WANG Fan. Establishment and Application of Sight Distance Computing Model Based on Support Vector Regression[J]. China Journal of Highway and Transport, 2018, 31(4): 105-113. |
| [12] |
文浩雄, 钟琨, 刘卓, 等. 高速公路中央分隔带横净距问题及对策[J]. 公路工程, 2013, 38(6): 20-23. WEN Hao-xiong, ZHONG Kun, LIU Zhuo, et al. Lateral Clear Distance Problems and Solutions of Median Divider in Highway[J]. Highway Engineering, 2013, 38(6): 20-23. |
| [13] |
张玥. 基于横向力系数的公路平曲线半径及超高取值方法研究[J]. 中外公路, 2015, 35(2): 5-9. ZHANG Yue. Research on Method of Determining Radius and Super Elevation of Highway Horizontal Curve Based on Lateral Force Coefficient[J]. China and Foreign Highway, 2015, 35(2): 5-9. |
| [14] |
梁友哲. 高等级公路平曲线外侧超车道停车视距的验算及改善措施[J]. 工程与建设, 2018, 32(4): 520-522, 545. LIANG You-zhe. Checking Calculation and Improvement Measures for Stopping Sight Distance of Overtaking Lane on High-grade Highway[J]. Engineering and Construction, 2018, 32(4): 520-522, 545. |
| [15] |
邢福东. 高等级公路适宜采用的平曲线半径分析[J]. 福建交通科技, 2020(5): 48-49. XING Fu-dong. Analysis of Horizontal Curve Radius Suitable for High-grade Highways[J]. Fujian Transportation Science and Technology, 2020(5): 48-49. |
| [16] |
尹和山. 高速公路互通式立交路线视距指标研究[J]. 工程与建设, 2017, 31(1): 81-82, 100. YIN He-shan. Study on Sight Distance Index of Highway Interchanges[J]. Engineering and Construction, 2017, 31(1): 81-82, 100. |
| [17] |
JTG D20-2017, 公路路线设计规范[S]. JTG D20-2017, Design Specifications for Highway Alignment[S]. |
| [18] |
JTG B01-2014, 公路工程技术标准[S]. JTG B01-2014, Technical Standard of Highway Engineering[S]. |
| [19] |
赵永平, 杨少伟, 赵一飞. 高速公路中央分隔带外侧超车道停车视距研究[J]. 公路, 2004(6): 39-42. ZHAO Yong-ping, YAN Shao-wei, ZHAO Yi-fei. Analysis of Passing Lane Stopping Sight Distance Outside Median Divider in Expressway[J]. Highway, 2004(6): 39-42. |
| [20] |
王晓楠, 王云泽, 苗慕楠, 等. 动态停车视距模型研究及应用[J]. 公路, 2015, 60(11): 151-155. WANG Xiao-nan, WANG Yun-ze, MIAO Mu-nan, et al. Study and Application of Dynamic Stopping Sight Distance Model[J]. Highway, 2015, 60(11): 151-155. |
| [21] |
杨帆, 白浩晨, 贺亚龙, 等. 高速公路中央分隔带停车视距评价方法研究[J]. 公路交通科技, 2018, 35(6): 45-51. YANG Fan, BAI Hao-chen, HE Ya-long, et al. Study on Method of Evaluating Stopping Sight Distance of Median Strip in Expressway[J]. Highway and Transportation Science and Technology, 2018, 35(6): 45-51. |
| [22] |
孟云龙. 高速公路曲线路段中央分隔带视距问题及交通安全设施改善措施研究[J]. 公路与汽运, 2017(3): 24-26. MENG Yun-long. Research on Visual Distance Problem of Central Separation Zone in Curved Section of Expressway and Improvement Measures of Traffic Safety Facilities[J]. Highways & Automotive Applications, 2017(3): 24-26. |
| [23] |
蒋利霞. 基于生存分析和离散选择模型的行人过街安全研究[D]. 重庆: 重庆大学, 2015. JIANG Li-xia. Study of Pedestrian Street-crossing Safety Based on Survival Analysis and Discrete Choice Model[D]. Chongqing: Chongqing University, 2015. |
| [24] |
徐进, 崔强, 常旭, 等. 苜蓿叶形互通立交进/出口的纵向驾驶行为特征[J]. 东南大学学报: 自然科学版, 2019, 49(6): 1205-1214. XU Jin, CUI Qiang, CHANG Xu, et al. Longitudinal Driving Behavior Characteristics at Approaching/Departing Areas of Clover Leaf Interchange[J]. Journal of Southeast University: Natural Science Edition, 2019, 49(6): 1205-1214. |
| [25] |
杨少伟, 张碧琴, 赵永平, 等. 道路勘测设计.第3版[M]. 北京: 人民交通出版社, 2009. YANG Shao-wei, ZHANG Bi-qin, ZHAO Yong-ping, et al. Road Survey and Design[M]. Beijing: China Communications Press, 2009. |
| [26] |
许金良, 杨宏志, 赵一飞, 等. 道路勘测设计. 第4版[M]. 北京: 人民交通出版社, 2016. XV Jin-liang, YANG Hong-zhi, ZHAO Yi-fei, et al. Road Survey and Design. 4th ed[M]. Beijing: China Communications Press, 2016. |
| [27] |
周海宇. 山区高速公路小半径平曲线隧道交通安全保障技术研究[D]. 西安: 长安大学, 2018. ZHOU Hai-yu. Research on Traffic Safety Assurance Technology of Small Radius Flat Curve Tunnel in Mountain Expressway[D]. Xi'an: Chang'an University, 2018. |
| [28] |
唐力焦. 基于高速公路几何线形与路侧安全设施的视线诱导技术研究[D]. 西安: 长安大学, 2019. TANG Li-jiao. Study on Line-of-sight Induction Technology Based on Freeway Geometric Alignment and Roadside Safety[D]. Xi'an: Chang'an University, 2019. |
 2021, Vol. 38
2021, Vol. 38
