扩展功能
文章信息
- 任春宁, 宋帅, 王佐, 林宣财, 李赞勇
- REN Chun-ning, SONG Shuai, WANG Zuo, LIN Xuan-cai, LI Zan-yong
- 基于调整缓和曲线参数的中间带宽度变化分幅过渡研究
- Study on Framing Transition of Width Change of Median Based on Adjustment of Transition Curve Parameters
- 公路交通科技, 2021, 38(9): 25-32
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(9): 25-32
- 10.3969/j.issn.1002-0268.2021.09.004
-
文章历史
- 收稿日期: 2021-05-06
高速公路中间带宽度增宽或减窄采用线性渐变过渡虽然符合现行规范中“条件受限制时的”规定,但由于采用线性渐变过渡与现行《公路路线设计规范》(JTG D20—2017)[1](以下简称现行《规范》)中其他规定不一致,因此多年来在行业内对采用线性渐变过渡是否存在安全隐患问题存在较大分歧。现行《规范》规定不一致的内容有:(1)不满足《规范》7.3.1“各级公路平面不论转角大小,均应设置圆曲线…”规定。(2)不满足《规范》7.4.1“…直线同小于表7.4.1不设超高的圆曲线最小半径径向相连处,应设置回旋线…”规定。(3)设置一处渐变段相当于在局部路段设置的2处小偏角,难以满足《规范》7.8.2“当路线转角小于或等于7时,应设置较长的平曲线,其长度应大于表7.8.2中规定的一般值规定。(4)当中间带宽度变化较大时,采用线性渐变过渡方式时,行车道中心线线形不够圆滑,路容较差。如果在直线路段采用线性渐变过渡,当增宽或减窄宽度较小时,渐变起终点折线之间存在极角变化,按《规范》规定的渐变率1/100计算极角变化值仅为0.57°;当增宽或减窄宽度较大时,中间带内外缘的行车道平面轨迹线在外观视觉上将出现较为明显的突变点。如果在圆曲线路段采用线性渐变过渡,中间带内外缘的行车道平面轨迹线在外观视觉上内侧突变点感觉不明显,外侧相对较为明显。所以有必要对高速公路中间带宽度变化过渡段过渡方式进行研究。
国外高速公路中间带宽度变化如何过渡研究资料非常少,美国A Policy on Geometric Design of Highway and Streets(《公路和街道几何设计策略》)[2]和日本《高速公路设计要领》[3]没有这方面的内容。国内对缓和曲线及超高过渡方式、方法的研究较多,对利用缓和曲线调整线形研究得较少。缓和曲线作为构成公路平面线形基本要素的重要组成部分,一方面有效的模拟了车辆转弯时的行驶轨迹,使车辆从直线向圆曲线或圆曲线向直线过渡时离心力逐渐变化,有助于车辆匀速行驶;另一方面缓和曲线的设置提供曲线加宽及超高过渡有利条件,对改善路容,避免圆曲线起终点处线形明显的转折具有显著效果,所以过渡段应尽量采用缓和曲线。杨轸等[4-5]建立了隧道洞口附近缓和曲线的计算模型,并结合车辆偏移阈值,根据几何关系确定隧道最小缓和曲线参数。曹友露[6]通过采用相关性分析方法,研究了交通事故与平曲线和缓和曲线组合之间地关系。研究表明,缓和曲线长度为2~3倍缓和曲线最小长度时,平曲线安全性最佳。范爽[7]以事故资料为依据, 全面分析了公路平面设计中各元素之间组合关系的安全性, 并提出了基于交通安全的高速公路平面设计指标及其组合。有部分学者通过研究驾驶人在不同平面线形情况下的驾驶员身体、心理特征去探究线形指标与事故率之间的关系[8-10]。程国柱等[11-13]基于仿真试验,针对道路几何指标,根据影响路侧安全程度进行排序,并分析了不同车型在平曲线路段的速度特性。涂圣文[14-15]等将平面线形与纵面线形进行组合,分析不同组合条件下的道路运行安全,得到易发生交通事故的平纵线形组合情况。张玥等[16-19]结合设计速度、圆曲线半径、横向力系数、超高值及过渡段的关系进行深入研究。
综上所述,因渐变过渡如何设置《规范》缺乏具体规定,可参考的研究成果也非常少,依据我国现行《规范》规定,高速公路中间带宽度增宽或减窄时应采用左右分幅线形设计,条件受限制时可采用渐变过渡。所以较多设计者从设计难度和减小工程规模考虑采用线性过渡。本研究重点基于调整缓和曲线参数实现左右分幅线形设计,使高速公路中间带宽度变化过渡符合规范相关规定,不得已才考虑采用线性渐变过渡,本研究可供设计时参考。
1 高速公路中间带宽度变化历次规范对过渡方式的修订及执行情况 1.1 历次规范的修订情况(1) 现行《规范》)中9.4.3条规定“整体式路基的中间带宽度宜保持等值。当中间带的宽度根据需要增宽或减窄时,应采用左右分幅线形设计。条件受限制,且中间带宽度变化小于3.0 m时,可采用渐变过渡,过渡段的渐变率不应大于1/100”。
(2)《公路路线设计规范》(JTG D20—2006)(简称2006年版《规范》)[20]中9.4.3条规定“整体式路基的中间带宽度宜保持等值。当中间带的宽度根据需要增宽或减窄时,应设置过渡段。过渡段以设在回旋线范围内为宜,长度应与回旋线长度相等。条件受限制时,过渡段的渐变率不应大于1/100”。
(3)《公路路线设计规范》(JTJ 011—94)(简称1994年版《规范》)[21]中6.3.3条规定“中间带的宽度一般情况下应保持等宽度,并不得频繁变更宽度。当中间带宽度受地形条件及其他特殊情况限制而减窄或增宽时,应设置过渡段。中间带的过渡段以设在回旋线范围内为宜,其长度应与回旋线长度相等”,如图 1所示。
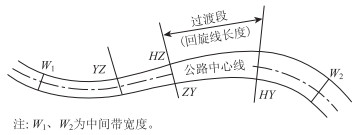
|
| 图 1 中间带宽度变化在缓和曲线范围过渡示意图 Fig. 1 Schematic diagram of transition of median width change in transition curve range |
| |
1.2 对规范的理解及执行情况
1994年版《规范》中6.3.3条对分离式断面中间带宽度宜大于4.5 m的规定,与现行《规范》规定左右分幅线形设计相一致;对中间带宽度变化值≤4.5 m时,过渡段以设在回旋线范围为宜,且长度应与回旋线长度相等的规定较为合理;2006年版《规范》增加了“条件受限制时,过渡段的渐变率不应大于1/100”的规定,使其在直线段或圆曲线路段采用线性渐变过渡被普遍认可;现行《规范》没有强调在缓和曲线路段渐变过渡。所以已建和在建高速公路中间带宽度变化较少在缓和曲线范围渐变过渡有着客观原因。现行《规范》规定应采用左右分幅线形设计,显然在强调采用左右分幅线形设计是为了保证行车道线形符合规范有关圆曲线、缓和曲线和小偏角转角线形等规定要求,是为了保证行车道线形不发生“突变”现象;保留“条件受限制”的规定,并将过渡段规范用词改为“渐变过渡”,一方面留有灵活余地,另一方面不局限于线性渐变,但渐变过渡宽度变化值限制在3.0 m内。
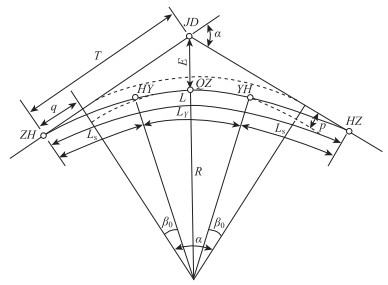
2 基于调整缓和曲线参数的中间带宽度变化分幅过渡研究 2.1 以中心线平曲线设计参数为基准的中间带内外缘缓和曲线计算模型根据回旋线作为缓和曲线的基本图式[22],如图 2所示,在平面存在转角的地方设置平曲线时,平曲线较设置单圆曲线存在一定的内移值p,计算式如下:
|
| 图 2 以中心线平曲线的回旋线作为缓和曲线的计算模型 Fig. 2 Calculation model which takes the spiral curve of centerline and horizontal curve as transition curve |
| |
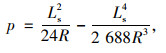
|
(1) |
式中,Ls为缓和曲线长度;R为缓和曲线所连接的圆曲线半径;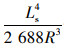

若中间带宽度变化控制因素在于圆曲线或直线时,通过调整前(后)缓和曲线参数来实现中间带宽度变化的线形过渡,其左右幅线形主要受p值大小的影响。假设标准路段为直线段,中间带单侧宽度为d,假设d=1;加宽段位于圆曲线,加宽值单侧为△b,则中间带宽度单侧值为(1+△b) m;根据左右分幅线形设计,平曲线内外缘参数R外,R,p外,p内分别如下:
中间带外缘边线平曲线内移值:p外=p-△b, 圆曲线半径R内=R-△b-1。
中间带内缘边线平曲线内移值:p内=p+△b,圆曲线半径R=R-△b-1。
根据式(1)的简化公式,平曲线缓和曲线长度Ls2=24Rp,则:

|
(2) |
式(2)可简化为:
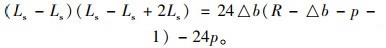
|
(3) |
令Ls-Ls=△Ls,则是式(3)可调整为:
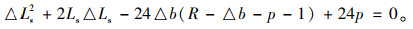
|
(4) |
求解式(4),得:
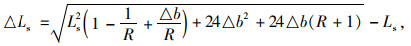
|
(5) |
同理得,
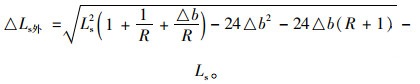
|
(6) |
由式(5)、(6)可知,通过缓和曲线参数调整实现中间带宽度变化,并符合左右分幅线形设计,过渡段内外缘缓和曲线长度与设计中心线圆曲线半径R、缓和曲线长度Ls及中间带宽度变化值△b相关。
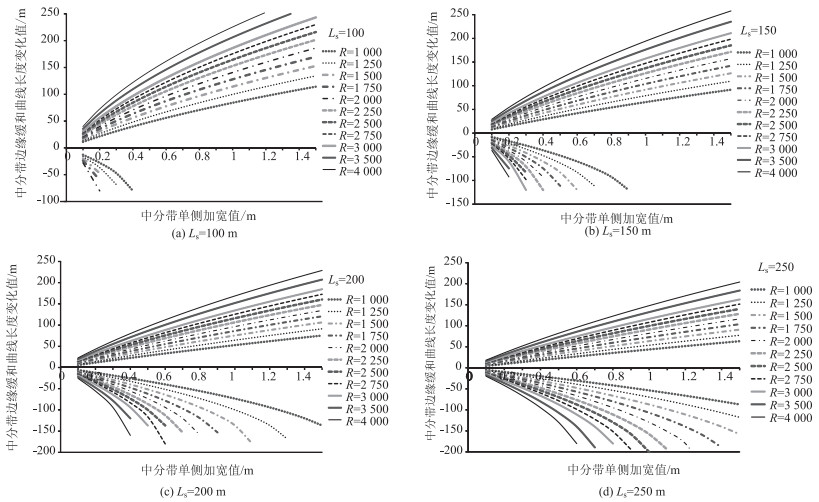
2.2 中间带宽度增宽值与中间带内外缘缓和曲线长度相关性研究假定设计中心线平曲线中缓和曲线长度分别为Ls=100,150,200,250 m时,圆曲线半径R=1 000~4 000 m,中间带单侧加宽值△b从0 m增加到1.5 m;根据式(5)、(6)计算得出中间带内外缘缓和曲线长度变化值△Ls,△Ls外,如图 3所示。
|
| 图 3 缓和曲线长度一定时,不同R值下△b与△Ls、△Ls外关系 Fig. 3 Relationships of △b with △Ls and △Ls外 with different Rs when length of transition curve is constant |
| |
由图 3可知:
(1) 当中间带单侧加宽值不断增加时,曲线内侧中间带边缘缓和曲线长度随之增加,所以曲线内侧缓和曲线较容易敷设,而曲线外侧中间带边缘缓和曲线长度则是随之不断减小;当中间带宽度变化值大于0.50 m时,曲线外侧较难符合敷设条件,如果缓和曲线长度减少值大于中心线缓和曲线长度,曲线将出现中断,即不连续现象,对此表明无法通过缓和曲线参数调整实现中间带宽度变化符合左右分幅线形设计的要求。
(2) 随着圆曲线半径的增加,曲线内、外侧中间带边缘缓和曲线长度变化值均不断增加;且随着中心线圆曲线半径增大,中间带内外缘缓和曲线长度增加或减小的幅度更大。当
(3) 随着中间带单侧加宽值的增加,曲线内外侧缓和曲线长度的变化基本呈线性变化,且其变化率随着设计中心的圆曲线半径增大不断增加。如当Ls=200 m,R=2 000 m,△b=0.9时,中间带外缘缓和曲线长度变化值已大于200 m,即无法通过缓和曲线参数调整进行过渡;而内缘缓和曲线长度变化值为88.3 m,缓和曲线长度为288.3 m;另外当内缘缓和曲线长度计算值过长时,可能使圆曲线长度缩短过多而变得过短,造成平曲线各单元长度不协调。
从以上分析可知,当中间带边缘缓和曲线长度计算值变化在±50 m时,采用缓和曲线参数调整实现中间带宽度变化能符合左右分幅线形设计相关规定的要求;当中间带内外缘缓和曲线长度变化值大于50 m时,采用调整中间带内外缘缓和曲线参数难以符合左右分幅线形设计要求。
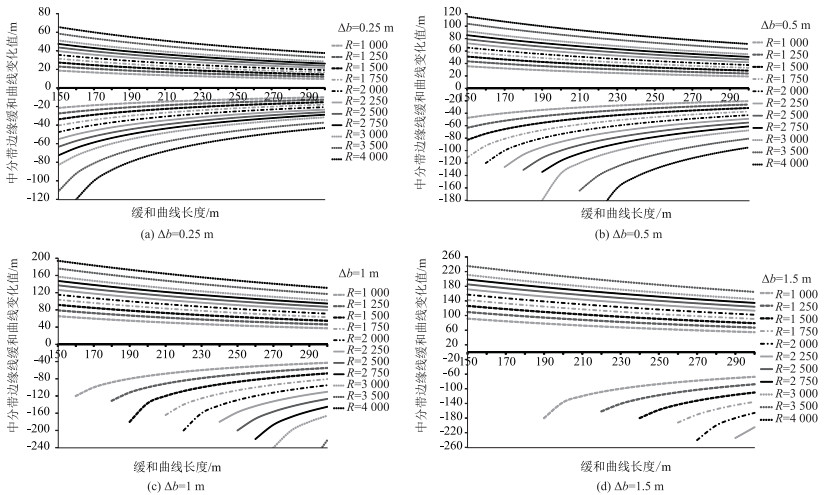
2.3 中心线缓和曲线长度变化与中间带内外缘缓和曲线长度相关性研究假定中间带单侧加宽值△b=0.25,0.5,1,1.5 m时,圆曲线半径R=1 000~4 000 m,缓和曲线长度Ls从150 m增加到300 m时,根据式(5)、(6)计算得出中间带内外缘缓和曲线长度变化值△Ls、△Ls外,如图 4所示。
|
| 图 4 中间带单侧加宽值一定时,不同R值下Ls与△Ls、△Ls外的关系 Fig. 4 Relationships of △b with △Ls and △Ls外 with different Rs when one side widening value of median is constant |
| |
由图 4可知:
(1) 随着中心线圆曲线半径的增加,中间带内外缘缓和曲线长度变化值均呈不断增加趋势。
(2) 随着中心线缓和曲线长度的增加,中间带内外缘缓和曲线长度变化值呈下降趋势,且内缘缓和曲线长度下降速度较外缘慢。如当△b=1.0,R=2 000 m时,Ls由150 m增加到300 m,中间带内缘缓和曲线长度变化值仅为44.088 m,外缘变化值为105.031 m, 即曲线中心缓和曲线长度每增加10 m,中间带内缘缓和曲线长度仅减少2.939 m,外缘减少7.00 m,且中心线缓和曲线长度不到200 m时,内缘缓和曲线计算值已经大于200 m,通过缓和曲线参数的调整无法实现中间带宽度过渡符合左右分幅线形设计要求。
(3) 随着中间带单侧加宽值的增加,中间带内外缘缓和曲线长度变化值也不断增加,当中间带单侧加宽值为1 m时,中间带内外缘缓和曲线长度变化值已达40 m,对缓和曲线长度的取值影响较大。故当中间带单侧宽度变化值小于0.5 m时,建议采用缓和曲线参数调整来实现中间带的宽度变化;当中间带宽度单侧宽度变化值小于1时,需结合设计中心线圆曲线半径和中间带内外缘缓和曲线参数计算结果分析确定。
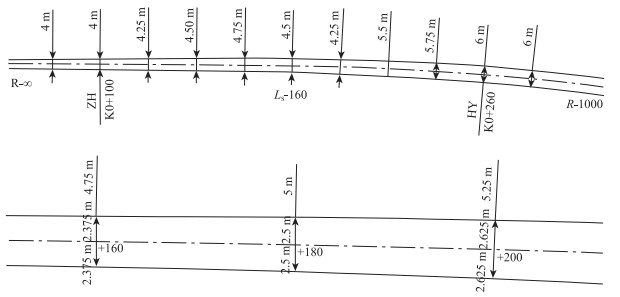
2.4 在缓和曲线上采用线性渐变的分幅过渡安全性分析当中间带单侧宽度变化值较大时,在缓和曲线长度范围通过调整缓和曲线参数难以实现左右分幅线形设计,这时可考虑在缓和曲线全段或一段采用线性渐变的分幅过渡,过渡段渐变率应不大于1/100,如图 5所示。
|
| 图 5 中间带宽度在缓和曲线上线性渐变的分幅过渡示意图 Fig. 5 Schematic diagram of framing transition of linear gradient of median width on transition curve |
| |
路线平面线形主要由直线、圆曲线和缓和曲线组成分析,其中直线、圆曲线路段曲率相同,中间带宽度变化在直线或圆曲线上渐变过渡,必然产生较短路段范围内曲率不连续及行车轨迹发生改变的可能;采用线性渐变过渡时,应首选在缓和曲线路段范围内渐变过渡,因为缓和曲线上任意一点的曲率本身就是变化的,在缓和曲线上线性渐变的分幅过渡避免了平曲线出现小偏角或原单圆曲线被拆分零散化,使路线线形保持连续性,保证交通安全。
3 应用案例 3.1 在高速公路沉管隧道前后路段中的应用某高速改造明挖隧道末端、敞开隧道、听海大道特殊结构桥梁、设计终点位于同一平曲线。其中明挖隧道中分带宽度要求5.2 m,末端可适当减小;听海大道特殊结构桥梁中间带宽度要求4.9 m;设计终点位于缓和曲线,衔接既有桥梁中间带宽度为2 m,该段落中间带宽度过渡较为复杂,限制因素较多。由于中间带宽度较既有桥梁的标准横断面增宽3.2 m,按照现行《规范》规定必须采用左右分幅线形设计。综合考虑控制因素,在明挖隧道末端的缓和曲线全段采用左右分幅线形设计,中间带宽度由5.2 m过渡至4.9 m,过渡段缓和曲线长度155 m;明挖隧道洞口段、敞开隧道,听海大道特殊结构桥梁中间带宽度保持4.9 m不变;终点段在缓和曲线上采用线性渐变的分幅过渡,中间带宽度由4.9 m渐变至2 m,渐变率1/117,衔接既有桥梁。该段高速公路中间带宽度变化分二次分幅进行,第1次过渡在缓和曲线上采用调整缓和曲线参数做到左右分幅线形设计; 第2次过渡也在缓和曲线上,但因该段为改扩建路段,既有缓和曲线长度较长,宽度变化值又偏大,难以通过调整缓和曲线参数实现左右分幅线形设计。经反复比较,最后采用在缓和曲线上线性渐变的分幅过渡方式进行渐变过渡,路线线形始终保持连续,保证了交通安全,见图 6。
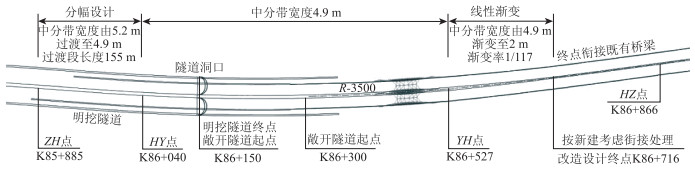
|
| 图 6 中间带宽度变化在缓和曲线上分幅过渡示意图 Fig. 6 Schematic diagram of framing transition of change of median width on transition curve |
| |
3.2 在超多车道高速公路中间带设墩路段中的推广应用
由于上跨高速公路的桥梁受行车视距、侧向余宽、桥墩防撞措施等的影响,较多高速公路中央分隔带不允许设置桥墩。随着我国经济高速增长的需要,改扩建双向六车道以上高速公路越来越多,包括新建高速公路考虑远期预留六车道以上改扩建条件。多车道高速公路如果都采用一跨跨越整体式六车道以上高速公路,因跨线桥桥梁跨径较大,特别是小角度交叉时桥梁工程规模增加明显。所以在大型枢纽互通式立交范围,被交叉高速公路与匝道连续上跨主线的桥梁较集中路段,或小角度交叉的重大桥梁工程,为了减小桥梁跨径和桥梁工程规模,可通过对高速公路局部路段中间带宽度增宽的措施以满足设墩要求;增宽过渡方式宜采用本研究推荐的调整两端缓和曲线参数的方式实现左右分幅线形设计。
4 结论(1) 现行《规范》规定中间带宽度变化应采用左右分幅线形设计,1994年版、2006年版《规范》均规定“过渡段以设在回旋线范围内为宜,长度应与回旋线长度相等”。这些规定都是考虑直线、圆曲线曲率都相同,为了避免因中间带宽度变化引起直线、圆曲线路段出现小偏角及原单曲线被拆分零散化的目的。
(2) 基于调整缓和曲线参数的中间带宽度变化分幅过渡主要研究结论有:①当中间带单侧宽度变化值小于0.5 m时,通过调整缓和曲线参数能实现中间带宽度变化过渡符合左右分幅线形设计;②当中间带宽度单侧变化值在0.5~1.0 m范围时,需进一步结合设计中心线圆曲线半径和中间带内外缘缓和曲线参数计算结果分析确定;③当中间带宽度单侧变化值大于1.0 m时,较难通过调整缓和曲线参数实现左右分幅线形设计。
(3) 当通过调整缓和曲线参数难以实现左右分幅线形设计时,可考虑在缓和曲线上采用线性渐变的分幅过渡方式过渡。因为缓和曲线上任意一点的曲率本身是变化的,在缓和曲线上渐变过渡不会出现小偏角或原单圆曲线被拆分零散化,前后路线线形依然保持连续性,交通安全有保障。
(4) 国内外对高速公路中间带宽度变化如何渐变过渡研究较少,应用案例说明本研究成果具有较高的实用价值,可供同行设计时参考。
| [1] |
JTG D20-2017, 公路路线设计规范[S]. JTG D20-2017, Design Specifications for Highway Alignment[S]. |
| [2] |
AASHTO. A Policy on Geometric Design of Highways and Streets[R]. Washington, D.C. : American Association of State Highway and Transportation Officials, 2011.
|
| [3] |
日本道路公团. 日本高速公路设计要领[M]. 西安: 陕西省旅游出版社, 1991. Japan Road Corporation. Essentials of Japanese Highway Design[M]. Xi'an: Shaanxi Tourism Publishing House, 1991. |
| [4] |
杨轸, 唐莹, 唐磊. 隧道出入口平面线形一致性[J]. 同济大学学报: 自然科学版, 2012, 40(4): 553-558. YANG Zhen, TANG Ying, TANG Lei. Consistency of Horizontal Alignment at Tunnel Entrance and Exit Zone[J]. Journal of Tongji University: Natural Science Edition, 2012, 40(4): 553-558. |
| [5] |
杨少伟, 洪玉川, 盘兵宏. 基于车辆偏移阈值的隧道洞口缓和曲线参数研究[J]. 中外公路, 2017, 37(8): 4-7. YANG Shao-wei, HONG Yu-chuan, PAN Bing-hong. Study on Transition Curve Parameters of Tunnel Portal Based on Vehicle Offset Threshold[J]. Journal of China & Foreign Highway, 2017, 37(8): 4-7. |
| [6] |
曹友露, 高建平. 圆曲线与缓和曲线组合对高速公路运营安全的影响[J]. 中外公路, 2016, 36(6): 300-305. CAO You-lu, GAO Jian-ping. Influence of Circular Curve and Transition Curve Combination on Expressway Operation Safety[J]. Journal of China & Foreign Highway, 2016, 36(6): 300-305. |
| [7] |
范爽. 高速公路平面线形指标及其组合安全性研究[D]. 西安: 长安大学, 2019. FAN Shuang. Study on Safety of Expressway Horizontal Alignment Index and Its Combination[D]. Xi'an: Chang'an University, 2019. |
| [8] |
张捷, 任作武, 朱守林. 草原公路直线段长度对驾驶员心率变异性的影响研究[J]. 科学技术与工程, 2014, 14(18): 135-139. ZHANG Jie, REN Zuo-wu, ZHU Shou-lin. Research on the Effect of Prairie Road Straight Line Length on Drivers' HRV[J]. Science Technology and Engineering, 2014, 14(18): 135-139. |
| [9] |
田林, 许金良, 贾兴利. 高海拔地区驾驶员心率-反向曲线间直线长度-车速关系分析[J]. 公路交通科技, 2015, 32(11): 138-142. TIAN Lin, XU Jin-liang, JIA Xing-li. Analysis of Relationship of Driver's Heart Rate with Straight Length in Reverse Curve and Vehicle Speed in High Altitude Area[J]. Journal of Highway and Transportation Research and Development, 2015, 32(11): 138-142. |
| [10] |
武士钥, 朱守林, 戚春华, 等. 基于驾驶员视觉特性的草原公路直线长度研究[J]. 内蒙古农业大学学报: 自然科学版, 2013, 34(6): 142-147. WU Shi-yue, ZHU Shou-lin, QI Chun-hua, et al. The Research on the Straight-line Length of Prairle highway Based on Human Visual Characteristics[J]. Journal of Inner Mongolia Agricultural University: Natural Science Edition, 2013, 34(6): 142-147. |
| [11] |
路宁. 道路线形与交通事故关系分析[J]. 交通标准化, 2012, 4(8): 120-122. LU Ning. Relationship between Road Alignment and Traffic Accident[J]. Transportation Standardization, 2012, 4(8): 120-122. |
| [12] |
范李, 李刚炎, 陈冉, 等. 基于横向力系数的汽车急转防侧翻车速计算模型与仿真[J]. 农业工程学报, 2016, 32(3): 41-47. FANG Li, LI Gang-Yan, CHEN Ran, et al. Speed Calculation Model and Simulation of Rollover Prevention in Condition of Extreme Turn Based on Lateral Force Coefficient[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(3): 41-47. |
| [13] |
程国柱, 程瑞, 徐亮. 基于路侧事故判别的公路平曲线车速限制研究[J]. 交通运输系统工程与信息, 2020, 20(1): 222-227, 240. CHENG Guo-zhu, CHENG Rui, XU Liang. Speed Limit in Curving Sections of Highway Based on Roadside Accidents Discriminant Analysis[J]. Journal of Transportation Systems Engineering and Information Technology, 2020, 20(1): 222-227, 240. |
| [14] |
涂圣文, 王冰, 邓梦雪, 等. 考虑平纵组合的事故预测模型在双车道公路线形安全分析中的应用[J]. 公路, 2019, 64(7): 196-203. TU Sheng-wen, WANG Bing, DENG Meng-xue, et al. Application of Accident Prediction Model in Safety Analysis of Two-lane Highway Alignment Considering Horizontal and Vertical Combination[J]. Highway, 2019, 64(7): 196-203. |
| [15] |
郭应时, 付锐, 袁伟, 等. 山区公路事故率与平面线形的关系[J]. 交通运输工程学报, 2012, 12(1): 63-71. GUO Ying-shi, FU Rei, YUAN Wei, et al. Relation between Accident Rate and Horizontal Alignment for Mountain Highway[J]. Journal of Traffic and Transportation Engineering, 2012, 12(1): 63-71. |
| [16] |
王浩, 孟祥海, 关志强. 山区高速公路几何线形与事故率关系研究[J]. 公路工程, 2011, 36(4): 89-92. WANG Hao, MENG Xiang-hai, GUAN Zhi-qiang. Research on Relationship Between Traffic Accident Rate and Geometric Alignment for Mountainous Freeway[J]. Highway Engineering, 2011, 36(4): 89-92. |
| [17] |
张玥. 基于横向力系数的公路平曲线半径及超高取值方法研究[J]. 中外公路, 2015, 35(2): 5-9. ZHANG Yue. Research on Value Method of Highway Horizontal Curve Radius and Superelevation Based on Transverse Force Coefficient[J]. Journal of China & Foreign Highway, 2015, 35(2): 5-9. |
| [18] |
涂文靖. 曲线超高计算的优化方法及应用[J]. 铁道建筑, 2019, 59(2): 120-125. TU Wen-jing. Optimization Method and Application of Curve Superelevation Calculation[J]. Railway Engineering, 2019, 59(2): 120-125. |
| [19] |
潘兵宏, 周海宇, 刘斌, 等. 基于CarSim仿真的超高过渡起点位置对比研究[J]. 铁道科学与工程学报, 2018, 15(3): 637-644. PAN Bing-hong, ZHOU Hai-yu, LIU Bin, et al. Comparative Study of Superelevation Starting Position Based on Car Simsimulation Model[J]. Journal of Railway Science and Engineering, 2018, 15(3): 637-644. |
| [20] |
JTG D20-2006, 公路路线设计规范[S]. JTG D20-2006, Design Specifications for Highway Alignment[S]. |
| [21] |
JTJ 011-94, 公路路线设计规范[S]. JTJ-94, Design Specifications for Highway Alignment[S]. |
| [22] |
杨少伟. 道路勘测设计. 2版[M]. 北京: 人民交通出版社, 2009. YANG Shao-wei. Road Survey and Design. 2nd ed[M]. Beijing: China Communications Press, 2009. |
 2021, Vol. 38
2021, Vol. 38
