扩展功能
文章信息
- 屈强, 李星, 吴明先, 潘兵宏, 王贵山
- QU Qiang, LI Xing, WU Ming-xian, PAN Bing-hong, WANG Gui-shan
- 基于行车稳定性的高速公路超高过渡方式对比研究
- Comparative Study on Expressway Super-elevation Transition Modes Based on Driving Stability
- 公路交通科技, 2021, 38(9): 15-24
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(9): 15-24
- 10.3969/j.issn.1002-0268.2021.09.003
-
文章历史
- 收稿日期: 2021-04-26
2. 长安大学 公路学院, 陕西 西安 710064
2. School of Highway, Chang'an University, Xi'an Shaanxi 710064, China
公路曲线路段往往是事故的高发路段。相关报告指出,在近年来发生的重大交通事故中,弯道路段事故数、死亡人数逐年增加。由货车主导的事故占比超过2/3,其中,有超过3成的事故发生在高速公路路段[1]。而超高过渡段的设置有利于车辆遵循曲线走向,实现车辆的平稳运行。当前对于超高过渡段的渐变方式研究,一般立足于已建成的高速公路运营及相关路线规范的完善。为了使渐变路段高程计算相对简单,易于施工,设计中常使用线性渐变;但对于长缓和曲线及S型曲线路段,线性渐变方式不能很好地处理路面积水及行车的安全问题,而曲线超高渐变方式有排水性能优越、行车稳定性好的特性。
目前,国内外学者对于超高渐变方式的研究成果丰富。美国AASHTO主编《公路与城市道路几何设计》、《日本公路技术标准的解说与应用》规定了超高过渡方式、超高渐变率等参数的取值,以及超高过渡段长度的计算公式[2-3]。Jeong等[4]针对反向曲线中间横坡为0断面处排水的不良特性,研究了纵度对超高雨水排放的影响。Jeong[5]建立了以二维有限体积扩散模型来模拟几何表面的流场,以探寻路面板流分布与路面横坡、纵坡等的关系。Zhang[6]基于安全边界提出了安全合理的超高渐变率。Fitzpatrick等[7]讨论了有关侧摩擦因子和过渡长度确定的方法。Arslan等[8]在车辆运动学方面美学过渡曲线与经典过渡曲线进行比较,推导了曲率和超高函数。在考虑大型车辆稳定性的基础上,对高速公路设计超高方式进行了评价,其中,重点在于对侧摩阻力、最小半径等因素和设计速度之间的关系进行重新评估。
国内,白钢等[9]依靠CarSim仿真软件对车辆的行驶稳定性进行研究,提出了高速公路几何设计指标的合理取值范围,但未考虑超高渐变下的车辆稳定性参数。姜康等[10]结合轮胎的受力、形变特点,推导了半挂汽车列车特性、圆曲线路段参数的耦合动力学模型,却忽略了排水及行车稳定性的效应。谢威等[11]构建了特殊路段的极限半径模型(如陡坡急弯路段及弯坡叠加路段),同时构建了急弯陡坡路段坡长限制模型等。杨永前等[12]分析了S形曲线超高过渡的两种过渡方法的适用性及可行性。潘兵宏等[13]介绍了不同有关超高过渡段起点的设置要点,同时基于行车稳定性参数指标,构建3类方式下的横向力系数、横向加速度变化率模型。傅兴春[14-15]等基于排水要求提出了适合各等级公路路面排水的超高渐变率。
综上研究成果可知,国内外对超高过渡段研究均基于数学模型分析,大部分缺乏行车稳定性的分析。为了改善公路线性超高过渡段的行车稳定性及其零坡断面排水性能,本研究建立多次抛物线、三角函数的正弦上半段、余弦下半段缓和曲线超高渐变模型。在CarSim当中以长距离缓和曲线为对象建立道路工况,研究上述3种不同超高渐变方式对横向稳定性的影响,并分析横向偏移值、横向加速度、侧倾角、横摆角速度等稳定性参数变化趋势和特点。通过对比线性过渡方式与曲线过渡方式下车辆的行车稳定性,提出可保障零坡断面排水通畅的超高过渡方式。
1 三种曲线超高过渡方式计算模型目前适合的“曲线型”超高过渡方式(以下简称曲线过渡方式)有以下3种:三次抛物线、上半波正弦型曲线、下半波余弦型曲线,不同过渡方式的线形上任一点的超高值采用如式(1)~(3)计算。
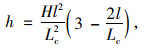
|
(1) |

|
(2) |
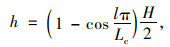
|
(3) |
式中,H为总超高;B为旋转轴至硬路肩外侧边缘的宽度;Lc为最小超高过渡段长度;l为超高过渡段中任一点至起点的距离;h为距离l处的高差。通过对上述公式中参数l求导,可得任一点的超高渐变率为:
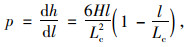
|
(4) |
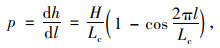
|
(5) |
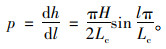
|
(6) |
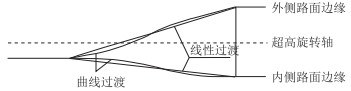
若继续对上述式(3)求导,可以发现曲线过渡方式的曲率变化率连续,即路面平纵线形平滑顺适。同时,这意味着经过超高过渡段起点和终点时,车辆不会出现明显的跳车、颠簸现象,保证了驾驶员的驾驶舒适性和安全性。曲线过渡方式同时适用于基本形和S形平曲线,如图 1、图 2所示。
|
| 图 1 单曲线的超高方式 Fig. 1 Superelevation mode of single curve |
| |
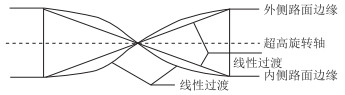
|
| 图 2 S形曲线的超高方式 Fig. 2 Superelevation mode of S-shaped curve |
| |
由图 1、2可以看出曲线过渡方式不仅可以保证行车顺适和路容美观,而且其中点为拐点且曲率连续,同时,此处路基边缘的纵向坡度、超高渐变率均达到最大值。因此需分析不同曲线过渡方式的最大超高渐变率。对式(4)~(6)经求导可得到3种曲线过渡方式的最大值,分别采用式(7)~(9)计算。其中,线性过渡方式的超高渐变率为定值H/Lc。
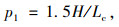
|
(7) |
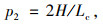
|
(8) |
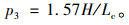
|
(9) |
显然,当超高过渡段长度相同时,多次抛物线、三角函数的正弦上半段、余弦下半段缓和曲线超高渐变率均大于线性过渡方式,其中,三角函数的正弦上半段为线性过渡方式的2倍。与线性渐变率为一定值不同,采用上述方法进行过渡的渐变率为连续变化的值,上述超高渐变方法都在回旋线中点达到临界值。
2 曲线过渡方式行车稳定性分析 2.1 车辆模型构建仿真时首先定义车辆模型。由于小客车速度较高,较货车受不同超高过渡方式的影响更大,因此本研究选用小客车作为仿真车型。根据《公路工程技术标准》[16]中规定的标准小客车的外观数据,结合CarSim自带的车辆材质库,新建了仿真车型的基本参数,如表 1所示。
| 参数 | 数值 | 参数 | 数值 | |
| 车身高度/m | 1.660 | 仿真车质量/kg | 1 370 | |
| 车身宽度/m | 2.000 | 转动惯量lxx/(kg·m -2) | 671.3 | |
| 质心横坐标/m | 1.110 | 俯仰惯量lyy/(kg·m -2) | 1 972.8 | |
| 质心纵坐标/m | 0.520 | 偏转惯量lzz/(kg·m -2) | 2 315.3 | |
| 车轴间距/m | 3.800 | 惯性积lxy/(kg·m -2) | 0 | |
| 车尾端横坐标/m | 5.200 | 惯性积lxz/(kg·m -2) | 0 | |
| 车尾端纵坐标/m | 0.500 | 惯性积lyz/(kg·m -2) | 0 | |
| 左前轮纵坐标/m | 0.340 | 回转半径Rx/m | 0.700 | |
| 左后轮纵坐标/m | 0.340 | 回转半径Ry/m | 1.200 | |
| 右前轮纵坐标/m | 0.325 | 回转半径Rz/m | 1.300 | |
| 右后轮纵坐标/m | 0.325 | 质心侧向坐标/m | 0 |
2.2 构建道路模型和仿真控制策略
建立道路模型时,需考虑道路的线形特征、路面构造、摩擦系数及环境4个方面。道路场景如图 3所示。

|
| 图 3 道路场景图 Fig. 3 Road scene |
| |
表 2给出了三次抛物线、上半波正弦型曲线过渡下的平曲线参数(由于下半波余弦型曲线过渡与三次抛物线过渡长度相似,二者仿真设置参数一致)。其中,超高最大值设定为6%(即一般地区),超高过渡方式为绕中央分隔带边缘旋转;并根据《公路路线设计规范》中规定的不同设计速度选择相应半径。为使不同线形间保持协调,宜将圆曲线与回旋线的长度尽量保持一致,圆曲线最长不能超过回旋线的2倍[17]。为满足最大、最小超高渐变率要求,仿真中取回旋线长度均超过极限值,具体设置长度如表 2所示。为使三次抛物线、上半波正弦型曲线的最大超高渐变率等于线性渐变的最大值,其长度等于1.5倍线性过渡段长度。
| 超高过渡方式 | 设计速度/ (km·h -1) | 半径/m | 直线长度/m | 缓和曲线长度/m | 圆曲线长度/m | 总长/ m |
| 三次抛物线过渡 | 80 | 500 | 198 | 198 | 198 | 594 |
| 120 | 1 200 | 264 | 264 | 264 | 792 | |
| 上半波正弦曲线过渡 | 80 | 500 | 264 | 264 | 264 | 792 |
| 120 | 1 200 | 352 | 352 | 352 | 1 056 | |
| 线性过渡 | 80 | 500 | 198 | 132 | 264 | 594 |
| 120 | 1 200 | 264 | 176 | 352 | 792 |
在CarSim的建模设置中,速度控制选用Target speed from path preview模式;制动控制采用No Open-loop Braking Pressure模式,车辆行驶挡位根据车辆即时行驶速度确定,行驶方向根据道路中线自行控制转向,转向系统当中的主传动器速比与变速器速比均按照规定选取,其他参数均采用软件提供的默认值。
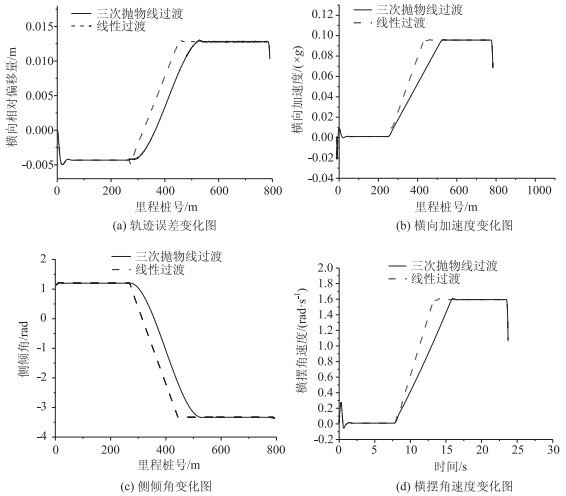
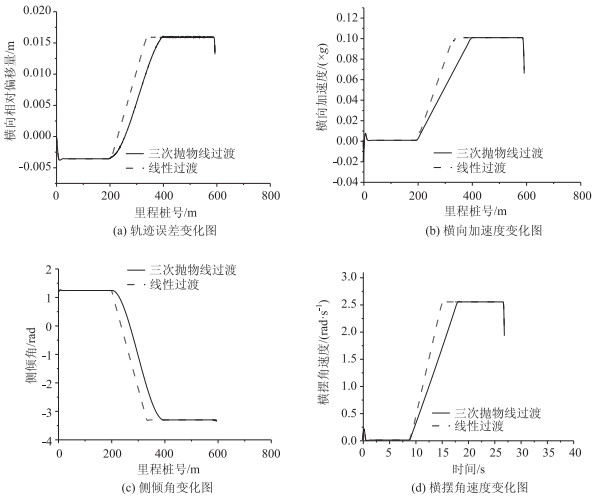
2.3 稳态参数的输出上述基础参数、控制策略等设定完毕后,运行CarSim进行仿真运行,得到衡量车辆稳定性的参数(横向加速度、横移值、横摆角速度、侧倾角)变化图。由于仿真试验过于冗杂及文章篇幅限制,无法展示所有工况下的结果,因此选取具有代表性的120,80 km/h设计速度下对应的仿真工况,经MATLAB等数据处理软件分析后,得到如图 4~5所示的三次抛物线过渡、图 6~7所示的下半波余弦型曲线和图 9~10所示的上半波正弦型曲线过渡3种过渡方式下的车辆稳定状态参数。
|
| 图 4 120 km/h设计速度下稳定性参数变化(三次抛物线过渡) Fig. 4 Change of stability parameters at design speed of 120 km/h (cubic parabola transition) |
| |
|
| 图 5 80 km/h设计速度下稳定性参数变化(三次抛物线过渡) Fig. 5 Change of stability parameters at design speed of 80 km/h (cubic parabola transition) |
| |
|
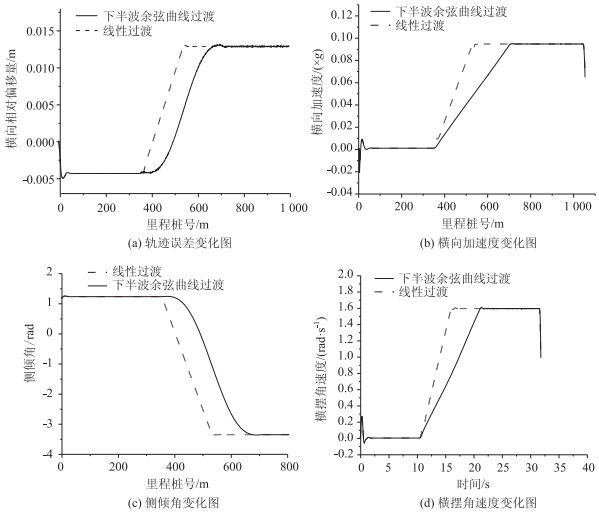
| 图 6 120 km/h设计速度下稳定性参数变化图(下半波余弦型曲线) Fig. 6 Change of stability parameters at design speed of 120 km/h (lower-half cosine curve) |
| |
|
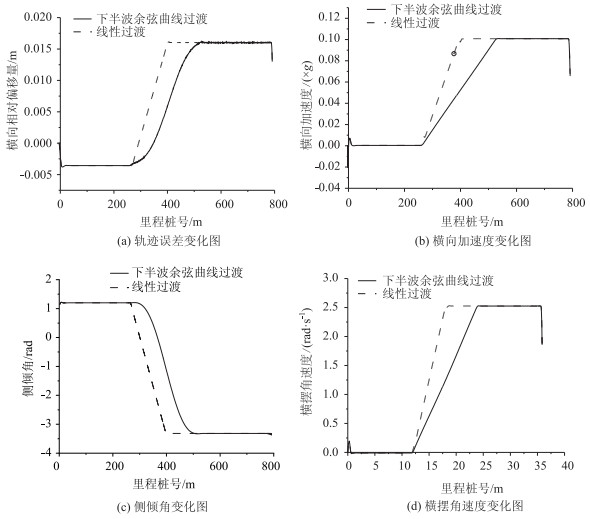
| 图 7 80 km/h设计速度下稳定性参数变化图(下半波余弦型曲线) Fig. 7 Change of stability parameters at design speed of 80 km/h (lower-half cosine curve) |
| |
|
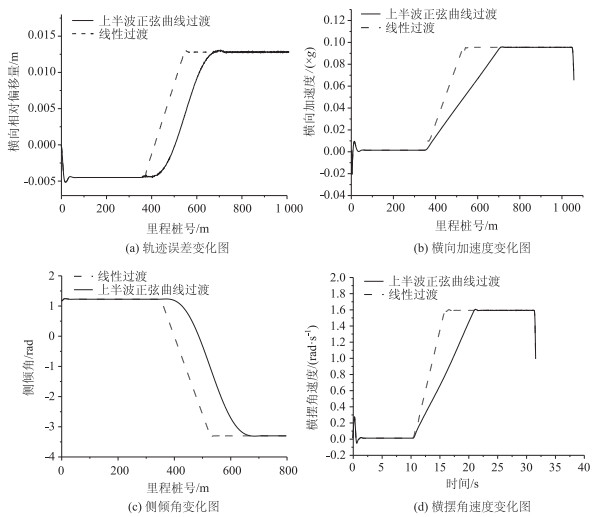
| 图 8 120 km/h设计速度下稳定性参数变化图(上半波正弦曲线) Fig. 8 Change of stability parameters at design speed of 120 km/h (upper-half sine-type) |
| |
|
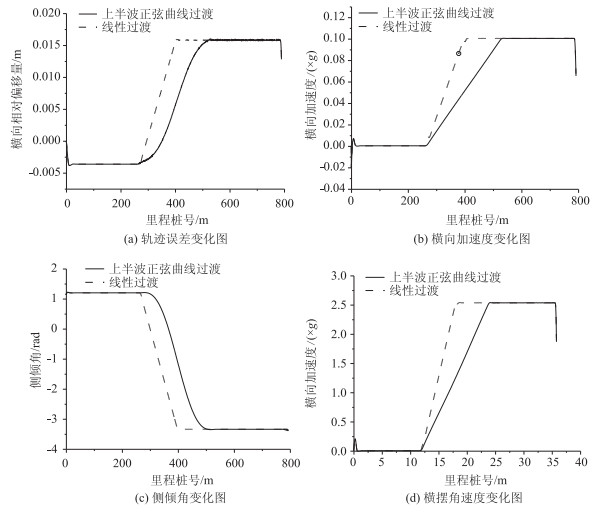
| 图 9 80 km/h设计速度下稳定性参数变化图(上半波正弦型曲线过渡) Fig. 9 Change of stability parameters at design speed of 80 km/h (upper-half sine-type) |
| |
由图 4~7可知:小客车在不同运行速度下,两类曲线过渡方式(三次抛物线、半波余弦型曲线过渡)下输出的稳定性参数变化趋势上保持一致,曲线型超高过渡段在同样的横断面高差条件下需要更长的曲线长度,因此车辆稳定性变化率小,在稳定性最高点处,曲线型与线形数值相同,所处曲线类型均为圆曲线。多次抛物线缓和曲线起终点处稳定性存在波动变化,三角函数的余弦下半段缓和曲线稳定性更好,车辆行驶更加平顺。
为使上半波正弦型曲线的最大超高渐变率等于线性渐变的最大值,其长度等于2倍线性过渡段长度。由图 8~9可知,设计速度为120 km/h,小客车的轨迹误差在-5~13 mm之间,横向加速度、侧倾角、横摆角速度等参数变化分别位于区间[-0.05~0.1](m·s-2),[-0.057 6 rad~-0.019 2 rad],[0~1.6](rad·s-1)。当超高过渡采用线性方式时,上述参数在缓和曲线端点存在波动,甚至突变,且变化率保持不变;正弦上半段过渡方式对行车平滑性呈现正改善,变化率小。设计速度为80 km/h时,轨迹误差增大,横向加速度、侧倾角变化不明显,横摆角速度增大,即小客车稳定性参数波动变大。
2.4 稳定性分析由仿真结果可知:(1)采用三次抛物线超高过渡方式时,整体稳定性优于其他方式,线性超高过渡方式总体稳定性不理想,不如三次抛物线和上半波正弦曲线,当采用线性超高过渡方式时,纵坡的起点和终点会产生突变,这是因为线性超高过渡会在曲线起终点位置产生附加坡度。(2)要实现车辆平顺稳定行驶,超高渐变需采用曲线渐变方式,并且超高过渡段恰好能在曲线起讫点处。
3 曲线过渡方式的排水分析超高过渡段会对道路排水产生较大影响,影响道路排水的因素是复杂且多样的。《公路路线设计规范》(JTG-D20—2017)(以下简称《路线规范》)[17]中规定道路纵向坡度与横向坡度的合成坡度需大于0.5%。当横断面为平坡时,无论道路纵坡设置成多大,路面水依然会向坡底聚集;但当横断面有一定大小横坡时,尽管路线纵坡为0,路面水也将沿横断面快速流往路基之外[18]。由此可见,合成坡度虽一定程度上影响路面的排水性能,但发挥主要作用的是横坡。下面从排水性能的角度分析3类超高过渡形式对超高过渡段路面的影响,从而选择更有利于路面排水的超高过渡方式。
3.1 小横坡段长度小横坡段是指超高区间的横坡处于[-0.3%, 0.3%]的路段。关于小横坡段,《日本高速公路设计要领》(简称《要领》)[19]的描述是:路段排水不畅区间,往往是直线向圆曲线过渡处或反向曲线拐点附近处。显然,当超高渐变率过小时,小横坡路段的长度就较长,横向排水路段的长度就更长,高速行车会因溅水、滑溜引发交通安全事故。当平曲线超高横坡区间为[-2%, 2%]时,其长度需收到限制,且最小渐变率要高于1/300;当超高横坡区间大于2%时,在满足最大超高渐变率的情况下,排水及行车舒适性将不再受最小渐变率取值的影响,因而不限制此类路段的最小超高渐变率。曲线上任一断面超高横坡计算公式可由式(1)~(3)计算得到,如式(10)~(13)。
三次抛物线[20]:
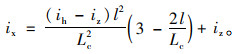
|
(10) |
上半波正弦型曲线:
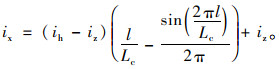
|
(11) |
下半波余弦型曲线:
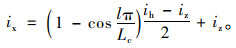
|
(12) |
线性渐变:
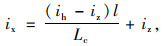
|
(13) |
式中, ix为缓和曲线上某点的超高横坡值;ih为全超高值;iz为路拱横坡值;l为超高过渡段上某点至超高起点的距离。[-2%, 2%]区间范围内的超高过渡段,不仅要满足最大超高渐变率,还要尽量缩短小横坡(即区间范围为[-0.3%, 0.3%])过渡区段的长度。
根据式(10)~(12)找到不同过渡方式下小横坡区间起讫点(-0.3%, 0.3%)在整个过渡区间长度上的位置坐标,进而得到3种曲线过渡方式下小横坡段长度与超高过渡段长度Lc之比,结果如表 3所示。
| iz | -2 | ||||||||
| ih | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 |
| l0x | 0.05 | 0.055 | 0.06 | 0.067 | 0.075 | 0.086 | 0.1 | 0.12 | 0.15 |
| l0p | 0.043 | 0.046 | 0.049 | 0.053 | 0.057 | 0.063 | 0.07 | 0.082 | 0.1 |
| 1.5l0p | 0.065 | 0.069 | 0.073 | 0.079 | 0.085 | 0.094 | 0.106 | 0.123 | 0.15 |
| l0z | 0.036 | 0.038 | 0.039 | 0.042 | 0.045 | 0.049 | 0.054 | 0.062 | 0.076 |
| l0y | 0.042 | 0.045 | 0.048 | 0.051 | 0.055 | 0.061 | 0.068 | 0.078 | 0.096 |
| Δl1 | -0.007 | -0.009 | -0.011 | -0.014 | -0.018 | -0.023 | -0.03 | -0.038 | -0.05 |
| Δl2 | 0.015 | 0.014 | 0.013 | 0.012 | 0.01 | 0.008 | 0.006 | 0.003 | 0 |
| Δl3 | -0.014 | -0.017 | -0.021 | -0.025 | -0.03 | -0.037 | -0.046 | -0.058 | -0.074 |
| Δl4 | -0.008 | -0.01 | -0.012 | -0.016 | -0.02 | -0.025 | -0.032 | -0.042 | -0.054 |
| 注:表中l0x,l0p,l0z,l0y为不同过渡方式下小横坡段长度与缓和曲线长度Lc的比值,如线性过渡、三次抛物线过渡、上半波正弦曲线、下半波余弦曲线过渡,Δl1,Δl2,Δl3,Δl4指3种曲线型过渡方式的小横坡段长度比(l0p,1.5l0p,l0z,l0y)分别与线性渐变的小横坡段长度比(l0x)的差值。 | |||||||||
由表 2可知:(1)过渡段长度相同时,线性过渡的小横坡段长度比曲线过渡长;(2)线性过渡小横坡段长度分别超三次抛物线、上半波正弦型曲线、下半波余弦型曲线过渡方式长度的16%~50%,39%~98%,19%~56%;(3)上半波正弦型曲线的小横坡段长度最短;(4)最大渐变率与线性过渡相同时,三次抛物线过渡的小横坡段长度是线性过渡的1~1.3倍。
3.2 零坡位置4类超高过渡方式的零坡位置可根据式(10)~(13)可以得到,见表 4。
| iz/% | -2 | |||||||||
| ih/% | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 零坡点距过渡段起点长度/ Lc | 线性 | 0.500 | 0.400 | 0.333 | 0.286 | 0.250 | 0.222 | 0.200 | 0.182 | 0.167 |
| 三次抛物线 | 0.500 | 0.433 | 0.387 | 0.353 | 0.326 | 0.305 | 0.287 | 0.272 | 0.259 | |
| 上半波正弦型曲线 | 0.500 | 0.449 | 0.414 | 0.388 | 0.367 | 0.350 | 0.336 | 0.323 | 0.313 | |
| 下半波余弦型曲线 | 0.500 | 0.436 | 0.392 | 0.359 | 0.333 | 0.312 | 0.295 | 0.280 | 0.268 | |
分析表 4可得到以下结论:
(1) 在其他变量保持不变的情况下,4种超高过渡方式的零坡位置有差异。
(2) 当超高过渡段长度相同时,线性过渡段的零坡位置最近,上半波正弦曲线最远。S形曲线采用线性过渡方式时零坡位置与长度成线性关系以消除反超高的影响,同时便于使平面线形拐点位置与零坡位置吻合。设置曲线型过渡方式下,零坡位置较难吻合于拐点位置处。因此,为控制小横坡段位置,满足路面排水要求,S形曲线型过渡段通常将以[-ih1, 2%],[-2% 2%],[2%, ih2]三区间分段设置。
4 结论为解决高速公路线性超高过渡段的行车稳定性不足和小横坡断面排水不良的问题,基于动力学软件CarSim仿真平台,分别构建三次抛物线、上半波正弦型、下半波余弦型曲线3种曲线型超高渐变仿真模型,以多车道高速公路的长缓和曲线的道路线形为试验路况,分析了零坡断面处的超高渐变率,验证了不同超高渐变方式下的行车稳定性,并输出了相应的稳定性参数变化情况。对比分析了线性过渡方式与曲线过渡方式的小横坡路段长度,研究主要结论如下:
(1) 渐变段长度相同时,三次抛物线、上半波正弦型、下半波余弦型过渡的超高渐变率是线性过渡超高渐变率的1.5,2,1.57倍。线性过渡方式的超高渐变率恒定,曲线过渡方式超高渐变率连续变化,都以过渡段中点为临界点,渐变率呈现轴对称分布,在中点处达到最大值,即在横坡为零的断面附近超高渐变率最大,能有效缩短小横坡路段的长度,有利于雨天的行车安全。
(2) 3种曲线过渡方式在超高过渡起终点附近的侧向加速度、横摆角速度曲线较线性过渡方式平滑连续。同时,通过分析对比3种曲线型过渡形式下小横坡段的长度,结果表明三次抛物线的过渡形式小横坡段的长度最短,更有利于雨天的行车安全。
(3) 建议将过渡段中最大超高渐变率与零坡断面位置相结合,可降低小横坡路段长度,增强路面排水。曲线超高方式对改善多车道高速公路长缓和曲线过渡段的稳定性及排水性能有重要意义。
受限于研究条件和篇幅,需要进一步验证实际车辆于雨天行驶这种不利的情况下曲线型过渡方式的合理性;由于超高过渡段设置方式可拓展到弧形路拱的范畴,可进一步从行车稳定性及排水性能来分析验证。
| [1] |
李方媛. 重特大道路交通事故致因机理及其风险行为研究[D]. 西安: 长安大学, 2014. LI Fang-yuan. Research on Cause Mechanism of Major Road Traffic Accidents and Its Risk Behaviors[D]. Xi'an: Chang'an University, 2014. |
| [2] |
日本道路协会. 日本公路技术标准的解说与运用[M]. 北京: 人民交通出版社, 1980. Japan Road Association. Interpretation and Application of Japanese Highway Technical Standards[M]. Beijing: Chinas Communications Press, 1980. |
| [3] |
AASHTO. A Policy on Geometric Design of Highways and Streets[R]. Washington, D. C. : AASHTO, 2011.
|
| [4] |
JEONG J. A Hydrodynamic Diffusion Wave Model for Stormwater Runoff on Highway Surfaces at Superelevation Transitions[D]. Austin: University of Texas at Austin, 2008.
|
| [5] |
JEONG J, CHARBENEAU R J. Diffusion Wave Model for Simulating Storm-water Runoff on Highway Pavement Surfaces at Superelevation Transition[J]. Journal of Hydraulic Engineering, 2010, 136(10): 770-778. |
| [6] |
ZHANG Z, CHENG J. Safety Margin-based Analysis on Road Superelevation Rate Selection[C]//15th COTA International Conference of Transportation Professionals. [S. l. ]: COTA, 2015.
|
| [7] |
FITZPATRICK K, KAHL K. A Historical and Literature Review of Horizontal Curve Design[R]. Austin: Texas Department of Transportation, 1992.
|
| [8] |
ARSLAN A, TARI E, ZIATDINOV R, et al. Transition Curve Modeling with Kinematical Properties: Research on Log-Aesthetic Curves[J]. Computer-Aided Design and Applications, 2014, 11(5): 509-517. |
| [9] |
白钢. 基于车辆行驶稳定性仿真的道路几何线形设计参数研究[D]. 长春: 吉林大学, 2013. BAI Gang. Study on Design Parameters of Road Geometric Alignment Based on Vehicle Driving Stability Simulation[D]. Changchun: Jilin University, 2013. |
| [10] |
姜康, 张梦雅, 陈一锴. 山区圆曲线路段半挂汽车列车行驶安全性分析[J]. 交通运输工程学报, 2015, 15(3): 109-117. JIANG Kang, ZHANG Meng-ya, CHEN Yi-kai. Driving Safety Analysis of Semi-trailer Train at Circular Curve Section in Mountain Area[J]. Journal of Traffic and Transportation Engineering, 2015, 15(3): 109-117. |
| [11] |
谢威. 基于车路耦合安全度模型的弯坡组合路段设计理论研究[D]. 重庆: 重庆交通大学, 2017. XIE Wei. Research of Curved Slope Road Design Theory Based on Vehicle-road Coupling Safety Model[D]. Chongqing: Chongqing Jiaotong University, 2017. |
| [12] |
杨永前, 黄红明. S形曲线超高过渡设计方法研究[J]. 中外公路, 2017, 37(6): 6-9. YANG Yong-qian, HUANG Hong-ming. Study on Ultra-high Transition Design Method of S-shaped Curve[J]. Journal of China & Foreign Highway, 2017, 37(6): 6-9. |
| [13] |
潘兵宏, 周海宇, 刘斌, 等. 基于CarSim仿真的超高过渡起点位置对比研究[J]. 铁道科学与工程学报, 2018, 15(3): 637-644. PAN Bing-hong, ZHOU Hai-yu, LIU Bin, et al. Comparative Study of Superelevation Starting Position Based on CarSim Simulation Model[J]. Journal of Railway Science and Engineering, 2018, 15(3): 637-644. |
| [14] |
傅兴春. 考虑排水的超高渐变率设计[J]. 中外公路, 2019, 39(5): 5-8. FU Xing-chun. Design of Ultra-high Gradient Considering Drainage[J]. Journal of China & Foreign Highway, 2019, 39(5): 5-8. |
| [15] |
张锋, 刘永旭, 杜晓博. 高速公路超高渐变段排水技术研究[J]. 华东公路, 2019(1): 44-48. ZHANG Feng, LIU Yong-xu, DU Xiao-bo. Research on Drainage Technology of Superhigh Gradient Section of Expressway[J]. East China Highway, 2019(1): 44-48. |
| [16] |
JTG B01-2014, 公路工程技术标准[S]. JTG B01-2014, Technical Standard of Highway Engineering[S]. |
| [17] |
JTG D20-2017, 公路路线设计规范[S]. JTG D20-2017. Design Specifications for Highway Alignment[S]. |
| [18] |
刘利民, 王智. 三次抛物线与线性超高渐变的对比研究[J]. 中外公路, 2018, 38(3): 1-3. LIU Li-min, WANG Zhi. Comparative Study of Three-order Parabola and Linear Superelevation Runoff[J]. Journal of China & Foreign Highway, 2018, 38(3): 1-3. |
| [19] |
日本道路公团. 日本高速公路设计要领[M]. 西安: 陕西旅游出版社, 1991: 125-155. Japan Road Corporation. Essentials of Japanese Highway Design[M]. Xi'an: Shaanxi Tourism Publishing House, 1991. |
 2021, Vol. 38
2021, Vol. 38
