扩展功能
文章信息
- 王佐, 王贵山, 李星, 吴善根, 王松
- WANG Zuo, WANG Gui-shan, LI Xing, WU Shan-gen, WANG Song
- 基于车辆悬挂系统的高速路圆曲线极限最小半径路段车辆稳定性仿真
- Simulation on Vehicle Stability of Limit Minimum Radius Section of Circular Curve on Expressway Based on Vehicle Suspension System
- 公路交通科技, 2021, 38(9): 9-14, 24
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(9): 9-14, 24
- 10.3969/j.issn.1002-0268.2021.09.002
-
文章历史
- 收稿日期: 2021-04-26
曲线路段的事故比其他路段多,研究表明在2012年和往后的6年里,弯道路段事故次数与死亡人数越来越多,数据中6.30%的原因是两货车相撞,货车事故占比是67.72%,高速公路事故占34.62%[1]。但这些弯道上的事故是否与圆曲线最小半径的取值有关呢?弯道上发生事故的原因较为复杂,既可能有驾驶人超速行驶的原因,也可能是弯道路段的超高设置不合理,影响车辆行车稳定性,导致过弯转向失控,发生侧滑甚至侧翻。《公路路线设计规范》(JTG-D20—2017)(以下简称《路线规范》)中列出的圆曲线极限最小半径(以下简称极限半径)计算模型中假设车辆为刚体(以下简称该计算模型为刚体模型),简化的刚体模型与装有悬挂系统的实际车辆之间存在差异,《路线规范》中采用刚体模型得到的极限半径是否满足具有悬挂系统车辆行驶的安全,若满足安全,安全余量如何等疑问需要解决。
目前,国内外相关学者研究了刚柔耦合下的曲线路段圆曲线最小半径计算模型。美国AASHTO主编的《公路与城市道路几何设计》(2011版,绿皮书)[2]提出了简化模型,并在此基础上分析了路面摩擦系数与超高的界定标准。Kordani等[3]采用仿真软件利用多重回归分析的方法研究,得出不同车型的侧向摩擦系数公式。Chang等[4]从车辆的悬架特性出发,研究基于悬架特性的弯道半径修正方程,并提出了既有公路曲线的评价方法。Haywood[5]等研究曲线路段车辆受力模型准确性,认为多个曲线设计速度受到最大允许超高限制。Craus等[6]从车辆悬架特性出发研究出基于悬架特性的曲线半径模型更合理。
张玥等[7]研究了横向力系数和半径的耦合,提供了平曲线半径以及相应超高横坡的推荐值,研究中忽略了悬挂装置的影响。范李等[8]研究涉及车辆悬挂效应的平曲线横向力系数并给出了危险阈值和车速之间的对应。罗京等[9]考虑悬挂系统推出该情况下半径计算方法,得出极限半径,但该研究缺少车辆稳定性仿真研究。范李等[10]考虑车辆过弯侧翻研究急转时车体的受力特性,改进横向力系数公式。张肖磊[11]在超高计算中引入可靠度理论,以车辆产生侧滑、倾覆等现象的极限状态为条件,建立安全超高计算模型。范爽[12]在事故资料调查和分析了公路平面设计元素组合安全性的基础上,提出了基于交通安全的高速公路平面设计指标及其组合。涂文靖[13]提出速度结合计算曲线超高。王磊[14]分析S路段中的高危段事故发生原因,研究超高渐变和零坡断面等。
目前国内外的部分研究立足于刚体模型对圆曲线最小半径的安全性分析,也有基于悬挂系统下圆曲线最小半径的分析,但大部分都没有针对车辆在弯道上行驶时稳定性指标进行分析评价,没有专门针对极限最小半径工况下的车辆稳定性分析。因此,本研究将首先构建基于车辆悬挂系统是公路极限半径计算模型(以下简称悬挂模型),然后根据《路线规范》中极限半径计算的参数,计算出基于悬挂模型的极限半径,最后分别在CarSim/TruckSim构建两种模型,研究两类模型的参数差异,分析特点,进而分析《路线规范》中的极限半径能否满足具有悬挂系统车辆的行驶稳定性要求。
1 悬挂模型的构建 1.1 代表车型的选择考虑到当前研究常为简单的客货分类研究,本研究对国内各级公路上的车辆运营状况进行调查分析,提出适宜我国公路车辆的分类。表 1~2为2018年调研高速公路上车型分布比例[15],表 2~3为2012—2018年我国高速公路不同类型货车占比变化情况。由表 1可以看出小客车占客车比例的96.08%,应将小客车作为客车的代表车型。由表 3可看出,铰接车占比逐年上升,逐渐承担其货车的主要市场。相比较而言,2,3,4轴货车占比变少。2018年铰接车占43.42%,其中,49 t的6轴铰接车成为高速公路货运的主要车型。故将6轴铰接车作为货车的代表车型。代表车型外部轮廓尺寸如表 4所示。
| 客座数量 | ≤7座 | ≥8座 |
| 客流转乘占比 | 63.52 | 36.48 |
| 车型占比 | 96.08 | 3.92 |
| 客流数占比 | 69.05 | 31.95 |
| 轴数 | 2轴 | 3轴、4轴 | 5、6轴铰接车 |
| 货运转运占比 | 7.32 | 8.86 | 83.82 |
| 轴类占比 | 40.75 | 14.54 | 44.71 |
| 车流量占比 | 34.23 | 16.52 | 49.25 |
| 年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
| 2轴4胎 | 11.32 | 12.68 | 13.05 | 13.16 | 12.03 | 11.57 | 12.54 |
| 2轴6胎 | 31.08 | 30.51 | 32.03 | 28.96 | 33.46 | 30.51 | 28.98 |
| 3轴、4轴货车 | 14.84 | 14.55 | 14.89 | 15.44 | 14.38 | 13.12 | 13.87 |
| 铰接车 | 41.75 | 41.83 | 41.21 | 42.13 | 38.95 | 43.67 | 43.42 |
| 代表车型 | 车长 | 车宽 | 后悬 | 前悬 | 轴距 | 车高 |
| 小客车 | 6 | 1.8 | 1.4 | 0.8 | 3.8 | 2 |
| 铰接列车 | 18.1 | 2.55 | 2.3 | 1.5 | 3.3+11 | 4 |
1.2 悬挂模型的构建
如图 1所示,悬挂系统下车辆离心力F使车向外微倾,悬挂装置变成内拉外伸,车体呈现绕P处旋转,载荷质心O点横向出现了偏移。内外车轮由于负载不平衡,导致抗侧翻能力下降。但悬挂系统的重心却比刚体更低。货车的载重大,悬架弹簧压缩更加严重,所以质心位置变低。综上,悬挂系统对货车更佳。本研究考虑多自由度建立悬挂系统曲线最小半径模型。
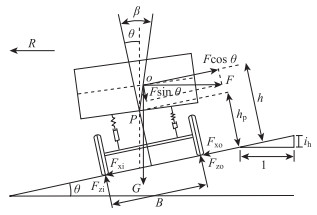
|
| 图 1 悬挂效应下车辆的受力特性 Fig. 1 Force characteristics of vehicle under suspension effect |
| |
(1) 悬挂模型
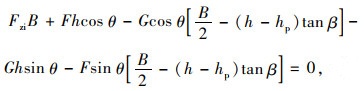
|
(1) |
式中,hp为车辆倾侧中心O距地面的高度;h为重心高度;Fzi地面对车辆作用反力;B为轮距;θ为路面超高下的横坡倾角,因θ较小,认为θ≈sin θ≈tan θ≈ih, cos θ≈1;β为车辆荷载质心的倾角;G为车辆自重。
将式(1)转化可得:
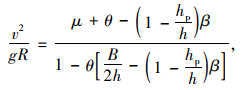
|
(2) |
式中,v为车辆速度;μ为路面摩擦系数;R为圆曲线半径;g为重力加速度。
车辆横摆角φ[16]用式(3)来描述:
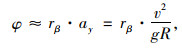
|
(3) |
式中,rβ为车辆的侧倾率;ay为车辆侧向加速度。联立(1)~(3)得:
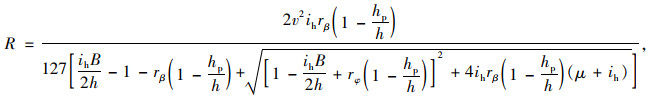
|
(4) |
式中,ih为道路超高。客车、货车的重心比分别为hp/h≈0.5, 0.25,侧倾率分别为rβ≈0.12,0.14 rad/g。一般汽车设计B/2h≈1,悬挂模型如式(5)所示。

|
(5) |
考虑到ih(μ+ih)值较小,在式(5)中几乎不影响曲线半径计算,故式(5)可简化为式(6):
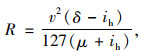
|
(6) |
式中δ为车型系数,客车δ=1.06,货车δ=1.105。
(2) 刚体模型
相对于悬挂模型,传统曲线最小半径计算方法的刚体模型如图 2所示。
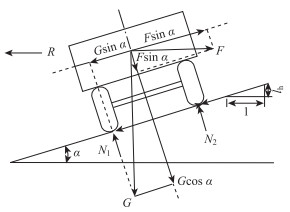
|
| 图 2 无悬挂效应下车辆的受力特性(刚体模型) Fig. 2 Force characteristics of vehicle without suspension effect (rigid body model) |
| |
刚体模型下圆曲线最小半径用(7)式计算。
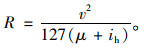
|
(7) |
行驶于圆曲线路段上的车辆横向力系数最大值应小于或等于横向摩阻系数μ。μ采取的值对应直接影响乘车心理、生理的感觉。
本研究利用交通运输部公路研究院的研究[17],考虑C级舒适度的情况下回归横向力系数阈值μ以及速度v的相关情况,见式(8)。
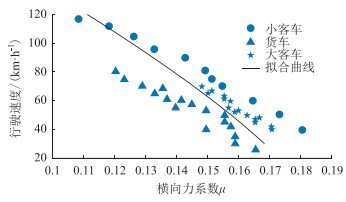
|
| 图 3 C级舒适度对应的横向力系数阈值 Fig. 3 Lateral force coefficient threshold corresponding to comfort level C |
| |
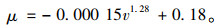
|
(8) |
利用式(8)可由速度v得C级横向力系数μ的阈值。
2 基于悬挂模型的圆曲线极限半径通过给定设计速度并计算相应的C级舒适度对应的横向力系数μ,并选取10%和8%两种最大超高值,可以计算出圆曲线最小半径极限值。查找《公路路线设计规范》(JTG D20—2017),圆曲线最小半径极限值总结如表 5~6所示。
| 设计速度/ (km·h -1) | 横向力系数 | 最大超高/% | 最小半径计算值/m | 最小半径推荐值/m | 《规范》最小半径极限值/m |
| 120 | 0.111 | 10 | 516 | 520 | 570 |
| 8 | 585 | 585 | 650 | ||
| 100 | 0.126 | 10 | 336 | 340 | 360 |
| 8 | 376 | 380 | 400 | ||
| 80 | 0.139 | 10 | 203 | 205 | 220 |
| 8 | 226 | 230 | 250 | ||
| 60 | 0.151 | 10 | 109 | 110 | 115 |
| 8 | 120 | 120 | 125 |
| 设计速度/ (km·h -1) | 横向力系数 | 最大超高/% | 最小半径计算值/m | 最小半径推荐值/m | 《规范》最小半径极限值/m |
| 80 | 0.139 | 10 | 212 | 215 | 220 |
| 8 | 236 | 240 | 250 | ||
| 60 | 0.151 | 10 | 113 | 115 | 115 |
| 8 | 126 | 130 | 125 |
对比表 5~6中圆曲线最小半径极限值计算结果和《规范》值的对比,可以看出计算结果略小于《规范》值。这说明计算结果是可靠的,规范对设计指标预留了安全余量。
3 极限半径下车辆稳定性分析由于表 5、表 6中提出极限最小半径稍低于《路线规范》,需对该半径下车辆的稳定性进行分析。本节基于CarSim软件构建车辆动力学仿真平台,在刚体模型与悬挂模型两者得出的半径下比较分析车辆的稳定性,表 7列出了半径的比较值。
| 设计速度/(km·h -1) | 120 | 80 | ||||||
| 圆曲线半径 | 刚体 | 悬挂 | 刚体 | 悬挂(客车) | 悬挂(货车) | |||
| 最小半径 | ihmax=10% | 570 | 520 | 220 | 205 | 215 | ||
| ihmax=8% | 650 | 585 | 250 | 230 | 240 | |||
3.1 构建车辆动力学仿真模型
CarSim/TruckSim仿真软件,可评估输出得到的车辆动力学效应参数,以实现车辆的稳定、舒适行驶。利用仿真软件对两种模型进行仿真来研究车辆稳定性。
(1) 车辆尺寸及荷载
如图 4所示,设定车辆模型是仿真的第一步,依据表 4进行拟定。在TruckSim平台上拟定如图 4(b)所示6轴货车。《集装箱外部尺寸和额定重量》(GB1413—2008)、《汽车、挂车及汽车列车外轮廓尺寸、荷载及质量限值》(GB1589—2016)给出长、宽、高为20 m,2.5 mm,4 m,满载49 t,同时利用荷载箱体模型来实现挂车的满载效应。
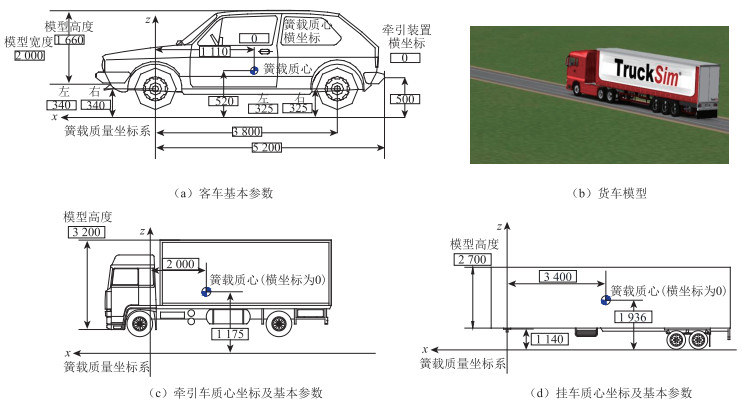
|
| 图 4 客货车质心坐标及基本参数(单位:mm) Fig. 4 Centroid coordinates and basic parameters of passenger car and truck(unit: mm) |
| |
(2) 构建道路模型
《路线规范》中规定回旋线、圆曲线、回旋线之长度比宜设计成1∶1∶1或1∶2∶1[18]。本研究中在不小于极限值的条件下定出的回旋线长度如表 8所示。
| 设计速度/ (km·h -1) | 超高/% | 圆曲线长度/m | 缓和曲线长度/m | 直线长度/m |
| 120 | 10 | 100 | 100 | 100 |
| 10 | 100 | 100 | 100 | |
| 80 | 100 | 70 | 70 | 70 |
| 8 | 70 | 70 | 70 |
在仿真软件利用断面渐变给出道路超高,设置示意如图 5所示。
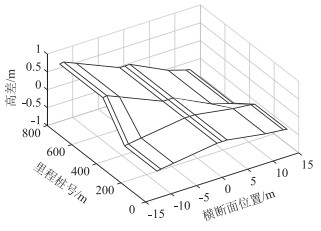
|
| 图 5 超高三维示意图 Fig. 5 Three-dimensional schematic diagram of superelevation |
| |
(3) 驾驶控制模型
仿真与超高相关,Target speed from path preview子模块控速,制动控制中,试验采用No Open-loop Braking Pressure模式自动换档。预瞄驾驶策略转向控制,运行轨迹采取行车道中线。主传动器速比设为25∶1,其他用默认值。
3.2 悬挂模型准确性及与刚体模型差异性分析(1) 稳态参数的输出
给定两模型的半径,依次输出得到衡量车辆的稳定性参数,如横向偏移值、横向加速度、横摆角速度以及侧倾角等。
(2) 稳定性分析
在高、低速情况下,基于刚性与悬挂刚体模型输出得到的4项稳定性参数走势无差别。
① 轨迹误差
相比刚体情况下,悬挂下的客、货车轨迹误差峰值稍大。而曲线段,刚体客、货车偏移距离并不稳定。
② 侧倾角的幅度值
刚体时两种情况下的侧倾角幅值浮动大,两模型浮动范围为-2°±4°。相对于刚体而言,悬挂车辆侧倾角峰值略。货车的两模型侧倾角变化曲线大致相同。
③ 横向加速度变化
两情况客车横向加速度走向相同,刚体车辆转弯半径增长时对应的横向加速度降低,稳定性更优。而货车的两种情况无明显差别。
④ 横摆角速度变化
当半径降低时,悬挂客车横摆角速度会增大,比较刚体情况下,差距减小。速度较低时最大值比刚体稍高。
由以上分析可知,基于悬挂刚体模型所计算出的圆曲线极限最小半径值具有合理性。
4 结论本研究引入考虑了悬挂系统,利用仿真,修正了横向力系数的情况下,给出客货车道路最小圆曲线半径在车辆装有悬挂时的推荐值。另外,基于动力学仿真平台,对刚体模型与悬挂模型在极限最小半径下的稳定性参数进行分析,讨论两类模型的差异性。主要研究结果如下:
(1) 本研究建立的超高悬挂模型计算得到的客车道路与货车道路的圆曲线极限最小半径稍低于《公路路线设计规范》(JTG D20—2017)。
(2) 侧倾角变化曲线误差在小半径曲线段浮动强烈,稳定性低。在仿真试验,装有悬挂的车辆稳定性更好,此结果在曲线半径更小的路段上显著。
(3) 刚性模型交互输出侧倾角的变化参数要略微低于独立悬挂的车体;车辆在进行减速时降低不利影响,安全呈正改善,适应性也更优。
| [1] |
李方媛. 重特大道路交通事故致因机理及其风险行为研究[D]. 西安: 长安大学, 2014. LI Fang-yuan. Research on Cause Mechanism of Major Road Traffic Accidents and Its Risk Behaviors[D]. Xi'an: Chang'an University, 2014. |
| [2] |
AASHTO. A Policy on Geometric Design of Highways and Streets[R]. Washington, D. C. : AASHTO, 2011.
|
| [3] |
KORDANI A A, MOLAN A M. The Effect of Combined Horizontal Curve and Longitudinal Grade on Side Friction Factors[J]. KSCE Journal of Civil Engineering, 2015, 19(1): 303-310. |
| [4] |
CHANG T H. Effect of Vehicles Suspension on Highway Horizontal Curve Design[J]. Journal of Transportation Engineering, 2001, 127(1): 89-91. |
| [5] |
HAYWOOD J C. Highway Alignment and Superelevation: Some Design-speed Misconceptions[J]. Transportation Research Record, 1980, 757: 22-25. |
| [6] |
CRAUS J, LIVNEH M. Superelevation and Curvature of Horizontal Curves[J]. Transportation Research Record, 1978, 685: 7-13. |
| [7] |
张玥. 基于横向力系数的公路平曲线半径及超高取值方法研究[J]. 中外公路, 2015, 35(2): 5-9. ZHANG Yue. Research on Valuing Method of Highway Horizontal Curve Radius and Superelevation Based on Transverse Force Coefficient[J]. Journal of China & Foreign Highway, 2015, 35(2): 5-9. |
| [8] |
范李, 李刚炎, 陈冉, 等. 客车急转工况下转向稳定的横向力系数与转弯半径计算[J]. 华南理工大学学报: 自然科学版, 2017, 45(2): 39-45, 51. FANG Li, LI GANG-Yan, CHEN Ran, et al. Calculation of Lateral Force Coefficient and Turning Radius for Bus Cornering Stability under Extreme Turn Conditions[J]. Journal of South China University of Technology: Natural Science Edition, 2017, 45(2): 39-45, 51. |
| [9] |
罗京, 张冬冬, 郭腾峰. 大型车辆横向稳定性对公路设计极限平曲线半径取值的影响分析[J]. 中国公路学报, 2010, 23(增1): 42-46. LUO Jing, ZHANG Dong-dong, GUO Teng-feng. Analysis for Influence of Large Vehicle's Lateral Stability on Ultimate Horizontal Curve Radius of Highway Design[J]. China Journal of Highway and Transport, 2010, 23(S1): 42-46. |
| [10] |
范李, 李刚炎, 陈冉, 等. 基于横向力系数的汽车急转防侧翻车速计算模型与仿真[J]. 农业工程学报, 2016, 32(3): 41-47. FANG Li, LI Gang-yan, CHEN Ran, et al. Speed Calculation Model and Simulation of Rollover Prevention in Condition of Extreme Turn Based on Lateral Force Coefficient[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(3): 41-47. |
| [11] |
张肖磊. 基于可靠度理论的高速公路平曲线超高设计研究[D]. 武汉: 武汉理工大学, 2019. ZHANG Xiao-lei. Research on Superelevation Design of Expressway Horizontal Curve Based on Reliability Theory[D]. Wuhan: Wuhan University of Technology, 2019. |
| [12] |
范爽. 高速公路平面线形指标及其组合安全性研究[D]. 西安: 长安大学, 2019. FAN Shuang. Study on Safety of Expressway Horizontal Alignment Index and Its Combination[D]. Xi'an: Chang'an University, 2019. |
| [13] |
涂文靖. 曲线超高计算的优化方法及应用[J]. 铁道建筑, 2019, 59(2): 120-125. TU Wen-jing. Optimization Method and Application of Curve Superelevation Calculation[J]. Railway Engineering, 2019, 59(2): 120-125. |
| [14] |
王磊. 高危路段S型曲线超高计算分析[J]. 兰州工业学院学报, 2016, 23(3): 40-43. WANG Lei. Calculation and Analysis of S Curve in High Risk Section[J]. Journal of Lanzhou Institute of Technology, 2016, 23(3): 40-43. |
| [15] |
交通运输部综合规划司. 中国高速公路运输量统计调查分析报告[R]. 北京: 人民交通出版社, 2018. Department of Comprehensive Planning of MOT. Statistical Investigation and Analysis Report of Expressway Traffic Volume in China[R]. Beijing: China Communications Press, 2018. |
| [16] |
GILLESPIE T D. Fundamentals of Vehicle Dynamics[M]. New York: Society of Automotive Engineers, Inc., 1992.
|
| [17] |
交通运输部公路科学研究院. 公路横向力系数[R]. 北京: 交通运输部公路科学研究院, 2002. Highway Research Institute of Ministry of Transport. Lateral Force Coefficient of Highway[R]. Beijing: Highway Research Institute of Ministry of Transport, 2002. |
| [18] |
JTG B20-2017, 公路路线设计规范[S]. JTG D20-2017, Design Specifications for Highway Alignment. |
 2021, Vol. 38
2021, Vol. 38
