扩展功能
文章信息
- 张锐, 帅斌, 黄文成, 于耀程, 许旻昊
- ZHANG Rui, SHUAI Bin, HUANG Wen-cheng, YU Yao-cheng, XU Min-hao
- 突发事故条件下道路交通流早发性失效机理研究
- Study on Mechanism of Road Traffic Flow Early-onset Breakdown under Sudden Accident
- 公路交通科技, 2021, 38(8): 140-148
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(8): 140-148
- 10.3969/j.issn.1002-0268.2021.08.019
-
文章历史
- 收稿日期: 2020-12-17
2. 西南交通大学 综合交通运输智能化国家地方联合工程实验室, 四川 成都 611756;
3. 西南交通大学 综合交通大数据应用技术国家工程实验室, 四川 成都 611756
2. National United Engineering Laboratory of Integrated and Intelligent Transportation, Southwest Jiaotong University, Chengdu Sichuan 611756, China;
3. National Engineering Laboratory of Integrated Transportation Big Data Application Technology, Southwest Jiaotong University, Chengdu Sichuan 611756, China
交通流失效是指当路段实际交通量达到或接近路段通行能力时,速度发生急速下降的现象[1],该现象广泛存在于交通系统中。近年来,诸多研究发现瓶颈路段上交通量未达到道路通行能力时亦有可能发生交通流失效,即早发性失效。交通流失效将对交通系统的稳定性造成较大影响,且该现象的发生往往伴随着交通流由自由流状态向拥挤状态的相位转变[2]。相对于普通的交通流失效,早发性失效的不确定性更强、预测难度更大。故深入理解早发性失效发生及演化机理,有利于交通管理者及时掌握路段交通流状态变化趋势并提前采取有效的管控措施,避免大规模拥堵及行车事故发生。
普通交通流失效的研究一般从失效发生原因、预测方法及相关应用3个方向展开。截至目前,交通流失效现象的内在机理尚未有定论,多数学者认为该现象不会在稳定流状态下发生,且具有随机性特点。部分学者针对匝道汇流等常发性瓶颈, 提出匝道上车流量的突然增加[3]及破坏性变道行为[4]是导致失效的重要致因。针对交通流失效的预测,诸多学者通过建立与路段交通流密度、流量相关的交通流失效概率模型[2, 5],建立数学解析模型推导交通流参数临界阈值[6],或采用机器学习、深度学习[7]相关方法对交通流失效进行预测。近年来,学者们利用交通流失效理论及既有研究成果在瓶颈路段交通流仿真[8-9]、管理控制策略制定[10]、路段通行能力计算[11]等领域进行了广泛应用,逐步拓展了交通流失效的相关研究。相比较而言,交通流早发性失效的研究则较为匮乏。Sun等[12]分析了上海市高架快速路匝道上利用线圈采集到的交通流数据,证明了早发性失效现象的存在,并在后续研究中基于交通流微观换道理论探讨了早发性失效的原因[13]。既有交通流早发性失效的研究中,研究场景基本集中于快速路匝道等常发性瓶颈,交通事故等偶发性瓶颈场景则少有涉及。早发性失效的内在原因探索则多站在交通流微观模型的视角,讨论个体车辆的驾驶行为,且目前尚缺乏针对早发性失效现象的预测研究。
本研究针对当前交通流早发性失效研究中存在的不足,站在系统及宏观视角,采用尖点突变模型讨论突发事故引起的偶发性瓶颈场景下交通流早发性失效的内在机理,并尝试为早发性失效预测提供新的方向及思路。
1 尖点突变模型的引入Thom在20世纪60年代提出了突变理论,该理论能够描述和解释光滑动力体系中稳定平衡状态的分歧问题。适宜运用突变理论进行研究的系统普遍具有5种特性,分别为突跳性、不可达性、多模态性、分歧性和滞后性[14]。基于以上特性,突变理论在交通流领域研究的适用性已得到充分论证,并且在近年来的研究中得到了多个方向的拓展[15-16]。
突变理论的优势在于能够在系统内复杂机理未知的情况下,直接解释和描述系统状态的不连续性变化。交通流受多种因素影响,且因素间相互作用关系复杂,属于典型的复杂巨系统。交通流早发性失效则是此巨系统中典型的状态不连续变化现象。故在对交通流系统内外影响因素进行细致刻画存在一定困难的条件下,引入突变理论对交通流早发性失效进行研究是较为适当的。
1.1 参数对应关系既有研究中,一般采用尖点突变模型对交通流3参数进行建模。
尖点突变模型包含以下3个函数[14]。
势函数:
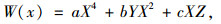
|
(1) |
平衡曲面:

|
(2) |
分叉集:
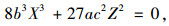
|
(3) |
式中,a, b, c为常参数;Y, Z为控制变量,决定系统状态的变化趋势;X为状态变量,描述系统的运行状态,会随控制变量的连续变化发生突跳。交通流实测数据显示速度更适合作为状态变量,占有率和交通量更适合作为控制变量。因此,本研究令速度为状态变量,交通量及时间占有率分别为控制变量。
1.2 突变平衡曲面及分叉集 1.2.1 定义突变平衡曲面是系统势函数驻点的集合,曲面上的点称为系统状态控制点,由1组三维变量(X, Y, Z)(1个状态变量X及2个控制变量Y, Z)所决定。多数情况下,状态变量X与控制变量组(Y, Z)一一对应。但存在一定区域,在控制变量确定的情况下,状态变量速度的取值不唯一,此时系统状态控制点无法由1组确定的三维变量唯一地确定位置,系统状态控制点可能在这些取值中发生跳跃,此区域称为突变区域。
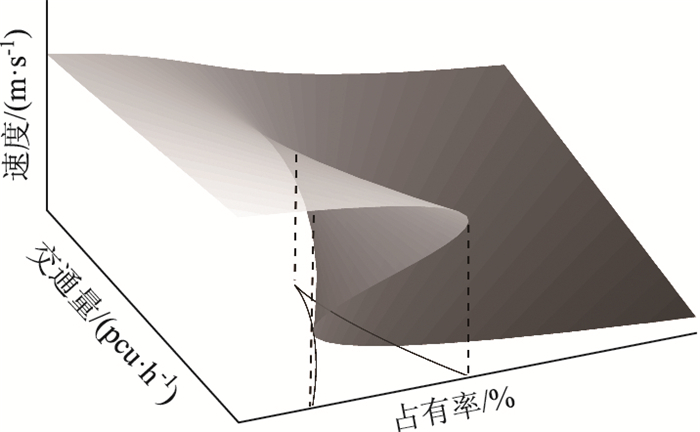
突变分叉集是突变区域内控制变量组(Y, Z)的集合,几何意义为突变平衡曲面上的突变褶皱曲面在控制平面上的映射区域(图 1),控制变量在控制平面上的变化影响着整个系统的运行状态。一旦控制变量进入分叉集,系统就进入了不稳定区间并将发生突变。
|
| 图 1 平衡曲面示意图 Fig. 1 Schematic diagram of equilibrium surface |
| |
1.2.2 映射关系分析
影响交通流系统的因素有人、车、路3方面,故同一线形设计的道路上同质性交通流系统可能的状态集合是一定的,即平衡曲面是确定的。随着交通运行状态的变化,系统状态控制点(由控制变量交通量、占有率及状态变量速度决定)在平衡曲面上运动,当其处于上、下叶非突变区域时,交通流分别处于自由流状态及非自由流状态,系统是稳定的。状态控制点进入突变区域时,状态变量速度的取值不唯一,交通流处于混沌流状态,交通流系统处于非稳定状态。
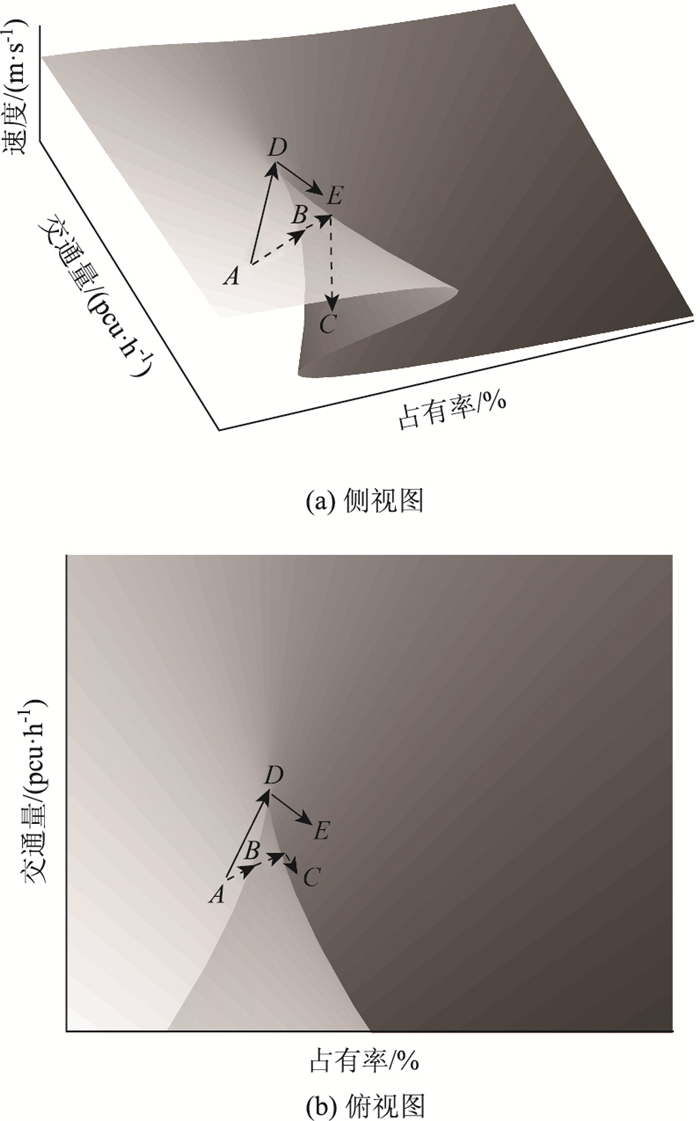
交通流系统状态控制点在平衡曲面上的不同运动路线与交通运行状态的不同演化过程相对应:(1)如图 2实线箭头所示,当系统初始状态位于平衡曲面上叶A点时,路段上车流呈现自由流状态。随着交通量、占有率的逐渐增大,系统状态控制点经D点附近由上叶过渡至下叶E点时,路段上车流由自由流状态变换至非自由流状态,此种拥堵产生的过程中,速度变化呈现近似连续或小幅度非连续变化的形式。
|
| 图 2 系统控制点运动示意图 Fig. 2 Schematic diagram of system control point motion |
| |
(2) 如虚线箭头所示,系统初始状态同样起始于A点(自由流状态),并朝着路段上交通量及密度变化向D点方向运动。由于某种原因(往往是瓶颈上游产生的交通波与瓶颈处由于换道产生的扰动结合, 导致下游交通流产生无法消解的扰动[17]),局部路段上密度及交通量发生急剧变化,导致系统状态控制点于B点进入了混沌区域并在较短的时间内跌至平衡曲面下叶C点。与上文所述缓慢的变换过程不同,此过程中速度以一种断崖式的方式下降,由自由流向非自由流的转换也是非连续的。
依据既有研究中针对交通流失效特征的描述,在上述2类演化过程中,系统状态控制点在远离道路通行能力的D点进入突变区域并发生的状态非连续性变化即对应交通流早发性失效;而在道路通行能力D点附近发生的交通流系统状态转换则对应普通交通流失效或未发生交通流失效的情况。由此可知,从交通流尖点突变模型出发,研究系统状态控制点在平衡曲面上的变化路线,即可分析和描述交通流早发性失效。
突发事故场景下,局部路段短时间内将形成瓶颈,原有的交通流系统突变平衡曲面也将发生相应改变。通过建立交通流尖点突变模型,对比发生与未发生事故条件下平衡曲面所发生的相关变化,进而深入分析其对系统控制点运动路线的影响,即可对突发事故条件下交通流早发性失效机理进行探索。
2 交通流尖点突变模型建立 2.1 模型建立 2.1.1 参数变换为避免交通流原始数据由于数量级存在差别导致拟合效果欠佳的情况,采用以下公式对交通流3参数进行线性变换[6, 8]:
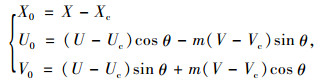
|
(4) |
式中,U, V, X分别为小时交通流率、时间占有率、速度的原始值;Uc,Vc,Xc分别为小时交通流率、时间占有率、速度的临界值(尖点顶点坐标);U0,V0,X0分别为变换后用于建立交通流尖点突变模型的交通流3参数;θ为旋转角度;m=Uc/Vc为归一化比例。小时交通流率计算公式为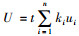
建立求解最优θ的模型如下:
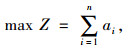
|
(5) |
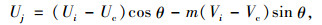
|
(6) |
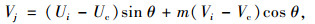
|
(7) |
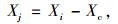
|
(8) |
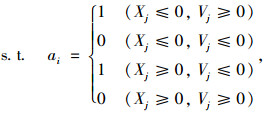
|
(9) |
式中,Ui, Vi, Xi分别为原始数据集中第i个交通流3参数数据;Uj, Vj, Xj分别为3参数变换后数据;ai为第i个交通流参数的状态变量。
2.1.2 参数拟合及分叉集推导依照尖点突变平衡曲面函数(式(2))建立以交通流3参数为变量的尖点突变平衡曲面模型,在参数a, b, c未知的情况下,需要依据处理后的散点采用最小二乘法完成参数拟合。
拟合得到参数分别为a0, b0, c0,则交通流尖点突变平衡曲面模型为:
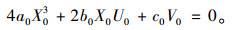
|
(10) |
对式(10)关于X求微分并与其联立消除X, 可推导得到分叉集函数:
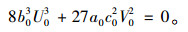
|
(11) |
结合式(4)对式(11)进行变换,将分叉集还原到原始数据的坐标系中:
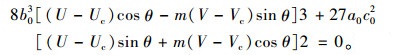
|
(12) |
由此得到原始数据坐标系中的分叉集。
2.2 分叉集相关特征计算由1.2.2节映射关系分析,在突变理论研究视角下, 交通流早发性失效现象和平衡曲面上的突变区域有直接联系,故分析突发事故条件下交通流早发性失效的机理,需要针对突变区域特征进行细致刻画,以便定量展现突变区域在突发事故条件下发生的变化。分叉集是突变区域在控制变量平面上的映射,本研究结合交通流系统状态控制点在平衡曲面上的运动变化特点及分叉集几何特征,定义分叉系数、包围系数及失效阈值边界对突变区域的相关特征进行描述。
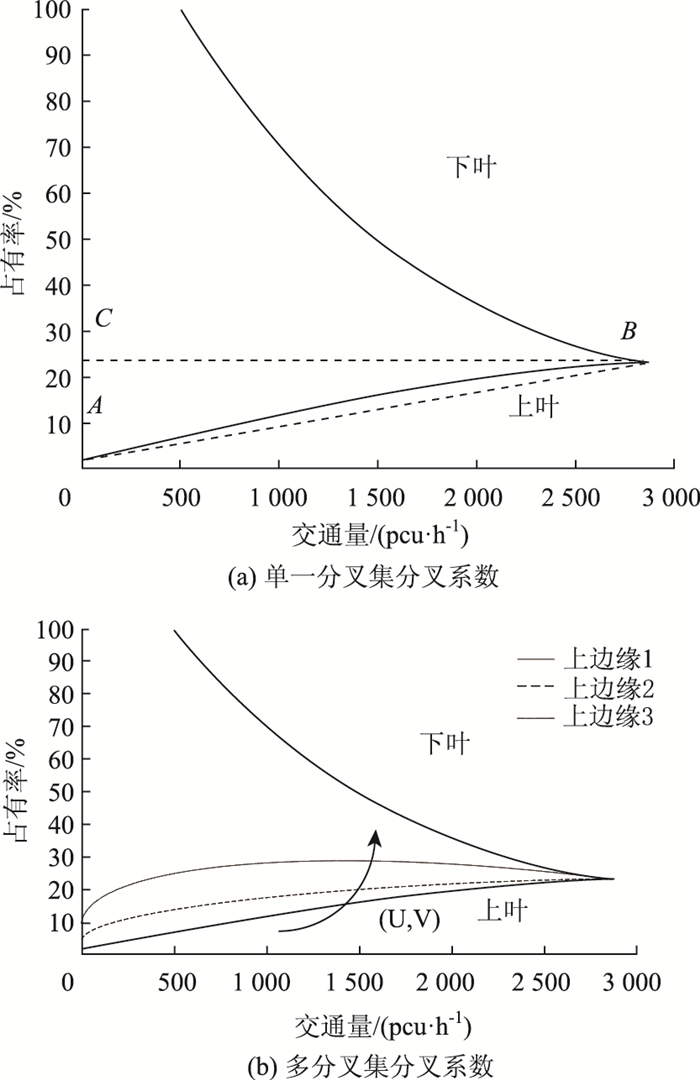
(1) 分叉系数:过临界点B的切线CB,与过B、分叉集上叶边缘与边界的交点A的AB构成的∠CBA(α),将其正切值定义为分叉系数(图 3(a))。同等情况下,当交通流系统状态控制点在上叶运动时,α越大,其在远离临界点B处坠入分叉集导致早发性失效发生的可能性越大。3个分叉集上边缘分叉系数α1>α2>α3(如图 3(b)),交通流系统控制点运动过程中进入3个分叉集的可能性由大到小依次为1,2,3。结合式(12)推导得到分叉系数的计算式(13),其中K和L是分叉计算系数,由常数项a0,b0,c0计算得到。
|
| 图 3 分叉系数示意图 Fig. 3 Schematic diagram of bifurcation coefficient |
| |
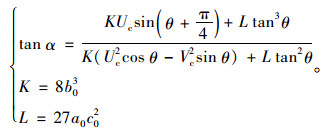
|
(13) |
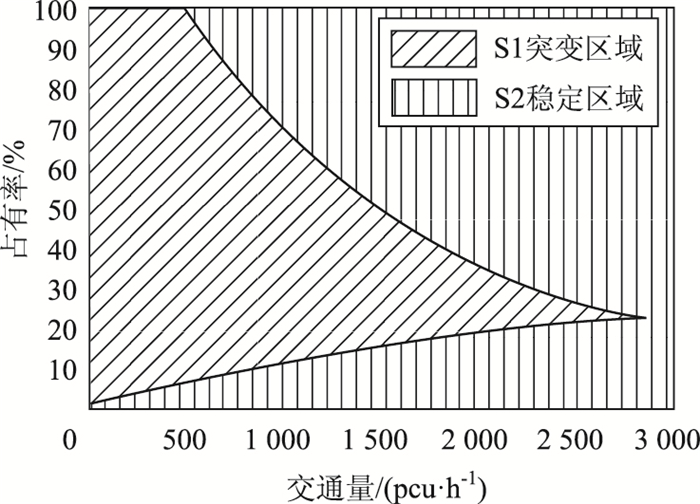
(2) 包围系数:分叉集曲线、2坐标轴所包围的区域为系统的突变区域。区域内散点数量较少且分布离散程度较大,整体呈现震荡、不稳定状态。交通流早发性失效现象发生时,系统状态控制点由上叶快速越过该区域落至下叶,故突变区域包围面积越大,由早发性失效引发的交通流状态变化程度越大。如图 4所示,将分叉集曲线、2坐标轴所确定的突变区域面积S1,与突变区域、稳定区域面积之和S1+S2的比值β定义为包围系数,其计算公式为:
|
| 图 4 包围系数示意图 Fig. 4 Schematic diagram of enclosure coefficient |
| |
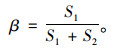
|
(14) |
(3) 失效阈值边界:依据交通流系统状态控制点在平衡曲面上的运动规律,将早发性失效发生过程中系统状态控制点由上叶向下叶运动时所越过的上叶边缘在控制平面的投影定义为失效阈值边界,其表达式为:
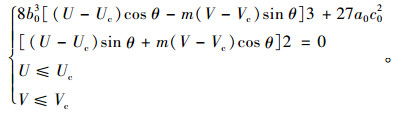
|
(15) |
当路段上交通流系统状态控制点接近失效阈值边界,即式(15)中8b03[(U-Uc)cos θ-m(V-Vc)sin θ]3+27a0c02[(U-Uc)sin θ+m(V-Vc)cos θ]2(系统状态值)取值为正且接近0时,易遇到扰动越过边界进入分叉集。即当式(15)取值由正值经0变为负时,交通流进入混沌流状态,可能发生早发性失效。
基于1.2.2节中的映射关系分析,对比同一路段上有、无事故条件下交通流系统的突变平衡曲面,结合分叉系数、包围系数及失效阈值边界,能够全面描述突发事故条件下交通流系统中发生的变化,进而揭示交通流发生早发性失效的机理,并尝试对早发性失效进行预测。
3 实例及仿真分析 3.1 实例数据来源本研究数据采集地点为成都市三环路北一段主路,数据采集日期为2019-10-28~2019-11-02。该路段晚高峰时段为17:00—19:00,为保证发生事故与未发生事故2种状况下交通流尖点突变模型的拟合准确性,对比2种状况下交通流状态的不同变化过程,进而对本研究所提出的交通流早发性失效机理进行验证,须记录路段交通流由自由流状态向非自由流状态变化的全过程数据,从而实现建模与分析。故选取晚高峰2 h、晚高峰前1 h,即16:00—19:00时段为数据采集具体时间。
路段特征:路段总长约3 km,双向8车道,车道宽3.75 m,限速80 km/h,交通流主要由小汽车、大客车及货车组成,交通流构成相对稳定。
数据采集情况:使用“川速微波”车辆检测器采集主路上东北-西南方向上的交通流数据,检测器采集周期为10 s,输出数据为过境车辆的平均速度、通过车辆数、平均时间占有率。数据采集期间,10月28日有事故发生,其余时间均无事故发生。
事故描述:事故为小型货车抛锚事故,发生于最右侧车道,距检测地约35 m,时间为16:27—17:15,共计48 min。事故发生于晚高峰开始前,初期路段车流量较小,路段通行状况受影响较小。随着路段上交通量逐步增大,过境车辆速度产生了明显变化,路段交通由畅通变化至拥堵的过程较为完整。
3.2 计算及分析采用事故发生全过程48 min中获取的数据建立事故条件下交通流尖点突变模型。由于交通流构成基本一致、检测地点及方法完全相同,将其余5 d中16:00—19:00内的数据合并建立未发生事故条件下交通流尖点突变模型,作为前者的对比组。依照第2部分中的步骤分别对其进行数据处理和计算,其中小时交通流率时间换算系数t=360,车辆换算系数ki参照既有文献,取值见表 1。
计算得到交通流尖点突变模型相关参数见表 2。
| 场景 | a0 | b0 | c0 | θ | Uc | Vc |
| 无事故 | 3.658×10-5 | 8.852×10-3 | 7.936 | -0.326 7 | 7 200 | 41.15 |
| 靠右单车道事故 | 2.325×10-2 | 1.11×10-2 | 1.202 | -0.053 4 | 5 760 | 51.05 |
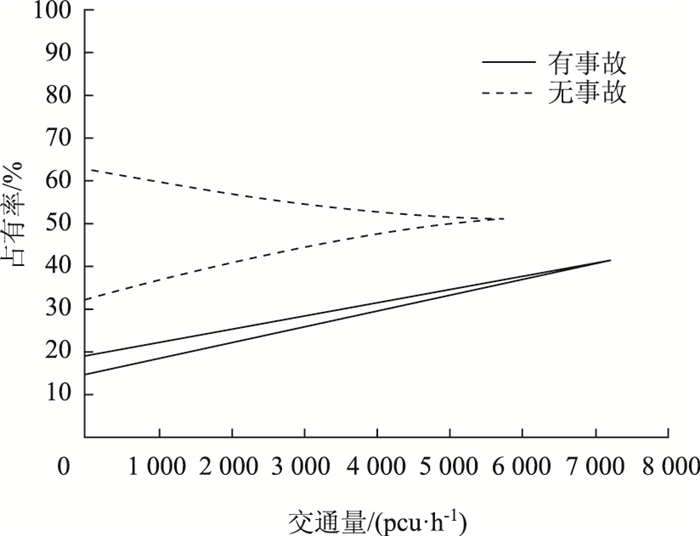
依据参数拟合结果推导并绘制平衡曲面,对比有、无事故2种情况下拟合得到的平衡曲面(图 5),前者对应突变区域的“褶皱”范围和上下叶间距明显增大,意味着系统状态控制点既有运动范围、上中下叶的相对位置由于事故影响发生改变,交通流状态演化趋势较未发生事故将有所不同。进一步推导得到2种状态下的分叉集函数,绘制图像(图 6),计算分叉系数、包围系数,见表 3。2种情况下的失效阈值边界如式(16)与式(17)所示。

|
| 图 5 平衡曲面示意图 Fig. 5 Schematic diagram of equilibrium surface |
| |
|
| 图 6 分叉集 Fig. 6 Bifurcation set |
| |
| 对比组 | 分叉系数 | 包围系数 |
| 无事故 | 3.75×10-3 | 0.117 64 |
| 靠右单车道事故 | 5.2×10-3 | 0.459 4 |
图 6、表 3及式(16)与式(17)中的结果进一步揭示了事故发生与否2种情况下交通流系统分叉集特征的变化,其对系统状态控制点运动路径带来的具体影响为:
(1) 有事故发生时,分叉集在交通量-占有率二维平面上的相对位置向占有率更高的方向移动,交通运行状态变差,最大小时交通量显著下降。
(2) 分叉集的分叉系数增大。相对未发生事故情况,交通流系统状态控制点在平衡曲面上叶运动时,受到同等强度扰动后更容易在距临界点较远的位置进入分叉集,导致交通流在路段流量远低于剩余最大通行能力时发生失效。
(3) 分叉集的包围系数增大,交通流系统中非平稳状态占比增加,交通流系统的整体稳定性降低。交通流早发性失效所导致的交通流状态变化程度更大,失效后路段通行速度更低,局部密度更大,易陷入拥堵状态。
(4) 依据计算得到的失效阈值边界,能够对2种情况下的交通流早发性失效进行预测,将路段交通量及占有率取值代入式(16)与式(17),计算结果满足临界阈值要求,交通流系统状态控制点将进入分叉集,交通流早发性失效有较大概率发生。
无事故条件下:
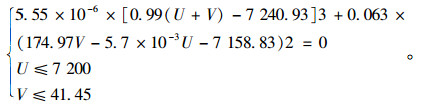
|
(12) |
事故条件下:
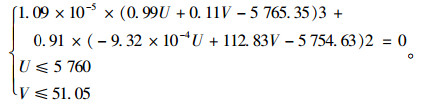
|
(13) |
为进一步验证3.2节中事故发生后交通流系统发生变化对系统状态控制点运动路径所带来的实际影响,总结突发事故条件下交通流早发性失效机理,截取6天中同一时段(16:27—17:15)的数据进行对比分析。
计算平均速度及标准差结果如下(表 4)。
| 日期 | 10-28 | 10-29 | 10-30 | 10-31 | 11-01 | 11-02 |
| 速度均值/(km·h-1) | 40.5 | 64.2 | 61.5 | 63.3 | 66.3 | 62.2 |
| 速度标准差 | 18.23 | 9.84 | 8.53 | 10.20 | 12.42 | 11.30 |
事故当天车辆平均速度相对其他时间大幅下降,速度标准差显著上升,此种变化与3.2节中分叉集在二维平面上相对位置的变化对应。分叉集相对位置向占有率增大方向改变表明路段上车头间距减小,平均速度降低,整体运行状态变差。而速度标准差增大则印证了事故发生后,分叉集包围系数增大导致交通流系统整体稳定性降低。
按有无事故2类整合,分别绘制短时交通流参数时序变化路径(图 7(a)、图 8(a))。

|
| 图 7 无事故交通流时序变化路径 Fig. 7 Temporal variation path of traffic flow without accident |
| |
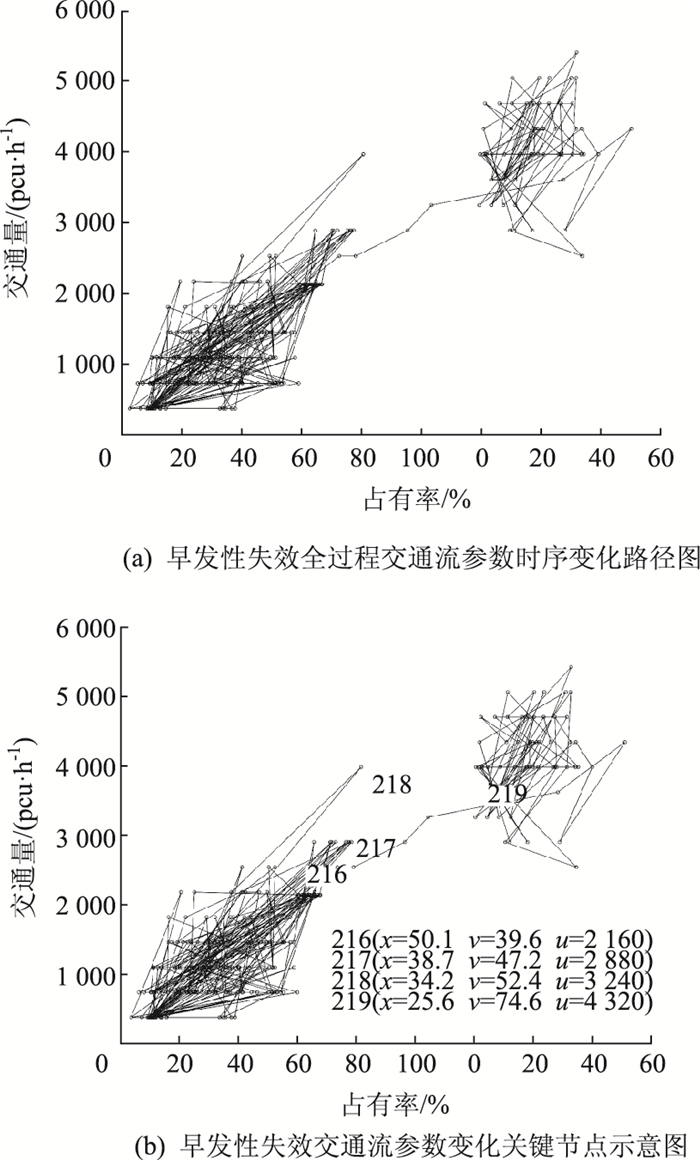
|
| 图 8 有事故交通流参数时序变化路径 Fig. 8 Temporal variation path of traffic flow with accident |
| |
无事故发生时,路段交通量并未达到路段通行能力上限(如图 7(a))。在占有率v∈[10, 25]、交通量u∈[500, 4 000]区域内存在部分离群散点,表明未发生事故条件下路段交通流受到一定程度的扰动影响,但对照图 6的分叉集范围,绝大部分扰动并未导致系统状态控制点运动路径变化进入分叉集,早发性失效也未发生。唯一1次失效发生过程如图 7(b)中编号104~106的点所示,此过程中速x由60 km/h迅速下降至43.1 km/h,占有率由12.7%变化至21.3%。将点104、点105对应的交通量及占有率代入式(16),系统状态值由正值变为负值,即系统状态控制点在点104处受到扰动,随局部交通量、占有率变化由点105进入分叉集,之后迅速变化至点106。然而该次早发性失效前后交通流状态变化程度较小,且在点106后迅速恢复了正常,并未导致拥堵发生。
事故条件下,道路通行状态发生了较大改变,过境车辆较少时交通流仍能保持自由流状态,随着过境车辆不断增多,交通流早发性失效发生(见图 8(a))。早发性失效发生前后交通流3参数的具体变化路径见图 8(b)编号216~219的点所示,在此过程中路段交通量远小于路段剩余通行能力,平均速度在0.5 min内由50.1 km/h急剧下降至25.6 km/h,占有率由39.6%变化为74.6%。将点216~219对应交通量及占有率代入式(17),系统状态值在点216为正,点217、点218为负,点219为正,即系统状态控制点在点216时处于平衡曲面上叶失效阈值边界附近,受到扰动后,由点217进入了分叉集,在短暂停留在点218后,迅速跳跃至点219并稳定在平衡曲面下叶上。此次失效发生过程中,交通流状态变化程度远大于未发生事故情况,且失效后速度最终稳定在了20 km/h左右,交通流相位发生了改变。
以上分析对3.2节所得出的结论及1.2.2节中的对应关系分析进行了论证。通过建立交通流尖点突变模型,能够从系统角度对交通流早发性失效的机理进行合理解释,即交通流系统状态控制点受扰动影响在交通量小于道路最大通行能力时进入分叉集,导致系统状态发生突变。而事故条件下交通流系统平衡曲面发生了较大改变,定量体现为分叉集的分叉系数和包围系数的增大,此种变化将使交通流系统状态控制点在变化过程中相对更容易在交通量远小于通行能力的情况下坠入分叉集导致早发性失效发生,且失效后交通流状态的改变将更剧烈,相位转变更彻底。基于此,通过计算交通流早发性失效阈值边界,能在一定程度上实现交通流早发性失效的预测与监控。
4 结论建立突发事故条件下交通流尖点突变模型,拟合突变平衡曲面、推导分叉集并采用定性、定量相结合的方法能够对突发事故下交通流早发性失效的机理进行全新解释,并采用确定失效阈值的方法对其进行预测。基于本研究介绍的方法,交通管理部门通过采集特定路段上不同类型事故的交通流数据,建立并分析常发事故相应的交通流尖点突变模型,能够掌握不同突发事故情况下的交通流演变规律,进而对交通流早发性失效进行预测,有效防止交通流状态快速改变导致的严重拥堵和二次事故的发生。
限于文章篇幅及数据采集手段,本研究仅针对单一路段实际数据进行了分析论证,并未对交通流早发性失效的具体概率计算进行详细研究。基于更多实测数据,对不同路段场景下突发事故引起的交通流早发性失效特征进行分析,针对分叉集内部早发性失效概率分布进行计算,引入交通流构成及其他因素分析其对概率分布的影响,是拓展本研究的重要方向。
| [1] |
《中国公路学报》编辑部. 中国交通工程学术研究综述·2016[J]. 中国公路学报, 2016, 29(6): 1-161. Editorial Department of China Journal of Highway and Transport. Review on China's Traffic Engineering Research Progress: 2016[J]. China Journal of Highway and Transport, 2016, 29(6): 1-161. |
| [2] |
郝媛, 孙立军, 徐天东. 交通流Breakdown现象与交通扰动演化模型[J]. 同济大学学报: 自然科学版, 2009, 37(9): 1178-1184. HAO Yuan, SUN Li-jun, XU Tian-dong. Traffic Breakdown Phenomenon and Evolution Model of Traffic Perturbation[J]. Journal of Tongji University: Natural Science Edition, 2009, 37(9): 1178-1184. |
| [3] |
ELEFTERIADOU A. A Probabilistic Model of Breakdown at Freeway-merge Junctions[J]. Transportation Research Part A: Policy & Practice, 1996, 30(1): 73. |
| [4] |
CASSIDY M J, RUDJANAKANOKNAD J. Increasing Capacity of an Isolated Merge by Metering Its On-ramp[J]. Transportation Research Part B: Methodological, 2005, 39(10): 896-913. |
| [5] |
BULLEN A G R. Strategies for Practical Expressway Control[J]. Transportation Engineering Journal of ASCE, 1972, 98(3): 599-605. |
| [6] |
KUHNE R, MAHNKE R, LUBASHEVSKY I, et al. Probabilistic Description of Traffic Breakdowns[J]. Physical Review E: Statistical Nonlinear & Soft Matter Physics, 2002, 65(6): 066125. |
| [7] |
FILIPOVSKA M, MAHMASSANI H S. Traffic Flow Breakdown Prediction Using Machine Learning Approaches[J]. Transportation Research Record, 2020, 2674(10): 560-570. |
| [8] |
CHEN X, LI T, MA Z, et al. Integrated Mainline and Ramp Signal Control for Expressway on-ramp Bottleneck with Unequal Lane-setting[J]. Journal of Intelligent Transportation Systems, 2020(1): 1-16. |
| [9] |
施俊庆, 程琳, 褚昭明, 等. 城市路网交通流元胞自动机模型研究[J]. 公路交通科技, 2015, 32(4): 143-149. SHI Qing-lin, CHENG Lin, ZHU Zhao-ming, et al. Cellular Automata Model of Urban Road Network Traffic Flow[J]. Journal of Highway and Transportation Research and Development, 2015, 32(4): 143-149. |
| [10] |
TU H, LI H, WANG Y, et al. When to Control the Ramps on Freeway Corridors? A Novel Stability-and-MFD-based Approach[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(6): 2572-2582. |
| [11] |
LORENZ M, ELEFTERIADOU L. A Probabilistic Approach to Defining Freeway Capacity and Breakdown[J]. Transportation Research Circular, 2000(E-C018): 84-95. |
| [12] |
SUN J, ZHANG J, ZHANG H M. Investigation of the Early-Onset Breakdown Phenomenon at Urban Expressway Bottlenecks in Shanghai[J]. Transportmetrica B: Transport Dynamics, 2014, 2(3): 215-228. |
| [13] |
SUN J, ZHAO L, ZHANG H M. Mechanism of Early-onset Breakdown at On-ramp Bottlenecks on Shanghai, China, Expressways[J]. Transportation Research Record, 2014, 2421(1): 64-73. |
| [14] |
丁庆华. 突变理论及其应用[J]. 黑龙江科技信息, 2008(35): 11-23. DING Qing-hua. Catastrophe Theory and Its Application[J]. Heilongjiang Science and Technology Information, 2008(35): 11-23. |
| [15] |
胡建荣, 何磊. 基于尖点突变理论的高速公路交通流状态判别方法[J]. 中国公路学报, 2017, 30(10): 141-148. HU Jian-rong, HE Lei. Freeway Traffic Flow Condition Criterion Method Based on Cusp Catastrophe Theory[J]. China Journal of Highway and Transport, 2017, 30(10): 141-148. |
| [16] |
LIN C, YU Y, WU D, et al. Traffic Flow Catastrophe Border Identification for Urban High-density Area Based on Cusp Catastrophe Theory: A Case Study under Sudden Fire Disaster[J]. Applied Sciences, 2020, 10(9): 3197. |
| [17] |
KERNER B S, KOLLER M, KLENOV S L, et al. Empirical Features of Spontaneous and Induced Traffic Breakdowns in Free Flow at Highway Bottlenecks[J]. Physics, 2015, 8(2): 136-141. |
| [18] |
辛泽昊. 面向交通网络分配的交叉口延误模型研究[D]. 南京: 东南大学, 2018. XIN Ze-hao. Research on Intersection Delay Model for Traffic Network Assignment[J]. Nanjing: Southeast University, 2018. |
 2021, Vol. 38
2021, Vol. 38
