扩展功能
文章信息
- 陈孟, 干可, 李凯, 陈非, 范庸
- CHEN Meng, GAN Ke, LI Kai, CHEN Fei, FAN Yong
- 基于实时多模态时空数据的时空图卷积网络精准鲁棒交通流预测模型
- A Spatial-temporal Graph Convolutional Network Model for Accurate and Robust Traffic Flow Prediction Based on Real-time Multimodal Spatial-temporal Data
- 公路交通科技, 2021, 38(8): 134-139, 158
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(8): 134-139, 158
- 10.3969/j.issn.1002-0268.2021.08.018
-
文章历史
- 收稿日期: 2020-08-18
作为现代智能交通系统研究中的核心问题,交通流预测旨在一定的时空范围内对车流量或者车速进行估计[1]。一种可靠的、准确的以及持久的交通流预测模型应具备以下3个功能:(1)旅客出行信息智能查询系统;(2)智能交通管制系统;(3)对以上两个系统的性能能给出科学的评估和未来的优化建议[1-2]。现有交通流预测模型可以大致分为时间序列预测法[3-5]、概率图模型[6-7]以及非参数策略[8-10]3类。其中前两类方法存在以下问题:(1)在缺少了具体的场景和人工评估背景下所构建的模型并不具有具体的场景针对性,而更多的是在一般场景下的概括描述;(2)相比于非参数策略,前两种策略无法捕捉交通时序中的非线性场景[11-14]。然而就非参数策略而言,以人工神经网络为代表,目前大多数人工神经网络的构建只有一个单隐藏层,原因在于多隐藏层的应用并不一定能够在相应的场景下成功地构建模型,在这一点上时间序列预测法中的线性构建策略比人工神经网络表现地更好[15-17]。因此针对人工神经网络的缺陷,研究人员主要通过混合神经网络和控制神经网络构建中的过拟合场景两个方面来解决。混合神经网络整合了不同的统计学方法和计算方法,其中最具代表性的是和时序预测策略的整合,Takagi-Sugeno模糊深度模型整合了模糊逻辑和前馈神经网络构建短期交通流模型[18-19],Stathopoulos等[20]在此基础上引入卡尔曼滤波对模型进行优化,Srinivasan等[21]则运用模糊过滤参数对数据进行聚类操作来作为前馈神经网络的输入参数,Tan等[22]利用传统的滑动平均和自回归滑动平均模型来作为神经网络的输入。尽管混合神经网络整合了不同的计算策略,但是同时需要高性能和高存储的计算设备作为支撑,另外硬件条件往往限制了混合神经网络策略真正的计算能力[23-25]。对于抑制过拟合策略而言,可以通过加噪的方式提高数据样本的质量,但这一方法同样需要大量的计算时间和算法处理,另一种常用的方式则是运用交叉验证,即把数据集划分为拟合数据集和验证数据集[26-27],前者用于神经网络学习而后者用于估计合法性误差,当错误率低于设定的阈值时训练终止。然而Liu等[28]证明即便是合理的交叉验证也未必能够避免过拟合现象,验证数据集往往并不具备足够的数据代表性来提供没有倾向的数据评估能力。
因此在本次研究中针对现有交通流预测方法的不足,提出了一种基于实时多模态时空数据的深度图神经网络策略来构建交通流的预测模型。首先采用时间图卷积网络模型对交通流数据的输入向量先后进行数据预处理和特征学习,并对输出结果用卡尔曼滤波进行矫正,从中挖掘交通流数据中的本质性规律,最后通过对该模型进行抽样以获取高层次的特征向量来预测交通流的状态。试验结果表明,该模型对交通流流量预测具有较好精度,是一种有效的交通流预测方法。
1 基于TK-GCN的交通流预测模型的构建 1.1 时间图卷积网络模型(T-GCN)传统的卷积神经网络(Convolutional Neural Networks, CNN)无法胜任由图策略构建城市道路的能力,因为城市道路图并不是二维空间网格,传统的CNN无法表现道路网络复杂的拓扑结构以及捕捉空间内部各个参数的依赖关系。因此针对传统CNN在表达城市道路交通流上的不足,中南大学的李海峰团队于2019年提出了时间图卷积网络(Temporal Graph Convolutional Network, T-GCN)模型[29],该模型同时集成了图卷积网络(Graph Convolutional Network, GCN)和门控递归单元(Gated Recurrent Unit, GRU),其中图卷积网络通过学习复杂的拓扑结构来捕获交通流图节点间的空间依赖关系,而门控递归单元通过学习交通数据的动态变化来捕获时间依赖关系。
1.2 空间依赖关系的描述在描述空间依赖关系中,GCN模型的构建通过邻接矩阵和特征矩阵在傅里叶域中构造了一个滤波器,该滤波器应用于图的各个节点上,通过它的一阶邻域捕获节点之间的空间特征,然后通过叠加多个卷积层来构建GCN模型:
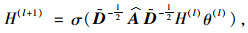
|
(1) |
式中,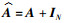
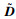
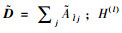
在这里采用两层GCN模型捕获空间依赖关系,如下所示:
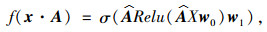
|
(2) |
式中, x为特征矩阵,A为邻接矩阵;w0和w1分别为第1层和第2层的单层GCN空间权重矩阵模型; Relu为线性整流函数。
1.3 时间依赖关系的描述而在时间依赖关系的描述中,由于长短期记忆网络(Long Short-term Memory, LSTM)对于数据要求较为漫长的训练时间,因此选用结构相对简单,整体训练速度相对较快的GRU模型从交通数据中获取时间相关性。因此对于整个T-GCN模型而言,GCN部分的某一时刻的输出进入特定的GRU模型中作为数据输入,经过GRU部分的更新门(Update Gate)和重置门(Reset Gate)的数据处理最终产生输出结果。
1.4 引入卡尔曼滤波对TK-GCN模型的构建由于实际场景交通流的时空演化具有非线性和不稳定的特质,且不同的深度置信网络所构建的混合模型内部的算法之间,并不能在复杂的场景条件和多参数的引用下实现很好的兼容和互补,因此本研究基于T-GCN模型,在T-GCN输出的结果输出过程中引入卡尔曼滤波对原有的模型进行改进,得到TK-GCN模型(Temporal Graph Convolutional Network with Kalman Filtering),旨在模拟降低因多参数的引入而产生的偏差[30]。
对于一个给定的路段Road,本研究定义其特征矩阵x,该矩阵由该路段的矩阵节点数n以及该节点属性特征p所构成,即历史时间序列的长度值,xt即表示在t时刻下该路段的观测图输入信号;而对于邻接矩阵A而言,其反映的是道路之间的交通流联系参数,因为Relu函数的归一化处理,其计算结果范围在0到1之间,0表示两条道路之间没有任何联系,而1表示两条道路有联系。邻接矩阵A,即为不同道路节点数n所构成。
因此整个交通流预测算法具体的流程如下所示:
(1) 获取某时刻下交通流状态的特征数据,根据函数构建特征数据集,原始数据集输入信号即可表示为{x(ti), i=1, 2, …, n}。
(2) 将该历史时间序列数据作为输入,利用图卷积网络捕获城市路网拓扑结构,获得空间特征。
(3) 将输出得到的具有空间特征的时间序列输入门控递归单元模型,通过单元间的信息传递获得动态变化,捕捉时间特征。
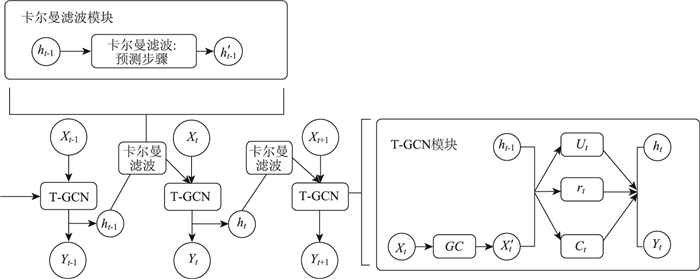
(4) 以全连接层的方式得到T-GCN输出预测结果{h′(ti), i=1, 2, …, n};得到的输出数据集经过卡尔曼滤波处理得到最终的输出预测结果。整个过程如图 1所示。在T-GCN模块当中,ht为t时刻传递出的隐藏值,GC为图卷积模块(Graph Convolution), Ut和rt分别为t时刻的更新门(Update Gate)和重置门(Reset Gate)。而在卡尔曼模块当中,ht和Yt-1对应的卡尔曼处理步骤定义为预测步骤(Prediction Step),Ct为将数据放缩到[-1, 1]范围内的tanh激活函数。
|
| 图 1 TK-GCN模型流程图 Fig. 1 Flowchart of TK-GCN model |
| |
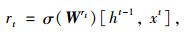
|
(3) |
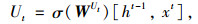
|
(4) |
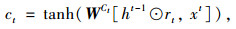
|
(5) |
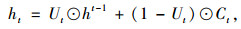
|
(6) |
式中, Wrt, WUt, WCt分别为更新门、计算重制门及代入激活函数tanh计算时所对应需要训练的矩阵。W为图卷积网络中需要训练的权重矩阵,每一层GRU的输入都考虑了上一层GRU的输出,从而捕获了路网交通流的时序关系。
在卡尔曼的滤波处理过程中,经过T-GCN输出得到的交通流初始隐藏输入信号序列{h′(ti), i=1, 2, …, n}可以转换成h′(t+1),而预测值在t时刻的交通流流量与该时刻前后的交通流流量相关,因此可得:
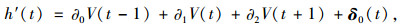
|
(7) |
式中, ∂0,∂1以及∂2分别为t前后即t-1,t以及t+1的矩阵参数; V为该时刻的交通流量; δ0为人工引入的参数噪音,这里定义为协方差矩阵。而t前后的交通流量V()做以下变换:
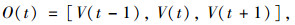
|
(8) |
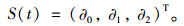
|
(9) |
而根据卡尔曼滤波,因此式(8)、(9)可以整合成:
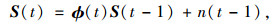
|
(10) |
式中,S(t)为t时刻的状态向量;ϕ(t)为t时刻对应的状态转移矩阵,n(t)为t时刻人工设计的噪音处理函数。
因此经过卡尔曼滤波处理的交通流量预测公式如下所示,其中β(t)即为观测矩阵:
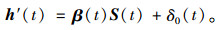
|
(11) |
由于T-GCN模块引入了卡尔曼滤波修正,因此式(3)~(6)中的隐藏输入信号ht-1修正为h′(t-1)。
2 试验结果及分析 2.1 试验数据该研究的试验数据、模型的仿真和验证工作基于川高系统视频智能分析平台(川高·智慧眼V2.0)实时记录了2019年5月1号—10月30日成都绕城高速公路绕东路段,选择绕东高速公路路段为主干道连接成都主城区共172条主要道路作为研究区域。试验数据主要包括两个部分:一是一个172×172的邻接矩阵,描述了道路之间的空间关系,每行表示1条道路,矩阵中的值表示道路之间的连接性。二是特征矩阵,描述了每条道路上的速度随时间的变化,每行代表 1条路,每列是不同时段道路上的交通速度。实时速度每间隔5 min采集1次,整个数据采集空间当中共包含397个采样点。由于交通流数据具有一定的规律性,且双休日和工作日分别呈现出不同的数据特性,为了充分利用数据之间的规律性,文中针对高速公路交通流预测的训练数据将排除双休日以及国家法定节假日的数据,并用实际数据进行验证工作。该数据由一个邻接矩阵和一个特征矩阵构成,通过智慧眼平台的摄像头位点之间的距离计算邻接矩阵。试验中,输入数据统一通过激活函数归一化进区间[0, 1]。另外,80%的数据作为训练集,剩下的20%作为测试集,以此作为模型的输入。基于以上数据,本研究预测未来10,20,30,40,50 min和60 min的交通速度。而为验证优化后的算法能够提高长时预测(30~60 min)的能力,同时不丢失短时预测(5~15 min)的水平。然而在实际高速公路路况当中,相比起城市道路的时刻都有相对稳定的车流量规律,高速公路连接城市部分的道路往往在全天呈现较大的规律性起伏,因此长时预测往往比短时预测更为满足生产需要,短时预测对于高速公路而言并不具有一定的参考意义。
本研究模型基于TK-GCN,模型训练过程中涉及的超参数包括:学习率、训练集容量以及隐藏层数。研究中,本研究将学习率设置为0.001,选择32个训练集,训练迭代次数为6 000从第20个epoch开始,每隔10个epoch学习率衰减为原来的1/10。在深度学习的架构中,不同的隐藏层数值的大小对预测精度有较大的影响,隐藏层层数需要大量的测试来选定。因此为了选择最优的隐藏层数值,针对不同的隐藏层数进行了尝试,通过比较预测结果来选择最优值。在反复验证的过程中发现,当隐藏层数的取值大于60时,均方误差的值不再发生显著的变化,所以将隐藏层数的上限值设置为60,最后输出层的节点数为{5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60},设计隐藏层数的值为40。整个模型通过自适应矩估计(Adaptive Moment Estimation, ADAM)优化器对模型进行训练。
2.2 性能指标与误差分析为了能够更好地分析和评价预测结果,本研究采用了绝对平均误差(Mean Absolute Error, MAE),相对平均误差(Mean Relative Error, MRE)以及决定系数(Coefficient of Determination, R2),3个指标定义如下所示:
绝对平均误差(MAE)
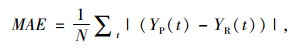
|
(12) |
相对平均误差(MRE)
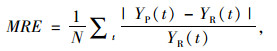
|
(13) |
决定系数(R2)
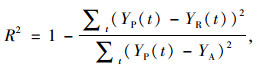
|
(14) |
式中,YP为交通流量的预测值;YR为交通流量的真实观测值;YA为统计区间内的平均值。MAE和MRE的值越小,代表预测值误差越小;R2计算相关系数,数值越大,预测结果越接近真实水平。本研究所提出的改进后TK-GCN模型与T-GCN模型、CRBM-DBN(Conditional Restricted Boltzmann Machine-deep Belief Nets)模型、LGCN-NGCN模型(Large-scale Learnable and Neighborhood-averaging Graph Convolutional Networks)以及FL-GCN-CNN模型(Functional linkable Graph Convolutional Networks with Convolutional Neural Networks)进行比较,由表 1可知,针对每种算法使用相同的数据集进行验证后发现,本研究提出的预测模型的误差性能明显优于同样基于深度置信网络的T-GCN、CRBM-DBN、LGCN-NGCN以及FL-GCN-CNN这些混合模型,表明了改进后的深度学习策略在交通流预测中的有效性。
| 预测模型 | 时间/min | 评价指标 | ||
| MAE | MRE | R2 | ||
| TK-GCN | 10 | 8.222 1 | 0.296 7 | 0.945 3 |
| 20 | 8.213 6 | 0.290 3 | 0.945 0 | |
| 30 | 8.862 6 | 0.376 4 | 0.944 2 | |
| 40 | 8.957 4 | 0.385 3 | 0.943 8 | |
| 50 | 8.802 0 | 0.367 9 | 0.942 1 | |
| 60 | 8.789 4 | 0.353 1 | 0.941 9 | |
| T-GCN | 10 | 10.761 3 | 2.157 3 | 0.879 6 |
| 20 | 10.758 7 | 2.142 2 | 0.864 3 | |
| 30 | 10.734 6 | 2.110 6 | 0.863 9 | |
| 40 | 10.711 0 | 2.108 7 | 0.862 0 | |
| 50 | 10.711 2 | 2.108 7 | 0.853 8 | |
| 60 | 10.710 3 | 2.108 0 | 0.852 6 | |
| CRBM-DBN | 10 | 10.842 7 | 2.181 3 | 0.879 5 |
| 20 | 10.894 2 | 2.182 0 | 0.878 2 | |
| 30 | 10.896 7 | 2.184 6 | 0.877 4 | |
| 40 | 10.899 8 | 2.185 2 | 0.876 8 | |
| 50 | 10.900 3 | 2.187 1 | 0.876 1 | |
| 60 | 10.900 4 | 2.187 4 | 0.876 1 | |
| LGCN-NGCN | 10 | 9.125 4 | 1.042 3 | 0.889 2 |
| 20 | 9.127 1 | 1.048 6 | 0.888 1 | |
| 30 | 9.128 1 | 1.049 7 | 0.887 2 | |
| 40 | 9.128 1 | 1.049 7 | 0.887 2 | |
| 50 | 9.128 1 | 1.049 7 | 0.887 2 | |
| 60 | 9.129 4 | 1.051 3 | 0.886 1 | |
| FL-GCN-CNN | 10 | 8.492 6 | 0.604 9 | 0.916 3 |
| 20 | 8.505 3 | 0.610 7 | 0.914 9 | |
| 30 | 8.544 9 | 0.638 4 | 0.910 3 | |
| 40 | 8.549 1 | 0.636 0 | 0.909 7 | |
| 50 | 8.550 3 | 0.642 6 | 0.908 4 | |
| 60 | 8.551 2 | 0.642 9 | 0.908 4 | |
2.3 交通流流量实际预测
由于其他基于深度置信网络的模型当中,FL-GCN-CNN相比之下预测精度较高,因此就真实交通流量的预测效果方面,仅仅就TK-GCN模型以及FL-GCN-CNN模型与实际交通流速度作比较。这里以2019年5月13日—2019年5月17日60 min交通流车速跟踪为例,对实际交通流量的预测由图 2可知,由于高速公路24 h的时段内始终都会有一定的车流量水平,两个模型对车流量的预测总体上与实际的交通流车速变化趋势相比相差不大,但是TK-GCN算法在波峰和波谷的预测表现,也就是上下高峰期时段交通流车速的预测,以及对交通流车速上升下降趋势预测表现,其所计算出的预测结果更吻合真实的交通流数据变化。
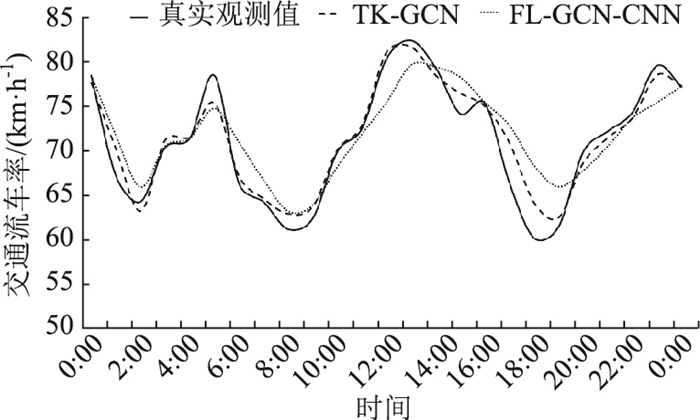
|
| 图 2 两种模型的交通流车速预测数据与真实交通流车速观测数据的对比 Fig. 2 Comparison of traffic flow speed prediction data of 2 models with measured real traffic flow speed data |
| |
3 结论
本研究基于改进后的时间图卷积网络模型(TK-GCN)应用于短时交通流预测。文中所介绍的方法利用图卷积网络(GCN)捕获路网拓扑结构,并对路网的空间依赖性进行建模;同时利用门控递归单元(GRU)捕获道路交通数据的动态变化,并对其时间依赖性进行建模,随后对预测数据进行卡尔曼滤波处理,从而挖掘交通流数据的本质特征;最后利用该模型对未来的交通流流量进行预测。试验结果表明,文中所构建的交通流流量预测模型与传统交通流预测模型相比,其预测数据值和实际测量的真实数据值偏差更小且更能吻合实际的交通流水平,证明该模型在交通流预测方面具有较高的预测精度。
| [1] |
LÜ Y S, DUAN Y J, KANG W W, et al. Traffic Flow Prediction with Big Data: A Deep Learning Approach[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(2): 865-873. |
| [2] |
SHI Q, ABDEL-ATY M. Big Data Applications in Real-time Traffic Operation and Safety Monitoring and Improvement on Urban Expressways[J]. Transportation Research Part C: Emerging Technologies, 2015, 58: 380-394. |
| [3] |
GHOSH B, BASU B, O'MAHONY M. Bayesian Time-series Model for Short-term Traffic Flow Forecasting[J]. Journal of Transportation Engineering, 2007, 133(3): 180-189. |
| [4] |
MOORTHY C K, RATCLIFFE B G. Short Term Traffic Forecasting Using Time Series Methods[J]. Transportation Planning and Technology, 1988, 12(1): 45-56. |
| [5] |
THOMAS T, WEIJERMARS W, BERKUM E V. Predictions of Urban Volumes in Single Time Series[J]. IEEE Transactions on Intelligent Transportation Systems, 2010, 11(1): 71-80. |
| [6] |
SUN S L, XU X. Variational Inference for Infinite Mixtures of Gaussian Processes with Applications to Traffic Flow Prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(2): 466-475. |
| [7] |
MA W, WANG R. Traffic Flow Forecasting Research Based on Bayesian Normalized Elman Neural Network[C]//2015 IEEE Signal Processing and Signal Processing Education Workshop (SP/SPE). Salt Lake City: IEEE, 2015: 426-430.
|
| [8] |
CASTRO-NETO M, JEONG Y S, JEONG M K, et al. Online-SVR for Short-term Traffic Flow Prediction Under Typical and Atypical Traffic Conditions[J]. Expert Systems with Applications, 2009, 36(3): 6164-6173. |
| [9] |
DELL'ACQUA P, BELLOTTI F, BERTA R, et al. Time-aware Multivariate Nearest Neighbor Regression Methods for Traffic Flow Prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(6): 3393-3402. |
| [10] |
YIN S, XIE X, SUN W. A Nonlinear Process Monitoring Approach with Locally Weighted Learning of Available Data[J]. IEEE Transactions on Industrial Electronics, 2017, 64(2): 1507-1516. |
| [11] |
ZHANG Y, ZHANG Y, HAGHANI A. A Hybrid Short-term Traffic Flow Forecasting Method Based on Spectral Analysis and Statistical Volatility Model[J]. Transportation Research Part C: Emerging Technologies, 2014, 43: 65-78. |
| [12] |
DIA H. An Object-oriented Neural Network Approach to Short-term Traffic Forecasting[J]. European Journal of Operational Research, 2001, 131(2): 253-261. |
| [13] |
ŚWIDERSKI A, JÓZ·WIAK A, JACHIMOWSKI R. Operational Quality Measures of Vehicles Applied for the Transport Services Evaluation Using Artificial Neural Networks[J]. Maintenance and Reliability, 2018, 20(2): 292-299. |
| [14] |
TORNATORE M. Data Analytics and Machine Learning Applied to Transport Layer[C]//2018 Optical Fiber Communications Conference and Exposition (OFC). San Diego: IEEE, 2018.
|
| [15] |
CHAN K Y, DILLON T S, SINGH J, et al. Neural-network-based Models for Short-term Traffic Flow Forecasting Using a Hybrid Exponential Smoothing and Levenberg-Marquardt Algorithm[J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(2): 644-654. |
| [16] |
RUTKA G. Neural Network Models for Internet Traffic Prediction[J]. Elektronika ir Elektrotechnika, 2015, 68(4): 55-58. |
| [17] |
DO L, TAHERIFAR N, VU H L. Survey of Neural Network-based Models for Short-term Traffic State Prediction[J]. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 2019, 9(1): e1285. |
| [18] |
HEYDARI G, VALI M, GHARAVEISI A A. Chaotic Time Series Prediction via Artificial Neural Square Fuzzy Inference System[J]. Expert Systems with Applications, 2016, 55: 461-468. |
| [19] |
KESKIN M E, TAYLAN D, TERZI Ö. Adaptive Neural-based Fuzzy Inference System (ANFIS) Approach for Modelling Hydrological Time Series[J]. Hydrological Sciences Journal, 2006, 51(4): 588-598. |
| [20] |
STATHOPOULOS A, DIMITRIOU L, TSEKERIS T. Fuzzy Modeling Approach for Combined Forecasting of Urban Traffic Flow[J]. Computer Aided Civil and Infrastructure Engineering, 2008, 23(7): 521-535. |
| [21] |
SRINIVASAN D, CHAN C W, BALAJI P G. Computational Intelligence-based Congestion Prediction for a Dynamic Urban Street Network[J]. Neurocomputing, 2009, 72(10/11/12): 2710-2716. |
| [22] |
TAN M C, WONG S C, XU J M, et al. An Aggregation Approach to Short-term Traffic Flow Prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2009, 10(1): 60-69. |
| [23] |
CHATTERJEE S, GHOSH S, DAWN S, et al. Forest Type Classification: A Hybrid NN-GA Model Based Approach[M]. New Delhi: Information Systems Design and Intelligent Applications, 2016: 227-236.
|
| [24] |
XIANG J, HAN X, DUAN F, et al. A Novel Hybrid System for Feature Selection Based on an Improved Gravitational Search Algorithm and k-NN Method[J]. Applied Soft Computing, 2015, 31: 293-307. |
| [25] |
XUE S, JIANG H, DAI L. Speaker Adaptation of Hybrid NN/HMM Model for Speech Recognition Based on Singular Value Decomposition[C]//The 9th International Symposium on Chinese Spoken Language Processing. Singapore: IEEE, 2014.
|
| [26] |
KARYSTINOS G N, PADOS D A. On Overfitting, Generalization, and Randomly Expanded Training Sets[J]. IEEE Transactions on Neural Networks, 2000, 11(5): 1050-1057. |
| [27] |
SETIONO R. Feedforward Neural Network Construction Using Cross Validation[J]. Neural Computation, 2001, 13(12): 2865-2877. |
| [28] |
LIU Y, STARZYK J A, ZHU Z. Optimized Approximation Algorithm in Neural Networks without Overfitting[J]. IEEE Transactions on Neural Networks, 2008, 19(6): 983-995. |
| [29] |
ZHAO L, SONG Y, ZHANG C, et al. T-GCN: A Temporal Graph Convolutional Network for Traffic Prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 1-11. |
| [30] |
钱伟, 杨慧慧, 孙玉娟. 相空间重构的卡尔曼滤波交通流预测研究[J]. 计算机工程与应用, 2016(14): 37-41. QIAN Wei, YANG Hui-hui, SUN Yu-juan. Kalman Filtering Traffic Flow Prediction Research Based on Phase Space Reconstruction[J]. Computer Engineering and Applications, 2016(14): 37-41. |
 2021, Vol. 38
2021, Vol. 38
