扩展功能
文章信息
- 龚彦峰, 王智勇, 张俊儒, 李树鹏, 张航
- GONG Yan-feng, WANG Zhi-yong, ZHANG Jun-ru, LI Shu-peng, ZHANG Hang
- 五车道大跨分岔隧道小净距段中夹岩柱支护效果研究
- Study on Supporting Effect of Middle Rock Pillars in Small Clear Distance Section of Long-span Forked Tunnel with Five lanes
- 公路交通科技, 2021, 38(8): 123-133
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(8): 123-133
- 10.3969/j.issn.1002-0268.2021.08.017
-
文章历史
- 收稿日期: 2020-11-13
2. 西南交通大学 土木工程学院, 四川 成都 610031
2. School of Civil Engineering, Southwest Jiaotong University, Chengdu Sichuan 610031, China
城市地下交通具有不受地面机动车、行人和天气的干扰,车辆通行效率高等优点,已成为当今城市地下空间开发利用的主要形式之一[1-2],而地下互通式立交则是担任连接地下交通网络的重要节点。城市互通地下立交可以分为平面交叉段和立体交叉段两部分。平面交叉段即分岔隧道,通常由大跨段、连拱段、小净距段以及分离段组成[3],主要特点是开挖面积大、扁平率低。厦门芦澳路—疏港通道地下互通立交隧道由单洞5车道隧道直接过渡至主洞3车道匝道2车道的小净距隧道,没有设置连拱隧道进行过渡,采取直接过渡的方式会导致大跨段与小净距段交界处的围岩应力更加复杂,在国内地下立交分岔隧道的修建中较为少见。因此对小净距段隧道的研究便十分必要,而中夹岩柱在施工中会出现二次应力场的叠加,从而出现应力集中,中夹岩柱的稳定性是小净距段隧道设计与施工的重点和难点[4],所以对中夹岩柱的加固处理变得尤为重要[5]。
近年来随着隧道跨度的逐渐增大,大跨隧道、连拱隧道、小净距隧道成为研究重点,对于小净距隧道中夹岩柱的研究主要集中在两个方面:(1)对中夹岩柱合理厚度即小净距隧道合理净距的研究;(2)对中夹岩柱不同加固措施的研究。刘芸[6]将中夹岩柱进行区域划分,并且对中夹岩柱的不同加固组合方式进行了研究,研究表明各种加固方法对于不同级别的围岩效果不同。张桂生[7]则建立了小净距隧道围岩的各项指标与净距敏感度之间的关系,提出了把敏感度突变阶段出现之前的净距作为合理净距。李建林[8]依托白羊沟特长隧道工程,通过有限元计算以及现场监测的方式确定了小净距段中夹岩柱的加固措施,最终采用预应力长锚杆(70 kN)及超前小导管注浆组合加固的方法确保了中夹岩柱的稳定性。赵秀绍[9]通过建立二维3台阶开挖数值分析模型,发现对于Ⅴ级软弱围岩,中夹岩柱的厚度应大于0.75倍隧道跨度,且隧道拱脚处为受力薄弱部位,应保证初期支护及时封闭。晏启祥[10]通过对软岩隧道下不同净距对中夹岩柱塑性区影响的分析研究得出,中夹岩柱塑性区的大小与净距密切相关,与此同时,隧道埋深以及围岩级别也是影响中夹岩柱塑性区的重要因素。李享松[11]建立了中夹岩柱的力学分析模型,推导出中夹岩柱破裂面的下滑力、抗滑力计算公式,最终采用安全系数作为中夹岩柱稳定的判据。
通过以上调研可知,针对不同的小净距隧道,不同的围岩级别,对中夹岩柱采取的加固措施不尽相同,各研究人员对于中夹岩柱稳定性的判断标准也不同。为了尽量减小开挖跨度,厦门芦澳路-疏港通道地下互通立交隧道由单洞5车道隧道直接过渡至主洞3车道匝道2车道的小净距隧道,不设置连拱隧道进行过渡。根据设计资料,小净距段隧道中夹岩柱最小厚度为1.2 m,中夹岩柱的厚度较小[3],施工力学机理较为复杂。基于此背景,对小净距段中夹岩柱最小厚度断面进行研究,对比分析不同加固措施对中夹岩柱的影响以及主洞隧道的力学特性,在此基础上提出相应的施工对策。
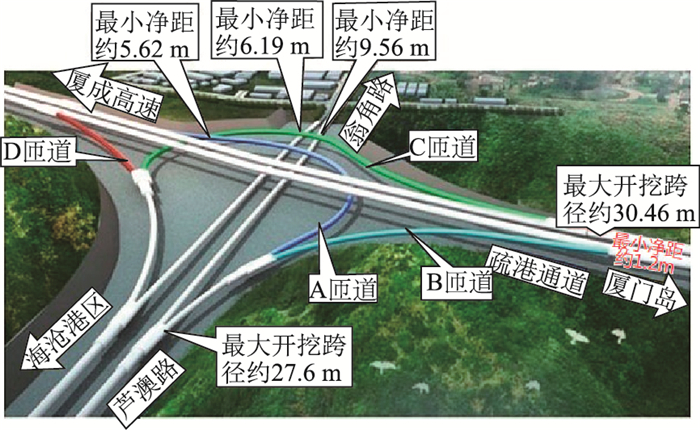
1 工程概况 1.1 工程背景厦门芦澳路—海沧疏港通道地下互通立交隧道位于厦门市海沧区,如图 1所示。芦澳路工程路线呈南北走向,起点接芦澳路跨南海3路跨线桥,路线往北穿越蔡尖尾山后,与疏港通道相交处设置A,B,C,D匝道隧道形成地下互通立交。疏港通道2#隧道左线长4 240 m,右线长4 250 m。分岔隧道则位于2#隧道右线,起讫里程为YK2+343~YK2+622.5,穿越花岗岩地层,为Ⅲ级围岩,最大埋深100 m。疏港分岔隧道采用4种断面逐步扩大过渡,过渡段不设置连拱隧道,由5车道大跨段直接过渡至3车道+2车道小净距段,小净距段最小夹岩厚度为1.2 m。
|
| 图 1 工程地理位置 Fig. 1 Geographic location of project |
| |
1.2 工程地质水文地质条件
疏港通道2#隧道穿越地层主要为花岗岩地层,进出口段地表分布第四系残-坡积层,隧址区构造发育,位于大帽山-石峰岩断裂带,处于石峰岩断块上。在多期构造应力作用下,岩体节理、裂隙较发育,岩体的完整性是在较完整到破碎这个区间内。分岔隧道通过燕山晚期第2次侵入花岗岩地层(γ53(1)b),中粗粒结构,块状构造,以中风化为主,节理、裂隙较发育,主要节理为N10~39°E/65~85°S,部分裂隙填充石英脉,岩体较完整,地下水为基岩裂隙水,主要赋存于花岗岩节理、裂隙中,综合围岩等级为Ⅲ级。
区内地貌属沿海低山丘陵地貌。地下水埋藏较浅,一般为1.0~5.0 m。对工程有影响的地下水主要在冲积层及部分构造储水带中。隧址区地表水较发育,水塘、水库零星分布,地表水流程短、泾流小,自成水系入海。岩体的完整性是在较完整到破碎这个区间内
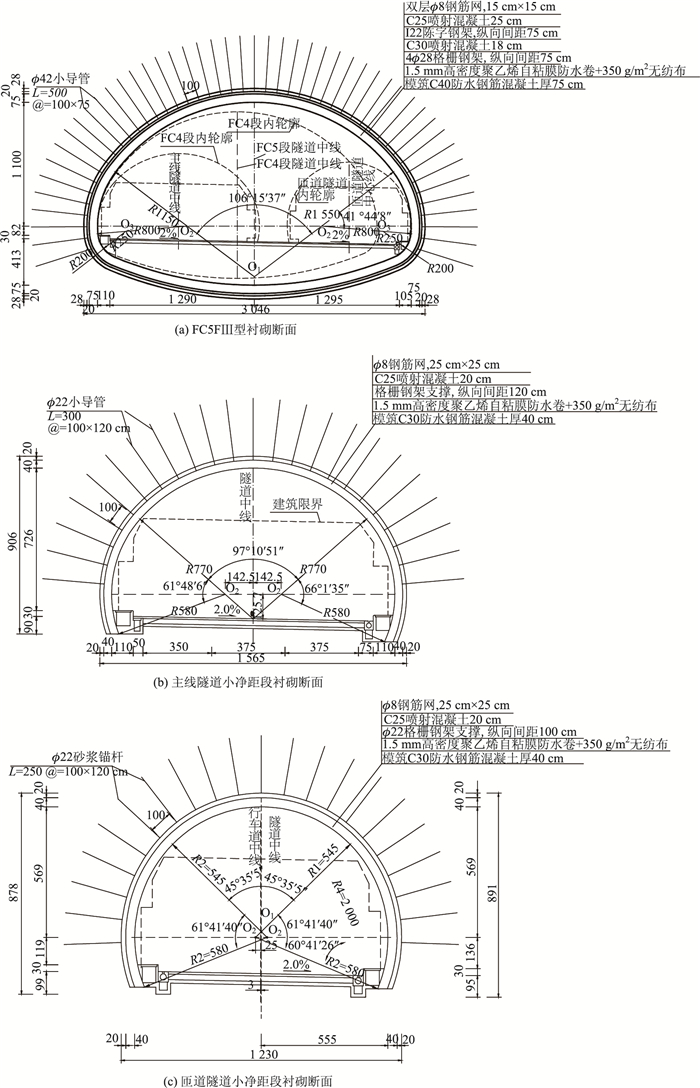
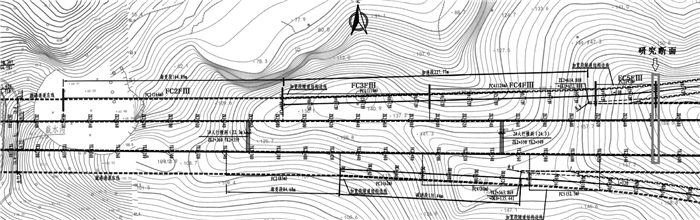
1.3 隧道设计参数及施工工法疏港通道分岔隧道采用4种断面(FC2FⅢ,FC3FⅢ,FC4FⅢ,FC5FⅢ)逐步扩大过渡,由大跨段直接过渡至小净距段,如图 2所示。最大过渡断面(FC5FⅢ),为单洞5车道设计,开挖跨度30.46 m,开挖面积450.41 m2,并采用双层初期支护+二次衬砌的支护设计,大跨段隧道衬砌断面如图 2(a)所示。主线隧道小净距段为单洞3车道设计,开挖跨度15.65 m,开挖面积122.53 m2,采用单层初期支护+二次衬砌的支护设计,主线隧道小净距段衬砌断面如图 2(b)所示。匝道隧道小净距段为单洞2车道设计,开挖跨度12.30 m,采用单层初期支护+二次衬砌的支护设计。匝道隧道衬砌断面如图 2(c)所示。整理疏港通道分岔隧道支护参数,如表 1所示。
|
| 图 2 隧道支护参数(单位: cm) Fig. 2 Tunnel support parameters(unit: cm) |
| |
| 疏港通道分岔隧道 | 施工段 | 支护类型 | 初期支护 | 二次衬砌/cm | ||
| 拱架/cm | 喷射混凝土/cm | |||||
| 大跨段 | 双层初支+ 二衬 | 工22b间距75+ϕ28格栅钢架间距75 | C25厚28+C30厚18 | C40厚75 | ||
| 小净距段 | 主洞隧道 | 单层初支+ 二衬 | ϕ22格栅钢架间距120 | C25厚20 | C30厚40 | |
| 匝道隧道 | 单层初支+ 二衬 | Φ22格栅钢架间距100 | C25厚20 | C30厚40 | ||
2 三轴压缩强度及变形试验 2.1 三轴压缩试验参数
本试验所用标准试件均取自现场掌子面,取样方法为现场钻芯,随后利用切石机进行加工。试样为天然含水状态下的中粗粒花岗岩标准试件,试件直径50 mm,高100 mm,如图 3所示。考虑到现场隧道埋深的影响,共设置5种围压工况,围压分别为:0,3,5,10,15 MPa。
|
| 图 3 花岗岩标准试样 Fig. 3 Standard granite samples |
| |
2.2 三轴试验结果分析 2.2.1 岩石抗剪强度指标计算
不同围压条件下的极限轴向应力,按公式(1)计算,得到计算结果如表 2所示。
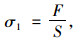
|
(1) |
| 试样 | 围压σ3/ MPa | 极限轴向应力σ1 /MPa | 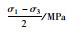 |
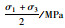 |
| 1 | 0 | 126.94 | — | — |
| 2 | 3 | 250.01 | 123.51 | 126.51 |
| 3 | 5 | 269.35 | 132.18 | 137.18 |
| 4 | 10 | 329.05 | 159.53 | 169.53 |
| 5 | 15 | 387.82 | 186.41 | 201.41 |
式中,σ1为极限轴向应力;F为轴向破坏荷载;S为试件横截面积。
由表 2可知,在有围压的情况下,随着围压增大,岩石试样极限轴向应力随之增大。通过试验得到试样单轴压缩强度σc=126.94 MPa。
以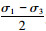
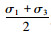
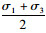
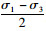

|
| 图 4 最佳关系曲线(单位: MPa) Fig. 4 Best relationship curve(unit: MPa) |
| |
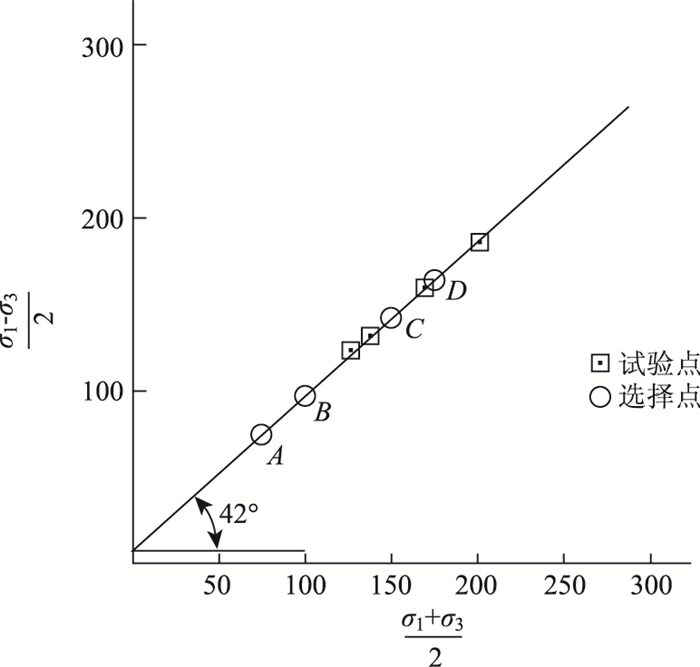
|
| 图 5 莫尔包络线 Fig. 5 Moiré envelope |
| |
| 编号 | 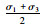 |
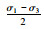 |
编号 | 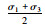 |
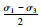 |
|
| A | 75 | 74.55 | C | 150 | 142.06 | |
| B | 100 | 97.05 | D | 175 | 164.56 |
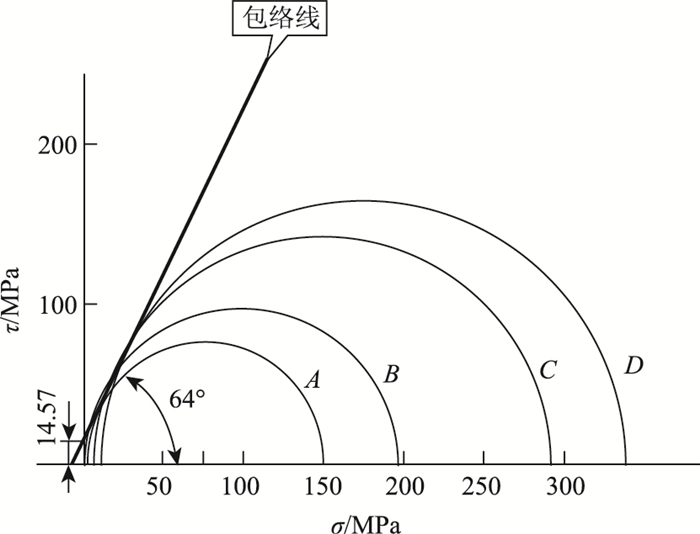
读取包络线在纵向轴上的截距和与横向轴之间的夹角,即可获得岩石黏聚力和内摩擦角,由图 5可知,岩石的内摩擦角为64°,黏聚力为14.57 MPa。
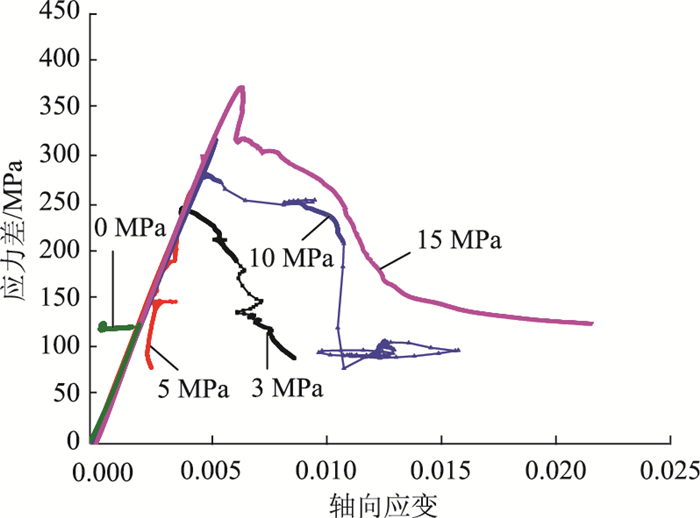
2.2.2 岩石应力-应变曲线图整理三轴压缩试验数据,以轴向应变值εas为横坐标,应力差(σ1-σ3)为纵坐标,绘制1~5试样的应力-应变关系曲线,如图 6所示。
|
| 图 6 1~5试样应力差-轴向应变关系曲线 Fig. 6 Curves of stress difference vs. axial strain of sample 1~sample 5 |
| |
由图 6可知,随着围压的增大,岩石试样峰值强度逐渐增大,超过峰值强度后,此时岩石试样内部裂隙继续发展,最后可以观察到峰值强度后的残余应变和残余强度曲线。同时可知,在无围压情况下,试样峰值强度远低于有围压的试样,岩石试样应力应变曲线几乎为直线,说明本工程花岗岩属于弹脆性岩石,无围压的情况下几乎不存在塑性状态。以上分析说明本工程花岗岩是弹脆性岩石,且岩石处于3向受力状态时的强度和稳定性远大于双向受力状态,应重点关注隧道施工时围岩是否及时处于3向受力状态。
2.2.3 岩石弹性模量和泊松比计算在应力差与轴向应变的关系曲线上(即图 6),确定直线段的起始点应力值σa和轴向应变εaa以及终点应力值σb和轴向应变εab。该直线段斜率为弹性模量,按式(2)计算,对应的弹性泊松比按式(3)计算:
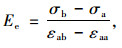
|
(2) |

|
(3) |
式中, Ee为岩石弹性模量;μe为岩石弹性泊松比;σa为应力与轴向应变关系曲线上直线段起始点的应力值;σb为应力与轴向应变关系曲线上直线段终点的应力值;εab为应力为σb时的轴向应变值;εaa为应力为σa时的轴向应变值;εab为应力为σb时的横向应变值;εaa为应力为σa时的横向应变值。
通过以上公式可计算出岩石弹性模量与泊松比,提取计算数据如表 4所示,花岗岩试样弹性模量与围压呈正相关。
| 试样编号 | σb | σa | εaa | εab | εca | εcb | 弹性模量/MPa | 泊松比 |
| 1 | 124.83 | 5.388 | 6.56×10-5 | 0.002 128 | 1.278×10-6 | 0.000 411 | 57 917.77 | 0.20 |
| 2 | 202.55 | 10.59 | 2.84×10-4 | 0.003 39 | 1.075×10-5 | 0.000 741 | 61 802.96 | 0.23 |
| 3 | 203.19 | 11.06 | 2.45×10-4 | 0.003 38 | 1.486×10-5 | 0.000 776 | 61 285.49 | 0.24 |
| 4 | 261.10 | 15.502 | 4.13×10-4 | 0.004 50 | 3.165×10-5 | 0.001 07 | 60 092.49 | 0.25 |
| 5 | 292.60 | 14.401 | 5.16×10-4 | 0.004 88 | 4.301×10-5 | 0.001 20 | 63 748.63 | 0.26 |
根据三轴试验得到岩块的物理力学参数,结合Hoek-Brown强度准则得到现场岩体的物理力学参数。Hoek-Brown等[12]人通过大量岩石三轴试验得到岩体强度普遍估计公式:

|
(4) |
式中, σ1为岩体破坏时最大主应力;σ3为岩体破坏时最小主应力;σc为完整岩块单轴抗压强度;mb, s为岩体Hoek-Brown参数;α为岩体特性决定的常数。
采用基于GSI(地质强度指标)的岩体参数Hoek-Brown估算方法,估算公式如下[12]:
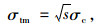
|
(5) |
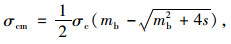
|
(6) |
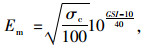
|
(7) |
式中, σtm为岩体抗压强度;σcm为岩体抗拉强度;Em为岩体弹性模量;GSI为岩体的地质强度指标。
结合Mohr-Coulomb强度准则,采用回归分析的方法,可以得出岩体内摩擦角φ和黏聚力c[13]:
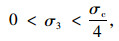
|
(8) |
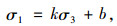
|
(9) |

|
(10) |
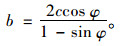
|
(11) |
由上述公式可知,岩体Hoek-Brown参数mb和s是确定岩体强度参数的关键,其值可以由下式得出:
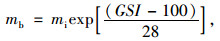
|
(12) |
式中mi为组成岩体完整岩块的Hoek-Brown参数,花岗岩为33。
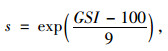
|
(13) |

|
(14) |
通过查询文献[13-16],并结合现场揭示的岩体结构类型和风化状态[17],得到施工现场岩体GSI值为55。根据三轴试验的结果,岩块单轴抗压强度σc=126.94 MPa。由式(12)~(14)可得mb=6.61;s=0.006 738;α=0.504。
由式(5)~(7)可得岩体抗压强度σtm=-10.41 MPa,岩体抗拉强度σcm=0.12 MPa,弹性模量Em=15.02 GPa。由式(4)可得:

|
(15) |
根据式(8),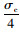
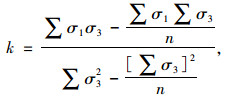
|
(16) |
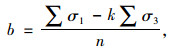
|
(17) |
将表 5中的数据代入公式(16)、(17)得k=5.67,b=31.15,将k, b的值代入公式(10)、(11)得φ=44.5°,c=6.54 MPa。汇总数值模拟采用的围岩物理力学参数如表 7所示。
| 试样编号 | 密度/ (kg·m-3) | 平均密度/ (kg·m-3) | 围压/ MPa | 轴向极限抗压强度/ MPa | 弹性模量/ MPa | 泊松比 | 黏聚力/ MPa | 内摩擦角/ (°) |
| 1 | 2 725.1 | 2 642.5 | 0 | 126.94 | 57 917.77 | 0.20 | 14.57 | 64 |
| 2 | 2 590.5 | 3 | 250.01 | 61 802.96 | 0.23 | |||
| 3 | 2 684.7 | 5 | 269.35 | 61 285.49 | 0.24 | |||
| 4 | 2 698.2 | 10 | 329.05 | 60 092.49 | 0.25 | |||
| 5 | 2 550.1 | 15 | 387.82 | 63 748.63 | 0.26 |
| σ3/MPa | σ1/MPa | σ1σ3 | σ32 |
| 0 | 10.213 58 | 0 | 0 |
| 6 | 77.415 79 | 464.494 7 | 36 |
| 12 | 112.737 8 | 1 352.854 | 144 |
| 18 | 141.356 9 | 2 544.423 | 324 |
| 24 | 166.476 | 3 995.425 | 576 |
| 30 | 189.349 2 | 5 680.475 | 900 |
| ∑=90 | ∑=697.55 | ∑=14 037.67 | ∑=1 980 |
| 类别 | 密度/ (kg·m-3) | 弹性模量/ GPa | 泊松比 | 黏聚力/ MPa | 内摩擦角/ (°) |
| 围岩 | 2 643 | 15.02 | 0.23 | 6.54 | 44.5 |
3 数值模拟 3.1 计算模型
数值计算采用大型岩土工程计算软件FLAC3D 5.0,对小净距隧道中夹岩柱的受力及位移情况进行计算分析。小净距隧道中夹岩柱的加固手段有:加长系统锚杆加固,预应力锚杆加固、对拉锚杆加固以及超前小导管注浆加固等[8]。通过对不同的支护手段进行组合,分析主匝道隧道拱顶位移、边墙位移、夹岩受力、隧道支护受力状态等情况,对不同支护手段的支护效果进行研究。不同支护手段组合工况如表 8所示。
| 工况 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 支护手段 | 毛洞 | 普通喷锚 | 普通喷锚+ϕ32对拉锚杆 | 普通喷锚+ϕ32预应力对拉锚杆(50 kN) | 普通喷锚+ϕ32预应力对拉锚杆(100 kN) | 普通喷锚+ϕ32预应力对拉锚杆(150 kN) | 普通喷锚+ϕ32预应力对拉锚杆(300 kN) |
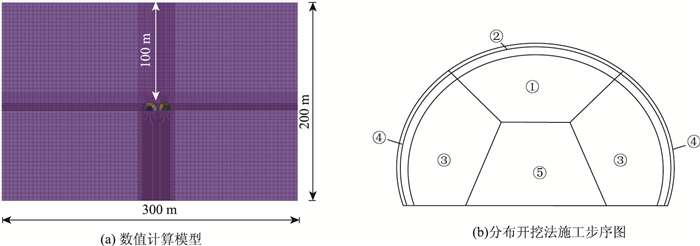
主洞隧道和匝道隧道净距为1.2 m,考虑到隧道开挖边界效应的影响(圣维南原理),模型尺寸为300 m(长)×200 m(高)×1 m(宽),隧道埋深以主线隧道为准为100 m,见图 7(a)。计算边界条件为模型顶部为自由面,其他5个面均约束法向位移。数值模拟中围岩采用弹塑性实体单元模拟,采用Mohr-Coulomb屈服准则,隧道初期支护采用弹性实体单元模拟;系统锚杆、对拉锚杆以及预应力对拉锚杆均采用Cable(锚索)单元模拟,二次衬砌为隧道承载储备本次计算不考虑模拟。主洞和匝道隧道系统锚杆采用ϕ22砂浆锚杆,环向间距为1 m,长度分别为3 m,2.5 m。对拉锚杆和预应力对拉锚杆直径为ϕ32,环向间距均为1 m。
|
| 图 7 数值计算模型与施工工法 Fig. 7 Numerical calculation model and construction method |
| |
主洞隧道和匝道隧道的开挖方法均采用分布开挖施工工法,施工工序如图 7(b)所示,施工工序为:(1)开挖①部;(2)施作①部初期支护②部;(3)开挖③部(预留核心土);(4)完成边墙初期支护④部;(5)开挖预留核心土⑤部。隧道施工顺序为先主洞隧道后匝道隧道,考虑到硬质围岩应力释放较快,故每开挖一步时围岩应力释放率取为70%[18],剩下围岩应力由初期支护承担。
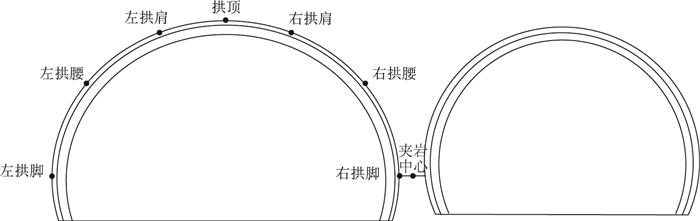
为了研究不同夹岩支护手段的支护效果,对主洞隧道拱顶和夹岩的位移、夹岩应力状态以及主洞隧道左拱脚、左拱腰、左拱肩、拱顶、右拱肩、右拱腰、右拱脚等部位受力情况进行了监测,如图 8所示。
|
| 图 8 监测点设置 Fig. 8 Layout of monitoring points |
| |
3.2 计算参数
围岩的计算参数由三轴试验进行修正后确定,如表 7所示。考虑到喷射混凝土和格栅钢架协调变形,并且初期支护以剪切破坏为主,故隧道初期支护参数采用等效刚度,将格栅钢架的弹性模量折算给C25喷射混凝土,见公式(18);初期支护材料力学参数根据《公路隧道设计规范》(JGT 3370.1—2018)选取。
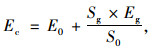
|
(18) |
式中,Ec为折算后的喷射混凝土弹性模量;E0为原C25喷射混凝土弹性模量;Sg为格栅钢架主筋的横截面积;Eg为格栅钢架主筋的弹性模量;S0为C25喷射混凝土的横截面积。
数值模拟采用的隧道支护参数如表 9所示,依据《锚杆喷射混凝土支护技术规范》(GB 50086—2001),砂浆锚杆的黏聚力C取2 MPa、内摩擦角φ取44°。
| 结构 | 弹性模量/GPa | 泊松比 | 密度/(kg·m-3) |
| 主洞初期支护(折算后) | 29.3 | 0.25 | 2 541 |
| 匝道初期支护(折算后) | 29.5 | 0.25 | 2 557 |
| 系统锚杆 | 200 | 0.30 | 7 850 |
| 对拉锚杆 | 200 | 0.30 | 7 850 |
| 预应力对拉锚杆 | 200 | 0.30 | 7 850 |
3.3 中夹岩柱支护效果分析 3.3.1 隧道关键点位移
表 10汇总了主洞拱顶和夹岩中心点的位移。从表 10中可以看出,由于围岩的强度较大,夹岩以弹性变形为主。
| 工况 | 拱顶位移/mm | 夹岩中心位移/mm | |||||||||
| 主洞完成开挖 | 匝道完成开挖 | 主洞完成开挖 | 匝道完成开挖 | ||||||||
| 竖直方向 | 水平方向 | 竖直方向 | 水平方向 | 竖直方向 | 水平方向 | 竖直方向 | 水平方向 | ||||
| 1 | -2.547 | -0.009 49 | -3.440 | -0.209 | 0.01 573 | 0.396 | 0.243 | 0.181 | |||
| 2 | -2.462 | -0.010 37 | -3.241 | -0.170 | 4.50×10-3 | 0.387 | 0.191 | 0.127 | |||
| 3 | -2.461 | -0.010 10 | -3.243 | -0.170 | 5.21×10-3 | 0.387 | 0.190 | 0.127 | |||
| 4 | -2.461 | -0.009 80 | -3.241 | -0.169 | 5.18×10-3 | 0.387 | 0.191 | 0.127 | |||
| 5 | -2.461 | -0.009 48 | -3.243 | -0.170 | 5.18×10-3 | 0.386 | 0.189 | 0.126 | |||
| 6 | -2.460 | -0.009 88 | -3.242 | -0.169 | 3.79×10-3 | 0.387 | 0.189 | 0.126 | |||
| 7 | -2.460 | -0.009 49 | -3.242 | -0.169 | 3.93×10-3 | 0.387 | 0.189 | 0.125 | |||
从拱顶位移来看,双洞开挖完成后,主洞拱顶竖直位移未支护情况下为3.44 mm,采取初期支护后位移为3.24 mm,减小幅度约为6%;主洞拱顶水平位移未支护情况下为0.209 mm,采取初期支护后位移为0.170 mm,减小幅度约为19%。当采取对夹岩加固手段时,随着锚杆预应力的增大,可以发现主洞拱顶位移也有减小的趋势,但减小程度相当有限,这表明隧道施工时,初期支护及时跟进和封闭能有效控制隧道位移变形。
从夹岩中心位移来看,双洞开挖完成后,夹岩中心竖直位移未支护情况下为0.243 mm,采取初期支护后为0.191 mm,减小幅度约为21.4%;夹岩中心水平位移未支护情况下为0.181 mm,采取初期支护后为0.127 mm,减小幅度约为29.8%。施加对拉锚杆和预应力对拉锚杆支护后,夹岩中心水平和竖直位移并没有明显减小。该结果表明,单纯增大预应力,夹岩中心位移减小程度有限。综上所述,初期支护及时闭合能有效减小夹岩位移,由于围岩强度较高,预应力对拉锚杆的支护效果对比对拉锚杆并没有明显提高。
3.3.2 夹岩应力状态考虑到岩体抗拉能力较小,故监测夹岩中心点左右侧岩体最小主应力变化情况,监测点均在同一条水平线上。图 9为采取不同支护手段下夹岩最小应力变化曲线。
|
| 图 9 各工况夹岩应力变化曲线 Fig. 9 Curves of stress of rock under different working conditions |
| |
为了方便描述,将距离夹岩中心距离为-0.6,-0.4,-0.2,0,0.2,0.4,0.6 m的监测点分别记为a,b,c,d,e,f,g测点。以工况1为例,当主洞开挖时,由于应力释放a(靠近主洞),b,c,d点应力迅速减小,夹岩由初始的3向受力状态变为双向受力状态。其中a点应力由-0.827 MPa,减小为-0.133 MPa,随着该点拉应力增大,摩尔应力圆向强度包络线移动,该点出现了剪切破坏,应力继续向深部转移,e,f,g点仍处于3向受力的状态。匝道隧道开挖后,测点应力呈“V”形分布,各测点应力均不同程度小于初始应力,同时也可以发现夹岩中心下部出现了应力集中的现象。
分析工况2~7结果可知,主洞开挖时,初期支护的支护阻力,使得a,b,c,d点处于3向受力的状态,对比工况1,4点的应力均有不同程度的增大。匝道隧道开挖完成后,测点应力呈“V”形分布,以测点c为例,工况2~7该测点应力分别为-0.805,-0.822,-0.862,-0.897,-0.932,-1.036 MPa相比未支护情况下测点应力为-0.720 MPa,应力增长幅度分别为11.8%,14.2%,19.7%,24.5%,29.4%,43.9%。此外,工况2~7中夹岩应力集中的区域也在逐渐变小。由以上分析可知,对夹岩及时的支护,保证夹岩处于3向受力的状态,能提高夹岩稳定性。相比隧道未支护的情况,采取对拉锚杆等支护手段时,夹岩最小主应力增大,使得摩尔应力圆朝着远离强度包络线的方向移动;当采用预应力对拉锚杆时,随着预应力增大,对夹岩受力状态的改善效果也越明显,应力集中的现象也有缓解,主要原因是预应力锚杆提供的预压应力,对夹岩有挟持作用,一定程度上减小了夹岩水平应力的损失,减少了主匝隧道开挖对夹岩的扰动。
3.3.3 主洞隧道受力情况表 11和表 12分列出了主匝隧道开挖完成后,不同夹岩支护条件下主洞隧道轴力和弯矩,根据轴力和弯矩可以求得主洞各部位的安全系数,如表 13所示。
| 工况 | 左拱脚 | 左拱腰 | 左拱肩 | 拱顶 | 右拱肩 | 右拱腰 | 右拱脚 |
| 2 | -1 144.69 | -476.82 | -208.36 | -52.95 | -42.90 | -625.19 | -3 363.80 |
| 3 | -1 144.69 | -476.98 | -208.28 | -52.96 | -42.98 | -624.92 | -3 363.55 |
| 4 | -1 144.84 | -476.85 | -208.37 | -52.8 | -42.84 | -623.41 | -3 362.63 |
| 5 | -1 144.72 | -476.75 | -208.18 | -52.78 | -42.80 | -621.63 | -3 360.37 |
| 6 | -1 144.36 | -476.48 | -208.17 | -52.81 | -43.00 | -619.88 | -3 359.66 |
| 7 | -1 144.65 | -476.45 | -207.82 | -52.83 | -42.37 | -615.40 | -3 355.57 |
| 工况 | 左拱脚 | 左拱腰 | 左拱肩 | 拱顶 | 右拱肩 | 右拱腰 | 右拱脚 |
| 2 | 1 464 | 279 | 699 | -155 | 466 | -216 | 2 225 |
| 3 | 1 463 | 280 | 700 | -155 | 465 | -217 | 2 217 |
| 4 | 1 473 | 278 | 707 | -156 | 467 | -273 | 2 155 |
| 5 | 1 463 | 279 | 700 | -154 | 464 | -254 | 2 173 |
| 6 | 1 463 | 279 | 700 | -157 | 467 | -267 | 2 153 |
| 7 | 1 464 | 279 | 699 | -148 | 464 | -306 | 2 085 |
| 工况 | 左拱脚 | 左拱腰 | 左拱肩 | 拱顶 | 右拱肩 | 右拱腰 | 右拱脚 |
| 2 | 3.332 | 7.984 | 18.373 | 72.251 | 88.629 | 6.085 | 1.132 |
| 3 | 3.332 | 7.981 | 18.38 | 72.243 | 88.477 | 6.087 | 1.132 |
| 4 | 3.331 | 7.983 | 18.373 | 72.465 | 88.745 | 6.104 | 1.132 |
| 5 | 3.332 | 7.985 | 18.389 | 72.488 | 88.843 | 6.121 | 1.133 |
| 6 | 3.333 | 7.989 | 18.390 | 72.453 | 88.425 | 6.138 | 1.133 |
| 7 | 3.332 | 7.990 | 18.421 | 72.407 | 89.716 | 6.184 | 1.135 |
分析表 11和表 12可以发现对夹岩采取加固措施后,主洞左侧结构轴力和弯矩基本没有变化;对比工况3~7,而随着预应力的增大右侧结构的轴力和弯矩有减小的趋势,说明对夹岩支护能一定程度改善隧道受力状态,减少匝道隧道施工对主洞隧道的扰动。分析表 13可知,主洞隧道初期支护不同部位的安全系数相差较大,安全系数由高到低依次是拱顶、右拱肩、左拱肩、左拱腰、右拱腰、左拱脚、右拱脚。左、右拱脚的安全系数相对较小,说明左右拱脚应力集中较大,尤其是右拱脚,其承受的轴力远大于其他部位,安全系数最小仅为1.132,左右拱脚是隧道受力最不利的部位,施工时应加强左右拱脚处支护。
4 结论(1) 本工程中的花岗岩属于弹脆性岩石,岩石处于3向受力状态时岩石强度和稳定性远大于双向受力状态,花岗岩试样弹性模量与围压呈正相关;结合Hoek-Brown及Mohr-Coulomb强度准则对三轴试验结果进行修正得到岩体物理力学参数。
(2) 初期支护及时闭合能有效减小夹岩位移,但中夹岩柱下部会出现应力集中现象,采用预应力对拉锚杆可以有效地缓解中夹岩柱的应力集中,施工中建议采用低预应力对拉锚杆。
(3) 主洞隧道初期支护不同部位的安全系数相差较大,左、右拱脚的安全系数相对较小,右拱脚安全系数最小仅为1.132,说明左右拱脚应力集中较大,左右拱脚是隧道受力最不利的部位,施工时应加强左右拱脚处支护。
(4) 岩石的强度和稳定性与围压关系较大,在对小净距隧道进行施工时,建议采取主动支护的手段,及时地对隧道以及中夹岩柱进行封闭支护,使得围岩尽快的处于3向受力状态。
| [1] |
钱七虎. 建设特大城市地下快速路和地下物流系统: 解决中国特大城市交通问题的新思路[J]. 科技导报, 2004, 22(4): 3-6. QIAN Qi-hu. Constructing Underground Expressway and Underground Logistics System of Metropolis in China[J]. Science & Technology Review, 2004, 22(4): 3-6. |
| [2] |
孙苗苗, 蒋丞武, 虞梦菲, 等. 伴随城市生长的地下交通空间布局与开发[J]. 地下空间与工程学报, 2019, 15(4): 980-989. SUN Miao-miao, JIANG Cheng-wu, YU Meng-fei, et al. Layout and Exploitation of Underground Traffic Space with City Growth[J]. Chinese Journal of Underground Space and Engineering, 2019, 15(4): 980-989. |
| [3] |
李术才, 王汉鹏, 郑学芬. 分岔隧道稳定性分析及施工优化研究[J]. 岩石力学与工程学报, 2008, 27(3): 447-457. LI Shu-cai, WANG Han-peng, ZHEN Xue-fen. Forked Tunnel Stability Analysis and Its Construction Optimization Research[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(3): 447-457. |
| [4] |
应国刚, 张素磊, 周明, 等. 基于预留支护假设的小净距隧道中央岩墙应力简化计算方法[J]. 公路交通科技, 2018, 35(12): 95-103. YING Guo-gang, ZHANG Su-lei, ZHOU Ming, et al. A Simplified Method for Calculating Stresses in Middle Rock Wall of Small Interval Tunnels Based on Reserved Supporting Hypothesis[J]. Journal of Highway and Transportation Research and Development, 2018, 35(12): 95-103. |
| [5] |
唐雨春, 徐林生, 金美海. 小净距隧道建设的若干问题综述[J]. 隧道建设, 2007, 27(1): 22-25. TANG Yu-chun, XU Lin-sheng, JIN Mei-hai. Comments on Construction of Closely-spaced Tunnels[J]. Tunnel Construction, 2007, 27(1): 22-5. |
| [6] |
刘芸, 周玉兵. 软岩小净距隧道中夹岩柱分区及加固方法研究[J]. 地下空间与工程学报, 2013, 9(2): 373-379. LIU Yun, ZHOU Yu-bing. Study on Partition and Reinforcement Method of Middle Rock Pillar in Soft Rock Tunnel with Small Clear Distance[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 9(2): 373-379. |
| [7] |
张桂生, 冯文件, 刘新荣, 等. Ⅴ级围岩下小净距隧道合理净距的探讨[J]. 地下空间与工程学报, 2009, 5(3): 582-586. ZHANG Gui-sheng, FENG Wen-jian, LIU Xin-rong, et al. Discussion on Reasonable Distance of Tunnel with Small Spacing in Ⅴ Grade Rock[J]. Chinese Journal of Underground Space and Engineering, 2009, 5(3): 582-586. |
| [8] |
李建林, 吴金刚, 毕强. 大跨度小净距公路隧道设计与施工方法研究[J]. 现代隧道技术, 2019, 56(5): 157-162, 227. LI Jian-lin, WU Jin-gang, BI Qiang. Study on the Design and Construction Method for the Large-span Highway Tunnel with Small Interval[J]. Modern Tunnelling Technology, 2019, 56(5): 157-162, 227. |
| [9] |
赵秀绍, 庄锦彬, 徐长节, 等. 浅覆大跨度小净距隧道中岩墙及初支力学特性研究[J]. 公路交通科技, 2015, 32(12): 100-107. ZHAO Xiu-shao, ZHUANG Jin-bin, XU Chang-jie, et al. Study of Mechanical Properties of Middle Rock Wall and Preliminary Lining of Shallow Buried Large Span Tunnel with Small Clear Distance[J]. Journal of Highway and Transportation Research and Development, 2015, 32(12): 100-107. |
| [10] |
晏启祥, 何川, 姚勇, 等. 软岩小净距隧道施工力学效应研究[J]. 地下空间与工程学报, 2005, 1(5): 693-697. YAN Qi-xiang, HE Chuan, YAO Yong, et al. Study on Mechanical Effect of Small-distance Tunnels Located at Soft Ground[J]. Chinese Journal of Underground Space and Engineering, 2005, 1(5): 693-697. |
| [11] |
李享松, 张心源, 覃娟, 等. 小净距隧道中夹岩安全系数法研究与验证[J]. 安全与环境学报, 2019, 19(6): 1898-1903. LI Xiang-song, ZHANG Xin-yuan, QIN Juan, et al. Pursuit and Verification of the Safety Coefficient of the Clamping Rock in the Short-distance Tunnel[J]. Journal of Safety and Environment, 2019, 19(6): 1898-1903. |
| [12] |
HOEK E, BROWN E T. Empirical Strength Criterion for Rock Masses[J]. Journal of the Geotechnical Engineering Division, 1980, 106(GT4): 1013-1035. |
| [13] |
苏永华, 封立志, 李志勇, 等. Hoek-Brown准则中确定地质强度指标因素的量化[J]. 岩石力学与工程学报, 2009, 28(4): 679-686. SU Yong-hua, FENG Li-zhi, LI Zhi-yong, et al. Quantification of Elements for Geological Strength Index in Hoek-Brown Criterion[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(4): 679-686. |
| [14] |
封立志. 隧道围岩力学参数估计及应用研究[D]. 长沙: 湖南大学, 2009. FENG Li-zhi. Study on Mechanical Parameters Estimation of Rock Mass and Application in Tunnel[D]. Changsha: Hunan University, 2009. |
| [15] |
CARRANZA-TORRES C, FAIRHUST C. The Elasto-plastic Response of Underground Excavations in Rock Masses that Satisfying the Hoek-Brown Failure Criterion[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(6): 777-809. |
| [16] |
SONMEZ H, ULUSAY R. Modification to the Geological Strength Index (GSI) and Their Applicability to Stability of Slopes[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(6): 743-760. |
| [17] |
HOEK E. 实用岩石工程技术[M]. 刘丰收, 等译. 郑州: 黄河水利出版社, 2002. HOEK E. Practical Rock Engineering[M]. LIU Feng-shou, et al translated. Zhengzhou: Yellow River Water Resources Press, 2002. |
| [18] |
孙亚奇, 杜守继. 山岭隧道开挖应力释放率研究[J]. 四川建筑科学研究, 2017, 43(3): 153-158. SUN Ya-qi, DU Shou-ji. Study of Stress Release Ratio of Mountain Tunnel Excavation[J]. Sichuan Building Science, 2017, 43(3): 153-158. |
 2021, Vol. 38
2021, Vol. 38
