扩展功能
文章信息
- 戴自然, 廖万辉, 周旭, 吴福飞, 杨冬升
- DAI Zi-ran, LIAO Wan-hui, ZHOU Xu, WU Fu-fei, YANG Dong-sheng
- 特大悬索桥现场隧道锚塞体的自平衡法承载特性研究
- Study on Bearing Characteristics of Site Tunnel Anchor Plug Body of Grand Suspension Bridge by Self-balance Method
- 公路交通科技, 2021, 38(8): 93-100
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(8): 93-100
- 10.3969/j.issn.1002-0268.2021.08.013
-
文章历史
- 收稿日期: 2021-02-03
2. 贵州省公路工程集团有限公司, 贵州 贵阳 550001
2. Guizhou Highway Engineering Group Co., Ltd., Guiyang Guizhou 550001, China
悬索桥[1-4]整体造型美观流畅,相比其他桥梁具有加固、维护和改建便利以及施工快捷的特点。锚塞体作为悬索桥的4大部件之一[5-7],在实际工程中,与围岩一起均要承受桥梁静载、行车动载和风荷载等其他不可遇见荷载的作用。因此,锚塞体和围岩在荷载作用下的安全性是悬索桥的关键问题之一[8-10]。
为了验证锚塞体和围岩在荷载作用下的安全性,国内学者张奇华采用现场和数值模拟发现,围岩破坏面主要发生在围岩接触面和锚体底部,扩散向外呈圆台桩发展[11]。李栋梁采用1∶10的原位模型试验,分析了围岩的变形和长期稳定性,并提出了浅埋软岩隧道锚的破坏形式[12]。童俊采用1∶10模型试验结合有限元分析,试验发现荷载达到8倍设计荷载时锚塞体发生破坏[13]。王东英采用Mindlin应力解,提出了隧道锚极限承载力的计算公式,通过实际工程,与室内试验验证其合理性[14]。王中豪基于隧道锚承载能力计算公式缺乏的问题,提出了承载能力非线性映射PSO-LSSVM模型,通过试验证明了PSO-LSSVM模型预测结果的合理性[15]。
自平衡法[16]是近些年来新发展的测桩承载力的方法,由于不需外部加载反力,以自身承载能力作为加载的反力,实现自我加载,可以在面临超大吨、边坡、水上等试验环境困难时,完成堆载法、锚桩法等传统加载方法难以完成的试验。然而用于隧道锚塞体的试验检测还不多见。为此,本研究借助自平衡测试方法,以开州湖大桥隧道锚塞体为例,采用现场模型试验验证现场隧道锚塞体自平衡的承载特性,为类似桥梁工程的长期安全性评价提供参考。
1 工程概况与地质构造 1.1 工程概况开州湖特大桥位于贵州黔北山地,地势总体西北高东南低,属浅切低山溶蚀、侵蚀地貌类型。桥长1 257 m,上部结构:3×30 m T梁+(1 100) m悬索桥+2×30 m T梁,孔跨布置:主桥为单跨1 100 m钢桁梁悬索桥;两岸主缆边跨分别为302, 143 m,主缆垂跨比1/10,主塔塔高分别为139,141 m,引桥为预应力混凝土T梁桥。下部结构:主塔采用薄壁空心钢筋混凝土桥塔,承台群桩基础;引桥墩为双柱式圆墩,圆桩基础;锚碇为重力式(瓮安岸)及隧道式锚(开阳岸)。开阳岸锚碇设计为隧道式嵌岩锚碇,设计以中风化基岩为基础持力层,锚碇抗滑移摩阻系数不小于0.6,锚碇混凝土与岩体接触面粘聚力不小于170 kPa。锚塞体单缆最大缆力2.56万t,抗拔安全系数不应小于2.0,设计围岩稳定安全系数不应小于4.0。
1.2 场区地质构造及岩土构成据《贵州省区域地质志》及1∶20万瓮安幅区域地质调查报告,项目区域区内位于扬子准地台-黔北台隆-遵义断拱-贵阳复杂构造变形区。桥区于K36+140处垂直跨越翁绍背斜轴部,背斜轴向北北东10°,近南北向展布,桥区核部地层为寒武系下统明心寺组、牛蹄塘组,两翼地层为寒武系下统金顶山组、清虚洞组。展布北段被北东向的顶兆冲断裂及其次生断裂切割,背斜轴部错动、平移,部分背斜轴与断裂重叠而隐伏。桥区两岸岩层倾向山内,背斜北西翼(开阳岸)岩层产状:325°∠25°,发育两组节理:J1:105°∠79°,J2:36°∠81°,背斜南东翼(瓮安岸)岩层产状90°∠20°,发育两组节理Jl:48°∠77°,J2:101°∠86°。根据赤平投影分析瓮安岸岩层与J1为内倾结构面,对岸坡影响小,J2为外倾结构面,在该结构面的作用下形成瓮安岸卸荷裂隙、开阳岸岩层与J1为内倾结构面,J2为外倾结构面。在该结构面的作用下形成错落体及陡崖。场区地层为上覆残坡积层(Q4el+dl)含碎石黏土、崩塌堆积层(Q4col)块石土,下伏基岩为寒武系(∈1q)清虚洞组白云岩、白云质灰岩;寒武系金顶山组(∈1j)页岩、泥质粉砂岩、泥岩、泥质灰岩;寒武系明心寺组(∈1m)粉砂质泥岩夹泥岩;寒武系牛蹄塘组(∈1n)碳质泥岩。
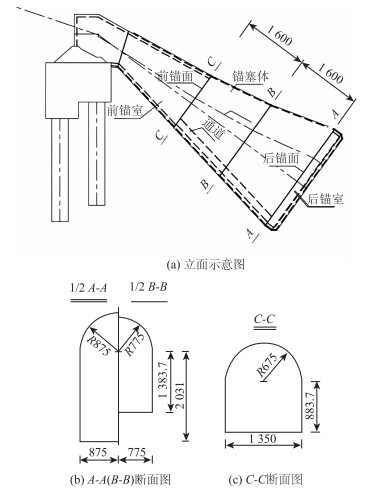
2 锚塞体模型的确定经过多次反复计算和结合施工情况,最终确定模型锚塞体按照实际体型进行1∶10比例缩小(如图 1~2所示)。据此确定双模型锚塞体的间距和尺寸(两模型锚塞体尺寸相同)。双模型锚塞体尾端距离1 150.0 mm,前端距离1 350.0 mm,长均为3 200.0 mm。断面为城门洞型,底端截面高为2 158.7 mm,宽为1 550.0 mm,前端截面高为1 558.7 mm,宽为1 350.0 mm。双模型锚塞体轴线倾角均为36.2°,单缆最大缆力256.0 t。
|
| 图 1 模型锚塞体(单位: mm) Fig. 1 Anchor plug model(unit: mm) |
| |
|
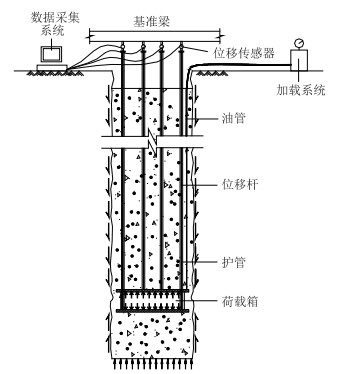
| 图 2 锚塞体自平衡试验 Fig. 2 Self-balance test of anchor plug body |
| |
模型锚塞体室试点制备应符合以下规定:(1)因开州湖大桥现场条件的限制,千斤顶及位移杆等部件均采用现场焊接组装; (2)千斤顶推力面与模型锚塞体倾斜度(36.2°)始终保持垂直,模型锚塞体的荷载反力部(底部基岩)应有足够强度且需大致凿平; (3)在浇注混凝土前,应清除内壁松散的碎石及其杂物; (4)制备一定比例的混凝土试件,并进行规范养护,在模型锚塞体试验前测试其抗压强度,当其强度达到C40及以上方可进行试验; (5)以锚塞体顶端为圆心,在半径为3 m的范围外搭设试验钢架,并将位移杆搭接固定到试验钢架上; (6)锚塞体原型的受力缆索通过转换装置施加在锚塞体底部,模型试验采用千斤顶后推法加载,其受力特征相似; (7)为模拟隧道锚的实际受力状态,采用后推法进行加载试验。传力钢垫板浇注在锚塞体模型的后部,然后安装千斤顶。试验反力由在锚塞体后部的试验支硐内浇注的混凝土后座提供。考虑到模型锚塞体的超载要求,混凝土后座设计可承受荷载不小于设计荷载的20倍。
3 试验方法 3.1 试验测试原理采用后推法测试技术对开州湖大桥进行试验测试,试验装置示意图如图 2所示。在模型锚塞体尾端位置安设千斤顶及位移杆(每个模型锚塞体下位移杆2个、上位移杆4个),沿着垂直作用方向加载,测试出模型锚塞体承载力和荷载—位移关系曲线表达式,从而计算得到模型锚塞体的极限承载力及荷载-位移关系曲线特性。
3.2 加载过程试验加载过程采用慢速维持荷载法对开州湖大桥进行测试。加载分级规定为:试验每级荷载的加载值为预估极限荷载承载力的1/10,第1级采用2倍分级荷载进行加载,第1 h内应在5,15,30,45,60 min各测读1次位移量,以后每隔30 min测读1次。卸载分级规定为:荷载最后一级荷载加载完成后,应分级将荷载卸载至0,每级卸载量按2倍分级荷载进行;每级荷载卸载后隔15 min测读1次,读2次后,隔30 min再读一次,即可卸下一级荷载,全部卸载后,隔3~4 h再读1次。荷载维持标准规定为:在加载和卸载时,应保持荷载传递均匀和连续,且无任何冲击荷载产生,每级荷载变化幅度不超过分级荷载±5%;每级荷载作用下每1 h内的位移增量不超过0.01 mm,并连续出现3次每级加载量为预估加载量的1/10,第1次按2倍分级荷载加载,见表 1。每级卸载为2倍加载值,见表 2。
| 试验级别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 加载值/kN | 5 120 | 7 680 | 10 240 | 12 800 | 15 360 | 17 920 | 20 480 | 23 040 | 25 600 |
4 结果与分析 4.1 锚塞体加载过程分析
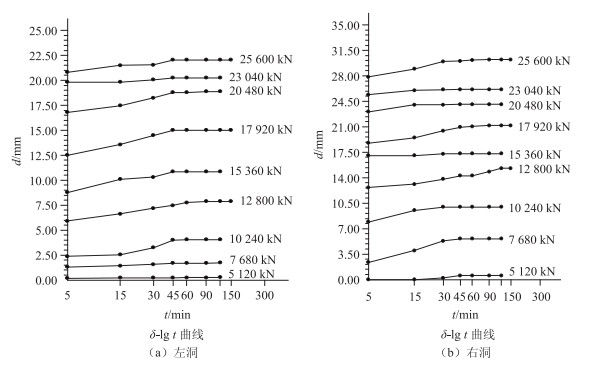
锚塞体的加载过程由图 3位移-时间对数曲线图可见,锚塞体在5 120~25 600 kN加载下,均恒加载300 min后,各级荷载作用下位移的变化规律有所不同。总体呈现出荷载值加载时间的延长,位移呈增大的趋势,位移基本发生在15~45 min,且每级荷载值加载下,其位移最大不超过5 mm。各级荷载增大后,其位移相对增大。对比左洞和右洞的加载-位移图发现,右洞在各级荷载加载下,其位移均高于左洞,部分高于5 mm。
|
| 图 3 位移-时间对数(δ-lg t)曲线 Fig. 3 Displacement-time logarithm (δ-lg t) curves |
| |
4.2 模型锚塞体抗拉试验
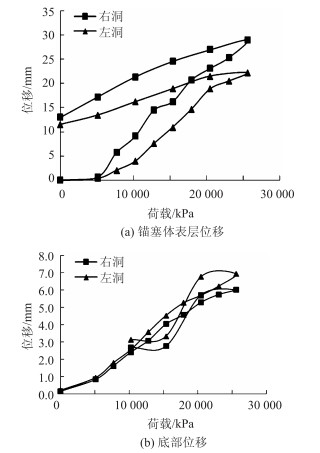
通过对模型锚塞体底部加载,其荷载-位移曲线如图 4所示。
|
| 图 4 荷载与位移关系 Fig. 4 Relationships between load and displacement |
| |
在底部荷载箱加载过程中,随着加载荷载从0增至25 600 kN时,模型锚塞体表层以及底部位移均呈增加的趋势。当极限荷载为25 600 kN,此时模型锚塞体的抗拔力为设计值的10倍,模型锚塞体及周围岩体无破坏迹象,两个模型锚塞体洞口位置出现轻微裂缝开展,荷载位移曲线为缓变形。模型锚塞体右洞表层位移为29.0 mm,模型锚塞体左洞表层位移为22.2 mm;右洞底部位移为12.9 mm,左洞底部位移为12.2 mm。在荷载箱卸载后,模型锚塞体右洞表层残留位移为13.0 mm,模型锚塞体左洞表层残留位移为11.5 mm;右洞底部位移为1.3 mm,左洞底部位移为0.95 mm。对比两个锚塞体的加、卸载过程也不难发现,右洞锚塞体在加、卸载过程中的位移均高于左洞,即使卸载完成后,仍表现出相同的规律。结合JTG/T D65-05—2015《公路悬索桥设计规范》[17]的要求和开州湖大桥的情况,该桥在运营阶段最大允许位移为11.0 mm,竖向变形为22.0 mm。通过试验发现,当锚塞体的抗拔力超过10倍设计值时,其位移量超过了允许值,经计算发现右、左洞锚塞体抗拔力分别是设计值的8倍和9倍其位移均不超过允许设计值。在设计中,要求抗拔安全系数不应小于2.0,围岩稳定安全系数不应小于4.0。本试验结果可达到8倍设计值,即安全系数达到8.0,远高于设计要求,可见开州湖大桥在运行中有足够的安全性。
4.3 锚塞体竖向抗拔承载力计算根据DBJ 52/T 079—2016《基桩承载力自平衡检测技术规程》[18]中对于桩竖向承载力极限值的计算办法,可计算出模型锚塞体的极限承载力,见式(1),模型锚塞体的极限承载力特征值可由式(2)计算:
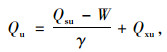
|
(1) |
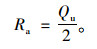
|
(2) |
式中,Qu为锚塞体的竖向极限承载力;W为锚塞体上段的自重;γ为锚塞体摩阻力的转换系数,取1.0;Qsu为锚塞体上段的极限承载力;Qxu为锚塞体下段的极限承载力;Ra为模型锚塞体的承载力特征值。
根据模型锚塞体的试验结果发现,当其位移量不超过允许位移值时,其荷载分别为20 480 kN和23 040 kN,极限荷载均为25 600 kN,模型锚塞体身的自重为547 kN。因此,模型锚塞体的竖向抗拔极限承载力特征值为12 526.5 kN。
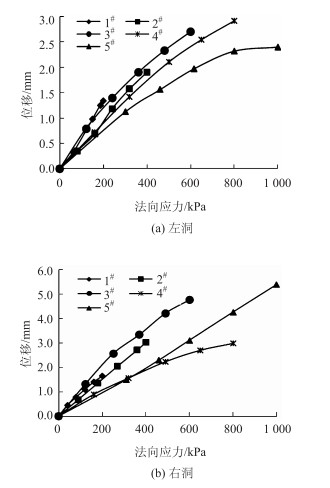
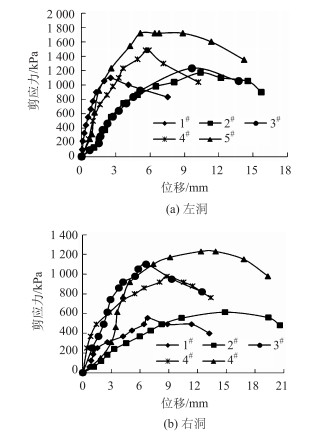
4.4 锚塞体摩擦角和黏聚力的确定开州湖大桥现场原位剪切试验的法向应力-位移关系曲线如图 5所示,剪应力-位移(τ-us)关系曲线如图 6所示。从图 5发现,法向应力从0增至1 000 kPa时,其位移不断增大,即应力越大,位移基本也越大。但在右洞中,法向应力加载至800 kPa时,其最大位移比法向应力为400 kPa时低0.05 mm。从整体来看,在各法向应力增大的过程中,左、右洞位移基本呈线性变化,且右洞的位移基本高于左洞。由图 6发现,当法向应力分别为200,400,600,800,1 000 kPa后,左、右洞剪切应力随位移的增加呈现出先增大后降低的变化趋势,即当剪切位移达到一定值后,混凝土试件与岩石接触面发生了一定程度的剪切破坏,其剪切应力也随之降低。
|
| 图 5 法向应力与法向位移(σ-un)关系 Fig. 5 Relationships between normal stress and normal displacement (σ-un) |
| |
|
| 图 6 剪应力与剪切位移(τ-us)关系曲线 Fig. 6 Relationships between shear stress and shear displacement(τ-us) |
| |
摩擦角和黏聚力通常采用最小二乘法来确定,分别如式(3)和式(4)所示:
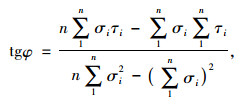
|
(3) |
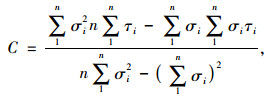
|
(4) |
式中,tg φ为摩擦系数;C为黏聚力;σi为正应力值,i,…,n;τi为与σi相对应的剪应力值,i=1, …, n;n为总次数。
根据开州湖大桥的试验结果代入式(3)和式(4),综合考虑建议左洞混凝土与岩体间的黏聚力381 kPa,右洞混凝土与岩体间的黏聚力369 kPa;左洞混凝土与岩体接触面摩擦系数0.77,右洞混凝土与岩体接触面摩擦系数1.44。结合两洞的实际情况,建议混凝土与岩体间的摩擦系数0.77和黏聚力369 kPa,高于设计中锚碇抗滑移摩阻系数不小于0.6和锚碇混凝土与岩体接触面黏聚力不小于170 kPa的取值要求。
4.5 模型锚塞体抗拔安全系数计算锚塞体抗拔安全系数根据JTG/T D65-05—2015《公路悬索桥设计规范》中的要求进行计算,如式(5)所示。
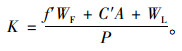
|
(5) |
式中,K为抗拔稳定系数;f′为摩擦系数;A为接触面积;C′为黏聚力;P为设计值;WL为结构自重沿拉拔方向的分量;WF为结构自重垂直于滑动面的分量。
在模型锚塞体中,接触面为33.8 m2,自重垂直分量为530 kN,自重沿拉拔分量为564 kN,结合现场摩擦角和粘聚力的取值,将其代入经公式(5),两个锚塞体的抗拔安全系数分别为5.3(左洞)和5.2(右洞)。在JTG/T D65-05—2015《公路悬索桥设计规范》中,锚塞体抗拔安全系数和围岩稳定安全系数分别不应小于2.0和4.0,本项目中,其安全系数均满足规范的要求。另外,在模型锚塞体抗拉加载试验中,右、左洞锚塞体抗拔力分别是设计值的8倍和9倍其位移均不超过允许设计值,因此,在不考虑摩擦参数时,其安全系数已经达到8.0和9.0。结合式(5)的计算结果不难发现,其安全系数满足JTG/T D65-05—2015《公路悬索桥设计规范》的相关要求,在实际运营中有足够的安全性。
5 结论(1) 锚塞体荷载值加载时间的延长,位移呈增大的趋势,位移基本发生在15~45 min,且每级荷载值加载下,其位移最大不超过5 mm,右洞在各级荷载加载下其位移均高于左洞,部分高于5 mm。
(2) 在加载过程中,模型锚塞体及周围岩体无破坏迹象,两个模型锚塞体洞口位置出现轻微裂缝开展,荷载位移曲线为缓变形。在加、卸载过程中,右洞锚塞体在加、卸载过程中的位移均高于左洞,即使卸载完成后,仍表现出相同的规律。经计算发现右、左洞锚塞体抗拔力分别是设计值的8倍和9倍其位移均不超过允许设计值,远高于抗拔安全系数和围岩稳定安全系数不应小于2.0和4.0的要求,验证了开州湖大桥在运行中有足够的安全性。
(3) 试验结果建议混凝土与岩体间的摩擦系数为0.77和黏聚力为369 kPa,采用各模型锚塞体的摩擦系数和黏聚力,确定两个模型锚塞体的的安全系数分别为5.3(左洞)和5.2(右洞),满足JTG/T D65-05—2015《公路悬索桥设计规范》中,锚塞体抗拔安全系数和围岩稳定安全系数分别不应小于2.0和4.0的要求。
| [1] |
毛伟琦, 胡雄伟. 中国大跨度桥梁最新进展与展望[J]. 桥梁建设, 2020, 50(1): 13-19. MAO Wei-qi, HU Xiong-wei. Latest Developments and Prospects for Long-span Bridges in China[J]. Bridge Construction, 2020, 50(1): 13-19. |
| [2] |
王鹏, 唐清华, 闫海青, 等. 空间缆索悬索桥吊索断裂时的强健性分析[J]. 公路交通科技, 2021, 38(4): 71-75, 91. WANG Peng, TANG Qing-hua, YAN Hai-qing, et al. Analysis on Robustness of Spatial Cable Suspension Bridge with Fracture of Slings[J]. Journal of Highway and Transportation Research and Development, 2021, 38(4): 71-75, 91. |
| [3] |
张海顺, 王玉银. 自锚式悬索桥先斜拉后悬索的体系转换模拟[J]. 公路交通科技, 2019, 36(1): 78-86. ZHANG Hai-shun, WANG Yu-yin. Simulation of System Transformation from Temporary Cable-stayed Bridge to Self-anchored Suspension Bridge[J]. Journal of Highway and Transportation Research and Development, 2019, 36(1): 78-86. |
| [4] |
沈锐利, 王文弟, 王路, 等. 基于可靠度理论的悬索桥预应力锚固系统时变计算方法研究[J]. 公路交通科技, 2019, 36(9): 57-64. SHEN Rui-li, WANG Wen-di, WANG Lu, et al. Study on Time-variant Calculation Method of Prestressed Anchor System of Suspension Bridge Based on Reliability Theory[J]. Journal of Highway and Transportation Research and Development, 2019, 36(9): 57-64. |
| [5] |
葛振才. 隧道锚技术在大型悬索桥中的应用[J]. 中国公路, 2021(1): 94-95. GE Zhen-cai. Application of Tunnel Anchor Technology in Large Suspension Bridge[J]. China Highway, 2021(1): 94-95. |
| [6] |
范一平. 压力型预应力锚索受力特性数值分析[J]. 公路交通科技, 2020, 37(9): 34-40. FAN Yi-ping. Numerical Analysis on Mechanical Characteristics of Pressure-type Prestressed Anchor Cable[J]. Journal of Highway and Transportation Research and Development, 2020, 37(9): 34-40. |
| [7] |
张可能, 李斌, 张洪亮, 等. 某隧道洞口段斜穿复合型滑坡体的综合治理及评价[J]. 公路交通科技, 2020, 37(5): 100-107. ZHANG Ke-neng, LI Bin, ZHANG Hong-liang, et al. Comprehensive Treatment and Evaluation of Inclined Composite Landslide in Portal Section of a Tunnel[J]. Journal of Highway and Transportation Research and Development, 2020, 37(5): 100-107. |
| [8] |
邓琴, 汤华, 吴振君, 等. 隧道锚-围岩系统承载特性的室内模型试验及畸变纠正[J]. 岩土力学, 2017, 38(增1): 247-254. DENG Qin, TANG Hua, WU Zhen-jun, et al. Research on Capacity Characteristics of Tunnel Anchorage and Distortion Correction[J]. Rock and Soil Mechanics, 2017, 38(S1): 247-254. |
| [9] |
于春. 坝陵河大桥隧道锚碇围岩稳定性及与上方公路隧道相互影响分析[J]. 四川建筑, 2008, 15(1): 106-108, 110. YU Chun. Analysis of Surrounding Rock Stability of Tunnel Anchorage of Baling River Bridge and Its Interaction with Upper Highway Tunnel[J]. Sichuan Architecture, 2008, 15(1): 106-108, 110. |
| [10] |
胡波, 曾钱帮, 饶旦, 等. 锚碇-围岩系统在拉剪复合应力条件下的变形规律及破坏机制研究: 以坝陵河特大岩锚悬索桥为例[J]. 岩石力学与工程学报, 2007, 26(4): 712-719. HU Bo, ZENG Qian-bang, RAO Dan, et al. Study on Deformation Law and Failure Mechanism of Anchorage-surrounding Rock System under Tensile-shear Complex Stresses: Taking Super-large Suspension Bridge on Baling River for Example[J]. Chinese Journal of rock Mechanics and Engineering, 2007, 26(4): 712-719. |
| [11] |
张奇华, 李玉婕, 余美万, 等. 隧道锚围岩抗拔机制及抗拔力计算模式初步研究[J]. 岩土力学, 2017, 38(3): 810-820. ZHANG Qi-hua, LI Yu-jie, YU Mei-wan, et al. Preliminary Study of Pullout Mechanisms and Computational Mode of Pullout Force for Rocks Surrounding Tunnel-type Anchorage[J]. Rock and Soil Mechanics, 2017, 38(3): 810-820. |
| [12] |
李栋梁, 刘新荣, 李俊江, 等. 浅埋软岩隧道式锚碇稳定性原位模型试验研究[J]. 岩土工程学报, 2017, 39(11): 2078-2087. LI Dong-liang, LIU Xin-rong, LI Jun-jiang, et al. Stability of Shallowly Buried Soft Rock Tunnel Anchorage by In-situ Model Tests[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(11): 2078-2087. |
| [13] |
童俊. 山区铁路悬索桥隧道锚模型试验稳定性研究[D]. 成都: 西南交通大学, 2017. TONG Jun. Study on Stability of Tunnel Anchor Model Test for Mountain Railway Suspension Bridge[D]. Chengdu: Southwest Jiaotong University, 2017. |
| [14] |
王东英, 汤华, 尹小涛, 等. 基于简化力学模型的隧道锚极限承载力估值公式[J]. 岩土力学, 2020, 41(10): 3405-3414. WANG Dong-ying, TANG Hua, YIN Xiao-tao, et al. Estimation Method of Ultimate Bearing Capacity of Tunnel-type Anchorage Based on Simplified Mechanical Model[J]. Rock and Soil Mechanics, 2020, 41(10): 3405-3414. |
| [15] |
王中豪, 郭喜峰, 杨星宇. 基于人工智能算法的隧道锚承载能力评价[J]. 西南交通大学学报, 2021, 56(3): 534-540. WANG Zhong-hao, GUO Xi-feng, YANG Xing-yu. Bearing Capacity Evaluation of Tunnel-type Anchorage Based on Artificial Intelligent Algorithm[J]. Journal of Southwest Jiaotong University, 2021, 56(3): 534-540. |
| [16] |
朱建民, 殷开成, 龚维明, 等. 中美欧自平衡静载试验标准若干问题探讨[J]. 岩土力学, 2020, 41(10): 3491-3499. ZHU Jian-min, YIN Kai-cheng, GONG Wei-ming, et al. Discussion about Several Issues of Bi-directional Load Testing in Chinese, American and European Standards[J]. Rock and Soil Mechanics, 2020, 41(10): 3491-3499. |
| [17] |
JTG/T D65-05-2015, 公路悬索桥设计规范[S]. JTG/T D65-05-2015, Specifications for Design of Highway Suspension Bridge[S]. |
| [18] |
DBJ 52/T 079-2016, 贵州省基桩承载力自平衡检测技术规程[S]. DBJ 52/T 079-2016, Technical Specification for Self-balance of Bearing Capacity Testing of Foundation Piles[S]. |
 2021, Vol. 38
2021, Vol. 38
