扩展功能
文章信息
- 陈双庆, 王树英, 吕文舒, 陈超云
- CHEN Shuang-qing, WANG Shu-ying, Lü Wen-shu, CHEN Chao-yun
- 无背索斜塔斜拉桥的模态分析及1:1内共振研究
- Modal Analysis and 1: 1 Internal Resonance Study on Inclined Pylon Cable-stayed Bridge without Backstay
- 公路交通科技, 2021, 38(8): 75-82, 100
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(8): 75-82, 100
- 10.3969/j.issn.1002-0268.2021.08.011
-
文章历史
- 收稿日期: 2020-09-21
2. 湖南文理学院, 湖南 常德 415000;
3. 中交水运规划设计院有限公司, 北京 100020;
4. 湖南省益阳公路桥梁建设有限责任公司, 湖南 益阳 413000
2. Hunan University of Arts and Science, Changde Hunan 415000, China;
3. CCCC Water Transportation Planning and Design Institute Co., Ltd., Beijing 100020, China;
4. Hunan Yiyang Highway and Bridge Construction Co., Ltd., Yiyang Hunan 413000, China
无背索斜塔斜拉桥造型奇特,吸引了众多学者对其研究和探索[1-2]。无背索斜塔斜拉桥不同于传统的直塔斜拉桥,由于取消了单侧拉索,其主要依靠主塔的倾斜来平衡主梁的恒载和活载,受力情况更为复杂,因此,无背索斜塔斜拉桥动力学特性的相关内容得到桥梁工程领域的关注[3]。
Starossek[4]在经典桥梁体系的基础上,提出了一种全新的斜拉桥体系概念,即采用倾斜塔来代替传统的垂直塔,通过讨论该体系的优缺点,指出该体系可以实现更大的跨度。彭旺虎等[5]总结国内外无背索斜塔斜拉桥,论述了塔梁平衡关系,推导得到了塔的合理倾角,为该类斜塔倾角的选取提供了理论依据。陈爱军等[6-7]比较了无背索斜拉桥与常规直塔斜拉桥力学的行为差异,从塔、梁和索的布置形式出发,分析了各种类型无背索斜塔斜拉桥的受力特性,并研究了斜塔柱的合理结构形式。刘永健等[8]针对无背索斜塔斜拉桥进行了静动力荷载试验,结合三维有限元模型的理论计算,从试验的角度研究了桥梁的静力和动力特性。蔡向阳等[9]基于无背索斜塔斜拉桥的受力特点,建立了用于评估竖弯刚度的双梁离散弹簧动力学模型,将普通钢索替换为CFRP索后,分析了斜拉索对整体竖弯刚度的影响。杨吉新等[10]以六安市寿春西路大桥为工程背景,通过有限元软件建立相应的有限元模型,模拟和计算了不同温度荷载下的截面应力情况,得出升温和降温作用下,桥塔将会产生较大的拉应力和较大的结构变形,对桥梁的安全产生不利影响。
从上述研究可以看出,目前对无背索斜塔斜拉桥的研究主要通过有限元模拟来实现。而斜拉索作为斜拉桥中重要的受力构件,对斜拉桥的动力学特性有着十分重要的影响,由于斜拉索具有阻尼低,重量轻的特点,容易在环境荷载(例如风雨荷载和车辆荷载等)下产生大幅振动[11-13],从而影响斜拉桥的动力学性能。因此,在建立有限元模型时,采用何种方法来模拟斜拉索是正确把握无背索斜塔斜拉桥动力学特性的关键。目前,建立斜拉桥的二维平面有限元模型主要有两种方法:第1种方法是斜拉索采用杆单元,但只将斜拉索划分为一段,即用一个杆单元模拟斜拉索[14-15]; 第2种方法是斜拉索采用杆单元并将斜拉索划分为多段,即将斜拉索离散为多个杆单元[14-15]。基于以上两种模型,苏潇阳等[16]对传统斜拉桥的力学性能进行了研究。而对于无背索斜塔斜拉桥,相关研究却未见到。
本研究以某无背索斜塔斜拉桥为工程背景,研究无背索斜塔斜拉桥频率、振型等模态特性,揭示了全局模态与局部模态,局部模态与局部模态之间的1∶1内共振关系。
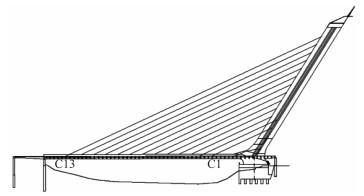
1 工程概况某斜拉桥位于长沙市,采用竖琴式无背索斜塔斜拉桥[9]。主梁采用钢-混凝土组合梁,挑梁间距为4~5 m,桥面宽33.2 m,主塔倾角为58°,主跨206 m,主塔桥面以上高度138 m。全桥共13对拉索,塔上索距为9.312 m,梁上索距12 m,横桥向两排,间距为6 m[9, 11],斜拉桥的立面示意图如图 1所示, 为表示方便,将斜拉索从里到外依次标记为C1, C2, …, C13,斜拉索索力如表 1所示。
|
| 图 1 某无背索斜塔斜拉桥立面图 Fig. 1 Elevation of an inclined pylon cable-stayed bridge without backstay |
| |
| 索号 | 索力/kN | 索号 | 索力/kN | |
| C1 | 6 620 | C8 | 4 777 | |
| C2 | 6 390 | C9 | 4 844 | |
| C3 | 6 255 | C10 | 4 892 | |
| C4 | 4 672 | C11 | 4 881 | |
| C5 | 4 688 | C12 | 4 927 | |
| C6 | 4 721 | C13 | 4 200 | |
| C7 | 4 736 |
2 模态分析
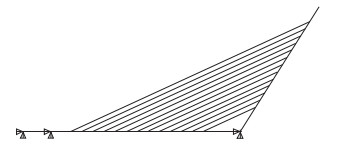
为了探究无背索斜塔斜拉桥的模态,利用有限元软件ANSYS建立相应的二维有限元模型,如图 2所示。采用两种不同的模型对斜拉索进行模拟,即OECS(one-element cable system,简称OECS)模型和MECS(multi-element cable system,简称MECS)模型,以探讨不同斜拉索模拟方法对无背索斜塔斜拉桥模态的影响。需要说明的是,建模时将塔的上端视为自由,塔的下端和主梁的两端视为固支,采用Earnst等效弹性模量考虑斜拉索的垂度影响。
|
| 图 2 无背索斜塔斜拉桥有限元模型 Fig. 2 Finite element model of inclined pylon cable-stayed bridge without backstay |
| |
2.1 OECS有限元模型
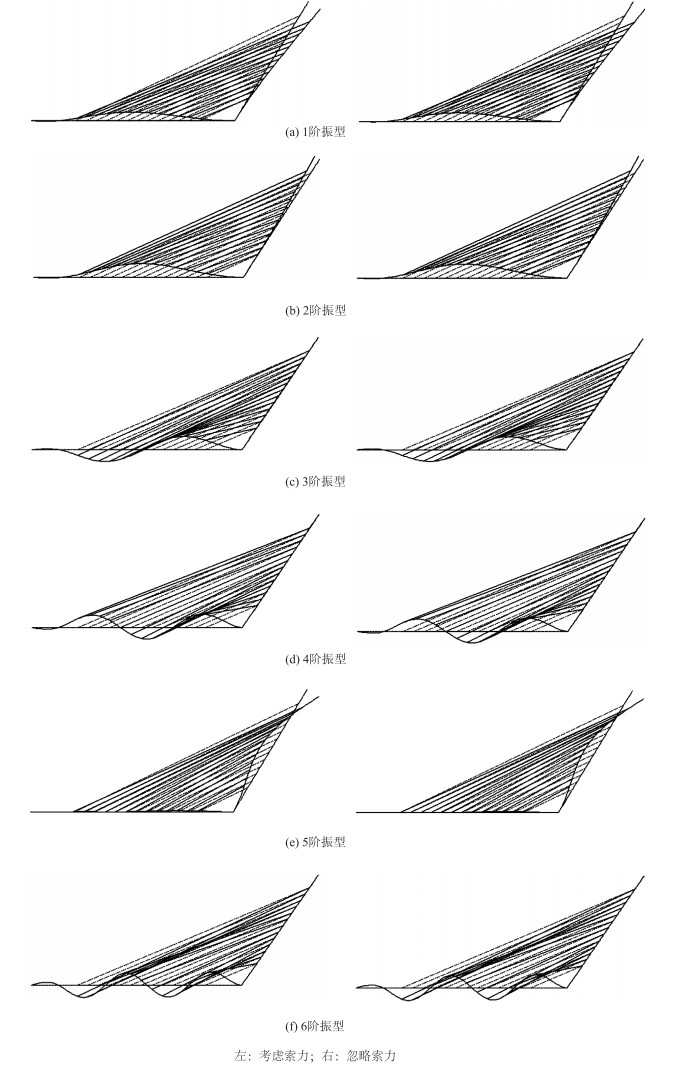
采用LINK10单元模拟斜拉索并划分为一段,主梁和主塔采用BEAM44模拟,总划分单元数为303,总划分节点数为291。表 2和图 3给出了是否考虑索力时,采用OECS有限元模型计算得到的斜拉桥前6阶频率和振型。观察图 3可以得出,振型均以梁和塔的振动为主,索的振动主要由主梁拖动所造成,这种振型一般被称作全局模态。表 2和图 3的结果表明,索力对全局频率和振型的影响很小,这是因为在OECS模型中,斜拉索被划分为一个单元,不会产生弯曲,OECS模型不能模拟出索的振动,此时斜拉索仅对主梁起到弹性支承的作用,因此,索力对全局频率和振型影响较小,这与文献[11, 18-19]得到的结果相同。斜拉桥作为一种柔性结构,刚度不足是其主要问题,所以通常需要在概念设计阶段对斜拉桥的竖弯刚度进行评估,而此种建模方法可以有效地识别出所需要的全局模态,节约了时间成本,因此在计算斜拉桥的模态时,如果只需要全局模态,可以采用此种方法建模,避免了筛选全局模态的麻烦。另外,表 2中列出了文献[17]计算的频率,可以看出其与本研究得到的频率十分接近,说明本研究结果的可靠度较高。
|
| 图 3 OECS模型斜拉桥前6阶振型 Fig. 3 First 6 orders mode shapes of cable-stayed bridge obtained by OECS model |
| |
| 横态序号 | 频率/Hz | 振型特征 | 文献[17]计算的频率/Hz | |
| 考虑索力 | 不考虑索力 | |||
| 1 | 0.369 6 | 0.369 2 | 梁1阶竖弯+塔侧弯 | 0.406 5 |
| 2 | 0.620 4 | 0.619 7 | 梁1阶竖弯+塔侧弯 | 0.629 7 |
| 3 | 1.042 9 | 1.042 4 | 梁2阶竖弯 | 1.067 3 |
| 4 | 1.819 6 | 1.819 2 | 梁3阶竖弯 | — |
| 5 | 2.175 2 | 2.175 9 | 塔2阶侧弯 | — |
| 6 | 2.919 2 | 2.919 0 | 梁4阶竖弯 | — |
2.2 MECS有限元模型
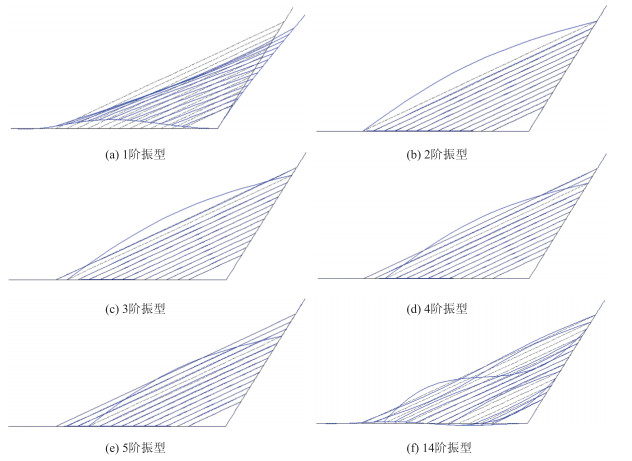
采用LINK10单元模拟斜拉索并将每根斜拉索划分为100段,总划分单元数为1 590,总划分节点数为1 578。表 3和图 4给出了采用MECS有限元模型计算得到的无背索斜塔斜拉桥前10阶频率和部分振型。对比表 2和表 3可以看出,第1阶频率几乎相同,这是因为第1阶模态是以主梁和主塔振动为主的全局模态,这说明采用MECS模型对全局模态的频率影响不大。对比图 4和图 3可以看到,由于将斜拉索划分为多段,使得MECS模型能够模拟斜拉索的振动,因此,图 4中存在斜拉索单独振动的振型(例如第2~5阶振型),这种振型称为局部模态,由于斜拉索是一种柔性结构,所以局部模态的频率较小,一般出现在低阶。除了全局模态和局部模态,还有第3种模态,如图 4中的第14阶振型所示,此时,梁、塔和索都发生了振动,这种模态称为混合模态,这是模态相互耦合的结果。仔细观察第14阶振型还可以看出,梁的振动形式与图 3中的第3阶振型相同,索的振动形式以C11的2阶振型为主,而根据表 2,第3阶频率为1.042 9 Hz,与C11的2阶频率(1.054 18 Hz,见表 4)很接近,这说明图 3中的第3阶模态与C11的2阶模态之间发生了1∶1内共振,此时将会发生模态间的能量传递并可能造成索的大幅振动。
|
| 图 4 MECS模型斜拉桥振型 Fig. 4 Mode shapes of cable-stayed bridge obtained by MECS model |
| |
| 模态序号 | 频率/Hz | 振型特征 |
| 1 | 0.372 44 | 梁1阶竖弯+塔侧弯 |
| 2 | 0.484 29 | C13索1阶面内 |
| 3 | 0.489 70 | C12索1阶面内 |
| 4 | 0.523 09 | C11索1阶面内 |
| 5 | 0.564 36 | C10索1阶面内 |
| 6 | 0.604 07 | C9索1阶面内 |
| 7 | 0.629 61 | C9索1阶面内+C8索1阶面内 |
| 8 | 0.672 36 | C8索1阶面内 |
| 9 | 0.737 89 | C7索1阶面内 |
| 10 | 0.822 95 | C6索1阶面内 |
| 振型 | 有限单元法/Hz | 张紧弦理论/Hz | 误差/% |
| C13 1阶 | 0.484 288 | 0.490 66 | 1.30 |
| C12 1阶 | 0.489 703 | 0.496 54 | 1.38 |
| C11 1阶 | 0.523 088 | 0.531 05 | 1.50 |
| C10 1阶 | 0.564 361 | 0.574 46 | 1.76 |
| C9 1阶 | 0.604 071 | 0.621 71 | 2.84 |
| C13 2阶 | 0.968 55 | 0.981 33 | 1.30 |
| C12 2阶 | 0.979 442 | 0.993 07 | 1.37 |
| C11 2阶 | 1.054 18 | 1.062 10 | 0.75 |
| C10 2阶 | 1.136 01 | 1.148 93 | 1.12 |
| C9 2阶 | 1.228 38 | 1.243 42 | 1.21 |
为了验证本研究模型的正确性,将局部模态频率与张紧弦理论算出的频率进行对比。根据张紧弦理论,张紧索的频率为:
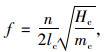
|
(1) |
式中,f为频率,n=1, 2, 3, …, lc为拉索长度;Hc为索力;mc为线密度。
基于上述理论,可以计算出斜拉索的自振频率并与本研究算出的频率进行对比,如表 4所示。从表中可以看出,本研究模型算出的局部模态频率与采用张紧弦理论算出的频率之间吻合非常好,说明本研究有限元模型可靠。
3 1∶1内共振分析 3.1 基本理论由于斜拉桥是一种高次超静定结构,对其整体进行非线性求解非常困难,所以一般只研究其中的基本构件,例如索梁模型。基于该模型,简要介绍采用多尺度法进行斜拉桥非线性内共振求解的基本理论。梁和索的运动方程可以写为[20]:
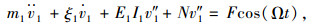
|
(2) |
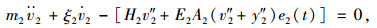
|
(3) |
式中,m,v,ξ,E和I分别为单位长度质量、横向位移、阻尼系数、弹性模量和惯性矩,下标‘1’和‘2’分别为梁和索;N和H2分别为梁和索的初始轴力;F和Ω分别为外激励的振幅和频率;A2为索的截面积;e2(t)为平均动应变,其表达式为:
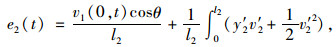
|
(4) |
式中,θ为索与梁的夹角; l2为拉索长度; y2为索的初始构型。
为探究更一般的规律,引入以下无量纲变量:
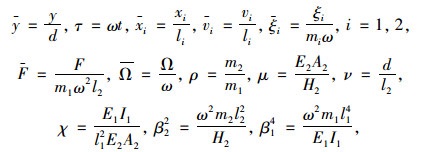
|
(5) |
式中,d为索的垂度;ω为面内自振频率。为便于书写,省略变量上方的横线,则式(2)和(3)可以另写为:
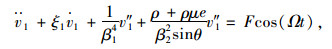
|
(6) |
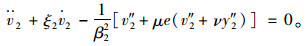
|
(7) |
根据文献[20],v1(x, t)和v2(x, t)可以写为:
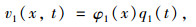
|
(8) |
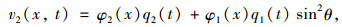
|
(9) |
式(8)~(9)中,φ1(x)和φ2(x)分别为梁和索的振型函数;q1(t)和q2(t)为梁和索广义坐标。
将式(8)和(9)代入式(6)和(7)并进行伽辽金积分,可以得到如下所示的常微分方程
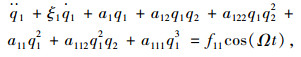
|
(10) |
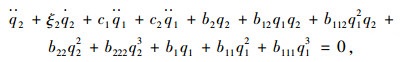
|
(11) |
式中,常系数可通过伽辽金离散后得到。
根据多尺度法,引入簿记参数ε和一个新的时间变量Ti-1=εi-1t。同时,将q1与q2一致展开为:
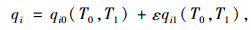
|
(12) |
式中,i=1, 2。
将式(12)代入式(10)和(11),并令ε的同次幂等于0:
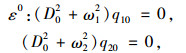
|
(13) |
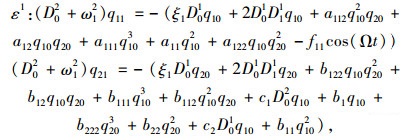
|
(14) |
式中,Dnm=∂m/∂Tn(m=1, n=0, 1)。
式(13)的解为:
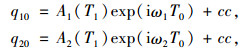
|
(15) |
式中cc为前面所有项的共轭。
将式(15)代入式(14),根据所考察的内共振关系,找到对应的久期项并令久期项为0。为方便求解,将A1与A2写为极坐标形式,即
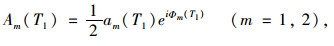
|
(16) |
式中,am(T1)和Φm(T1)可通过可解性条件求得。将式(16)代入久期项,最终可以求得系统稳态解。
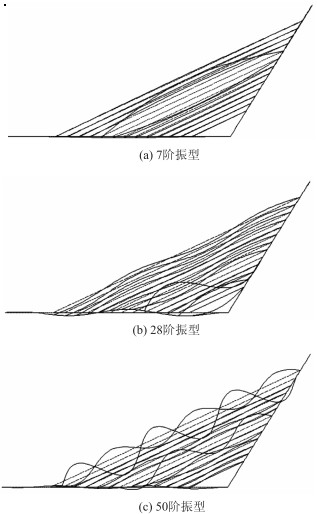
3.2 有限元分析基于以上理论可以定量对内共振进行分析,而采用有限元法可以定性对无背索斜塔斜拉桥中存在的各种内共振关系进行把握,由于MECS模型更能全面地揭示出斜拉桥的全部模态,所以本节的分析都是基于MECS模型。由表 3可知,无背索斜塔斜拉桥的频率非常密集,而且斜拉索的数量众多,不可避免地会导致某阶局部模态频率与全局模态频率之间呈现倍比关系,从而引发各种形式的内共振。图 5(a)为2阶全局模态与C9的1阶模态之间的1∶1内共振,由于1阶模态在各阶模态中占有重要的地位,所以与索1阶模态间的内共振一直是斜拉桥非线性动力学的研究问题之一。由表 2可以知道,2阶全局模态的频率为0.620 4 Hz,注意到C9的1阶模态频率为0.604 071 Hz(见表 4),两者十分接近,从而导致了1∶1内共振,由于C8的1阶频率与C9相近,导致图 5(a)中也激起了C8的1阶模态。
|
| 图 5 全局模态与局部模态间的内共振 Fig. 5 Internal resonances between global and local modes |
| |
除了上述所说的全局模态与索的1阶模态之间的内共振,还存在全局模态与索的高阶模态之间的内共振。图 5(b)给出了无背索斜塔斜拉桥第28阶振型,其频率为1.829 31 Hz。从图中可以看到,梁的振动形式与图 3中的第4阶振型类似,索的振动则以C5的2阶振型为主,同时还伴有其余斜拉索的高阶振型振动。根据表 2,第4阶全局模态的频率为1.819 6 Hz,而C5的2阶频率为1.861 29 Hz,两者很接近,这说明此时4阶全局模态和C5的2阶模态之间发生了1∶1内共振,一旦梁的4阶模态被激起,主梁就会在索端给斜拉索施加一个参数激励,从而激起C5的2阶模态。由于索的数量多,频率比较密集,短索的低阶频率可能与长索的高阶频率相近,从而也会激起长索的高阶模态,图 5(c)进一步验证了这种现象。图 5(c)为第6阶全局模态与局部模态间的1∶1内共振,从图中可以明显看到短索的低阶模态和长索的高阶模态同时被激起,此时索与梁之间不仅会发生能量传递,短索与长索之间也会通过梁发生能量间的传递,使得无背索斜塔斜拉桥的非线性行为变得更加复杂。
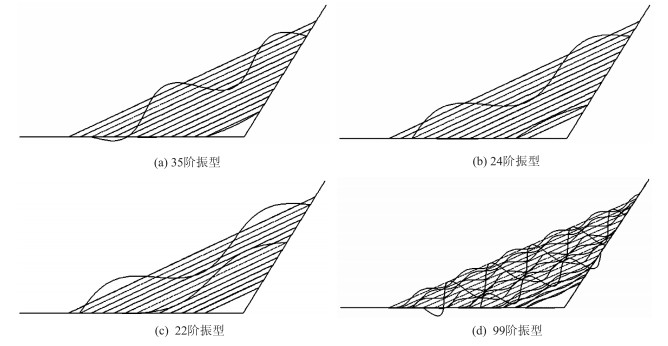
除了全局模态与局部模态间的内共振,索与索之间,即局部模态和局部模态之间也存在复杂的内共振关系。由于短索的自振频率比同阶的长索的自振频率大,因此,很容易出现短索的低阶模态与长索的高阶模态之间的1∶1内共振。图 6(a)中,C1的1阶模态和C11的4阶模态同时被激起,由于C1的1阶模态频率为2.083 85 Hz,C11的4阶模态频率为2.120 60 Hz,两者十分接近,所以此时发生了1∶1内共振。同样,图 6(b)给出了C2的1阶模态与C11的3阶模态之间的1∶1内共振,这样的内共振模式还有很多,在特定的条件下均有可能引起不同索之间的内共振。除此之外,索的高阶模态之间也存在1∶1内共振,例如图 6(c)所示的C7的2阶模态与C12的3阶模态。甚至出现更为复杂的内共振现象,从图 6(d)中可以看到多根索的高阶模态之间同时被激起了内共振,这在一定程度上解释了为什么实际工程中一根斜拉索的振动往往会导致其余多根索的大幅振动,此时容易导致斜拉索的疲劳和拉索保护层的破坏,降低斜拉索的使用寿命,甚至影响斜拉桥的行车安全,工程中应特别注意设计参数规避相应的共振区,以避免此类现象的发生。
|
| 图 6 局部模态与局部模态间的内共振 Fig. 6 Internal resonances between local and local modes |
| |
4 结论
(1) OECS模型简单方便,但采用OECS模型只能计算出无背索斜塔斜拉桥的全局振型和频率,不能模拟斜拉索的振动,当只需要斜拉桥的全局模态时,可以采用此种建模方法,避免了筛选全局模态的麻烦,从而节约时间成本。
(2) MECS模型能够模拟斜拉索的振动,对全局振型、频率的计算结果影响不大,能准确有效地计算出无背索斜塔斜拉桥的全部平面内模态。MECS模型与OECS模型配合使用,可以快速确定全局模态与局部模态间的内共振关系。
(3) 在一定条件下,全局模态与索的低阶和高阶模态间会发生1∶1内共振,不同索的高阶模态以及高阶与低阶模态间也会发生1∶1内共振,由于无背索斜塔斜拉桥频率的密集性,甚至有可能激起多根索的振动,工程中应注意避免此现象的发生。
| [1] |
琚明杰, 刘世明, 刘永健. 索力随机误差对组合梁无背索斜拉桥受力影响[J]. 公路交通科技, 2016, 33(10): 60-66. JU Ming-jie, LIU Shi-ming, LIU Yong-jian. Influence of Random Deviation of Cable Tension Force on Stress State of Composite Girder Cable-stayed Bridge without Back-stay[J]. Journal of Highway and Transportation Research and Development, 2016, 33(10): 60-66. |
| [2] |
刘世明, 刘永健. 无背索曲塔曲梁斜拉桥参数敏感性分析[J]. 公路交通科技, 2014, 31(2): 54-68. LIU Shi-ming, LIU Yong-jian. Analysis of Parameter Sensitivity for Curved-pylon and Curved-girder Cable-stayed Bridge without Back-stay[J]. Journal of Highway and Transportation Research and Development, 2014, 31(2): 54-68. |
| [3] |
邓露, 王维. 公路桥梁动力冲击系数研究进展[J]. 动力学与控制学报, 2016, 14(4): 289-300. DENG Lu, WANG Wei. Research Progress on Dynamic Impact Factors of Highway Bridges[J]. Journal of Dynamics and Control, 2016, 14(4): 289-300. |
| [4] |
STAROSSEK U. Cable-stayed Bridge Concept for Longer Spans[J]. Journal of Bridge Engineering, 1996, 1(3): 99-103. |
| [5] |
彭旺虎, 邵旭东, 李立峰, 等. 无背索斜拉桥的概念、设计与施工[J]. 土木工程学报, 2007, 40(5): 26-33. PENG Wang-hu, SHAO Xu-dong, LI Li-feng, et al. The Concept, Design, and Construction of Cable-stayed Bridges without Backstays[J]. China Civil Engineering Journal, 2007, 40(5): 26-33. |
| [6] |
陈爱军, 邵旭东. 无背索竖琴式斜拉桥合理结构体系分析[J]. 中外公路, 2009, 29(4): 89-95. CHEN Ai-jun, SHAO Xu-dong. Reasonable Structural System Analysis of Harp-type Cable-stayed Bridges without Backstay[J]. Journal of China and Foreign Highway, 2009, 29(4): 89-95. |
| [7] |
陈爱军, 邵旭东. 无背索竖琴式斜拉桥混凝土斜塔柱合理结构型式分析[J]. 公路工程, 2007, 32(4): 130-135. CHEN Ai-jun, SHAO Xu-dong. Analysis on the Reasonable Structure of Inclined Concrete Pylon of Harp-shaped Cable-stayed Bridge with No Backstays[J]. Highway Engineering, 2007, 32(4): 130-135. |
| [8] |
刘永健, 杨健, 梁鹏, 等. 无背索斜塔斜拉桥荷载试验[J]. 长安大学学报: 自然科学版, 2009, 29(5): 59-63. LIU Yong-jian, YANG Jian, LIANG Peng, et al. Field Load Testing of Inclined Tower Cable-stayed Bridge without Back-stays[J]. Journal of Chang'an University: Natural Science Edition, 2009, 29(5): 59-63. |
| [9] |
蔡向阳, 苏潇阳, 康厚军, 等. 无背索斜拉桥竖弯刚度评估模型与方法研究[J]. 振动与冲击, 2018, 37(19): 104-111. CAI Xiang-yang, SU Xiao-yang, KANG Hou-jun, et al. Evaluation Model and Method for Vertical Bending Stiffness of a Cable-stayed Bridge without Backstays[J]. Journal of Vibration and Shock, 2018, 37(19): 104-111. |
| [10] |
杨吉新, 杨蒋鹤立, 周兴宇, 等. 双斜塔无背索斜拉桥拉索温度效应分析[J]. 武汉理工大学学报: 交通科学与工程版, 2018, 42(6): 911-914. YANG Ji-xin, YANG JIANG He-li, ZHOU Xing-yu, et al. Analysis of Cable Temperature Effect of Double Inclined Tower Cable-stayed Bridge Without Back Cable[J]. Journal of Wuhan University of Technology: Transportation Science and Engineering Edition, 2018, 42(6): 911-914. |
| [11] |
GATTULLI V, MORANDINI M, PAOLONE A. A Parametric Analytical Model for Non-linear Dynamics in Cable-stayed Beam[J]. Earthquake Engineering & Structural Dynamics, 2010, 31(6): 1281-1300. |
| [12] |
GATTULLI V, LEPIDI M. Localization and Veering in the Dynamics of Cable-stayed Bridges[J]. Computers & Structures, 2007, 85(21): 1661-1678. |
| [13] |
赵跃宇, 王连华, 陈得良, 等. 斜拉索面内振动和面外摆振的耦合分析[J]. 土木工程学报, 2003, 36(4): 65-69. ZHAO Yue-yu, WANG Lian-hua, CHEN De-liang, et al. Coupled Analysis of Out-of-plane Oscillation and In-plane Vibration for Stay Cable[J]. China Civil Engineering Journal, 2003, 36(4): 65-69. |
| [14] |
ABDEL-GHAFFAR A M, KHALIFA M A. Importance of Cable Vibration in Dynamics of Cable-stayed Bridges[J]. Journal of Engineering Mechanics, 1991, 117(11): 2571-2589. |
| [15] |
CAETANO E, CUNHA A, TAYLOR C A, et al. Investigation of Dynamic Cable-deck Interaction in a Physical Model of a Cable-stayed Bridge. Part II: Seismic Response[J].Earthquake Engineering & Structural Dynamics, 2000, 29(4): 499-521. |
| [16] |
苏潇阳, 康厚军, 丛云跃, 等. 不同斜拉索模型对多塔斜拉桥力学性能的影响[J]. 公路工程, 2017, 42(2): 42-46. SU Xiao-yang, KANG Hou-jun, CONG Yun-yue, et al. Influence of Different Cable Models on Mechanical Performance of Multi-tower Cable-stayed Bridge[J]. Highway Engineering, 2017, 42(2): 42-46. |
| [17] |
陈爱军. 大跨无背索竖琴式斜拉桥合理结构型式研究[D]. 长沙: 湖南大学, 2005. CHEN Ai-jun. Research on Reasonable Structure of Long-span Harp-shaped Cable-stayed Bridge without Backsaty[D]. Changsha: Hunan University, 2005. |
| [18] |
SU X Y, KANG H J, GUO T D, et al. Dynamic Analysis of the In-plane Free Vibration of a Multi-cable-stayed Beam with Transfer Matrix Method[J]. Archive of Applied Mechanics, 2019, 89: 2431-2448. |
| [19] |
彭雪林. 基于健康监测的大跨度斜拉桥基准有限元模型[D]. 福州: 福州大学, 2003. PENG Xue-lin. Baseline Finite Element Model of Large Span Cable-stayed Bridges for Health Monitoring[D]. Fuzhou: Fuzhou University, 2003. |
| [20] |
WEI M H, XIAO Y Q, LIU H T, et al. Nonlinear Responses of a Cable-beam Coupled System under Parametric and External Excitations[J]. Archive of Applied Mechanics, 2014, 84: 173-185. |
 2021, Vol. 38
2021, Vol. 38
