扩展功能
文章信息
- 鲁志强, 陈贺, 张永华, 郑福坤, 乔文号
- LU Zhi-qiang, CHEN He, ZHANG Yong-hua, ZHENG Fu-kun, QIAO Wen-hao
- 基于数值仿真的重力式锚碇承载机制研究
- Study on Load-bearing Mechanism of Gravity Anchorage Based on Numerical Simulation
- 公路交通科技, 2021, 38(8): 67-74
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(8): 67-74
- 10.3969/j.issn.1002-0268.2021.08.010
-
文章历史
- 收稿日期: 2020-04-15
2. 云南交投公路建设第三工程有限公司, 云南 昆明 650041;
3. 中国科学院武汉岩土力学研究所 岩土力学与工程国家重点试验室, 湖北 武汉 430071;
4. 中国科学院大学, 北京 100000
2. YCIC Highway Construction Third Engineering Co., Ltd., Kunming Yunnan 650041, China;
3. State Key Laboratory of Geomechanics and Geotechnical Engineering, Institute of Rock and Soil Mechanics of CAS, Wuhan Hubei 430071, China;
4. University of Chinese Academy of Sciences, Beijing 100000, China
悬索桥因其跨越能力强、受力性能好和景观效果好等优点[1-5],常作为千米级大跨度桥梁的推荐方案。重力式锚碇依靠自身承载,对周围环境的依赖性低,适应范围较广,适用于平地和山区,既能应用于岩性较好的场区,也适用于软弱岩层[6-7],作为悬索桥主缆锚固的主要结构型式被广泛应用于实际工程。重力式锚碇依靠自身巨大的重力抵抗主缆垂直方向的拉力,水平力则依靠重力锚底面同地基的摩阻力来抵抗,在保证悬索桥安全运营方面发挥重要作用。因此,对悬索桥重力式锚碇承载机制研究就显得尤为必要。
重力式锚碇的承载属于结构和地基相互作用问题,影响其承载性能的因素主要包括:锚碇结构形式、锚碇位置以及工程区域地基的地质特征和力学特性[8-12]。目前对重力式锚碇承载机制研究主要通过以下3种手段:(1)模型试验:重力式锚碇模型试验能够针对特定的锚碇结构形式、地层条件进行研究,能够完整地揭示重力式锚碇承载过程中的变形破坏规律。李永盛[13]开展了江阴长江大桥北锚碇1∶100的室内模型试验,根据观测结果分析了锚碇结构的变形机制和岩土体的受力破坏模式。李家平[14]根据相似理论对宁波庆丰悬索桥重力式锚碇开展了室内相似模型试验,试验表明:在锚索力作用下,锚碇不仅向前水平位移,而且产生前端下沉、后端隆起的刚性转动。(2)理论分析:重力式锚碇理论研究多基于简化力学模型或是借鉴地基基础的研究经验。尹小涛[15]依托普立特大桥宣威岸重力式锚碇,提出了一种基于简化力学模型的重力式锚碇安全评价方法,评价了宣威岸重力式锚碇抗倾覆、抗滑移、基底应力和变形等多方面的安全性。朱栓来[16]分析了传统的抗滑稳定系数法及分项系数法的现实及客观性,提出了锚碇设计采用分项系数法的合理性及必要性。(3) 数值模拟:数值仿真不仅可以针对特定的工程锚碇模型进行锚碇-地基联合承载特性分析,还可以分析不同结构类型的锚碇,对于研究重力式锚碇的承载机制十分重要。尹小涛[17]基于普宣高速宣威岸重力式锚碇,采用FLAC3D有限元软件,利用数值仿真分析了重力式锚碇和地基的力学机制和破坏模式。林荣安[18]针对武汉阳逻长江大桥南锚碇进行有限元仿真,计算分析了锚碇的基底应力、抗滑稳定性、抗倾覆稳定性、沉降及变位,计算结果均满足规范要求。
基于上述认识,本研究依托于普立特大桥宣威岸重力锚工程,采用FLAC3D软件建立宣威岸重力锚数值模型,分析锚碇的受力和承载机制,为重力式锚碇的优化设计和安全监测提供指导。
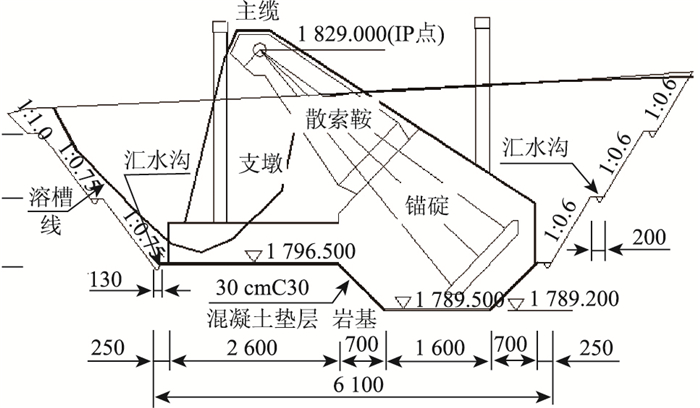
1 背景介绍 1.1 工程概况普立特大桥为云南省普宣高速控制性工程,全长为1 040 m,横跨宝山镇和普立镇两个乡镇,主桥桥型为单跨双塔悬索桥方案,矢跨比为1/10,主缆横向布置2根,主缆横桥向中心间距26 m。宣威岸重力锚工程主要由支墩、锚块、散索鞍、主缆等部分组成,具体见图 1。锚碇四周地层从下至上依次是中风化白云质灰岩、中厚层夹薄层白云质灰岩、第四系残坡积覆盖层,支墩基底溶蚀沟槽发育。
|
| 图 1 重力式锚碇设计方案(单位: cm) Fig. 1 Design scheme of gravity anchorage(unit: cm) |
| |
1.2 数值仿真模型
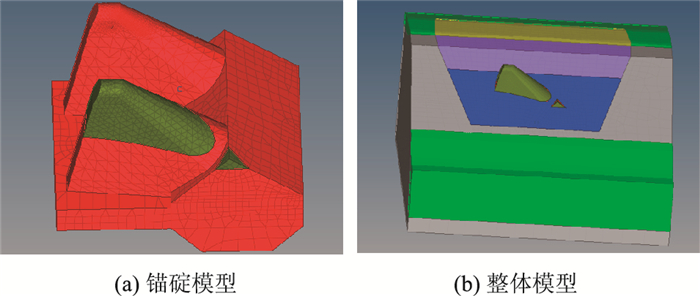
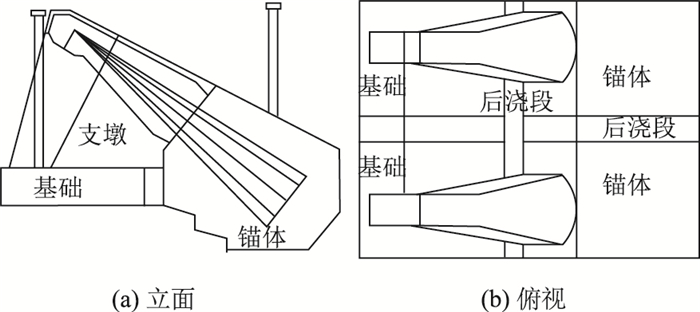
通过FLAC3D软件建立宣威重力锚工程三维数值模型见图 2,重力锚模型长61 m,宽度56 m,高22 m,锚碇几何尺寸见图 3。为研究重力式锚碇的承载机制设计平底锚碇和齿坎锚碇两种类型,每种锚碇考虑回填和不回填两种工况。
|
| 图 2 重力式锚碇数值模型 Fig. 2 Numerical model of gravity anchorage |
| |
|
| 图 3 重力式锚碇几何尺寸 Fig. 3 Geometric dimensions of gravity anchorage |
| |
整个模型由四面体单元、六面体单元和五面体单元组合剖分网格,共划分215 440个单元,2 125个节点。模型底面边界采用固定约束,侧边为法向约束,表观自由。锚碇选用弹性本构,岩土体采用弹塑性本构,选用考虑拉破坏的摩尔-库伦模型。不同地层岩体及材料的物理力学参数建议值由设计和勘察提供,具体计算参数见表 1。
| 岩体名称 | 天然重度/(kN·m-3) | 内摩擦角/(°) | 黏聚力/MPa | 弹性模量/GPa | 泊松比 | 抗拉强度/MPa | |
| 覆盖层 | 18.9 | 27.0 | 0.035 | 0.038 | 0.35 | 0.0 | |
| 灰岩溶蚀带 | 强风化 | 26.0 | 35.0 | 0.75 | 3.0 | 0.24 | 0.4 |
| 中风化 | 26.5 | 40.0 | 0.85 | 8.0 | 0.22 | 0.7 | |
| 微风化 | 27.5 | 45.0 | 1.05 | 10.0 | 0.20 | 1.5 | |
| 锚体 | 25.0 | 35.0 | 1.50 | 30.0 | 0.20 | 1.1 | |
| 锚-岩界面 | 25.0 | 34.3 | 0.71 | 7.89 | 0.23 | 0.6 | |
| 回填土 | 19.5 | 32.0 | 0.020 | 0.030 | 0.35 | 0.0 | |
2 重力式锚碇承载机制分析 2.1 应力演化机制研究
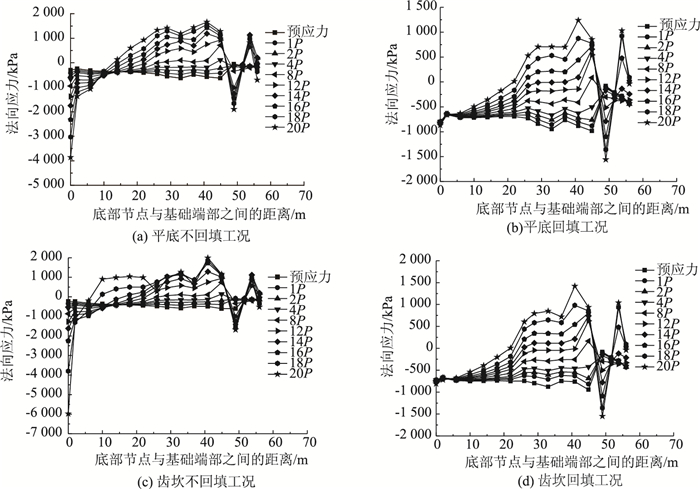
结构基底拉应力作为重力式锚碇安全性评价的一个重要指标,对于结构安全起着至关重要的作用,为了更直观对比不同工况下锚碇应力的变化,现将超载作用下不同加载阶段的基底轴线应力响应数据整理成图 4和图 5。
|
| 图 4 不同工况法向应力随荷载变化曲线 Fig. 4 Curves of normal stress vs. load under different working conditions |
| |
|
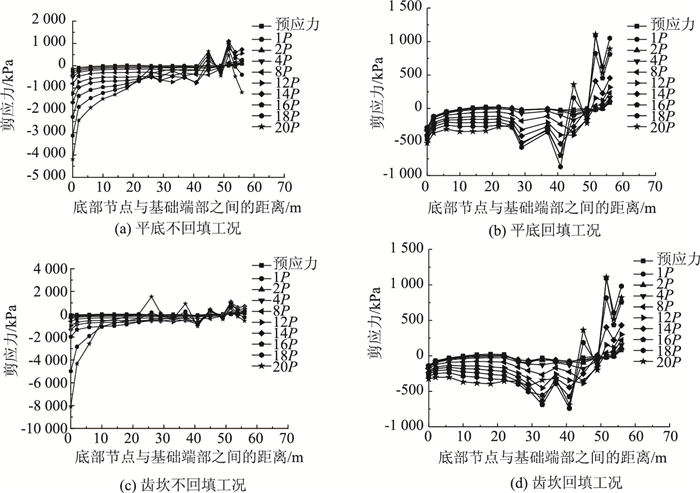
| 图 5 不同工况剪应力随荷载变化曲线 Fig. 5 Curves of shear stress vs. load under different working conditions |
| |
通过位移随荷载变化曲线图中曲线簇的疏密程度可以判断出不同工况下重力式锚碇的极限承载力见表 2,其中P代表设计缆力,P为95 824 kN。
| 工况 | 极限承载力 |
| 平底不回填工况 | 8 P |
| 平底回填工况 | 12 P |
| 齿坎不回填工况 | 12 P |
| 齿坎回填工况 | 16 P |
| 注:P为设计荷载。 | |
平底不回填工况基底最大应力为1 900 kPa,平底回填工况基底最大应力为1 560 kPa,齿坎不回填工况基底最大应力为1 990 kPa,齿坎回填工况基底最大应力为1 420 kPa,因此回填可以有效抑制基底应力的增长,齿坎也可以在一定程度降低基底应力的发展。
综上,齿坎的存在能够改善锚碇的受力状态,显著提高锚碇的承载能力,回填不仅可以提高锚碇的承载性能还可以有效抑制锚碇应力的发展。
2.2 变形演化机制研究为对比不同工况下锚碇位移的变化,现将超载作用下不同加载阶段的基底轴线位移响应数据整理成图 6和图 7。
|
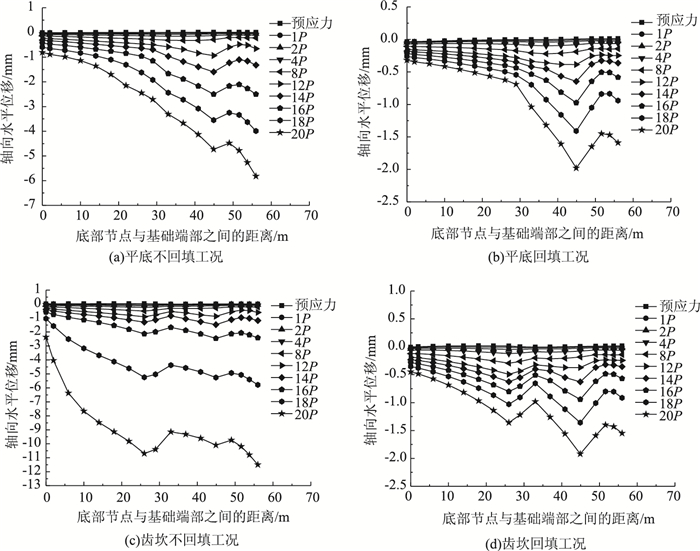
| 图 6 水平位移随荷载变化曲线 Fig. 6 Curves of horizontal displacement vs. load |
| |
|
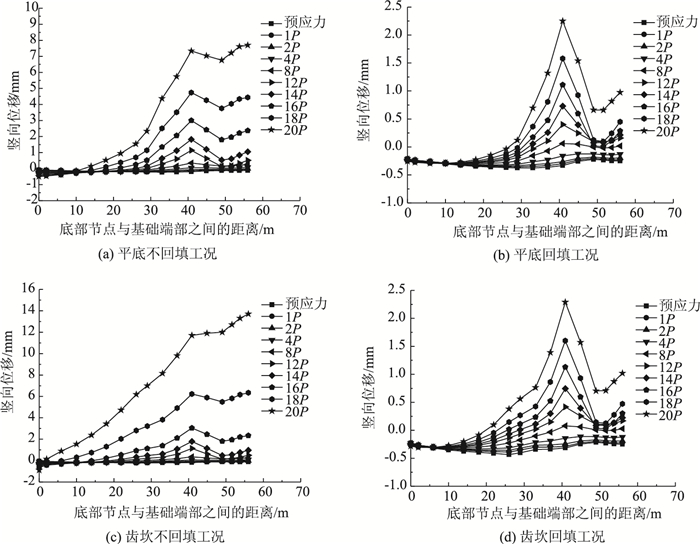
| 图 7 竖向位移随荷载变化曲线 Fig. 7 Curves of Vertical displacement vs. load |
| |
通过位移随荷载变化曲线图中曲线簇的疏密程度可以判断出不同工况下重力式锚碇的极限承载力见表 3。位移曲线所得结论同应力荷载曲线所得遥相呼应。
| 工况 | 极限承载力 |
| 平底不回填工况 | 8 P |
| 平底回填工况 | 12 P |
| 齿坎不回填工况 | 12 P |
| 齿坎回填工况 | 16 P |
从图 6、图 7可以看出回填不仅能够显著提高锚碇的承载性能,还能够有效控制锚碇位移的发展,最多可以减小10倍左右。齿坎不回填工况锚碇的水平位移为11.5 mm、竖向位移超过14 mm,进行回填处理后锚碇的水平位移仅为1.5 mm、竖向位移小于2 mm。
综上所述,回填不仅可以提高锚碇的承载性能,还可以有效抑制锚碇位移的发展。
2.3 渐进破坏特征研究为分析工程荷载作用下平底不回填工况重力式锚碇的渐进破坏特征,现将不同工程荷载下锚碇的纵剖面塑性区云图整理如图 8所示。
|
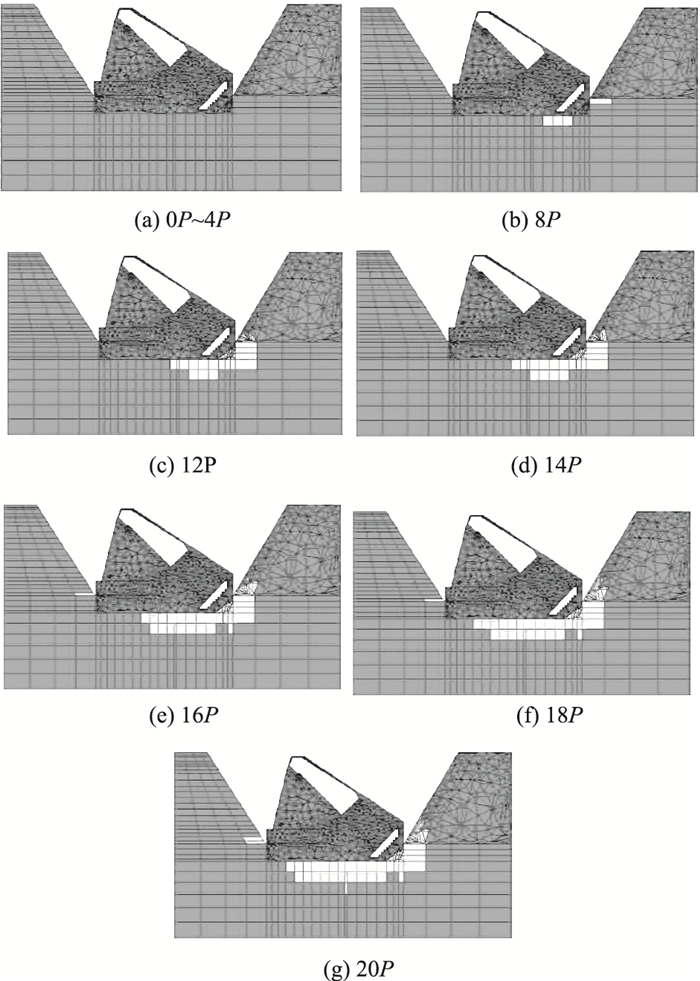
| 图 8 平底不回填工况塑性区云图 Fig. 8 Nephograms of plastic area of flat bottom without backfilling |
| |
由图 8可知,当主缆拉力达到8P时,锚碇基底开始出现塑性区;12P时锚碇基底拉应力塑性区进一步发展,基底局部剪切破坏;14P时锚碇基底开始出现拉应力塑性区,且基底基本贯通;16P时基底塑性区完全贯通,拉应力区明显;18P~20P时进入完全破坏状态。塑性区的发展进一步证明了平底不回填工况的极限承载力约为8P,这同前述章节应力和位移随荷载变化曲线确定的极限承载力相呼应。
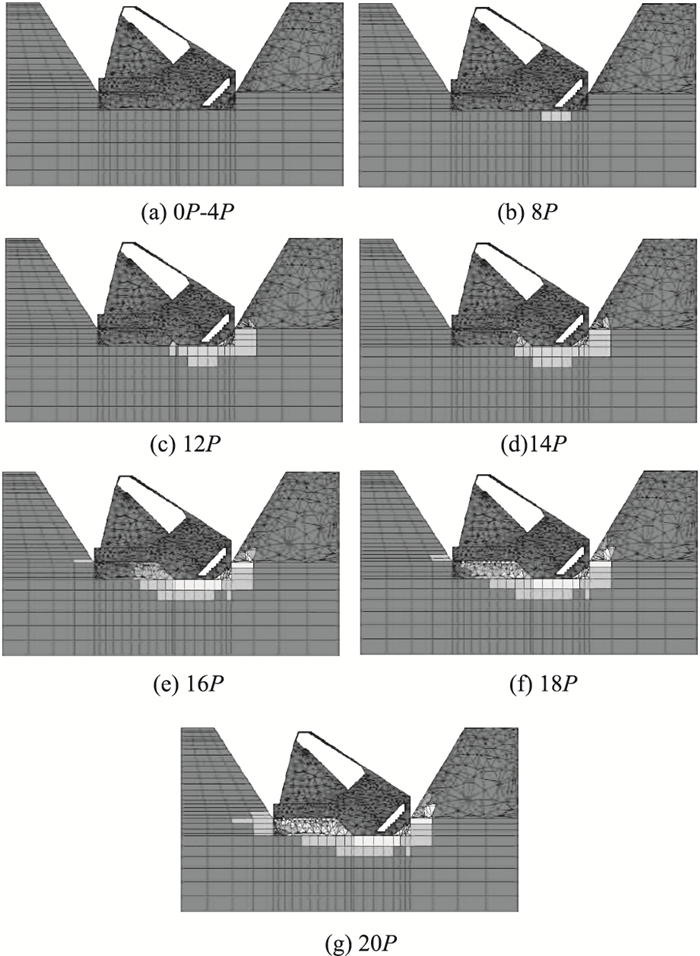
为分析工程荷载作用下齿坎不回填工况重力式锚碇的渐进破坏特征,现将不同工程荷载下锚碇的纵剖面塑性区云图整理如图 9所示。
|
| 图 9 齿坎不回填工况塑性区云图 Fig. 9 Nephograms of plastic area of ridges without backfilling |
| |
由图 9可知, 主缆拉力达到8P时,锚碇基底开始出现塑性区。12P时锚碇基底基本贯通;14P时锚碇齿坎部斜面接触面也开始出现塑性,且基本贯通;荷载增加至16P时齿坎局部剪切破坏;18P~20P时齿坎基本贯通剪切破坏。这说明考虑基底的摩擦效应齿坎不回填工况的极限承载力约为8P,若考虑到齿坎的夹持效应则锚碇在16P之前都是安全的。
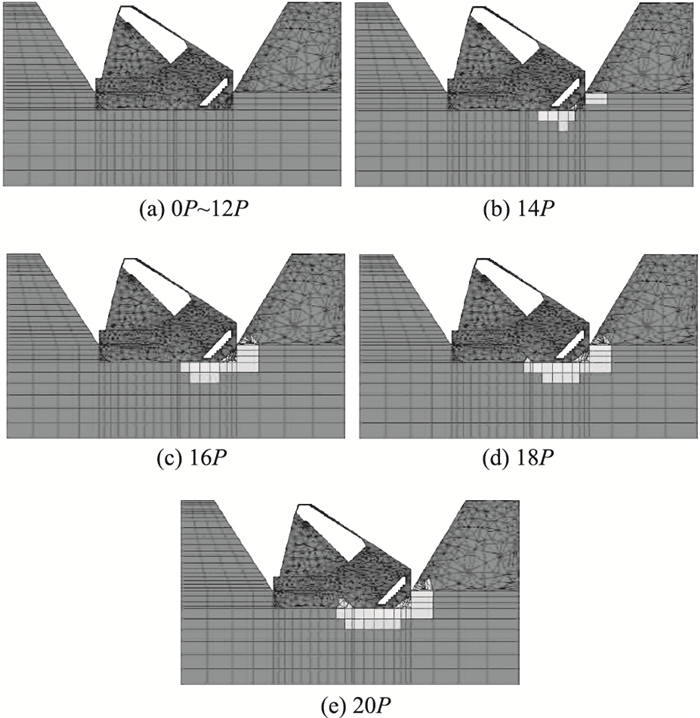
为分析工程荷载作用下齿坎回填工况重力式锚碇的渐进破坏特征,现将不同工程荷载下锚碇的纵剖面塑性区云图整理如图 10所示。
|
| 图 10 齿坎回填工况塑性区云图 Fig. 10 Nephograms of plastic area of ridges with backfilling |
| |
由图 10可知,当主缆拉力小于12P时锚碇基底尚未出现塑性区;当荷载增加到14P时锚碇底部开始出现塑性区;随着荷载继续增加到16P时锚碇底部塑性区进一步发展且基底完全贯通;当主缆拉力为18P时齿坎部位开始出现塑性区;20P后塑性区进一步发展,齿坎部位塑性区基本贯通,齿坎剪切破坏。因此齿坎回填工况的极限承载力可达16P~18P。
对比回填工况和不回填工况可知:回填能够较大幅度提高锚碇的承载能力,以齿坎锚碇为例,不回填工况8P时开始出现塑性区,而回填工况14P才开始出现塑性区,不回填工况极限承载力约为12P,进行回填处理后锚碇极限承载力提升至16P~18P。
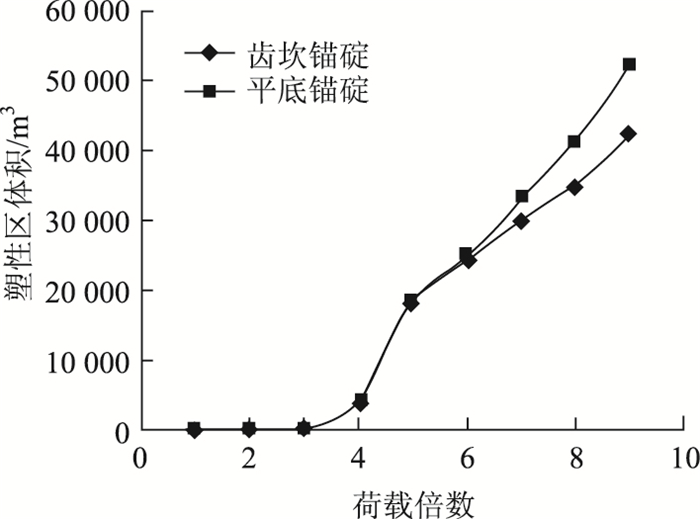
为了对比是否存在齿坎对于锚碇系统破坏的影响,两种工况塑性区体积变化曲线见图 11。
|
| 图 11 不同工况塑性区体积曲线 Fig. 11 Volume curves of plastic zone under different working conditions |
| |
从图 11可以看出当主缆拉力在0P~4P之间时平底锚碇和齿坎锚碇基本未产生塑性区,此时外荷载小于锚碇基底的摩擦力;当主缆拉力介于4P~12P之间时平底锚碇塑性区体积略大于齿坎锚碇,这是由于平底锚碇极限承载力低,因此较早出现塑性区,塑性区发展也稍快;当主缆拉力大于12P后齿坎锚碇塑性区逐渐大于平底锚碇并且差距随荷载增加而增大,这是由于平底锚碇进入塑性屈服阶段,塑性区增长较慢,而齿坎锚碇此时开始调动齿坎接触面处岩体联合承载,齿坎接触斜面开始进入塑性阶段。
塑性区图也说明了齿坎锚碇不仅仅依靠摩擦效应承载(主要是初期),齿坎夹持岩体的承载能力在大荷载作用下居主导作用。
3 结论(1) 通过塑性区扩展、基底应力变化、变形特性分析等确定不同工况的极限承载力。平底不回填工况的极限承载力约为8P,平底回填工况约为12P,齿坎不回填工况约为12P,齿坎回填工况约为16P。
(2) 齿坎的存在能够改善锚碇的受力状态,显著提高锚碇的承载能力。回填不仅可以提高锚碇的承载性能,还可以有效抑制锚碇位移的发展。重力式锚碇通过齿坎和回填土的约束作用能够充分调动基础和四周岩土体联合承载,使其安全性能大大提高。
(3) 平底锚碇主要依靠基底摩擦承载,塑性区仅在锚碇底部发展,最终的破坏模式表现为滑移失稳;齿坎锚碇在荷载初期也是依靠摩擦承载,随着荷载的增加齿坎调动围岩联合承载的效应逐渐发挥,塑性区的变化规律也表现为荷载初期塑性区在锚碇底部发展,大荷载作用下锚碇齿坎处岩体则开始逐渐进入塑性,最终的破坏模式为齿坎处岩体的剪切破坏和锚碇的倾覆破坏。
本研究通过数值仿真模拟计算了有无齿坎和是否回填对于锚碇承载性能、基底应力变化以及位移发展的影响,分析了重力式锚碇的齿坎和回填覆土对于锚碇承载性能的影响,有助于清晰重力式锚碇承载机制,并且为类似工程重力式锚碇优化设计提供思路。
| [1] |
周孟波. 悬索桥手册[M]. 北京: 人民交通出版社, 2003: 105-219. ZHOU Meng-bo. Manual of Suspension Bridges[M]. Beijing: China Communications Press, 2003: 105-219. |
| [2] |
雷俊卿. 悬索桥设计[M]. 北京: 人民交通出版社, 2002. LEI Jun-qing. Design of Suspension Bridge[M]. Beijing: China Communications Press, 2002. |
| [3] |
严国敏. 现代悬索桥[M]. 北京: 人民交通出版社, 2002. YAN Guo-min. Modern Suspension Bridge[M]. Beijing: China Communications Press, 2002. |
| [4] |
翟晓亮, 朱青, 钱程, 等. 山区峡谷大跨度钢桁梁悬索桥抗风性能研究[J]. 公路交通科技, 2020, 37(11): 56-62. ZHAI Xiao-liang, ZHU Qing, QIAN Cheng, et al. Study on Wind-resistance Performance of Steel Truss Girder Suspension Bridges in Mountainous Canyon[J]. Journal of Highway and Transportation Research and Development, 2020, 37(11): 56-62. |
| [5] |
沈锐利, 王文弟, 王路, 等. 基于可靠度理论的悬索桥预应力锚固系统时变计算方法研究[J]. 公路交通科技, 2019, 36(9): 57-64. SHEN Rui-li, WANG Wen-di, WANG Lu, et al. Study on Time-variant Calculation Method of Prestressed Anchor System of Suspension Bridge Based on Reliability Theory[J]. Journal of Highway and Transportation Research and Development, 2019, 36(9): 57-64. |
| [6] |
钱冬生, 陈仁福. 大跨度悬索桥的设计与施工[M]. 成都: 西南交通大学出版社, 1999. QIAN Dong-sheng, CHEN Ren-fu. Design and Construction of Long-span Suspension Bridge[M]. Chengdu: Southwest Jiaotong University Press, 1999. |
| [7] |
张杰, 钱冬生. 大跨悬索桥塔和锚碇的合理设计[J]. 桥梁建设, 2000(4): 20-22. ZHANG Jie, QIAN Dong-sheng. Rational Design of Long Span Suspension Bridge Towers and Anchorages[J]. Bridge Construction, 2000(4): 20-22. |
| [8] |
JTG/T D65-05-2015, 公路悬索桥设计规范[S]. JTG/T D65-05-2015, Specifications for Design of Highway Suspension Bridge[M]. |
| [9] |
JTG 3363-2019, 公路桥涵地基与基础设计规范[S]. JTG 3363-2019, Specifications for Design of Foundation of Highway Bridges and Culverts[S]. |
| [10] |
范菊. 悬索桥锚旋系统及接触摩擦问题的研究[D]. 大连: 大连理工大学, 2012. FAN Ju. Study of Suspension Bridge Anchorage System and Contact Friction[D]. Dalian: Dalian University of Technology, 2012. |
| [11] |
赵启林, 陈斌, 卓家寿. 悬索桥锚碇及地基基础中的力学问题研究动态[J]. 水利水电科技进展, 2001, 21(1): 22-26. ZHAO Qi-lin, CHEN Bin, ZHUO Jia-shou. Developments in Mechanical Analysis of Suspension Bridges' Anchorage and Foundation[J]. Advances in Science and Technology of Water Resources, 2001, 21(1): 22-26. |
| [12] |
吉林, 眭峰, 王保田. 润扬大桥锚碇基岩摩阻力试验研究[J]. 岩石力学与工程学报, 2004, 23(2): 256-260. JI Lin, SUI Feng, WANG Bao-tian. Testing Study on Base Resistance of the Anchors at Runyang Yangtze Bridge[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(2): 256-260. |
| [13] |
李永盛. 江阴长江公路大桥北锚碇模型试验研究[J]. 同济大学学报: 自然科学版, 1995, 20(2): 134-140. LI Yong-sheng. Experimental Study on the North Anchorage of the Jiangyin Yangtze Bridge[J]. Journal of Tongji University: Natural Science Edition, 1995, 20(2): 134-140. |
| [14] |
李家平, 李永盛, 王如路. 悬索桥重力式锚碇结构变位规律研究[J]. 岩土力学, 2007, 28(1): 145-150. LI Jia-ping, LI Yong-sheng, WANG Ru-lu. Research on Displacement of Anchorage of Suspension Bridge[J]. Rock and Soil Mechanics, 2007, 28(1): 145-150. |
| [15] |
尹小涛, 严飞, 周磊, 等. 重力式锚碇水平极限承载力估值公式探讨[J]. 铁道工程学报, 2017, 34(1): 41-46. YIN Xiao-tao, YAN Fei, ZHOU Lei, et al. Exploration on the Horizontal Limit Bearing Capacity Formula of Gravity Anchorage[J]. Journal of Railway Engineering Society, 2017, 34(1): 41-46. |
| [16] |
朱栓来. 悬索桥锚碇设计采用分项系数法的建议[J]. 西南公路, 2011(4): 19-21. ZHU Shuan-lai. Suggestion of Using Partial Coefficient Method for Anchorage Design of Suspension Bridge[J]. Southwest Highway, 2011(4): 19-21. |
| [17] |
尹小涛, 严飞, 周磊, 等. 悬索桥重力式锚碇结构-地基联合承载机制[J]. 交通运输工程学报, 2017, 17(2): 1-11. YIN Xiao-tao, YAN Fei, ZHOU Lei, et al. Joint Bearing Mechanism of Structure and Foundation for Gravity Anchor Block of Suspension Bridge[J]. Journal of Traffic and Transportation Engineering, 2017, 17(2): 1-11. |
| [18] |
林荣安. 悬索桥重力式锚碇系统受力分析及其优化[D]. 西安: 长安大学, 2008. LIN Rong-an. Stress Analysis and Optimization of Gravity Anchorage System of Suspension Bridge[D]. Xi'an: Chang'an University, 2008. |
 2021, Vol. 38
2021, Vol. 38
