扩展功能
文章信息
- 王天鹏, 张建仁, 王磊, 马亚飞
- WANG Tian-peng, ZHANG Jian-ren, WANG Lei, MA Ya-fei
- 模糊失效准则下桥梁拉索锈蚀时变可靠性分析
- Analysis on Time-varying Reliability of Corroded Bridge Cables Based on Fuzzy Failure Criterion
- 公路交通科技, 2021, 38(8): 59-66
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(8): 59-66
- 10.3969/j.issn.1002-0268.2021.08.009
-
文章历史
- 收稿日期: 2020-09-09
2. 中南林业科技大学 土木工程学院, 湖南 长沙 410004
2. School of Civil Engineering, Central South University of Forestry and Technology, Changsha Hunan 410004, China
桥梁的拉索直接承受主梁的恒载及活载,对外界侵害比较敏感。国内外近年来有多座桥梁的缆索因耐久性不足而更换,经济损失巨大,甚至由于拉索断裂而发生安全事故[1]。为了保证桥梁安全,对锈蚀严重的拉索必须进行更换,保守的更换措施固然可以保证拉索服役期的安全,但频繁更换拉索,不仅成本巨大,还会造成不良的社会影响。
国内外学者对拉索服役期的可靠性评估进行了一系列研究。Betti[2]基于悬索桥缆索锈蚀状况的调查结果,通过试验分析了不同负载和环境条件下高强钢丝的腐蚀过程,指出钢丝的严重脆化不是单纯由吸氢引起的(氢脆),由腐蚀引起的钢丝表面的不均匀性才是主因。采用钢丝锈蚀程度分级的概念对拉索进行可靠性评估,由于方法直观被国内外学者所大量采用[3-4],但存在同等级的钢丝强度变异系数较大的问题。Zhu[5]考虑Daniel效应和断丝概率提出了基于斜拉索运营期安全系数的可靠度评估模型。兰成明[6]根据锈蚀钢丝强度的概率分布采用统计强度理论建立了平行钢丝索承载能力评定方法。Hou[7]根据索力和车辆荷载的监测结果对斜拉索进行了可靠性分析,但上述研究均对拉索的锈蚀演化考虑不足,本质上仍是静态模型。Faber[8]提出基于拉索腐蚀、疲劳损伤超声检测数据的强度概率修正方法并建立了可靠度评估框架,Elachachi[9]从丝、股、索等多个尺度建立缆索强度模型,提出了多尺度时变可靠度评估方法,马小利[10]在二者研究的基础上,发展深化了钢丝锈蚀时变概率模型,提出概率分枝约界方法解决了计算中的关键问题。E.Karanci[11]进行了不同腐蚀环境下钢丝的腐蚀速率试验,结合世界各国碳钢腐蚀速率的试验数据,建立了带有径向基核函数的支持向量回归模型预测钢丝腐蚀速率,根据监测数据给出了缆索剩余强度的估算方法。刘沐宇[12]分析了钢丝之间微动疲劳导致的磨损,为钢绞线拉索的可靠性分析提供了有益的参考。
上述研究成果为桥梁拉索的时变可靠性分析奠定了基础,但在既有的研究中都采用了清晰的失效准则,即拉索由可靠状态到失效状态是突变的。在实际工程中,拉索由可靠状态到失效状态往往是渐变的,之间存在一个过渡的模糊区域。采用清晰的失效准则可能会导致评估结果出现偏差,比如过早的更换拉索而造成经济浪费。本文在已有研究成果的基础上,提出模糊失效准则下桥梁拉索的锈蚀时变可靠度计算模型,以期将拉索服役期间的可靠性评估建立在更科学的基础上,从而为桥梁缆索的耐久性分析和更换策略提供参考。
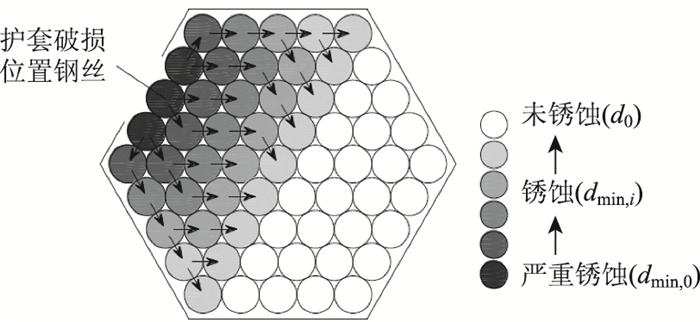
1 拉索截面的锈蚀演化模型根据国内外学者对桥梁缆索截面锈蚀分布的调查结果[4, 13],钢丝的锈蚀首先发生在缆索护套的破损处,此处表层钢丝锈蚀最为严重,进而由表及里,逐渐沿截面周向和径向扩展,如图 1所示。
|
| 图 1 拉索截面钢丝锈蚀扩展规律 Fig. 1 Corrosion propagation rule of steel wire in cable section |
| |
为准确描述拉索在截面上的锈蚀分布规律,徐俊[4]定义了钢丝锈蚀扩散比r,其表达式为:
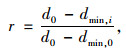
|
(1) |
式中,d0为钢丝的公称直径;dmin, 0为护套破损处表层钢丝的最小直径;dmin, i为距离表层钢丝第i层钢丝锈蚀后的最小直径。文献[4]分别拟合了拉索径向和周向钢丝锈扩散比r的均值和标准差:

|
(2) |
由拟合结果可知,拉索截面径向和周向钢丝锈蚀扩散比十分接近。为方便计算,假定径向和周向钢丝锈蚀扩散比相等,第i层钢丝的锈蚀扩散比ri服从正态分布,均值为0.856i,标准差为0.4。因此距离表层钢丝第i层钢丝锈蚀后的最小直径dmin, i的计算式为:
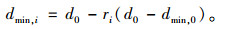
|
(3) |
设距离表层钢丝第i层钢丝的数量为ni,缆索共有j层钢丝,则锈蚀拉索的有效截面积为:
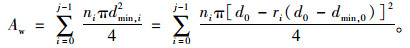
|
(4) |
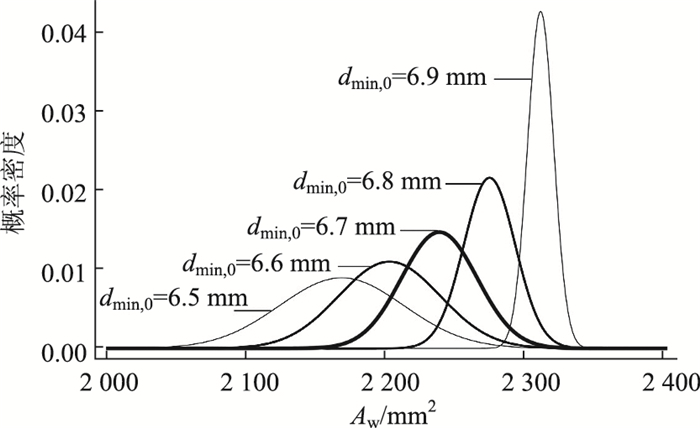
以图 1所示的拉索截面为例,设钢丝公称直径为7 mm,采用Monte Carlo方法对不同dmin, 0时锈蚀拉索的有效面积进行模拟,经过试算,模拟次数为5 000次时均值已经稳定。对模拟结果进行统计分析,不同dmin, 0条件下锈蚀拉索有效面积的概率分布均能通过99%的K-S正态分布检验。由图 2所示的模拟结果可知,随着锈蚀程度的增加,拉索有效面积均值明显减小,变异性增大,表明拉索的力学指标逐步劣化。
|
| 图 2 锈蚀拉索有效面积概率密度分布 Fig. 2 Probability density distribution of effective area of corroded cable |
| |
2 锈蚀拉索抗力退化模型
拉索抗力退化的随机过程记为R(t),一般可简化为:

|
(5) |
式中,g(t)为拉索抗力退化的随机过程,当不考虑维修加固时,是从1开始单调递减的函数;R0为拉索初始时刻的抗力,其计算式为:
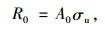
|
(6) |
式中,A0为拉索初始时刻的截面积;σu为考虑Daniel效应的钢索平均抗拉强度,其随着钢丝数量的增加而减小。已有的研究成果表明[8, 14],随着钢索平均强度的衰减,其强度变异系数迅速减小,对于中等数量钢丝的拉索可忽略其变异性,所以可认为σu是与钢丝数量有关的定值。采用多项式对文献[14]的数值仿真结果进行拟合,当钢丝抗拉强度标准值为1 670 MPa时,σu的计算式为:
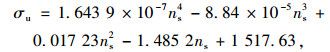
|
(7) |
式中ns为拉索所包含的钢丝数。
根据锈蚀拉索有效截面Aw的演化规律,由式(4)得到拉索抗力退化的随机过程为:
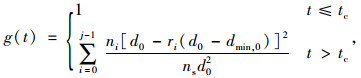
|
(8) |
式中tc为钢丝锈蚀的起始时刻,即护套出现破损的时刻。
护套破损处表层钢丝暴露于大气环境下,其锈蚀后的直径dmin, 0计算式为:
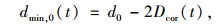
|
(9) |
式中Dcor(t)为t年后的累积腐蚀深度,遵循幂函数规律:
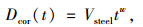
|
(10) |
式中,Vsteel为第1年的腐蚀速率;w为长期腐蚀指数,表征腐蚀的发展趋势,我国不同地区气候环境下碳钢的腐蚀速率参数如表 1所示[15]。
| 参数 | 武汉 | 青岛 | 江津 | 琼海 |
| 气候环境特征 | 一般城市 | 温带海洋 | 污染城市 | 湿热城市 |
| Vsteel/(mm·a-1) | 0.047 | 0.058 | 0.083 | 0.024 |
| w | 0.39 | 0.57 | 0.45 | 1.03 |
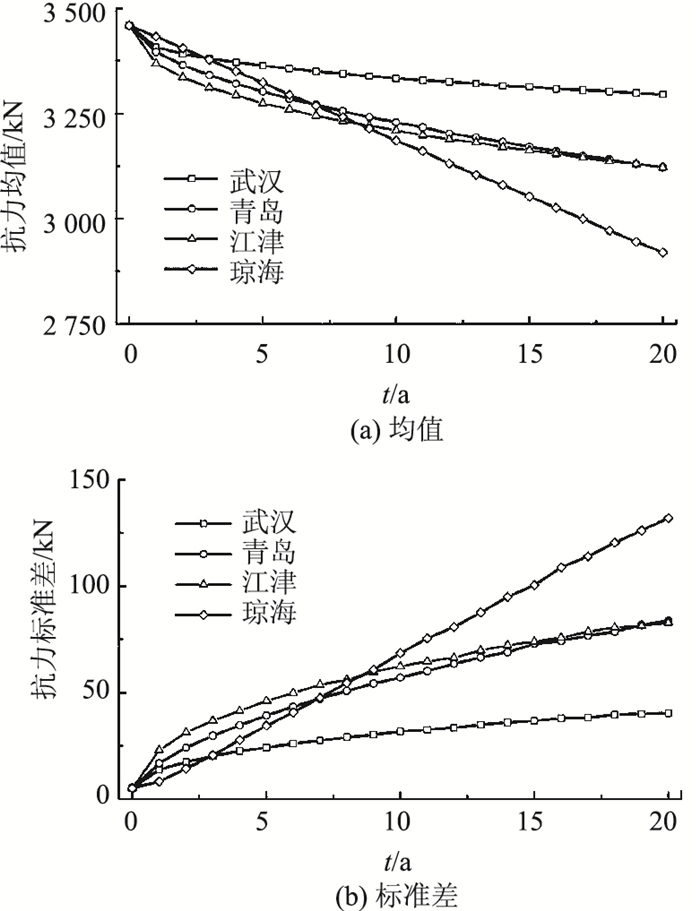
仍以图 1所示的PES7-61拉索截面为例,其中钢丝抗拉强度标准值为1 670 MPa,d0=7 mm,ns=61,设tc=0,采用Monte Carlo方法由式(5)~(10)计算不同地区拉索抗力均值、标准差随时间的变化曲线,如图 3所示。
|
| 图 3 拉索抗力退化曲线 Fig. 3 Cable resistance degradation curves |
| |
由图 3结果可知,拉索抗力的均值为时间的单调降函数,标准差为时间的单调增函数,抗力退化过程为非平稳随机过程。在腐蚀初期,Vsteel是抗力退化的主要因素,但从长远看,长期腐蚀指数w则影响更大。当w值小于1时,随着时间增加抗力退化速率有所减缓;当w值大于1时,抗力退化为加速过程。海洋性和工业性污染环境对拉索锈蚀初期抗力影响较大,湿热的气候环境则对拉索抗力退化的长期过程更为不利。
需要说明的是,钢丝的镀锌层起着屏蔽和阴极保护作用,理论上应具有较好的防腐效果,但由于锌层厚度的均匀性缺乏严格的控制和检验,制作过程中的磕碰、刮擦在所难免,且在服役阶段还存在钢丝间的磨损。另有研究表明[16]:随着钢丝张力的增加,其腐蚀速率也明显增大,原因之一就是随着钢丝应力的增加,镀锌层表面产生微裂纹并迅速扩展,使腐蚀介质更易进入。因此,镀锌层一般仅作为钢丝在拉索制作期间的防腐保障,而不作为使用阶段的防腐保障。所以本研究在拉索锈蚀模拟过程中未考虑钢丝镀锌层的影响。
3 锈蚀拉索时变可靠度计算 3.1 拉索模糊失效的隶属函数当现象或事件本身概念不清晰或没有明确的界限时,使得事件存在模糊性和不分明性,相应的事件称为模糊事件,相应的集合称为模糊集合。设x为论域U上的一个元素,
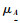

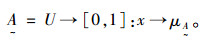
|
(11) |
该映射使任意一个x∈U对应一个确定的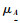

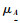
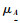
考虑拉索抗力退化和运营期间实际索力的安全系数为:
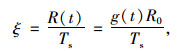
|
(12) |
式中,ξ为拉索运营期的安全系数;Ts为运营期间拉索的索力值。根据规范规定[17],运营状态斜拉索的安全系数应不小于2.5,即:
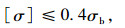
|
(13) |
式中,[σ]为斜拉索的容许应力;σb为钢丝的抗拉标准强度。根据美国后张法协会斜拉桥委员会对拉索服役状态的规定[18],对服役拉索的静力强度分级界限可选取拉索设计允许应力(0.4σb)、允许应力超荷1.25倍(0.5σb)、强度抗力系数点(0.65σb)3个特殊点的应力比值,具体强度状态指标和对应的处理方式如表 2所示。
| 评价等级 | 状态指标 | 处理方式 | 使用状态 | 对应安全系数 |
| Ⅰ级 | 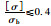 |
安全适用,不必采取措施 | 继续使用 | ξ≥2.5 |
| Ⅱ级 | 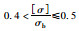 |
基本安全适用,可不必采取措施 | 改善使用 | 2.0≤ ξ<2.5 |
| Ⅲ级 | 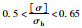 |
影响安全和正常使用,应采取措施 | 变更使用 | 1.54<ξ<2.0 |
| Ⅳ级 | 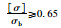 |
危及安全或不能正常使用,必须采取措施 | 停止使用 | ξ≤1.54 |
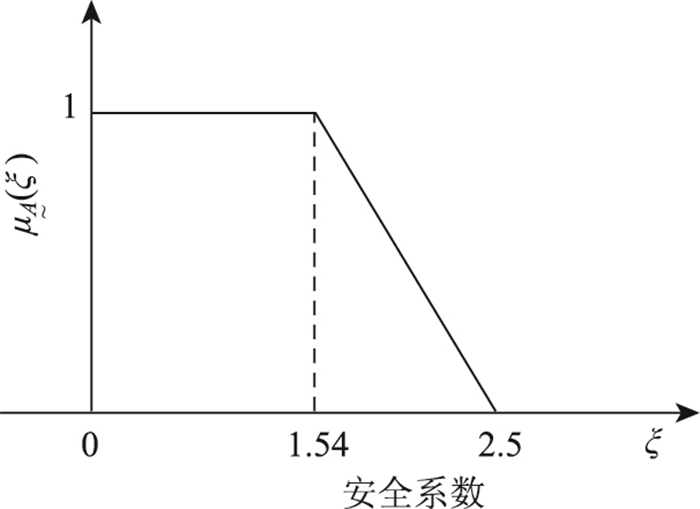
由表 2可知,当ξ≥2.5时拉索安全,当ξ≤1.54时拉索可认为拉索完全失效。而当1.54 < ξ < 2.5时,拉索的失效为一模糊随机事件。以ξ为失效判据,模糊失效的隶属函数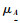
|
| 图 4 模糊失效的隶属函数 Fig. 4 Membership function of fuzzy failure |
| |
拉索模糊失效的隶属函数表达式为:
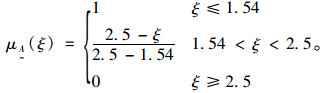
|
(14) |
设安全系数ξ的概率密度函数为f(ξ),则模糊失效准则下拉索的失效概率为[19]:
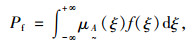
|
(15) |
式(15)是一个高维积分,计算十分复杂,因此引入新的随机变量X,其累积分布函数为FX(ξ)=1- 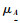
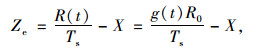
|
(16) |
式(16)只含有随机变量,可采用常规的概率可靠度求解方法进行计算,如JC法。对于本文还可采用Monte Carlo方法计算失效概率:
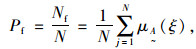
|
(17) |
式中N是模拟次数。通过试算可知,两种方法计算结果十分接近,只是当失效概率较低时,Monte Carlo方法的计算量较大。
上述是不变模糊可靠度的计算方法,考虑到拉索抗力和荷载效应的时变性,把服役期(0, T)内分割成m个较小时段Δti, i=1, 2, …, m,每个时段内结构抗力和可变荷载都是时不变的,都可以用随机变量表示。采用时不变可靠度计算方法可计算出每个时段内的失效概率Pf(Δt)和可靠度ψ(Δt),则在(0, T)时期内的失效概率为[20]:
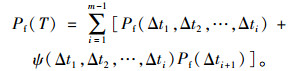
|
(18) |
于是(0, T)时期内的可靠指标为:
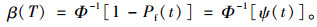
|
(19) |
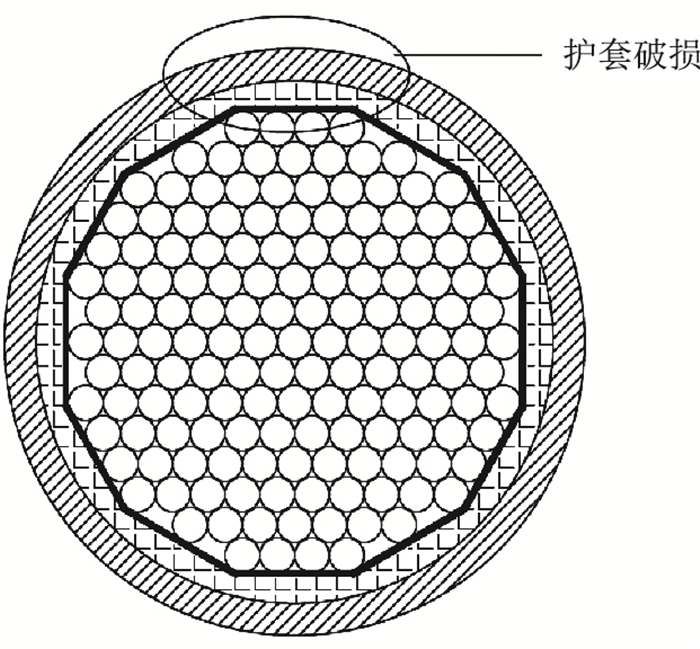
某斜拉桥B01号斜拉索规格为PES7-151,钢丝抗拉强度为1 670 MPa,运营10年后HDPE护套在图 5所示位置发生破损,引发局部钢丝锈蚀,即tc=10。1年内的索力监测结果显示,索力服从极值Ⅰ型分布,均值为3 059 kN,标准差为36.5 kN。考虑Daniel效应的拉索钢丝平均抗拉强度为1 467.33 MPa。大气腐蚀环境参数按表 1武汉地区取值,拉索设计基准期为20 a,以年为单位将拉索设计基准期分割为m=20个时段,计算服役期不同时段内拉索的时变可靠度。
|
| 图 5 PES7-151拉索截面图 Fig. 5 Pes7-151 cable section |
| |
计算拉索设计基准期内的时不变可靠指标以进行比较,其中拉索设计基准期T内的索力最大值概率分布函数为[21]:
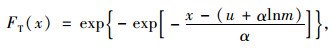
|
(20) |
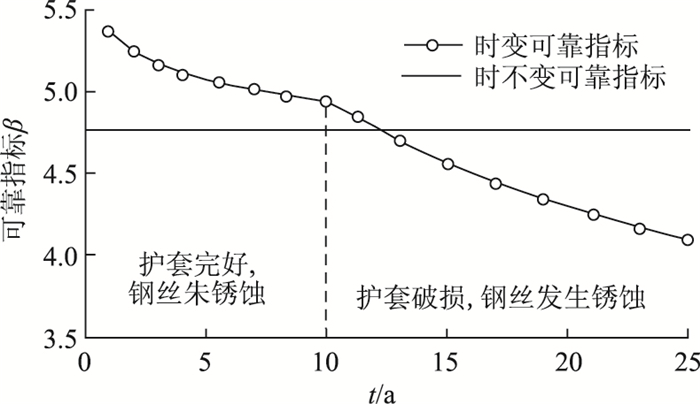
式中u, α为索力截口概率分布参数,本研究中为1年内索力最大值分布参数。利用Mathematica软件编制计算程序,拉索的时变可靠指标计算结果如图 6所示。
|
| 图 6 时变可靠指标与时不变可靠指标 Fig. 6 Time-varying reliability indicator and time-invarying reliability indicator |
| |
由图 6可知,拉索的时变可靠指标在服役期内分为两个时段:第1时段钢丝未锈蚀,拉索抗力未发生变化,可靠指标虽有下降但较为平缓;第2时段钢丝发生锈蚀,拉索抗力发生衰减,时变可靠指标明显下降,2年后已低于时不变可靠指标。
取不同的安全系数确定清晰失效准则下的功能函数为:
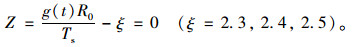
|
(21) |
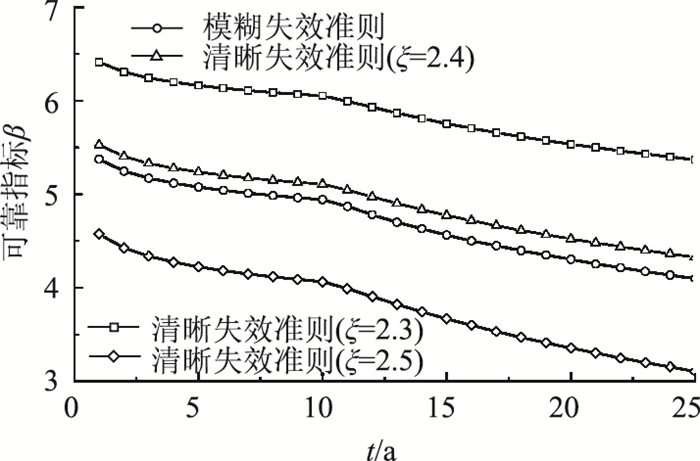
计算清晰失效准则下的时变可靠指标,与模糊失效准则的比较结果如图 7所示。
|
| 图 7 模糊失效准则与清晰失效准则下的时变可靠指标 Fig. 7 Time-varying reliability indicators based on fuzzy failure criterion and clear failure criterion |
| |
由图 7可见,由于清晰失效准则“非黑即白”的特性,取不同安全系数的时变可靠指标差别较大。取ξ=2.3时,显然高估了锈蚀拉索的安全性;取ξ=2.5则显得保守,过早地更换拉索有可能造成不必要的浪费。取ξ=2.4时虽然二者较为接近,但本研究方法考虑了拉索失效的模糊性,在无法确定构件清晰失效准则的情况下更为适用。
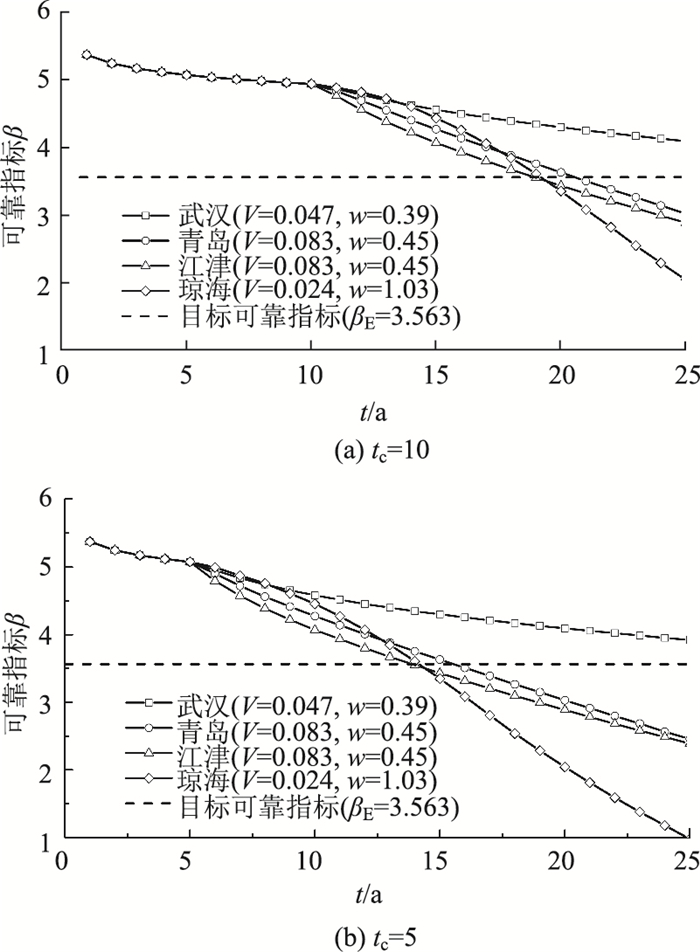
为比较不同气候环境条件下拉索时变可靠性的变化规律,并分析在钢丝锈蚀发生后拉索的服役寿命,取文献[22]给出的我国已建公路桥梁承载能力评估目标可靠指标的建议值βE=3.563,即认为β(T)<βE时拉索失效。分别以不同的钢丝锈蚀起始时刻和腐蚀速率参数进行计算,结果如图 8所示。
|
| 图 8 不同地区拉索的时变可靠指标 Fig. 8 Time-varying reliability indicators of cables in different areas |
| |
由图 8可知,在护套发生局部破损后,不同地区拉索可靠指标的变化规律遵循钢丝锈蚀程度的变化规律。在一般城市环境下,由于腐蚀速率随时间增加有所减缓,所以在拉索设计基准期内(20 a),时变可靠指标仍大于目标可靠指标。但对于其他腐蚀环境更为恶劣的地区,钢丝发生锈蚀后拉索的服役寿命仅为8~10 a,当tc < 10时,拉索寿命将小于设计基准期。本研究仅考虑护套局部破损,若出现环向开裂,周边钢丝同时发生腐蚀,则拉索抗力退化更为迅速。根据我国桥梁换索状况的调查结果[1],采用热挤PE护套的拉吊索在不到20 a就进行更换的桥梁,主要集中在广西、四川、福建、广东等腐蚀环境较为恶劣的地区,并都伴随着护套的损伤,可见推迟钢丝锈蚀的初始时间是保证拉索服役寿命的关键。
5 结论针对桥梁拉索耐久性问题日益突出的现状,本文对服役拉索的时变可靠性问题进行了探索性研究,得出如下结论:
(1) 根据钢丝的腐蚀速率和拉索截面的锈蚀扩展规律,以服役期拉索的安全系数为失效判据,提出了模糊失效准则下桥梁拉索锈蚀时变可靠度分析模型。该模型能够反映拉索在不同腐蚀环境、不同服役时间内可靠性的变化规律。由于考虑了拉索可靠状态到失效状态的渐变性,模糊失效准则下时变可靠指标的渐变规律更好,与工程实际更为相符,一定程度上避免了清晰失效准则下安全系数选取不当可能造成的决策失误。
(2) 算例分析表明,锈蚀拉索的时变可靠指标具有明显的时段区分,当拉索防护失效后,可变可靠指标进入第2时段,即随着钢丝锈蚀程度的变化产生不同程度的下降。在腐蚀环境较为恶劣的地区,护套发生局部破损后拉索的服役寿命仅为8~10 a,若护套寿命小于10 a,拉索寿命将不满足20 a的使用年限。由于钢丝锈蚀的不可逆性,避免缆索护套在施工过程中产生损伤并在运营期加强检测,避免钢丝发生锈蚀是保证其耐久性的关键。
(3) 本研究旨在提出一种基于模糊失效准则的服役拉索可靠性分析方法,故对于锈蚀拉索的抗力退化模型进行了简化。在实际工程中,钢丝的点蚀通常伴随着均匀腐蚀同时发生,加之钢丝镀锌层、疲劳断裂、氢脆等因素的影响,使得拉索抗力的退化过程十分复杂。在本研究时变可靠性模型的基础上,考虑多种影响因素和检测手段,准确描述拉索抗力的退化规律,据此对模型参数进行修正将是今后重点研究的内容。
| [1] |
张劲泉, 李承昌, 郑晓华, 等. 桥梁拉索与吊索[M]. 北京: 人民交通出版社, 2013: 9-13. ZHANG Jin-quan, LI Cheng-chang, ZHENG Xiao-hua, et al. Bridge Cables and Slings[M]. Beijing: China Communications Press, 2013: 9-13. |
| [2] |
BETTI R, WEST A C, VERMAAS G, et al. Corrosion and Embrittlement in High-strength Wires of Suspension Bridge Cables[J]. Journal of Bridge Engineering, 2005, 10(2): 151-162. |
| [3] |
CAMO S. Probabilistic Strength Estimates and Reliability of Damaged Parallel Wire Cables[J]. Journal of Bridge Engineering, 2003, 8(9): 297-311. |
| [4] |
徐俊. 拉索损伤演化机理与剩余使用寿命评估[D]. 上海: 同济大学, 2006: 60-82. XU Jun. Damage Evolution Mechanism and Remained Service Lives Evaluation of Stayed Cables[D]. Shanghai: Tongji University, 2006: 60-82. |
| [5] |
ZHU J S, XIAO R C, HE L Z. Probability Evaluation Method for Cable Safety of Long-span Cable-stayed Bridges[J]. Journal of Southeast University: English ed, 2007, 23(1): 92-97. |
| [6] |
兰成明, 李惠, 鞠杨. 平行钢丝拉索承载力评定[J]. 土木工程学报, 2013, 46(5): 31-38. LAN Cheng-ming, LI Hui, JU Yang. Bearing Capacity Assessment for Parallel Wire Cables[J]. China Civil Engineering Journal, 2013, 46(5): 31-38. |
| [7] |
HOU N, SUN L, CHEN L. Cable Reliability Assessments for Cable-Stayed Bridges using Identified Tension Forces and Monitored Loads[J]. Journal of Bridge Engineering, 2020, 25(7): 1-12. |
| [8] |
FABER M H, ENGELUND S, RACKWITZ R. Aspects of Parallel Wire Cable Reliability[J]. Structural Safety, 2003, 25(2): 201-225. |
| [9] |
ELACHACHI S M, BREYSSE D, YOTTE S, et al. A Probabilistic Multi-scale Time Dependent Model for Corroded Structural Suspension Cables[J]. Probabilistic Engineering Mechanics, 2006, 21(3): 235-245. |
| [10] |
马小利, 王立彬, 丁盛. 平行钢索的锈蚀时变失效概率分析[J]. 工程力学, 2012, 29(4): 210-216. MA Xiao-li, WANG Li-bin, DING Sheng. Time-dependent Failure Probability Analysis of Corroded Parallel Wire Cable[J]. Engineering Mechanics, 2012, 29(4): 210-216. |
| [11] |
KARANCI E, BETTI R. Modeling Corrosion in Suspension Bridge Main Cables. Ⅱ: Long-Term Corrosion and Remaining Strength[J]. Journal of Bridge Engineering, 2018, 23(6): 04018026-1-15. |
| [12] |
刘沐宇, 陈齐风, 吴志强. 考虑微动疲劳的斜拉桥钢绞线斜拉索时变可靠性分析[J]. 土木工程学报, 2012, 45(7): 141-147. LIU Mu-yu, CHEN Qi-feng, WU Zhi-qiang. Time-dependent Reliability Analysis of Strand Cables of Cable-stayed Bridges Considering Fretting-fatigue Factor[J]. China Civil Engineering Journal, 2012, 45(7): 141-147. |
| [13] |
FURUYA K, KITAGAWA M, NAKAMURA S I, et al. Corrosion Mechanism and Protection Methods for Suspension Bridge Cables[J]. Structural Engineering International, 2000, 10(3): 189-193. |
| [14] |
徐宏, 黄平明. 平行钢丝拉索Daniel效应分析[J]. 铁道科学与工程学报, 2008, 5(2): 38-41. XU Hong, HUANG Ping-ming. Analysis of Daniel Effect for Parallel Wire Cable[J]. Journal of Railway Science and Engineering, 2008, 5(2): 38-41. |
| [15] |
曹楚南. 中国材料的自然环境腐蚀[M]. 北京: 化学工业出版社, 2004: 92-98. CAO Chu-nan. Natural Environment Corrosion of Chinese Materials[M]. Beijing: Chemical Industry Press, 2004: 92-98. |
| [16] |
YANG W J, YANG P, LI X M, et al. Influence of Tensile Stress on Corrosion Behavior of High-strength Galvanized Steel Bridge Wires in Simulated Acid Rain[J]. Material and Corrosion, 2012, 63(5): 401-408. |
| [17] |
JTG/T D65-01-2007, 公路斜拉桥设计细则[S]. JTG/T D65-01-2007, Guidelines for Design of Highway Cable-stayed Bridge[S]. |
| [18] |
PTI Committee DC-45. Recommendations for Stay Cable Design, Testing and Installation[S]. 5th ed. Farminton Hills: Post-Tensioning Institut, 2007.
|
| [19] |
姜潮, 刘敏, 韩旭, 等. 一种考虑失效准则模糊性的时变可靠度分析方法[J]. 机械科学与技术, 2015, 34(11): 1699-1704. JIANG Chao, LIU Min, HAN Xu, et al. A Time Varying Reliability Analysis Method Considering Fuzzy Failure Criterion[J]. Mechanical Science and Technology for Aerospace Engineering, 2015, 34(11): 1699-1704. |
| [20] |
秦权, 贺瑞, 杨小刚. 在时变结构可靠度领域中有必要澄清一个错误概念[J]. 工程力学, 2009, 26(8): 201-204. QIN Quan, HE Rui, YANG Xiao-gang. Clarification of a Wrong Concept in the Field of Time-varying Structural Reliability[J]. Engineering Mechanics, 2009, 26(8): 201-204. |
| [21] |
沈锐利, 王文弟, 王路, 等. 基于可靠度理论的悬索桥预应力锚固系统时变计算方法研究[J]. 公路交通科技, 2019, 36(9): 57-64. SHEN Rui-li, WANG Wen-di, WANG Lu, et al. Study on Time-variant Calculation Method of Prestressed Anchor System of Suspension Bridge Based on Reliability Theory[J]. Journal of Highway and Transportation Research and Development, 2019, 36(9): 57-64. |
| [22] |
尤吉, 房涛, 付公康. 公路桥梁承载能力评估目标可靠指标计算[J]. 世界桥梁, 2013, 41(3): 73-76. YOU Ji, FANG Tao, FU Gong-kang. Calculation of Targeting Reliability Index for Bearing Capacity Evaluation of Highway Bridges in China[J]. World Bridges, 2013, 41(3): 73-76. |
 2021, Vol. 38
2021, Vol. 38
