0 引言

低温条件下道路结冰后，湿滑对城市道路和高速公路交通安全构成威胁，会影响人们正常出行及增大交通事故发生概率而导致巨大的经济损失。资料表明，随着高速公路里程数的增加，由低温引起的高速公路事故发生频率呈逐年增长趋势。因此，考虑道路下垫面状况的改变，进行微小尺度范围温度的精细化预报一直是待攻克的难题和关注的热点。准确预报路面温度变化，可为道路维护(如撒盐融冰融雪等)和实施交通管制提供可靠决策信息依据，促进对低温天气的快速响应和及时处置，对保障交通出行安全、减少交通事故发生和财产损失具有重要意义。

江苏省位于我国大陆东部沿海，南北狭长，在30°45′N~35°20′N，116.18°18′E~121°57′E之间，处南北分界线之间，地貌由平原、水域和低山丘陵组成。江苏省高速公路是我国华东地区重要的交通枢纽，通车里程于2019年达4 865 km，高速公路密度位居全国前5名。研究表明，道路结冰是我国公路交通的主要气象灾害，在江苏省占主要灾害第3位^[1]，因此研究江苏省高速公路地温的变化具有很高的代表性。

关于地表温度预报方法已有很多研究，国外20世纪80年代就开始有报道^[2]，随后90年在欧洲和北美迅速发展，相继研制出一些道路结冰预报模型并得到了应用^[3-6]，如：较著名的加拿大METRo模型^[2]、RoadSurf模型^[3]、荷兰KNMI-RWM模型^[5]等，模型中除路面积水/雪模块外，路面温度预报模型是其重要组成部分。这些模型大多基于地表能量平衡方程，模型参数多，能量通量计算过程中会带来误差传递，影响了温度预测精度。为了能够做出精准的预报预警，研究人员采用统计分析方法，将路面附近气象要素^[7-11] (如风、气温和云量、地形等)的影响纳入考虑范围，同时基于实时自动气象站的数据应用也受到重视^[12-14]。对路面温度和路面状况的监测预警与预报研究也日益受到重视，在路面温度预测模型方面已取得较多研究成果^[15-16]。然而，能量平衡法^{[13-14, 17-19]}虽然通用性强，但是建模需要输入参数多、且不易获取而影响了模型的精确度，降低了适用性，特别是材料的热力学参数，建模过程复杂。统计分析方法^[20-21]虽建模需要输入参数少，建模过程简单，但是存在预估公式地域适用性差的缺点，难以达到道路预警服务要求。

本研究在上述温度预报模型研究与应用的基础上，综合考虑数值天气预报模式要素输出信息(天气背景)、路面实时气象观测信息(反映道路状况局地变化)和路面温度变化特征，建立一套具有反映温度机理性变化特征能力的路面温度预测模型并进行验证，并且寻找其中路面热特性参数B₀在时空范围上的变化，提升24 h、微小尺度范围内的逐时路面温度预报精度，预报时效提前3 h以上，以期为业务化应用奠定基础。

1 材料与方法 1.1 资料来源

收集了2016—2017年江苏省高速公路气象监测站的自动气象观测资料，包括2 m高度的空气温度、露点温度、降水、风速、路面状况、地面温度、10 m空气温度、相对湿度等气象要素，约240多个站点。以高速公路路线、经纬度和途经城市等为筛选条件，选择了4条高速公路(京沪高速公路、沈海高速公路、常合高速公路和长深高速公路)上的13个站点，对比同一条高速公路上不同纬度上预报方程的效果，途经同一城市不同高速公路上B值，以及同一纬度上不同高速公路上B值效果等。应用2016年的资料建立地表温度预测方程并确定模型中的参数，然后用2017年高速公路路面温度数据进行验证。

1.2 预报方法 1.2.1 低温预报方程的建立

使用正弦函数模型^[22]做地表日温的预测，该模型将12-dl/2 < t_i < 12+dl/2(dl为日长，t_i为台站真太阳时)记为白天，则白天t_i时刻温度T_i可表示为：

(1)

式中，T_max和T_min分别为日最高、最低路面温度；p为日最高温度出现的时刻与正午时刻之间的小时数，这里取p=2.0 h。

夜间，路面净辐射能量损失R_n与路面温度梯度和路面热特性有密切关系。根据胡继超^[23]的研究，该关系可以表示为：

(2)

式中，κ为导温率；ρ为路面材料密度；c为比热容；z为深度。

将式(2)写成差分形式，可得到夜间地表(z=0)的温度T_i为：

(3)

式中，T_i为夜间时刻t_i时待预报的温度；T₀为日落后2 h的温度。

另有：

(4)

式中，a和b为系数，这里取a=0.66，b=0.14；e为水汽压；σ为斯蒂芬波尔兹曼常数，这里取σ=5.67×10^-8 W/(m²·k⁴)；T为夜间地表平均温度；C_n为云量(云占天空百分比)；c₁为参数。

可得：

(5)

令：

(6)

则：

(7)

式中，T_i为夜间t_i时刻待预报的温度；T₀为日落后2 h的温度。根据历史观测资料及路面材质信息，可以确定T₀和路面热特性参数B₀。

由式(1)与式(7)可得地表温度预报方程：

(8)

这样，根据上面的系列公式，就可以预报从当天日落时刻开始，未来24 h内逐时或任意给定时刻t_i的道路温度值。

1.2.2 参数值B₀的确定

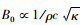
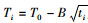
在式(7)中，路面热特性参数，主要与路面建筑材料的热特性有关。参数B值的物理含义为夜间每小时高速公路路表降温的幅度。有2种途径确定参数B和B₀值：一是可根据高速公路路面材料的ρ，c，κ值，先计算得到B₀值，然后依据天气状况计算得到B值；另一途径是根据历史气象观测资料用公式反演出B值，再根据B=B₀R_n推算出B₀。本研究将2种途径得到的B₀进行了对比，用统计回归方法分析它们的一致性，确定B₀值的合理范围。

下面是收集高速公路路表常用材料^[24]及水和冰^[25]的ρ，c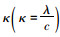，值，并由此计算与下垫面特征有关的B₀值。

1.3 预报效果评价指标

本研究利用路面温度预报值与实测值进行对比研究。用预报值(模拟值)与实测值之间的相关系数r、平均偏差MBE、均方差误差RMSE和模型效率ME来描述模型模拟效果。

(9)

(10)

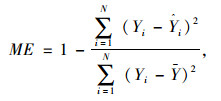
(11)

式中，为模拟值；Y_i为观测值；Y为观测平均值；N为观测样本数。相关系数R越大，平均偏差与标准差越低，模型效率越接近于1，说明该算法的预报效果越好。

2 预报结果与差异分析 2.1 参数B₀值的计算结果及分析

先利用观测资料根据计算得到B值，再由B=B₀R_n，在晴天无云的情况下，去除B中R_n的影响，则可得到与高速公路路表建筑材料有关的B₀值，将求得的各站点路面热特性参数B₀值列于表 3。

(1) 表 3中由实测数据反演得到的热特性参数B₀的计算结果变化于3.17~3.67之间，将其与表 2中用路面热特性值ρ，c，κ值推算得到的B₀(在3.6左右)进行比较可知，二者能很好地吻合，表明表 3中热特性参数B₀的计算结果是合理的。(2)分析同一高速公路路面由实测数据反演得到的热特性参数B₀，二者非常相似，这是它们的建筑材质一致导致的必然结果。(3)不同高速公路因建筑材质不一样，路面热特性参数B₀明显不同，从表 3得到，G15沈海高速公路段B₀值约为3.63，比G25长深高速公路B₀值(3.53)略高，比G2沪宁高速公路段上B₀值(3.25)高约10%。而S38常合高速的B₀值(3.21)最低。

B值绝对值的变化与其所在经纬度和月份有关，由B值计算公式：(1-c₁C_n)，B₀值不变时，温度升高时B值随之升高。在同一站点，B值随着月份的增加而增加，下半年则呈现出相反的趋势，这是因为不同季节路表温度不同，因而同一站点呈现出B值随月份变化而发生相应改变的现象。

2.2 单站逐时温度预报效果检验

应用路面温度逐时预报方程对高速公路路面温度进行预报。取1 h作为时间步长，以1 h时间间隔的气象要素观测资料作为实测值，以预报起报时的高速公路路面温度实况值作为计算未来24 h高速公路路面温度初始值。在本模型中，以日出日落为界限将每天分为白天和夜间2个部分，白天应用正弦函数对地温进行预测，夜间以日落时间为预报起报时间，利用当天的最高地温和前一天的最低地温计算夜间逐时的高速公路路面温度预报值，对各站点2月份的逐时地温预报效果进行检验。

如表 4所示，13个站点温度预报方程的预测值与实测值相关系数r均大于0.91，平均偏差MBE的绝对值小于1.2，标准差较小，模型效果基本达到0.75以上，预报方程效果好，可以较准确地预测高速公路路面温度。

由表 4，选择相关系数最高(M9340，r=0.962)和最低(M9266，r=0.919)的2个站点作为代表性站点分析方程模拟效果，绘制逐时地表温度实测值和预测值的对比图。由图 1可见，2个测站的路面温度预测值与实测值吻合程度非常高，路面预报方程不仅可以很好地预测高速公路地表温度的变化趋势，而且二者偏差很小，尤其在晴朗的夜间。

由图 1，本研究对地表温度的预测可以很好地预测出地表温度逐时变化趋势，结合气象要素实测数据做误差分析。在晴朗干燥的夜间，实测值与预报值拟合较好，误差相对较小；在多云与阴天天气条件下，当日日较差较小，由于云的保温作用，R_n发生变化，夜间降幅度不大，预测值仍是以下降趋势为主，但预报值相比实测值较小。在阴天或多云后的晴天，预测值比实测值偏大，可能是因为多云日日较差较小，影响了当日预报效果。

选取M9340站点2月份夜间地温预报值与实测值做不同天气状况下的具体分析。如图 2、表 5所示，晴朗夜间方程预报效果极佳，预报值与实测值偏差在1 ℃以内的达到72%，偏差2 ℃内的达到92%，偏差在3 ℃内的达到100%。多云、阴天天气状况下的高速公路地表温度预报可以较好地体现地表温度发展趋势，偏差在3 ℃以内的达到92%。

2.3 最低温预报效果检验

以2017年1月至4月、10月至12月13个站点的气象观测资料为本研究建立的预报方程最低温度预报效果的检验数据。图 3是所选测站路面日最低温度实测值与预报值的散点图，其中预报值与实测值数据点比较集中，且其拟合线与45°等值线很吻合，说明该方程预报精度较高。由表 6可知，由预报方程得到的最低温度预报值与实测值相关系数达0.96，均方差误差小于2 ℃，平均偏差为0.08 ℃，模型效果达0.9。实测值与预报值偏差在1 ℃内的为45.23%，偏差为2 ℃内的为75.82%，偏差在3 ℃内的达92%，预报结果可作为高速公路最低温预报的参考值。

3 结论

(1) 本研究建立的预报方程具有较好的实用性和较高的预测精度，晴朗夜间高速路面温度预测值与实际值偏差在1 ℃以内的比例达到72%，阴天和多云天气时高速路面温度预测值与实际值偏差在2 ℃以内比例达到76%。模拟值与实测值相关系数高，均方根差值小，模型模拟效果好，表明模型具有很好的预测能力，可以用来进行路表温度的预测。

(2) 预报方程的参数B₀值仅与路面状况ρ，c，κ有关，因此随着高速公路路表性质发生改变时，B₀值也会相应发生变化。本研究确定了江苏段内可用于路面低温预报方程的B₀值。B值在B₀的基础上考虑了局地小气候的影响，与R_n有关，随温度发生变化，同一季节纬度升高B值绝对值逐步增大、同一地点随着整体气候逐渐变暖，B值绝对值也在逐步增加。总地来说，B值绝对值随高速公路地表最低温度增大而增大。由于地表温度随月份变高，夜间R_n负值会变大，B值的绝对值是变大的。

(3) 文中提出的地面温度预报方程在晴天天气状况下预报效果良好，冷平流发生时，地面平衡状态发生改变，预报值相对实测值偏高。降水发生或路面结冰时路面干湿状况发生改变，下垫面参数ρ，c，κ变化，B₀随之改变，根据表 2，有积水或冰雪路面的B₀值为2.07和2.28，比干燥路面B₀值小。由此推断当路面积水或积冰发生时，路面温度下降幅度相对小些，这一推测有待更多的观测资料来验证。