扩展功能
文章信息
- 张俊红, 贾宏杰, 周启迪, 朱小龙, 林杰威
- ZHANG Jun-hong, JIA Hong-jie, ZHOU Qi-di, ZHU Xiao-long, LIN Jie-wei
- 基于自适应变分模态分解的扩展工况传递路径分析方法
- An Operational-X Transfer Path Analysis Method Based on Adaptive Variational Modal Decomposition
- 公路交通科技, 2021, 38(7): 138-144, 158
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(7): 138-144, 158
- 10.3969/j.issn.1002-0268.2021.07.018
-
文章历史
- 收稿日期: 2020-10-09
2. 天津仁爱学院, 天津 301636;
3. 潍柴动力股份有限公司, 山东 潍坊 261016
2. Tianjin Renai College, Tianjin 301636, China;
3. Weichai Power Co., Ltd., Weifang Shandong 261061, China
汽车作为一个复杂的机械系统,在运行过程由于多个激励点经不同的传递路径合成导致汽车内部产生声振问题。在车辆研发过程中,为优化整车NVH(Noise, Vibration, Harshness)性能,需要综合考虑所有激励和传递路径。传递路经分析[1]可有效解决上述问题。经过20多年的发展,在TPA的基础上衍生出了多种分析方法,如工况传递路径分析(Operational Transfer Path Analysis,OPA)[2]和扩展工况传递路径分析(Operational-X Transfer Path analysis,OPAX)等[3]。其中,OPAX[4]兼顾TPA的高精度和OPA的高效率,被广泛应用于工程和科研领域。
OPAX进行参数化建模的过程,需要采集大量的工况数据[5-6]。因测试环境存在偶发性的冲击和外界干扰噪声,导致采集数据掺杂一定的噪声信号,有效的弱特征振动信号可能会被掩盖,使OPAX分析精度出现较大的偏差,无法准确获得各条传递路径的贡献度。因此,为剔除干扰信号,保证有效信号的识别精度,需要对采集到的信号进行去噪处理。
目前常用的去噪方法包含小波变换(WT)、经验模态分解(EMD)、变分模态分解(VMD)等[7-9]。WT基于积分理论,在分解信号的过程中过分依赖于小波基的选择,不具有自适应性[10]。EMD弥补了WT的不足,可自适应的将复杂的信号分解为多个本征模态函数(Intrinsic Mode Function,IMF),但EMD在理论上缺乏严格的证明,分解信号过程中存在包络误差、模态混淆等问题[11]。文献[12]在传统维纳滤波理论的基础上提出了变分模态分解(Variational Mode Decomposition,VMD),该方法具有坚实的数学基础,在处理非线性非平稳信号时具有很大的优势。然而,VMD方法中的模态个数K和惩罚因子α需要人为预设,并且缺乏标准。
针对VMD参数优化问题,汤周杰等[13]通过融合鲁棒独立分量优化VMD中的模态个数K,但没有考虑惩罚因子α的影响。鄢小安等[14]利用瞬时能量分配-置换熵作为目标函数分别对VMD中的参数K和α进行优化,然而忽略了K和α之间的耦合影响,可能会引起局部最优结果。肖怀硕等[15]采用傅立叶频谱包络作为优化目标函数对参数K和α同时优化,但该目标函数对非稳态信号适应性较差。唐贵基等[16]以Shannon熵作为适应度函数,采用粒子群优化算法对VMD进行优化。然而以Shannon熵为适应度函数的优化结果鲁棒性较差。多尺度模糊熵可以衡量时间序列在不同尺度因子下的复杂程度和维数变化时产生新信息的概率大小,考虑到采集信号中包含具有规律性的振动信号和随机性很强的干扰信号,将多尺度模糊熵作为判断信号特征的指标,用于振动信号的分解去噪。PSO具有较高的计算效率,但是全局搜索能力较差,容易陷入局部最优解[17]。模拟退火算法[18]具有概率突跳能力,使粒子在停止进化的位置重新产生粒子进行迭代计算,可有效避免局部最优。
为了削减OPAX在信号采集过程干扰噪声的影响,提高分析精度,本研究提出一种基于自适应变分模态分解和巴氏距离的优化OPAX方法。该方法考虑到多尺度模糊熵能够较好地表征非稳态复杂信号,将其作为适应度函数;采用模拟退火粒子群算法(Simulated Annealing Particle Swarm Optimization,SAPSO)进行信号自适应变分模态分解,最后通过巴氏距离计算原始信号和分解信号概率密度函数的相似性进行相关模态筛选,实现信号去噪。
1 AVMD-BD和OPAX方法原理 1.1 AVMD-BD降噪算法 1.1.1 AVMD算法文献[12]已详细介绍了VMD算法的原理,本研究不再赘述。VMD方法在处理信号时需要预先设定模态个数K和惩罚参数α,参数选择不准确会导致信号产生过分解、欠分解和模态混叠的问题。针对VMD参数优化的问题,由于PSO算法存在着全局搜索能力较差、易陷入局部最优解、精度较差等问题,借鉴模拟退火算法中的概率突跳能力,使粒子跳出已搜索的最优区域,在更大空间中开展搜索。
基于此,本研究综合考虑SAPSO算法全局搜索优势,以及多尺度模糊熵在提取复杂非稳态信号的优势[19-20],提出一种以最小IMF多尺度模糊熵为适应度值的SAPSO搜索算法进行VMD自适应参数寻优。
粒子群算法的进化方程为:
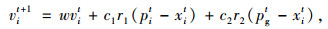
|
(1) |
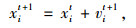
|
(2) |
式中,vit为第i个粒子在第t代的速度;xit为第i个粒子在第t代的位置; w为惯性权重;i为第i个粒子;t为第t代;pit为第i个粒子在第t代的最优点;pg为粒子最佳位置;c1和c2为加速度常数;r1和r2为2个相互独立的随机函数,r1, r2∈U[0, 1]。
为提高粒子群算法的搜索效率,使得在搜索空间中随机产生的粒子j以较大的概率处于最优点附近,采用模拟退火算法生成。
模拟退火的基本思想为:从一个给定解开始,以当前粒子最佳位置pg为初始状态,即xjt+1=pg,同时选择初始温度T=T0,从最佳位置的邻域中随机产生其他解。
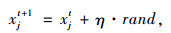
|
(3) |
式中,η为扰动幅值参数;rand为随机变量。
计算上述2个粒子位置引起的适应值变化量ΔE,若ΔE≤0,按照Tt+1=qTt(0<q<1)接受xjt+1为新位置;否则就不降温,xjt+1仍为xjt。
AVMD算法中SAPSO的参数设置如表 1所示。其中M为粒子的种群规模;N为迭代次数;w为惯性权重;T为初始温度;q为退火系数;c1和c2为学习因子;V为粒子移动的速度范围。
| M | 40 | N | 40 | |
| w | [0.4, 0.9] | T/ | 5 000 | |
| c1=c2 | 1.496 2 | q | 0.7 | |
| Vmax | 2 | Vmin | -2 |
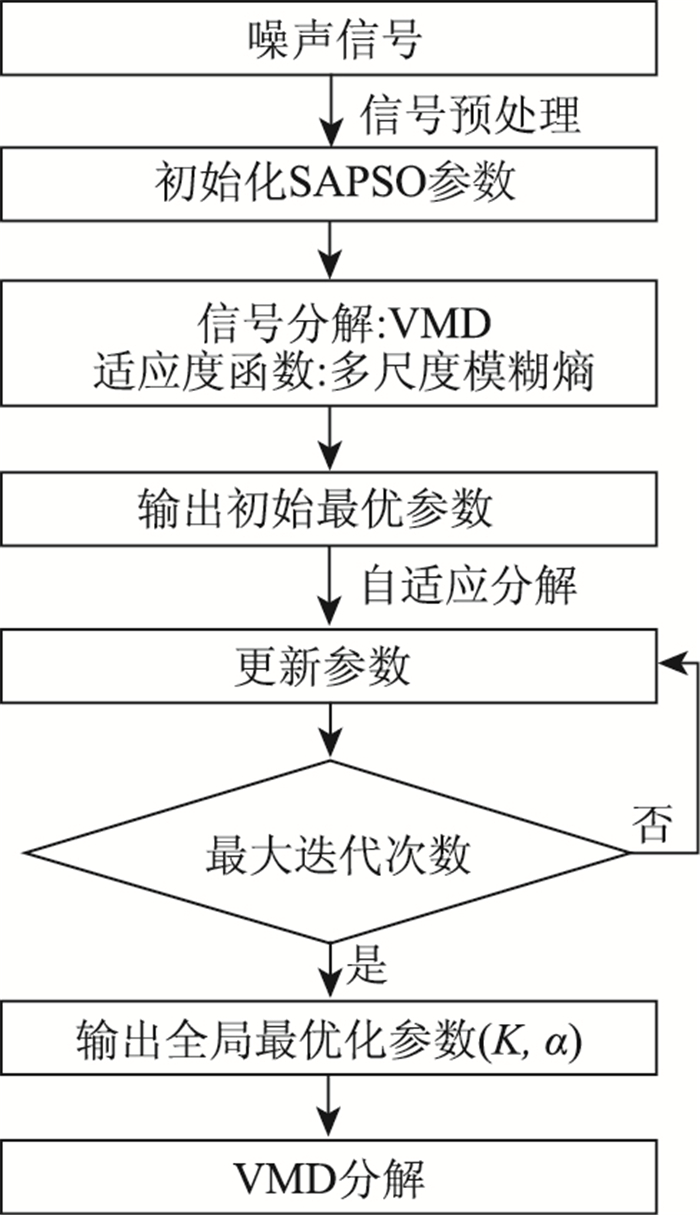
AVMD算法自适应获取最优参数流程见图 1,具体步骤如下:
|
| 图 1 AVMD算法优化流程 Fig. 1 Flowchart of optimization by AVMD algorithm |
| |
(1) 确定SAPSO中的所有初始化参数。
(2) 计算每个粒子的适应度。
(3) 对比粒子的适应度和最好位置pg,如较好,设置为当前最好位置。
(4) 当pg=xjt+1,则第j个粒子停止进化,用模拟退火算法生成xjt+1。
(5) 根据(3)和(4)对其他粒子的速度和位置进行优化。
(6) 满足停止条件输出最优结果。
1.1.2 相关模态的选择概率密度函数(Probability Density Function,PDF)[21]可以反映不同信号分布之间的区别。本研究采用核密度估计的方法获取每个分解信号和原始信号的PDF。计算信号之间的相似性作为区分相关模态的依据。巴氏距离[22]是2个统计样本之间的重叠量的距离测量,用于计算2个样本之间的相对接近程度。巴氏距离的定义如下:
在定义域X中,概率分布Q和P的巴氏距离的定义为:
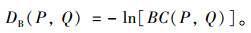
|
(4) |
对于离散概率分布:
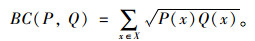
|
(5) |
对于连续概率分布:
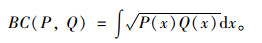
|
(6) |
可以看出,DB越小表示概率分布越接近,即模态分量与输入信号更相关。
输入信号和模态分量之间相似性的定义为:
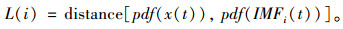
|
(7) |
通过评估2个相邻IMF之间距离的斜率来确定相关模式。当斜率显著增加时,表明该IMF之后发生的相似性迅速降低。定义θ为2个相邻的IMF与输入信号之间的最大斜率,表达式为:
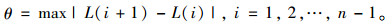
|
(8) |
如在IMFm和IMFm+1之间产生最大斜率,则通过式(9)获得滤波后的信号y(t)。
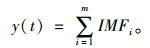
|
(9) |
传统的TPA通常使用逆矩阵法求解工作载荷,其理论公式为:
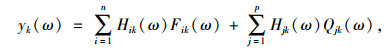
|
(10) |
式中,yk(ω)为目标点k的总贡献量;ω为频率;n为传递路径数量;Hik(ω)和Hik(ω)分别为不耦合的主动端与响应端之间的结构和声学频率响应函数矩阵;Fik(ω)和Qjk(ω)分别为作用在主动端的结构载荷和声学载荷。
OPAX方法是在传统TPA方法基础上演化而来的,与传统TPA方法的主要区别在于使用了参数化模型进行载荷识别,同时借鉴了OPA方法的优点,大量采用实测工况数据进行建模,减少了FRF的测试工作量,在保证结果精度的同时节省了建模时间。
在整车系统中,动力总成作为激励源为主动侧,车身结构为被动侧,中间的耦合元件为悬置,起到支撑及隔离振动的作用,目标点是某点在某自由度上的振动。对于目标点的振动响应,被动侧在耦合点的每个自由度到响应点均会形成1条独立的传递路径。考虑纵向、侧向和垂向3个方向自由度。任一方向的频响函数可以表示为:
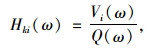
|
(11) |
式中,Vi(ω)为结构表面的振动加速度;Q(ω)为麦克风处的体积速度。
已知某传递路径上的系统频响函数和工作载荷,该路径对目标位置噪声的贡献yki(ω)可以表示为:
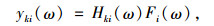
|
(12) |
式中,k为响应点的表示符号;Hki(ω)为第i条传递路径上的频响函数;Fi(ω)为第i条路径上的工作载荷。
Vi(ω)直接影响频响函数的计算精度,进而影响传递路径分析的计算结果。
如果有n条传递路径,则目标点的总响应可认为是多条路径分贡献量的线性叠加,可以表示为:
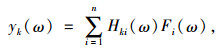
|
(13) |
式中yk(ω)为目标点k的响应。
2 仿真试验与分析考虑到振动信号中包含多种成分,同时测试环境中存在偶发性的冲击和外界干扰噪声。本研究仿真试验由2部分组成:(1)验证AVMD算法的准确性。由于高斯白噪声中包含多种不确定分量,无法验证AVMD分解结果的准确性,因此模拟信号x(t)由包含明确特征的多分量和非高斯信号组成。(2)验证AVMD-BD去噪效果的有效性。在信号x(t)中增加高斯白噪声模拟外界干扰噪声的影响。
2.1 AVMD算法验证为验证AVMD算法的准确性,模拟信号x(t)由4类信号叠加而成。
针对下式的仿真信号进行分解:
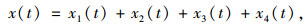
|
(14) |
式中,x1(t)=cos(16πt); x2(t)=cos(40πt); x3(t)=cos(100πt); 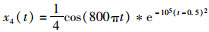
采用PSO-VMD和SAPSO-VMD这2种方法对上述信号进行分解,计算得到的最优参数组合为[K=5, α=436]和[K=4, α=674],从优化参数组合中可以看出,PSO-VMD的K=5,而原始信号中只有4组信号,表明该方法出现过分解现象。SAPSO-VMD可以准确分解4个模拟信号。上述分析结果表明,SAPSO-VMD可以有效分离混合信号,为后续通过巴氏距离挑选相关模态奠定良好的基础。
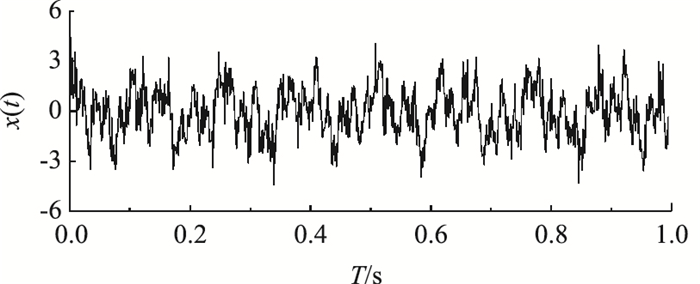
2.2 AVMD-BD算法验证用于计算频响函数的信号中若掺杂干扰噪声会严重影响OPAX的计算精度。为验证AVMD-BD算法在信号去噪效果中的有效性,本研究在式(14)信号的基础上叠加高斯白噪声来进行模拟仿真。模拟信号时域结果如图 2所示。
|
| 图 2 模拟信号仿真 Fig. 2 Analog signal simulation |
| |
用AVMD对上述模拟信号进行分解,计算得到最佳的参数优化组合为[K=16,α=3 052]。
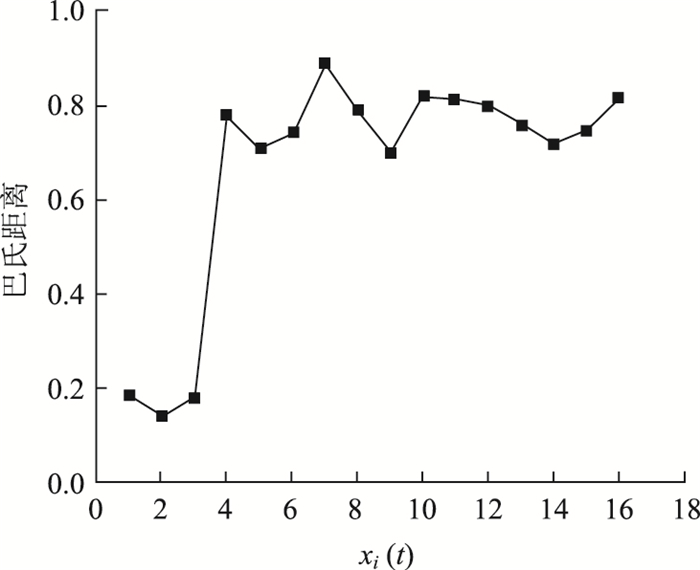
为了有效地剔除干扰参量,实现信号的精确去噪,在采用巴氏距离进行特征模态选择时,首先利用核密度估计的方法获得输入信号与每个模态分量的pdf。其次根据式(4),得到信号之间的巴氏距离,如图 3所示。可以看出,巴氏距离将分解信号分为2组,每组中的xi(t)与输入信号之间的距离相对集中,从x3(t)到x4(t)的过程中,斜率显著增加,表明x4(t)后发生的相似性迅速减少。另外,从x4(t)到x16(t)与原始信号之间的距离相对较远,均可以认为是远离原始信号的非相关模态。x1(t)到x3(t)即为相关模态,通过重构相关模态,从而得到去噪后的模拟信号。
|
| 图 3 各分解信号与模拟含噪信号之间的巴氏距离 Fig. 3 BD between each decomposed signal and analog noisy signal |
| |
3 AVMD-BD-OPAX效果验证 3.1 OPAX模型建立及工况数据采集
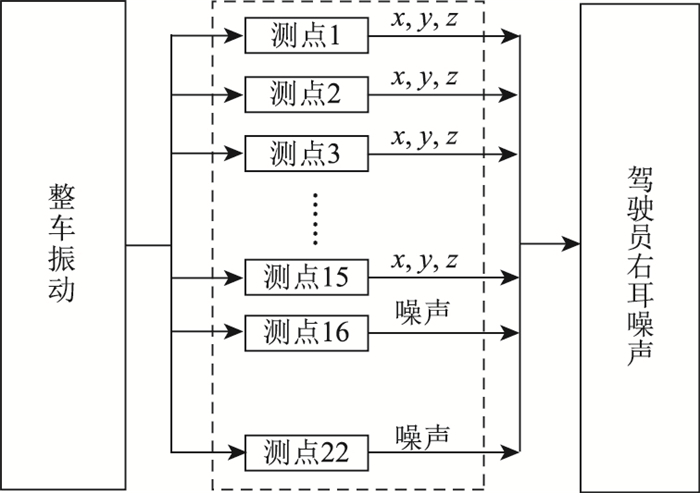
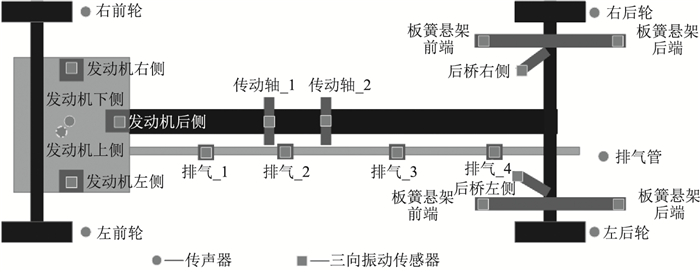
本研究选取的试验对象为某国产轻型客车,装载一款4缸柴油发动机,发动机排量为2.0 L,额定乘员为21人。动力总成悬置共有3个,传动轴悬置有2个,排气悬置有4个,后轮钢板弹簧悬置左右共有6个。整车动态试验在90 km/h匀速工况进行测试,利用数采系统(LMS,SCADAS 05)和LMS TEST.LAB软件对数据进行采集与分析。试验中在悬置主被动端分别安装三向加速度传感器(PCB,356A26)进行振动信号采集,在车轮、发动机进排气端和驾驶员右耳布置传声器(PCB,378B02)进行噪声信号采集,传递路径分析模型如图 4所示,包括15×3+7=52条传递路径。传感器安装位置如图 5所示。
|
| 图 4 传递路径分析模型示意图 Fig. 4 Schematic diagram of transfer path analysis model |
| |
|
| 图 5 测点布置示意图 Fig. 5 Schematic diagram of measuring point arrangement |
| |
3.2 频响函数的测量
采用声学互易法进行频响函数的测量。将体积声源作为输入信号放置在车内驾驶员位置,测取整车37个测点处的信号。对去噪后的信号利用式(11)计算相应传递路径的频响函数。
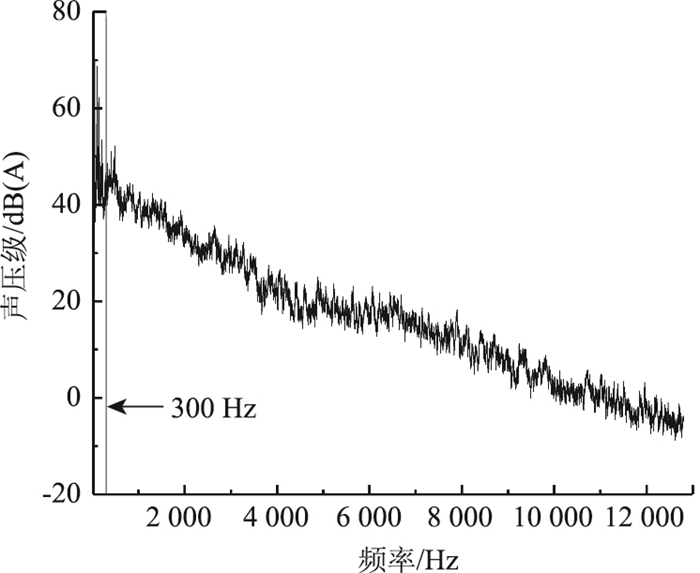
3.3 AVMD-BD-OPAX结果图 6为车辆90 km/h匀速行驶工况下驾驶员右耳噪声的平均功率谱。可以看出,噪声能量主要集中在0~300 Hz的中低频区域。因此主要关注该区域的优化结果。
|
| 图 6 驾驶员右耳噪声平均功率谱 Fig. 6 Average power spectrum of driver's right ear noise |
| |
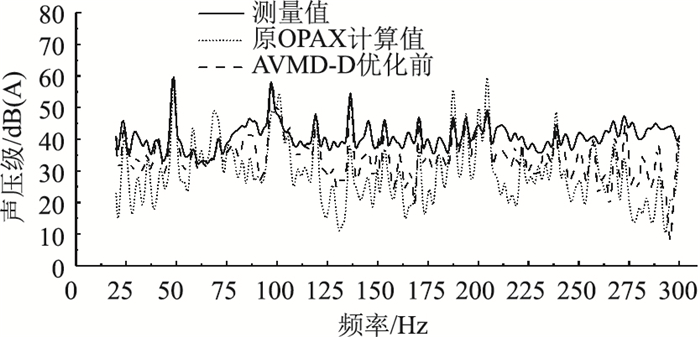
将目标点处的实测信号作为参考值,对比验证本研究所提方法的准确性和优越性。图 7为原始OPAX计算值和AVMD-BD优化后OPAX计算值。可以明显看出,优化前后所得结果的走势与实测值基本一致,在采用AVMD-BD降噪后所得结果与实测值的吻合程度更高,在40~280 Hz频率段内尤为明显。
|
| 图 7 原OPAX方法与改进后方法的计算结果 Fig. 7 Calculation results of original OPAX method and improved method |
| |
为进一步验证AVMD-BD方法在振动信号去噪处理中的有效性,以信噪比SNR和均方根误差RMSE来作为评判的依据。其中均方根误差越小,信噪比越大,表征信号的去噪效果越好。
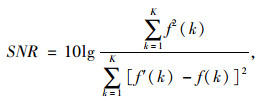
|
(15) |
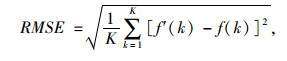
|
(16) |
式中,f′(k)为去噪信号;f(k)为原始信号;k为信号长度。
表 2列出了AVMD-BD降噪优化后相对于实测信号的SNR和RMSE。可以明显看出,在采用AVMD-BD降噪优化后,信噪比提升了71.2%,均方根误差减小了66.9%。说明本研究所提的降噪优化方案可有效提高OPAX方法的计算精度。
| 比较方法 | 优化前 | 优化后 |
| SNR | 8.941 5 | 15.308 9 |
| RMSE | 21.494 6 | 7.119 0 |
在40~280 Hz内振动响应较大,且有8个比较明显的峰值,这也是工程研究人员最为关心的问题。
表 3中列出了在8处峰值频率处,计算值和实测值之间的相对误差。结果显示经AVMD-BD优化后的OPAX误差均控制在5%以内,表明优化后OPAX计算结果的精确性得到有效提高。
| 频率/Hz | 原OPAX方法/% | 优化后的OPAX方法/% |
| 48.5 | 1.73 | 0.46 |
| 97 | 17.89 | 2.42 |
| 119 | 8.11 | 1.04 |
| 136.5 | 31.64 | 4.03 |
| 153.5 | 20.13 | 4.03 |
| 170.5 | 21.57 | 3.75 |
| 204.5 | 20.92 | 0.89 |
| 239 | 7.59 | 4.72 |
4 结论
本研究针对采用扩展传递路径分析(OPAX)进行频响函数计算时,由于存在干扰信号导致频响函数计算准确性低进而影响OPAX计算精度的问题,提出了一种基于自适应变分模态分解和巴氏距离的优化OPAX方法。该方法提高了传递路径分析的精确性。具体结论如下:
(1) 提出了一种基于模拟退火粒子群算法的自适应变分模态分解方法,该方法考虑到多尺度模糊熵能够较好地表征非稳态复杂信号,将其作为适应度函数;利用模拟退火算法的概率突跳能力,可有效避免局部最优。通过仿真信号分析,将其与PSO-VMD进行对比,结果表明,AVMD可以有效分离混合信号中的各个模态,其分解结果优于PSO-VMD。
(2) 采用巴氏距离可以有效识别信号分量与有效信号的相关性,实现高信噪比的信号重构。重构信号的走势与原信号基本一致,且波形更加光滑,降噪效果明显。
(3) 提出了一种基于AVMD-BD的OPAX优化方法。试验分析结果表明,优化后的计算值更加接近实测值,优化后OPAX计算值的信噪比提高了71.2%,均方根误差减小了66.9%,在峰值频率处的误差均控制在5%以内。
| [1] |
VAN DER SEIJS M, DE KLERK D, RIXEN D J. General Framework for Transfer Path Analysis: History, Theory and Classification of Techniques[J]. Mechanical Systems and Signal Processing, 2016, 68/69: 217-244. |
| [2] |
DOVYDAS V, DMITRI T, JONAS B. Application of Vibro-acoustic Operational Transfer Path Analysis[J]. Applied Acoustics, 2019, 154: 201-212. |
| [3] |
龙岩. 基于改进传递路径分析方法的动力总成悬置系统优化设计[D]. 长春: 吉林大学, 2010. LONG Yan. Optimum Design of Engine Mounting System Based on Improved Transfer Path Analysis[D]. Changchun: Jilin University, 2010. |
| [4] |
JANSSENS K, GAJDATSY P, GIELEN L, et al. OPAX: A New Transfer Path Analysis Method Based on Parametric Load Models[J]. Mechanical Systems and Signal Processing, 2011, 25(4): 1321-1338. |
| [5] |
YE S, HOU L, ZHANG P, et al. Transfer Path Analysis and Its Application in Low-frequency Vibration Reduction of Steering Wheel of a Passenger Vehicle[J]. Applied Acoustics, 2020, 157: 107021. |
| [6] |
宋海生. 基于扩展OPAX传递路径方法的轻型客车振动控制研究[D]. 长春: 吉林大学, 2012. SONG Hai-sheng. Research Vibration Control of Light Bus Based on Improved Operational-X Transfer Path Analysis[D]. Changchun: Jilin University, 2012. |
| [7] |
赵玲, 刘小峰, 娄路. 复小波分解联合SVD提取振动信号非平稳特征[J]. 振动、测试与诊断, 2015, 35(4): 672-676. ZHAO Ling, LIU Xiao-feng, LOU Lu. The Feature Extraction Method of Non-stationary Vibration Signal Based on SVD-complex Analytical Wavelet Demodulation[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(4): 672-676. |
| [8] |
汪莹鹤, 王保田. 基于小波降噪与最小二乘支持向量机的公路软基沉降预测模型[J]. 公路交通科技, 2008, 25(6): 40-43, 49. WANG Ying-he, WANG Bao-tian. A Settlement Prediction Model for Soft Foundations Based on Wavelet De-noising and LSSVM[J]. Journal of Highway and Transportation Research and Development, 2008, 25(6): 40-43, 49. |
| [9] |
李义罡, 焦朋朋, 乔伟栋. 基于改进粒子群优化BP神经网络的弯道转向行为预测[J]. 公路交通科技, 2019, 36(10): 128-136. LI Yi-gang, JIAO Peng-peng, QIAO Wei-dong. Prediction of Steering Behaviors on Curves Based on BP Neural Network Optimized by Modified PSO[J]. Journal of Highway and Transportation Research and Development, 2019, 36(10): 128-136. |
| [10] |
ZHOU Z, HUA D, WANG Y, et al. Improvement of the Signal to Noise Ratio of Lidar Echo Signal Based on Wavelet De-noising Technique[J]. Optics and Lasers in Engineering, 2013, 51(8): 961-966. |
| [11] |
YANG G, LIU Y. EMD Interval Thresholding Denoising Based on Similarity Measure to Select Relevant Modes[J]. Signal Process, 2015, 109: 95-109. |
| [12] |
ZOSSO D, DRAGOMIRETSKIY K. Variational Mode Decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. |
| [13] |
张俊红, 汤周杰, 林杰威, 等. IVMD融合Robust ICA的内燃机噪声源分离[J]. 振动、测试与诊断, 2020, 40(1): 28-34, 201. ZHANG Jun-hong, TANG Zhou-jie, LIN Jie-wei, et al. Noise Source Separation of Internal Combustion Engine Based on IVMD-Robust ICA Method[J]. Journal of Vibration, Measurement & Diagnosis, 2020, 40(1): 28-34, 201. |
| [14] |
YAN X, JIA M, ZHAO Z. A Novel Intelligent Detection Method Forrolling Bearing Based on IVMD and Instantaneous Energy Distribution-permutation Entropy[J]. Measurement, 2018, 130: 435-447. |
| [15] |
XIAO H S, WEI J C, LIU H S, et al. Identification Method for Power System Low-frequency Oscillations Based on Improved VMD and Teager-Kaiser Energy Operator[J]. IET Generation, Transmission & Distribution, 2017, 11(16): 4096-4103. |
| [16] |
唐贵基, 王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J]. 西安交通大学学报, 2015, 49(5): 73-81. TANG Gui-ji, WANG Xiao-long. Parameter Optimized Variational Mode Decomposition Method with Application to Incipient Fault Diagnosis of Rolling Bearing[J]. Journal of Xi'an Jiaotong University, 2015, 49(5): 73-81. |
| [17] |
雷秀娟, 付阿利, 孙晶晶. 改进PSO算法的性能分析与研究[J]. 计算机应用研究, 2010, 27(2): 453-458. LEI Xiu-juan, FU A-li, SUN Jing-jing. Performance Analyzing and Researching of Improved PSO Algorithm[J]. Application Research of Computers, 2010, 27(2): 453-458. |
| [18] |
刘海波, 王和平, 沈立顶. 基于SAPSO优化灰色神经网络的空中目标威胁估计[J]. 西北工业大学学报, 2016, 34(1): 25-32. LIU Hai-bo, WANG He-ping, SHEN Li-xiang. Target Threat Assessment Using SAPSO and Grey Neural Network[J]. Journal of Northwestern Polytechnical University, 2016, 34(1): 25-32. |
| [19] |
CHEN W, WANG Z, XIE H, et al. Characterization of Surface EMG Signal Based on Fuzzy Entropy[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering, 2007, 15(2): 266-272. |
| [20] |
CHEN W, ZHUANG J, YU W, et al. Measuring Complexity Using FuzzyEn, ApEn, and SampEn[J]. Medical Engineering & Physics, 2009, 31(1): 61-68. |
| [21] |
KOMATY A, BOUDRAA A O, AUGIER B, et al. EMD-based Filtering Using Similarity Measure between Probability Density Functions of IMFs[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 63(1): 27-34. |
| [22] |
MA W P, YIN S X, JIANG C L, et al. Variational Mode Decomposition Denoising Combined with the Hausdorff Distance[J]. Review of Scientific Instruments, 2017, 88(3): 35109. |
 2021, Vol. 38
2021, Vol. 38
