扩展功能
文章信息
- 周昆, 荆迪菲, 荆林立, 宋佳康, 陈跃文
- ZHOU Kun, JING Di-fei, JING Lin-li, SONG Jia-kang, CHEN Yue-wen
- 基于节点承载力的高密度路网诱导路径选择方法
- An Approach for Selecting Guidance Route of High-density Road Network Based on Node Capacity
- 公路交通科技, 2021, 38(7): 124-130
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(7): 124-130
- 10.3969/j.issn.1002-0268.2021.07.016
-
文章历史
- 收稿日期: 2021-03-18
2. 同济大学 道路与交通工程教育部重点实验室, 上海 201804;
3. 云南省昭通市大永高速公路建设指挥部, 云南 昭通 657305
2. Key Laboratory of Road and Traffic Engineering of Ministry of Education, Tongji University, Shanghai 201804, China;
3. Dali-Yongsheng Expressway Construction Headquarters, Zhaotong Yunnan 657305, China
随着我国经济的快速发展,我国道路工程建设取得了长足的进步,东部地区一些省份路网密度及复杂程度越来越高,已形成高密度路网结构。高密度路网的概念是相对于建设前期两点之间的单一路线而言的,两点之间的出行可能在路网中存在多个可选择路径,出行阻抗差异化的减小是构成高密度路网的条件[1]。高密度路网内相邻交叉口间关联性高,交通需求集中且交通运行环境复杂,路网系统稳态易被打破,导致路网通行效率下降和事故发生概率上升[2],高密度路网的形成对道路管理提出了更高的要求。
交通诱导系统是智能交通系统的核心组成部分[3],其以路网的交通分配结果为基础,结合路网动态信息对驾驶员进行路径诱导,实现行驶车辆在路网中的均衡分布,从而有效地缓解道路交通拥堵,是道路管理者最为青睐的策略[4]。合理有效的路径诱导策略将有助于缓解交通拥挤状况、改善交通运行状态、提高交通系统运行效率[5]。智能交通系统的发展推动了最优路径问题的研究,传统的最优路径算法如Dijkstra算法[6]、深度优先搜索算法等,均具有很高的计算复杂度和搜索空间,但其所规划路径仅仅是数学意义上的最短路径,很难满足实际路径诱导需求[7],且计算过程收敛较慢,计算时间冗余,所以很难在实际交通诱导系统中应用。路网主要由网络节点和道路构成,节点即道路上的间断点,包括交叉口、匝道出入口和互通式立交等[8]。与一般路网相比,高密度路网中包含更多等级节点和道路,驾驶员面对路径选择时,往往会避免在不同等级的道路间频繁地切换行车,更倾向于选择与目的地有直接通路的,能承载、转换高密度交通流的,由高等级节点和道路组成的路线。即便该路线不是常规意义上的最优路径,却更加符合驾驶员的驾驶偏好和期望[9]。
路网节点评估是路网运营管理和交通诱导的基础。传统的路网运营管理主要以道路为单位,忽略了路网节点的重要性,路网中的高等级节点会对路网的动力学过程产生重要影响[10],将直接影响路网的服务水平和交通运行效率,直接关系到路网路径诱导方案的合理性与可靠性。国内外学者关于路网节点评估展开了大量研究,劳潮惠等[11]将城市作为节点,提出基于运输需求理论选取人口数量、人均收入等指标进行灰色聚类的公路网节点层次划分方法。Chen等[12]、Kermarrec等[13]采用节点中心性指标对节点重要度进行评估。Geisberger等[14]提出了根据道路等级和节点使用率指标对路网节点进行重要度排序的方法。程光权等[15]提出了一种基于复杂网络中节点失效状态演化模型的节点重要度评估方法,该方法通过破坏网络拓扑结构来分析网络连通性变化情况,从而进一步量化节点的重要程度。以上节点评估方法在实际公路网中具有一定的适用性,但节点特征指标的选取和评估方法更侧重路网结构拓扑信息分析等单一静态指标,没有考虑路网节点转换、承载交通流等的节点承载力情况,且没有体现高密度路网的无标度特征和行为自组织特征[16]下节点评价指标阈值的不确定性。
基于此,综合考虑高密度路网的复杂交通背景,对路网节点的结构、交通运行状态进行综合度量,并采用TOPSIS法实现对节点承载力的量化;参照重力模型和交通分配的方法将节点间的承载力分配到路段上,并基于路段实际条件修正,得到路段承载力;综合节点承载力和路段承载力,最终提出面向驾驶员偏好的并满足驾驶员期望的,基于节点承载力的高密度路网诱导路径选择方法。
1 高密度路网节点承载力评估 1.1 高密度路网模型构建高密度路网的概念常被用于城市道路,本研究所研究的高密度路网是指路网两点之间存在多条行程时间或行驶路程相当的行车路径构成的网络[17],具有路网密度高、交通流大、城镇密集、交通风险传播迅速等特征。高密度路网中相邻节点距离近,由不同道路通过节点以一定的拓扑关系构成,具有明显的网络特性,因此本研究应用图论的方法建立路网模型,以便对路网进行分析。
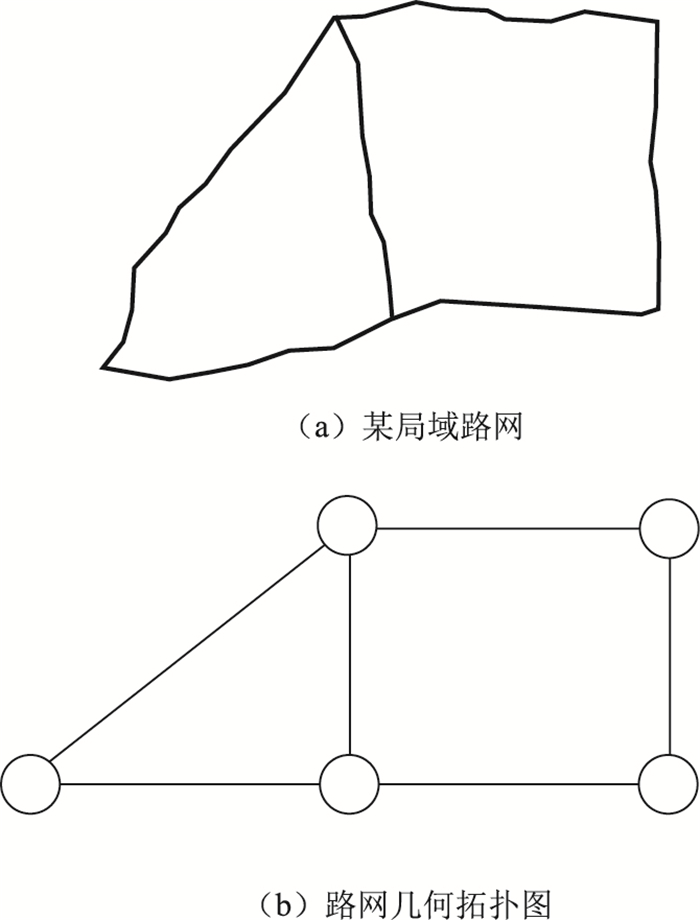
路网模型的构建首先需要对路网进行结构化选取,传统的基于语义等级的选取方法仅考虑道路等级、类型等信息[18],选取效果难以满足本研究要求。由于高密度路网由节点和路段通过一定的拓扑关系构成,具有明显的网络特性,因此本研究基于图论的方法构建路网的无向拓扑模型,对道路网进行结构化选取,即将道路上的间断点如交叉口、匝道出入口和互通式立交等视为节点,用圆圈表示;节点间的道路用线段表示。以某局域路网为例,路网几何拓扑图如图 1所示。
|
| 图 1 路网几何拓扑图示例 Fig. 1 An example of road network geometric topology |
| |
高密度路网的拓扑结构模型为式(1):
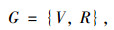
|
(1) |
式中,G为路网模型集合;V为路网中n个节点的集合,vi为路网中第i个节点(1≤i≤n);R为路段集合,rij为路网中直接连接节点vi和vj(i≠j)的路段;L为路径集合,lij为路网中直接连接节点vi和vj(i≠j)的路径。
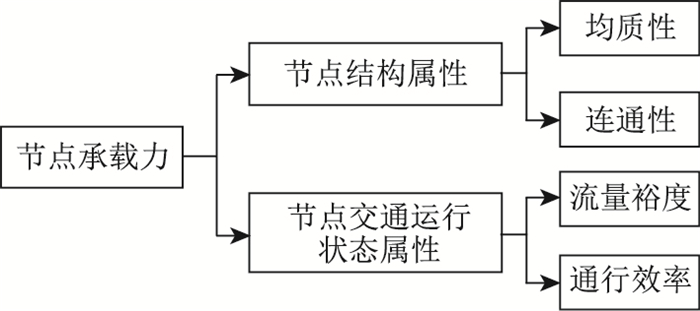
1.2 节点承载力度量高密度路网节点的评价指标应从多方面综合反映节点属性,因此构造节点承载力指标,分别从结构属性和交通运行状态属性两个方面对节点进行评价。其中,结构属性指基于拓扑理论的物理属性,主要表现为节点的均质性、连通性,分别表征节点在路网中的分布情况和节点相互作用关系;交通运行状态属性指路网运营状态下交通流在节点上的特征属性,主要表现为节点的流量裕度、通行效率,分别表征节点承载、转换交通流的能力。高密度路网节点承载力度量体系如图 2所示。
|
| 图 2 高密度路网节点承载力度量体系 Fig. 2 Node capacity measuring system for high-density road network |
| |
1.2.1 节点结构特征指标
(1) 均质性
高密度路网为无标度网络,路网的异质性对节点结构属性及路网内交通流行为均存在影响。节点vm的介数bm定义为路网中所有最短路径经过vm的路径数量,本研究选用节点介数对路网均质性进行表征,其反映了节点在路网中分布的均匀程度,节点分布越均匀,路网结构性能越好。节点均质性计算公式为:
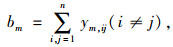
|
(2) |
式中,bm为节点vm的介数; n为路网节点总数,min(l)ij表示路网中起终点分别为vi和vj的最短路径,对于vm∈min(l)ij,ym, ij=1表示该最短路径经过节点vm,否则ym, ij=0。
(2) 连通性
高密度路网的优点在于其良好的节点间连接性和路径选择性,路网中节点的连通性对路网运行效率存在影响。本研究选用节点连通度om对节点连通性进行表征,即与节点vm直接相连的其他节点数目,om越大,表明vm与路网中其他节点的关联程度越紧密。节点连通性计算公式为:
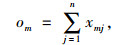
|
(3) |
式中,om为节点vm的连通度; n为路网节点总数,xmj表示节点vm和vj间连通性,xmj=1表示节点vm和vj存在路段直接连通,否则xmj=0。
1.2.2 节点交通状态特征指标(1) 流量裕度
节点流量裕度qm是单位时间T内节点vm的通行能力Cm与经过节点vm的实际交通量Qm的差值,反映了节点通行能力对实际运行交通量的适应程度,可有效表征路网的畅通性。节点流量裕度计算公式为:
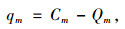
|
(4) |
式中qm,Cm,Qm单位均为pcu/h。
(2) 通行效率
节点通行效率em定义为单位时间T内通过节点vm的实际交通量Qm在单位时间T内行驶路程,即单位时间内节点承载、转换交通量与平均行程速度S的乘积,可综合表征节点的服务水平和服务交通量的高效性。节点通行效率计算公式为:
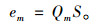
|
(5) |
路网节点承载力评价是多因素决策问题,传统的层次分析模型和模糊综合评价法的主观性很强,跟实际情况有一定偏差。TOPSIS法(Technique for Order Preference by Similarity to Ideal Solution,优劣解距离法)是一种常用的综合评价法,能通过多种指标数据共同评估样本优劣[19]。该方法对数据分布和样本含量没有严格限制,数据计算简单易行,广泛应用于交通研究领域[20-21]。因此本研究提出一种基于TOPSIS算法的综合评价方法,将模糊层次分析法的思想与n维欧氏距离结合,用“加权欧氏距离”对节点承载力进行评价。
1.3.1 指标集构建及标准化假设路网中存在n个节点,各节点层次均由d个指标共同评价,αmt是节点m的第t个属性指标的数值。由于量纲及量级的不同,各指标间不可度量。为尽可能反映实际情况,采用倒数法对指标数值进行趋势一致化处理后为:
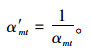
|
(6) |
采用比重法对指标数值进行无量纲化处理为:
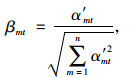
|
(7) |
式中,α′mt为趋势一致化后的指标数值;βmt为无量纲化后的指标数值。
1.3.2 指标权重确定采用1~9标度法构造判断矩阵,求解判断矩阵得出最大特征根λmax所对应的特征向量W,Saaty建议的重要性语言量化标度见表 1。
| 因素x与y相较 | 标度值 |
| x与y同等重要 | 1 |
| x比y稍微重要一些 | 3 |
| x比y重要一些 | 5 |
| x比y重要得多 | 7 |
| x比y极端重要 | 9 |
| x比y处于以上相邻判断区间内 | 2,4,6,8 |
一致性检验[22]通过后,向量各元素即为各指标权重值wt,按式(8)计算可得加权后的指标数值。
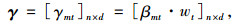
|
(8) |
式中γmt为加权后的指标数值。
1.3.3 节点承载力评价分别采用式(9)、式(10)计算节点样本距最优节点样本的距离EDm+、距最劣节点样本的距离EDm-,采用节点样本到最优样本点的接近度表征节点承载力Hm,计算公式如式(11)所示。
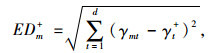
|
(9) |
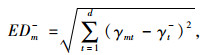
|
(10) |
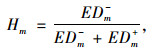
|
(11) |
式中,γt+为最优节点样本加权后的指标数值;γt-为最劣节点样本加权后的指标数值。
节点承载力高的节点往往与多个节点间存在直接通路,具备良好的连通性,且通行效率高,能承载、转换高密度交通流,属于路网中的关键节点;节点承载力低的节点有效运输能力和服务水平相对较低,位于路网相对边缘的位置,属于路网中的重要节点或一般节点。
2 基于节点层次的最优路径算法 2.1 基于节点承载力的路段承载力评价基于图论理论,路径是一系列节点由路段相连构成的集合[22],因此路段承载力同样影响诱导路径的选择。基于节点承载力和路段实际交通条件,构造路段承载力指标对路段进行评价,方法如下:
Step1:基于重力模型法,将路段起、终节点之间的承载力分布到路段上,构造承载力吸引量分布矩阵为:
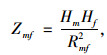
|
(12) |
式中,Zmf为节点vm,vf的承载力吸引量;Rmf为路段rmf的长度;Hm, Hf分别为节点vm,vf的节点承载力。
Step2:采用交通分配的方法将承载力吸引量分布矩阵在路网上进行分配,即可得到承载力在路段上的累积值——初始路段承载力P′mf。
Step3:选取路段设计速度、路段的单向车道数对路段承载力进行修正,修正后的值即为路段承载力Pmf为:
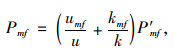
|
(13) |
式中,umf为路段rmf的设计速度;u为路网中所有路段的平均设计速度;kmf为路段rmf的单向车道数;k为路网中所有路段的平均单向车道数。
2.2 诱导路径的确定方法诱导路径的选择本质上是查找最优路径问题,本研究定义最优路径为承载力最优路径,即由承载力均优的节点和路段构成的,符合驾驶员驾驶期望的路径。基于节点承载力和路段承载力,可设计出高密度路网区诱导路径的确定方法,具体步骤如下:
Step1:构建路网拓扑化模型。
Step2:基于路网中节点的结构属性、交通运行状态属性计算节点承载力。
Step3:基于节点承载力计算路网中路段承载力,并从路段实际交通条件层面进行修正。
Step4:确定出行起终点,在路网中规划多条诱导路径,计算路径中包含的节点和路段的承载力并排序,最优路径可由式(14)求得:
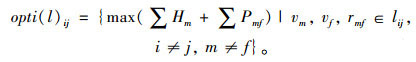
|
(14) |
为验证本研究所提算法的有效性,本研究构造一高密度路网,同时应用本研究算法与传统Dijkstra算法进行最优路径的搜索比较。Dijkstra算法是典型最短路径算法,采用广度优先搜索思想,以起始点为中心向外层层扩展,直到扩展到终点为止。
3.1 路网结构与交通运行状态信息本研究构建的高密度路网结构模型如图 3所示。
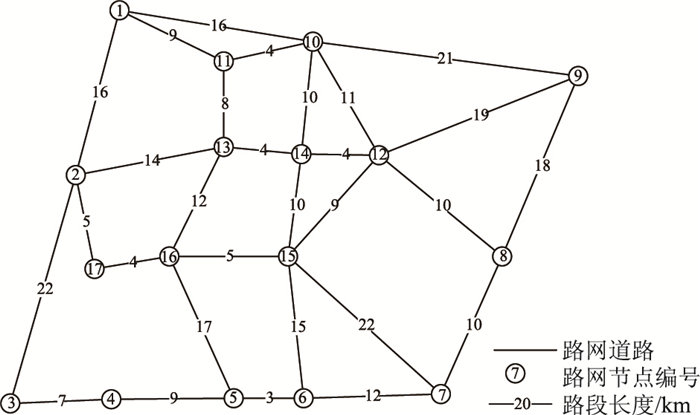
|
| 图 3 路网结构模型 Fig. 3 Road network structure model |
| |
各节点间OD分布如表 2所示。
| 节点 | v1 | v2 | v3 | v4 | v5 | v6 | v7 | v8 | v9 | v10 | v11 | v12 | v13 | v14 | v15 | v16 | v17 |
| v1 | 0 | 326 | 16 | 9 | 2 | 54 | 6 | 2 | 1 | 7 | 21 | 9 | 22 | 10 | 5 | 7 | 9 |
| v2 | 332 | 0 | 206 | 196 | 33 | 222 | 77 | 120 | 13 | 113 | 270 | 90 | 47 | 40 | 51 | 21 | 4 |
| v3 | 14 | 189 | 0 | 87 | 20 | 8 | 16 | 117 | 6 | 55 | 77 | 12 | 5 | 3 | 16 | 3 | 1 |
| v4 | 10 | 198 | 85 | 0 | 56 | 7 | 108 | 1 | 13 | 101 | 8 | 6 | 22 | 1 | 16 | 1 | 1 |
| v5 | 2 | 36 | 19 | 57 | 0 | 2 | 6 | 11 | 4 | 80 | 1 | 2 | 3 | 2 | 6 | 2 | 2 |
| v6 | 56 | 221 | 8 | 6 | 12 | 0 | 37 | 1 | 12 | 7 | 18 | 10 | 3 | 3 | 6 | 33 | 12 |
| v7 | 7 | 78 | 15 | 107 | 5 | 35 | 0 | 2 | 3 | 18 | 5 | 3 | 1 | 1 | 6 | 1 | 2 |
| v8 | 2 | 120 | 122 | 2 | 1 | 1 | 3 | 0 | 1 | 13 | 57 | 5 | 2 | 1 | 9 | 1 | 3 |
| v9 | 2 | 13 | 7 | 12 | 4 | 22 | 2 | 1 | 0 | 66 | 4 | 7 | 0 | 3 | 92 | 6 | 3 |
| v10 | 7 | 110 | 58 | 102 | 83 | 7 | 18 | 14 | 68 | 0 | 53 | 61 | 4 | 19 | 106 | 5 | 2 |
| v11 | 21 | 264 | 82 | 8 | 1 | 18 | 5 | 59 | 4 | 57 | 0 | 106 | 98 | 21 | 44 | 13 | 4 |
| v12 | 9 | 87 | 7 | 6 | 51 | 9 | 3 | 3 | 6 | 60 | 103 | 0 | 11 | 108 | 275 | 72 | 8 |
| v13 | 22 | 51 | 5 | 11 | 2 | 4 | 1 | 2 | 1 | 4 | 101 | 9 | 0 | 30 | 4 | 2 | 2 |
| v14 | 10 | 43 | 2 | 1 | 1 | 3 | 26 | 1 | 2 | 18 | 25 | 104 | 29 | 0 | 35 | 14 | 3 |
| v15 | 5 | 49 | 14 | 16 | 6 | 5 | 6 | 10 | 88 | 102 | 41 | 274 | 5 | 35 | 0 | 126 | 99 |
| v16 | 12 | 21 | 2 | 1 | 2 | 1 | 1 | 2 | 7 | 5 | 14 | 78 | 1 | 14 | 120 | 0 | 190 |
| v17 | 1 | 4 | 3 | 12 | 14 | 1 | 10 | 2 | 3 | 1 | 4 | 9 | 2 | 2 | 96 | 192 | 0 |
3.2 节点承载力计算结果
根据式(2)~(11)计算节点承载力如表 3所示。
| 节点 | 距最优节点样本的距离 | 距最劣节点样本的距离 | 节点承载力 | 节点承载力排序 |
| v1 | 5 641.99 | 2 784.06 | 0.33 | 7 |
| v2 | 4 195.892 | 3 064.459 | 0.422 | 2 |
| v3 | 5 339.814 | 2 516.33 | 0.32 | 14 |
| v4 | 5 544.487 | 2 693.971 | 0.327 | 11 |
| v5 | 5 575.671 | 2 722.639 | 0.328 | 10 |
| v6 | 5 066.76 | 2 315.881 | 0.314 | 17 |
| v7 | 5 747.423 | 2 884.47 | 0.334 | 6 |
| v8 | 5 930.338 | 3 064.604 | 0.341 | 3 |
| v9 | 5 766.684 | 2 903.097 | 0.335 | 5 |
| v10 | 5 103.349 | 2 339.47 | 0.314 | 16 |
| v11 | 5 511.691 | 2 664.34 | 0.326 | 12 |
| v12 | 5 470.04 | 2 627.323 | 0.324 | 13 |
| v13 | 5 864.926 | 2 999.369 | 0.338 | 4 |
| v14 | 5 628.984 | 2 771.9 | 0.33 | 8 |
| v15 | 2 930.566 | 5 931.851 | 0.669 | 1 |
| v16 | 4 492.373 | 2 206.343 | 0.329 | 9 |
| v17 | 5 123.313 | 2 353.221 | 0.315 | 15 |
3.3 最优路径计算结果分析
以节点v1至节点v6为例,根据式(12)~(14)得出的最优路径途经节点为v1,v10,v14,v15,v6;采用传统Dijkstra算法得出的最优路径途经节点为v1,v2,v17,v16,v15,v6。Dijkstra算法规划的路径途经低级节点v17,驾驶员需频繁切换道路,平均行车速度低,不符合驾驶员行车期望。由基于节点承载力的最优路径算法得出的路径虽比Dijkstra算法稍长,但是由高等级节点和道路组成的路径,这样的规划结果更符合实际交通诱导系统需求,更能体现驾驶人员选路偏好。
4 结论随着道路工程建设的发展,我国部分地区已形成高密度路网结构。为了使路网运管水平能跟上路网建设程度,本研究提出节点承载力指标,综合考虑高密度路网节点的结构属性和交通运行状态属性,采用节点均质性、连通性、流量裕度、通行效率综合表征高密度路网节点属性,并采TOPSIS法量化节点承载力。路段承载力同样影响诱导路径的选择,本研究基于重力模型法和交通分配计算路段承载力,并给出诱导路径的确定方法。
本研究提出的方法可对高密度路网节点进行评估,运管人员可基于节点承载力制订路网运管方案,充分发挥高密度路网连接性与选择性好的优势,最大限度地提高路网的通行能力,具有很重要的现实意义。本研究向高速公路运营管理者提出了新的管理理念,可以指导现代交通诱导系统的建设并保障现代路网的安全有序运行,具有重要的实用价值。
| [1] |
黄勤威. 复杂路网条件下高速公路互通区指路标志内容设计研究[D]. 福州: 福州大学, 2017. HUANG Qin-wei. Guide Design for Expressway Interchange under Condition of Complex Road Network[D]. Fuzhou: Fuzhou University, 2017. |
| [2] |
胡晓健, 王炜, 陆建, 等. 控制排队长度的高密度路网信号优化模型[J]. 控制理论与应用, 2010, 27(12): 1693-1698. HU Xiao-jian, WANG Wei, LU Jian, et al. Traffic Signal Control Model Based on Queue Management in High-density Network[J]. Control Theory & Applications, 2010, 27(12): 1693-1698. |
| [3] |
KUMAR P, SINGH V, REDDY D. Advanced Traveler Information System for Hyderabad City[J]. IEEE Transactions on Intelligent Transportation Systems, 2005, 6(1): 26-37. |
| [4] |
李志林, 邱红桐, 封春房, 等. 基于路网分层的协同诱导路径搜索算法[J]. 公路交通科技, 2017, 34(1): 143-148. LI Zhi-lin, QIU Hong-tong, FENG Chun-fang, et al. A Cooperative Guidance Path Searching Algorithm Based on Hierarchical Road Network[J]. Journal of Highway and Transportation Research and Development, 2017, 34(1): 143-148. |
| [5] |
张春勤. 道路交通动态信息发布策略研究[D]. 长春: 吉林大学, 2011. ZHANG Chun-qin. Research on Traffic Dynamic Information Dissemination Strategies[D]. Changchun: Jilin University, 2011. |
| [6] |
DIJKSTRA E W. A Note on Two Problems in Connection with Graphs[J]. Numerische Mathematics, 1959, 1(1): 269-271. |
| [7] |
苏海滨, 王继东. 交通网络中多路径优化选择算法的研究[J]. 公路交通科技, 2007, 24(9): 109-111. SU Hai-bin, WANG Ji-dong. Study on Multi-path Optimization Routing Algorithm in Traffic Network[J]. Journal of Highway and Transportation Research and Development, 2007, 24(9): 109-111. |
| [8] |
邹文杰, 翁剑成, 荣建, 等. 基于空间相关性分析的路网评价区域划分方法[J]. 北京工业大学学报, 2012, 38(4): 90-95. ZOU Wen-jie, WENG Jian-cheng, RONG Jian, et al. Spatial Autocorrelation Theory-based Road Network Regional Division[J]. Journal of Beijing Polytechnic University, 2012, 38(4): 90-95. |
| [9] |
苏海滨, 王继东, 侯朝桢. 道路网络分层的快速路径诱导算法[J]. 火力与指挥控制, 2008(7): 108-111. SU Hai-bin, WANG Ji-dong, HOU Zhao-zhen. A Fast Route Guidance Algorithm Based on the Layered Road Network[J]. Fire Control & Command Control, 2008(7): 108-111. |
| [10] |
范文礼. 基于复杂网络理论的连锁故障建模与预防研究[D]. 成都: 西南交通大学, 2014. FAN Wen-li. Modeling and Prevention of Cascading Failures Based on Complex Network Theory[D]. Chengdu: Southeast Jiaotong University, 2014. |
| [11] |
劳潮惠, 吴群琪, 王芳. 公路网节点层次划分方法[J]. 交通运输工程学报, 2013, 13(2): 80-85. LAO Chao-hui, WU Qun-qi, WANG Fang. Division Method of Node Level for Highway Network[J]. Journal of Traffic and Transportation Engineering, 2013, 13(2): 80-85. |
| [12] |
CHEN D, LÜ L, SHANG M S, et al. Identifying Influential Nodes in Complex Networks[J]. Physica A: Statistical Mechanics and Its Applications, 2012, 391: 1777-1787. |
| [13] |
KERMARREC A M, MERRER E L, SERICOLA B, et al. Second Order Centrality: Distributed Assessment of Nodes Importance in Complex Networks[J]. Computer Communications, 2011, 34(5): 619-628. |
| [14] |
GEISBERGER R, SANDERS P, SCHULTES D, et al. Contraction Hierarchies: Faster and Simpler Hierarchical Routing in Road Networks[C]//International Workshop on Experimental and Efficient Algorithms. Berlin: Springer, 2008: 319-333.
|
| [15] |
程光权, 陆永中, 张明星, 等. 复杂网络节点重要度评估及网络脆弱性分析[J]. 国防科技大学学报, 2017, 39(1): 120-127. CHENG Guang-quan, LU Yong-zhong, ZHANG Ming-xing, et al. Node Importance Evaluation and Network Vulnerability Analysis on Complex Network[J]. Journal of National University of Defense Technology, 2017, 39(1): 120-127. |
| [16] |
王建伟, 付鑫, 马暕. 复杂路网条件下高速公路收费费率计算方法[J]. 中国公路学报, 2010, 23(1): 105-110. WANG Jian-wei, FU Xin, MA Jian. Calculated Method of Expressway Toll Rate under Condition of Complex Road Network[J]. China Journal of Highway and Transport, 2010, 23(1): 105-110. |
| [17] |
王晓飞. 灾变条件下通道路网运营安全管理及应急处置研究[D]. 上海: 同济大学, 2008. WANG Xiao-fei. Research on Operation Safety Management and Emergency Disposal against Disastrous Conditions of Freeway Corridor[D]. Shanghai: Tongji University, 2008. |
| [18] |
JIANG B, CLARAMUNT C. Topological Analysis of Urban Street Networks[J]. Environment and Planning B: Planning and Design, 2004, 31(1): 151-162. |
| [19] |
ZELENY M, COCHRANE J L. Multiple Criteria Decision Making[M]. New York: McGraw-Hill, 1982.
|
| [20] |
LI Y, ZHAO L, SUO J. Comprehensive Assessment on Sustainable Development of Highway Transportation Capacity Based on Entropy Weight and TOPSIS[J]. Sustainability, 2014, 6(7): 4685-4693. |
| [21] |
WANG Y, CHEN K M. Comprehensive Evaluation for Urban Rail Transit Network Based on TOPSIS Model[J]. Applied Mechanics & Materials, 2014, 587/588/589: 1862-1866. |
| [22] |
彭祖增, 孙韫玉. 模糊(Fuzzy)数学及其应用[M]. 武汉: 武汉大学出版社, 2002. PENG Zu-zeng, SUN Yun-yu. Fuzzy Mathematics and Its Applications[M]. Wuhan: Wuhan University Press, 2002. |
 2021, Vol. 38
2021, Vol. 38
