扩展功能
文章信息
- 邝先验, 吴玉刚, 刘平, 张建华, 陈奕希
- KUANG Xian-yan, WU Yu-gang, LIU Ping, ZHANG Jian-hua, CHEN Yi-xi
- 考虑速度空间横向伸缩效应的混合交通流模型
- A Mixed Traffic Flow Model Considering Stretching Effect of Transverse Space Caused by Vehicle Speed
- 公路交通科技, 2021, 38(7): 114-123
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(7): 114-123
- 10.3969/j.issn.1002-0268.2021.07.015
-
文章历史
- 收稿日期: 2020-10-09
在城市道路特别是老城区的次干道、支路等路段,由于空间受限,道路宽度较窄,机动车道与非机动车道通常不设置硬隔离带。非机动车灵活,车道意识较弱,在这类路段占用机动车道行驶的现象较为普遍[1-3],非机动车又存在并行现象,造成各类车辆之间的干扰十分明显,车辆延误也因此加剧。
建立细致的模型并分析其交通特性具有重要现实意义, 如一方面,可以对机非混合路段交通流的影响因素有更深刻的认识,有助于抓重点并对实际交通流实施改进方法;另一方面,在智能交通的大背景下,可以为未来利用5G物联网、大数据等技术,识别并分类车辆冲突行为,提供一定理论基础。
交通流的建模方法中,元胞自动机(CA)通过引入描述交通特性的规则,利用计算机进行数值模拟再现交通流中各种物理现象,在交通流仿真建模领域受到学者们的极大青睐[4]。在机动车流研究方面,最经典的模型是NS模型[5],其后衍生出一系列改进模型如CD[6]模型、STCA[7]模型等;在非机动车流研究方面,贾斌等[4]认为非机动车速度小、车道概念弱的特性更适合采用多值模型(MCA)进行仿真,其中最具代表性的是EBCA[8-9]模型。
目前基于CA的机非混合交通流模型,大多采用NS的改进模型。文献[10]分析了车辆数和换道行为对交通流的影响;文献[11-12]验证了非机动车最大速度多样性,并考虑了机动车鸣笛效应区域的影响;文献[13]设计了基于路宽的压缩概率公式。
由于机动车更适合采用NS模型,非机动车更适合采用MCA模型,近年来,NS-MCA的耦合模型受到研究者的关注。文献[14]设计了公交车站台处车辆混行的耦合规则;文献[15]考虑了交叉口处右转机动车对自行车的冲突;文献[16]细化了交叉口处机非干扰下车辆的行为。这些耦合模型仅模拟了路段中特定交通场景下的机非混行现象,但目前对整个路段采用耦合模型仿真的较少。
基于上述已有的研究成果,对于机非混行路段的交通流,以往的模型大多只关注车辆的纵向位置关系,在横向位置上侧重关注换道规则[6-7]和机非之间的干扰[11-12],但没有综合考虑非机动车之间的横向干扰,以及干扰造成的道路横向空间的变化,这就会导致仿真得出的交通流与实际交通有所差异,因而如何较精确地描述不同车辆间存在的横向干扰需要更深入地研究。
实际交通中,车辆在不同速度下,所需要的横向通行空间会不同,导致道路横向空间的容量(非机动车数量)发生可逆的变化,本研究称其为车辆速度-空间横向伸缩效应(SST: Speed-Strictive Effect of Transverse Space)。SST具体是指车辆速度越快,需要占据的横向通行空间就会更大,导致横向空间的容量被压缩,反之横向空间容量得到扩张。一方面,对于高速非机动车,骑行者为追求驾驶环境的安全、舒适,所需要的道路横向通行空间更大,道路剩余横向空间减小,对空间容量造成横向压缩效应。此时,若通行的车道宽度不足,车辆将会减速以减小对道路宽度的占用,减速实际上是增大了安全通行的宽度。另一方面,机动车速度较慢时对非机动车的横向干扰较小,非机动车道横向空间“外溢”到机动车道的一部分,横向剩余空间容量增加,非机动车可行驶在机非分割线处的中间地带,造成了横向扩张效应,反之快速的机动车将完全占据机动车道的横向空间,使得非机动车道横向空间难以扩张。
此外,传统的MCA模型是对整个非机动车路段进行元胞划分,不考虑元胞内车辆的换道行为,而在机非混行路段中,非机动车存在频繁的越线换道行为,如主动换道、受机动车压力时的换道等,因此需要针对这些情况在MCA模型中引入合适的换道规则。机动车出于安全考虑,在受到横向非机动车的干扰较大时,为了防止非机动车的突然换道,其自身加速度也会受限,因此如何界定车辆之间的横向干扰是MCA模型需要解决的问题。
综合上述分析,本研究主要通过对机非混行路段车辆的特征进行分析,建立SST-CA耦合模型。其中机动车考虑一般车型的交通流,非机动车考虑快、慢车混合的两轮车流,引入可伸缩的元胞空间容量规则、舒适驾驶空间、换道方式等影响规则,以真实反映该机非混行路段的交通流特征,分析机非干扰特性、空间横向伸缩效应、混合交通的偏析[17]现象等。
1 模型 1.1 机非混行路段模型文章研究的机非混行路段,如图 1(a)所示,其中Lane0为非机动车道,Lane1为机动车道,车道宽均为3.5 m,两车道的划分标志为机非分割线,非机动车可以越线行驶至机动车道,机动车只能在机动车道行驶,机动车和非机动车存在相互干扰。图 1(b)、(c)是实际交通流中典型的横向伸缩效应,由图 1(b)所示的横向压缩效应为非机动车道设计可容纳3辆车并行驾驶时,骑行者更倾向于少于3辆并行驾驶,当大于等于2辆并行驾驶时,易发生越线换道;图 1(c)展现的横向扩张效应为非机动车道设计仅可容纳1辆车并行驾驶,此时并行的骑行者占据机动车道靠近非机动车道的空间行驶,机动车若要超车,需向相反方向偏移,给骑行者让出一定空间,以避免发生碰撞。
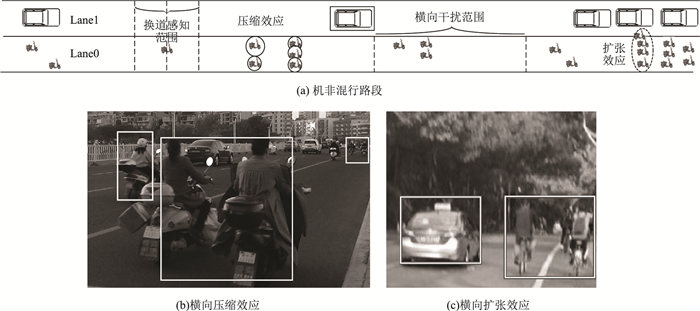
|
| 图 1 机非混行路段示意图 Fig. 1 Schimetic diagram of mixed traffic section |
| |
1.2 非机动车流模型(SST-EBCA)
非机动车在传统的EBCA模型中只有前进规则,不考虑多车道的换道行为,本研究考虑速度为3 cells/s和2 cells/s的快、慢两轮车,以非机动车追求安全、舒适、高速驾驶为越线换道动机,设计换道规则。此外,无论是换道还是前进过程,相应的元胞空间容量都会根据实际情况伸缩变化。
1.2.1 非机动车越线(违法)换道规则从换道动机和换道空间角度设计换道规则,并考虑非机动车主动换道时在保持车辆速度下,对横向空间造成的压力相对较大,横向压缩效应明显。将非机动车的换道分为受迫型换道、舒适型换道、自由型换道。换道需要前提条件:目标位置的元胞空间存在剩余容量。

|
(1) |
式中,Cet为元胞空间实时容量;Cej+u(ok)为另一条车道(ok)第j+u格元胞容量。
(1) 受迫型换道:仅有非机动车从Lane1换至Lane0,此时受到机动车的干扰。
换道条件:若dfm≤deffectf或dbm≤deffectb, 则当Rand(X) < ppre时换道。dfm, dbm为非机动车与前、后方机动车之间的距离。deffectf, deffectb为骑行者前后的感知距离,实际中该参数对于不同骑行者在不同交通条件会发生变化,本研究取为固定值。Rand(X)为服从0~1均匀分布的随机变量。
(2) 舒适型换道:借鉴机动车的换道动机[7],本研究结合骑行者换道灵活,以及对周围感知[18]也更加敏感,注重安全、舒适驾驶的特性,会综合判断本、邻车道前后方空间是否满足舒适驾驶条件才会选择换道,且不像机动车追求完全占据道路横向空间(如图 1所示的换道感知范围)。
本研究定义舒适驾驶条件:
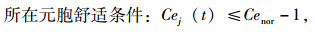
|
(2) |
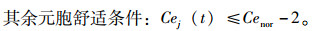
|
(3) |
故定义舒适驾驶空间:所在元胞与目标位置之间的元胞都满足舒适驾驶条件时,该元胞空间为舒适驾驶空间。Cenor为元胞空间常态容量, 前方的舒适驾驶距离dfc如式(4)所示,同理也可推导出后方、邻道前方、邻道后方的舒适驾驶距离dbc, dlrfc, dlrbc。
若Cej(t)≤Cenor-1,则当Ce++j≤Cenor-2时,
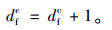
|
(4) |
换道条件:若dfc≤deffectf或dbc≤deffectb,且满足dlrfc>deffectf, dlrbc>deffectb时,则当Rand(X) < pcf时进行换道。pcf为舒适换道概率。
(3) 自由型换道:当Lane0和Lane1都满足舒适驾驶条件时,骑行者由不同城市,不同道路,不同交通流特征条件下的违法意愿,随机选择换道。
换道条件:若本车道dfc>deffectf且dbc>deffectb,邻车道dlrfc>deffectf, dlrbc>deffectb,则当Rand(X) < pfre时进行换道。pfre为自由换道概率。
此外,当发生受迫型换道时,Lane0车辆会感受到Lane1车辆的换道意愿,从而压缩道路剩余空间,目标元胞空间容量扩张。而舒适型换道和自由型换道建立在另一条车道驾驶条件更加安全、舒适上,因此目标元胞空间容量压缩。上述换道方式相互独立,判断优先级为:(1)>(3)>(2)。
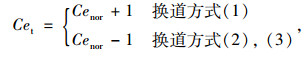
|
(5) |
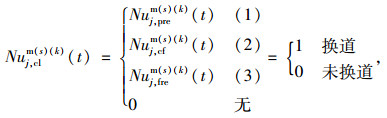
|
(6) |
式中Nuj, clm(s)(k)为换道前进s格的非机动车数。
1.2.2 非机动车运行规则在考虑前进规则时,同样考虑车辆速度导致的横向伸缩效应,本研究假设速度为3 cells/s的非机动车会实际在道路中占据较大的横向空间,设为2 cells,而小于该速度的非机动车占据的横向空间设为1 cells。当元胞中存在车辆没有换道或前进时,若此时机动车对非机动车的干扰很小,非机动车道横向空间容量也会扩张,非机动车为了追求更快的速度,在扩张概率prev下前进。
判断式为:非机动车邻道感知范围(deffectb, deffectf)内, Vlim为机动车慢速阈值,若满足:
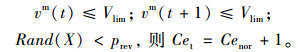
|
(7) |
Step 1:计算换道后前进3格元胞的车辆数:
按s=3, i=1, 2, 3, k=0, 1,Cej+i(ok)(t)=Cej+i(ok)(t)+A×Nuj, clm(s)(k)(t)为车辆所在车道,更新式(5)、(6)、(8)、(9)。
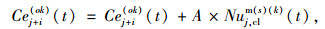
|
(8) |
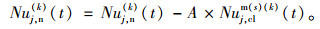
|
(9) |
当s=3时,常数A=2,否则A=1。Cej+i(ok)(t)为经过元胞的容量;Nuj, clm(s)(k)为换道前进s格元胞的非机动车数;Nuj, n(k)为更新后剩余的非机动车数。
Step 2:计算前进3格元胞的车辆数
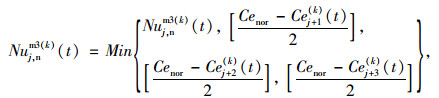
|
(10) |
式中[]为向下取整符号。
按s=3, i=1, 2, 3, k=0, 1,更新式(8)、(9)。在前进步中,式(8)中ok=k。
当满足式(7),且Nuj, clm3(0)(t)=0时,若Min{[Cet-Cej+1(0)(t)], [Cet-Cej+2(0)(t)], [Cet-Cej+2(0)(t)]}≥2,则更新Nuj, nm3(0)(t)以及式(8)、(9)。
Step 3:计算换道后前进2格元胞的车辆数
按s=2, i=1, 2, k=0, 1更新式(5)、(6)、(8)、(9)。
Step 4:计算前进2格元胞的车辆数
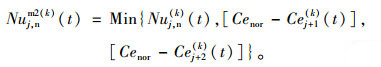
|
(11) |
按s=2, i=1, 2, k=0, 1, 更新式(8)、(9)。
当满足式(7),且Nuj, clm2(0)(t)=0时,若
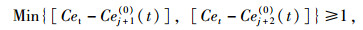
|
更新Nuj, nm2(0)(t)以及式(8)、(9)。
Step 5计算换道后前进1格元胞的车辆数
按s=1, i=1, k=0, 1更新式(5)、(6)、(8)、(9)。
Step 6计算前进1格元胞的车辆数
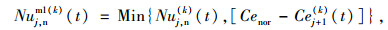
|
(12) |
按s=1, i=1, k=0, 1更新式(8)、(9)。
当满足式(7),且Nuj, clm1(0)(t)=0时, 若[Cet-Cej+1(0)(t)]≥1,更新Nuj, nm1(0)(t)以及式(8)、(9)。
Step 7元胞更新
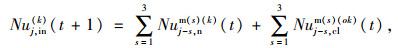
|
(13) |
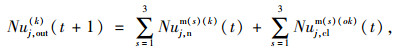
|
(14) |
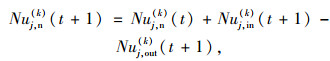
|
(15) |
式中, Nuj, in(k), Nuj, out(k)为驶入、驶出的非机动车数。
1.3 机动车流模型(SST-NS)SST-NS模型的改进之处主要是针对机动车受到非机动车的纵向、横向干扰的加减速规则,其中横向干扰的考虑驾驶员对邻道前侧一定范围内空间容量的判定。另外考虑到机动车为了使NS-MCA能较好耦合,针对机动车也引入元胞空间容量的确定条件,机动车速度相对较大,因而具有很强的横向压缩效应,在超过慢速阈值后就会完全占据机动车道横向空间。
Step 1:加速受限规则
机动车受邻道非机动车的干扰较大时,出于安全考虑相应的最大加速度会减小。对于邻道前方的vmaxm格元胞的非机动车,如果超过一定比例R的非机动车占据空间大于或等于Cenor格元胞,机动车可能受到影响,无法正常加速行驶。
当Cej+i(k)(k)≥Cenor, i=0, 1, …vmaxm时, nd=nd+1, 若nd>=R(vmaxm+1)且Rand(X) < pd,
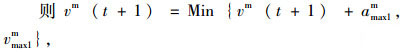
|
(16) |
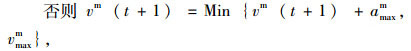
|
(17) |
式中,nd为对一定范围内元胞空间容量大于或等于Cenor的元胞的计数;pd为机动车受非机动车影响概率;amax1m, vmax1m为机动车受到横向干扰时的最大加速度与车速。
Step 2主动减速规则
机动车受到前方机动车或非机动车的干扰会主动减速,以避免与前车发生碰撞,相较于前方为机动车,前方为非机动车时应具有更大的减速度,用距离表示就是机动车对非机动车保持的安全距离, 该距离表示为Δgapn。
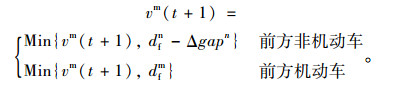
|
(18) |
Step 3随机慢化规则
机动车在行驶过程中会概率pslowm, 发生随机减速现象:若Rand(X) < pslowm,则:
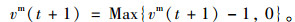
|
(19) |
Step 4车辆运动更新
机动车在道路横向空间具有明显速度横向压缩效应,超过慢速阈值Vlim后,非机动车道无法扩张。
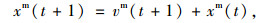
|
(20) |
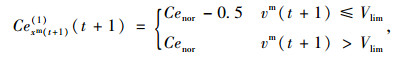
|
(21) |
式中,xm(t)为t时刻机动车m的位置;Cexm(t+1)(1)(t+1)为t+1时刻机动车m实际占据空间。
2 数值模拟与结果分析 2.1 仿真设置仿真建立在周期性边界条件下,分别设定一条机动车道和非机动车道,每个元胞长2 m,宽3.5 m,道路总长L=500 cells, 常态元胞空间容量Cenor=3, vmax1m=6, vmaxm=9, amax1m=2, amaxm=3, Vlim=2, Δgapn=2, deffect=5。非机动车快慢车比例为7∶3, R=0.5, 相关概率: pd=pcf=0.6, pfree=pslown=pslowm=0.2, prev=0.3, ppre=1。机动车道初始只有机动车且为致密分布,非机动车道初始只有非机动车且为随机分布,仿真总时间步为25 500,每个时间步为1 s。为排除初始化设置带来的暂态效应影响,数据取仿真得到的最后500个时间步的平均值。计算机动车平均的密度ρm、速度vm、流量qm∶ρm=Num,
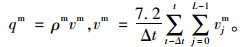
|
(22) |
非机动车平均的密度ρn(k)、速度vn(k)、流量qn(k):
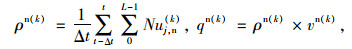
|
(23) |
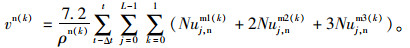
|
(24) |
首先通过非机动车密度对机动车流的影响进行交通流基本图的分析(km, kn为机动车、非机动车归一化后密度),由图 2(a)可知随着kn的提升,qm呈现下降趋势,自由流向拥堵流相位转变的临界密度逐渐滞后,这主要是由于ρm较低时受非机动车干扰明显,无法满足机动车需求的驾驶空间。此时Lane1剩余道路空间较多,非机动车在有限的感知范围内可能发生换道,但由于两类车速度差距较大,机动车快速迫近非机动车时必会减速,因而对机动车流的影响特别明显。而在ρm上升后,非机动车感知范围内出现机动车的可能性也更大,难以完成换道,故此时机动车受非机动车影响很小。另外在图 2(b)中,kn大于0后,vm受非机动车影响很大,难以保持在高速状态,但在ρm上升到一定值后,非机动车很难满足换道条件,机动车重新占据道路主权,反而使vm有小幅度的反弹,该幅度在kn越小时相对明显。
|
| 图 2 不同kn下机动车流基本曲线 Fig. 2 Basic curves of motor vehicle flow under different kn |
| |
2.3 机动车流的影响
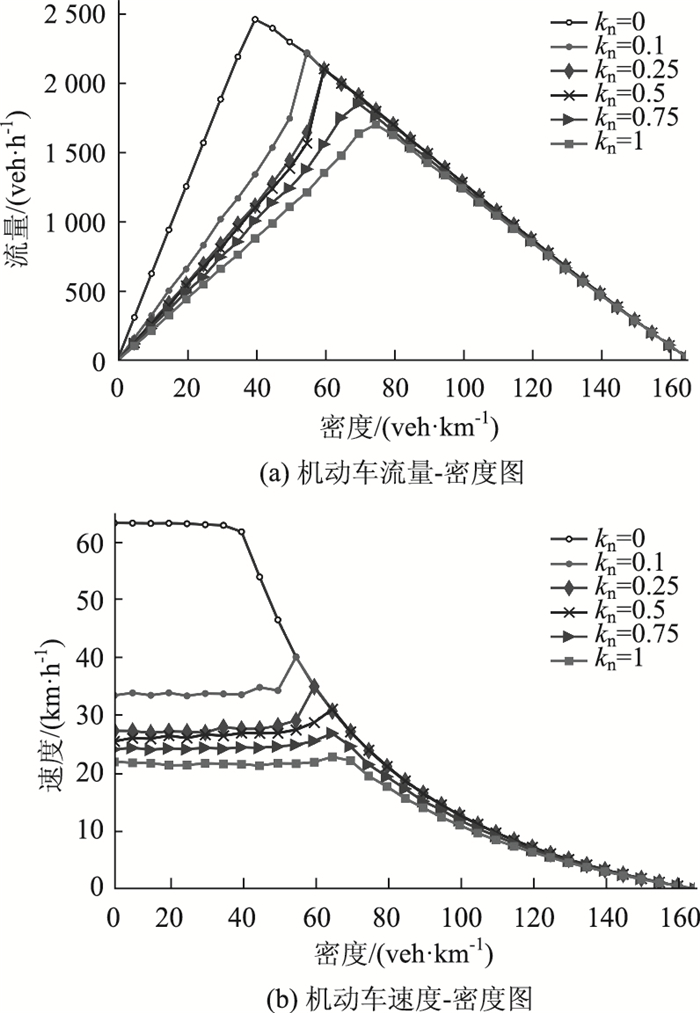
如图 3(a)所示,在ρn(0)相对较低时,Lane0车辆几乎不受km影响,原因是Lane0条件很舒适,骑行者偏向于行驶在Lane0。而当ρn(0)上升到φ1后,流量达到峰值,饱和流相位对应密度范围扩大, φ2密度之后才发生相位的转变,这是由于ρn(0)在(φ1, φ2)内,Lane0的条件虽然不能满足舒适驾驶,但骑行者换至Lane1,缓解了Lane0压力,非机动车流因而能稳定在峰值状态, 可这种换道作用有限,在φ2密度后,Lane0压力继续上升后,qn(0)开始下降,此时不同的km对非机动车影响表现出差异性。km在(0, 0.5)区间内,随着km的上升非机动车选择在Lane0行驶的也越来越多,使得qn(0)呈现下降趋势,而km在(0.75, 1)区间,此时vm较慢,横向压缩效应较弱,Lane0横向空间得以扩张,反而使qn(0)得以上升。由图 3(b)可知,km在0.2时对vn(0)影响较大,vn(0)随着其密度的升高而降低,km在0.2~0.6时影响幅度降低,但其在0.6~1时,vn(0)又会有小幅度的升高,此时道路主权分配回归正常,车辆各行其道,但由于机动车对非机动车干扰很小,两车道间隙被骑行者利用,非机动车速度得以小幅回升。
|
| 图 3 不同km下Lane0处非机动车流基本图 Fig. 3 Basic curves of non-motor vehicle flow at Lane0 under different km |
| |
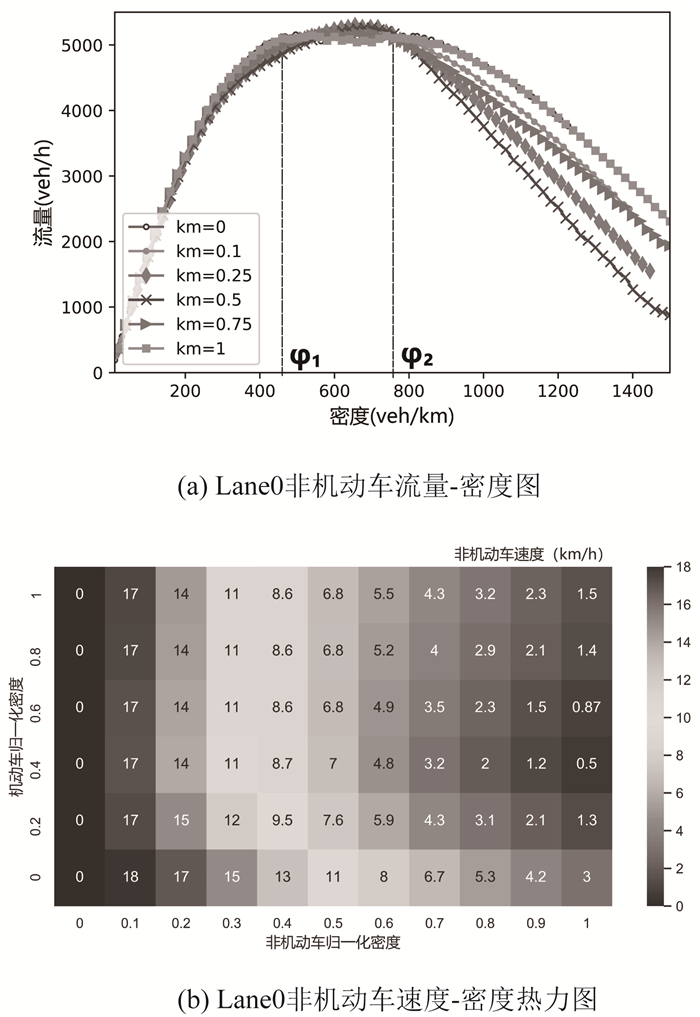
2.4 横向空间的变化
图 4中Occupy表示Lane0横向空间容量(非机动车数量),从图 4可以看出本研究建立的SST模型,相较于传统EBCA模型,更符合实际交通场景。
|
| 图 4 不同km下非机动车密度对Lane0处Occupy的影响 Fig. 4 Influence of non-motor vehicle density on Occupy at Lane0 under different km |
| |
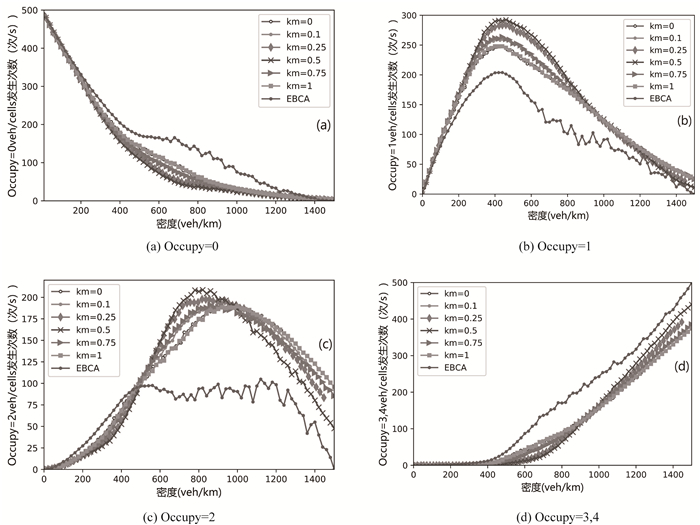
图 4(a)展现了Lane0横向空间无车辆出现发生的次数,可以看出SST模型充分利用了道路的横向空间无车辆的元胞,特别是在中等密度下与EBCA模型对比。图 4(b)表现了横向空间非机动车数量为1的总数,SST模型在不同密度下几乎都高于EBCA模型。图 4(c)中EBCA模型只在ρn(0)较低时,其数量略高于SST模型,而在密度提升后,横向空间非机动车数量为2的总数明显高于EBCA模型,这是由于SST模型中非机动车会乐于追求道路中横向空间中存在小于等于2辆的舒适空间。图 4(d)可以看出,在ρn(0)提升后,道路空间有限,更多的非机动车不得不并行驾驶,在这种道路拥堵条件下,EBCA模型的非机动车没有更多的选择,因而横向空间非机动车数量为3的数量在不同km下均高于SST模型横向空间非机动车数量3和4的总和。
横向扩张效应在道路中平均每秒发生的次数可表示为SST模型中元胞容量为4的平均次数,结合图 5(a),可以分析得出Lane0横向扩张现象只在ρn(0)于中、高密度时发生,且随着ρn(0)的提升呈现上升趋势,km主要影响其上升幅度,km处于相对中等密度时对非机动车影响较为明显。横向压缩效应在SST模型中表示为车辆占据元胞容量与元胞中实际车辆数的差值,从图 5(b)可知,Lane0横向压缩现象发生的次数随着非机动车的密度先上升后下降,这与交通流中自由流向拥堵流相位转变很类似,伴随着非机动车运行的整个过程。
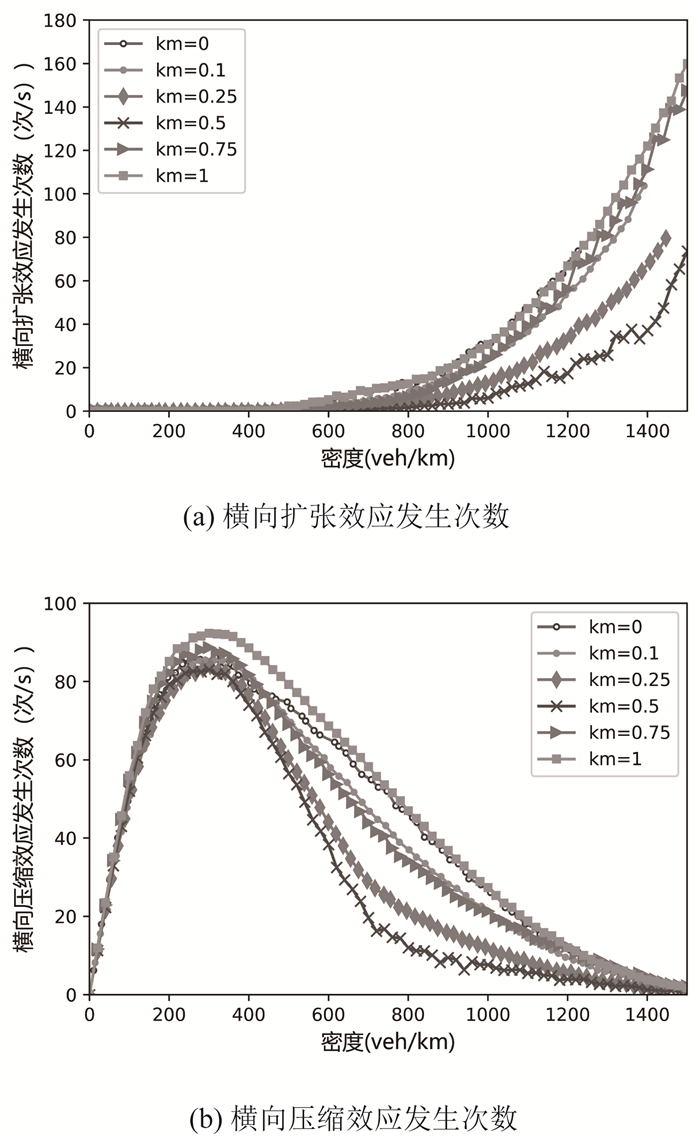
|
| 图 5 不同km下非机动车密度对Lane0横向伸缩效应发生次数的影响 Fig. 5 Influence of non-motor vehicle density on occurrence of transverse stretching at Lane0 under different km |
| |
2.5 时空图分析
图 6是SST模型中机动车流最后500 s的时空分布图,纵轴自上而下时间步逐渐扩大,横轴自左向右代表机动车道1~500个元胞,图 6(a)~(f)分别是机动车,非机动车在各特定密度下的时空分布图。

|
| 图 6 特定km, kn下,Lane1机动车流时空分布图 Fig. 6 Space-time distributions of motor vehicle flow at Lane1 under specific km and kn 注:浅灰色代表非机动车,深黑色代表慢速行驶的机动车,且对应横向Lane0没有扩张,深灰色代表快速行驶的机动车或者慢速行驶的机动车且对应横向Lane0存在扩张。 |
| |
由图 6(a)分析可知两种车辆密度都较低时,存在非机动车换道至Lane1,并在Lane1呈现带状分布,形成了“塞子”,阻碍了后方快速的机动车,不同于双车道机动车之间,引起偏析现象的原因是快车换道的超车行为,机非混合交通流是由速度慢的非机动车主导的,其先占道再让道才使得快速的机动车完成超车,而快速的机动车也会在非机动车换道前保持与其安全距离。
从图 6(b)可知,在ppre很低时,尽管两车都处于较低密度,但阻塞的扩大还是很明显。另外结合图 7(舍去初始较大值点),ppre对机动车的高速度状态下有明显的影响,并随着km的增大而影响扩大,vm随着ppre的降低而降低,这种影响在ppre较高(0.8, 1)时不太明显。而当两类车都处于高密度时,ppre几乎不对vm造成影响。
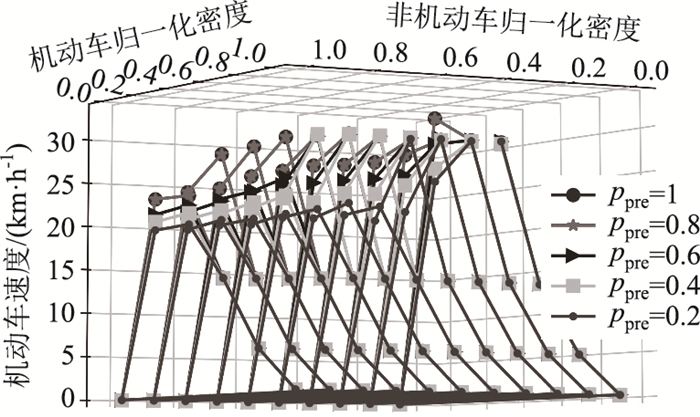
|
| 图 7 不同车辆密度下ppre对机动车速度的影响 Fig. 7 Influence of ppre on vehicle speed under different vehicle densities |
| |
偏析现象在km提升到中、高后基本消散(图 6(c)、(d)),这是由于在本研究设定的规则下,非机动车是以安全、舒适为前提才会选择换道,机动车在Lane1具有优先权,因而基本能够维持在正常的流量下。当km很低时,kn的上升(图 6(e))会使得越线换道的非机动车变多,图示的非机动车条带也会变宽,强化了偏析效应,空白部分的增多,主要是机动车为与非机动车保持安全距离导致的,在该种情形下道路空间难以得到有效利用。此外,当非机动车和机动车都在高密度时(图 6(f)),由于vm很慢对非机动车的横向干扰较小,非机动车又较灵活,因此Lane0横向扩张现象较为明显。
3 结论机非混合交通流是我国城市道路,特别是支路,次干道存在的一种普遍交通形式,建立模型并对其进行分析具有重要现实意义。本研究以机非混行路段(无隔离带)、非机动车与机动车为对象建立的SST模型,充分考虑了骑行者违法换道带来的交通冲突和舒适驾驶空间以及道路横向空间的变化。数值模拟的结果表明,道路横向空间实际容量是引起机非混合交通流变化的关键因素,其又受到车辆类型、速度、舒适驾驶心理等的影响。而这些参数本质上都可以通过一系列变化用速度来体现的,这也一定程度上简化了模型。通过与EBCA模型的对比,SST模型更能反映道路空间横向伸缩效应与骑行者舒适驾驶心理。此外,机非混合交通流中偏析效应主导方为非机动车,非机动车换道意愿的降低和其密度上升都会强化该效应。本研究建立的SST模型可以为机非混合交通流的建模方式,城市中该路段的细致规划设计以及骑行者违法换道意愿的控制提供参考,在后续研究中将针对实际交通场景,如加入公交站台、路边停车位等,校正元胞参数,进行更深层次的分析。
| [1] |
林贵宝, 马荣国, 杨泞珲. 机非划线分割道路自行车交通流对机动车运行的影响[J]. 公路交通科技, 2016, 33(1): 112-118. LIN Gui-bao, MA Rong-guo, YANG Ning-hui. Impact of Bicycle Traffic on Vehicle Operation on Divided Road[J]. Journal of Highway and Transportation Research and Development, 2016, 33(1): 112-118. |
| [2] |
张邻, 黄选伟, 吴伟明. 机非混行驾驶行为博弈分析[J]. 公路交通科技, 2014, 31(12): 116-123. ZHANG Lin, HUANG Xuan-wei, WU Wei-ming. Game Analysis of Drivers' Behaviors in Mixed Traffic[J]. Journal of Highway and Transportation Research and Development, 2014, 31(12): 116-123. |
| [3] |
CHEN J X, LI Z B, JIANG H, et al. Simulating the Impacts of On-street Vehicle Parking on Traffic Operations on Urban Streets Using Cellular Automation[J]. Physica A: Statistical Mechanics and Its Applications, 2017, 468: 880-891. |
| [4] |
贾斌, 高自友, 李克平, 等. 基于元胞自动机的交通系统建模与模拟[M]. 北京: 科学出版社, 2007. JIA Bin, GAO Zi-you, LI Ke-ping, et al. Models and Simulations of Traffic System Based on Theory of Cellular Automaton[M]. Beijing: Science Press, 2007. |
| [5] |
李珣, 赵征凡, 刘瑶, 等. 车路协同下带诱导车速的单车道改进NS模型[J]. 公路交通科技, 2018, 35(2): 101-108. LI Xun, ZHAO Zheng-fan, LIU Yao, et al. An Improved NS Model for Single Lane with Induce Speed under Situation of Cooperative Vehicle Infrastructure System[J]. Journal of Highway and Transportation Research and Development, 2018, 35(2): 101-108. |
| [6] |
邱夫成, 兰时勇, 李毅. 基于元胞自动机的多车道机非混合道路交通流[J]. 计算机与现代化, 2015(3): 65-70. QIU Fu-cheng, LAN Shi-yong, LI Yi. Multi-lane Mixed Road Traffic Flow Based on Cellular Automata Model[J]. Computer and Modernization, 2015(3): 65-70. |
| [7] |
李娟, 曲大义, 刘聪, 等. 基于元胞自动机的车辆换道行为研究[J]. 公路交通科技, 2016, 33(11): 140-145. LI Juan, QU Da-yi, LIU Cong, et al. Study on Vehicle Lane-changing Behavior Based on Cellular Automaton[J]. Journal of Highway and Transportation Research and Development, 2016, 33(11): 140-145. |
| [8] |
XUE S Q, JIA B, JIANG R, et al. An Improved Burgers Cellular Automaton Model for Bicycle Flow[J]. Physica A: Statistical Mechanics and Its Applications, 2017, 487: 164-177. |
| [9] |
夏亮, 郭廷龙, 刘仰, 等. 基于多值CA模型的两轮车加速过程建模与分析[J]. 公路交通科技, 2017, 34(1): 112-119. XIA Liang, GUO Ting-long, LIU Yang, et al. Simulation and Analysis of Two-wheel Vehicle Acceleration Based on Multi-value CA Model[J]. Journal of Highway and Transportation Research and Development, 2017, 34(1): 112-119. |
| [10] |
游诗广, 肖文, 陈宇光. 基于NaSch模型的混合交通流研究[J]. 公路工程, 2017, 42(3): 64-69, 76. YOU Shi-guang, XIAO Wen, CHEN Yu-guang. Mixed-Traffic Flow Study Based on NaSch Model[J]. Highway Engineering, 2017, 42(3): 64-69, 76. |
| [11] |
冯雪, 王喜富. 考虑自行车流特性的机非混合交通流元胞自动机仿真[J]. 公路交通科技, 2016, 33(3): 132-137. FENG Xue, WANG Xi-fu. Simulation of Mixed Traffic Flow by Cellular Automaton Considering Bicycle Flow Characteristics[J]. Journal of Highway and Transportation Research and Development, 2016, 33(3): 132-137. |
| [12] |
冯雪, 王喜富, 李美羽. 考虑鸣笛效应的城市路段机非混合交通流模拟[J]. 北京交通大学学报, 2015, 39(3): 56-61. FENG Xue, WANG Xi-fu, LI Mei-yu. Simulation of Mixed Traffic Flow under the Influence of Honk Effect[J]. Journal of Beijing Jiaotong University, 2015, 39(3): 56-61. |
| [13] |
JIN S, XU L, XU C, et al. Lane Width-based Cellular Automata Model for Mixed Bicycle Traffic Flow[J]. Computer-Aided Civil and Infrastructure Engineering, 2019, 34(8): 696-712. |
| [14] |
ZHAO X M, JIA B, GAO Z Y, et al. Traffic Interactions between Motorized Vehicles and Nonmotorized Vehicles Near a Bus Stop[J]. Journal of Transportation Engineering, 2009, 135(11): 894-906. |
| [15] |
LI X G, GAO Z Y, JIA B, et al. Modeling the Interaction between Motorized Vehicle and Bicycle by Using Cellular Automata Model[J]. International Journal of Modern Physics C, 2009, 20(2): 209-222. |
| [16] |
张兴强, 汪滢, 胡庆华. 交叉口混合交通流元胞自动机模型及仿真研究[J]. 物理学报, 2014, 63(1): 90-97. ZHANG Xing-qiang, WANG Ying, HU Qing-hua. Research and Simulation on Cellular Automaton Model of Mixed Traffic Flow at Intersection[J]. Acta Physica Sinica, 2014, 63(1): 90-97. |
| [17] |
南天伟, 毛保华, 陈志杰, 等. 基于元胞自动机的城市混合非机动车流特性模拟研究[J]. 公路交通科技, 2014, 31(1): 104-109. NAN Tian-wei, MAO Bao-hua, CHEN Zhi-jie, et al. Urban Mixed Non-motor Vehicle Flow Character Simulation Based on Cellular Automata[J]. Journal of Highway and Transportation Research and Development, 2014, 31(1): 104-109. |
| [18] |
李黎山, 李冰, 成卫. 基于空间比和感知密度的混合自行车交通流模型[J]. 交通运输系统工程与信息, 2019, 19(1): 104-110, 150. LI Li-shan, LI Bing, CHENG Wei. Mixed Bicycle Traffic Flow Model Based on Space Split and Perceived Density[J]. Journal of Transportation Systems Engineering and Information Technology, 2019, 19(1): 104-110, 150. |
 2021, Vol. 38
2021, Vol. 38
