扩展功能
文章信息
- 谢立广, 杨群
- XIE Li-guang, YANG Qun
- 关于隧道结构的安全推演及寿命预测
- Safety Deduction and Life Prediction of Tunnel Structure
- 公路交通科技, 2021, 38(7): 107-113
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(7): 107-113
- 10.3969/j.issn.1002-0268.2021.07.014
-
文章历史
- 收稿日期: 2020-01-15
2. 成都师范学院, 四川 成都 611130
2. Chengdu Normal University, Chengdu Sichuan 611130, China
准确地掌握结构变异与安全的关系,科学地评定隧道的剩余寿命,并在恰当的时机进行维护,已成为各国地下工程领域的重要课题。日本从20世纪80年代起,在铁路隧道、水工隧道中引入了健全度概念,对结构的剩余寿命进行评估,获得了实质性进展;美国则以结构损伤度的概念进行结构物损伤的评估方法的研究,也取得了一定的进展[1]。
近年来,国内也逐渐重视隧道寿命预测课题并着手相关研究,孙富学[2]提出了以裂缝限值和承载力分别作为衡量隧道结构寿命终结标准, 并分别对不同准则下结构寿命进行预测,通过比较确定衬砌结构最终寿命的方法;杨艳青[3]建立的运营隧道衬砌结构剩余寿命评估模型,以衬砌混凝土强度为可变参数,结合隧道衬砌结构当前状况计算衬砌结构内力,并以三截面破坏作为衬砌结构剩余寿命终结的标准;薛振年[4]建立了一种基于荷载结构法的在役公路隧道剩余寿命评估模型,分析了在役公路隧道常见病害及其对剩余寿命评估模型基本参数的影响;刘恒[5]结合特定隧道所处的地下环境,按裂缝限值准则和承载力限值准则进行隧道寿命预测;王海彦[6]针对我国西南山区隧道常见硫酸盐侵蚀环境,建立了混凝土抗硫酸盐侵蚀的耐久寿命预测模型,并对各种胶凝材配方混凝土的耐久寿命进行了预测。刘强[7]针对临海隧道所处的碳化环境和硫酸盐侵蚀环境,进行了相关耐久性试验,研究得出了混凝土渗水高度、氯离子扩散系数和抗压强度等规律,并对特定隧道的衬砌结构进行使用寿命分析。总体而言,目前的研究大致可以分为两类;一类是材料耐久性研究,它基于特定的隧道服役环境,专注于钢筋混凝土材料的耐久性,而未考虑隧道结构体系的受力特点,视构件寿命为隧道寿命,或相对保守;另一类是结构安全性研究,它根据设定的隧道病害发展或材料劣化历程,求解结构受力和安全性的变化,但未考虑因果转换,也值得商榷。实际上,材料劣化、环境恶化与结构受力之间或彼此影响,共同主宰了隧道全寿命周期的演变历程,故本研究尝试结合前述两类研究并考虑各种因素的相互作用,重在反映隧道结构的内力演变和安全性演变,可为完善相关研究提供新的思路。
本研究的主要内容有两项:一为钢筋混凝土偏压构件的安全性演变;二为隧道衬砌结构的内力及安全性演变。前者基于目前钢筋混凝土材料耐久性的研究成果,分析了材料劣化过程对偏压构件安全性演变的影响规律;后者在前者基础上,建立了隧道结构体系受力演变模型,分析了材料劣化及病害发展过程等对隧道结构内力和安全性演变的影响规律。
1 隧道衬砌结构的安全性演变 1.1 安全性的判断标准如何界定隧道寿命终结或进行寿命预测,目前尚没有统一的技术标准;孙富学[2]认为,只要结构安全系数不小于规范规定值,从技术角度而言,结构就是安全的,即满足安全耐久性要求的。因此,界定结构安全系数等于规范规定值为安全承载寿命准则的极限状态。杨艳青[3]假定,衬砌结构有3个不同位置的截面发生破坏为衬砌结构承载能力寿命终结的标志;薛振年[4]假定,当衬砌结构某截面破坏且破坏时应力水平达到极限应力的80%时,认为衬砌结构破坏,即衬砌结构承载能力寿命终止。本研究采用综合安全系数作为承载寿命的衡量标准,规范要求的安全系数限值适用于设计阶段,它考虑了荷载的不确定性,与寿命“预测”的特点是比较契合的;但对于实测的荷载作用和结构抗力,综合安全系数小于规范要求的限值,并不意味着截面破坏甚至隧道寿命终结。
根据力学分析的结果,隧道衬砌承受弯矩M、轴力N和剪力Q等内力的综合作用;多数情况下,控制衬砌结构承载能力极限状态验算的是弯矩M和轴力N。为简明起见,本研究选择验算正截面承载能力极限状态。根据规范[8]10.4.4,隧道支护结构按承载能力极限状态校核时可按综合安全系数法验算结构强度。验算可采用综合安全系数法,可按式(1)计算综合安全系数K。
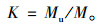
|
(1) |
式中,Mu为衬砌受弯承载力极限值,取决于衬砌计算轴力N和结构设计;M为衬砌计算弯矩。
1.2 材料性能经时变化 1.2.1 受力钢筋锈蚀钢筋锈蚀是导致混凝土结构性能退化的最主要原因[9];钢筋锈蚀量的计算可采用理论模型或经验模型,理论模型考虑的因素较为全面,但其中参数难于确定,实用性较差;经验模型便于应用,但缺乏足够的理论依据,且不同的研究考虑的因素各不相同,局限性也较大。故宜按规范[10]附录C,将两者结合起来,提出了一般环境钢筋锈蚀深度、速率和年限的系列计算公式。利用这些公式,受拉钢筋的有效截面面积As可按式(2)估算[9-10]。
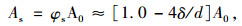
|
(2) |
式中,φs为钢筋截面面积系数;A0为钢筋截面面积初值;δ为钢筋锈蚀深度,可按式(3)估算;d为钢筋直径。
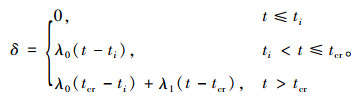
|
(3) |
式中,λ0, λ1为保护层锈胀开裂前后钢筋年平均锈蚀速率;ti为结构建成至钢筋开始锈蚀的时间;tcr为结构建成至保护层锈胀开裂的时间。
1.2.2 混凝土强度劣化混凝土结构的服役年限,必须考虑混凝土强度劣化的影响[11];一般来说,混凝土强度在初期随时间增大,但增长速度逐渐减慢,在后期则随时间下降,可按式(4)估算。
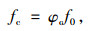
|
(4) |
式中, φc为混凝土强度系数,可按式(5)计算;f0为混凝土强度初值。
根据研究,经年混凝土强度仍服从正态分布,混凝土抗压强度系数可按下式估算[11]。
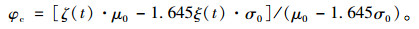
|
(5) |
式中,μ0为混凝土实测28 d强度的平均值;σ0为混凝土实测28 d强度的标准差;ζ(t)、ξ(t)为随时间变化的函数。
1.2.3 材料劣化变速上述“受力钢筋锈蚀”和“混凝土强度劣化”反映的是自然条件下的材料劣化过程,某些特殊原因可能导致劣化加速或延缓;为反映材料劣化速度改变,也为更好地利用现有研究成果,本研究引入材料劣化变速系数m,如式(6)所示:
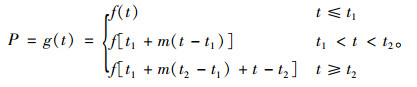
|
(6) |
式中,t1为变速劣化开始时间;t2为变速劣化结束时间;f(t)为正常劣化作用函数,如式(2)中的φs和式(4)中的φc;g(t)为变速劣化作用函数;m为材料劣化变速系数,m < 1.0,延缓劣化,m>1.0,加速劣化。
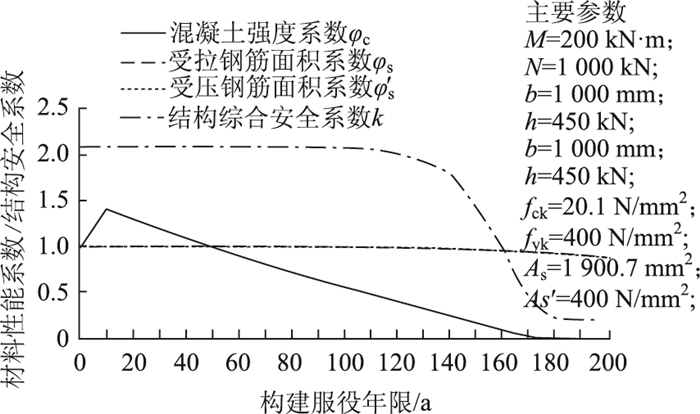
1.3 算例及分析根据某隧道力学分析的结果,选取最不利受力截面进行承载力验算,结构内力值(弯矩和轴力)恒定不变,材料参数值(钢筋面积、钢筋强度和混凝土强度等)按正常环境经时变化,计算的主要参数及结果如图 1所示。
|
| 图 1 正常环境衬砌结构的安全性演变 Fig. 1 Safety evolution of lining structure in normal environment |
| |
由图 1可以看出:隧道建成后大约前50 a,实际混凝土强度高于设计值,但结构综合安全系数并未相应增加。这是由于隧道衬砌是按“适筋”原则设计的,结构破坏总是从钢筋屈服开始,受“钢筋”的制约,单纯提高混凝土强度并不能提高结构的安全性。
计算表明:隧道建成后大约70 a,钢筋开始锈蚀,衬砌结构综合安全系数即随之降低;大约120 a,混凝土强度系数约为0.40,钢筋面积系数约为0.98,衬砌结构综合安全系数略大于2.0,视为预测的寿命终点。由于隧道的设计寿命大多为100 a,故可认为,在正常情况下,钢筋混凝土材料的耐久性能满足隧道设计寿命的要求。
计算表明,综合安全系数受钢筋锈蚀的影响比混凝土劣化要大很多,延缓钢筋锈蚀是隧道预防性养护的工作重点之一。假设从第10 a起,受拉钢筋因为某种原因锈蚀速度增加为正常速度的两倍,则大约在第90 a,衬砌结构综合安全系数已不足2.0,预测的隧道寿命不能满足设计要求。
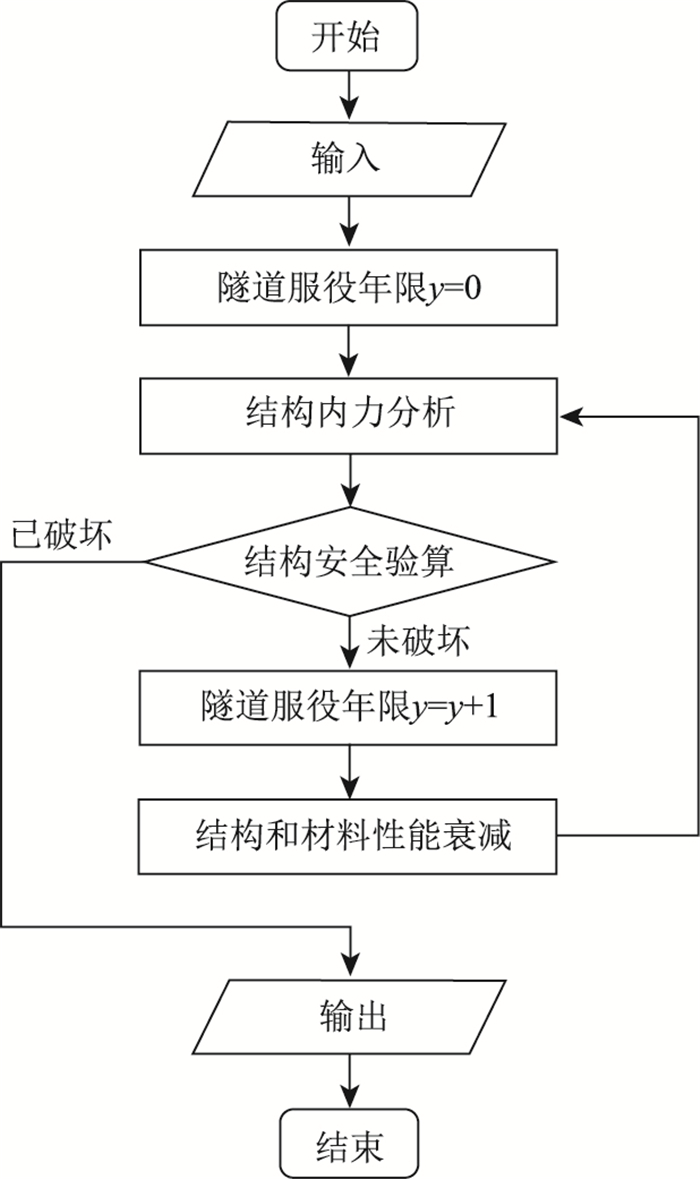
2 隧道结构体系受力演变模型 2.1 演变模型概述在隧道的全寿命周期范围内,材料劣化、环境恶化与结构受力之间或彼此影响[12-15]。材料劣化,比如钢筋锈蚀、混凝土强度劣化,无疑会改变结构的安全性,可能诱发或加剧各种病害,进而引起环境恶化;环境恶化,比如地层松动或变位、地下水位涨落,必然改变结构受力,进而改变结构安全性;而结构受力和安全性反过来也会影响材料劣化和环境恶化的进程,比如结构裂缝或破损扩展可能加速钢筋锈蚀,诱发衬砌背后的水土流失,进而引起地层松动或变位。为反映隧道全寿命周期的历程,研究材料劣化及病害发展过程等对隧道结构内力和安全性演变的影响规律,本研究建立了隧道结构体系受力演变模型。该模型的计算按时间递进,包括3个环节,分别为力学分析、结构验算和性能衰减,涉及的参数均为变量,或为时间的函数,或为彼此的函数。3个环节之间存在参数接龙和因果循环的关系,力学分析的结果用于结构验算,结构验算的结果用于确定性能衰减的速度,性能衰减的结果用于结构的力学分析,具体的计算流程如图 2所示。
|
| 图 2 隧道结构体系受力演变计算流程图 Fig. 2 Flowchart of calculating force evolution of tunnel structure system |
| |
2.2 力学分析模型
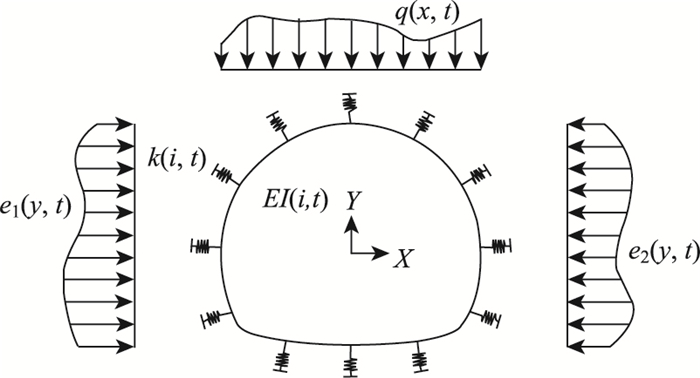
力学分析采用隧道通用结构力学模型,分析结果将用于结构验算。如图 3所示,相关力学参数均为与时间相关的函数变量,其中,隧道拱顶垂直分布压力函数为q(x, t),侧墙水平分布压力函数为e1(y, t)和e2(y, t),地层径向抗力分布函数为k(i, t), 衬砌刚度分布函数为EI(i, t);如果需要,还可以考虑地层切向抗力分布函数k′(i, t);上述(x, y),i分别指某点的坐标和位置,两者是一一对应的关系。
|
| 图 3 隧道通用结构力学模型 Fig. 3 General structural mechanical model of tunnel |
| |
2.3 结构验算项目
结构验算的项目包括结构安全验算和裂缝宽度验算,分别按式(1)和式(7)计算;结构安全验算的结果用于安全判断和寿命预测,裂缝宽度验算的结果为调整结构性能提供参数。
隧道衬砌属于偏心受压构件,考虑长期作用影响的最大裂缝宽度可按下式计算[16]:
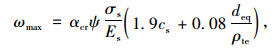
|
(7) |
式中,σcr为构件受力特征系数;ψ为裂缝间纵向受拉钢筋应变不均匀系数;σs为受拉钢筋等效应力;Es为钢筋的弹性模量;cs为最外层受拉钢筋外边缘至底边的距离;deq为受拉钢筋的等效直径;ρte为配筋率。
2.4 性能衰减假定 2.4.1 性能衰减概述性能衰减包括结构性能衰减和材料性能衰减;其中结构性能衰减的结果用于力学分析,涉及地层抗力弱化、衬砌刚度退化等内容。材料性能衰减的结果用于结构验算,涉及受力钢筋腐蚀、混凝土强度劣化和材料劣化变速等内容,如2.2节所述。
2.4.2 地层抗力弱化隧道建成后,结构与围岩之间可能存在漫长的寻求平衡的协调过程,多数情况下,这种协调或许是有利的。计算表明,隧道结构体系总能在某种程度趋向更为合理地受力,当然也有例外,比如长期伴泥渗漏可能导致衬砌背后的地层抗力弱化甚至空洞。目前尚无研究涉及地层抗力弱化的经时规律,为简化分析,假定按式(8)估算地层抗力值kr。
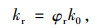
|
(8) |
式中,φr为地层抗力系数,按式(9)计算;k0为地层抗力初值,可按《规范》[17]取值。
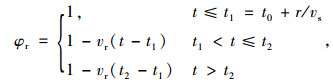
|
(9) |
式中,t0为病害点地层抗力弱化开始时间;t1为波及点地层抗力弱化开始时间;t2为地层抗力弱化结束时间;vr为地层抗力弱化速度;vs为地层抗力弱化效应扩散速度;r为地层抗力弱化效应扩散范围。
2.4.3 衬砌刚度退化钢筋混凝土构件经历一段使用期后, 构件的受拉区出现裂缝, 对构件的截面刚度产生影响。对钢筋混凝土超静定结构而言, 截面刚度的变化不仅影响结构的变形性能, 还会影响到构件间的内力分布[18]。隧道衬砌刚度值Bl(即图 3中的EI)可按下式估算。
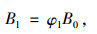
|
(10) |
式中, φl为衬砌刚度系数,按式(11)计算;B0为衬砌刚度初值。
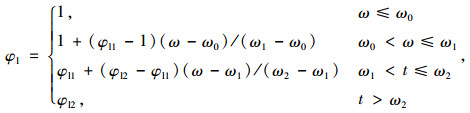
|
(11) |
式中,ω为计算裂缝宽度,按式(7)计算;ω0,ω1,ω2为裂缝宽度限值;φl1,φl2为衬砌刚度系数。
3 受力演变模型的算例及分析 3.1 计算案例概况某公路隧道V级围岩段,二衬断面如图 4所示;衬砌截面高度h=0.45 m,地层抗力基准值k0=150 MPa/m,衬砌混凝土强度等级C30,截面采用双层配筋,内外层主筋面积As=A′s=1 900.7 mm2;限于篇幅,其他参数不一一赘述。

|
| 图 4 隧道二衬断面(单位: cm) Fig. 4 Section of tunnel secondary lining(unit: cm) |
| |
另外需指出,隧道荷载若能按实测数据取值做具体分析当然很好,但各实测数据往往差别较大不便于总结规律。为简明起见,下述所有计算案例的分布压力按规范[17]推荐的松散荷载计算取值,不考虑经时变化。
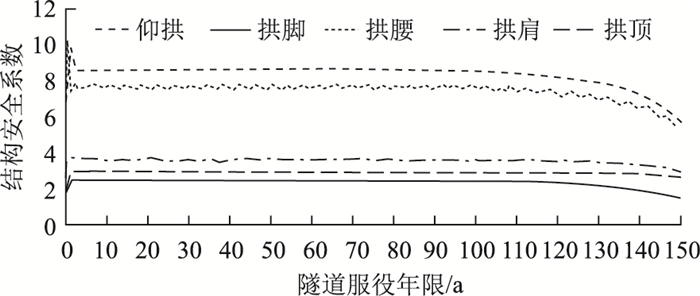
3.2 隧道自然老化隧道自然老化需按一般大气环境考虑受力钢筋锈蚀及混凝土强度劣化,以及荷载裂缝所导致的衬砌刚度退化等情况。为便于对比分析,钢筋锈蚀及混凝土强度劣化过程与图 1大致相同,此处不再赘述。经程序计算,隧道结构体系的安全演变如图 5所示,其中选取仰拱、拱脚、拱腰、拱肩及拱顶等特征部位为代表,来反映隧道整体的变化。
|
| 图 5 基于隧道自然老化的安全性演变 Fig. 5 Safety evolution based on natural aging of tunnel |
| |
由图 5可以看出,仰拱、拱脚、拱腰、拱肩及拱顶等部位的安全系数在隧道建成初期有短暂的调整,中期是相对漫长的稳定状态,后期安全系数逐渐降低,一直到最不利位置的安全系数降至2.0以下,隧道寿命共延续130~140 a。
隧道建成初期衬砌因受力产生荷载裂缝,裂缝导致衬砌刚度退化,刚度退化导致内力重分布,进而改变结构安全系数。由图 5可以看出,在初期的内力调整过程中,拱脚、拱顶和拱肩等相对偏危险部位的安全系数不变或略有提高,这表明衬砌荷载裂缝并不意味着隧道结构体系受力的恶化。究其原因,相对较大的衬砌内力产生较大的荷载裂缝,进而导致较大的刚度退化,而相对较小的衬砌刚度只能分担较少的结构内力,按此规律将逐渐趋于平衡。隧道后期结构受力基本上是稳定的,结构的安全系数逐渐降低的原因是材料性能劣化,结构的耐久性取决于材料的耐久性。
综上可认为,按裂缝宽度验算的公式,隧道衬砌出现裂缝几乎不可避免,但不必对此过于担心,因为隧道结构体系具有一定的自我调节能力,“偏爱”合适的稳定的内力分布。不过需要注意,裂缝是否存在发展迹象,在本算例中裂缝是趋于稳定的,若实测裂缝发展则可能是由于荷载加剧或围岩不稳定,应予以重视。还要注意,裂缝是否引起或诱导材料的加速劣化。
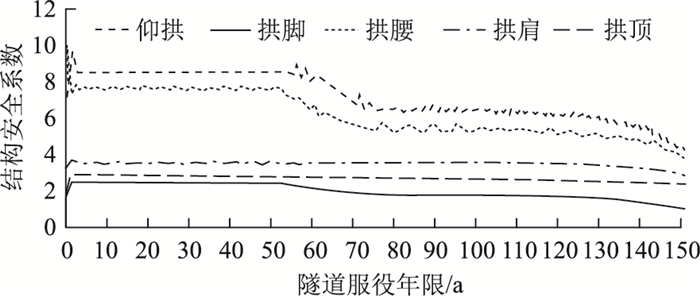
3.3 局部地层弱化分别选取仰拱、拱脚、拱腰等位置,研究局部地层弱化对隧道结构受力演变的影响;为便于对比分析,统一假定:地层弱化开始时间为50 a,结束时间为75 a,地层抗力弱化速度为0.02/a, 弱化效应扩散速度为0.2 m/a。经计算,拱脚处地层弱化的不利影响更为明显,如图 6所示。
|
| 图 6 基于拱脚地层弱化的安全性演变 Fig. 6 Safety evolution based on weakening of arch foot stratum |
| |
计算表明,地层弱化会影响结构的安全性演变,且对弱化附近区域的影响相对较大。总体上看,地层弱化的影响是不利的,尤其是拱脚处地层弱化的危害最大,可能导致结构安全性降低而不能满足设计寿命的要求。从现场反馈的情况看,拱脚处衬砌开裂渗漏的现象较为普遍,有可能导致地层弱化,值得相关养护部门重视。
4 结论本研究首先基于目前钢筋混凝土材料耐久性的研究成果,分析了材料劣化过程对隧道衬砌安全性演变的影响规律;然后在此基础上建立了隧道结构体系受力演变模型,该模型可以考虑材料劣化、环境恶化与结构受力之间的相互影响,是本研究提出的新思路;最后利用该模型分析了材料劣化及病害发展过程等对隧道结构内力和安全性演变的影响规律。
研究表明:
(1) 钢筋混凝土材料具有良好的耐久性,正常情况下能满足隧道设计寿命的要求;就隧道衬砌配筋而言,结构安全性的演变过程受钢筋锈蚀的影响比混凝土劣化要大很多,延缓钢筋锈蚀是隧道预防性养护的工作重点之一。
(2) 隧道衬砌出现裂缝会导致衬砌刚度退化,从而改变结构的内力分布,但一般不至于引起结构内力的明显恶化;对衬砌裂缝不必过于担心,但需注意,裂缝是否存在发展迹象,是否引起或诱导材料的加速劣化。
(3) 总体上看,局部地层弱化的影响是不利的,尤其是拱脚处地层弱化的危害最大,可能导致结构安全性降低而不能满足设计寿命的要求;维持围岩的稳定以及衬砌背后的密实性,是保障隧道结构安全性和使用寿命的前提条件。
本研究通过算例验证了隧道结构体系受力演变模型的可操作性,但相关研究仅处于起步阶段;因此利用了以往钢筋混凝土材料耐久性的研究成果,同时为简化分析,还采用了若干假定,这些既有成果与假定是否符合隧道的实际情况,尚需深入研究和完善。
| [1] |
关宝树, 高波. 地下结构剩余寿命评估方法研究的现状和发展[J]. 西部探矿工程, 1994, 6(4): 12-16. GUAN Bao-shu, GAO Bo. Status and Development of Research on Evaluation Method of Remaining Life of Underground Structures[J]. West-China Exploration Engineering, 1994, 6(4): 12-16. |
| [2] |
孙富学, 荣耀. 隧道衬砌结构耐久寿命预测研究[J]. 地下空间与工程学报, 2006, 2(3): 358-360. SUN Fu-xue, RONG Yao. Study on Tunnel Lining Service-life Prediction[J]. Chinese Journal of Underground Space and Engineering, 2006, 2(3): 358-360. |
| [3] |
杨艳青. 运营隧道健康诊断及剩余寿命评估研究[D]. 北京: 北京交通大学, 2012. YANG Yan-qing. Study on Health Diagnosis and Evaluation of Residual Life for Operation Tunnel[D]. Beijing: Beijing Jiaotong University, 2012. |
| [4] |
薛振年, 李杰, 马成斌, 等. 基于荷载-结构法的公路隧道剩余寿命评估模型[J]. 筑路机械与施工机械化, 2018, 35(9): 148-152. XUE Zhen-nian, LI Jie, MA Cheng-bin, et al. Assessment Model of Remaining Life of Highway Tunnel Based on Load-structure Method[J]. Road Machinery Construction Mechanization, 2018, 35(9): 148-152. |
| [5] |
刘恒, 王秀英. 大跨隧道衬砌结构耐久性寿命预测[J]. 混凝土, 2009(8): 28-29, 46. LIU Heng, WANG Xiu-ying. Large-span Structure of the Tunnel Lining Durability Forecast[J]. Concrete, 2009(8): 28-29, 46. |
| [6] |
王海彦, 仇文革, 杜立峰, 等. 隧道衬砌混凝土抗硫酸盐侵蚀耐久寿命预测模型研究[J]. 现代隧道技术, 2014, 51(3): 91-97. WANG Hai-yan, QIU Wen-ge, DU Li-feng, et al. Durability Prediction Model for Tunnel Lining Concrete Under Sulfate Corrosion[J]. Modern Tunnelling Technology, 2014, 51(3): 91-97. |
| [7] |
刘强, 黄绵松, 金峰. 临海隧道混凝土结构耐久性和使用寿命研究[J]. 北京交通大学学报, 2018, 42(6): 1-8. LIU Qiang, HUANG Mian-song, JIN Feng. Study on Durability and Service Life of Concrete Structure of Coastal Tunnel[J]. Journal of Beijing Jiaotong University, 2018, 42(6): 1-8. |
| [8] |
JTG/T D70-2010, 公路隧道设计细则[S]. JTG/T D70-2010, Guidelines for Design of Highway Tunnel[S]. |
| [9] |
牛荻涛. 混凝土结构耐久性与寿命预测[M]. 北京: 科学出版社, 2002. NIU Di-tao. Durability and Life Prediction of Concrete Structure[M]. Beijing: Science Press, 2002. |
| [10] |
GB/T 51355-2019, 既有混凝土结构耐久性评定标准[S]. GB/T 51355-2019, Standard for Durability Assessment of Existing Concrete Structures[S]. |
| [11] |
牛荻涛, 王庆霖. 一般大气环境下混凝土强度经时变化模型[J]. 工业建筑, 1995, 25(6): 36-38. NIU Di-tao, WANG Qing-lin. Models of Concrete Strength Changing with Time in General Air Environment[J]. Industrial Construction, 1995, 25(6): 36-38. |
| [12] |
巴明芳, 薛涛, 黄国阳, 等. 公路隧道低水胶比衬砌混凝土碳化耐久性预测与分析[J]. 公路交通科技, 2018, 35(9): 56-62. BA Ming-fang, XUE Tao, HUANG Guo-yang, et al. Prediction and Analysis of Carbonation Durability of Lining Concrete with Low Water-cement Ratio for Vehicle Tunnels[J]. Journal of Highway and Transportation Research and Development, 2018, 35(9): 56-62. |
| [13] |
张素磊, 丰权章, 应国刚, 等. 公路隧道渗漏水成因及新型排水材料现场试验研究[J]. 公路交通科技, 2013, 30(10): 86-91, 140. ZHANG Su-lei, FENG Quan-zhang, YING Guo-gang, et al. Study of Causes of Highway Tunnel Leakage and Field Test of New Drainage Material[J]. Journal of Highway and Transportation Research and Development, 2013, 30(10): 86-91, 140. |
| [14] |
薛晓辉, 张军, 姚广, 等. 公路隧道衬砌注浆加固力学特性研究[J]. 公路交通科技, 2017, 34(4): 93-100. XUE Xiao-hui, ZHANG Jun, YAO Guang, et al. Study on Mechanical Property of Highway Tunnel Lining Grouting Reinforcement[J]. Journal of Highway and Transportation Research and Development, 2017, 34(4): 93-100. |
| [15] |
邹育麟, 何川, 周艺, 等. 重庆高速公路现役营运隧道渗漏水病害统计及成因分析[J]. 公路交通科技, 2013, 30(1): 86-93, 101. ZOU Yu-lin, HE Chuan, ZHOU Yi, et al. Statistics and Cause Analysis of Leakage Diseases in Operating Expressway Tunnels in Chongqing[J]. Journal of Highway and Transportation Research and Development, 2013, 30(1): 86-93, 101. |
| [16] |
GB50010-2010, 混凝土结构设计规范(2015版)[S]. GB50010-2010, Code for Design of Concrete Structures (2015 Edition)[S]. |
| [17] |
JTG3370.1-2018, 公路隧道设计规范(第1册土建工程)[S]. JTG3370.1-2018, Specifications for Design of Highway Tunnels (Section 1 Civil Engineering)[S]. |
| [18] |
顾祥林, 许勇, 张伟平. 钢筋混凝土梁开裂后刚度退化研究[J]. 结构工程师, 2005, 21(5): 20-23. GU Xiang-lin, XU Yong, ZHANG Wei-ping. Study on Stiffness Deterioration of RC Beams after Cracking[J]. Structural Engineers, 2005, 21(5): 20-23. |
 2021, Vol. 38
2021, Vol. 38
