扩展功能
文章信息
- 石州, 罗彦斌, 陈建勋, 刘伟伟, 于海涛
- SHI Zhou, LUO Yan-bin, CHEN Jian-xun, LIU Wei-wei, YU Hai-tao
- 软弱围岩隧道锁脚锚管力学特性现场模拟试验
- Field Simulation Test on Mechanical Characteristics of Feet-lock Anchor Pipes for Soft Surrounding Rock Tunnel
- 公路交通科技, 2021, 38(7): 96-106, 123
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(7): 96-106, 123
- 10.3969/j.issn.1002-0268.2021.07.013
-
文章历史
- 收稿日期: 2020-11-13
2. 广东省交通集团有限公司, 广东 广州 510000
2. Guangdong Provincial Traffic Groupco., Ltd., Guangzhou Guangdong 510000, China
软弱围岩隧道开挖过程中,围岩自稳能力差,开挖工序繁杂,施工过程中极易发生钢架扭曲、断裂、喷射混凝土开裂、掉块、仰拱隆起、二次衬砌开裂、掉块,甚至垮塌等病害问题[1-4]。锁脚锚管作为软弱围岩隧道建设中的一种常用支护手段,在控制隧道变形沉降和提高结构稳定性方面发挥了重要作用,其结构简单、操作方便、经济适用,因此被广泛应用于以分部开挖法施工的软弱围岩隧道工程建设中[5-6]。其结构力学承载特性及合理支护参数的选取已经成为国内外隧道研究人员普遍关注和重点研究的问题[7-10]。
近些年来,国内外专家学者和工程技术人员,通过理论分析[11-13]、数值模拟[14-16]和工程实践等[17-23]方法对锁脚锚管展开了一系列研究。黄彬等[18]根据中南铁路的大量黄土隧道的施工经验分析了锁脚锚管控制隧道拱部下沉和水平收敛的作用效果,指出锁脚锚管的打设长度和角度对隧道变形有显著影响。赖金星等[19]通过对比相同地层中分别采用与不采用锁脚锚管施工的隧道拱顶下沉与水平收敛的现场实测结果,证实了黄土隧道中锁脚锚管可以有效控制隧道变形。王道远等[20]通过高地应力隧道“刚性强支”下变形控制现场试验研究了锁脚锚管在软弱围岩环境下的力学及变形特性。
尽管锁脚锚管在软弱围岩隧道变形控制和大变形灾害处治中应用广泛,但目前对于锁脚锚管的作用机理和受力特性的研究仍不够全面和深入,尤其对于锁脚锚管在围岩荷载作用下的受力判别以及应变和位移的分布变化规律等方面缺乏系统的研究,大多相关研究是采用数值模拟或者通过监测隧道变形而间接反映锁脚锚管的作用效果,缺乏对其更为直接、有针对性的试验研究,并且对于软弱围岩条件下锁脚锚管的合理打设角度、长度等力学参数缺乏符合工程实际的定量化分析研究。同时,由于隧道中锁脚锚管属于隐蔽型的支护措施,结构受力复杂,操作空间狭小,现有的结构受力测试方法和传感器无法直接应用于锁脚锚管的现场测试。因此,需要寻求一种能够模拟隧道中锁脚锚管实际传力机制和准确测量锚管力学及变形特性的试验方法,对复杂环境条件下锁脚锚管的内力分布规律及结构变形特性进行研究。
本试验借鉴传感器外贴、导线内引的思路,提出采用非电量电测法对锁脚锚管的受力变形进行测量,设计出一套可以模拟隧道中钢架对锁脚锚管竖向作用力的试验装置,并在某隧道左洞附近边坡对锁脚锚管进行了现场模拟试验。通过分析不同打设角度下锁脚锚管的实测应变及相应的弯曲应变,揭示了锁脚锚管的内力和变形分布及荷载响应情况,并结合不同打设角度下锁脚锚管端部位移和试验前后的变形情况,对锁脚锚管的力学作用机理和结构承载特性进行了系统全面的研究。
1 锁脚锚杆模拟试验设计本试验选取与隧道围岩土质相同的黄土边坡来模拟隧道围岩,通过加载装置在锁脚锚管端部加载模拟钢架对锁脚锚管的竖向作用,采用在锁脚锚管管壁外粘贴箔式电阻应变片、导线内引的方式测量管身应变。本试验仅研究空心锚管在端部竖向荷载作用下管身的应变分布特性及锚管变形规律,不考虑注浆效果的影响。为研究锁脚锚管在不同打设角度下的力学特性,进而研究锁脚锚管的合理打设长度和角度及揭示锁脚锚管的应变与位移分布规律,本现场试验锁脚锚管的打设角度分别为0°,30°,45°和60°。
1.1 试验锚管设计为尽可能准确地模拟隧道中的锁脚锚管,本试验采用与剪子岔2号隧道中相同规格的无缝钢管制作试验锚管。试验锚管相关物理力学参数如表 1所示。选用量程为±20 000 με的BE120-5 AA电阻应变片进行锚管应变监测。试验锚管测点布置如图 1所示,每个断面上测点布置图如图 2所示。为降低钻孔对锚管截面强度的影响,锚管测点截面圆周上、下孔与左、右孔2对钻孔交错布置;通过对应变片粘贴位置的管壁进行微抛光,并用脱脂棉沾取丙酮溶剂进行擦洗来增加电阻应变片与锚管管壁的接触面积并避免贴好的应变片脱胶;将应变片的导线在管内通过钻孔穿引后,用电烙铁将应变片引线和导线在接线端子上焊接在一起并及时在测点处涂刷3~5 mm厚的环氧树脂胶覆盖应变片、导线进行保护;最后在锁脚锚管进孔端安装一个长3 cm锥底圆周直径为51 mm的钢锥头,以保护锁脚锚管内部导线在整个试验过程中完好无损。具体流程如图 3所示。
| 内径/mm | 长度/m | 外径/mm | 弹性模量/GPa | 屈服强度/MPa | 变形系数/m |
| 43 | 2.5 | 51 | 200 | 205 | 2.776 |

|
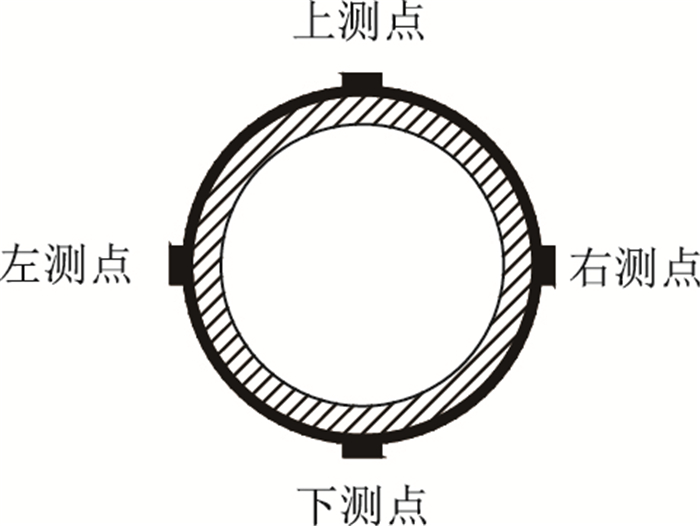
| 图 1 锚管测点布置图(单位: cm) Fig. 1 Layout of measuring points on anchor pipe(unit: cm) |
| |
|
| 图 2 各断面测点布置图 Fig. 2 Layout of measuring points at each section |
| |

|
| 图 3 试验锚管设计安装 Fig. 3 Design and installation of test anchor pipe |
| |
为抵消沿锚管长度方向土体温度不同而产生的误差,本次试验取与锚管相同的钢管制作了温度补偿块,利用机床从钢管上切割宽度为2 cm,L=2.5 m的板条,将贴好应变片的温度补偿块放置在L=2.5 m,ϕ26 mm,壁厚为2 mm的镀锌管内。
1.2 现场试验隧址区位于陕北黄土高原南部,地貌以黄土台塬、黄土梁峁-沟壑为主。隧道围岩由上更新统马兰组黄土(Q3col)组成,围岩单一,为Ⅴ级围岩。本试验的试验场地为黄(陵)延(安)高速剪子岔二号隧道左洞洞口附近的高陡边坡,试验以与隧道围岩土质相同的边坡模拟围岩,试验区域的土层为上更新统马兰组黄土(Q3col),湿陷性不明显,自然边坡整体稳定性好,土体呈硬塑状。现场对试验边坡黄土取样并进行室内试验测定,土样的工程性质指标如表 2所示。
| 指标 | 重度γ/(kN·m-3) | 弹性模量E/MPa | 黏聚力c/kPa | 内摩擦角φ/(°) |
| 参数 | 16.7 | 31 | 35 | 22 |
为了避免相邻锁脚锚管在试验加载过程中产生相互影响,相邻两钻孔中心间距设置为100 cm,采用钻头直径为70 mm的TY28型号钻机现场钻取了4根不同角度的锚管试验钻孔,同时用同样方法钻取角度为30°的温度补偿块埋设钻孔;安设好的锚管与温度补偿块均静置1 h以上,并在此时间段内进行零漂检测。
现场试验时通过自主研发的加载装置和反力装置在锁脚锚管端部竖向加载模拟钢架对锁脚锚管的竖向作用,通过锚管端部施加荷载的层级变化来模拟锁脚锚管在不同埋深及不同荷载条件下的力学承载机制,如图 6所示。锁脚锚管管身应变采用电阻应变片测试,应变数据通过TST3821E无线遥测静态电阻应变仪采集;锚管端部位移采用SW-40型手持式激光测距仪并结合白纸描点测量,如图 7所示。

|
| 图 6 加载装置及反力装置安装 Fig. 6 Installation of loading device and reaction device |
| |

|
| 图 7 端部位移测量仪器布置 Fig. 7 Arrangement of measuring instrument for end displacement |
| |
2 锁脚锚模拟试验结果分析
模拟试验测试结束后,通过统计测试数据发现,4根锁脚锚管共80个测点以及温度补偿块上的5个测点均成活(成活率100%),说明采用“外贴内引法”和非电量电测法进行锁脚锚管应变测试是可行的。以下对试验数据进行分析。
2.1 锁脚锚管各断面测点应变分布变化规律锁脚锚管各断面测点应变实际上是拉(压)弯组合应变,其分布变化规律主要从两个方面进行分析,即各级荷载作用下锁脚锚管的测点应变沿锚管长度的分布规律和锁脚锚管各方位测点应变随端部荷载的变化规律。同时根据隧道工程中锁脚锚管以竖向变形为主的承载作用机制,本试验中仅对锁脚锚管横截面上下部应力应变分布规律进行重点分析研究。下面分别对这两个方面测点应变的分布变化规律进行分析。
2.1.1 各级荷载下测点应变沿锚管长度的分布规律(1) 各级荷载下上部测点应变沿锚管长度的分布规律
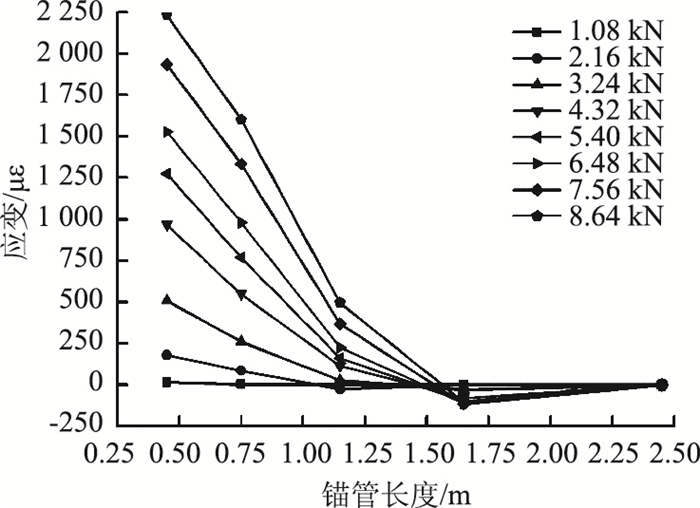
图 8~图 11分别为不同打设角度的锁脚锚管在各级荷载作用下其上部测点的应变沿锚管长度的分布情况,因上部及下部应变对称分布,此处仅以上部应变为例进行分析。
|
| 图 8 0°打设锚管上部测点应变沿锚管长度分布曲线 Fig. 8 Curves of strain distribution at upper measuring point along length of anchor pipe at 0° angle |
| |
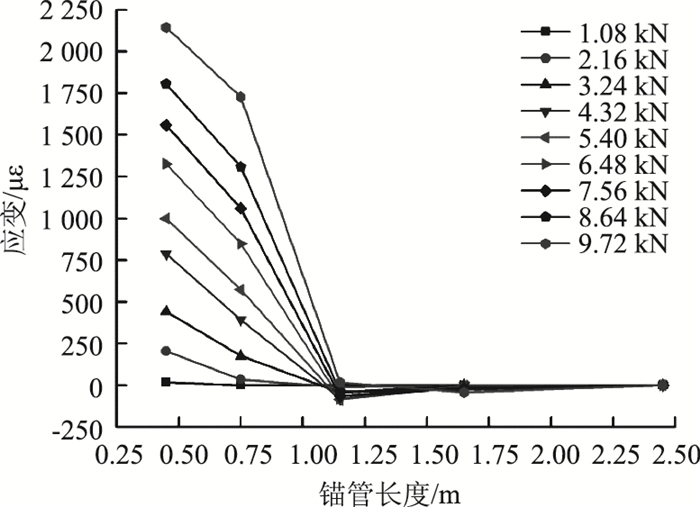
|
| 图 9 30°打设锚管上部测点应变沿锚管长度分布曲线 Fig. 9 Curves of strain distribution at upper measuring point along length of anchor pipe at 30° angle |
| |
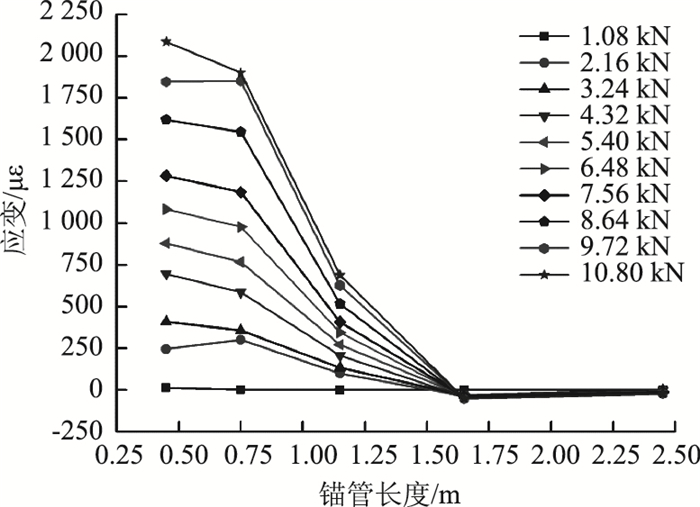
|
| 图 10 45°打设锚管上部测点应变沿锚管长度分布曲线 Fig. 10 Curves of strain distribution at upper measuring point along length of anchor pipe at 45° angle |
| |
|
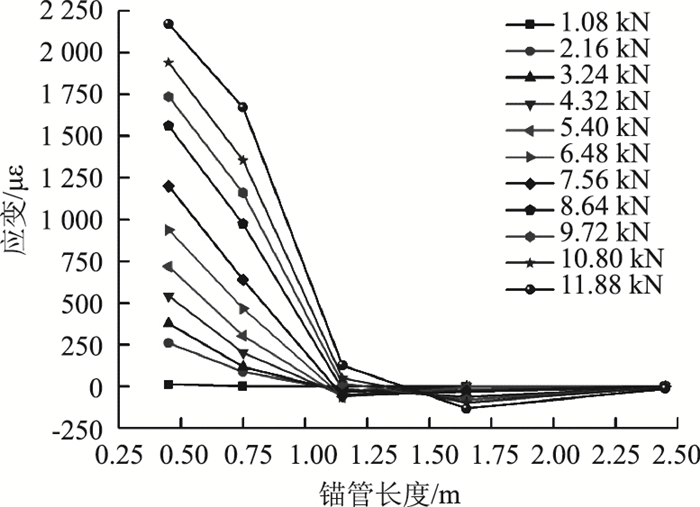
| 图 11 60°打设锚管上部测点应变沿锚管长度分布曲线 Fig. 11 Curves of strain distribution at upper measuring point along length of anchor pipe at 60° angle |
| |
对于上部测点的应变,由图 8~图 11可知:(1) 打设角度相同时,各级荷载作用下锁脚锚管上部测点应变沿锚管长度的分布规律基本一致,即在断面1处为最大正应变,随着锚管长度的增加应变迅速衰减直至减为0,然后应变变为负应变并沿着锚管长度缓慢变化最终趋于0;(2) 当荷载相同时,锚管相同位置处的测点应变大小随着打设角度的增大而减小;(3) 锁脚锚管端部荷载传递长度因锚管打设角度不同而异,当锁脚锚管的打设角度为45°时,端头荷载传递长度最大,此角度打设的锁脚锚管能更好地将荷载传递到围岩中且锁脚锚管受力相对更加均匀。
2.1.2 各断面不同方位处测点应变随锚管端部荷载的变化规律(1) 锁脚锚管0°打设时不同方位测点荷载-应变分布规律
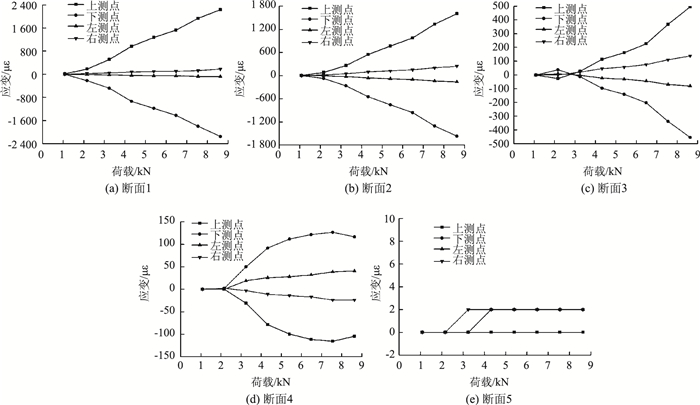
图 12为打设角度0°时锁脚锚管不同方位测点荷载-应变分布情况。
|
| 图 12 0°打设锚管不同方位测点荷载-应变分布曲线 Fig. 12 Load-strain distribution curves of measurement points on anchor pipe at 0° angle |
| |
对于打设角度为0°的锁脚锚管,由图 12可知:①锁脚锚管5个断面中各测点应变在数值上与端部荷载基本呈正相关;②同一荷载下,各个测点均为断面1(靠近加载点)应变值最大,断面5(远离加载点)应变值最小,且从断面1到断面5应变值递减,说明锁脚锚管将其承受的端部竖向荷载沿其长度方向逐渐向围岩深部传递;③同一荷载下,同一断面的上、下测点应变值均远远大于左、右测点的应变值,且上、下测点应变值大小相近,说明锁脚锚管主要依靠其竖向弯折变形来承受荷载;④断面5的测点应变很小(2 με),可以忽略不计,说明荷载传递到锚管底部附近时已经消散殆尽,所以对于0°打设的锁脚锚管,长度2.5 m能够满足承载要求。
(2) 锁脚锚管30°打设时不同方位测点荷载-应变分布规律
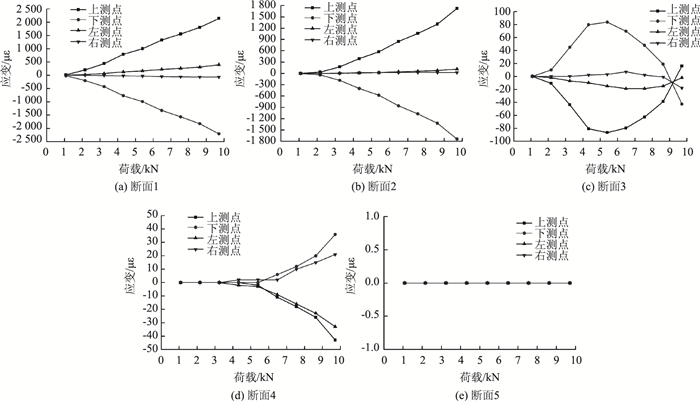
图 13为打设角度30°时锁脚锚管不同方位测点应变荷载-应变分布情况。
|
| 图 13 30°打设锚管不同方位测点荷载-应变分布规律 Fig. 13 Load-strain distribution rules of measurement points on anchor pipe at 30° angle |
| |
对于打设角度为30°的锁脚锚管,由图 13可知:①断面1、断面2和断面4上各个测点应变在数值上与端头荷载基本呈正相关,而断面3的测点应变随着荷载先增大到峰值后逐渐减小,说明断面3处锚管随着受力和变形的持续进行,其承载方式发生了改变(先加载后卸载);②同一荷载下,各测点的应变值基本呈现为从断面1(靠近加载点)到断面5(远离加载点)逐级递减的分布规律,说明锁脚锚管将其承受的端部竖向荷载沿其长度方向逐渐向围岩深部传递;③同一荷载下,同一断面的上、下测点应变值基本均大于左、右测点的应变值,且对于断面1和断面2,上、下测点应变远远大于左右测点应变,说明锁脚锚管尤其是靠近加载端的部分主要依靠其竖向弯折变形来承受荷载;④断面5的测点应变为0,说明锚管尾端部分并未承受荷载,所以对于30°打设的锁脚锚管,长度2.5 m能够满足承载要求。
(3) 锁脚锚管45°打设时不同方位测点荷载-应变分布规律
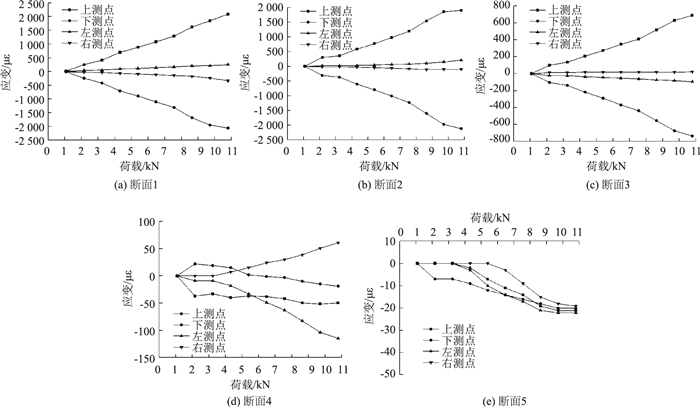
图 14为打设角度为45°时锁脚锚管不同方位测点荷载-应变分布情况。
|
| 图 14 45°打设锚管不同方位测点荷载-应变分布曲线 Fig. 14 Load-strain distribution curves of measurement points on anchor pipe at 45° angle |
| |
对于打设角度为45°的锁脚锚管,由图 14可知:①断面1、断面2和断面3各测点应变在数值上与端头荷载基本呈正相关。断面4和断面5的各测点应变均较小;②同一荷载下,各测点的应变值基本呈现为从断面1(靠近加载点)到断面5(远离加载点)逐级递减的分布规律,说明锁脚锚管将其承受的端部竖向荷载沿其长度方向逐渐向围岩深部传递;③同一荷载下,前3个断面的上、下测点应变值均远远大于左、右测点的应变值,说明锁脚锚管尤其是靠近加载端的部分主要依靠其竖向弯折变形来承受荷载;④断面5各测点应变最大值为-20 με左右,应变值较小,可以忽略不计,所以对于45°打设锁脚锚管,长度2.5 m能够满足承载要求。
(4) 锁脚锚管60°打设时不同方位测点荷载-应变分布规律
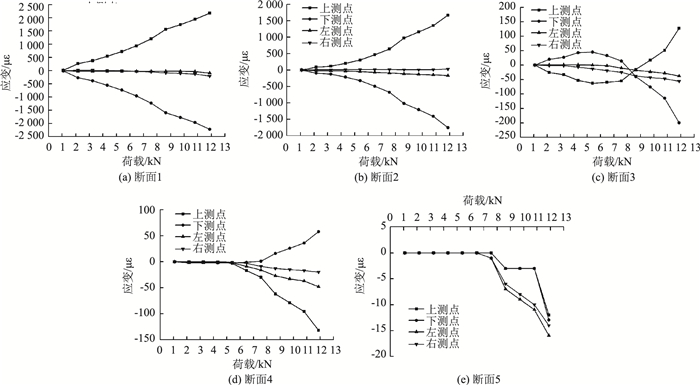
图 15为打设角度为60°时锁脚锚管不同方位测点荷载-应变分布情况。
|
| 图 15 60°打设锚管不同方位测点荷载-应变分布曲线 Fig. 15 Load-strain distribution curves of measurement points on anchor pipe at 60° angle |
| |
对于打设角度为60°的锁脚锚管,由图 15可知:①断面1和断面2各测点应变在数值上与端头荷载基本呈正相关;②同一荷载下,各个测点的应变值基本呈现为断面1(靠近加载点)到断面5(远离加载点)逐级递减的分布规律,说明锁脚锚管将其承受的端部竖向荷载沿其长度方向逐渐向围岩深部传递;③同一荷载下,前4个断面的上、下测点应变值基本均远远大于左、右测点的应变值,说明锁脚锚管尤其是靠近加载端的部分主要依靠其竖向弯折变形来承受荷载;④断面5的测点最大应变为-15 με左右,应变值较小,所以对于60°打设锁脚锚管,长度2.5 m能够满足承载要求。
综合图 16~图 19,可以得到不同打设角度下锁脚锚管测点应变随端部荷载的变化规律如下:①不同打设角度下各锁脚锚管均表现为其各个断面的测点应变随着荷载的增加而随之增大,说明锁脚锚管能有效对其端部荷载作出响应;②相同荷载下,各测点应变值从断面1到断面5递减,上、下测点应变值一般远远大于左、右测点的应变值,说明锁脚锚管能有效将其承受的端部竖向荷载沿其长度方向逐渐向围岩深部传递,且锚管主要靠其距加载点较近部分的竖向弯折变形承受荷载;③在同一端部荷载下,随着打设角度的增大,各锚管的最大应变值相应减小,且应变为0的断面位置逐渐向锚管深部位置移动,说明增大锁脚锚管的打设角度有利于将端部竖向荷载传递至围岩深处;④无论锁脚锚管以小角度(0°和30°)打设还是大角度(45°和60°)打设,端部荷载传递至锚管1.5 m位置左右时管身应变已衰减至很小,且管尾处应变可忽略不计,所以锁脚锚管的打设长度可取为2.5 m左右。

|
| 图 16 锁脚锚管上下弯曲应变沿锚管长度分布曲线 Fig. 16 Distribution curves of bending strains of upper and lower parts of foot-lock anchor pipe along pipe length |
| |
|
| 图 17 锁脚锚管上下弯曲应变随端部荷载的变化曲线 Fig. 17 Distribution curves of bending strains of upper and lower parts of foot-lock anchor pipe varying with end load |
| |
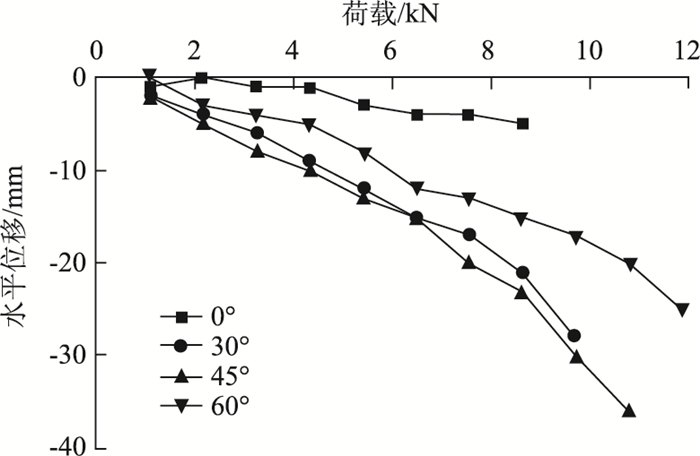
|
| 图 18 锁脚锚管端部水平位移随荷载的变化曲线 Fig. 18 curves of horizontal displacement at end of foot-lock anchor pipe varying with load |
| |

|
| 图 19 试验前后锚杆对比图 Fig. 19 Comparison of bolt states before and after test |
| |
2.2 锁脚锚管各断面弯曲应变的分布变化规律
根据材料力学及锚杆轴力分析可知,各断面的上下弯曲应变可由式(1)计算得到:
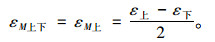
|
(1) |
下面根据各测点应变对弯曲应变进行计算,并对其分布规律进行分析。
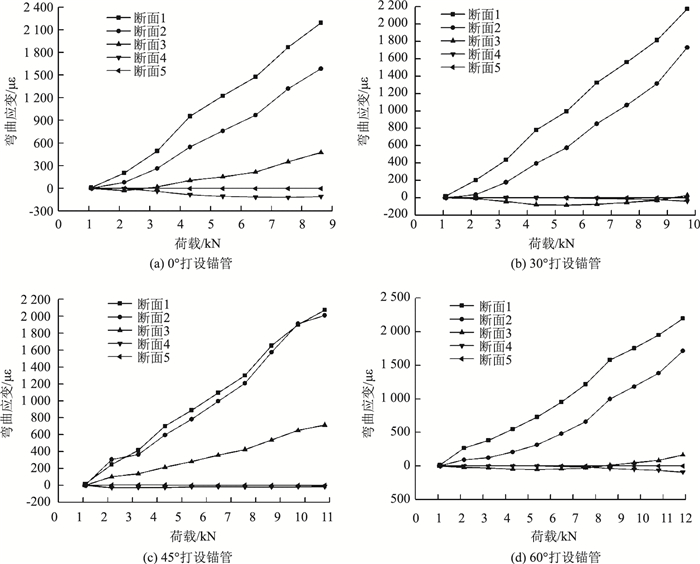
2.2.1 各级荷载下弯曲应变沿锚管长度的分布规律图 16(a)~(d)分别为不同打设角度下锁脚锚管各断面上下弯曲应变沿锚管长度的分布情况。
对于锁脚锚管上下弯曲应变,由图 16(a)~(d)可知:(1) 打设角度一定时,各级荷载作用下锁脚锚管上下弯曲应变沿锚管长度的分布规律基本一致,即弯曲应变随着锚管长度的增加而迅速衰减直至趋于零,说明锚管主要为其加载点附近的部分管段承受弯矩。(2)当荷载相同时,对于同一断面,其上下弯曲应变值随着打设角度的增大而减小,其原因是随着打设角度的增大,竖向荷载在锚管端部的横向分力随之减小,这一分布规律表明增大锁脚锚管的打设角度有助于减小其管身的竖向弯矩。(3)锁脚锚管端部荷载的传递长度因锚管打设角度而异,此处用上下弯曲应变第一零点长度来衡量(某一荷载作用下弯曲应变为零对应的断面的最小锚管长度),打设角度分别为0°,30°,45°和60°时,荷载为8.64 kN对应弯曲应变第一零点长度分别为1.50,1.15,1.65和1.40 m,容易得知,当锁脚锚管的打设角度为45°时,端部荷载的传递长度最大,此时锁脚锚管的竖向承载力发挥得最极致。
2.2.2 各个断面的弯曲应变随端部荷载的变化规律(1) 锁脚锚管各断面上下弯曲应变随端部荷载的分布规律
图 17(a)~(d)分别为不同打设角度下锁脚锚管各断面上下弯曲应变随端部竖向荷载的分布情况。
对于锁脚锚管各断面上下弯曲应变,由图 17(a)~(d)可知:(1) 任意打设角度下,锁脚锚管各个断面的上下弯曲应变在数值上与端部荷载基本呈正相关。(2) 同一打设角度时,各断面上下弯曲应变值随着断面距离加载点的距离增大而减小,说明锁脚锚管能有效将其承受的端部竖向荷载沿其长度方向逐渐向围岩深部传递。(3) 断面1和断面2的上下弯曲应变远远大于其他3个断面的弯曲应变,说明锁脚锚管主要靠加载端部附近部分承受弯矩。(4) 在相同的端部荷载下,锁脚锚管同一断面处的上下弯曲应变随着打设角度的增大而减小,说明增大锁脚锚管的打设角度有助于改善锁脚锚管的弯矩受力状态。
2.3 锁脚锚管端部水平位移随端部荷载的变化规律不同端部荷载作用下锁脚锚管的端部水平位移如图 18所示。
对于各端部荷载作用下锁脚锚管的端部水平位移,由图 18可知:(1) 对于打设角度为30°,45°和60°的锁脚锚管,其端部水平位移随着荷载的走势基本一致,且在加载前期,锚管端头水平位移增速都较慢,随着荷载的逐渐增大,水平位移增速相应增大,说明随着荷载的持续施加和增大,锚管的弯曲变形和管周围岩的破坏进入了快速演变阶段。(2) 当荷载相同时,锚管端部水平位移随着打设角度的不同而不同,当打设角度为45°时其水平位移为最大,打设角度为0°时其水平位移为最小。
2.4 试验前后锁脚锚管与围岩变形对比分析为了更好地研究锁脚锚管整体的变形破坏特点,试验结束后,利用挖掘机将试验锚管整体小心挖出。以下对锁脚锚管的变形情况和围岩的破坏情况进行分析研究。图 19为不同打设角度下锁脚锚管试验前后的变形对比图。图 20为围岩孔口附近试验前后的变形破坏对比图。
由图 19可知,锁脚锚管的变形主要在靠近加载点的一定管身范围内发生弯折变形。经测量,折弯点均位于距锚管端部55 cm左右的位置,说明锁脚锚管主要靠其孔口附近部分承受荷载。建议在隧道锁脚锚管施工过程中注意保护孔口附近的围岩,必要时可以采用一定的施工措施如围岩注浆等方法对围岩进行加固。
由图 20可知,孔口附近均发生了不同程度的围岩剥离破坏,且破坏区域主要集中在钻孔的下部,说明孔口附近围岩主要是在锁脚锚管的竖向挤压下产生了塑性变形和剥离破坏,所以隧道锁脚锚管施工时应注意保护孔口附近围岩,最好对孔口附近尤其钻孔下部围岩施加适当的补强措施。

|
| 图 20 试验前后围岩对比 Fig. 20 Comparison of surrounding rock states before and after test |
| |
3 结论
本研究根据现场模拟试验对锁脚锚管的力学作用机理和结构承载特性进行了系统全面的分析研究,主要结论如下:
(1) 不同打设角度下锁脚锚管各方位测点应变沿锚管长度的分布规律与不同荷载下各测点应变的变化规律基本一致,均为加载端的锚管应变较大并沿管身向围岩深部递减。同时,随着打设角度的增大,各锚管应变峰值随之减小,应变峰值部位与管端距离随之变大,大角度打设的锁脚锚管受力更均匀,且将端部荷载传递到围岩更深部位置。不同打设角度下锁脚锚杆末端应变值均接近于0,因此锁脚锚管打设长度取为2.5 m左右可满足工程建设要求。
(2) 在端部竖向荷载作用下,锁脚锚管的弯曲应变随着锚管长度增加而迅速衰减,锁脚锚管主要靠管口附近部位抵抗弯矩。锁脚锚管的上下弯曲应变曲线和测点应变曲线在走势及数值大小上均较为接近,锁脚锚管在端部竖向荷载作用下主要依靠其竖向抗弯刚度提供承载力。
(3) 锁脚锚管端部水平位移随着荷载的走势基本一致,在加载前期锚管端头水平位移增速均较慢,随着荷载的逐渐增大,水平位移增速相应增大。当荷载相同时,锚管端部水平位移随着打设角度的不同而不同,当打设角度为45°时其水平位移为最大,打设角度为0°时其水平位移为最小。
(4) 锁脚锚管的变形破坏主要为集中在孔口附近的弯折破坏,锁脚锚管主要依靠其抗弯刚度提供承载力。孔口围岩的塑性变形和剥离破坏集中在锚管下方部位,主要由锚管的竖向挤压变形引起。因此锁脚锚管施工时应注意保护孔口部位(尤其是钻孔下部)围岩的完整与强度,必要时可对孔口附近围岩进行加固。
| [1] |
陈建勋. 软弱地层隧道初期支护技术-钢架喷网锁脚锚杆组合结构[M]. 北京: 科学出版社, 2011. CHEN Jian-xun. Tunnel Support Structure Made up of Steel Frame and Shotcrete and Steel Mesh and Feet-lock Rock Bolt[M]. Beijing: Science Press, 2011. |
| [2] |
关宝树, 赵勇. 软弱围岩隧道施工技术[M]. 北京: 人民交通出版社, 2011. GUAN Bao-shu, ZHAO Yong. Tunnel Construction Technology in Weak Surrounding Rock[M]. Beijing: China Communications Press, 2011. |
| [3] |
陈子全, 何川, 吴迪, 等. 高地应力层状软岩隧道大变形预测分级研究[J]. 西南交通大学学报, 2018, 53(6): 1237-1244. CHEN Zi-quan, HE Chuan, WU Di, et al. Study of Study of Large Deformation Classification Criterion for Layered Soft Rock Tunnels under High Geostres[J]. Journal of Southwest Jiaotong University, 2018, 53(6): 1237-1244. |
| [4] |
BIZJAK K F, PETKOVŠEK B. Displacement Analysis of Tunnel Support in Soft Rock around a Shallow Highway Tunnel at Golovec[J]. Engineering Geology, 2004, 75(1): 89-106. |
| [5] |
陈建勋, 王超, 罗彦斌, 等. 高含水量土质隧道不设系统锚杆的试验研究[J]. 岩土工程学报, 2010, 32(5): 815-820. CHEN Jian-xun, WANG Chao, LUO Yan-bin, et al. Experimental Research on High-water-content Soil Tunnel without Systematic Bolts[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(5): 815-820. |
| [6] |
周宇. 锁脚锚管和仰拱注浆对控制大断面海底隧道位移的有效性分析[J]. 岩石力学与工程学报, 2007(增2): 3830-3834. ZHOU Yu. Validity Analysis of Locking Anchor Pipe and Grouting in Inverted Arch for Displacement Control of Large-section Subsea Tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2007(S2): 3830-3834. |
| [7] |
梁辉如, 王永东, 燕新, 等. 锁脚锚管-钢拱架在软岩隧道中的力学稳定性研究[J]. 北京交通大学学报, 2020, 44(4): 34-41. LIANG Hui-ru, WANG Yong-dong, YAN Xin, et al. Research on Mechanical Stability of Feet-lock Pipe and Steel Arch in Soft Rock Tunnel[J]. Journal of Beijing Jiaotong University, 2020, 44(4): 34-41. |
| [8] |
CHEN L J, ZHANG Y L, MA Z Y. Analytical Approach for Support Mechanism of Feet-lock Pipe Combined with Steel Frame in Weak Rock Tunnels[J]. KSCE Journal of Civil Engineering, 2016, 20(7): 2965-2980. |
| [9] |
BOBET A, EINSTEIN H H. Tunnel Reinforcement with Rockbolts[J]. Tunnelling and Underground Space Technology, 2011, 26(1): 100-123. |
| [10] |
陈建勋, 刘伟伟, 陈丽俊, 等. 绿泥石片岩地层大跨度公路隧道大变形控制及合理支护形式现场试验[J]. 中国公路学报, 2020, 33(12): 212-223. CHEN Jian-xun, LIU Wei-wei, CHEN Li-jun, et al. In-situ Experimental Study on Large-deformation Control and Reasonable Support Forms for a Large-span Highway Tunnel in Chlorite Schist[J]. Chinese Journal of Highway and Transport, 2020, 33(12): 212-223. |
| [11] |
罗彦斌, 陈建勋. 软弱围岩隧道锁脚锚杆受力特性及其力学计算模型[J]. 岩土工程学报, 2013, 35(8): 1519-1525. LUO Yan-bin, CHEN Jian-xun. Mechanical Characteristics and Mechanical Calculation Model of Tunnel Feet-lock Bolt in Weak Surrounding Rock[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(8): 1519-1525. |
| [12] |
陈丽俊, 张运良, 马震岳. 锁脚锚管合理打设角度的理论研究[J]. 岩石力学与工程学报, 2015, 34(7): 1334-1344. CHEN Li-jun, ZHANG Yun-liang, MA Zhen-yue. Theoretical Research on Reasonable Installation Angle of Feet-lock Pipes[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(7): 1334-1344. |
| [13] |
陈丽俊, 张运良. 锁脚锚管受力分析的双参数弹性地基梁模型[J]. 岩石力学与工程学报, 2016, 35(5): 989-999. CHEN Li-jun, ZHANG Yun-liang. Double Parameters Elastic Foundation Beam Model of Feet-lock Pipes[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(5): 989-999. |
| [14] |
邓国华, 邵生俊, 陶虎, 等. 锁脚锚管对土质隧道围岩变形和支护内力的影响研究[J]. 土木工程学报, 2010, 43(1): 108-113. DENG Guo-hua, SHAO Sheng-jun, TAO Hu, et al. A Study of the Effects of Locking Tremies on the Internal Force of Tunnel Support and the Deformation of Surrounding Soil[J]. China Civil Engineering Journal, 2010, 43(1): 108-113. |
| [15] |
赵德安, 蔡小林, SWOBODA G, 等. 锚杆单元及其在黄土隧道计算中的若干问题[J]. 岩石力学与工程学报, 2004, 23(24): 4183-4189. ZHAO De-an, CAI Xiao-Lin, SWOBODA G, et al. Some Problems Associated with Analysis of Tunnels in Loess Using Bolt Elements[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(24): 4183-4189. |
| [16] |
曾超. 大断面海底隧道异常变形控制措施研究[J]. 岩土力学与工程学报, 2007, 26(11): 2170-2175. ZENG Chao. Study on Abnormal Deformation Controlling Measures for Large Cross-section Subsea Tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(11): 2170-2175. |
| [17] |
谭忠盛, 杨旸, 陈伟, 等. 中老铁路高地应力软岩隧道大变形控制技术研究[J]. 铁道学报, 2020, 42(12): 171-178. TAN Zhong-sheng, YANG Min, CHEN Wei, et al. Large Deformation Control Technology of High Geostress Soft Rock Tunnel of China-Laos Railway[J]. Journal of the China Railway Society, 2020, 42(12): 171-178. |
| [18] |
黄彬. 大断面黄土隧道土石分界段施工技术[J]. 现代隧道技术, 2013, 50(1): 139-142. HUANG Bin. Construction Techniques for a Large-section Loess Railway Tunnel at the Dividing Line of Loess and Rock[J]. Modern Tunnelling Technology, 2013, 50(1): 139-142. |
| [19] |
赖金星, 樊浩博, 来弘鹏, 等. 软弱黄土隧道变形规律现场测试与分析[J]. 岩土力学, 2015, 36(7): 2003-2012, 2020. LAI Jin-xing, FAN Hao-bo, LAI Hong-peng, et al. In-situ Monitoring and Analysis of Tunnel Deformation Law in Weak Loess[J]. Rock and soil Mechanics, 2015, 36(7): 2003-2012, 2020. |
| [20] |
王道远, 刘佳, 张逴, 等. 高地应力深埋隧道断裂破碎带大变形控制方法现场试验研究[J]. 岩土工程学报, 2020, 42(4): 658-666. WANG Dao-yuan, LIU Jia, ZHANG Chuo, et al. Field Tests on Large Deformation Control Method for Surrounding Rock of Deep Tunnel in Fault Zone with High Geostress[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(4): 658-666. |
| [21] |
郭吉平. 软弱碎裂岩体中隧道锚杆支护优化分析[J]. 中外公路, 2016, 36(6): 188-192. GUO Ji-ping. Optimization Analysis of Tunnel Bolt Support in Weak and Fractured Rock Mass[J]. Journal of China & Foreign Highway, 2016, 36(6): 188-192. |
| [22] |
王亚琼, 汪珂, 孙铁军, 等. 软弱围岩隧道塌方段力学性状测试与数值分析[J]. 应用力学学报, 2015, 32(3): 384-389, 4. WANG Ya-qiong, WANG Ke, SUN Tie-jun, et al. Test and Numerical Study on Mechanical Properties of Tunnel Collapse in Soft Surrounding Rock[J]. Chinese Journal of Applied Mechanics, 2015, 32(3): 384-389, 4. |
| [23] |
陈建勋, 刁鹏升, 陈丽俊, 等. 软弱围岩隧道施工过程荷载释放特性[J]. 中国科技论文, 2018, 13(7): 840-846. CHEN Jian-xun, DIAO Peng-sheng, CHEN Li-jun, et al. Stress Release Characteristics during the Construction Process of Soft Rock Tunnel[J]. China Sciencepaper, 2018, 13(7): 840-846. |
 2021, Vol. 38
2021, Vol. 38
