扩展功能
文章信息
- 薛锋, 胡萍, 黄宇
- XUE Feng, HU Ping, HUANG Yu
- 基于组合模型的公路隧道交通安全评价
- Traffic Safety Evaluation of Highway Tunnel Based on Combined Model
- 公路交通科技, 2021, 38(7): 85-95
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(7): 85-95
- 10.3969/j.issn.1002-0268.2021.07.012
-
文章历史
- 收稿日期: 2020-10-09
2. 西南交通大学 综合交通大数据应用技术国家工程实验室, 四川 成都 611756;
3. 西南交通大学 综合交通运输智能化国家地方联合工程实验室, 四川 成都 611756;
4. 成都市交通发展研究院, 四川 成都 610017
2. National Engineering Laboratory of Application Technology of Integrated Transportation Big Data, Chengdu Sichuan 611756, China;
3. National United Engineering Laboratory of Integrated and Intelligent Transportation, Southwest Jiaotong University, Chengdu Sichuan 611756, China;
4. Chengdu Communications Development Academe, Chengdu Sichuan 610017, China
隧道是公路交通的瓶颈,具有行车环境封闭性的特点,因其交通环境的特殊性,公路隧道交通安全事故频频发生[1-2]。在隧道里,行驶中的车辆往往处于一个较为危险的交通环境,车辆密度、车速、内部光线、空间、交通安全设施等因素都有可能是引发交通事故的危险源。
当前,有关隧道安全评价的研究侧重于隧道建设时期,如隧道的施工安全、施工方法等,部分的安全评价侧重于隧道的照明、消防等单一方面[3-6]。欧美、日本等国家对隧道运营安全尤为重视,如基于事故和火灾发生的概率,按照隧道长度划分公路隧道安全等级[7]。涉及公路隧道交通安全评价体系的构建主要集中在两方面,一方面是以隧道运营环境安全视角,从驾驶员相对不可控的客观条件方面构建评价体系。郭延永等[8]考虑气候和道路环境等因素,建立了从道路、交通、环境以及气候的公路隧道交通安全评价体系;胡群芳等[9]针对隧道运营结构安全,从运营养护角度构建了以结构设计、结构现状、养护维修等3方面组成的公路隧道安全指标体系;钱勇等[10]认为交通工程设施对隧道安全影响较大,着重考虑道路、交通运营、交通工程设施以及气候4方面的评价指标。另一方面是从公路隧道安全全方位考虑,针对驾驶员的特性因素综合评价。方守恩等[11]通过分析隧道群路段特征断面车辆的速率变化和驾驶员实车试验数据,提出一种基于速率差和心率增长的安全评价方法;胡江碧等[12]通过对驾驶员自身参数以及相关特性分析,建立了视认距离与亮度需求的关系模型,得出夜间隧道入口段照明满足驾驶员安全行车的需求阈值;杜志刚等[13]通过大量的隧道进出口处视觉适应试验,从驾驶员的视觉特性角度构建公路隧道进出口行车安全评价指标。涉及公路隧道交通安全评价方法可分为定性评价和定量评价两大类。欧洲国家一般采用定性和定量相结合的安全评价方法且应用相对成熟,如成立于2000年的Euro Test机构的基于风险潜势和安全潜势的安全评价方法;我国高速公路隧道的建设起步较晚,定性安全评价方面主要集中在交通流理论、声学理论、空气动力学等,形成了一定的评价标准和指标体系[14];定量安全评价方面主要采用适当的数学模型,其中运用模糊评价和灰色评价的研究较为广泛[15],大都较为主观。学者们就降低误差、尊重客观事实这一评价特性,杨健等[16]针对高速公路隧道安全提出了基于改进DSmT的综合评价方法;Qu等[17]提出了一种有趣的方法来开发公路隧道定量风险评估(QRA)软件工具,并对新加坡公路隧道交通安全进行了应用评估;Kazaras等[18]分析了隧道基础设施对交通安全的风险性,引入STAMP模型对传统的隧道交通风险评估方法做出了补充。公路隧道交通事故的发生是由多种相互关联的风险源耦合导致的,单一的因素不具备表征公路隧道整体交通安全的条件,且公路隧道交通安全评价是多要素、多层次,具有复杂随机性的、定量与定性结合的综合评价问题。针对此问题,本研究引入能够准确揭示各种因素之间相互关系的决策实验室法[19](Decision Making Trial and Evaluation Laboratory,DEMATEL),DEMATEL是通过运用图论与矩阵的方法分析复杂系统中元素的结构关系,但并未考虑各个元素权重的影响,而层次分析法(Analytic Hierarchy Process,AHP)在计算各影响因素权重时能够比较各因素的影响程度大小,因此,设计AHP-DEMATEL模型来优化评价指标的权重,能够较为全面地考虑风险因素之间的依存关系,避免单个专家意见的局限性,同时能够克服干扰性因素引起的评价误差。在针对某些指标的模糊性和随机性特性时,本研究引入云模型的概念以期得到各个指标的隶属度,实现定性与定量不确定性之间的映射与转换[20]。
鉴于此,本研究从交通流因素、隧道因素、交通工程设施因素、其他因素4个方面,从定性和定量两个视角构建公路隧道交通安全指标体系,提出基于AHP-DEMATEL和云模型的组合评价方法。模型首先通过敏感性分析和德尔菲法筛选出评价指标;然后利用AHP-DEMATEL组合方法,考虑指标间的相关性优化指标权重,并采用云模型解决指标间的耦合性、模糊性和随机性,突出隶属度;最后通过模糊数学运算联立求解,得到隧道交通安全的综合评价结果,以期为公路隧道交通安全的管理者提供决策理论依据。
1 评价指标的建立 1.1 评价指标体系的初始确定公路隧道及隧道群,一般位于大山、河流等特殊地理区段上,具有线形复杂多变、视距不良、洞内能见度低等特点。遵循科学性、独立性、可操作性、目的性等原则构建公路隧道交通安全评价体系,结合《公路隧道设计规范》(JTG D70/2—2014)[21]以及现有影响公路隧道交通安全状态的各种因素,以交通安全评价、隧道交通环境评价等已有相关研究成果及相关技术规范为依据[22-25],从交通流、交通工程设施、隧道条件、气候环境4个方面构建公路隧道交通安全评价初始指标体系,如表 1所示。
| 准则层 | 因素层 | 指标特征 | 准则层 | 因素层 | 指标特征 |
| 交通流因素 | 车辆密度 | 反映公路隧道交通安全与交通流之间的动态因素 | 隧道因素 | 最小平曲线半径 | 反映隧道交通安全与隧道线形结构内在因素 |
| 行驶车速 | 曲线段长度占比 | ||||
| 平均车速 | 最大纵坡值 | ||||
| 设计车速 | 隧道进出口线形 | ||||
| 大型车占比 | 隧道长度 | ||||
| 载重率 | 连续坡长 | ||||
| 交通工程设施因素 | 交通诱导设施 | 反映公路隧道交通安全与相关设施的静态因素 | 路面抗滑性 | ||
| 交通监控设施 | 路面排水性 | ||||
| 消防设施 | 其他因素 | 年不良气候天数 | 反映影响公路隧道交通安全随机因素 | ||
| 中央控制设施 | 隧道能见度 | ||||
| 通风与照明设施 | 隧道内外侧风速 | ||||
| 紧急呼叫设施 | 等效声级 |
1.2 评价指标的筛选
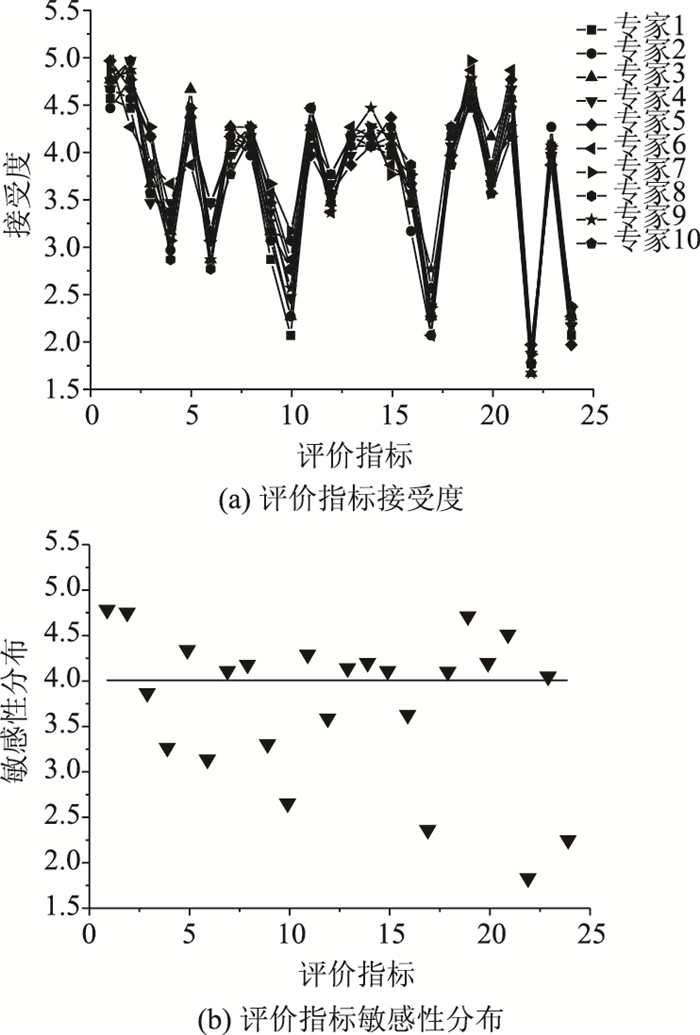
公路隧道交通安全评价影响因素众多且指标构成复杂,初步建立的公路隧道交通安全评价指标体系其信息具有重叠性,是一个复杂的综合性评价问题。因此,考虑将经济学中的敏感性分析引入德尔菲法(Delphi Method)进行指标筛选[15],通过调查问卷的方式邀请从事公路隧道交通安全管理领域的资深专家,专家比例为20%的路桥企业高工,80%的高等院校研究公路隧道安全方面的科研人员,从“系统性、科学性、目的性、可持续发展性、简明性”5个维度对评价指标打分,最后取每位专家针对各维度的打分总和作为一位专家的打分结果。在收集群体专家决策意见后进行敏感性因素筛选前,为有效降低专家对某一领域的偏爱而产生的误差,一方面结合领域内高质量文献中的指标进行二次确定,另一方面将某一高分值指标单独进行多专家再评估取最后均值,以此缩小评价结果误差,使敏感性因素更符合客观事实。通过指标筛选,得到公路隧道交通安全评价指标的总平均认可程度和敏感性分布,如图 1所示。
|
| 图 1 筛选评价指标 Fig. 1 Screening evaluation indicators |
| |
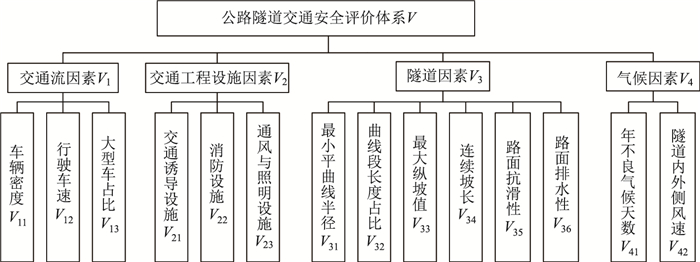
经济学中,把不确定性因素以及对目标函数影响程度较大的因素称为敏感性因素。引用文献[15]的参数设置方式,本研究中指标敏感性分布值大于或等于4即为敏感性因素。因此,以公路隧道交通安全为顶层目标,结合图 1结果,筛选出14个敏感性因素,最终建立公路隧道交通安全评价体系,如图 2所示。
|
| 图 2 公路隧道交通安全评价体系 Fig. 2 Highway tunnel traffic safety evaluation system |
| |
根据公路隧道交通安全评价体系,同时参考相关研究成果[7-14],建立公路隧道交通安全综合评价等级标准。在因素层中,车辆密度、行驶车速、大型车占比、最小平曲线半径、曲线段长度占比、最大纵坡值、连续坡长、隧道内外侧风速这8个指标为定量指标,其余6个指标为定性指标。将公路隧道交通安全综合评价转化为评分制,并构建各指标的分级标准,见表 2。
| 指标 | 非常安全(Ⅰ) | 安全(Ⅱ) | 轻度危险(Ⅲ) | 危险(Ⅳ) | 重度危险(Ⅴ) |
| V11 | 0~0.3 | 0.3~0.55 | 0.55~0.75 | 0.75~1.0 | ≥1.0 |
| V12 | 20~60 | 60~80 | 80~90 | 90~100 | 100~120 |
| V13 | 0~0.2 | 0.2~0.4 | 0.4~0.6 | 0.6~0.8 | 0.8~1 |
| V21 | 0.8~1.0 | 0.6~0.8 | 0.4~0.6 | 0.2~0.4 | 0~0.2 |
| V22 | 0.8~1.0 | 0.6~0.8 | 0.4~0.6 | 0.2~0.4 | 0~0.2 |
| V23 | 0.8~1.0 | 0.6~0.8 | 0.4~0.6 | 0.2~0.4 | 0~0.2 |
| V31 | 80~100 | 60~80 | 40~60 | 20~40 | 0~20 |
| V32 | 0~20 | 20~40 | 40~60 | 60~80 | 80~100 |
| V33 | 0~3 | 3~4 | 4~6 | 6~7 | 7~10 |
| V34 | 1.72~2.53 | 2.53~3.25 | 3.25~5.57 | 5.57~6.74 | 6.74~10 |
| V35 | 80~100 | 60~80 | 40~60 | 20~40 | 0~20 |
| V36 | 80~100 | 60~80 | 40~60 | 20~40 | 0~20 |
| V41 | 0~20 | 20~30 | 30~40 | 40~50 | ≥50 |
| V42 | ≤4 | 4~8 | 8~12 | 12~16 | 16~20 |
2 公路隧道交通安全组合评价方法
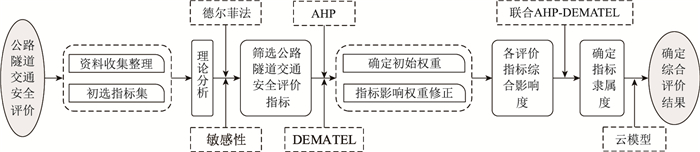
考虑公路隧道交通安全评价具有模糊性、综合性的特性,而传统的AHP法未能排除同级指标间的信息干扰,只讨论了下层指标对上层指标的影响;DEMATEL方法只仅考虑一种指标对剩余所有指标的影响。将两种方法结合则形成优势互补,既考虑单个因素对其他指标的影响,又可讨论下层指标对上层指标的影响,使得到的指标权重更准确[26]。根据表 2等级标准,检测并获取具有科学性、可靠性的隧道交通安全评价指标的效应量。
Step 1:利用AHP-DEMATEL法获取指标综合影响度;
Step 2:根据正态云模型获得指标隶属度;
Step 3:应用模糊数学运算,得到综合评价结果,识别隧道交通安全状态。具体方法和步骤如图 3所示。
|
| 图 3 公路隧道交通安全组合评价方法 Fig. 3 Combined evaluation method for highway tunnel traffic safety |
| |
2.1 确定初始权重Wi
层次分析法(AHP)常应用于多指标评价问题,将复杂问题的结构转变为具有递阶层次的模型,其主要计算公式步骤如下:
(1)构建影响因素判断矩阵。采用1-9标度法对同一层次中的影响因素进行两两比较,构建元素重要度的判断矩阵Aij=[aij],见式(1)(其中,aij为元素i与元素j相对于上一层次目标的比较结果,aii=1)。
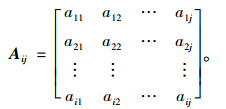
|
(1) |
(2) 运用求和法计算判断矩阵的最大特征值λmax和相应的特征向量,见式(2)。
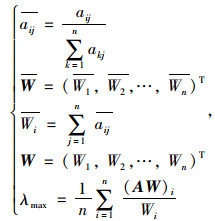
|
(2) |
式中,aij为判断矩阵每列归一化处理后的指标;Wi为归一化处理后的判断矩阵按行相加的指标;W为Wi组成的列向量;W为向量W归一化处理后的结果,即对应的特征向量,其中,i, j=1, 2, …, n。
2.2 指标影响权重的修正DEMATEL法即决策与试验评价实验室法,其目的在于提炼复杂系统中的主因素,简化其层次结构间所产生的方法论。引入DEMATEL法可优化AHP方法得出的基础权重:通过评价系统中各因素之间的逻辑关系,构建直接影响矩阵,从而得到各因素的影响度(fi)、被影响度(ei)和中心度(hi)[19]。
(1) 构建各因素之间具有影响程度等级的有向图。系统因素间的相互影响程度等级用0~4表示。0分为没有影响,1分为影响弱,2分为影响较强,3分为影响强,4分为影响很强,具体表现形式如图 4所示。
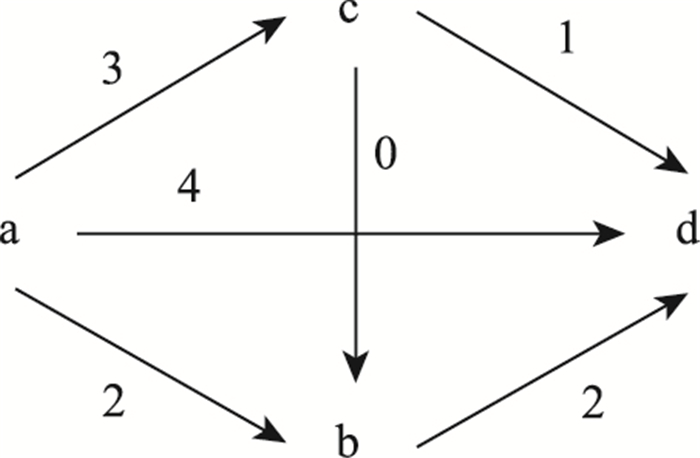
|
| 图 4 指标影响程度有向图 Fig. 4 Directed graph of indicator influence degree |
| |
(2) 建立直接影响矩阵N=[Nij](其中Nij为第i个元素对第j个元素的直接影响程度)。经规范化处理得到规范化直接影响矩阵B,随后求得综合影响矩阵T,见式(3)(其中I为单位矩阵)。
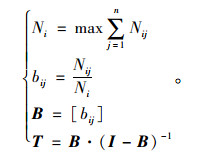
|
(3) |
(3) 计算各指标的fi,ei,hi,见式(4)。
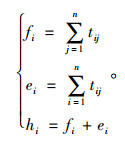
|
(4) |
(4) 联合AHP-DEMATEL法。由AHP法求得的公路隧道交通安全各指标初始权重wi和DEMATEL法求得的隧道交通安全中心度hi,计算各评价指标综合影响度αi,并将综合影响度αi大于0.05的影响因素划分为关键因素,见式(5)。
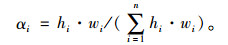
|
(5) |
云模型在描述指标的随机性、模糊性以及两者间的耦合作用可起到较优的效果,同时能够实现评价状态集与评价指标之间的不确定性映射,其最为核心的两个内容是云发生器和云的3个数字特征Ex(期望值)、En(熵值)、He(超熵值),其符号含义与特征如表 3所示。模型首先通过3个数字特征Ex,En,He整体产生1个云粒度,以实现定性概念到定量数值的转换,即正向云发生器;之后通过已得到的数据转换成云的3个数字特征Ex,En,He实现定性概念,如图 5所示。
| 符号 | 含义 | 特征 |
| Ex | 云的重心位置 | 反映定性概念的点 |
| En | 定性概念不确定性的量度 | 反映云滴的离散程度和定性概念的模糊性 |
| He | 熵的不确定性量度 | 反映定性概念中不确定性的凝聚性 |
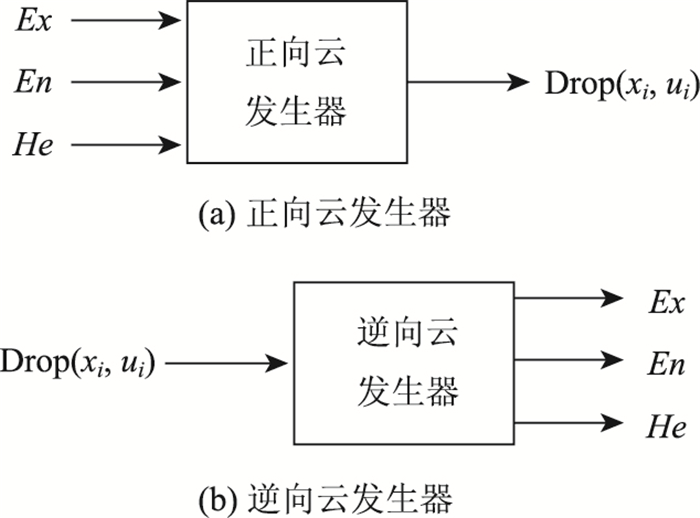
|
| 图 5 云发生器 Fig. 5 Cloud generator |
| |
设定量论域U由有限个具体数值所组成,C表示定量论域U上的定性概念。若存在定量值x∈U为定性概念C的一次随机实现,满足:x~N(Ex, En2),且En~N(En, He2)[14],且x对C的确定度满足:
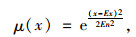
|
(6) |
则x在论域U上的分布称为正态云。
(1) 通过云模型得到公路隧道交通安全评价指标的Ex,En,He。其中,He为常数,根据评价指标的模糊性进行取值;Ex可根据划分的隧道交通安全等级标准区间(xij1, xij2)计算得到,见式(7)。
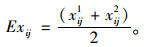
|
(7) |
(2)根据公路隧道交通安全评价等级的区间边界值存在模糊性以及相邻两个安全等级有一半归属度的特性,其熵值求解见式(8)。
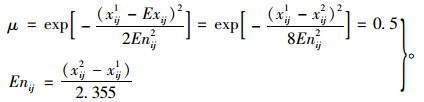
|
(8) |
(3) 生成各评价等级的云图。计算得到公路隧道交通各安全等级正态云模型的3个数字特征Ex,En,He后,通过Matlab编程生成对应的评价指标的隶属度云图。
(4) 构建评价指标隶属度矩阵。根据公路隧道交通安全评价指标所生成对应的隶属度云图,可以得到具体的某一指标在对应的安全等级下的隶属度,即可以构建各指标在不同安全等级下的隶属度矩阵B。
2.4 确定综合评价结果构建综合评价矩阵Z。将各指标综合影响权重矩阵α和隶属度矩阵B进行模糊数学运算,构建综合评价矩阵Z,见式(9)。根据正态云模型隶属度最大原则,即得公路隧道交通安全等级评级结果。
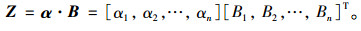
|
(9) |
二峨山隧道位于四川省内,地处龙泉山脉。二峨山山顶海拔高度784.5 m,隧道全长2 302 m,日均断面车流量约为8 000辆,隧道进口设计标高537.18 m,出口设计标高514.92 m,双向四车道,设计时速40 km/h。
3.1 计算综合权重及确定关键因素因公路隧道交通安全评价体系的各层次因素计算初始权重的方法一致,故本研究仅构建准则层的各因素判断矩阵及求解过程,因素层各指标权重可依据准则层计算方法求得。
(1) 根据德尔菲法并结合式(1),得到准则层判断矩阵A:
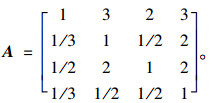
|
(10) |
(2) 通过公式(2)计算得到其特征向量W=(0.450, 0.171, 0.260, 0.119)T,特征值λ=4.072。
(3) 根据构建的准则层判断矩阵阶数为4,CI=0.024,CR=0.027,且CR的值小于0.1,符合一致性检验。
(4) 根据准则层计算步骤,也可求出因素层指标权重,结果见表 4。
| 准则层 | 权重 | 因素层 | 权重 | 初始权重 |
| V1 | 0.450 | V11 | 0.326 | 0.147 |
| V12 | 0.455 | 0.205 | ||
| V13 | 0.218 | 0.098 | ||
| V2 | 0.171 | V21 | 0.402 | 0.069 |
| V22 | 0.223 | 0.038 | ||
| V23 | 0.375 | 0.064 | ||
| V3 | 0.260 | V31 | 0.137 | 0.036 |
| V32 | 0.192 | 0.050 | ||
| V33 | 0.129 | 0.034 | ||
| V34 | 0.171 | 0.044 | ||
| V35 | 0.188 | 0.049 | ||
| V36 | 0.183 | 0.048 | ||
| V4 | 0.119 | V41 | 0.428 | 0.051 |
| V42 | 0.572 | 0.068 |
(5) 借鉴文献[25]提出的权重计算方法,以V11,V12,V13者为例,利用Matlab编程计算直接影响矩阵N、规范矩阵B、综合影响矩阵T;对各指标进行相似计算,再应用式(3)~(4)计算各指标的影响度、被影响度、中心度,结果见表 5。
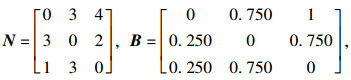
|
(11) |
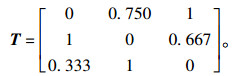
|
(12) |
| 指标 | 影响度 | 被影响度 | 中心度 |
| V11 | 2.323 | 1.212 | 3.535 |
| V12 | 2.421 | 1.231 | 3.652 |
| V13 | 1.876 | 0.678 | 2.554 |
| V21 | 1.523 | 0.356 | 1.879 |
| V22 | 1.139 | 0.332 | 1.471 |
| V23 | 1.478 | 0.325 | 1.803 |
| V31 | 2.389 | 1.128 | 3.517 |
| V32 | 2.312 | 2.219 | 4.531 |
| V33 | 2.561 | 2.136 | 4.697 |
| V34 | 2.121 | 1.293 | 3.414 |
| V35 | 2.561 | 2.211 | 4.772 |
| V36 | 1.873 | 0.556 | 2.429 |
| V41 | 1.572 | 0.478 | 2.050 |
| V42 | 1.211 | 0.382 | 1.593 |
根据得到的各指标初始权重以及中心度,应用公式(5)计算可得各指标综合影响权重:
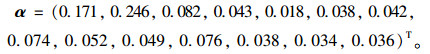
|
(13) |
其中综合影响权重αi大于0.05的评价指标有车辆密度(V11)、行驶车速(V12)、大型车占比(V13)、曲线段长度占比(V32)、最大纵坡值(V33)、路面抗滑性(V35),是影响隧道交通安全的关键性指标。
3.2 构建隶属度矩阵正态云模型最关键一步就是确定公路隧道交通安全评价正态云标准,根据公式(7)、公式(8)计算得到14个指标在5种评价等级对应下的3个具体的数字特征Ex,En,He,结果见表 6。
| 指标 | 非常安全(Ⅰ) | 安全(Ⅱ) | 轻度危险(Ⅲ) | 危险(Ⅳ) | 重度危险(Ⅴ) |
| V11 | (0.15, 0.127, 0.02) | (0.425, 0.106, 0.02) | (0.65, 0.085, 0.02) | (0.875, 0.106, 0.02) | (1.5, 0.424, 0.02) |
| V12 | (40, 16.985, 0.1) | (70, 8.492, 0.1) | (85, 4.246, 0.1) | (95, 4.246, 0.1) | (110, 8.493, 0.1) |
| V13 | (0.1, 0.085, 0.01) | (0.3, 0.085, 0.01) | (0.5, 0.085, 0.01) | (0.7, 0.085, 0.01) | (0.9, 0.085, 0.01) |
| V21 | (0.9, 0.085, 0.01) | (0.7, 0.085, 0.01) | (0.5, 0.085, 0.01) | (0.3, 0.085, 0.01) | (0.1, 0.085, 0.01) |
| V22 | (0.9, 0.085, 0.01) | (0.7, 0.085, 0.01) | (0.5, 0.085, 0.01) | (0.3, 0.085, 0.01) | (0.1, 0.085, 0.01) |
| V23 | (0.9, 0.085, 0.01) | (0.7, 0.085, 0.01) | (0.5, 0.085, 0.01) | (0.3, 0.085, 0.01) | (0.1, 0.085, 0.01) |
| V31 | (90, 8.493, 0.1) | (70, 8.493, 0.1) | (50, 8.493, 0.1) | (30, 8.493, 0.1) | (10, 8.493, 0.1) |
| V32 | (10, 8.493, 0.1) | (30, 8.493, 0.1) | (50, 8.493, 0.1) | (70, 8.493, 0.1) | (90, 8.493, 0.1) |
| V33 | (1.5, 1.274, 0.05) | (3.5, 0.424, 0.05) | (5, 0.849, 0.05) | (6.5, 0.424, 0.05) | (8.5, 1.274, 0.05) |
| V34 | (2.1, 0.344, 0.02) | (2.89, 0.306, 0.02) | (4.41, 0.985, 0.02) | (6.2, 0.497, 0.02) | (8.37, 1.384, 0.02) |
| V35 | (90, 8.493, 0.1) | (70, 8.493, 0.1) | (50, 8.493, 0.1) | (30, 8.493, 0.1) | (10, 8.493, 0.1) |
| V36 | (90, 8.493, 0.1) | (70, 8.493, 0.1) | (50, 8.493, 0.1) | (30, 8.493, 0.1) | (10, 8.493, 0.1) |
| V41 | (10, 8.493, 0.1) | (25, 4.246, 0.1) | (35, 4.246, 0.1) | (45, 4.246, 0.1) | (60, 8.493, 0.1) |
| V42 | (2, 1.699, 0.05) | (6, 1.699, 0.05) | (10, 1.699, 0.05) | (14, 1.699, 0.05) | (18, 1.699, 0.05) |
根据表 6得到的各指标在对应安全等级评价标准下的数字特征,依据各指标综合影响度大于0.05,将其视为关键因素的条件。得到关键因素为:车辆密度、行驶车速、大型车占比、曲线段长度占比、最大纵坡值、路面抗滑性。通过编程生成列举的6个关键因素在对应等级下的正态云图,进而计算不同等级对应的隶属度,结果如图 6所示。
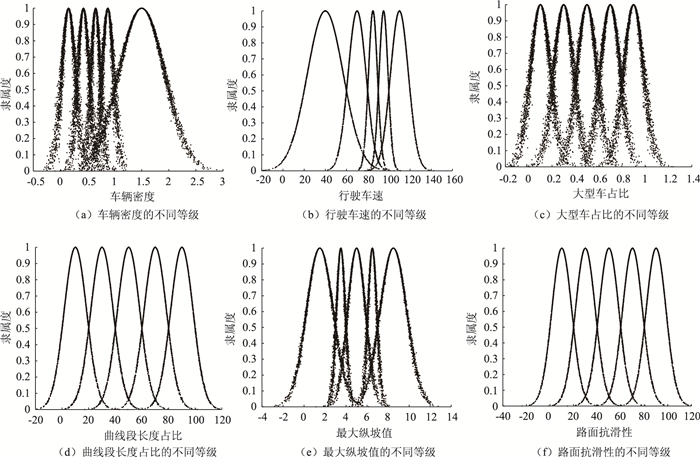
|
| 图 6 6个关键因素正态云图 Fig. 6 Normal cloud diagram of 6 key factors |
| |
根据图 6关键指标因素的云图显示,可以较为直观的得到6个关键因素在不同等级下云图的期望值对应云模型分布中心,云滴的离散程度(熵值)较小且云滴的厚度(超熵值)也较小,说明生成的模型模糊性和不确性较小,即模型生成的隶属度稳定。随后,根据生成的云模型隧道交通安全评价体系中各指标的正态云图,采用隶属度公式(6)进行计算。由于云模型通常具有一定程度的随机性,为了保证隶属度计算结果的可靠性,在编程计算时,利用500次加权平均的方式生成各指标综合隶属度,结果见表 7。
| 指标 | 非常安全(Ⅰ) | 安全(Ⅱ) | 轻度危险(Ⅲ) | 危险(Ⅳ) | 重度危险(Ⅴ) |
| 车辆密度 | 0.030 | 0.759 | 0.222 | 0.006 | 0.006 |
| 行驶车速 | 0.496 | 0.499 | 0.006 | 0 | 0 |
| 大型车占比 | 0.212 | 0.835 | 0.017 | 0.009 | 0 |
| 最小平曲线半径 | 0.500 | 0.499 | 0.002 | 0 | 0 |
| 曲线段长度占比 | 0.002 | 0.521 | 0.479 | 0.002 | 0 |
| 连续坡长 | 0.146 | 0.487 | 0.498 | 0.0002 | 0 |
| 最大纵坡值 | 0.007 | 0.597 | 0.469 | 0 | 0 |
| 年不良气候天数 | 0.499 | 0.499 | 0.002 | 0 | 0 |
| 交通诱导设施 | 0.450 | 0.540 | 0.007 | 0.003 | 0 |
| 消防设施 | 0.340 | 0.620 | 0.040 | 0 | 0 |
| 通风与照明设施 | 0.420 | 0.560 | 0.020 | 0 | 0 |
| 路面抗滑性 | 0.230 | 0.740 | 0.030 | 0 | 0 |
| 路面排水性 | 0.350 | 0.580 | 0.060 | 0.010 | 0 |
| 隧道内外侧风速 | 0.620 | 0.360 | 0.020 | 0 | 0 |
3.3 综合评价结果
将所求得到的隧道交通安全指标综合权重矩阵α与隶属度矩阵B进行模糊数学运算,得到最终公路隧道交通安全评价结果,如表 8所示。
| 安全状态 | 非常安全(Ⅰ) | 安全(Ⅱ) | 轻度危险(Ⅲ) | 危险(Ⅳ) | 重度危险(Ⅴ) |
| 数据值 | 0.324 | 0.595 | 0.096 | 0.002 | 0.001 |
表 8数据结果显示,该公路隧道安全状态处于非常安全等级的数据值为0.324,处于安全等级的数据值为0.595,处于轻度危险等级的数据值为0.096,处于危险等级的数据值为0.002,处于重度危险等级的数据值为0.001。根据云模型最大隶属度归属原则,结果表明二峨山隧道交通安全评价等级为Ⅱ级。依据隧道现场调研结果,二峨山隧道各项运行指标均符合设计规范,隧道内各设施正常运行,日常养护及运作情况比较良好,隧道内的细小问题能及时有效解决,隧道整体交通安全状态比较良好,调研结果与论文综合评价结果相吻合,检验了评价结果的可靠性。
4 结论我国隧道建设和使用越来越多,其主被动安全也引起人们的广泛关注和研究,隧道交通安全在多个方面都存在不确定性,所以隧道交通安全评价不单单只是不确定性中的随机性或模糊性的某一方面,更是复合型的不确定性评价问题。论文基于组合模型上科学性及可行性的考量,从权重、隶属度、敏感因素云模型图、模糊度运算、综合评价结果层层递进,得到隧道交通安全评价结果,并且本研究采用的AHP-DEMATEL和云模型对公路隧道交通安全进行评价,考虑了指标间的耦合性和模糊性,评价结果和隧道现实情况一致,显示评价方法是合理、可行的。该方法具有一定优势,具体表现在:
(1) 将敏感性分析引入德尔菲法进行指标筛选。以德尔菲法为主要理论依据,引入经济学中“敏感性”的概念,以总平均认可程度对评价指标进行敏感性分析,对评价指标进一步筛选,最终定量地确立公路隧道运行环境安全综合评价指标体系。该评价方式简捷且具有较强的实用性,评价指标意义清晰且评价值获取较为容易。
(2) 克服了指标间的模糊性。采用AHP-DEMATEL结合的方法来确定隧道交通安全各评价指标的综合影响度,既避免了传统AHP方法因素之间的相互影响,又克服了DEMATEL方法在等值权重上计算的不足,所得的指标权重更优。
(3) 评价结果更为直观。对比文献[14],[22],[24],[27]评价方法所得结果可知,利用AHP-DEMATEL和云模型组合评价的结果更直观且更具可靠性,因为云模型不仅得到了各指标的3个数字特征Ex,En,He,还将指标的云图在不同等级下的离散程度(熵)和厚度(超熵)直接展现出来,使评价结果更具说服力。
| [1] |
赖金星, 张鹏, 周慧, 等. 高速公路隧道交通事故规律研究[J]. 隧道建设, 2017, 37(1): 37-42. LAI Jin-xing, ZHANG Peng, ZHOU Hui, et al. Study of Rules of Traffic Accidents in Expressway Tunnels[J]. Tunnel Construction, 2017, 37(1): 37-42. |
| [2] |
邬洪波, 周荣贵, 廖军洪, 等. 高速公路隧道进口段的安全评价技术[J]. 公路交通科技, 2012, 29(10): 126-132. WU Hong-bo, ZHOU Rong-gui, LIAO Jun-hong, et al. Study of Rules of Traffic Accidents in Expressway Tunnels[J]. Journal of Highway and Transportation Research and Development, 2012, 29(10): 126-132. |
| [3] |
代言明, 胡彦杰, 邓敏, 等. 基于模糊网络分析法的公路隧道火灾风险综合评价模型[J]. 安全与环境学报, 2016, 16(4): 57-61. DAI Yan-ming, HU Yan-jie, DENG Min, et al. Comprehensive Road Tunnel Fire Risk Assessment Model Based on the FAND[J]. Journal of Safety and Environment, 2016, 16(4): 57-61. |
| [4] |
刘辉, 孙世梅. 基于改进LEC法的公路隧道施工安全评价研究[J]. 现代隧道技术, 2015, 52(1): 26-32, 61. LIU hui, SUN Shi-mei. Study on the Construction Safety Assessment of Highway Tunnels Based on the Improved LEC Method[J]. Modern Tunnelling Technology, 2015, 52(1): 26-32, 61. |
| [5] |
吴森阳, 胡学兵. 公路隧道运营安全等级评估研究[J]. 地下空间与工程学报, 2018, 14(增1): 363-370. WU Sen-yang, HU Xue-bing. Study on Safety Evaluation of Road Tunnel Operation[J]. Chinese Journal of Underground Space and Engineering, 2018, 14(S1): 363-370. |
| [6] |
周兵, 王传生, 刘芳亮, 等. 城市交通隧道运营安全风险评估模型及管理系统研究[J]. 公路交通科技, 2021, 38(1): 97-103. ZHOU Bing, WANG Chuan-sheng, LIU Fang-liang, et al. Study on Risk Assessment Model and Management System for Urban Traffic Tunnel Operation Safety[J]. Journal of Highway and Transportation Research and Development, 2021, 38(1): 97-103. |
| [7] |
《中国公路学报》编辑部. 中国隧道工程学术研究综述·2015[J]. 中国公路学报, 2015, 28(5): 1-65. Editorial Department of China Journal of Highway and Transport. Review on China's Tunnel Engineering Research: 2015[J]. China Journal of Highway and Transport, 2015, 28(5): 1-65. |
| [8] |
郭延永, 刘攀, 吴瑶, 等. 山区高速公路隧道交通运行环境安全评价[J]. 武汉理工大学学报, 2013, 35(7): 53-58. GUO Yan-yong, LIU Pan, WU Yao, et al. Safety Evaluation of Mountain Freeway Tunnels' Traffic Operation Environment[J]. Journal of Wuhan University of Technology, 2013, 35(7): 53-58. |
| [9] |
胡群芳, 周博文, 王飞, 等. 基于模糊层次分析的公路隧道结构安全评估技术[J]. 自然灾害学报, 2018, 27(4): 41-49. HU Qun-fang, ZHOU Bo-wen, WANG Fei, et al. Structural Safety Assessment Technology of Long Highway Tunnel Based on Fuzzy Analytic Hierarchy Process[J]. Journal of Natural Disasters, 2018, 27(4): 41-49. |
| [10] |
钱勇, 马健霄, 赵顗, 等. 基于集对可拓物元模型的公路隧道运营环境安全评价方法[J]. 森林工程, 2020, 36(1): 87-95. QIAN Yong, MA Jian-xiao, ZHAO Yi, et al. Safety Evaluation Method for Highway Tunnel Operation Environment Based on Set-pair Extension Matter Element Model[J]. Forest Engineering, 2020, 36(1): 87-95. |
| [11] |
方守恩, 邬洪波, 廖军洪, 等. 山区高速公路隧道群路段安全评价[J]. 同济大学学报: 自然科学版, 2013, 41(5): 693-699. FANG Shou-en, WU Hong-bo, LIAO Jun-hong, et al. Safety Evaluation of Freeway Tunnel Groups in Mountainous Areas[J]. Journal of Tongji University: Natural Science Edition, 2013, 41(5): 693-699. |
| [12] |
胡江碧, 张晓芹, 郭达. 基于安全视认的夜间公路隧道入口段光环境研究[J]. 北京理工大学学报, 2016, 36(5): 487-490, 497. HU Jiang-bi, ZHANG Xiao-qin, GUO Da. Research on the Tunnel Entrance Night Light Environment of Highway Tunnel Based on Visual Safety[J]. Transactions of Beijing Institute of Technology, 2016, 36(5): 487-490, 497. |
| [13] |
杜志刚, 徐弯弯, 向一鸣. 基于视线诱导的公路隧道光环境优化研究框架[J]. 中国公路学报, 2018, 31(4): 122-129. DU Zhi-gang, XU Wan-wan, XIANG Yi-ming. Research on Light Environment Improvement Framework of Highway Tunnel Based on Visual Guidance[J]. China Journal of Highway and Transport, 2018, 31(4): 122-129. |
| [14] |
史晓花, 杜志刚, 郑展骥, 等. 公路隧道中部视错觉减速标线的优化[J]. 公路交通科技, 2016, 33(3): 89-96. SHI Xiao-hua, DU Zhi-gang, ZHENG Zhan-ji, et al. Optimization of Optical Illusion Deceleration Markings in Middle of Highway Tunnel[J]. Journal of Highway and Transportation Research and Development, 2016, 33(3): 89-96. |
| [15] |
陈红, 周继彪, 王建军, 等. 公路隧道运行环境安全评价指标与方法[J]. 长安大学学报: 自然科学版, 2013, 33(4): 54-61, 74. CHEN Hong, ZHOU Ji-biao, WANG Jian-jun, et al. Safety Evaluation Indexes and Method for Traffic Environment of Highway Tunnels[J]. Journal of Chang'an University: Natural Science Edition, 2013, 33(4): 54-61, 74. |
| [16] |
杨健, 阳富强, 沈斐敏. 基于改进DSmT的公路隧道行车安全综合评价方法研究[J]. 中国安全科学学报, 2016, 26(8): 116-121. YANG Jian, YANG Fu-qiang, SHEN Fei-min. Comprehensive Evaluation of Highway Tunnel Traffic Safety Based on Improved DSmT[J]. China Safety Science Journal, 2016, 26(8): 116-121. |
| [17] |
QU X, QIANG M, YUANITA V, et al. Design and Implementation of A Quantitative Risk Assessment Software Tool for Singapore Road Tunnels[J]. Expert Systems with Applications, 2011, 38(11): 13827-13834. |
| [18] |
KAZARAS K, KIRYTOPOULOS K, RENTIZELAS A. Introducing the STAMP Method in Road Tunnel Safety Assessment[J]. Safety Science, 2012, 50(9): 1806-1817. |
| [19] |
瞿英, 路亚静, 刘紫玉, 等. 基于AHP-DEMATEL法的权重计算方法研究[J]. 数学的实践与认识, 2016, 46(7): 38-46. QU Ying, LU Ya-jing, LIU Zi-yu, et al. Research on the Weight Calculation Method Based on the AHP-DEMATEL Method[J]. Mathematics in Practice and Theory, 2016, 46(7): 38-46. |
| [20] |
张秋文, 章永志, 钟鸣. 基于云模型的水库诱发地震风险多级模糊综合评价[J]. 水利学报, 2014, 45(1): 87-95. ZHANG Qiu-wen, ZHANG Yong-zhi, ZHONG Ming. A Cloud Model Based Approach for Multi-hierarchy Fuzzy Comprehensive Evaluation of Reservoir-induced Seismic Risk[J]. Journal of Hydraulic Engineering, 2014, 45(1): 87-95. |
| [21] |
JTG D70/2-2014, 公路隧道设计规范(第2册交通工程与附属设施)[S]. JTG D70/2-2014, Specifications for Design of Highway Tunnels (Section 2 Traffic Engineering and Affiliated Facilities)[S]. |
| [22] |
国威, 潘晓东, 蒋曙豪. 基于相对差异函数的隧道群交通安全评价[J]. 同济大学学报: 自然科学版, 2013, 41(1): 101-105. GUO Wei, PAN Xiao-dong, JIANG Shu-hao. Relative Difference Function-based Traffic Safety Assessment of Tunnel Groups[J]. Journal of Tongji University: Natural Science, 2013, 41(1): 101-105. |
| [23] |
谭泽斌. 基于可拓云模型的隧道交通安全评价研究[D]. 武汉: 华中科技大学, 2019. TAN Ze-bin. Research on Tunnel Traffic Safety Evaluation Based on Extension Cloud Model[D]. Wuhan: Huazhong University of Science and Technology, 2019. |
| [24] |
BASSAN S. Overview of Traffic Safety Aspects and Design in Road Tunnels[J]. IATSS Research, 2016, 40(1): 35-46. |
| [25] |
VENKATARAMAN N S, ULFARSSON G F, SHANKAR V N. Extending the Highway Safety Manual (HSM) Framework for Traffic Safety Performance Evaluation[J]. Safety Science, 2014, 64: 146-154. |
| [26] |
章光, 武晓炜, 胡少华, 等. 基于AHP-DEMATEL的混凝土重力坝健康诊断[J]. 安全与环境学报, 2019, 19(5): 1489-1496. ZHANG Guang, WU Xiao-wei, HU Shao-hua, et al. On the Strength Identification and Determination of the Concrete Gravity Dam Based on the AHP-DEMATEL Model[J]. Journal of Safety and Environment, 2019, 19(5): 1489-1496. |
| [27] |
王景春, 张法, 林佳秀. 基于改进云模型的公路施工安全防护系统评价[J]. 中国安全科学学报, 2017, 27(8): 73-78. WANG Jing-chun, ZHANG Fa, LIN Jia-xiu. Evaluation of Safety Protection System in Highway Construction Based on Improved Cloud Model[J]. China Safety Science Journal, 2017, 27(8): 73-78. |
 2021, Vol. 38
2021, Vol. 38
