扩展功能
文章信息
- 王欲敏, 杨未蓬, 周丹, 邬江红
- WANG Yu-min, YANG Wei-peng, ZHOU Dan, WU Jiang-hong
- 高温沥青混合料摊铺时正交异性钢桥面板温度响应分析
- Analysis on Temperature Response of Orthotropic Steel Bridge Deck during Paving of High-temperature Asphalt Mixture
- 公路交通科技, 2021, 38(7): 60-68
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(7): 60-68
- 10.3969/j.issn.1002-0268.2021.07.009
-
文章历史
- 收稿日期: 2020-06-30
2. 绵竹市公路工程质量监督所, 四川 德阳 618200;
3. 浙江公路技师学院, 浙江 杭州 310023;
4. 重庆交通大学 土木工程学院, 重庆 400074
2. Mianzhu Highway Engineering Quality Supervision Institute, Deyang Sichuan 618200, China;
3. Zhejiang Highway Technician College, Hangzhou Zhejiang 310023, China;
4. School of Civil Engineering, Chongqing Jiaotong University, Chongqing 400074, China
目前,大、中跨径的桥梁大多采用正交异性桥面板钢箱梁体系,沥青混合料常用来作为钢桥面板上的铺装层。浇注式沥青混凝土由于具有优良的疲劳性能、抗老化性能、变形随从能力和一次摊铺成型的特点[1-2],逐渐从其他桥面铺装材料选型中脱颖而出,但在摊铺沥青过程中为了保持混合料的流动性和自密实效果,常需要采用高温摊铺的方式,摊铺温度往往高达220~260 ℃。由于钢桥面所采用的钢材是一种传热性能好,热膨胀系数较高的材料,对温度变化极为敏感,如此高的摊铺温度势必会使得钢箱梁结构在局部高温下产生温差,引起结构温度变形和内力,从而对铺装层的摊铺质量埋下隐患,由于钢桥面的受高温形成凹洞或凸起,特容易造成铺装层局部厚度过薄的现象[3]。
已有学者研究了太阳辐射、气温等环境因素对桥梁温度场分布的影响[4-6],但没有涉及到高温沥青摊铺过程对钢桥面的影响,也有学者[7-11]研究了沥青混凝土摊铺作用对钢-混组合连续箱梁桥的温度场分布,但是这一温度分布规律并不适用于正交异性板桥面板钢箱梁结构。针对这个问题,杜明峰[12]借助ANSYS有限元软件建立了双箱单室钢箱梁及扁平钢箱梁节段瞬态传热模型,对浇注式沥青混凝土摊铺过程中钢箱梁温度场的时空分布特征进行分析;钱振东[3]课题组建立了高温沥青摊铺下钢箱梁的瞬态热传导数值模型,模型中考虑自重、二期荷载及日照温度荷载,并将动态温度荷载数值施加在摊铺区,进而进行温度效应分析;Wang J F、沈聪等[13-14]建立高温曲线钢箱梁桥面铺装层的有限元模型,结合实测数据对有限元模型的仿真数据进行验证对比,但其没有考虑接触界面处防水黏结层的接触热阻参数。本研究结合某长江大桥在浇注式沥青混凝土摊铺过程中实测数据,基于瞬态温度场理论和热力学边界假设条件,确定数值模拟所需的各项热力学参数,并建立相应的温度场有限元模型,在验证模拟方法的可靠性之后,进一步分析高温摊铺下正交异性钢桥面板温度场的时空变化规律。
1 瞬态温度场理论热传导问题分为稳态热传导和瞬态热传导问题,其关键因素在于其变量是否与时间相关。在浇注式沥青摊铺过程中,摊铺机就相当于一个移动热源,同时钢桥还会受太阳福射、空气对流换热和辐射换热等作用,与时间相关,应属于瞬态热传导问题。由于计算过程的复杂性和因素的多变性,运用传统的解析方法求解温度场存在较大困难。现有限元方法在传热学中已有较为成熟的应用,可解决导热微分方程等复杂问题。
根据热传导理论,三维瞬态温度分布T(x, y, z, t),应满足如下控制微分方程:
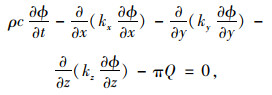
|
(1) |
式中, ρ为材料密度;c为比热容;kx,ky,kz为沿着x,y,z方向的热传导系数; Q为内部热源。
一般来说,导热问题还需满足以下3类边界条件:
(1) 初始温度场:
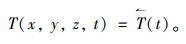
|
(2) |
(2) 热流密度:
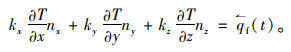
|
(3) |
(3) 和环境对流换热:
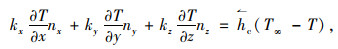
|
(4) |
式中,nx,ny,nz为边界外法线的方向余弦值;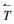
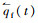
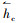
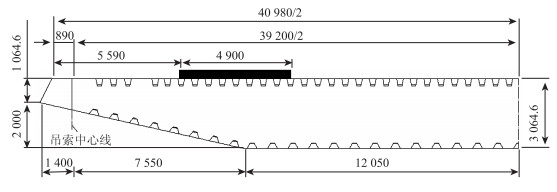
某长江大桥全长1 520 m,主桥主跨880 m,标准宽度为38.0 m。顶板采用U肋和横隔板形成的正交异性板结构体系,钢箱梁截面参数见图 1。桥面铺装采用总厚度为7.2 cm的浇注式沥青混凝土铺装技术体系:2 mm厚MMA防水体系+3.5 cm厚浇注式沥青混凝土GA-10+3.5 cm厚SMA-10。目标测试对象为靠近桥侧的摊铺带钢箱梁(如图 1黑色区域所示),摊铺中心距离钢箱梁边缘8.04 m,宽度为4.9 m,摊铺速度为2 m/min。温度测试示意图如图 2所示。
|
| 图 1 钢箱梁参数(单位:mm) Fig. 1 Parameters of steel box girder(unit: mm) |
| |

|
| 图 2 温度测试 Fig. 2 Temperature test |
| |
2.2 测点布置
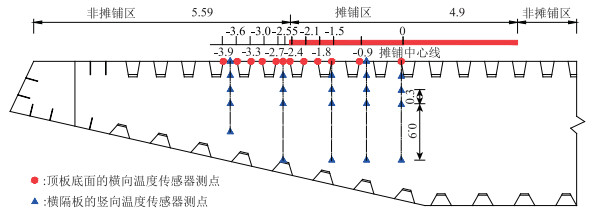
为了测试钢箱梁在沥青摊铺过程中温度变化,传感器采用特制的接触型电阻温度传感器。共布设49个温度传感器:顶板底面1个纵向断面(摊铺带中心线,间距4×1.5 m)、顶板底面2个横向断面(横隔板位置和两个横隔板中间位置)。图 3为横隔板断面测点布置。
|
| 图 3 横隔板断面测点布置(单位:m) Fig. 3 Layout of measuring points on cross-section of diaphragm (unit: m) |
| |
2.3 测试方法
由于测试断面距离摊铺起始端距离较小,当摊铺开始时,即进行读数。测量时间是从早上8点开始,以30 s间隔时间在线测试10 h左右的时间,然后离线进行测试,直至温度与空气温度相同时为止,总测试时间为26 h。
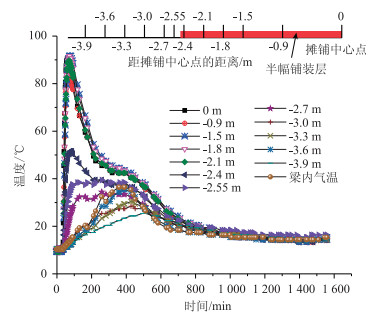
2.4 测试结果典型温度曲线图 4中典型温度曲线的参考点选取跨中顶板底面,对各个横向测点进行了连续26 h的温度变化测试,从图中可以看出:(1)位于摊铺区域的顶板峰值温度高于非摊铺区,摊铺区的峰值温度大约在35 min达到最大值为92 ℃; (2)桥面板沿横向温度传递有明显滞后现象,从摊铺区域向非摊铺区域,钢板达到温度峰值的时间逐渐后延; (3)随着时间推移,温度在顶板影响范围逐渐增大,最终影响大致在摊铺左右各1 m,摊铺4.9 m铺装块下影响范围7 m左右。
|
| 图 4 跨中顶板底面横向温度变化 Fig. 4 Transverse temperature change of bottom of mid-span roof |
| |
3 有限元数值模拟方法 3.1 温度场热力学边界条件假设
(1) 初始温度场
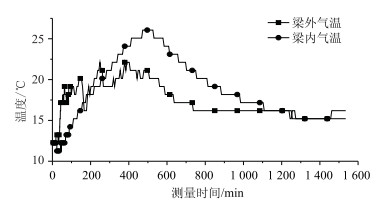
测试当天环境温度变化曲线如图 5所示,梁体结构的初始温度和环境初始温度是一致,即11 ℃;沥青混凝土铺装层的实际温度为240 ℃。
|
| 图 5 温度-时间变化曲线 Fig. 5 Temperature-time curves |
| |
(2) 太阳辐射量
模型中考虑太阳辐射日变化,查询相关资料确定了现场试验当天的正午最大辐射q0=455 W/m2,并依据文献[15]的研究成果,选取了太阳辐射日变化过程的近似函数。
(3) 辐射换热
结构体除了吸收外界短波辐射以外,自身也在不断发射辐射波,与周围环境形成辐射换热。钢箱梁与大气接触处的表面均设置辐射换热面,还需要确定结构表面发射率ε,通常沥青铺装常取0.81,箱梁表面取0.4。
(4) 对流换热
根据文献[16],对流换热系数的表达式为:
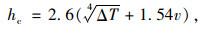
|
(5) |
式中,ΔT为箱梁温度与环境温度的温差; v为经过箱梁表面的风速。
已有研究表明,在估算最不利温度效应时,钢箱梁外侧风速近似取为1 m/s[17],沥青混合料施工温度与环境温差达到229 K,钢箱表面对流换热系数hc为14 W/(m2·K)。钢箱的侧面及底面由于太阳辐射小,假设温差ΔT均为0,则计算出对流换热系数hc为4.1 W/(m2·K),而箱梁内部为自然对流,空气流动较小,故不考虑对流换热。
3.2 防水黏结层导热系数铺装层与钢桥面板之间的防水黏结层在热传导分析中起着一定的阻热作用。在有限元建模分析中,如考虑将防水黏结层按实体单元建模,并赋予相应热参数,但由于厚度方向尺寸相比其他方向的尺寸过小,极易造成求解方程病态奇异,与实际结果相差较大。结合以往力学分析[18-19],本节将防水黏结层的厚度忽略不计,在模型中通过设置防水层的界面热阻参数(导热系数的倒数),以体现出防水黏结层的阻热效应。
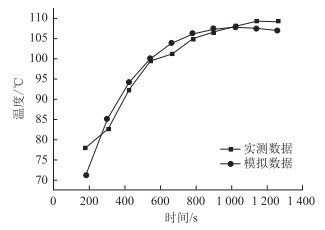
基于试验-仿真模拟方法,选取文献[20]中所用室内模型及其钢板温度变化试验数据,借助Abaqus建立相应的室内传热有限元模型,在模型中设置不同的界面热阻参数值,分别计算相应的温度变化。基于最小二乘法的优化方法,再将模拟温度与实测温度的误差平方和作为选择依据,以误差平方和最小的热阻值作为最适宜的热阻系数,得到界面热阻值为0.007 94 (m2·K)/W。将室内模型对应的模拟温度与实测温度对比,从图 6中可看出,两条曲线的变化趋势基本一致,因此可将此界面热阻参数代入钢箱梁有限元模型,以模拟铺装层与钢板之间的热传导作用。
|
| 图 6 温度-时间曲线对比图 Fig. 6 Comparison of temperature-time curves |
| |
3.3 有限元模型结果与现场试验结果对比分析
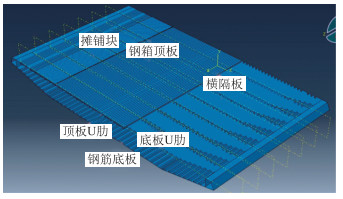
采用ABAQUS有限元软件建立一段纵向长为24 m的正交异形板钢箱梁模型。钢箱顶板、U肋、隔板,均采用D4R四节点传热四边形壳单元模拟,铺装块采用DC3D8实体单元来模拟35 mm的铺装层。计算模型示意图如图 7所示。本节仅考虑高温沥青摊铺和日照引起的温度荷载,其余模型中所用尺寸和各项计算参数见表 1。
|
| 图 7 模型示意图 Fig. 7 Schematic diagram of model |
| |
| 项目 | 参数值 | 项目 | 参数值 |
| 顶、底板厚度/mm | 16 | 正午最大辐射/ (W·m-2) |
455 |
| 顶板U肋及底板U 肋间距/m |
0.6/0.9 | 桥面及铺装表面换热系 数/[W·(m2·K)-1] |
14 |
| U肋厚度/mm | 8 | 底面及侧面换热系数/ [W·(m2·K)-1] |
4.1 |
| 横隔板间距/m | 3 | 沥青铺装层、箱梁发射率 | 0.81/0.4 |
| 横隔板厚度/mm | 10 | 界面热阻值/ [(m2·K)·W-1] |
0.007 94 |
在浇注式沥青混凝土摊铺现场试验中,摊铺机等同于一个连续移动的热源,而在有限元模拟中则考虑将整个连续摊铺过程离散化,即采用生死单元法模拟摊铺机作为移动热源向前传递温度的过程,并在铺装层和钢桥面板接触面中设置热传递接触属性:将纵向24 m长的铺装层等分为8块,将全部铺装层单元设置为无效单元,然后设置8个分析步,并在每个分析步中依次激活相应的铺装层单元[20]。
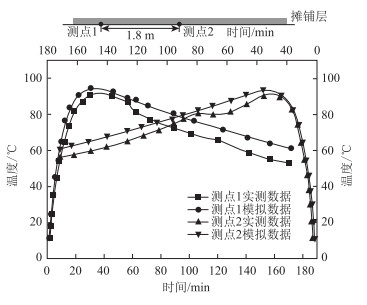
本节主要研究高温摊铺下钢箱梁在升温阶段和高温阶段中温度场的变化规律,将实测数据与模拟数据进行对比,由图 8可知,摊铺区域顶板底面的模拟温度和实测温度在升温阶段拟合较好,验证了采用生死单元法的有限元建模方法能够有效地模拟高温摊铺下钢箱梁的升温变化过程,因此可将此模型用于温度场的计算。
|
| 图 8 跨中顶板温度对比图 Fig. 8 Comparison of temperatures at mid-span roof |
| |
4 典型温度场分析 4.1 温度场竖向分布规律
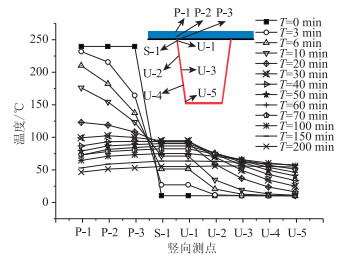
图 9表示的是开始摊铺后,位于跨中截面摊铺区域中心处竖向测点在不同时刻的温度变化分布情况。P-1,P-2,P-3为铺装层测点,沿厚度方向的3等分点,S-1为顶板的测点,U-1~U-5为U肋测点,沿竖向的5等分点。可以得到:(1)铺装层与钢板、U肋之间的温差随着时间的增加而逐渐减小,在30 min左右基本趋于一致;(2)U肋的温度的升温速率慢于与铺装层直接接触的钢桥面板;(3)铺装层、钢板、U肋的温度大约在150 min基本稳定。
|
| 图 9 不同时刻竖向测点温度分布 Fig. 9 Distribution of temperatures at vertical measuring points at different time |
| |
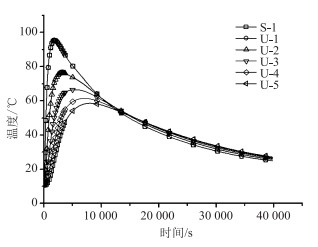
由图 10中跨中截面S-1和U-1的温度-时间曲线可知:(1)钢桥面板上测点S-1在整个摊铺过程中与测点U-1温度分布情况相同,大约在30 min时达到最高温度95 ℃;(2)由U-1~U-5的温度-时间曲线可知,沿着U肋竖向温度传递的滞后现象随时间变化越来越明显,各个测点达到的峰值温度逐步降低,且所经历的时间越多;(3)对于U肋结构还需考虑由温差引起的温度应力,对比U-1和U-2温度-时间曲线,可得到在17.8 min左右达到最大温差74 ℃,形成的温差将会对结构稳定性造成不利影响。
|
| 图 10 竖向测点温度-时间曲线 Fig. 10 Temperature-time curves of vertical measuring points |
| |
4.2 温度场横向分布规律
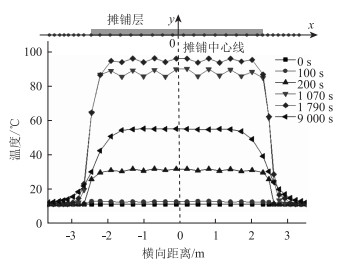
图 11表示的是跨中顶板在几个特殊时刻沿横向温度分布曲线,包括摊铺开始时(0 s)、铺装层摊铺中某时刻(100,200 s)、U肋达到最大温差时(1 070 s)、摊铺区域顶板温度达到最大时(1 790 s)、整体温度稳定时(9 000 s)。可以得到:(1)不同时刻的横向温度分布规律基本一致,其横向温度曲线大致形成了一个以摊铺中心线为对称中心的对称图形。(2)温度曲线中锯齿形是顶板下方U肋导致,U肋处钢桥面温度较其他部位略低;(3)随着时间推移,顶板温度的影响范围逐渐增大,最终影响大致在摊铺边缘左右各1 m,也就是摊铺4.9 m宽的铺装层所对应的影响范围为7 m左右。
|
| 图 11 不同时刻横向测点温度分布 Fig. 11 Distribution of temperatures at transverse measuring points at different time |
| |
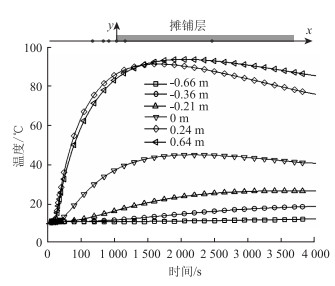
图 12为跨中顶板在摊铺边缘-0.66~0.24 m范围内各个测点的温度变化曲线,0 m为摊铺边缘。可以得到:(1)摊铺区域从内到外,顶板温度峰值时间逐渐后延,且峰值温度逐渐降低;(2)摊铺区域内(0.24 m)、外(-0.21 m)温度差别较大,大约在70 ℃;(3)对摊铺区域中心(2.64 m)和摊铺边缘(0 m)的温度-变化曲线进行对比分析,两测点的温度变化规律大致相同,仅是峰值温度上的差异:摊铺边缘顶板大约在35 min左右达到峰值温度,为45 ℃,与摊铺中心顶板的峰值温度相比,相差50 ℃。
|
| 图 12 横向测点温度-时间曲线 Fig. 12 Temperature-time curves of transverse measurement points |
| |
4.3 温度场纵向分布规律
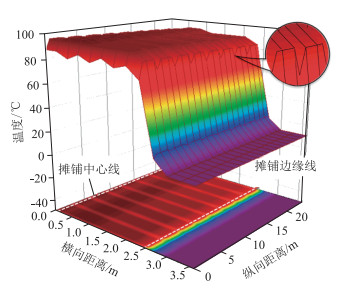
图 13中为顶板在1 070 s时温度分布三维图和温度水平投影图,横向距离原点为摊铺中心,纵向距离原点为摊铺起点。可以得到:(1)纵向各截面的横向温度变化规律类似;(2)由于摊铺时间差,同一时刻沿纵向有一定温度差;(3)纵向温度分布三维图中锯齿形是由顶板下方横隔板导致,致使横隔板处顶板的纵向温度有着规律性的降低,温差在6~7 ℃,纵向影响范围大约为横隔板附近各0.6 m,但离摊铺边缘线越远,横隔板所造成的影响逐渐减小。
|
| 图 13 纵向温度分布三维图(1 070 s) Fig. 13 Three-dimensional diagram of longitudinal temperature distribution (1 070 s) |
| |
5 最不利温度荷载作用下的正交异性钢桥面板温度力学响应 5.1 有限元模型概况
本节将针对性地研究高温摊铺下对钢箱梁力学响应及变形效应的影响,不计钢箱梁自重,只考虑沥青混凝土产生的温度荷载,通过将上文正交异性板钢箱梁温度场分析模型导出钢箱梁温度变化数据,作为应力场分析模型中温度荷载。应力场计算模型在温度场模型的基础上,尺寸参数保持不变,添加钢材和沥青混凝土的材料参数,见表 2。在应力场分析模型中需要设置边界条件,在吊杆位置处约束钢箱梁的竖向位移,在钢箱梁的跨中中心位置处约束钢箱梁的横向位移和纵向位移,在这种约束条件下,模型在纵向和横向上可以自由地进行伸缩,对于节段箱梁而言,该边界条件最为接近实际工作状态的约束方式。
| 材料 | 弹性模量/MPa | 泊松比 | 膨胀系数/(×10-5) |
| 钢材 | 2.1×105 | 0.3 | 1.2 |
| 沥青 | 1 500 | 0.2 | 1.4 |
5.2 最不利温度荷载作用下的正交异性钢桥面板温度力学响应
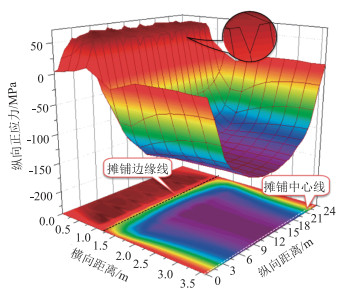
摊铺引起的温度应力主要集中分布于摊铺区域附近。图 14表示的是顶板纵向正应力达到最大值时(1 790 s)三维分布图和水平投影图,横向距离原点为距摊铺边缘线1.2 m处,纵向距离原点为摊铺起点。可以得到:(1)位于摊铺区域的顶板主要受压应力,其纵向正应力由摊铺中心线沿两侧向摊铺区边缘横向递减,同时纵向正应力在纵向上由跨中截面向两侧递减,最大压应力位于摊铺中心线处跨中截面附近,最大压应力温度增量为139 MPa;(2)位于非摊铺区的顶板主要受拉应力,以距摊铺区边缘线0.36 m处顶板为例,最大拉应力温度增量为70 MPa;(3)纵向正应力分布三维图中锯齿形是由顶板下方横隔板导致,致使横隔板处顶板的纵向正应力有着规律性的降低,约为8 MPa。
|
| 图 14 纵向正应力分布三维图 Fig. 14 Three-dimensional diagram of longitudinal normal stress distribution |
| |
摊铺边缘处的应力较为复杂,以左侧的摊铺边缘线为例,分别选取左右两侧各3 m范围内的顶板为研究对象,图 15表示的是钢桥面板纵向应力沿横向分布图。可以得到: (1)钢桥面板沿横向的纵向应力以摊铺边缘线为分界线由拉应力过渡到压应力,主要是因为摊铺区域的顶板在温度作用下热胀产生局部的拉伸变形,使得温度相对较低的非摊铺区受拉出现拉应力,而非摊铺区的顶板反过来限制摊铺区顶板变形,摊铺区顶板出现压应力;(2)钢桥面板的1/4截面和跨中截面的应力变化趋势相同,表明摊铺时纵向各截面影响基本一致,影响温度应力的主要为桥面板与摊铺层的横向位置关系。

|
| 图 15 纵向应力沿横向分布图 Fig. 15 Transverse distribution of longitudinal stresses |
| |
6 结论
本研究以瞬态温度场理论和热力学边界假设条件为基础,基于试验-数值模拟方法得到界面热阻参数,采用生死单元法建立相应的温度场有限元模型,分析了高温摊铺下正交异性钢桥面板温度场时空变化规律。
(1) 通过与实测数据进行对比,验证了该模拟方法的可靠性,可为类似高温摊铺下桥梁结构的模拟方法提供参考。
(2) 研究结果表明,在开始摊铺浇注式沥青混凝土30 min左右,摊铺区域处跨中钢桥面板上达到最高温度95 ℃;大约在17.8 min左右,U肋上下端达到最大温差74 ℃,在结构中必须考虑由U肋温差引起的温度应力。因此,在施工过程计算和施工监测中应重点关注摊铺过程15~30 min后的U肋与顶板相交部位。
(3) 随着摊铺过程的进行,顶板温度的横向影响范围逐渐增大,最终影响在摊铺边缘左右各约1 m,摊铺区域中心和摊铺边缘的温度差别较大,大约在50 ℃。
(4) 横隔板处顶板的纵向温度较其他截面低,温差在6~7 ℃,纵向影响范围大约为横隔板附近各0.6 m,但离摊铺边缘线越远,横隔板所造成的影响逐渐减小。
| [1] |
王朝辉, 陈谦, 高志伟, 等. 浇注式沥青混凝土现状与发展[J]. 材料导报, 2017, 31(5): 135-145. WHANG Chao-hui, CHEN Qian, GAO Zhi-wei, et al. Review on Status and Development of Gussasphalt Concrete[J]. Materials Reports, 2017, 31(5): 135-145. |
| [2] |
赵国云, 邵强, 闫东波. 钢桥面铺装浇注式沥青混合料级配性能[J]. 公路交通科技, 2013, 30(6): 75-81. ZHAO Guo-yun, SHAO Qiang, YAN Dong-bo. Gradation Performance of Gussasphalt Mixture for Steel Bridge Deck Paving[J]. Journal of Highway and Transportation Research and development, 2013, 30(6): 75-81. |
| [3] |
钱振东, 胡靖, 刘龑, 等. 浇注式沥青混凝土摊铺温度对钢箱梁力学响应及变形效应影响[J]. 土木工程学报, 2015, 48(2): 96-102. QIAN Zhen-dong, HU Jing, LIU Yan, et al. Influence of Gussasphalt Concrete Paving Temperature on Mechanical Responses and Deformation Effects of Steel Box Girder[J]. China Civil Engineering Journal, 2015, 48(2): 96-102. |
| [4] |
孙君, 李爱群, 丁幼亮. 润扬长江大桥钢箱梁的温度分布监测与分析[J]. 公路交通科技, 2009, 26(8): 94-98. SUN Jun, LI Ai-qun, DING You-liang. Observation and Research on Temperature Distribution in Steel Box Girders of Runyang Yangtse River Bridge[J]. Journal of Highway and Transportation Research and Development, 2009, 26(8): 94-98. |
| [5] |
丁幼亮, 王晓晶, 王高新, 等. 珠江黄埔大桥钢箱梁温度长期监测与分析[J]. 东南大学学报: 自然科学版, 2012, 42(5): 945-949. DING You-liang, WANG Xiao-jing, WANG Gao-xin, et al. Long-term Temperature Monitoring and Analysis of Steel Box Girders of Pearl River Huangpu Bridge[J]. Journal of Southeast University: Natural Science Edition, 2012, 42(5): 945-949. |
| [6] |
REIS A, LOPES N, REAL P V. Shear-bending Interaction in Steel Plate Girders Subjected to Elevated Temperatures[J]. Thin-Walled Structures, 2016(104): 34-43. |
| [7] |
孙金, 冯小青, 唐焱, 等. 高温沥青摊铺时钢-混叠合梁桥温度场有限元分析[J]. 中外公路, 2018, 38(3): 216-221. SUN Jin, FENG Xiao-qing, TANG Yan, et al. Finite Element Analysis of Temperature Field of Steel-mixed Composite Beam Bridge during High Temperature Asphalt Paving[J]. Journal of China and Foreign Highway, 2018, 38(3): 216-221. |
| [8] |
IM C K, CHANG S P. Estimating Extreme Thermal Loads in Composite Bridge Using Long-term Measured Data[J]. International Journal of Steel Structures, 2004(4): 25-31. |
| [9] |
刘其伟, 朱俊, 唐蓓华, 等. 沥青高温摊铺时钢筋混凝土箱梁的温度分布试验[J]. 中国公路学报, 2007, 20(4): 96-100. LIU Qi-wei, ZHU Jun, TANG Bei-hua, et al. Experiment on Temperature Distribution of Reinforced Concrete Box Girder under Asphalt High Temperature Paving[J]. China Journal of Highway and Transport, 2007, 20(4): 96-100. |
| [10] |
刘其伟, 丁峰, 朱俊, 等. 钢-混凝土组合箱梁沥青摊铺温度场试验[J]. 东南大学学报: 自然科学版, 2006, 36(4): 572-575. LIU Qi-wei, DING Feng, ZHU Jun, et al. Temperature Field Caused by Bituminous Deck Pavement of Steel-concrete Composed Box Girder Bridge[J]. Journal of Southeast University: Natural Science Edition, 2006, 36(4): 572-575. |
| [11] |
董旭, 邓振全, 李树忱, 等. 大跨波形钢腹板箱梁桥日照温度场及温差效应研究[J]. 工程力学, 2017, 34(9): 230-238. DONG Xu, DENG Zhen-quan, LI Shu-chen, et al. Research on Sun Light Temperature Field and Thermal Difference Effect of Long Span Box Girder Bridge with Corrugated Steel Webs[J]. Engineering Mechanics, 2017, 34(9): 230-238. |
| [12] |
杜明峰. 沥青摊铺对正交异性钢桥面箱梁的温度效应及对结构的影响分析[D]. 成都: 西南交通大学, 2018. DU Ming-feng. Temperature Effect on Orthotropic Steel Deck Box Girder during Asphalt Concrete Paving and Its Influence on Structures[D]. Chengdu: Southwest Jiaotong University, 2018. |
| [13] |
WANG J F, XU Z Y, FAN X L, et al. Thermal Effects on Curved Steel Box Girder Bridges and Their Countermeasures[J]. Journal of Performance of Constructed Facilities, 2016, 04016091. |
| [14] |
沈聪, 高培伟, 张辉. 钢箱梁大桥桥面铺装温度场有限元分析研究[J]. 公路工程, 2018, 43(3): 21-25. SHEN Cong, GAO Pei-wei, ZHANG Hui. Research on Temperature field of Steel Deck Pavement by Finite Element[J]. Highway Engineering, 2018, 43(3): 21-25. |
| [15] |
LI H, HARVEY J. Numerical Simulation and Sensitivity Analysis of Asphalt Pavement Temperature and Near-surface Air Temperature Using Integrated Local Modeling[C]//The 90th Annual Meeting of Transportation Research Board. Washington, D.C. : TRB, 2010: 11-3125.
|
| [16] |
顾颖, 李亚东, 姚昌荣. 太阳辐射下混凝土箱梁温度场研究[J]. 公路交通科技, 2016, 33(2): 46-53. GU Ying, LI Ya-dong, YAO Chang-rong. Research of Temperature Field of Concrete Box Girder under Solar Radiation[J]. Journal of Highway and Transportation Research and Development, 2016, 33(2): 46-53. |
| [17] |
李前名. 预应力混凝土箱梁桥温度场及温度应力的分析与研究[D]. 成都: 西南交通大学, 2006. LI Qian-ming. Analysis and Research on Temperature Field and Temperature Stress of Prestressed Concrete Box Girder Bridge[D]. Chengdu: Southwest Jiaotong University, 2006. |
| [18] |
张磊. 南京长江第四大桥钢桥面浇注式沥青铺装研究[D]. 济南: 山东大学, 2015. ZHANG Lei. Research on Steel Deck Gussasphalt Pavement on Fourth Nanjing Yangtze River Bridge[D]. Jinan: Shandong University, 2015. |
| [19] |
樊叶华, 黄卫, 王敬民, 等. 江阴大桥钢桥面柔性防水黏结层特性分析[J]. 公路交通科技, 2007, 24(6): 33-36. FAN Ye-hua, HUANG Wei, WANG Jing-min, et al. Research on Interface Cohesiveness of the Waterproofing System for Jiangyin Bridge[J]. Journal of Highway and Transportation Research and Development, 2007, 24(6): 33-36. |
| [20] |
刘阳. 高温摊铺下钢桥桥面温度场及温度效应分析[D]. 南京: 东南大学, 2015. LIU Yang. Analysis on Temperature Field and Effect of Steel Bridge Deck during Asphalt Pavement Paving[D]. Nanjing: Southeast China University, 2015. |
 2021, Vol. 38
2021, Vol. 38
