扩展功能
文章信息
- 王秀兰, 张云龙, 柴生波, 蒲广宁
- WANG Xiu-lan, ZHANG Yun-long, CHAI Sheng-bo, PU Guang-ning
- 双缆多塔悬索桥主缆垂跨比的合理取值
- Reasonable Value of Sag-span Ratio of Main Cable in Double-cable Multi-pylon Suspension Bridge
- 公路交通科技, 2021, 38(7): 51-59
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(7): 51-59
- 10.3969/j.issn.1002-0268.2021.07.008
-
文章历史
- 收稿日期: 2020-06-03
2. 中交二航局第二工程有限公司, 重庆 400016;
3. 西安建筑科技大学 土木工程学院, 陕西 西安 710054
2. China Communications 2nd Navigational Bureau 2nd Engineering Co., Ltd., Chongqing 400016, China;
3. School of Civil Engineering, Xi'an University of Architecture and Technology, Xi'an Shaanxi 710054, China
近十年来,国内外先后建造了泰州长江大桥、马鞍山大桥以及鹦鹉洲长江大桥、韩国新世纪大桥,温州瓯江北口大桥等多塔悬索桥,伴随这一新兴结构的出现,多塔悬索桥也成为当今桥梁工程的研究热点[1]。建造多塔悬索桥面临的主要问题是“中塔效应”,多塔悬索桥的中塔缺乏边主缆的有效约束,使多塔体系刚度不足,受到不平衡活载时,加劲梁挠度过大,影响其使用性能[2];若中塔刚度较大,则会使主缆与中塔鞍座的抗滑稳定性降低,影响结构安全[3-4],增加抗滑板的措施可以增大主缆与中塔之间的抗滑稳定性[5-7],但提高中塔刚度必然增大中塔塔底弯矩,降低多塔悬索桥的经济性。并且,仅在恒活载比值超过一定限值时,才存在使结构变形及主缆抗滑同时满足的中塔刚度[8]。为了解决多塔悬索桥的这些问题,国内外学者从缆索的布置形式出发对传统的单缆结构进行了改进。Gimsing[9]提出了双层主缆的构想,通过在同一索面设置垂度不同的两根主缆,共同承担桥面荷载。双缆多塔悬索桥为解决多塔悬索桥结构刚度不足的问题提供了新的解决思路,然而,作为一种新型桥梁结构,其结构参数的选取尚缺乏相关研究。
双缆体系的提出引起广泛关注,众多学者对其一些力学特性进行了研究。Gimsing、Georgakis[9]比较了双缆多塔悬索桥与传统的三塔悬索桥体系以及A字形桥塔多跨悬索桥的变形及主缆用钢量,认为双缆体系的主缆用钢量将比传统体系多约20%,桥塔材料用量减小约15%,但未给出相关依据;陈艾荣、陈文明[10]比较了包括双缆体系在内的几种新型缆索体系,认为双缆体系非常适合应用于大跨度悬索桥;张新军[11]通过研究,认为双缆体系具有良好的结构动力特性,抗风稳定性高于传统悬索桥;肖汝诚[12]研究了活载作用下双缆多塔悬索桥的变形及桥塔受力,认为双缆多塔悬索桥在刚度方面具有优势,活载引起的桥塔剪力及弯矩均远小于传统多塔悬索桥;柴生波研究了均布荷载在双缆中的分配原理[13],推导了双缆体系对桥塔的约束刚度表达式[14-15],发现双缆体系对桥塔的约束作用远大于传统悬索桥体系,采用双缆体系可有效增大结构刚度并减小中塔受力,并进一步指出双缆体系并不会增加主缆的用钢量[16];张清华等[17]对比分析了传统悬索桥和双缆体系竖向刚度的差异,发现双缆体系能够有效提高结构竖向刚度,大幅减小中塔塔顶两侧主缆不平衡水平力;王秀兰、柴生波通过构建等效弹簧模型,推导了大跨度双缆悬索桥的最大挠度计算方法[18],提出了采用同一根主缆作为相邻两跨的上缆和下缆的一种新型的双缆布置方案,推导出了双缆悬索桥的抗滑移安全系数[19],并以主缆抗滑系数以及加劲梁挠度作为控制指标,推导出了中塔刚度的上、下限值的解析方式[20]。
双缆体系能有效提高多塔悬索桥结构刚度已成共识,但由于双缆体系中结构参数的合理取值尚不明确。特别是双缆的垂跨比取值,对结构刚度、及主缆抗滑均有重要影响。为明确双缆悬索桥的上下缆垂跨比的合理取值,本研究采用“上缆变下缆”的主缆布置形式,根据现有理论确定满足要求的桥塔刚度,拟定不同主缆垂跨比的双缆悬索桥模型,通过数值模拟研究主缆垂跨比对结构变形、主缆抗滑稳定性的及主缆用钢量的影响,并与传统多跨悬索桥进行对比,推荐适宜的主缆垂跨比。
1 双缆体系参数取值原则多塔悬索桥最不利荷载工况为其中一个主跨满布荷载,其余各跨均不加载,此时中塔塔顶承受的不平衡水平力最大,主缆抗滑稳定性降至最低,加劲梁挠度达到最大。对这一荷载工况下的结构变形及主缆抗滑,已有相关研究成果[18-20]。
1.1 主缆面积根据活载作用下双缆的受力特点,采用相同主缆作为相邻两跨的上缆和下缆的设计[19],可以有效解决双缆体系的主缆抗滑问题。
根据图 1所示的三塔两跨双缆悬索桥示意图,A, B为两根主缆。At,Ab共用同一根主缆,分别为相邻两跨的上缆和下缆,因此面积相等,主缆面积为Ac,根据文献[19]有:
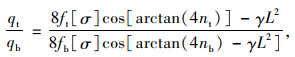
|
(1) |
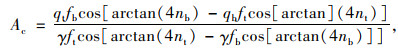
|
(2) |
|
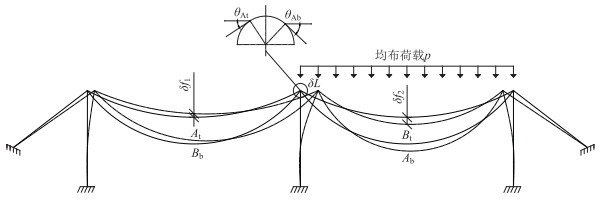
| 图 1 双缆多塔悬索桥变形 Fig. 1 Deformation of double-cable multi-pylon suspension bridge |
| |
式中, qt,qb分别为上缆和下缆承担的恒载大小;ft,fb分别为上缆和下缆垂度;nt,nt分别为上缆和下缆的垂跨比;L为主跨跨度;Ac为主缆面积;γ为主缆重度;[σ]为主缆容许应力值。式(1)确定的上下缆荷载分配比例可以确保恒载状态下主缆在中塔鞍座两侧缆力相等。
1.2 中塔刚度双缆体系的中塔刚度上、下限值分别由主缆在中塔的抗滑安全系数及结构刚度决定。在活荷载作用下双缆多塔悬索桥主缆变形如图 1所示,以加劲梁的最大允许挠度值确定中塔刚度的下限值[20]。
假定边塔位移为0,可以得到中塔刚度下限值Kt,min表达式如下:

|
(3) |
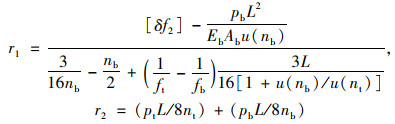
|
式中,pt,pb为上缆和下缆所承担的活荷载,pb=pu(nb)/[u(nb)+u(nt)];Kt为桥塔刚度;Kc为主缆对桥塔提供的纵向刚度;[δf2]为跨中挠度最大允许值。
随着桥塔刚度的增大,相邻两跨主缆不平衡水平力增大,主缆抗滑安全性降低,以主缆抗滑安全系数确定中塔刚度的上限值[20]。
采用加载跨下缆和非加载跨上缆控制双缆体系的抗滑设计,可以得到中塔刚度上限值Kt,max表达式如下:

|
(4) |
式中,X=r3r5r6+r3r5;Y=r3r6wt+r5r6fb+r4r5r6-r5ft+r3wb+r3pb;Z=r6wtfb+r4r6wt-wbft-pbft。
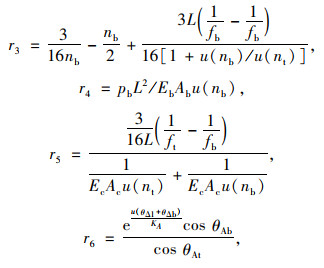
|
式中,θAt,θAb为塔顶处非加载跨上缆和加载跨下缆与水平线的夹角;wt,wb为上、下缆分别承担的恒载集度(包含主缆自重)。
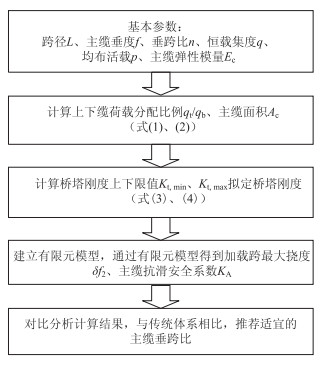
2 双缆体系主要参数的确定 2.1 研究流程已有研究发现,双缆垂跨比取值对结构刚度、主缆在中塔的抗滑稳定性均有重要影响。为明确双缆多塔悬索桥主缆垂跨比合理取值范围,首先需拟定满足结构变形及主缆抗滑要求的双缆多塔悬索桥结构参数。本研究采用研究流程如图 2所示。
|
| 图 2 研究流程 Fig. 2 Research process |
| |
根据“上缆变下缆”的缆索布置方式,拟定三塔悬索桥,单个主跨长度L=1 000 m,桥面恒载集度为240 kN/m,下缆垂跨比取为1/9~1/5,上缆垂跨比取为1/15~1/11,从加载跨跨中挠度和主缆抗滑安全系数两个方面分析主缆垂跨比对双缆体系力学性能的影响,从而确定适宜的主缆垂跨比。
2.2 恒载分配比及主缆面积恒载分配比例是双缆体系设计中的关键参数,根据《公路悬索桥设计规范》[21]对主缆安全系数的要求,令恒载作用下主缆应力为600 MPa,通过式(1)、式(2)对上下缆荷载分配比例和主缆面积进行计算,计算结果如表 1和表 2所示。
| nb=1/9 | nb=1/8 | nb=1/7 | nb=1/6 | nb=1/5 | |
| nt=1/15 | 0.564 | 0.504 | 0.446 | 0.393 | 0.344 |
| nt=1/14 | 0.614 | 0.548 | 0.486 | 0.429 | 0.374 |
| nt=1/13 | 0.671 | 0.599 | 0.531 | 0.467 | 0.409 |
| nt=1/12 | 0.736 | 0.657 | 0.582 | 0.513 | 0.448 |
| nt=1/11 | 0.811 | 0.724 | 0.642 | 0.565 | 0.494 |
| nb=1/9 | nb=1/8 | nb=1/7 | nb=1/6 | nb=1/5 | |
| nt=1/15 | 0.375 | 0.348 | 0.321 | 0.293 | 0.266 |
| nt=1/14 | 0.364 | 0.338 | 0.312 | 0.286 | 0.260 |
| nt=1/13 | 0.351 | 0.328 | 0.303 | 0.279 | 0.254 |
| nt=1/12 | 0.338 | 0.316 | 0.293 | 0.270 | 0.247 |
| nt=1/11 | 0.324 | 0.304 | 0.283 | 0.261 | 0.239 |
| 注:表中主缆面积Ac为两根主缆面积之和。 | |||||
由表 1可以看出,上下缆荷载分配比例随着上缆垂度的增大和下缆垂度的减小而增大;由表 2可以看出,主缆面积随着上缆垂度和下缆垂度的增大而减小。
2.3 中塔刚度上、下限值中塔刚度的取值是多塔悬索桥设计中的关键力学问题,根据《公路悬索桥设计规范》要求,加劲梁挠跨比不得超过1/250,主缆抗滑安全系数K不得小于2。通过式(3)、式(4),以主缆抗滑安全系数和加劲梁挠度作为控制指标,计算双缆三塔悬索桥中塔刚度的上、下限值,以确定适宜的中塔刚度取值,计算结果如表 3所示。
| 中塔刚度下限值Kt,min | nb=1/9 | nb=1/8 | nb=1/7 | nb=1/6 | nb=1/5 |
| nt=1/15 | -7.91 | -16.05 | -25.21 | -33.88 | -41.85 |
| nt=1/14 | -2.10 | -10.11 | -18.64 | -27.57 | -36.45 |
| nt=1/13 | 3.20 | -4.03 | -12.41 | -21.60 | -30.34 |
| nt=1/12 | 7.39 | 1.03 | -6.91 | -15.18 | -24.77 |
| nt=1/11 | 10.53 | 5.38 | -1.36 | -9.52 | -18.52 |
| 中塔刚度上限值Kt,max | nb=1/9 | nb=1/8 | nb=1/7 | nb=1/6 | nb=1/5 |
| nt=1/15 | 22.18 | 19.89 | 18.24 | 17.89 | 18.26 |
| nt=1/14 | 21.80 | 19.94 | 18.39 | 18.07 | 18.90 |
| nt=1/13 | 20.68 | 18.98 | 18.13 | 18.18 | 19.32 |
| nt=1/12 | 19.59 | 18.32 | 18.11 | 17.75 | 19.75 |
| nt=1/11 | 17.99 | 16.95 | 16.81 | 17.62 | 19.57 |
| 注:中塔刚度计算值为负值,说明即使中塔不提供抗推刚度,结构变形仍可满足要求。 | |||||
表 3可以看出,中塔刚度取值范围随着上缆垂度的减小和下缆垂度的增大而增大,当上下缆垂度相差较大时,中塔刚度下限值为负值,这使得双缆悬索桥在设计过程中可以采用柔性塔,解决了中塔刚度过大导致主缆抗滑安全性降低的问题。
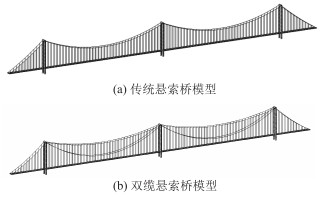
3 数值模拟为分析垂跨比对双缆多塔悬索桥挠度和主缆抗滑安全系数的影响,采用Midas civil建立三塔两跨传统悬索桥和双缆悬索桥有限元模型(图 3),主要构件材料如表 4所示。用受拉桁架单元模拟主缆及吊杆,用梁单元模拟桥塔及加劲梁,加劲梁采用单梁模型,加劲梁与吊杆用钢臂连接。
|
| 图 3 多塔悬索桥模型 Fig. 3 Finite element model of multi-pylon suspension bridge |
| |
| 主要构件 | 材料类型 | E/GPa | γ/(kN·m-3) |
| 桥塔 | C50 | 34.5 | 26 |
| 加劲梁 | Q345 | 206 | 78.5 |
| 主缆 | 高强钢丝 | 205 | 78.5 |
| 吊杆 | 高强钢丝 | 205 | 78.5 |
悬索桥各主跨长度均为1 000 m,桥面恒载集度为240 kN/m,根据表 1中荷载在上、下缆中的分配比例确定上下缆分别承担的恒载集度。为了便于对比,传统悬索桥和双缆悬索桥桥塔高度均取250 m,对其中一个主跨施加均布荷载,活载集度为p=40 kN/m。根据表 3确定的中塔刚度,在上下限值范围内,分别取3个不同的中塔抗推刚度Kt=1 000,5 000,10 000 kN/m(均为两根塔柱的抗推刚度之和),对不同垂跨比进行研究,传统悬索桥主缆垂跨比分别取1/12~1/9,双缆悬索体系上缆垂跨比取1/15~1/11,下缆垂跨比取1/9~1/5。传统悬索桥主缆面积取值原则与双缆体系相同,恒载作用下主缆应力水平为600 MPa。由于边跨主缆对边塔提供的纵向约束刚度较大,且随着边中跨比而改变,因此模型中约束边塔塔顶位移,以消除边中跨比的影响。加劲梁刚度在大跨度悬索桥中作用有限,加劲梁截面惯性矩取较小值,本例中加劲梁惯性矩取为0.96 m4,表 5列出了部分垂跨比下的结构参数。
| 结构类型 | 垂跨比 | 主缆垂度/m | 主缆截面面积/m2 | 吊杆面积/m2 | 恒载集度/(kN·m-1) |
| 传统悬索桥 | 1/9 | 111.11 | 0.264 | 4.4×10-3 | 240 |
| 1/10 | 100.00 | 0.299 | 4.4×10-3 | 240 | |
| 1/11 | 90.91 | 0.336 | 4.4×10-3 | 240 | |
| 1/12 | 83.33 | 0.374 | 4.4×10-3 | 240 | |
| 双缆悬索桥 | 1/11,1/5 | 200.00,90.91 | 2×0.120 | 1.36×10-3,2.74×10-3 | 79.36,160.64 |
| 1/12,1/5 | 200.00,83.33 | 2×0.125 | 1.27×10-3,2.84×10-3 | 74.25,165.75 | |
| 1/11,1/6 | 166.67,90.91 | 2×0.130 | 1.48×10-3,2.62×10-3 | 86.65,153.35 | |
| 1/12,1/6 | 166.67,83.33 | 2×0.134 | 1.39×10-3,2.72×10-3 | 81.37,158.63 | |
| 1/11,1/7 | 142.86,90.91 | 2×0.140 | 1.60×10-3,2.50×10-3 | 93.84,146.16 | |
| 1/12,1/7 | 142.86,83.33 | 2×0.148 | 1.51×10-3,2.60×10-3 | 88.29,151.71 | |
| 1/11,1/8 | 125.00,90.91 | 2×0.151 | 1.72×10-3,2.38×10-3 | 100.79,139.21 | |
| 1/12,1/8 | 125.00,83.33 | 2×0.158 | 1.63×10-3,2.48×10-3 | 95.16,144.84 | |
| 1/11,1/9 | 111.11,90.91 | 2×0.162 | 1.84×10-3,2.26×10-3 | 107.48,132.52 | |
| 1/12,1/9 | 111.11,83.33 | 2×0.169 | 1.75×10-3,2.36×10-3 | 101.75,138.25 | |
| 注:垂跨比、主缆垂度、吊杆面积、恒载集度等参数在双缆悬索桥中分别为上、下主缆对应的参数。传统悬索桥主缆面积为单根主缆面积,双缆采用上缆变下缆,故上下主缆面积相等。 | |||||
3.1 加劲梁挠度
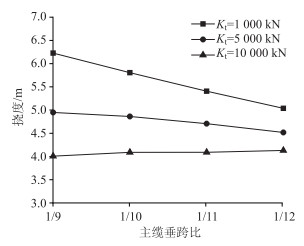
传统悬索桥加劲梁加载跨最大挠度如图 4所示。由图 4可知,当Kt=1 000 kN/m时,传统多塔悬索桥加劲梁挠度为5.04~6.22 m;Kt=10 000 kN/m时,加劲梁挠度为4.02~4.14 m;加劲梁挠跨比均大于4 m(挠跨比大于1/250)。为使加劲梁挠度满足要求,进一步增大桥塔刚度至Kt=10 200 kN/m时,主缆垂跨比为1/9,加劲梁挠跨比才降至1/250。
|
| 图 4 传统多塔悬索桥加劲梁挠度(单位:m) Fig. 4 Deflection of stiffening girder in traditional multi-pylon suspension bridge(unit: m) |
| |
双缆多塔悬索桥加劲梁加载跨最大挠度如图 5所示。由图 5可知,当Kt=1 000 kN/m时,双缆多塔悬索桥加劲梁挠度为1.37~5.22 m;Kt=10 000 kN/m时,加劲梁挠度最大值为1.24~3.81 m。比较图 5(a)~(c)可以看出,双缆体系的结构刚度主要取决于主缆垂跨比,结构变形随着上缆垂度的减小和下缆垂度的增大而减小。

|
| 图 5 双缆多塔悬索桥加劲梁挠度(单位:m) Fig. 5 Deflection of stiffening girder in double-cable multi-pylon suspension bridge(unit: m) |
| |
比较图 4、图 5可以看出,传统体系加劲梁挠度均超过4 m,挠跨比大于1/250,结构刚度过低。采用双缆体系时,当Kt=1 000 kN/m时,仅少数垂跨比加劲梁挠度不满足要求,当上下缆垂度分别取1/15,1/5时,加劲梁挠度为1.19 m,远小于传统多塔悬索桥。双缆多塔悬索桥其缆索体系刚度远大于传统悬索桥,当采用合理的垂跨比时,双缆体系的加劲梁挠度远小于传统体系。
当Kt=1 000 kN/m时,采用不同主缆垂跨比时,传统多塔悬索桥挠度值最大降低19%,双缆多塔悬索桥挠度值降低74%;当Kt=10 000 kN/m时,改变主缆垂跨比,传统多塔悬索桥挠度值降低3%,双缆多塔悬索桥挠度值降低了67%。桥塔刚度从1 000 kN/m增大至10 000 kN/m,采用不同主缆垂度的传统多塔悬索桥挠度值降低了22%~36%;双缆多塔悬索桥挠度值降低了10%~25%。由此可见,传统多塔悬索桥结构刚度主要由中塔刚度控制,双缆多塔悬索桥的刚度主要由主缆垂跨比控制,桥塔刚度对双缆体系的刚度影响较小。桥塔刚度较柔时,可以通过增大上下缆垂度差值来提高结构刚度(增大下缆垂度,或减小上缆垂度)。上下缆垂度应保持一定差值(采用较小下缆垂度的同时,不宜采用较大的上缆垂度)。双缆多塔悬索桥可以采用较柔的中塔,中塔刚度取值的可行范围远大于传统悬索桥。
3.2 主缆抗滑安全系数由于采用上缆变下缆的主缆布置时,主缆抗滑稳定性由加载跨下缆及非加载跨上缆控制[19],图 7中计算结果均为此主缆的抗滑安全系数。
主缆抗滑安全系数可由《公路悬索桥设计规范》中计算公式求得[21]:
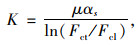
|
(5) |
式中,μ为主缆与槽底或隔板间的摩擦系数,泰州长江大桥μ取为0.2[7];αs为主缆与鞍槽的包角,αs=θct+θcl其中θct,θcl分别为塔顶处两侧主缆与水平线的夹角;Fct为塔顶处加载跨主缆拉力;Fcl为塔顶处非加载跨主缆拉力。抗滑安全系数模型值通过模型中塔顶两侧加载跨下缆和非加载跨上缆内力值以及两根缆索与鞍座的包角由式(5)求得。
传统悬索桥主缆抗滑安全系数如图 6所示。由图 6可知,当Kt=1 000 kN/m时,传统多塔悬索桥主缆抗滑安全系数为5.87~8.44;Kt=10 000 kN/m时,主缆抗滑安全系数为2.4~3.25。传统多塔悬索桥主缆抗滑安全系数受桥塔刚度影响较大。

|
| 图 6 传统多塔悬索桥抗滑安全系数 Fig. 6 Antiskid safety coefficient of traditional multi-pylon suspension bridge |
| |

|
| 图 7 双缆多塔悬索桥抗滑安全系数 Fig. 7 Antiskid safety coefficient of double-cable multi-pylon suspension bridge |
| |
双缆多塔悬索桥主缆抗滑安全系数如图 7所示。由图 7可知,当Kt=1 000 kN/m时,双缆多塔悬索桥主缆抗滑安全系数为2.47~5.33;Kt=10 000 kN/m时,主缆抗滑安全系数为2.07~2.50。主缆抗滑安全系数随着桥塔刚度的增大而减小。通过图 7(a)~ 图 7(c)可以看出,主缆抗滑安全系数随着下缆垂度的减小而增大。图 7(a)可以看出,桥塔刚度较小时,主缆垂度对双缆体系的主缆抗滑性能影响较大,主缆抗滑安全系数随着上缆垂度的增大而增大;图 7(c)可以看出,桥塔刚度较大时,若采用较小的下缆垂跨比(下缆垂跨比1/9~1/7),随着上缆垂跨比的增大,主缆抗滑安全系数先增大后减小。
比较图 6、图 7(a)~图 7(c)可知,桥塔刚度对传统体系悬索桥主缆抗滑影响较大,而对双缆多塔悬索桥主缆抗滑稳定性的影响相对较小。
3.3 单个主跨主缆用钢量本研究采用“上缆变下缆”的布置方案,与文献[16]中的研究相比,上、下缆荷载分配比例以及主缆面积为定值,主缆面积按恒载状态下,跨中主缆应力为600 MPa确定。模型值与理论值结果一致,通过模型中对单元质量的计算结果,单个主跨主缆用钢量如图 8、图 9所示。

|
| 图 8 主缆用钢量与垂跨比的关系 Fig. 8 Relationship between steel consumption and sag-span ratio of main cable |
| |

|
| 图 9 双缆体系用钢量与垂跨比的关系 Fig. 9 Relationship between steel consumption and sag-span ratio in double-cable system |
| |
传统单根主缆悬索桥每个主跨主缆用钢量在4 400~6 100 t之间,而双缆体系悬索桥用钢量在4 200~6 200 t之间,双缆体系与传统体系多跨悬索桥主缆用钢量均与主缆垂跨比有关,随着主缆垂跨比的减小,主缆用钢量增大。双缆体系主缆用钢量随着下缆垂度和上缆垂度的减小而增大,这是因为随着上、下缆垂度的减小,上缆与下缆之间的恒载分配比例增大,主缆水平力增大,从而导致主缆用钢量增大。
传统多跨悬索桥随着主缆垂跨比从1/9减小至1/12时,单个主跨主缆用钢量从4 414.9 t增大至6 077.1 t。若采用双缆体系,当上下缆垂跨比分别为1/11,1/5时,单个主跨主缆用钢量为4 241.4 t;当上下缆垂跨比分别为1/15,1/9时,单个主跨主缆用钢量为6 155.3 t。由此可见,双缆体系悬索桥主缆用钢量与传统体系用钢量基本一致,当采用较大的上下缆垂度时,双缆体系的用钢量甚至小于传统体系多跨悬索桥。
4 结论(1) 双缆体系的结构刚度主要取决于主缆垂跨比,结构变形随着上缆垂度的减小和下缆垂度的增大而减小;上缆垂跨比增大或下缆垂跨比减小时,主缆对中塔的纵向约束刚度减小,桥塔刚度对结构变形影响较大。
(2) 垂跨比对主缆滑抗滑性能的影响取决于塔的刚度,主缆抗滑安全系数随着桥塔刚度的增大而减小,随着下缆垂跨比的减小而增大。桥塔刚度较小时,主缆垂跨比对双缆体系的主缆抗滑性能影响较大,主缆抗滑安全系数随着上缆垂跨比的增大而增大;桥塔刚度较大,下缆垂跨比较小时,随着上缆垂跨比的增大,主缆抗滑安全系数先增大后减小。
(3) 与传统悬索桥体系相比,双缆体系加劲梁变形和主缆抗滑稳定性受桥塔刚度的影响较小。当采用合理的垂跨比时,双缆体系的加劲梁挠度远小于传统体系,同时主缆抗滑稳定性可以满足设计要求,桥塔刚度的可行性范围远大于传统多跨悬索桥,双缆多塔悬索桥的中塔可以采用柔性桥塔。
(4) 双缆体系悬索桥主缆用钢量与传统体系用钢量基本一致,主缆用钢量随着下缆垂度和上缆垂度的增大而减小。当采用较大的上、下缆垂度时,双缆体系的用钢量甚至小于传统体系悬索桥。
(5) 在双缆悬索桥设计中,下缆垂跨比适宜取值为1/8~1/6,上缆垂跨比适宜取值为1/14~1/11。当桥塔刚度较小时,以加劲梁挠度为主要控制指标,应增大上、下缆垂度差值;当桥塔刚度较大时,以主缆抗滑安全性为主要控制指标,应减小上、下缆垂度差值。
| [1] |
CHOI D H, GWON S G, NA H S. Simplified Analysis for Preliminary Design of Towers in Suspension Bridges[J]. Journal of Bridge Engineering, 2014, 19(3): 4013007. |
| [2] |
YOSHIDA O, OKUDA M, MORIYA T. Structural Characteristics and Applicability of Four-span Suspension Bridge[J]. Journal of Bridge Engineering, 2004, 9(5): 453-463. |
| [3] |
王秀兰, 柴生波. 三塔悬索桥中塔适宜刚度[J]. 北京工业大学学报, 2019, 45(4): 353-358. WANG Xiu-lan, CHAI Sheng-bo. Stiffness Value of the Middle Tower in Triple-tower Suspension Bridges[J]. Journal of Beijing University of Technology, 2019, 45(4): 353-358. |
| [4] |
DANIEL R A, DOOREN F V, MEIJER R D. Comparison of a Single and Double Main Span Suspension Bridge for the Western Scheldt Crossing[C]//34th International Symposium on Bridge and Structural Engineering. Venice: IABSE, 2010: 9-16.
|
| [5] |
张清华, 李乔. 悬索桥主缆与鞍座间摩擦特性试验研究[J]. 土木工程学报, 2013, 46(4): 85-92. ZHANG Qing-hua, LI Qiao. Study on Cable-saddle Frictional Characteristics of Long-span Suspension Bridges[J]. China Civil Engineering Journal, 2013, 46(4): 85-92. |
| [6] |
张清华, 李乔, 周凌远. 悬索桥主缆与鞍座摩擦特性理论分析方法[J]. 中国公路学报, 2013, 46(1): 44-50. ZHANG Qing-hua, LI Qiao, ZHOU Ling-yuan. Theoretical Analysis of Cable-saddle Friction Characteristics for Suspension Bridges[J]. China Journal of Highway and Transport, 2013, 46(4): 85-92. |
| [7] |
张清华, 程震宇, 贾东林, 等. 悬索桥主缆与鞍座抗滑移安全系数的确定方法[J]. 中国公路学报, 2017, 30(7): 41-49. ZHANG Qing-hua, CHENG Zhen-yu, JIA Dong-lin, et al. Method for Determining Anti-slip Safety Factors between Main Cable and Saddle in Suspension Bridge[J]. China Journal of Highway and Transport, 2017, 30(7): 41-49. |
| [8] |
CAO H Y, QIAN X D, ZHOU Y L, et al. Feasible Range for Midtower Lateral Stiffness in Three-tower Suspension Bridges[J]. Journal of Bridge Engineering, 2018, 23(3): 06017009. |
| [9] |
GIMSING N J, GEORGAKIS C T. Cable Supported Bridges[M]. 3rd ed. Chichester: John Wiley, 2012.
|
| [10] |
陈艾荣, 陈文明. 多跨悬索桥的性能[C]//中国公路学会桥梁和结构工程分会2001桥梁学术研讨会论文集. 北京: 人民交通出版社, 2001: 561-566. CHEN Ai-rong, CHEN Wen-ming. Performance of Multi-span Suspension Bridge[C]//Bridge Academic Seminar of Bridge and Structural Engineering Commission of China Highway & Transportation Society in 2001. Beijing: China Highway & Transportation Society, 2001: 561-566. |
| [11] |
张新军, 陈兰, 赵孝平. 三塔悬索桥的缆索体系及其抗风稳定性[J]. 浙江工业大学学报, 2010, 38(4): 437-441. ZHANG Xin-jun, CHEN Lan, ZHAO Xiao-ping. Cable System and Wind Stability of Three-tower Suspension Bridges[J]. Journal of Zhejiang University of Technology, 2010, 38(4): 437-441. |
| [12] |
肖汝诚. 桥梁结构体系[M]. 北京: 人民交通出版社, 2013. XIAO Ru-cheng. Bridge Structure System[M]. Beijing: China Communications Press, 2013. |
| [13] |
柴生波, 肖汝诚, 孙斌. 双缆悬索桥体系的力学特性(Ⅰ)[J]. 华南理工大学学报: 自然科学版, 2011, 39. CHAI Sheng-bo, XIAO Ru-cheng, SUN Bin. Mechanical Properties of Double-cable Suspension Bridge System (Ⅰ)[J]. Journal of South China University of Technology: Natural Science Edition, 2011, 39(12): 159-164. |
| [14] |
柴生波, 肖汝诚. 双缆悬索桥体系的力学特性(Ⅲ)[J]. 华南理工大学学报: 自然科学版, 2013, 41(8): 120-126. CHAI Sheng-bo, XIAO Ru-cheng. Mechanical Properties of Double-main Cable Suspension Bridge(Ⅲ)[J]. Journal of South China University of Technology: Natural Science Edition, 2013, 41(8): 120-126. |
| [15] |
CHAI S B, XIAO R C, LI X N. Longitudinal Restraint of a Double-cable Suspension Bridge[J]. Journal of Bridge Engineering, 2014, 19(4): 1-7. |
| [16] |
柴生波, 王秀兰, 任翔. 双缆多跨悬索桥力学性能及主缆用钢量研究[J]. 建筑科学与工程学报, 2015, 32(6): 74-81. CHAI Sheng-bo, WANG Xiu-lan, REN Xiang. Study on Mechanical Properties and Steel Consumption of Double-cable Multi-span Suspension Bridge[J]. Journal of Architecture and Civil Engineering, 2015, 32(6): 74-81. |
| [17] |
张清华, 张莹, 程震宇, 等. 双缆悬索桥的静力特性及其关键影响因素[J]. 西南交通大学学报, 2020, 55(2): 238. ZHANG Qing-hua, ZHANG Ying, CHENG Zhen-yu, et al. Static Behavior and Key Influencing Factors of Double-cable Suspension Bridge[J]. Journal of Southwest Jiaotong University, 2020, 55(2): 238. |
| [18] |
WANG X L, CHAI S B, XU Y. Deformation Characteristics of Double-cable Multispan Suspension Bridges[J]. Journal of Bridge Engineering, 2016, 21(4): 06015007. |
| [19] |
WANG X L, CHAI S B, XU Y. Sliding Resistance of Main Cables in Double-cable Multispan Suspension Bridges[J]. Journal of Bridge Engineering, 2017, 22(3): 06016011. |
| [20] |
WANG X L, CHAI S B. Determining the Middle Tower Stiffness Value in an In-plane Double-cable Triple-tower Suspension Bridge[J]. Journal of Bridge Engineering, 2018, 23(7): 06018001. |
| [21] |
JTG/T D65-05-2015, 公路悬索桥设计规范[S]. JTG/T D65-05-2015, Specifications for Design of Highway Suspension Bridge[S]. |
 2021, Vol. 38
2021, Vol. 38
