扩展功能
文章信息
- 周日彪, 庞明宝, 王雄杰
- ZHOU Ri-biao, PANG Ming-bao, WANG Xiong-jie
- 基于K-shell的特大城市公交换乘优惠与线网规划协同优化
- Coordination Optimization of Transfer Pricing Discount and Network Planning for Public Transport of Megalopolis Based on K-shell
- 公路交通科技, 2021, 38(6): 141-148
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(6): 141-148
- 10.3969/j.issn.1002-0268.2021.06.018
-
文章历史
- 收稿日期: 2020-11-26
2. 天津市道路运输管理局, 天津 300384
2. Tianjin Road Transport Authority, Tianjin 300384, China
采取各种措施提高公交出行比例是国内外学者对特大城市抑制交通拥堵、建设绿色宜居城市的共识,其中建设并运行“轨道交通为骨架,汽车公交为辅助”的高效公交系统是其基本要求。但近年来随着我国很多特大城市轨道交通的大规模投入运营,出现严重问题:(1)汽车公交客流量急剧下降,企业亏损严重。轨道交通分担较远比例,共享单车分担较近距离的出行,特别是非通勤时间段汽车公交上座率极低。(2)若大幅度调整(主要是减少常规)汽车公交线路,又会增加乘客的等车时间和换乘次数与费用,使得部分乘客因“广义出行费用增加”而选择其他如小汽车出行方式,无法实现公交高比例出行的目标。而解决这一问题的关键点是在进行“大幅度降低常规公交线路数量,增加接驳和通勤公交线路数量”的汽车公交线网调整的同时,辅助以“公交换乘优惠”政策使其与线网调整协同优化,使得乘客不因“可能的换乘”造成其广义出行费用增加或过多增加,从而继续选择公交出行,直接达到公交线网优化目的的同时,继续保持和增加公交出行量,提升公交综合服务水平并降低公交企业不必要的亏损(政府补贴)。
理论研究分3部分:(1)汽车公交线网规划调整。分为汽车公交-汽车公交间[1-4]和基于轨道交通的汽车公交线网调整等[5-7],但多为对单条汽车线路的调整,较少从全网和定量的角度进行公交线网优化,较少涉及基于换乘优惠下的城市公交与轨道线网的一体化研究。(2)公交换乘优惠[8]。分两种:一是根据实际采取的政策分析,运用数理统计的方法对实施效果进行评述;二是基于问卷调查分析换乘优惠的影响,研究出行者意向,主要从宏观角度分析且模型的目标函数较单一。(3)换乘优惠与线网协同优化[9-11]。多为对轨道交通票价、汽车公交票价与其自身线网单方面的研究,不涉及换乘优惠与线网协同优化方面。
线网调整的关键点之一是换乘站的确定问题,已有考虑共享单车城市轨道交通社区接驳规划[12]、物元法评价模型法[13]、基于双层规划的公交站设置规划[14]等,这些主要是针对数量较少的公交站点研究,并不适用于特大城市公交线网调整。实际上公交系统作为复杂网络,采用节点重要度指标选择公交站点是公交规划的基本方法之一[15]。而在复杂网络节点重要度的各种定义中,K-shell分解法(K-shell decomposition)由于比度中心性和介数中心性更准确[16],适用于大规模网络的分析,且考虑了节点在网络的全局连通性,得到较多应用,但不涉及公交网络。而若将K-shell分解法应用于特大城市公交主要换乘站的选择问题,节点Ks值越高,表示节点位于网络的核心位置,重要性程度越高,以此类节点作换乘站的参考,实现公交换乘网络优化的目的。基于此,本研究以含轨道交通的特大城市公交网络为研究对象,基于K-shell分解法确定保留下的骨干公交线路,构思其余公交线路候选集合;建立换乘优惠方案下汽车公交线网调整优化双层规划模型,并优化求解,最后通过实例予以验证分析。
1 换乘优惠与线网规划协同优化设计 1.1 换乘优惠设计需考虑换乘优惠对象、换乘优惠时段、优惠幅度和优惠次数,采用模式有限时免费换乘、打折优惠换乘、定额优惠换乘、定额优惠后再享受折扣等。城市轨道交通票价采用分段制,汽车公交分为一票制或分段制。设Pμ为票价率; φrs为公交票制0-1变量,若采用分段制φrs=1,采用一票制φrs=0, Pε和Pθ分别为分段制和一票制的汽车公交票价率。
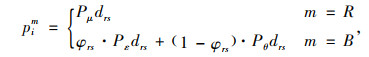
|
(1) |
式中,pim为票价函数;I为乘客种类集合,i∈I,其中老年卡乘客公交段免费,即p=0,地铁段按正常优惠规则计费;普通卡乘客按正常优惠规则计费;m为交通方式的子集,M为交通方式的集合,m∈{Bus, Rail},B和R分别为汽电车公交和轨道交通。
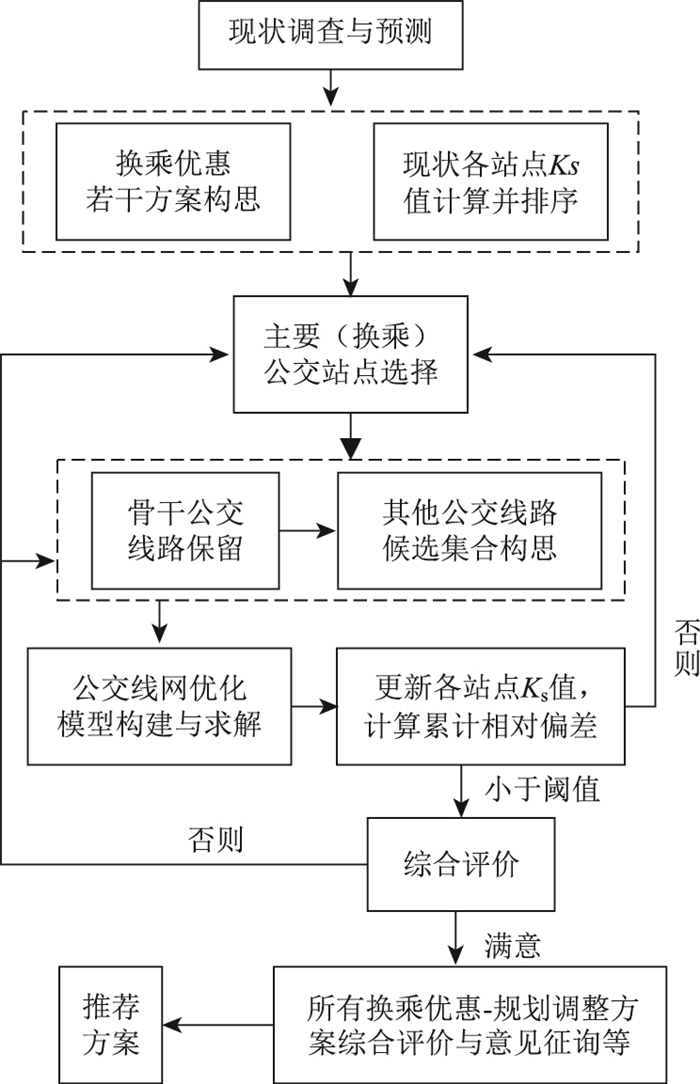
1.2 协同优化设计考虑到特大城市公交系统的复杂性,本协同优化设计流程如图 1所示,其中轨道交通-汽车公交间换乘优惠含,但线网调整仅为汽电车公交。
|
| 图 1 换乘优惠与线网协同优化设计流程 Fig. 1 Design process of transfer pricing discount and cooperative optimization of line network |
| |
(1) 确定换乘优惠对象、幅度等,构思若干换乘优惠方案,对每一个换乘优惠方案,转向(2)。
(2) 使用K-shell分解法计算各公交站点Ks值并排序;结合实际,选择Ks值大的前面站点(其总数占站点总数一定比例,如15%)作为重要节点,作为规划调整时的主要换乘站点予以保留。
(3) 对连接这些主要节点的汽车公交线路,结合已有公交系统和城市实际,规划调整时予以选择保留。一般来说,这些线路无论是快速公交还是常规公交,依然是城市骨干公交线路。
(4) 构思其余汽车公交线路候选集合。其中部分为常规公交,主要为接驳线路和通勤线路。
(5) 构建“其余汽车公交线路选择”双层规划模型,并求解得到优化后的规划调整方案。
(6) 返回(2),重新计算各个公交站点Ks值,若所有公交站点Ks值“上一步计算值与本次计算值的相对偏差”累加小于阈值如2%,转向(7);否则,重复(2)~(6)。
(7) 对该规划调整方案进行综合评价,若满意,返回(1)进行下一个换乘优惠方案的规划调整;若不满意,返回(2),调整对该换乘优惠方案下的重要站点选择比例,调整保留下的公交线路,调整候选的公交线路集合,得到新的规划调整方案。
(8) 对所有换乘优惠-规划调整方案进行综合评价,并征求意见,不断反馈形成最终方案。
2 基于K-shell分解法的重要节点选择城市公交网络(包括轨道交通、公交等)G=(N,A),其中N为节点(公交站、地铁站)集合,n为具体节点;A为节点间无权向网络连接边的集合,定义如下:
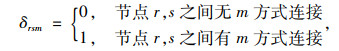
|
(2) |
式中,δrsm为循环决策变量,当δrsm=0时,可消除理论上任意两点间的自连接。
采用K-shell分解法[17-18]计算各公交站点Ks值并排序,具体步骤:
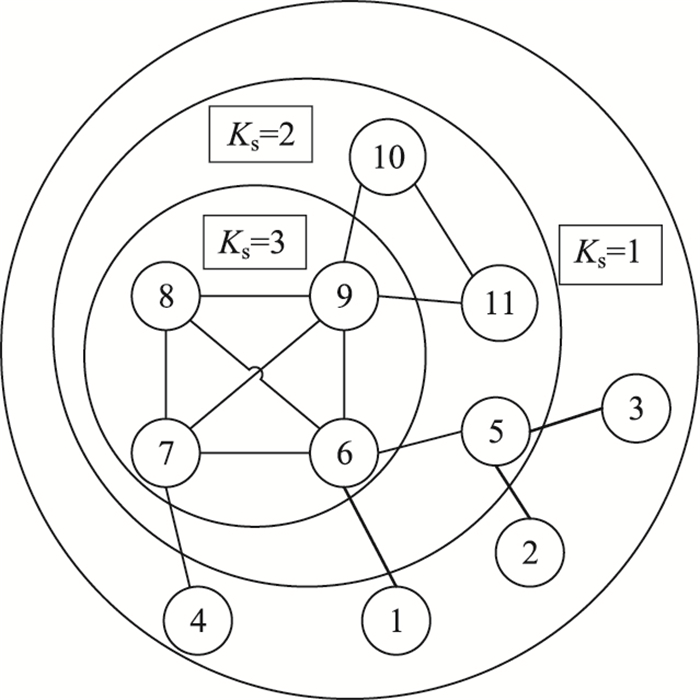
(1) 找到网络G中度数为1的节点及边,删除度为1的节点及边,得到子网络G1,再选取子网络G1中度为1的节点,将度为1的节点和边删除得到子网络G2,重复上述操作,直到网络中不再新出现度为1的节点,此时将所有删除的节点作为网络的第1层,记为Ks=1。如图 2中的节点4,2,3,1为第1层,记为1-shell。
|
| 图 2 K-shell分解法示例 Fig. 2 An example of K-shell decomposition |
| |
(2) 递归地删除网络中节点度数小于等于2的节点及其相连的边得到子网络G3,之后更新网络并重新计算度,记为Ks=2。如图 2中的节点5,10,11为第2层,记为2-shell。同时对同一层节点辅助于度中心性进行排序, 即从大到小排序为5,10,11。
(3) 对于更新之后的网络,重复上述操作,直到网络中的所有节点都被赋予Ks值,记为Ks=k。
(4) 结合实际,选择Ks值大的前面站点(其总数占站点总数一定比例,如15%)作为重要节点,作为规划调整时的主要换乘站点予以保留。而此类站点在实际中包括“火车站、高铁站、地铁站、汽车站、已有换乘中心等客流量较大的综合站场”,也包括其他站点。
3 汽车公交线网优化模型 3.1 汽车公交线网模型建立符号说明:xa为路段a断面流量; t1,t2,t3,t4,t5分别为乘客步行时间、等车时间、上(下)车时间、车内行驶时间、换乘时间;λ为时间价值转化系数; umik为第i类乘客的换乘优惠幅度;Ca为路段a最大公交流量;K,Knr,Ktrs s分别为路径集合、直达路径集合、换乘路径集合;Cnrs, km为OD对rs间路径k直达广义费用;δrs, a, km为0-1变量,当路段a在OD对rs间路径k上m方式时,δrs, a, km=1,否则为0;Ctrs, km为rs间路径k换乘广义费用;δrs, T, km为0-1变量,路段a在rs间路径k上m方式在T处换乘时,δrs, T, km=1,否则δrs, T, km=0;ti, T, mk为换乘点T处第k条线路第i类乘客以m方式的换乘广义费用;fm是方式m的发车频率;Vm是交通方式m的平均行驶速度;frs, im为OD对rs间线路客流量;qrsi为OD对rs间第i类出行者需求量,drs为空间距离;qrsm为m方式的出行量,qrs为总出行量;Drs(·)为出行量需求函数,Drs-1(·)为其反函数;C0固定成本;C1车辆运营成本;RB为行驶车辆数;CTB为车辆循环周期;yk为0-1变量,当线路k被确定为规划线路时,yk=1,反之为0。
路段a广义费用ta为乘客步行时间、等车时间、上(下)车时间和车内行驶时间和票价的线性组合[19],即:
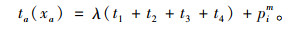
|
(3) |
乘客使用某种方式m时的平均等车时间为:
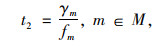
|
(4) |
式中,参数γm的值取决于交通方式m的车距和乘客的到达分布时间,γm一般取0.5。
乘客选择交通方式m时的车内行驶时间为:
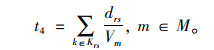
|
(5) |
在第k条线路第i类乘客m方式的线路换乘点T需要换乘时,其广义费用为:
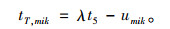
|
(6) |
若不需要换乘,即k∈Knrs,则OD对rs之间路径k的广义费用为:
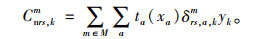
|
(7) |
若需要换乘,即k∈Ktrs,则OD对rs之间路径k的广义费用为:
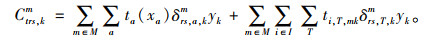
|
(8) |
本优化模型是在对现状骨干线路保留的基础上,对“其余汽车公交线路”选择的模型,优化目标以系统广义出行成本最小化、公交出行量最大化和公交亏损最小化建立多目标函数,同时受到单线目标和线网整体因素等制约。
(1) 系统广义出行成本最小化:
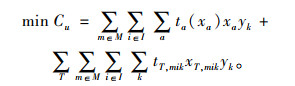
|
(9) |
(2) 出行总量最大化
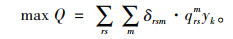
|
(10) |
(3) 公交企业成本亏损最小化
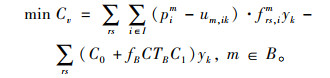
|
(11) |
综上,多目标问题转化为单目标,上层模型为:
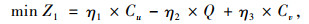
|
(12) |
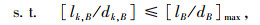
|
(13) |
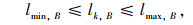
|
(14) |
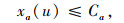
|
(15) |
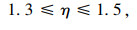
|
(16) |

|
(17) |
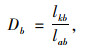
|
(18) |
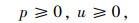
|
(19) |
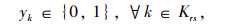
|
(20) |
式中,η1,η2,η3分别为各目标的偏重程度或权重;式(13)为线路非直线系数约束,规定其最大值为1.4;式(14)为公交线路长度约束,其中lmin, B、lmax, B分别为最小和最大长度;式(15)为路段a公交的最大通行能力约束;式(16)为乘客平均换乘系数约束,一般换乘不超过3次;式(17)为线网密度约束,S1为市中心区,S2为市边缘区;式(18)为公交线网覆盖率约束;式(19)为换乘优惠和票价的非负性约束,式(20)为0-1整数决策变量。
下层模型:采用基于弹性需求多方式多用户均衡配流模型,具体为:
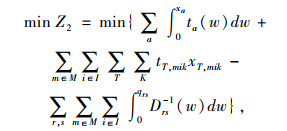
|
(21) |
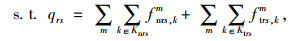
|
(22) |
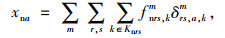
|
(23) |
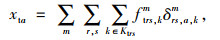
|
(24) |
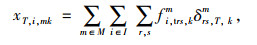
|
(25) |
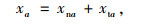
|
(26) |
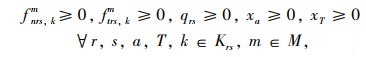
|
(27) |
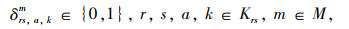
|
(28) |
式中,fnrs, km为r,s间m方式第k条路径上的直达需求量;ftrs, km为r,s间m方式第k条路径的换乘量;Krs为OD对rs之间所有的路径集合;xna为直达线路的路段流量;xta为换乘线路的路段流量;xT, mk为换乘点的线路流量;xa为路段a流量之和,式(27)为流量的非负性,δrs, a, km为0-1整数决策变量。
3.2 优化算法采用浮点遗传算法(Floating Genetic Algorithm, FGA)求解。
Step 1:各参数的输入。种群规模为MN、变异概率为pm、交叉概率pc及最大迭代次数NN。
Step 2:随机产生初始种群。设置进化代数Gen=0, 将初始种群Y(0)=[y1(0), y2(0),…, yMN(0)]代入下层模型中,输出线路流量,并计算目标函数值min(-C(0))、min(T(0))、min(-F(0)), 上标0表示第0代。
Step 3:计算各个个体的适应度值。依据适应值的大小,按照遗传算法规则进行淘汰和复制,然后进行选择、交叉、变异等遗传操作,产生新一代群体Y(k)。
Step 4:更新目标函数值。将新一代种群Y(k)代入式(21)~(28),输出其对应的线路流量,并更新目标函数值min(-C(k))、min(T(k))、min(-F(k))。
Step 5:若迭代次数达到最大迭代次数Gen>NN,将最后代数的最优个体解作为最优解,否则令k=k+1,转向Step 3。
4 应用分析 4.1 应用背景以天津市中心城区的轨道交通和汽车公交线网为例。截至2018年底投入运营的地铁线路6条,工作日均客流量110万人次/ d。中心城区汽车公交线路518条(快速和常规416条,接驳102条),线路长度750 km, 公交站点2 401个,公交出行量136万人次/d,平均长度25.8 km,公交换乘率为1.09,中心城区公交出行量占机动化出行总量比例58.1 %(不含步行),公交一卡通使用率72.5%;中心城区公交普通车8 km以下为1元/人次,8~10 km为1.5元/人次,10 km以上为2元/人次;空调车一律为2元/人次。其中公交普通卡九五折优惠, 老年卡免费。
4.2 基于K-shell分解法的公交站节点分析采用K-shell分解法(具体使用Pajek软件)对天津中心城区公交网络节点进行K-shell分解和计算对比,按其所得值从高到低进行排序,表 1是现状部分Ks值排名在前的站点(根据网路节点的重要性分15层),在优化过程中依据该排序确定主要换乘站点和保留骨干线路,调整其余线路,再依据调整后的规划方案,更新各站点Ks值,不断重复。
| 序号 | 公交站点名 | Ks值 | 度中心性 |
| 1 | 鼓楼东 | 15 | 50 |
| 2 | 城厢东路 | 15 | 42 |
| 3 | 马庄 | 14 | 34 |
| 4 | 北仓 | 14 | 31 |
| 5 | 北仓礼堂 | 14 | 28 |
| 6 | 海光寺 | 13 | 38 |
| 7 | 荣业大街 | 13 | 34 |
| 8 | 时代广场 | 13 | 34 |
| 9 | 侯台村 | 13 | 30 |
| 10 | 鞍山西道地铁站 | 13 | 28 |
| 11 | 学苑路 | 13 | 28 |
| 12 | 百货大楼 | 13 | 27 |
| 13 | 柳苑公寓 | 13 | 27 |
| 14 | 陞安大街 | 13 | 26 |
| 15 | 中铁十八局 | 13 | 24 |
| 16 | 轻化所 | 13 | 24 |
| 17 | 南市食品街 | 13 | 24 |
| 18 | 天拖地铁站 | 13 | 22 |
| 19 | 灰堆 | 13 | 22 |
| 20 | 南门外大街 | 13 | 20 |
4.3 协同优化过程评价与分析
经计算λ≈0.43元/min(由天津市居民人均可支配收入与居民工作时间确定),取η1∶η2∶η3=3∶1.5∶1, 乘客换乘平均走行时间为2.38 min,平均候车时间为4.85 min,上下车时间忽略不计。汽车公交和轨道交通(地铁)的车容量分别为40,245人/车,固定成本和间接成本忽略不计,运营成本分别为275,1 200元/h,平均行驶速度分别为15,36 km/h。
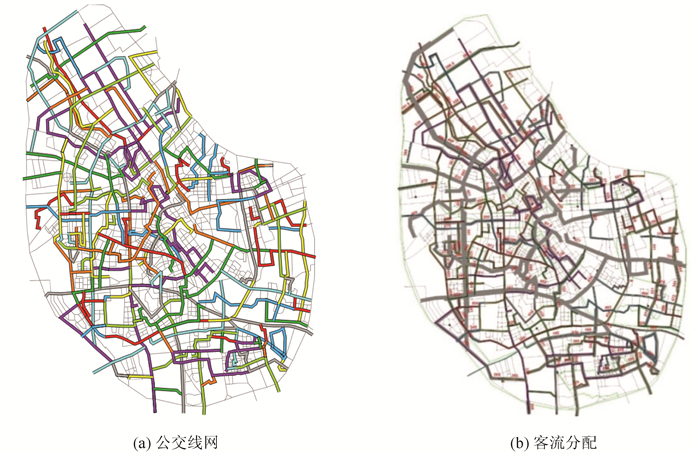
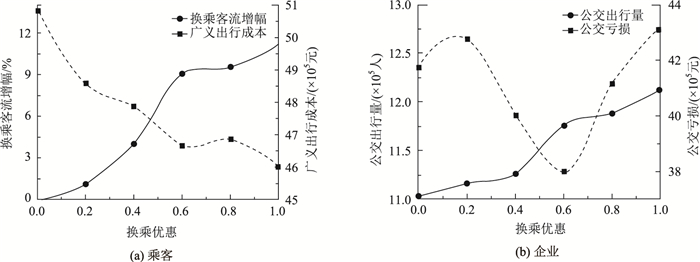
采用打折优惠换乘,1 h内公交以2元票价为基准,换乘优惠对象为使用IC卡、二维码、银联、NFC等支付方式的普通乘客和使用老年卡的乘客,其中老年卡乘客公交段免费。对不同的换乘优惠幅度,优化结果、客流分配和线网调整评价指标如表 2所示(为协同优化方案中的规划调整方案),基于TransCAD弹性用户均衡配流模型的天津市中心城区的客流分布如图 3所示,换乘优惠比例对乘客和公交企业影响如图 4所示。
| 换乘优惠幅度/% | 广义出行成本/元 | 出行总量/(人·d-1) | 公交亏损/元 | 目标函数/元 | 乘客换乘系数 | 公交换乘出行量/(人·d-1) | 公交线网密度/(km·km-2) | 公交分担率/% |
| 0 | 5 087 702 | 2 515 742 | 4 295 616 | 15 785 109 | 1.15 | 528 485 | 2.68 | 56.45 |
| 20 | 4 858 420 | 2 535 099 | 4 276 382 | 14 848 994 | 1.26 | 534 578 | 2.82 | 59.01 |
| 40 | 4 788 579 | 2 672 938 | 4 004 467 | 14 260 797 | 1.35 | 549 895 | 2.78 | 60.45 |
| 60 | 4 647 870 | 2 780 048 | 3 857 635 | 13 631 173 | 1.44 | 565 812 | 2.75 | 63.03 |
| 80 | 4 786 652 | 2 768 331 | 4 298 472 | 14 505 932 | 1.47 | 578 768 | 2.72 | 65.55 |
| 100 | 4 699 895 | 2 892 141 | 4 394 864 | 14 156 338 | 1.58 | 601 862 | 2.69 | 69.32 |
|
| 图 3 天津市中心城区客流分布 Fig. 3 Distribution of passenger flow in central area of Tianjin |
| |
|
| 图 4 换乘优惠折扣对乘客和公交企业的影响 Fig. 4 Influence of transfer pricing discount on passengers and public transport enterprise |
| |
(1) 换乘优惠的实施增加公交的出行量,同时对线网的调整降低公交的亏损。但优惠幅度不宜过大,这样会增加公交企业的亏损,不利于整体社会效益。从目标函数可以判断出换乘优惠选60%较合理,公交分担率增加了10.55%。
(2) 图 4(a)为不同换乘优惠对乘客的影响,可以看出换乘优惠幅度的增大,换乘客流增幅呈现“
慢-快-慢”的趋势,乘客票价成本虽减少,但换乘优惠伴随着线网的调整,导致乘客的换乘时间增加,相应的换乘时间成本加大,如换乘优惠为80%时,从而对于乘客是不利的,而100%时公交企业亏损严重,是企业不能承担的;图 4(b)为换乘优惠对于公交企业的影响:可看出随着换乘优惠的增加,部分线路变短和接驳线路增加,增加了出行者的出行次数,但整体对于社会效益是有利的,公交客流量增大,企业亏损减少。
参照文献研究,考虑4种方式进行对比:一是不换乘优惠和规划调整;二是只有换乘优惠;三是只有规划调整;四是本方案,结果如表 3所示。其中方式1、2公交线路有518条(快速和常规419条,接驳99条),平均长度为25.8 km,方式3优化后汽车公交线路484条(快速和常规368条,接驳116条),线路平均长度22.4 km, 方式4优化后汽车公交线路465条(快速和常规334条,接驳131条),线路平均长度20.5 km。
| 方式 | 换乘优惠幅度/% | 广义出行成本/元 | 出行总量/(人·d-1) | 公交亏损/元 | 目标函数 | 线路重复系数 | 换乘出行率/% | 公交分担率/% |
| 现状 | — | 5 088 796 | 2 461 742 | 4 123 288 | 15 697 063 | 12.09 | 18.32 | 58.10 |
| 1 | — | 5 407 680 | 2 355 654 | 5 298 542 | 17 988 101 | 12.09 | 16.86 | 48.85 |
| 2 | 60 | 5 343 257 | 2 493 971 | 5 051 472 | 17 340 287 | 12.09 | 22.25 | 50.02 |
| 3 | — | 5 087 702 | 2 515 742 | 4 295 616 | 15 785 109 | 9.42 | 23.18 | 56.45 |
| 4 | 60 | 4 647 870 | 2 780 048 | 3 857 635 | 13 631 173 | 10.06 | 24.36 | 63.03 |
(3) 由方式1~方式4对比可看出,若维持现状,公交分担率将从现在的58.10%下降到48.85%,公交企业直接运营成本(亏损)从412.328 8万元增加到529.854 2万元,其他指标也变差;方式2和3通过单一方式调整,可增加乘客乘坐公共交通的出行比例,但方式2增加了企业成本,方式3会降低线路重复系数,但增加了乘客的出行时间,将乘客从公交出行转向其他方式出行,不是我们追求的目标;而本换乘优惠与线网的协同优化方式与前3种相比,系统广义出行成本分别降低14.05%,13.01%和8.65%,公交分担率分别增加29.03%,26.01%和11.66%,公交企业亏损分别降低27.19%,23.63%和10.20%,线路断面更加均衡,负载效率更加平均,日均客运量增加,说明线网与站点空间分布合理,线网优化效果还是比较明显的。
5 结论建立换乘优惠与汽车公交线网调整协同优化模型,其中采用K-shell分解法选择重要节点,确定保留的骨干公交线路。该换乘优惠与线网协同优化方法,可有效组合多重模式的公共交通系统,实现协同配合,提高公共交通出行率;此外,该方法在适度加大居民换乘率的同时,提升公交网络的整体运营水平,有效平衡客流分布,优化资源配置,降低乘客的出行成本和政府的补贴,为构建多层次、多模式、一体化的公共交通体系提供具体实施举措。
| [1] |
AN K, LO H K. Two-phase Stochastic Program for Transit Network Design under Demand Uncertainty[J]. Transportation Research Part B: Methodological, 2016, 84: 157-181. |
| [2] |
CIPRIANI E, GORI S, PETRELLI M. Transit Network Design: A Procedure and an Application to a Large Urban Area[J]. Transportation Research Part C: Emerging Technologies, 2012, 20(1): 3-14. |
| [3] |
陈维亚, 刘晓飞, 吴良江. 数据驱动的公交网络动态优化调整方法[J]. 交通运输系统工程与信息, 2017, 17(6): 114-119. CHEN Wei-ya, LIU Xiao-fei, WU Liang-jiang. Data-driven Optimization Methods for Dynamic Transit Network Adjustment[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(6): 114-119. |
| [4] |
黄敏. 多层次公交线网拓扑结构分析[J]. 公路交通科技, 2010, 27(5): 93-99. HUANG Min. Analysis on Topology Frame of Multi-level Transit System Network[J]. Journal of Highway and Transportation Research and Development, 2010, 27(5): 93-99. |
| [5] |
张恺伦. 基于轨道交通的常规公交线网优化研究[D]. 兰州: 兰州交通大学, 2016. ZHANG Kai-lun. Study on Net Optimization of Conventional Bus Transportation Based on Rail Transit[D]. Lanzhou: Lanzhou Jiaotong University, 2016. |
| [6] |
陈鹏, 严新平, 李旭宏, 等. 轨道交通与常规公交计划调度协调模型[J]. 吉林大学学报: 工学版, 2011, 41(4): 950-955. CHEN Peng, YAN Xin-ping, LI Xu-hong, et al. Schedule Coordination Model between Rail Transit and Bus Transit[J]. Journal of Jilin University: Engineering and Technology Edition, 2011, 41(4): 950-955. |
| [7] |
陈阳. 特大城市多层次地面公交网络优化实用方法研究[D]. 南京: 南京林业大学, 2018. CHEN Yang. Study on Practical Method for Optimization of Multi-level Bus Network in Megacities[D]. Nanjing: Nanjing Forestry University, 2018. |
| [8] |
张悦. 考虑出行方式选择行为的公共交通换乘优惠研究[D]. 重庆: 重庆交通大学, 2016. ZHANG Yue. Analysis of Transfer Fare Discount under Consideration of Travel Mode Choosing Behavior of Public Transport[D]. Chongqing: Chongqing Jiaotong University, 2016. |
| [9] |
刘杰, 何世伟, 宋瑞, 等. 基于社会经济效益最大化的轨道交通票价优化[J]. 吉林大学学报: 工学版, 2011, 41(5): 1268-1272. LIU Jie, HE Shi-wei, SONG Rui, et al. Optimization of Railway Transit Ticket Price Based on Maximization of Social-economic Benefit[J]. Journal of Jilin University: Engineering and Technology Edition, 2011, 41(5): 1268-1272. |
| [10] |
LI Z C, LAM W H K, WONG S C. Transportation and Traffic Theory 2009:Golden Jubilee[M]. Boston: Springer, 2009: 495-516.
|
| [11] |
刘秉政, 葛颖恩, 曹凯. 基于地铁与公交站间距差异的票价及换乘优惠优化[J]. 交通运输系统工程与信息, 2016, 16(3): 113-119. LIU Bing-zheng, GE Ying-en, CAO Kai. Optimizing Fares and Transfer Pricing Discounts for a Subway and Bus Corridor Considering Difference in Stop Distance between Two Service[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(3): 113-119. |
| [12] |
靳爽, 庞明宝. 考虑共享单车的城市轨道交通社区接驳规划与公交调度综合优化[J]. 公路交通科技, 2020, 37(2): 123-129. JIN Shuang, PANG Ming-bao. Integrated Optimization of Community Connection Planning and Bus Dispatching for Urban Rail Transit Considering Shared Bicycle[J]. Journal of Highway and Transportation Research and Development, 2020, 37(2): 123-129. |
| [13] |
任其亮, 孙丰瑞, 王亚龙. 城市公共交通便捷性评价模型研究[J]. 公路交通科技, 2015, 32(2): 127-133. REN Qi-liang, SUN Feng-rui, WANG Ya-long. Study on Evaluation Model of Urban Public Transport Convenience[J]. Journal of Highway and Transportation Research and Development, 2015, 32(2): 127-133. |
| [14] |
庞明宝, 张思林, 李春霞. 城市公交站设置双层规划[J]. 公路交通科技, 2013, 30(3): 118-124. PANG Ming-bao, ZHANG Si-lin, LI Chun-xia. Bi-level Programming of Urban Bus Stop Locating[J]. Journal of Highway and Transportation Research and Development, 2013, 30(3): 118-124. |
| [15] |
孟婕. 基于节点重要度和线网结构特征的城乡公交线路布局研究[D]. 北京: 北京交通大学, 2015. MENG Jie. Lines Layout Research of Urban-rural Public Transit Based on Node Importance and Network Structure Characteristics[D]. Beijing: Beijing Jiaotong University, 2015. |
| [16] |
KITSAK M, GALLOS L K, HAVLIN S, et al. Identification of Influential Spreaders in Complex Networks[J]. Nature Physics, 2010, 6(11): 888-893. |
| [17] |
BROWN P E, FENG J. Measuring User Influence on Twitter Using Modified k-shell Decomposition[C]//Proceedings of the 5th International AAAI Conference on Weblogs and Social Media. Menlo Park: AAAI, 2011: 18-23.
|
| [18] |
CARMI S, HAVLIN S, KIRKPATRICK S, et al. A Model of Internet Topology Using k-shell Decomposition[J]. Proceedings of the National Academy of Sciences, 2007, 104(27): 11150-11154. |
| [19] |
王镜, 邵春福, 毛科俊. 公交换乘优惠的双层规划模型[J]. 中国公路学报, 2008, 21(2): 93-97. WANG Jing, SHAO Chun-fu, MAO Ke-jun. Bi-level Programming Model for Transfer Benefit of Public Transportation[J]. China Journal of Highway and Transport, 2008, 21(2): 93-97. |
 2021, Vol. 38
2021, Vol. 38
