扩展功能
文章信息
- 蔡晓禹, 吕亮, 杜蕊
- CAI Xiao-yu, LÜ Liang, DU Rui
- 基于组合模型的车辆出行特征模式划分
- Classification of Vehicle Travel Feature Modes Based on Combined Model
- 公路交通科技, 2021, 38(6): 129-140
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(6): 129-140
- 10.3969/j.issn.1002-0268.2021.06.017
-
文章历史
- 收稿日期: 2020-10-12
2. 山地城市交通系统与安全重庆市重点实验室, 重庆 400074
2. Chongqing Key Laboratory of Traffic System & Safety in Mountainous Cities, Chongqing 400074, China
随着区域一体化进程的加快,城市出行需求增长迅速,私家车作为城市交通的主要组成部分,具有灵活、机动的优势。在综合运输竞争日益激烈的背景下,研究私家车的出行特征,有助于改善城市交通组织,为城市智能的交通发展奠定基础。
近些年,RFID(射频识别技术)在交通领域中被广泛挖掘应用,主要体现在公路收费、停车场管理、车辆身份识别等方面[2-3]。根据相关外文文献,美国在RFID的应用方面处于相对领先的地位,英国、德国、瑞士、瑞典、日本等国均具有较为成熟且先进的RFID产品,如美国的E-Zpass收费、新家坡的不停车收费以及英国伦敦的交通拥堵费。此外德国也研究了RFID技术在交通信息采集方面的重要应用,德国柏林交通管理中心在2000年建立基于RFID技术的交通信息采集系统。21世纪初,RFID逐渐进入中国市场,并得到了政府的大力支持。2019年6月,伴随着《中国RFID技术政策白皮书》的发布,我国的RFID技术进入了国家产业发展战略层面。现如今,我国的RIFD技术发展相对成熟的城市有南京、杭州、无锡、深圳和重庆等地。上海、杭州、重庆等多个城市依靠设置在道路上的RFID系统对公交进行实时监控,实现对车辆到站、离站时间的预测,以及配合红绿灯实现公交优先通行等。随着我国电子车牌国家标准的即将出台以及物联网技术的持续发展,RFID技术将会在自动驾驶、智能交通管理、智慧城市发展中具有更加广阔的应用前景。
不同时间段里城市人群移动的动态变化规律,体现了城市交通流体变化规律,隐含城市地域功能性信息等,其实质是对城市居民出行特征的研究分析。因此,车辆出行特征研究在城市建设规划等方面具有重要的意义,同时也是制订交通政策的科学依据。据相关国外研究,Sini Guo等[4]人主要研究轨迹数据的分割技术,从而分析车辆行为,提取商务信息,提出了一种集二元理论和牛顿法相结合的高效数据值算法来获取最优值。Zun Wang等[5]学者利用GPS数据中瞬时速度分布的变化系数来测量行程时间可靠性,提出旅行时间可靠性与道路密度的模型。Csáji等[6]基于大约10万组手机信令数据发掘了葡萄牙用户的活动模式。MingqiLv等[7]人提出一种序列模式挖掘算法,通过考虑估计的空间接近度,从单元轨迹数据集中挖掘运动模式。A. Ladino等[8]就提出了一种行程时间的动态聚类模型,利用聚类的质心级别与趋势变化规律来预测出行的旅行时间。Justin van Dijk[9]以轨迹数据提取利用不同的4种机器学习算法来识别轨迹数据中的活动点和旅行点,引入局部密度概念并评估了4种算法的性能。在国内的研究中,董宏辉等[10]人依据轨迹数据研究出行者的出行方式。充分挖掘GPS数据,提出两种基于相似性度量和窗口的转换点识别方法,然后将该方法运用到BP神经网络、决策树、KNN和支持向量机(SVM)4种识别交通出行的算法中,最后比较得出采用SVM识别交通出行方式能够取得最优结果。丁玲等[11]研究了在公共交通优先政策下对出行个体行为的影响。研究根据分析将出行个体划分为了3类,并采用聚类的方法将出行个体进行划分。再基于非集计模型对出行行为进行分析,研究综合考虑了交通状态影响以及公共交通优先策略影响下,出行个体的行为变化。
1 车辆出行轨迹分析城市车辆出行是出行者利用私家车、公交车以及出租车等方式在不同道路间的出行过程。本研究基于轨迹数据分析重点分析私家车及出租车辆的活动特点。
对于私家车轨迹研究,随机选取了近千辆私家车个体进行轨迹信息可视化定性分析。通过大量对私家车轨迹的观察,发现私家车出行集中呈现某些统计特征,即私家车轨迹检测数据大部分较短,但是大部分完整的RFID点位数据存在规律性。根据大量私家车出行轨迹分析,定性主要可以分析出存在两类典型出行特征情况。
根据出行轨迹可视化分析,可知存在一部分私家车群体在不同工作日内的出行会呈现高度重叠现象,例如周一至周五每天的出行时间以及轨迹基本一致,仅存在细微差别,特别是早高峰和晚高峰时期,例如图 1中给出了车辆编号为1005406和102563的私家车个体在2017年19日周四以及2017年20日周五的全天出行轨迹空间变化图。从图中可以看出该类型私家车个体工作日内的轨迹是相似的,有极高的重现性。一般这种具有规律性的车辆出行时间集中在7:00—8:00以及18:00—19:00之间,即早晚交通高峰时期,首次出行后会在固定区域活动或驻留较长时间,再进行1~2次折返,出行时间一般为1~2 h,并且这类私家车出行者占总体数目较多。总体来说,这类私家车用户出行需求较大,出行时间较为稳定,出行空间分布固定。
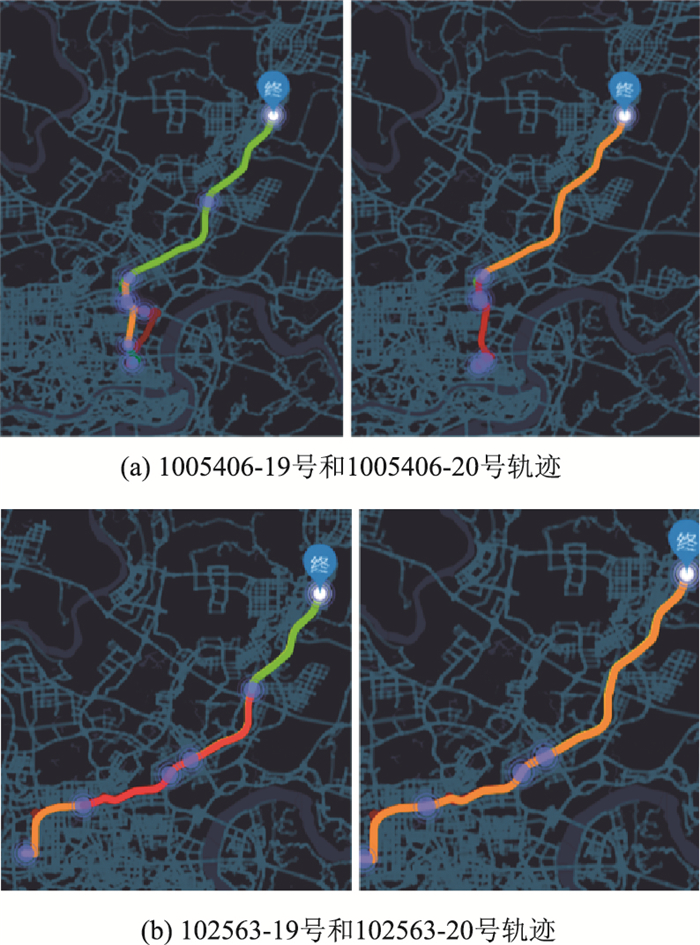
|
| 图 1 典型私家车Ⅰ轨迹空间 Fig. 1 Trajectory spaces of typical private car I |
| |
还有部分私家车工作日内每天的轨迹与之前类型的私家车完全不同,这些私家车用户的轨迹相比较下十分混乱,且经过的卡口点位较高,轨迹路径随机性也较高,但是起讫点基本一致。这种情况的私家车轨迹显示该车辆出行时间一般集中在早晨7:00—8:00或者下午13:00—14:00,被检测的时间分布较为均匀,其在道路网络的运行时间较大,且逗留位置较多即出行轨迹存在较多的断点,但驻留时间不长,如图 2中车辆编号为1008533(a)和1021804(b)的私家车个体在2017年19日周四以及2017年20日周五的全天出行轨迹空间变化图。从图上可看出这类私家车用户出行时间较为不固定,出行的空间分布较为紊乱,随机性高。但从大量类似出行特征的用户轨迹统计发现这类用户在道路网运行时间较大,虽然出行路径轨迹随机性高重复率低,但存在区域集中的现象,说明该类型用户拥有区域选择偏好。
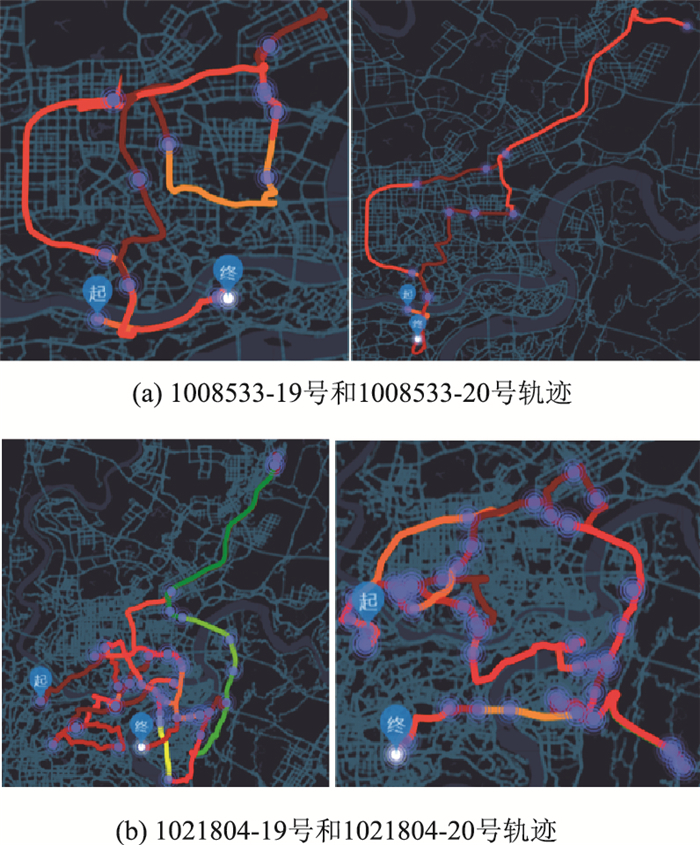
|
| 图 2 典型私家车Ⅱ轨迹空间展示图 Fig. 2 Trajectory spaces of typical private car II |
| |
对于出租车轨迹研究,本研究随机选取了数百辆出租车个体进行轨迹信息可视化定性分析。发现出租车工作日内出行轨迹空间分布极为广泛,大多数出租车出行时间极早几乎全天24 h都在路上运行,因此在道路网络运行时间较长。且出租车的轨迹空间分布不仅广泛,一般跨越4~5组团区域,而且轨迹路径组成较为复杂、随机性高。但根据大量出租车数据的统计分析可见大量的出租车驾驶员一般会在熟悉的区域跑动,因此轨迹存在聚集的现象,如图 3(b)172639出租车一周工作日的轨迹多出现在南岸区、巴南区。由此可以推测部分出租车驾驶员出行具有个体偏好的活动区域。
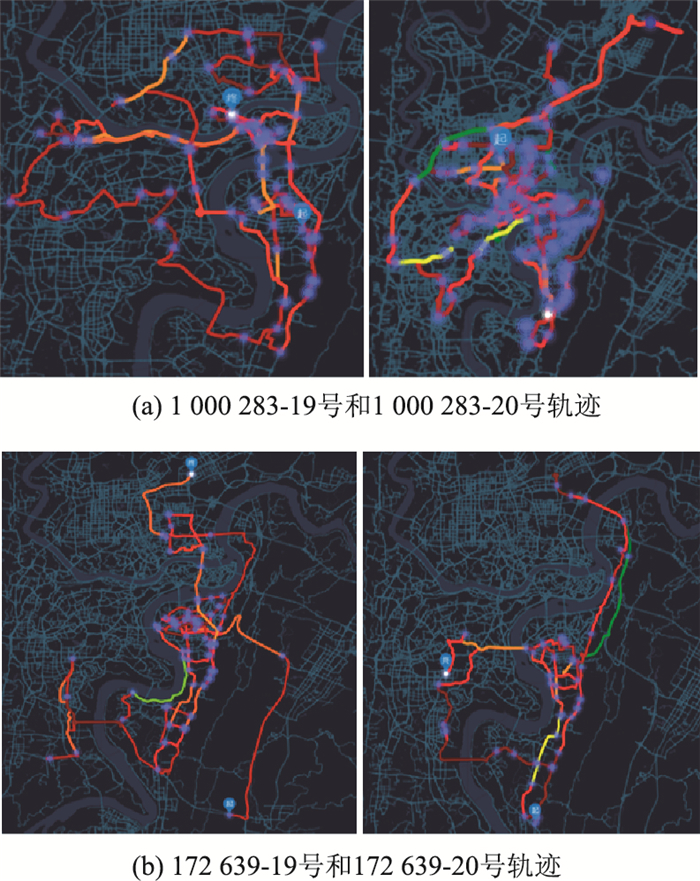
|
| 图 3 典型出租车轨迹空间 Fig. 3 Trajectory spaces of typical taxi |
| |
2 车辆出行特征指标分析
从轨迹数据的定性分析可知轨迹数据特征中直接或间接得包含了此出行轨迹与其他出行轨迹的差异性和共同处。出行轨迹的特征指标指对原始出行轨迹数据进行分析研究后,从中得到的可以表征出行特点的一系列具有代表意义的向量值。在对出行数据研究过程中可以提取出很多特征属性,其中包含一些目前研究不需要的指标;特征指标相互之间也会存在各种关联,有的相互补充,有的相互依赖,有的相互重复。在研究过程中为了减少不必要的重复,减少建模的复杂性和可行性,还需要对数据特征指标进行分析,剔除冗余或与研究不太相关的特征指标,以选取更加适合、完善的特征指标序列进行研究分析[12-14]。出行特征指标提取的详细研究分析过程如图 4流程所示。
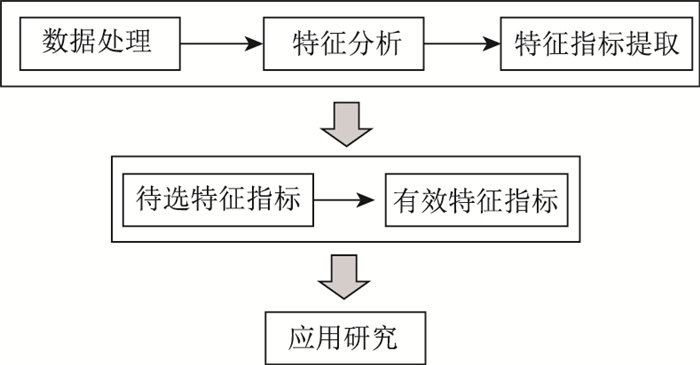
|
| 图 4 特征指标提取研究过程 Fig. 4 Study process of characteristic indicator extraction |
| |
出租车类型车辆较其他类型车辆在轨迹重复率指标中总体较低,在网时间总体分布很高的特点。这是因为出租车在出行轨迹上具有极大的随机性,但基于大数据轨迹的统计分析,发现出租车出行总体分布会存在偏好区域,即出租车会在偏好的区域内更频繁地活动。实际情况下,出租车在空载的情况下,一般会无目的地运行在道路上寻找乘客,但在一段时间内出租车需求少,出租车驾驶员会根据经验前往乘客较多的区域。另一方面,不同区域的乘客虽然出发点和目的地不相同,但根据概率也会存在概率高的出发点以及目的地。因此提出“热点活动区域”出行特征,分析出租车群体的最大概率活动区域。在研究车辆出行特征指标时提出热点活动区域指标,热点活动区域指标主要针对轨迹的出现空间选择偏好进行刻画,该指标体现了车辆个体最大概率出现的区域。根据上述对出行特征指标的差异性分析,最终选取出行频次、在网时间、轨迹重复率、以及首次出行时段、出行结束时段等指标变量构成出行特征的指标向量,见表 1。
| 特征指标称 | 特征指标描述 |
| 首次出行时段 | 车辆首次被检测到出行的时段 |
| 出行结束时段 | 车辆末次被检测到出行的时段 |
| 出行频次 | 一天时间内车辆的出行轨迹被驻留行为打断后出行段次数 |
| 在网时间 | 车辆一天24 h内在道路网上行驶的总时间 |
| 轨迹重复率 | 车辆出行轨迹点重复次数与总轨迹点个数的比值 |
| 干线影响区选择偏好 | 车辆个体对某选定干线道路的使用程度 |
| 热点活动区域 | 车辆个体在某选定区域内活动情况 |
3 车辆出行特征模式划分 3.1 改进CFSFDP聚类算法原理
CFSFDP聚类算法(clustering by fast search and find of density peaks)的基本步骤是:首先将多维数据集进行距离和密度计算,再选取聚类中心,最后对数据集中非聚类中心点进行归类操作[15-16]。
(1) 局部密度ρi
局部密度ρi具有两种计算方式,即Cut-off kernel (截止内核算法)和Gaussian kernel (高斯算法),其中当数据规模较大时,局部密度应该当用截止内核算法,当数据规模较小时,利用高斯算法计算局部密度ρi。
Cut-off kernel (截止内核算法):
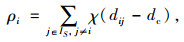
|
(1) |
其中函数
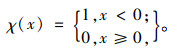
|
(2) |
参数dc>0为截断距离(cutoff distance),需聚类前研究设定。
由公式(1)可知,实际上ρi求得S数据集中与xi之间的距离小于截断距离dc(不包含xi本身)的个数。
Gaussian kernel (高斯算法):
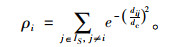
|
(3) |
截止内核算法为离散值而高斯算法为连续值,相对来说高斯算法更小可能产生冲突(即不同数据点具有相同的局部密度)。
(2) 距离δi
距离δi的计算公式为:

|
(4) |
其中{qi}i=1N表示{ρi}i=1N的一个降序排列的下标集合,即:
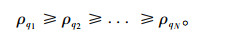
|
(5) |
由计算公式可知,当xi是具有局部密度的数据点时,δi表示xi与S数据集中距离最大的数据点的距离值;否则,δi表示在所有局部密度大于xi的数据点中,与xi距离最小的那些数据点的距离值。
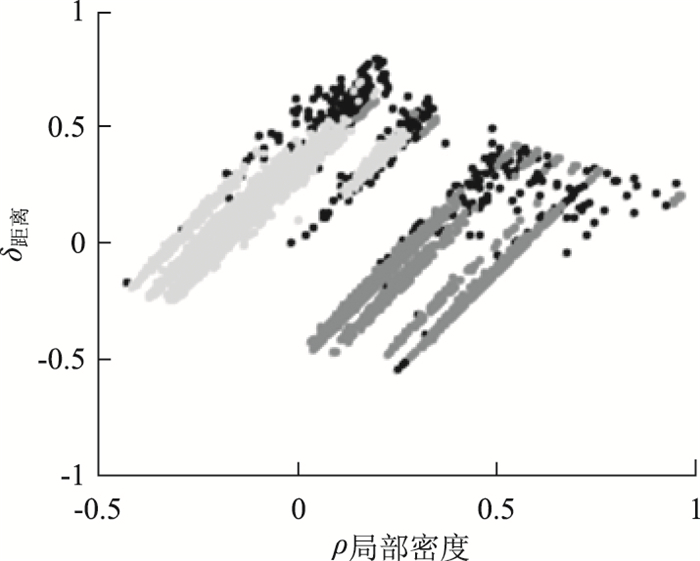
在计算了所有数据点的局部密度ρi和距离δi之后,以ρ为横轴,δ为纵轴,将二元点集{(ρi, δi)}i=1N对应做出聚类决策图,参考图 5(a)中的例子(例子中包含了28个二维数据点),做决策图如图 5(b)。从决策图可以看出来,元素1与元素10同时具有较大的ρ值和δ值,而这两个元素也是图 5(a)数据集中的两个聚类中心。从图 5(a)散点图可以看出元素26,27,28在原始数据集中是噪声点(离群点),这3个元素在图 5(b)中反映的特点是:δ值很大,但是ρ值很小。

|
| 图 5 决策图实例及示意图 Fig. 5 Example and schematic diagram of decision-making diagram |
| |
3.2 BP神经网络识别模型
人工神经网络(artificial neural network),是由大量处理单元通过广泛互联而构成的网络体系。神经网络的快速发展使得其成为模式识别强有力的工具。神经网络主要分为前馈神经网络和循环神经网络[17]。本研究介绍的BP神经网络模型属于多层前馈神经网络,能够实现从输入到输出的映射功能,数学理论证明三层的神经网络以任意精度逼近任何非线性连续函数,这使得BP神经网络具有较强的非线性映射能力。
BP神经网络可以由BP和前馈神经网络两个部分组成[18],BP指的是Back Propagation(逆向传播),即误差的逆向传播,以及信号的前向传播。其学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小,BP网络得结构示意图见图 6。

|
| 图 6 构建BP神经网络模型 Fig. 6 Building a BP neural network model |
| |
3.3 基于组合模型的出行特征模式划分
出行特征群体辨识主要由3部分内容组成:(1)RFID轨迹数据的预处理与出行指标参数的选取,主要包括对出行群体的轨迹分析、预判断和出行指标的提取;(2)基于出行特征指标的聚类分析,主要是针对选取的出行特征指标进行基于峰值密度的聚类分析,再根据分类结果分析划分群体的具体性质;(3)出行特征群体的识别,主要介绍BP神经网络出行特征识别模型。出行特征群体的辨识是先分出租车、私家车、货车3种车辆类型,分别进行群体的划分和识别训练过程,针对不同车辆类型的出行特征分布特点进行出行特征群体的研究,每一种车辆类型选取的出行特征指标因车辆类型的运行特点和分析角度有所不同,本研究先将全面考虑所有出行特征可能的不同分布,再利用聚类思想将选取的出行特征指标进行研究分析,再进行群体识别。具体的车辆出行特征辨识方法结构如图 7所示。

|
| 图 7 出行特征群体辨识方法结构 Fig. 7 Structure of travel characteristic group recognition method |
| |
4 案例分析 4.1 数据来源
本研究试验分析数据来源于重庆市城市交通大数据工程技术研究中心。研究数据主要来源于道路安装的RFID设备检测器,数据类型包含车辆RFID检测数据、RFID卡口经纬度数据,详见表 2。
| 数据内容 | 检测卡口名称 | 车辆行驶方向 | 车辆编码 | 时间 | 车辆信息 | 卡口设备情况 | 卡口经纬度坐标 |
| RFID数据 | √ | √ | √ | √ | √ | √ | √ |
数据覆盖范围主要为重庆市主城区,其中覆盖北碚组团、西永组团、西彭组团、蔡家组团、沙坪坝组团、空港组团、悦来组图、礼嘉组团、人和组团、观音组团、渝中组团、大杨石组团、南坪组团、大渡口组团、李家沱组团、茶园组团以及界石组团。重点研究区域选定为机场路干线影响区,其实际地理位置位于人和组团内,覆盖范围实际是围绕机场路以及机场路所能在交通方面直接影响的区域,详细范围以及范围内RFID卡口分布如图 8所示。各组团区域划分以及所在区域内RFID卡口布设点位分布如图 9所示。
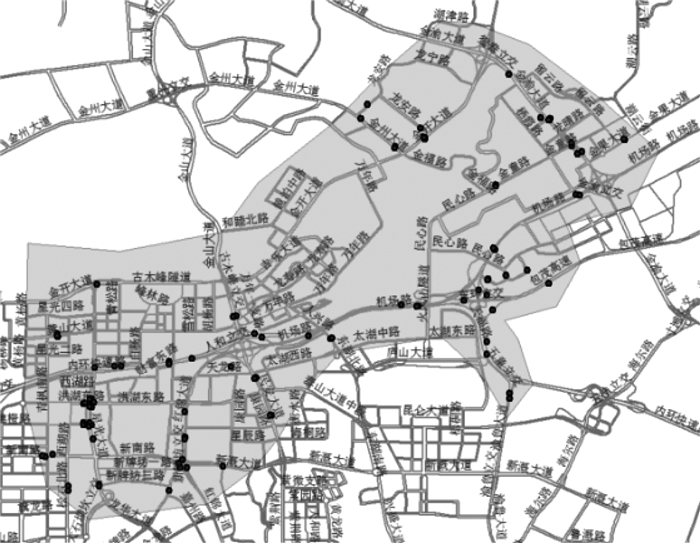
|
| 图 8 干线影响区范围及RFID卡口 Fig. 8 Scope of mainline affected area and RFID gates |
| |

|
| 图 9 组团及RFID卡口布设 Fig. 9 Grouping and layout of RFID gates |
| |
4.2 私家车出行群体辨识
由于智能交通的发展,新型智能交通打车APP的出现,使得越来越多的私家车多向性的发展为商用运营车辆。合理规划管理商用运营车辆群体,可以更高效率地提高车辆的使用率,提高运行效率。根据相关文献可知,商用运行车辆的在网时间一般小于出租车个体,但比通勤出行需求的车辆运行时间长,且出行频次较高,同时运行轨迹与出租车相似随机性高,因此轨迹重复率指标值较低。由此可知,选取的出行特征指标可以满足商用运行车辆的识别要求。
私家车群体的试验对象来源于重庆市主城区2017年10月17号—10月22号的RFID数据。由于样本数据过大会造成程序运行需要大量时间,系统运行负荷大易崩溃现象。因此经过多次试验后,随机选取26 165组完整有效处理后数据样本,提取出行频次、在网时间、轨迹重复率、首次出行时段、出行结束时段出行特征指标进行聚类分析。数据样本详见表 3。
| ID | 首次出行时段 | 出行频次/(次·d-1) | 在网时间/s | 出行结束时段 | 轨迹重复率 |
| 100 975 | 05:00—07:00 | 2 | 3 555 | 05:00—07:00 | 0.522 |
| 1 003 994 | 07:00—09:00 | 4 | 2 365 | 17:00—19:00 | 0.462 |
| 1 004 047 | 09:00—12:00 | 2 | 4 550 | 19:00—22:00 | 0.889 |
(1) 私家车群体划分
由前节模型说明可知,CFSFDP算法的输入参数是指标相互之间的距离。为便于计算在计算指标之间的距离前,首先需要对特征向量组数据进行编号,详见表 4。
| 序号 | 出行特征向量 |
| 1 | (2, 2, 3 555, 2, 0.522) |
| 2 | (3, 4, 2 365, 6, 0.462) |
| 3 | (4, 2, 4 550, 7, 0.889) |
| 类型 | 出行频次(次·d-1) | 在网时间/h | 轨迹重复率 | 首次出行时段 | 出行结束时段 | 群体定义 |
| A | 3-5 | [1,4] | [0.18,0.46] | 07:00—09:00 | 22:00—24:00 | 商用私家车出行者 |
| B | 2-3 | [0.4,1.3] | [0.4,0.83] | 07:00—09:00 | 17:00—19:00 | 通勤私家车出行者 |
| C | 2-4 | [0.7,1.9] | [0.27,0.7] | 07:00—09:00 | 19:00—22:00 | 其他私家车出行者 |
本章节使用欧式距离公式来计算指标向量之间的距离,详见式(1)。
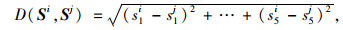
|
(1) |
式中,Si, Sj表示两组不相同的特征向量组,其中i, j < N(N为样本总量)。s1i~s5i分别表示出行频次、在往时间、轨迹重复率、首次出行时段、出行结束时段出行的指标值。将特征向量之间的距离作为模型输入,进行CFSFDP算法聚类计算。聚类结果显示私家车存在3个聚类中心,分别为:
聚类中心A:总包含元素2 669个,其中核心元素2 669,无噪声元素。
聚类中心B:总包含元素12 491个,其中核心元素12 491,无噪声元素。
聚类中心C:总包含元素11 005个,其中核心元素11 005,无噪声元素。
图 10展示了不同类别数据在二维图上的分布情况,需要特别说明的是,图 10中的X轴与Y轴仅代表一种二维空间中的度量,没有特定的含义。有图可见,改进后的局部密度计算方法是的每个数据点的值符合实际,避免了错误的分配,减少了私家车的噪声数据,且不同类型数据存在明显分离。
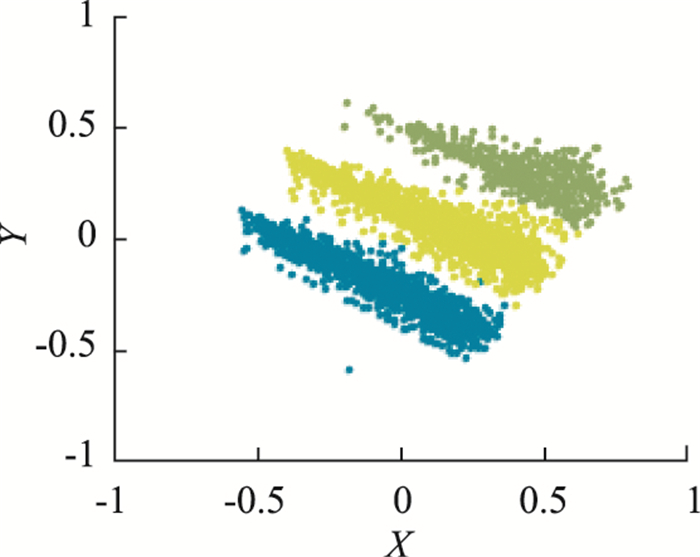
|
| 图 10 私家车CFSFDP算法分类数据二维展示 Fig. 10 Two-dimensional display of classification data obtained by CFSFDP algorithm |
| |
(2) 聚类结果分析及群体定义
由聚类算法结果可知26 165辆私家车样本被划分为3类。为了精准地认识这3种类型的出行特征,需要对选取的5个出行特征指标进行详细的分析。对聚类结果的3类私家车样本分别从5个指标展开对比分析研究不同的特征规律,可以准确定义3类出行特征群体。本研究为比较分析私家车不同群体的特征差异性,绘制参数比较图,详见图 11~图 16。

|
| 图 11 私家车出行群体出行频次比较 Fig. 11 Comparison of travel frequencies of travel groups |
| |
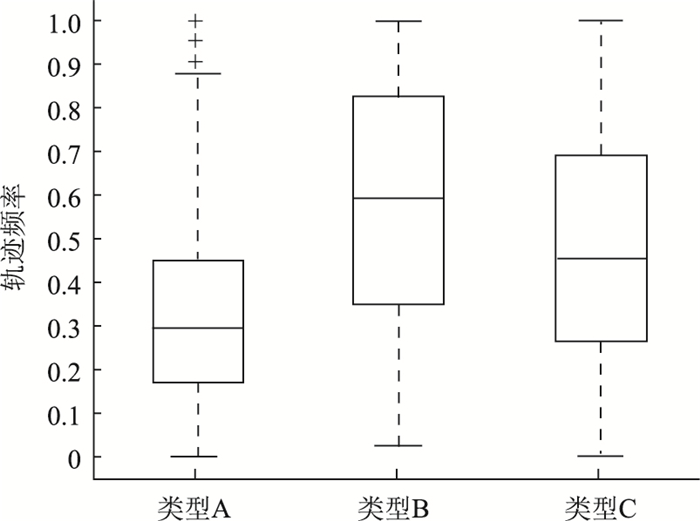
|
| 图 12 私家车出行群体轨迹重复率比较 Fig. 12 Comparison of travel group trajectory repetition rates |
| |
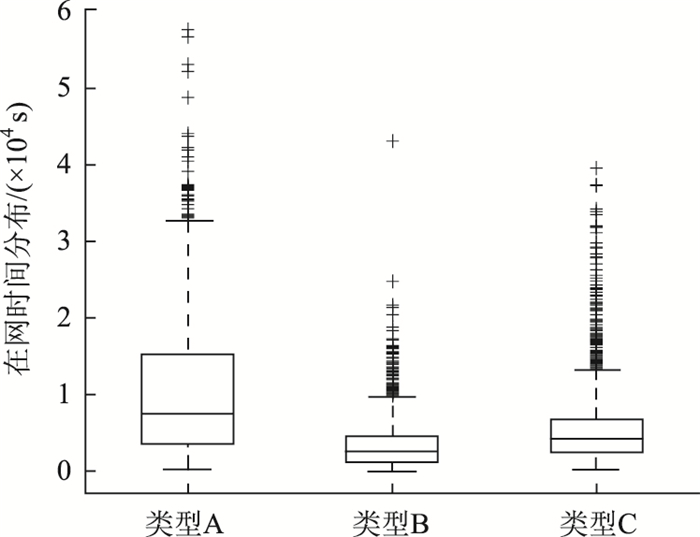
|
| 图 13 私家车出行群体在网时间比较 Fig. 13 Comparison of online time of travel groups |
| |

|
| 图 14 类型A出行时段 Fig. 14 Travel time of Type A |
| |
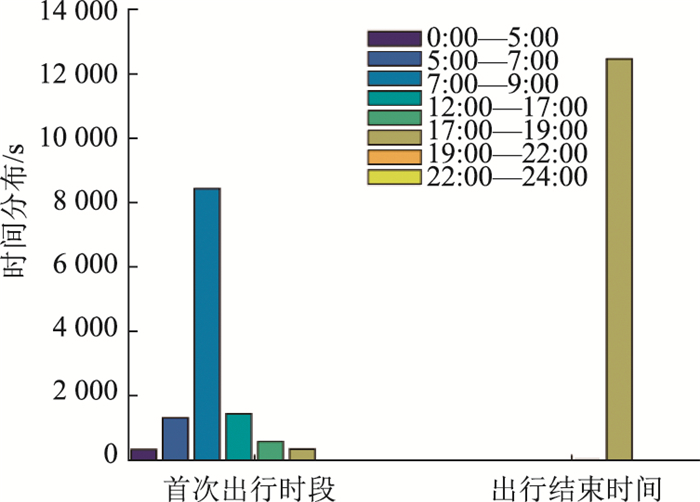
|
| 图 15 类型B出行时段 Fig. 15 Travel time of Type B |
| |

|
| 图 16 类型C出行时段 Fig. 16 Travel time of Type C |
| |
① 出行频次
类型A:该分类有较高的出行频次,基本集中3~5次/d,平均4次/d。
类型B:该分类有较低的出行频次,基本集中2~3次/d,平均2次/d。
类型C:该分类在出行频次上集中2~4次/d,平均3次/d,出行频次分布处于中间水平。
② 轨迹重复率
类型A:该类型有较低的轨迹重复率,分布集中在[0.18,0.46],平均在0.3左右,说明该类私家车驾驶员每天的行程不太一样,具有多变性和偶然性。
类型B:该分类有较高的轨迹重复率,基本集中[0.4,0.83],平均在0.7左右,据相关分析轨迹重复率在0.7左右,即代表该类私家车驾驶员具有极高的轨迹重现性。
类型C:该类型在轨迹重复率集中[0.27,0.7],轨迹重复率处于中间水平。
③ 在网时间
类型A:该类型有较高的在网时间,分布集中在[3 609,15 340],平均在7 503 s,即2 h左右。说明该类私家车驾驶员每天在行程上花费大量的时间。
类型B:该分类有较低的在网时间,基本集中[1 296,4 642],平均在2 688 s,即0.7 h左右。代表该类私家车驾驶员在行程上所费时间较少,对于车辆的依赖性较低。
类型C:该类型在网时间指标集中[2 387, 6 773],平均4 325 s,驾驶员在网时间处于中间水平。
④ 出行时段分布
类型A:该类型首次出行时段较高集中在07:00—09:00时段,出行结束时间基本集中在22:00—24:00时段。其中00:00—05:00出行的车辆分布较其他类型多。
类型B:该类型首次出行时段较高集中在07:00—09:00时段,出行结束时间基本集中在17:00—19:00时段。
类型C:该类型首次出行时段较高集中在07:00—09:00时段,出行结束时间基本集中在19:00—22:00时段。
类型A出行频次高,轨迹分布较离散且在网时间较高的特点看,该类型接近于私家车商用的司机特性,例如(滴滴车等),因此类型A在本研究定义为商用私家车出行群体。
类型B出行频次低,平均2次/d,出行的轨迹重现性高且在网时间较短的特点看,该类型接近于通勤私家车司机的特性,例如(即基本上班和下班用车),因此类型B在本研究定义为通勤私家车出行群体。
类型C各特征指标都处于中间水平的特点看,该类型是介于类型A和类型B之间的,因此类型C在本研究定义为其他私家车出行群体。
⑤ 群体识别结果
私家车出行群体识别性能函数见图 17,网络经过设定的296次训练达到设定的期望误差。私家车10 466组测试数据识别结果中准确识别出10 173组数据,将类型A识别为类型B的有7组、类型B识别为类型C的有89组数据,将类型A识别为类型C的有20组,类型C识别为类型A的有59组,将类型C识别为类型B的有113组数据,将类型B识别为类型A的有5组,因此测试集的识别准确率高达97.2%。
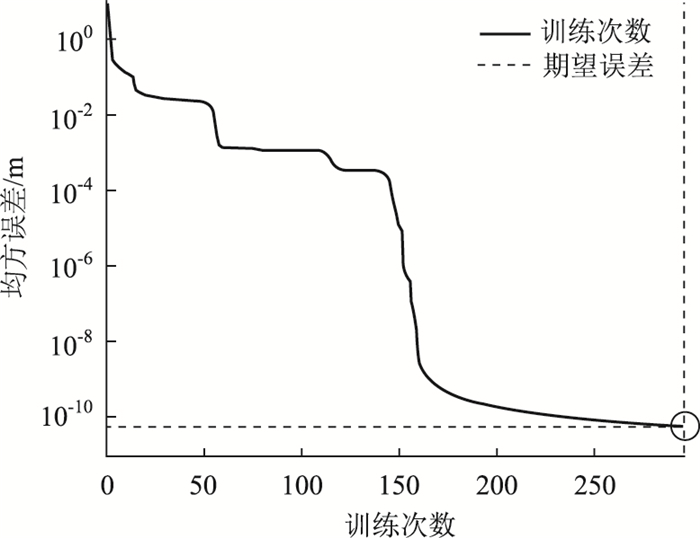
|
| 图 17 私家车出行群体识别性能函数 Fig. 17 Performance function for private car travel group recognition |
| |
4.3 出租车出行群体辨识
出租车群体的试验对象来源于重庆市主城区2017年10月17日至10月22日的RFID数据,经数据处理后,共获取14 866组完整有效处理后数据样本。根据前文对出行特征的差异分析,本研究最终选取轨迹重复率、在网时间、热点活动区域及干线影响区活动偏好4个指标构成模型的特征向量。
(1) 出租车群体划分
将出租车出行特征群体分类提取的4种特征指标(轨迹重复率、在网时间、热点活动区域及干线影响区活动偏好),进行聚类分析,得到结果如下:
① 聚类中心F:总包含元素5 562个,其中核心元素5 199,噪声元素有363。
② 聚类中心G:总包含元素9 304个,其中核心元素8 669,噪声元素有635。
由图 18可知聚类的两种群体具有部分噪声点,这可能由于部分出行车辆出行独特性造成,但是这种独特体较少,且可有不同,不能代表为一类群体,只能证明存在特殊情况。
|
| 图 18 出租车分类数据二维展示 Fig. 18 Two-dimensional display of taxi classification data |
| |
(2) 聚类结果分析及群体定义
① 在网时间
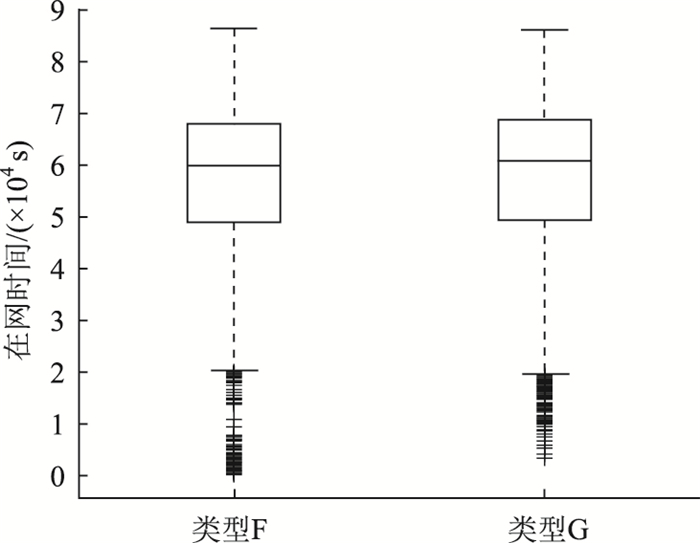
类型F:相比类型G,该分类有存在较多样本的在网时间较短,从箱图比较上看略微低于类型G,但总体分布相差并不大。
类型G:同理对比类型F,该分类总体上略微比类型F的在网时间长。
出租车的两种分类群体对于在网时间指标上,相差不大都集中位于[14,20]区间。这与前章分析也较为符合,由于出租车时商业运营车辆,基本全天都处于路网运营,极少由于特殊原因在网时间短的,见图 19。
|
| 图 19 出租车出行群体在网时间比较 Fig. 19 Comparison of online time of taxi travel groups |
| |
② 轨迹重复率
类型F:对比类型G,该类型的轨迹重复率略低,且部分重复率 < 0.05的样本比类型G多,分布集中在[0.203,0.278]区间,平均处于0.242左右,见图 20。

|
| 图 20 出租车出行群体轨迹重复率比较 Fig. 20 Comparison of trajectory repetition rates of taxi travel groups |
| |
类型G:对比类型F,该分类轨迹重复率略高,基本集中[0.238,0.308]区间,平均在0.272左右,整体分布略高于类型F。类型F相对比类型G在轨迹重复率的特征上较低,说明类型G更偏向于在固定区域活动,但总体都处于很低的状况,这是由于出租车的运营性质决定出租车轨迹的随机性以及广泛性,极少存在重复率很高或者重复率很低的情况,因此单独来看也不足以划分为一种常规群体。
③ 热点活动区域
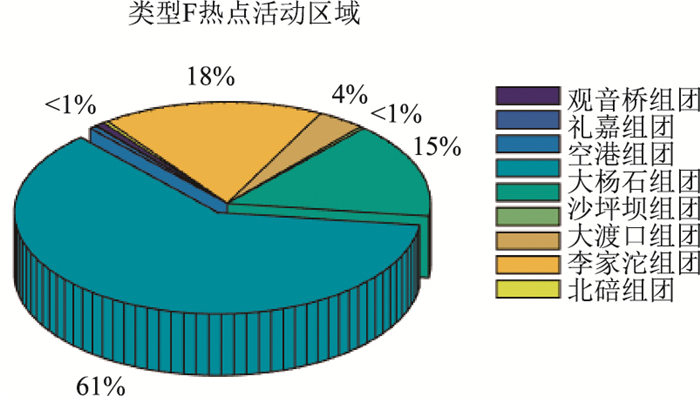
类型F:该类型出租车热点活动区域为大杨石组团、沙坪坝组团、李家沱组团、大渡口组团、空港组团、西永组团以及北碚组团。其中该群体出租车的热点活动区域集中分布在大杨石组团,占全部的61%,其次是李家沱组团,占据了18%的比例;以及沙坪坝组团,占比15%,见图 21。
|
| 图 21 类型F热点活动区域分布 Fig. 21 Distribution of hotspot activity area type F |
| |
类型G:该类型出租车热点活动区域为渝中组团、南坪组团、观音桥组团、人和组团、礼嘉组团以及空港组团。其中该群体出租车的热点活动区域集中分布在观音桥组团,占全部的68%;以及南坪组团,占据了21%的比例,见图 22。

|
| 图 22 类型G热点活动区域分布 Fig. 22 Distribution of hotspot activity area Type G |
| |
类型G与类型F两个分类在热点活动区域分布上有相交区域(观音桥组团、礼嘉组团),但是在大部分区域上不是相同的。类型F的热点活动区域集中在重庆城区中部和北面,类型G则是集中在西面。
④ 干线影响区选择偏好
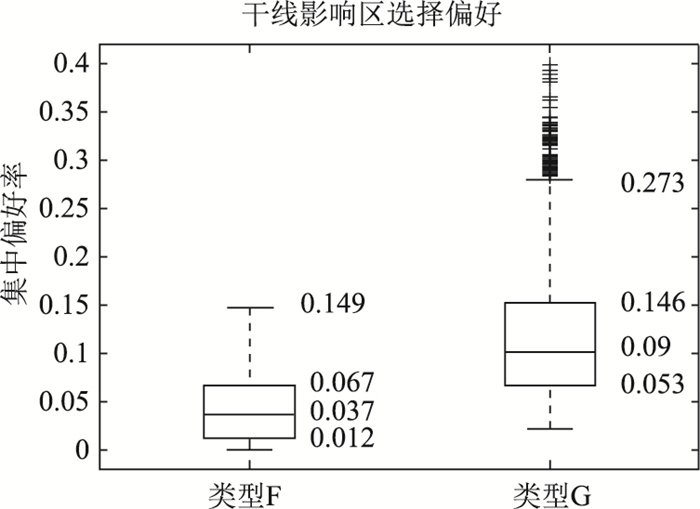
类型F:干线影响区偏好小于类型G, 其集中在[0.012, 0.067]之间,平均值为0.037,见图 23。
|
| 图 23 出租车出行群体干线影响区选择偏好比较 Fig. 23 Comparison of selection preferences of taxi travel groups affected by main line |
| |
类型G:该分类较多的经过干线影响区,偏好指标在[0.053, 0.146],分布高于类型F。
综上所述,类型F与类型G在干线影响区选择偏好特征上存在较大的差别,干线影响区选择偏好虽然也存在加大的随机性,与出租车的热点活动区域以及出租车驾驶员住址有着一定的关系。相临近的区域偏向选择干线影响区。
类型F出行区域集中在重庆中部以及南部,且干线影响区选择偏好较小的特点看,该类型出租车较少经过干线影响区,因此类型F在本研究定义为其他区域偏好出租车群体。
类型G出行区域集中在重庆西部,且干线影响区选择偏好较大的特点看,该类型干线影响区的影响想对较大,因此类型G在本研究定义为干线影响区偏好出租车群体。出租车的出行特征群体分类主要存在的差异性主要体现在运行活动区域上,由表 6分析可知出租车中类型G(干线影响区偏好群体)的活动热点区域集中在渝中组团、南坪组团、观音桥组团、人和组团以及空港组团。
| 类型 | 在网时间/h | 轨迹重复率 | 干线影响区偏好 | 热点活动区域 | 群体 |
| F | [14,20] | [0.2,0.28] | [0.012, 0.067] | 大杨石组团 | 其他区域偏好出租车群体 |
| G | [0.24,0.31] | [0.053, 0.146] | 观音桥组团 | 干线影响区偏好出租车群体 |
(三)群体识别结果
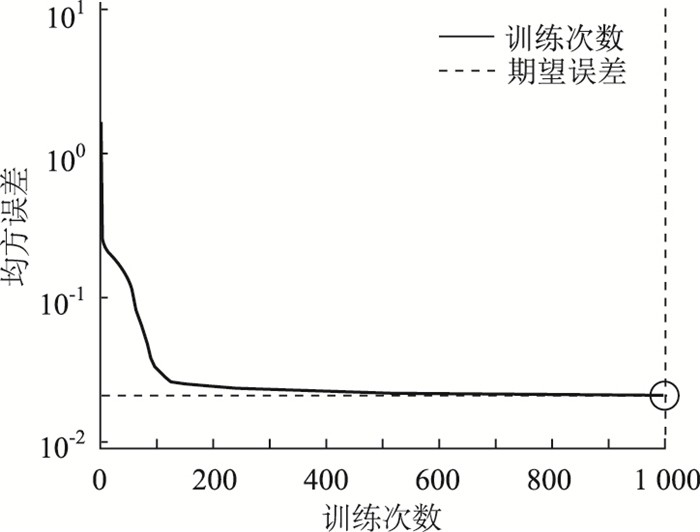
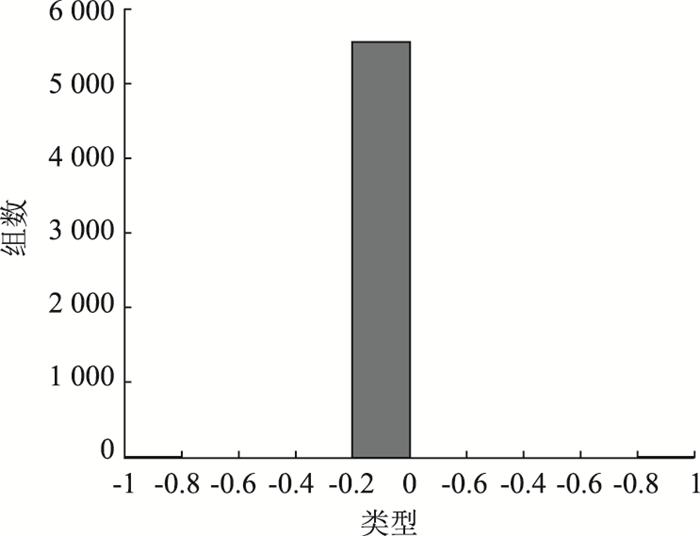
出租车特征群体得识的性能函数见图 24,从图中可以看出实际网络经1 000次可以较精准达到期望目标。出租车5 946组测试数据识别结果见图 25,其中准确识别出5 897组数据,将类型F识别为类型G的有32组数据,将类型G识别为类型F的有17组,因此测试集的识别准确率高达99.18%。
|
| 图 24 出租车出行群体识别性能函数 Fig. 24 Performance function for taxi travel group recognition |
| |
|
| 图 25 出租车特征群体识别结果 Fig. 25 Taxi characteristic group recognition result |
| |
5 结论
本研究主要开展轨迹数据驱动的出行特征指标分析以及出行特征群体辨识建模两大部分研究工作。通过RFID轨迹数据,基于数据统计分析研究了出行特征指标提取方法,由此建立车辆出行特征辨识指标体系。针对私家车、出租车的出行特点进行出行特征指标的定制提取,采用基于密度峰值的聚类算法(CFSFDP)以及BP组合模型,对特征指标进行聚类分析,再集合BP神经网络算法,建立出行特征群体识别模型。以重庆主城区内私家车、出租车为试验对象,基于RFID数据分别提取出行频次,轨迹重复率、首次出行时间、出行结束时间等指标进行聚类分析和识别建模,最终实现车辆的不同出行特征模式的辨识,具有较好的应用前景,具体体现在以下几个方面:
(1) 本研究对车辆出行特征进行了详细的研究及分类,能够有效辨识不同的车辆群体,为下一步预测不同群体的出行时长、路径选择,以及掌握车辆的OD出行等方面提供了数据支撑;
(2) 城市交通流的变化规律,其实质就是对城市居民出行特征的研究分析。不同的群体有着不同的出行特性,只有追踪车辆出行轨迹的溯源,才能从根本上对交通流进行管控,为解决干线拥堵问题奠定了重要基础;
(3) 探究车辆运动轨迹的溯源,挖掘车辆的出行特征,不仅是精准掌握车辆出行OD和进行合理的路网资源配置的前提,同时也能够更加紧密地结合城市道路交通管控,为城市道路交通个性化智能管控提供理论依据。
| [1] |
VISHNEVSKY V, KOZYREV D, RYKOV V. New Generation of Safety Systems for Automobile Traffic Control Using RFID Technology and Broadband Wireless Communication[C]//Communications in Computer and Information Science. Moscow: Springer International Publishing, 2014: 145-153.
|
| [2] |
LIU D L, ZHU X B, XU K L, et al. An Application of RFID Technology in Traffic Congestion Management[J]. Applied Mechanics and Materials, 2014, 2987(1030): 3954-3957. |
| [3] |
BYSHOV N, SIMDIANKIN A, USPENSKY I, et al. Method of Traffic Safety Enhancement with Use of RFID Technologies and Its Implementation[J]. Transportation Research Procedia, 2017, 20: 107-111. |
| [4] |
GUO S, LI X, CHING W K, et al. GPS Trajectory Data Segmentation Based on Probabilistic Logic[J]. International Journal of Approximate Reasoning, 2018, 103(12): 227-247. |
| [5] |
WANG Z, GOODCHILD A, MCCORMACK E. A Methodology for Forecasting Freeway Travel Time Reliability Using GPS Data[J]. Transportation Research Procedia, 2017, 25: 842-852. |
| [6] |
CSÁJI B C, BROWET A, TRAAG V A, et al. Exploring the Mobility of Mobile Phone Users[J]. Physica A: Statistical Mechanics and Its Applications, 2013, 392(6): 1459-1473. |
| [7] |
LV M, CHEN L, CHEN T, et al. Discovering Individual Movement Patterns from Cell-id Trajectory Data by Exploiting Handoff features[J]. Information Sciences, 2019, 474: 18-32. |
| [8] |
LADINO A, KIBANGOU A Y, WIT C, et al. A Real Time Forecasting Tool for Dynamic Travel Time from Clustered Time Series[J]. Transportation Research Part C: Emerging Technologies, 2017, 80(7): 216-238. |
| [9] |
VAN DIJK J. Identifying Activity-travel Points from GPS-data with Multiple Moving Windows[J]. Computers, Environment and Urban Systems, 2018, 70(7): 84-101. |
| [10] |
董宏辉, 孙晓亮, 贾利民, 等. 多模态的交通流量预测模型[J]. 吉林大学学报: 工学版, 2011, 41(3): 645-649. DONG Hong-hui, SUN Xiao-liang, JIA Li-min, et al. Multimode Traffic Volume Prediction Model[J]. Journal of Jilin University: Engineering and Technology Edition, 2011, 41(3): 645-649. |
| [11] |
丁玲. 公共交通优先策略下考虑交通状态的出行行为研究[D]. 南京: 东南大学, 2016. DING Ling. Research on Travel Behavior Considering Traffic State under Public Transportation Priority Strategy[D]. Nanjing: 2016. |
| [12] |
MENGISTU K T, HANNEMANN M, BAUM T, et al. Hierarchical HMM-based Semantic Concept Labeling Model[C]//Spoken Language Technology Workshop. Goa, India: IEEE, 2009.
|
| [13] |
YU D, DENG L. Deep Learning and Its Applications to Signal and Information Processing[J]. IEEE Signal Processing Magazine, 2011, 28(1): 145-154. |
| [14] |
SAMANTA O, BHATTACHARYA U, PARUI S K. Smoothing of HMM Parameters for Efficient Recognition of Online Handwriting[J]. Pattern Recognition, 2014, 47(11): 3614-3629. |
| [15] |
张文开. 基于密度的层次聚类算法研究[D]. 合肥: 中国科学技术大学, 2015. ZHANG Wen-kai. Research on Hierarchical Clustering Algorithm Based on Density[D]. Hefei: University of Science and Technology of China, 2015. |
| [16] |
RODRIGUEZ A, LAIO A. Clustering by Fast Search and Find of Density Peaks[J]. Science, 2014, 344(6191): 1492-1496. |
| [17] |
丛爽. 面向MATLAB工具箱的神经网络理论与应用[M]. 合肥: 中国科学技术大学出版社, 2009. CONG Shuang. Neural Network Theory and Application for MATLAB Toolbox[M]. Hefei: University of Science and Technology of China Press, 2009. |
| [18] |
张青贵. 人工神经网络导论[M]. 北京: 中国水利水电出版社, 2004. ZHANG Qing-gui. Introduction to Artificial Neural Network[M]. Beijing: China Water & Power Press, 2004. |
 2021, Vol. 38
2021, Vol. 38
