扩展功能
文章信息
- 任翔, 齐洋, 王璐, 黄平明, 宋飞
- REN Xiang, QI Yang, WANG Lu, HUANG Ping-ming, SONG Fei
- 截面几何参数对混凝土薄壁桥塔温度应力的影响
- Influence of Sectional Geometric Parameters on Thermal Stress in Concrete thin-walled Bridge Pylon
- 公路交通科技, 2021, 38(6): 78-87
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(6): 78-87
- 10.3969/j.issn.1002-0268.2021.06.011
-
文章历史
- 收稿日期: 2020-07-09
2. 长安大学 桥梁与隧道陕西省重点实验室, 陕西 西安 710064
2. Key Laboratory of Bridge and Tunnel of Shaanxi Province, Chang'an University, Xi'an Shaanxi 710064, China
进入21世纪后,大跨径桥梁得到迅速的发展,结构跨度不断增大,混凝土桥墩、桥塔高度逐渐增高,体积逐渐增大。多数桥梁建成运营后混凝土薄壁箱型桥墩、桥塔出现了竖向裂缝[1-4]。而开裂是大体积混凝土结构中一个影响结构安全性和耐久性的关键问题[5]。
相关研究发现桥塔结构内外表面日照温差荷载引起温度应力是导致桥塔开裂的重要因素[6-9],且裂缝宽度会随索塔内外表面温差的变化而变化,发生闭合和扩展现象[10-13]。表明塔壁内外表面的日照温差是产生温度应力的主要原因。因此,日照温差应力对于混凝土薄壁桥塔结构的影响不可忽视。截面几何参数对混凝土薄壁结构塔壁内外表面的温差应力有较大的影响,其相关研究较少。张运波等[14]分析了双肢矩形薄壁空心墩不同截面形状对其温度应力的影响,发现温度应力随着墩壁截面形状的变化而变化。傅理文,汪劲丰等[15]以某公路桥方形桥墩出现开裂为背景,通过对圆形、方形、矩形3种截面形状下的温度效应进行对比,发现圆形截面可降低温度开裂的风险。武利群[16]研究了箱梁截面几何参数对箱梁顶板日照温差应力的影响,发现顶板越厚、底板越薄、腹板越高,顶板受力越有利。
本研究利用ANSYS的热分析功能对某混凝土薄壁箱型桥塔温差应力进行研究,分析几何参数对混凝土薄壁桥塔温差应力的影响,找不同截面几何参数影响的敏感性,为该类结构设计提供一定的参考依据。
1 桥塔结构研究对象为某跨径为960 m钢箱梁悬索桥混凝土桥塔。该桥位于北纬30.57°,东经111.39°,结构方位角为82°。南北塔塔肢均为空心矩形箱结构,南塔承台以上高度为142.227 m,设3道横梁,北塔承台以上高度为112.415 m,设2道横梁,南北塔顶横桥方向5 m宽,从塔顶到塔底不变;顺桥向6 m宽,从塔顶按1∶100的坡度加宽至承台,塔顶横桥向等宽为5 m。南、北塔顶部壁厚均为0.7 m,南塔底部宽度为1.0 m,北塔底部壁厚度0.8 m。本研究选取研究截面布置及尺寸如图 1所示。其中图 1(c)中L为顺桥走向外侧塔壁长度,6~8.84 m;B为横桥走向外侧塔壁宽度,等宽5 m;t为塔壁厚度,等厚0.8 m。

|
| 图 1 矩形空心桥塔典型截面(单位:cm) Fig. 1 Typical section of rectangular hollow pylon (unit: cm) |
| |
2 分析方法 2.1 温度应力计算方法
结构热力耦合分析方法有直接法和间接法。直接法考虑了温度、结构位移自由度,并引入温度场和应力场的边界条件,进行一次性的耦合分析。由于高度非线性的桥塔温度场以及其箱形结构面-面辐射热分析的复杂性,增加计算难度,且由于力学边界的不准确性会使结果有一定的误差。而间接法是根据热传导方程得到节点热流率向量,再将其作为荷载引入应力场求解方程,最后通过求解方程计算应力场[17],如下:
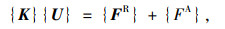
|
(1) |
式中,{K}为总刚矩阵;{U}是节点位移矩阵;{FR}为反力矢量;{FA}={Fnd}+{Fac}+ 
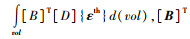
模型初始条件采用桥塔内部温度及环境温度的实测值,塔壁厚度温差采用一天内正温差和负温差最大的时刻作为分析荷载。实测温差在不同厚度的塔壁处应是不同的,大量学者基于实测数据发现,温度在桥塔、桥墩等柱状结构壁厚方向的分布模型一般有直线型、双折线和指数分布,其中与指数分布最为接近[16, 18-23],当壁厚达到一定数值时,温度随厚度变化不大[21-23]。我国铁路规范[24]也有类似的规定,当顶板和腹板厚度≥26 cm时,温度曲线就趋于稳定。本研究通过现场实测数据发现当桥塔壁厚大于0.24 m时温差变化不大,而文中分析的桥塔壁厚在0.2~1.6 m之间,为了简化计算,本研究在模拟时只考虑了不同方位上的温差,对不同壁厚时的温差进行了简化处理,方便计算。
2.2.2 边界条件有限元模型温度边界条件采用第二类边界条件。第二类边界条件是已知物体边界上的热流密度[25-26],即

|
(1) |
式中,q(t)为Γ边界上总的热流密度,由太阳辐射、对流换热和长波辐射3部分组成,以热量流入为正,流出为负;Kn为边界平面外法线方向的热传导系数;T为温度。
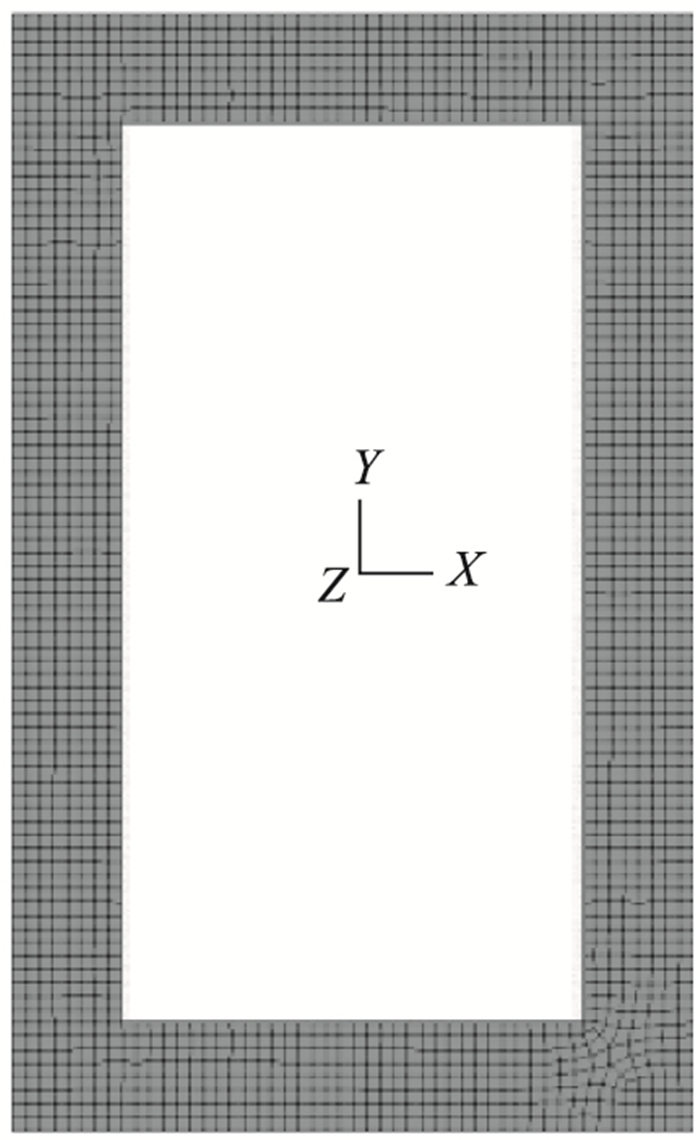
2.3 桥塔材料参数及模型桥塔采用C50混凝土,采用砂岩做骨料,查询规范[27]可得,导热系数取值为10.6 kJ/(m·h·℃),比热容取值为0.96 kJ/(kg·℃),线膨胀系数为10-5。有限元模型及结构离散见图 2。混凝土桥塔采用平面有限元模型,单元选择PLANE42四节点四边形单元,网格采用自由划分,单元长度为0.1 m。
|
| 图 2 桥塔塔壁截面网格划分 Fig. 2 Meshing of pylon wall section |
| |
2015年1月29日至2月4日对某悬索桥混凝土桥塔南塔肢进行了为期一周的温度场测试,选取了2015年1月30日上午10时和1月31日凌晨2时的正温差和负温差作为外荷载,分析不同截面几何参数对南侧塔壁内外表面温度应力的影响,如表 1所示。
| 时间 | 温差/℃ | |||
| 东侧塔壁 | 南侧塔壁 | 西侧塔壁 | 北侧塔壁 | |
| 10:00 am | 1.8 | 7.7 | 7.4 | 2.0 |
| 2:00 am | -8.1 | -6.5 | -5.5 | -6.4 |
温度荷载以约束的形式施加在桥塔塔壁内外表面,按二维温度场计算,先求解桥塔截面温度分布,然后转化成结构单元求解温度应力。
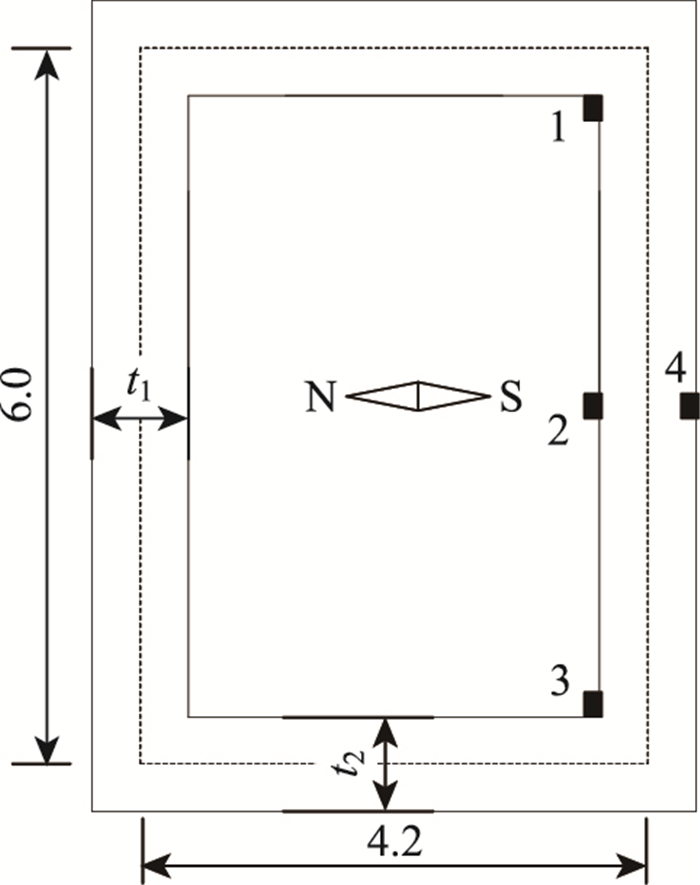
3 温度应力分析 3.1 塔壁厚度对温度应力的影响南、北塔壁厚度为t1,东、西塔壁厚度为t2,如图 3所示。通过改变塔壁厚度分析塔壁厚度方向温差对塔壁内外表面温度应力的影响。塔壁厚度选择两种工况:工况1,4个塔壁厚度均相等;工况2,2个对边塔壁厚度相等,相邻2个塔壁厚度不相等。
|
| 图 3 桥塔温度应力分析截面及测点(单位:m) Fig. 3 Analysis section and measuring points of thermal stress of bridge pylon (unit: m) |
| |
3.1.1 等厚度变化
图 3所示,塔壁温度应力分析截面中线的长度为6.0 m,宽度为4.2 m,且保持不变。t1=t2且从0.2~1.2 m每0.1 m一个等级变化。将塔壁厚度0.80 m的截面作为基准截面,用于与其他不同截面厚度下的温度应力进行比较分析。塔壁内表面在中线、两个角隅处及外表面中线处设置了温度应力观察点。
(1) 塔壁正温差
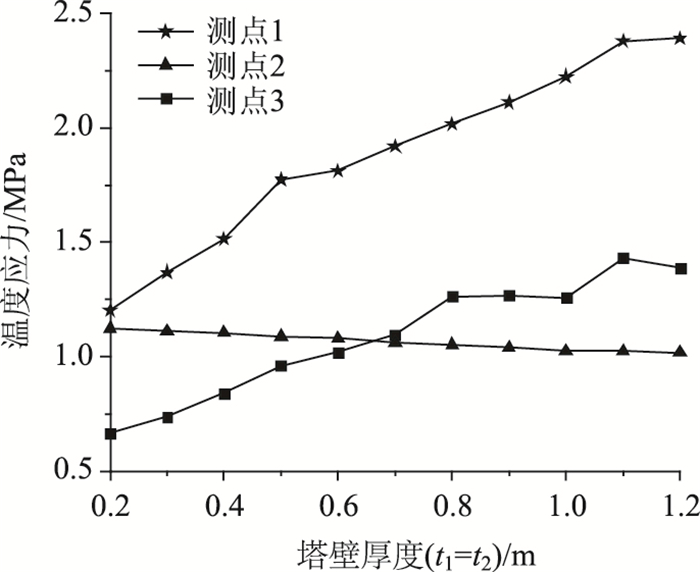
图 4给出了正温差作用下南侧塔壁不同厚度的塔壁内侧表面温度应力分布。
|
| 图 4 南侧塔壁在不同厚度下内表面应力分布 Fig. 4 Stress distribution on the inner surface of the south pylon wall under different thickness |
| |
图 4可以看出,塔壁正温差荷载作用下,南侧塔壁内表面的最大温度应力出现在位置1处,且位置1,3处的温度应力均大于其他位置。
随着塔壁厚度的增大,南侧塔壁位置1,3处的温度应力逐渐增大。当塔壁厚度为0.8 m(基准截面)时,位置1,3处的温度应力分别为2.03 MPa和1.26 MPa;当塔壁厚度为0.2 m时,位置1,3处的温度应力分别为1.19 MPa和0.66 MPa,相比于基准截面减小约41%和48%;而塔壁厚度为1.2 m时,温度应力分别为2.39 MPa和1.38 MPa,相比基准截面增大约15%和9.5%。位置2处的温度应力随着壁厚的增大而逐渐减小,且变化较为缓慢。综上可知,塔壁等厚度变化对南侧塔壁内表面角隅处的温度应力的影响较大。
(2) 塔壁负温差
图 5给出了负温差下南侧塔壁不同厚度的塔壁外侧表面温度应力分布。

|
| 图 5 南侧塔壁不同厚度下外表面温度应力 Fig. 5 Thermal stresses on outer surface of south pylon wall with different thicknesses |
| |
由图 5看出,在负温差作用下,4个塔壁等厚度变化对南侧塔壁外表面位置4的温度应力影响很小。
3.1.2 不等厚度变化桥塔温度应力分析截面及测点仍采用图 3所示截面,基准截面塔壁厚度t1=t2,其对比截面塔壁厚度t1≠t2。t2保持不变取值为0.8m,t1变化,塔壁厚度比t1/t2分别取0.5,0.6,0.8,1.2,1.5,1.8和2.0变化。
(1) 塔壁正温差
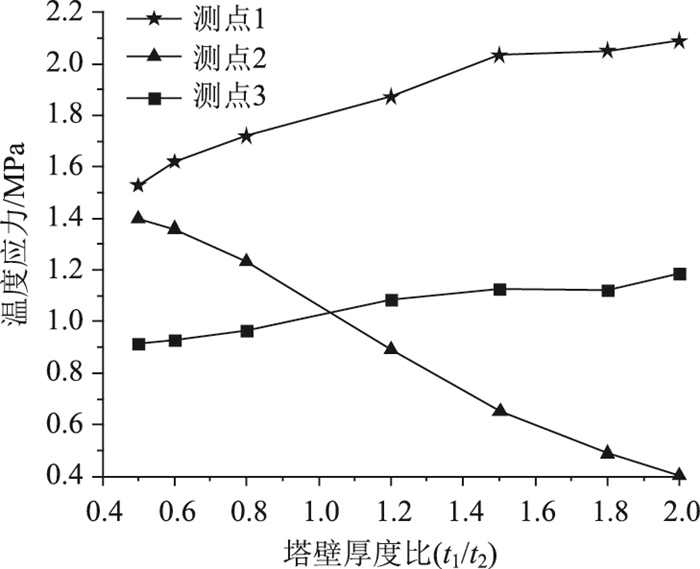
图 6给出了相邻塔壁不同厚度比对南侧塔壁内侧表面上温度应力的影响。
|
| 图 6 不同厚度比下南塔壁内表面的温度应力 Fig. 6 Thermal stresses on inner surface of south pylon wall with different thickness ratios |
| |
由图 6可以看出,相邻塔壁不同厚度比下,塔壁正温差荷载引起的最大温度应力仍出现在南侧塔壁内表面测点1处,同时内表面测点1,3处的温度应力均比其他位置处的温度应力大。
随着塔壁厚度比的逐渐增大,南侧塔壁内表面测点1,3处的温度应力也随之增大,而内表面测点2处及其他位置处的温度应力随塔壁厚度的增大而逐渐减小。
与基准截面(t1/t2=1),当塔壁厚度比为0.6时,南侧塔壁1,3处的温度应力分别降低了约16%和14%,位置2处的温度应力增大约为22%;当塔壁厚度比为2.0时,南侧塔壁1,3处的温度应力分别增大了约7%和8.5%,位置2处的温度应力减小约63%。
塔壁内表面测点1,3处的温度应力的变化幅度比塔壁内表面中心处的温度应力的变化幅度要小。增大塔壁厚度比可以大幅度地减小南侧塔壁内表面中心位置处的温度应力,但同时增大了角隅处的温度应力。因此,在选择塔壁厚度比时,不宜太大。
(2) 塔壁负温差
图 7给出了相邻塔壁不同厚度比对南侧塔壁外侧表面上温度应力的影响。

|
| 图 7 不同厚度比下南侧塔壁外表面温度应力 Fig. 7 Thermal stresses on outer surface of south pylon wall with different thickness ratios |
| |
图 7可以看出,南侧塔壁外表面位置2的温度应力随厚度比t1/t2的增大而逐渐减小,变化幅度较大。在正温差下位置4处的温度应力与图 6中位置2处的温度应力结果相似。
3.2 塔壁长宽比对温度应力的影响图 1所示,桥塔温度应力分析截面的4个塔壁厚度均为0.8 m,且保持不变。东侧和西侧塔壁截面中线长度为B,保持B=4.2 m不变,南侧和北侧塔壁截面中线长度为L,L变化。
基准截面尺寸为L=4.2 m,B=4.2 m,其余对比截面塔壁截面中线处的长宽比L/B分别取1,1.2,1.5,1.8,2.0,2.2和2.5,分别计算相应的温度应力,并与基准截面下的温度应力进行对比分析。塔壁温度应力观察点仍参照图 3。
(1) 塔壁正温差
图 8给出了塔壁不同长宽比下正温差荷载对南侧塔壁内侧表面上温度应力的影响。

|
| 图 8 南侧塔壁内表面温度应力 Fig. 8 Thermal stress on inner wall surface of south pylon wall |
| |
图 8可以看出,改变塔壁截面长宽比对改善塔壁截面温度应力的效果不明显。
(2) 塔壁负温差
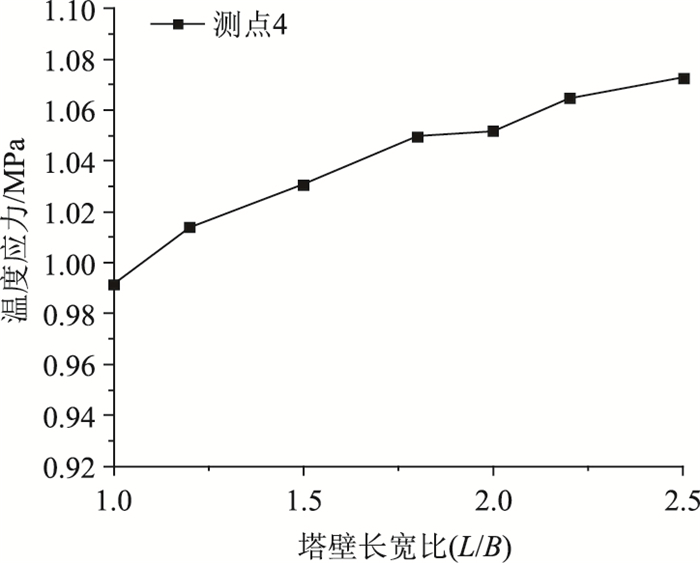
图 9给出了塔壁不同长宽比下负温差荷载对南侧塔壁外侧表面的温度应力的影响。
|
| 图 9 南侧塔壁外表面温度应力 Fig. 9 Thermal stress at outer wall surface of south pylon wall |
| |
图 9可以看出,负温差作用下,塔壁长宽比对塔壁外表面的最大温度应力的影响非常小,这与正温差作用下的结果是一致的。
3.3 塔壁截面不同倒角对温度应力的影响从前面分析可以看出,在塔壁内侧表面角隅处存在温度应力集中现象,为了减小结构在截面角隅处产生的应力集中现象,采用角隅处倒角的方式来降低应力集中。
塔壁截面倒角拟选择两种工况:工况1,只对内侧截面角隅处倒角;工况2,对内侧、外侧截面角隅处同时倒角。
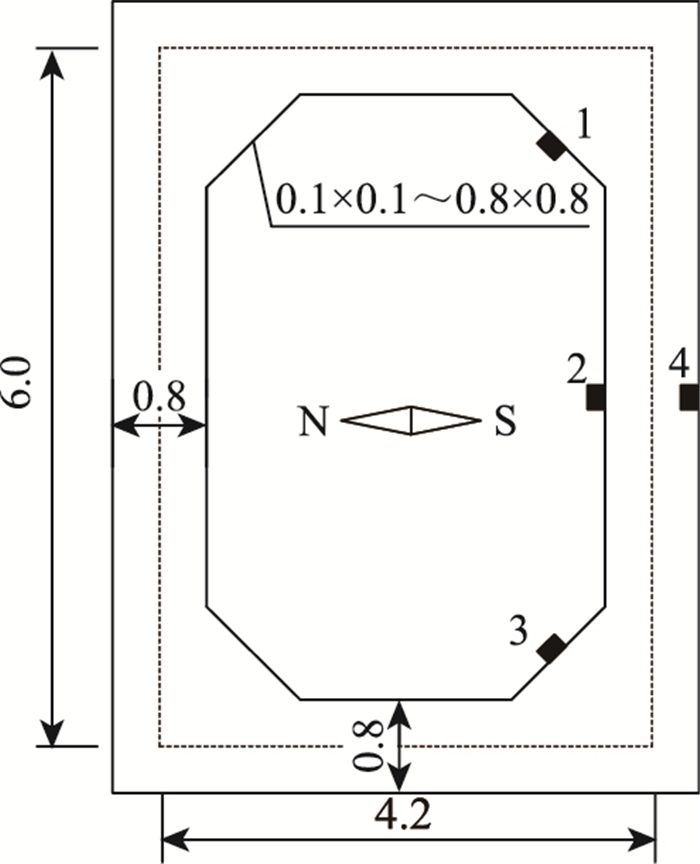
3.3.1 内侧截面角隅处倒角如图 10所示,桥塔塔壁中线长度为6.0 m,宽度为4.2 m,4个塔壁厚度为0.8 m,且保持不变。基准截面为内表面未倒角,对比截面为内表面4个倒角相同,且倒角尺寸从0.1 m×0.1 m到0.8×0.8 m每0.1 m一个等级变化。
|
| 图 10 内表面角隅处倒角及温度应力观察点(单位:m) Fig. 10 Chamfering at corners of inner surface and observation points of thermal stress (unit: m) |
| |
(1) 塔壁正温差
图 11给出了正温差荷载作用下内表面角隅处不同倒角的南侧塔壁内侧表面上温度应力分布。
|
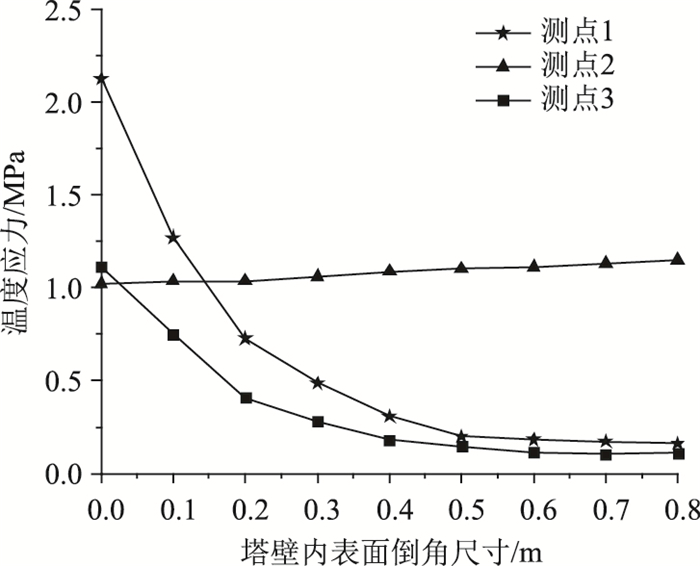
| 图 11 不同截面倒角下南侧塔壁内表面温度应力分布 Fig. 11 Distribution of thermal stresses at inner surface of south pylon wall under different sectional chamfers |
| |
图 11可以看出,塔壁内侧表面角隅处倒角后,南侧塔壁内侧表面1,3处的温度应力均比基准截面的温度应力大幅度减小。
当倒角尺寸为0.1 m×0.1 m~0.3 m×0.3 m范围变化时,角隅处的温度应力下降较大,当倒角尺寸为0.3 m×0.3 m时,相对于基准截面,测点1的温度应力2.14 MPa降低到0.74 MPa,减小约65%;测点3的温度应力从1.13 MPa降低到0.42 MPa,减小约63%。
当倒角尺寸超过0.5 m×0.5 m时,角隅处的温度应力变化不明显。除角隅处,其他部位的温度应力随着倒角尺寸的增大而增大,但增大幅度较小。表明在塔壁内侧表面角隅处倒角能有效地降低角隅处的应力集中,但较大的倒角尺寸增大截面厚度且增加了混凝土用量,造价提高。
(2) 塔壁负温差
图 12给出了负温差荷载作用下外表面角隅处不同倒角的南侧塔壁内侧表面上温度应力分布。
|
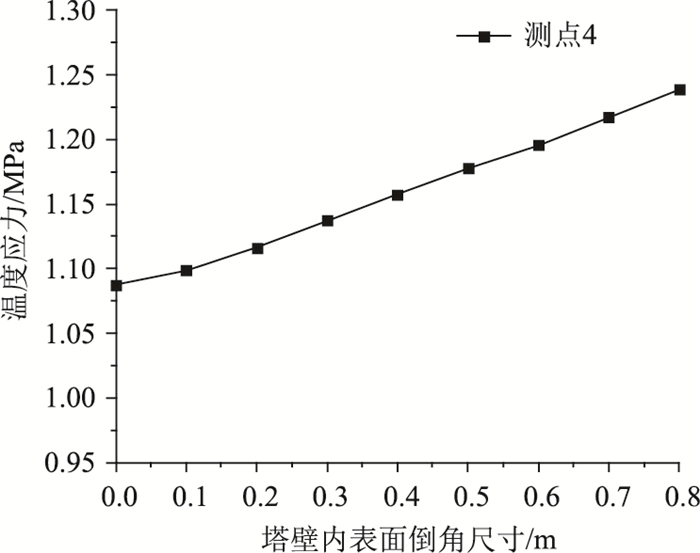
| 图 12 不同截面倒角下南侧塔壁外表面温度应力 Fig. 12 Distribution of thermal stresses at outer surface of south pylon wall under different sectional chamfers |
| |
图 12可以看出,随着塔壁内侧表面倒角尺寸的逐渐增大,南侧塔壁外侧表面温度应力也随之增大。与基准截面计算结果相比,当倒角尺寸为0.8 m×0.8 m时,其塔壁外表面位置4处的温度应力从1.09 MPa增大到1.24 MPa,增大约12%。由此表明,负温差状况下在塔壁内侧表面4个角隅处倒角会增大表面温度应力,但是增大幅度不大。
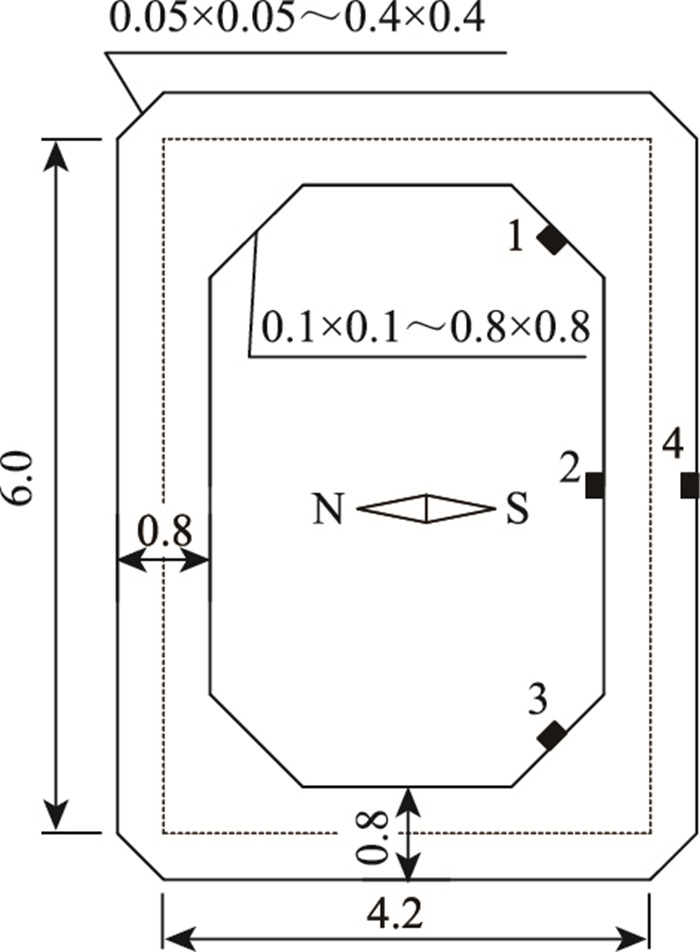
3.3.2 内、外两侧截面角隅处倒角在图 10的基础上增加了外表面角隅处的倒角,倒角尺寸从0.05 m×0.05 m到0.4 m×0.4 m,每0.05 m一个等级变化,与外侧倒角从0.1~0.8 m变化相对应,共8个工况,初始工况为内外侧均未倒角。如图 13所示。
|
| 图 13 内外两侧截面角隅处倒角(单位:m) Fig. 13 Chamfers at inner and outer corners in cross-section (unit: m) |
| |
(1) 塔壁正温差
图 14给出了内、外表面倒角在正温差下南侧塔壁内侧表面上的温度应力分布。
|
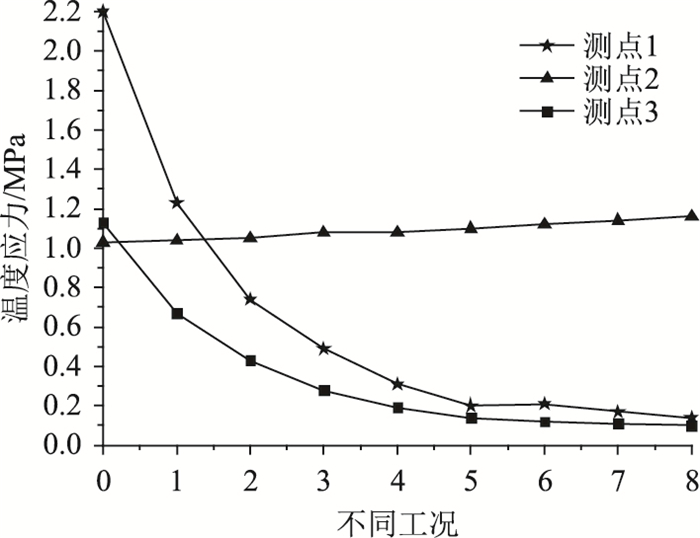
| 图 14 南侧塔壁内表面温度应力 Fig. 14 Thermal stress on inner surface of south pylon wall |
| |
图 14可以看出,塔壁内、外表面角隅处倒角对南侧塔壁内表面的温度应力的影响与内侧表面角隅处倒角的分析结果几乎一致。
(2) 塔壁负温差
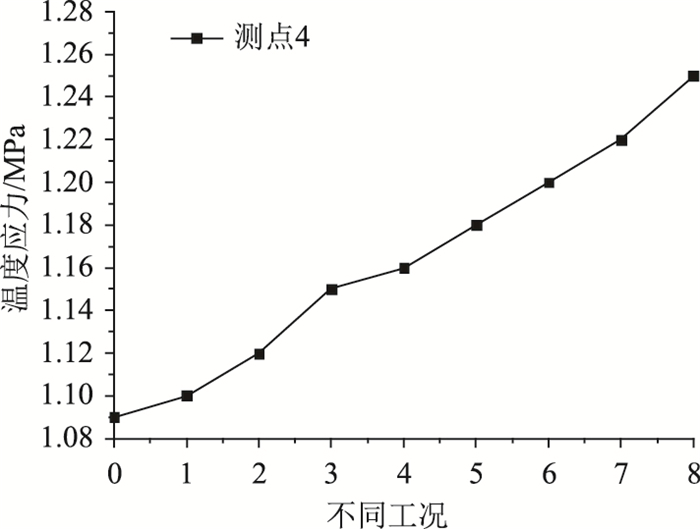
图 15给出了内、外表面倒角在负温差下南侧塔壁内侧表面上的温度应力分布。
|
| 图 15 南侧塔壁外表面温度应力 Fig. 15 Thermal stress on outer surface of south pylon wall |
| |
图 15可以看出,在负温差作用下,塔壁内外两侧表面角隅处倒角尺寸对南侧塔壁外表面位置4处的温度应力的影响与内侧表面角隅处倒角的分析结果一致。
4 结果分析前述研究发现,塔壁厚度比t1/t2以及倒角的大小是影响桥塔截面温度应力的重要因素。但截面参数的变化会改变混凝土的体积和抗压刚度发生变化。因此,设计桥塔截面时需要综合考虑降低温度应力和增加桥塔造价两个因素。
4.1 塔壁厚度3.1.2节分析表明,在正负温差下,塔壁厚度比t1/t2已经成为影响塔壁表面温度应力的重要因素。因此,在不同塔壁厚度比t1/t2情况下,对混凝土体积和南侧桥塔的抗压刚度(EA)进行分析。
在表 2中,混凝土体积和桥塔抗压刚度随着塔壁厚度比的增长而快速增长。对比参考截面(塔壁厚度比为1),当塔壁厚度比为2时,2位置处(仅列出正温差下的结果)的温度应力减小了大约63%,同时混凝土体积和桥塔抗压刚度分别增长了59.7%和64.6%。然而,当塔壁厚度比为0.5时,温度应力增加约27.1%,而混凝土体积和桥塔抗压刚度分别下降了约29.8%和32%。结果表明,较大的塔壁厚度比可以降低桥塔中心处温度应力,但同时会导致角隅处温度应力集中,混凝土体积增加,塔壁长宽比变小,从而导致桥塔的抗压刚度降低。
| t1/t2 | 混凝土体积/m3 | 温度应力/MPa | EA/(×107 kN) |
| 0.5 | 1 982.1 | 1.4 | 22.1 |
| 0.6 | 2 150.9 | 1.4 | 24.2 |
| 0.8 | 2 488.6 | 1.2 | 28.4 |
| 1.0 | 2 826.3 | 1.1 | 32.5 |
| 1.2 | 3 164.0 | 0.9 | 36.7 |
| 1.5 | 3 670.6 | 0.7 | 43.1 |
| 1.8 | 4 177.2 | 0.5 | 49.3 |
| 2.0 | 4 514.9 | 0.4 | 53.5 |
4.2 内侧截面角隅处倒角
第3.3节分析表明,倒角可以大大减少南塔壁内表面角隅的温度应力。表 3显示了不同倒角尺寸下,桥塔的混凝土体积、温度应力和抗压刚度。
| 倒角尺寸/m | 混凝土体积/m3 | 温度应力/MPa | EA/ (×107 kN) |
|
| 位置1 | 位置3 | |||
| 0×0 | 2 686.2 | 2.1 | 1.1 | 32.4 |
| 0.1×0.1 | 2 689.0 | 1.3 | 0.8 | 32.5 |
| 0.2×0.2 | 2 697.6 | 0.7 | 0.4 | 32.7 |
| 0.3×0.3 | 2 711.8 | 0.5 | 0.3 | 33.1 |
| 0.4×0.4 | 2 731.7 | 0.3 | 0.2 | 33.5 |
| 0.5×0.5 | 2 757.3 | 0.2 | 0.1 | 34.2 |
| 0.6×0.6 | 2 788.6 | 0.2 | 0.1 | 34.9 |
| 0.7×0.7 | 2 825.6 | 0.2 | 0.1 | 35.8 |
| 0.8×0.8 | 2 868.3 | 0.2 | 0.1 | 36.8 |
与参考截面(无倒角)相比,当倒角大小从0.1 m×0.1 m变化到0.3 m×0.3 m(如表 3所示),位置1和3处的温度应力会迅速减小。当倒角尺寸大于0.3 m×0.3 m时,桥塔的混凝土体积增加约1%。当倒角大小变为0.5 m×0.5 m时,位置1和3处的温度应力基本保持不变,但混凝土体积仍随着倒角变大而继续逐渐增大;当倒角在0.3 m×0.3 m~0.5 m×0.5 m之间时,改变倒角尺寸对于温差应力及混凝土体积的影响均较小,因此建议在此区间内选取倒角尺寸。
5 结论为了降低混凝土桥塔内外表面温度应力,本研究介绍了桥塔截面几何参数,如塔壁厚度、塔壁长宽比和倒角大小,对混凝土桥塔的温度应力的影响。结果如下:
(1) 塔壁厚度比t1/t2是重要设计参数,其取值不宜太大;
(2) 改变塔壁截面长宽比对改善塔壁截面温度应力的效果不明显;
(3) 倒角应设计在内侧截面角隅处,其尺寸建议在0.3 m×0.3 m~0.5 m×0.5 m之间进行取值。
| [1] |
马春生, 王萍. 某大桥桥塔裂缝成因分析[J]. 公路, 2002(8): 44-47. MA Chun-sheng, WANG Ping. Analysis of Crack Causes of Certain Bridge Tower[J]. Highway, 2002(8): 44-47. |
| [2] |
甘应朋. 夷陵大桥斜拉桥主塔下塔柱裂缝分析与处理[J]. 交通科技, 2004(3): 51-53. GAN Ying-peng. Analysis and Treatment of Cracks in Lower Column of Main Pylon of Yiling Bridge Cable-stayed Bridge[J]. Transportation Science and Technology, 2004(3): 51-53. |
| [3] |
梁合兴, 何庭蕙, 劳晓春, 等. 连续刚构梁桥薄壁柔性墩身裂缝产生原因[J]. 暨南大学学报: 自然科学与医学版, 2005, 26(1): 110-113. LIANG He-xing, HE Ting-hui, LAO Xiao-chun, et al. Preliminary Research on the Cause of the Cracks in Thin-walled Flexible Piers of Continuous Rigid Frame Bridges[J]. Journal of Jinan University: Natural Science & Medicine Edition, 2005, 26(1): 110-113. |
| [4] |
郭升烈. 湘江大桥薄壁空心墩墩身裂缝成因与预防控制[J]. 城市道桥与防洪, 2008(3): 58-59. GUO Sheng-lie. Forming Cause of Crack on Thin-wall Hollow Pier Body of Main Span for Xiangjiang River Bridge and Its Preventive Control Measures[J]. Urban Roads Bridges and Flood Control, 2008(3): 58-59. |
| [5] |
DO T A. Influence of Footing Dimensions on Early-Age Temperature Development and Cracking in Concrete Footings[J]. Journal of Bridge Engineering, 2015, 20(3): 06014007. |
| [6] |
任翔, 黄平明, 韩万水. 混凝土薄壁箱形结构横向温度应力解析计算方法[J]. 中国公路学报, 2012, 25(1): 76-82. REN Xiang, HUANG Ping-ming, HAN Wan-shui. Transverse Temperature Stress Computation Method of Concrete Thin-wall Box-shape Structure[J]. China Journal of Highway and Transport, 2012, 25(1): 76-82. |
| [7] |
任翔, 何青, 佟阳, 等. 混凝土桥塔温度场和空间应力场分析[J]. 郑州大学学报: 工学版, 2011, 32(2): 62-65. REN Xiang, HE Qing, TONG Yang, et al. Temperature and Stress Fields Analysis of Concrete Bridge Tower[J]. Journal of Zhengzhou University: Engineering Science Edition, 2011, 32(2): 62-65. |
| [8] |
任翔, 黄平明. 温度场作用下混凝土桥塔Ⅰ型裂纹开裂面应力场分析[J]. 世界桥梁, 2011(6): 50-53. REN Xiang, HUANG Ping-ming. Analysis of Cracking Surface Stress Field of Type I Crack of Concrete Bridge Tower Under Action of Temperature Field[J]. World Bridges, 2011(6): 50-53. |
| [9] |
任翔, 佟阳, 何青, 等. 薄壁箱形混凝土桥塔温度应力场分析[J]. 广西大学学报: 自然科学版, 2011, 36(1): 121-127. REN Xiang, TONG Yang, HE Qing, et al. Thermal Stress Fields of Thin-walled Box Girder Concrete Bridge Tower[J]. Journal of Guangxi University: Natural Science Edition, 2011, 36(1): 121-127. |
| [10] |
靳敏超, 冯仲仁, 刘吉波, 等. 斜拉桥索塔裂缝的温变特性研究[J]. 公路, 2010(1): 39-42. JIN Min-chao, FENG Zhong-ren, LIU Ji-bo, et al. A Study on Temperature Variation Characteristics of Tower Cracks of Cable-Stayed Bridge[J]. Highway, 2010(1): 39-42. |
| [11] |
谢尚英. 广州猎德大桥索塔日照温度效应分析[J]. 桥梁建设, 2007(2): 72-75. XIE Shang-ying. Analysis of Sunshine Temperature Effect on Tower of Liede Bridge in Guangzhou[J]. Bridge Construction, 2007(2): 72-75. |
| [12] |
代璞, 钱永久. 斜拉桥H形截面混凝土桥塔短期温度特性[J]. 西南交通大学学报, 2014, 49(1): 59-65. DAI Pu, QIAN Yong-jiu. Short-Term Temperature Characteristics of H-Shaped Section Concrete Pylon of Cable-stayed Bridge[J]. Journal of Southwest Jiaotong University, 2014, 49(1): 59-65. |
| [13] |
BRANCO F A, MENDES P A. Thermal Actions for Concrete Bridge Design[J]. Journal of Structural Engineering, 1993, 119(8): 2313-2331. |
| [14] |
张运波, 蔡亭亭, 刘洋. 截面形状对双肢薄壁墩温度场的影响分析[J]. 铁道工程学报, 2015, 32(3): 41-45. ZHANG Yun-bo, CAI Ting-ting, LIU Yang. Effects Analysis of the Cross-sectional Shape on Double-limb Thin-walled Piers' Temperature Field[J]. Journal of Railway Engineering Society, 2015, 32(3): 41-45. |
| [15] |
傅理文, 汪劲丰, 程伟平, 等. 方形混凝土桥墩裂缝成因分析及对策[J]. 浙江大学学报: 工学版, 2010, 44(9): 1738-1745. FU Li-wen, WANG Jin-feng, CHENG Wei-ping, et al. Causes and Treatments of Quadrate Concrete Pier's Crack[J]. Journal of Zhejiang University: Engineering Science Edition, 2010, 44(9): 1738-1745. |
| [16] |
武立群. 混凝土箱梁和空心高墩温度场及温度效应研究[D]. 重庆: 重庆大学, 2012. WU Li-qun. Analysis of Temperature Field and Temperature Effect for Concrete Box Girder and Hollow High Pier[D]. Chongqing: Chongqing University, 2012. |
| [17] |
樊启武, 钱永久. 采用间接耦合法分析斜拉桥索塔瞬态温度应力场[J]. 石家庄铁道大学学报: 自然科学版, 2008, 21(1): 18-22. FAN Qi-wu, QIAN Yong-jiu. Analysis of Transient Temperature Gradient and Thermal Stress Field of Cable-stayed Bridge Tower by means of Indirect Coupling[J]. Journal of Shijiazhuang Railway Institute: Natural Science Edition, 2008, 21(1): 18-22. |
| [18] |
顾斌, 谢甫哲, 钱海, 等. 长江下游地区倒Y形混凝土桥塔的三维日照温场及其效应[J]. 中南大学学报: 自然科学版, 2020, 51(1): 248-260. GU Bin, XIE Fu-zhe, QIAN Hai, et al. 3D-temperature Field and Its Effect of Inverted Y-shaped Concrete Pylon in Lower Yangtze Region[J]. Journal of Central South University: Science and Technology Edition, 2020, 51(1): 248-260. |
| [19] |
张宁, 刘永健, 刘江, 等. 高原高寒地区H形混凝土桥塔日照温度效应[J]. 交通运输工程学报, 2017, 17(4): 66-77. ZHANG Ning, LIU Yong-jian, LIU Jiang, et al. Temperature Effects of H-shaped Concrete Pylon in Arctic-alpine Plateau Region[J]. Journal of Traffic and Transportation Engineering, 2017, 17(4): 66-77. |
| [20] |
雷素敏, 吕贤良, 章开东. 空心薄壁墩温度效应有限元分析[J]. 铁道建筑, 2019, 59(5): 47-50. LEI Su-min, LÜ Xian-liang, ZHANG Kai-dong. Finite Element Analysis of Temperature Effect of Hollow Thin-walled Pier[J]. Railway Engineering, 2019, 59(5): 47-50. |
| [21] |
戴公连, 唐宇, 刘勇, 等. 高墩三维日照温度场数值模拟及试验研究[J]. 铁道工程学报, 2016, 33(11): 57-62. DAI Gong-lian, TANG Yu, LIU Yong, et al. Numerical Simulation and Test Analysis of Three-dimensional Solar Temperature Field of Hollow Tall-piers with Rounded Rectangular Cross Section[J]. Journal of Railway Engineering Society, 2016, 33(11): 57-62. |
| [22] |
戴公连, 唐宇, 刘勇, 等. 高铁圆端形空心高墩日照温度场数值分析[J]. 桥梁建设, 2016, 46(6): 67-72. DAI Gong-lian, TANG Yu, LIU Yong, et al. Numerical Analysis of Solar Radiation Temperature Fields of Round End Hollow Tall Pier for High-Speed Railway Bridge[J]. Bridge Construction, 2016, 46(6): 67-72. |
| [23] |
杨美良, 吕寻博, 段志岳. 山区空心薄壁高墩日照温度效应[J]. 长沙理工大学学报: 自然科学版, 2015, 12(2): 29-36. YANG Mei-liang, LÜ Xun-bo, DUAN Zhi-yue. Sunshine Temperature Field of Mountain Hollow Thin-walled High Piers[J]. Journal of Changsha University of Science and Technology: Natural Science Edition, 2015, 12(2): 29-36. |
| [24] |
TB 10002.3-2005, 铁路桥涵钢筋混凝土和预应力混凝土结构设计规范[S]. TB 10002.3-2005, Code for Design on Reinforced and Prestressed Concrete Structure of Railway Bridge and Culvert[S]. |
| [25] |
张元海, 李乔. 桥梁结构日照温差二次力及温度应力计算方法研究[J]. 中国公路学报, 2004, 17(1): 49-52. ZHANG Yuan-hai, LI Qiao. Study of the Method for Calculation of the Thermal Stress and Secondary Force of Bridge Structure by Solar Radiation[J]. China Journal of Highway and Transport, 2004, 17(1): 49-52. |
| [26] |
王勖成. 有限单元法基本原理和数值方法[M]. 北京: 清华大学出版社, 1997. WANG Xu-cheng. Basic Principle and Numerical Method of Finite Element Method[M]. Beijing: Tsinghua University Press, China, Beijing, 1997. |
| [27] |
JTG D60-2015, 公路桥涵设计通用规范[S]. JTG D60-2015, General Specifications for Design of Highway Bridges and Culverts[S]. |
 2021, Vol. 38
2021, Vol. 38
