扩展功能
文章信息
- 秦幼林, 许崇帮, 高晓静, 赵凡
- QIN You-lin, XU Chong-bang, GAO Xiao-jing, ZHAO Fan
- 膨胀岩本构力学模型研究进展及展望
- Study Progress and Prospect of Constitutive Mechanical Model of Swelling Rock
- 公路交通科技, 2021, 38(6): 23-31
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(6): 23-31
- 10.3969/j.issn.1002-0268.2021.06.004
-
文章历史
- 收稿日期: 2020-11-02
2. 中铁十一局集团有限公司, 重庆 400037
2. China Railway 11 th Bureau Group Co., Ltd., Chongqing 400037, China
膨胀是一种岩石-水相互作用的现象[1],水进入岩石结构导致岩石体积增加。根据膨胀机理的不同,膨胀通常分为两类:黏土矿物吸水导致体积增大的物理膨胀,硬石膏吸水转化为石膏导致体积增大的化学膨胀,据此,将膨胀岩分为两类:物理膨胀岩和化学膨胀岩。物理膨胀岩即常见的软岩中的黏土岩,如泥岩、泥灰岩、页岩、凝灰岩、红层泥岩等,化学膨胀岩常见的有硬石膏岩、含硬石膏泥灰岩等。在工程实践中,岩石膨胀常导致边坡岩体吸水膨胀失稳,建筑物地基不均匀胀缩变形开裂;隧道底板隆起、行车中断及衬砌裂损[2]。
我国存在大量且分布广泛的膨胀岩,在20多个省市中均有膨胀岩分布[3],国外膨胀岩广泛分布在瑞士西北部与德国西南部和西班牙等地区,膨胀岩的存在对许多工程特别是隧道造成了破坏,导致隧道运营被迫中断,耗费了巨大的维修费用[4]。
对膨胀问题的研究始于20世纪70年代初,起因是德国的Wagenburg公路隧道和瑞士的Belchen公路隧道穿越了膨胀岩岩层,引发了一系列工程问题。从那时起,各国学者进行了一系列有关膨胀岩的研究项目,这些项目涉及的问题、所采用的方法、调查的规模和所涉及的学科等方面都有所不同。在微观尺度上,矿物学家对黏土颗粒,硬石膏和石膏晶体之间的相互作用进行了理论和试验研究。除在微尺度上进行了科学研究外,对实验室(中尺度)及实际工程(宏观尺度)的膨胀现象也进行了大量的研究。
自1972年以来,众多学者提出了一系列简化的理论模型来描述膨胀岩的膨胀行为,为工程设计提供了合理的依据。逐渐地,学者们开始考虑膨胀过程观察到的时间依赖性,Anagnostou[5]开始尝试使用耦合模型来模拟膨胀岩的力学行为。Wittke[6]、Gysel[7]、Einstein[8]、Anagnostou[9-10]从物理-化学-机械角度研究本构模型。缪协兴等[11]提出的湿度应力场理论为膨胀岩本构模型的研究开辟了新方向。
膨胀岩本构模型对各类遭遇膨胀岩的工程的设计及施工具有重要工程现实意义。国内外学者对膨胀岩本构模型进行了广泛的研究,随着膨胀岩对各类工程危害的不断凸显,对现有的膨胀岩本构模型研究进行全面、系统的研究、归纳和总结具有重要的工程意义。
1 膨胀岩本构模型研究根据本构模型推导原理及方法,膨胀岩本构模型主要分为3类:一是基于试验数据拟合应力应变关系的半经验法;二是基于连续介质力学的应力应变分析方法的连续介质力学类本构模型;三是从热力学基本定律出发建立表征应力应变关系的热力学定律类模型。
1.1 半经验法类本构模型半经验法类膨胀岩本构模型一般先通过室内膨胀岩试验得到应力-应变关系的经验公式,再结合数学、力学理论分析建立最终的膨胀岩本构模型。第一个描述膨胀岩膨胀行为的半经验法类本构模型是在认识和量化膨胀行为的试验基础上得到的。1970年,Huder和Amberg用固结仪进行了侧限条件下的膨胀岩试验,1972年Grob提出了侧限条件下膨胀岩Huder-Amberg一维本构模型,也即Grob定律[12]。
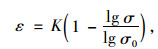
|
(1) |
式中,ε为轴向膨胀应变;σ为轴向膨胀应力;σ0为最大膨胀应力;K为σ=0.1 MPa时的轴向膨胀应变。
Huder-Amberg一维膨胀岩本构模型已得到世界范围内的公认,并被广泛应用于隧道仰拱的设计[13]。但是,该本构模型的不足在于本构模型建立在泥灰岩(膨胀不包含化学膨胀)试验基础上。因此,该本构模型能较好表征泥灰岩(物理膨胀岩)的膨胀行为,对于化学膨胀岩其适用性并不确定[14]。另外,该本构模型不足之处在于模型本身受到试验模型的限制,在试验基础上推导的本构模型仅适用于特定的环境[11]:膨胀部分岩体均匀吸水,周围岩体是刚性的;膨胀部分岩体与周围岩体无摩擦光滑接触;周围岩体中的应力场(例如原岩应力场)不会作用到膨胀部分岩体上。这种特定环境仅仅存于试验模型中,实际工程中膨胀岩体吸水的范围和程度都是变化的。并且,Huder-Amberg一维本构模型只适用于膨胀岩不再吸收任何水分,即膨胀岩吸水达到饱和状态,膨胀达到稳定状态后的情况[15],无法反映整个膨胀过程的应力-应变关系。
刘晓丽等[16]考虑了膨胀随时间变化的非稳定阶段,并发现Huder-Amberg一维本构模型中当σ→0,ε→∞时存在的数学奇异性问题,修正后的本构模型为

|
(2) |
式中,ε∞为岩石膨胀最终膨胀率;k为岩石膨胀吸水系数;σ0为最大膨胀应力;t为时间;ε,σ为t时刻的膨胀应变、应力。
上述本构模型中为了避免数学奇异性问题,从而在lg(1+σ),lg(1+σ0)式中引入了参数“1”。但是,该参数并没有明确的物理意义;同时,该模型未考虑岩石的初始含水率的影响。大量研究表明:不同的初始含水率引起的膨胀应变不同[17],因此,该膨胀模型仅适用于某一固定初始含水率的情况。
邓建华等[18]考虑到进行膨胀岩试验时,无论是自由膨胀试验还是侧限膨胀试验都要预先施加一定的压力,而这部分预压力没有记入试验数据中,从而导致了σ=0时产生了数学函数的奇异性。基于上述试验事实,提出了修正的Huder-Amberg一维本构模型。
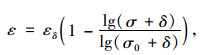
|
(3) |
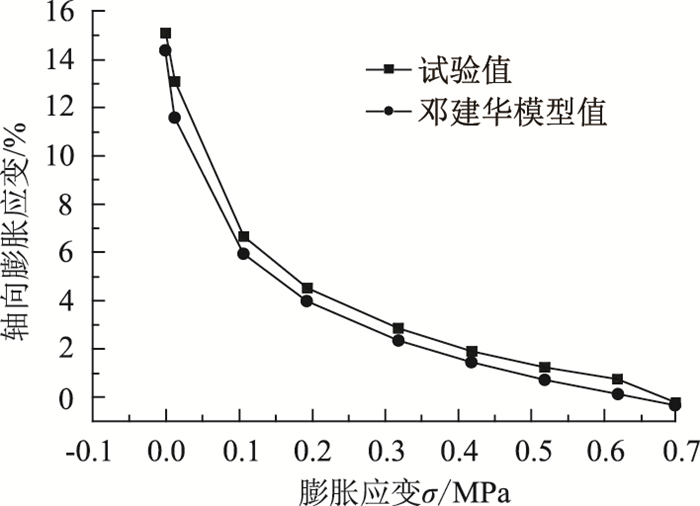
式中,εδ为膨胀参数;σ0为最大膨胀应力;ε,σ为膨胀应变、应力;δ为自由膨胀时施加的轴向膨胀应力,一般根据规范取值,通常取0.01 MPa[19]。
邓建华本构模型与膨胀岩石膨胀试验值的对比如图 1所示。由图 1可见,采用式(3)的本构模型与试验结果比较接近,因而该修改模型能够更准确地描述侧限条件下膨胀岩的膨胀规律。
当考虑膨胀岩初始含水率,即考虑吸水变化过程时,岩石的膨胀应变取决于吸水量w。本构模型中考虑吸水量的变化时,Huder-Amberg一维膨胀模型在岩石未完全饱和,膨胀处于非稳定阶段的情况时也是有效的,克服了Huder-Amberg无法应用于膨胀岩非稳定膨胀阶段的不足。引入含水量的Huder-Amberg一维膨胀模型[20]变为:
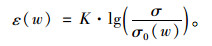
|
(4) |
其中

|
(5) |
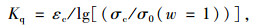
|
(6) |
式中,ε(w)为膨胀应变;σ为膨胀应力;εc为最大膨胀应变;σc为最小的膨胀应力;σ0(w=1)代表岩石吸水饱和时的膨胀应力,也即为侧限膨胀试验的最大膨胀应力[15];Kq为膨胀岩的膨胀参数。
在用Huder-Amberg一维本构模型进行计算时,只考虑了垂直应力的影响,这将引起存在很大的误差。因为,另外两个方向上的应力也对膨胀存在影响[21]。随后,Pregl[22]在Huder-Amberg的膨胀试验基础上假定径向应力与轴向应力符合金尼克条件[16],同时,假设膨胀应变是由应力第一不变量引起(该假设的正确性后来得到了试验验证),推导出了三维的膨胀本构模型。
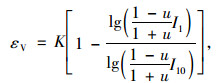
|
(7) |
式中,εV为体积膨胀应变;u为膨胀岩的泊松比;I1为应力第一不变量;I10为应力第一不变量最大值。
其他学者也在三维膨胀本构模型研究方面做了大量的工作:Wittke[23]基于Kiehl推导饱和各向同性膨胀本构模型的方法,考虑膨胀过程吸水的三维本构模型为:
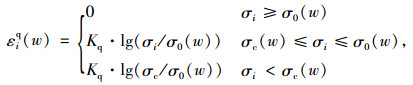
|
(8) |
式中,i=1, 2, 3;εiq(w),σi分别为膨胀主应变和主正应力;σc为最小的膨胀应力;σ0(w)为岩石吸水饱和时的膨胀应力;Kq为膨胀岩的膨胀参数。
左清军等[24-25]基于泥质板岩侧限膨胀试验发现膨胀应变不仅与膨胀应力相关,还与最大膨胀应力与最小膨胀应力之差有关,建立了能分段描述泥质板岩的基于时间效应的三维膨胀本构模型。
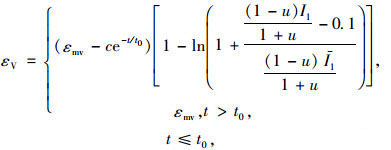
|
(9) |
式中,εmv为最大体积膨胀率;c为拟合系数;t0为最大体积膨胀率对应的时间;u为膨胀岩材料泊松比;I1-为最大、最小膨胀压力所对应的应力第一不变量之差。
杨庆等[26]在三维膨胀本构模型中考虑了吸水率和轴向应力的影响,并且,认为轴向应力对膨胀性围岩的膨胀过程起着决定性的作用,通过试验拟合得到包含吸水率与应力的本构模型。
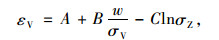
|
(10) |
式中,w为吸水率;A,B,C为材料的膨胀特性常数。
部分学者从其他角度建立了膨胀岩本构模型。傅学敏等[27]借助电镜扫描,从微观机理方面分析膨胀岩石颗粒的微观变化,并且在大量验证性试验的基础上,提出采用膨胀元件、弹性元件、黏性元件和塑性元件并联组合的模型来模拟膨胀过程中的力学行为。
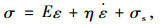
|
(11) |
式中,σ为某一时刻的膨胀应力;ε为某一时刻的膨胀应变;
基于试验揭露的黏土质页岩所具有的低透水性、高黏塑特性,Bonini等[28]认为建模时需要采用考虑弹性、塑性和黏性行为分量的本构关系,提出基于Mohr-Coulomb屈服准则的黏弹性、塑性模型(CVISC)来表征黏土质页岩膨胀的力学特性和时变特性,本构模型如下:
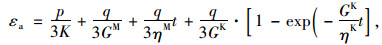
|
(12) |
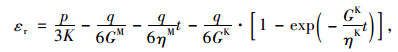
|
(13) |
式中,εa为轴向膨胀应变;εr为环向膨胀应变;K为体积模量;ηM为Maxwell动力黏度;GM为Maxwell剪切模量;ηK为Kelvin为动力黏度;GM为Kelvin剪切模量;c为黏聚力;σt为单轴抗拉强度。
陈宗基等[29]认为膨胀确实是与时间有关的体积增加,但同时强调矿物和物理、化学试验的重要性,考虑物理化学和力学过程联合作用后的本构模型为
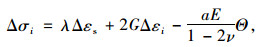
|
(14) |
式中,i=1, 2, 3;εs为膨胀总应变;a取决于膨胀过程中出露面的比表面积参数;λ,G为弹性理论中的拉梅常数;E为膨胀岩的弹性模量;Θ为黏土矿物之类膨胀活动性很强的物质的参数。
从上述各种半经验法类膨胀岩本构模型看出,半经验法类膨胀岩本构模型都是在特定的试验基础上建立膨胀岩本构模型。通过这种方法建立的本构模型具有一定的不足。首先,基于试验模型得到的本构模型必然反过来会受到试验模型的限制,该类本构模型仅适用于类似试验时的特定环境,这种特定的试验环境与工程实际情况存在着较大差别,运用于实际工程时存在一定的误差。其次,在分析和计算岩体遇水作用之后产生的应力应变场方面缺少完备、严谨的数学、力学基础。
1.2 连续介质力学类本构模型众多学者从物理-化学-机械角度研究岩石膨胀,使本构模型的研究不单纯依靠试验数据,而是先从数学、力学、物理、化学理论角度分析建立本构模型,然后结合试验验证本构模型,这是研究膨胀岩本构模型的另外一种思路。例如Anagnostou[10]介绍了一种基于连续介质应力分析的模型,将岩石膨胀描述为一个耦合的水力-机械过程。
对于地下工程来讲,例如隧道工程,隧道开挖后,隧道附近会形成松散带,导致渗透性增加。考虑应力-应变行为、剪胀、渗漏、吸水膨胀等多因素耦合后,本构模型的研究变得困难。此时,Anagnostou[5]将隧道多因素耦合产生的膨胀视为一个水力-机械耦合过程,充分考虑渗流的作用后,能够真实地反映所观察到的膨胀。
弹性本构模型为:
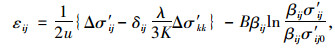
|
(15) |
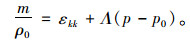
|
(16) |
其中
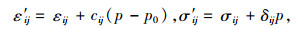
|
(17) |
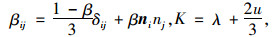
|
(18) |
式中,λ,u为弹性理论的Lame常数[30];δ为Kronecker符号;B,β为膨胀相关的参数;p0,p为初始孔隙水压力及孔隙水压力;εij,σij为初始应变、应力;Λ,cij为岩石颗粒压缩性、水压缩性、岩石孔隙率有关的材料常数;ni为垂直于层理平面的单位矢量;m为含水质量。
对于弹塑性阶段,增量弹塑性形式本构模型为:
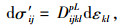
|
(19) |
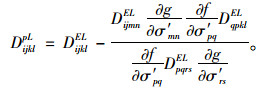
|
(20) |
其中
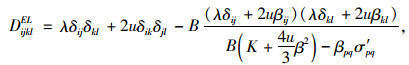
|
(21) |
式中,f,g分别表示屈服函数和塑性势函数,其余参数见式(15)~(18)。
Anagnostou[5]本构模型在考虑了实际的渗流之后,模型可分别根据渗流条件的不同计算不同部位的膨胀,例如隧道中底板、边墙和顶拱的膨胀;此外,由于考虑了渗流,可以模拟膨胀变形随时间变化的发展过程。同时,该耦合本构模型还考虑到了膨胀岩各向异性的性质。并且,该本构模型中考虑了水进入岩石后,岩石有效孔隙水压力的改变,考虑到了膨胀是由有效应力而不是总应力的变化引起的,这是目前其余膨胀岩本构模型都不具备的。该模型在瑞士隧道设计建模分析中得到了较好的应用[31]
Bonini等[28]提出基于经典塑性理论流动法则的弹黏塑性Lemaitre模型(VIPLA)来表征黏土质页岩膨胀的力学特性和时变特性。
VIPLA本构模型为:
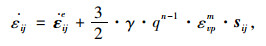
|
(22) |
式中,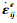
李安润等[32]以滇中地区龙川江河谷红层泥岩为研究对象,在研究了饱水-失水循环条件下红层泥岩的蠕变特性后,提出将广义开尔文体与非线性黏塑性体以及胡克体串联得到红层泥岩剪切蠕变本构模型(LCJN)。
当σ0≤σL时,非线性黏塑性体不发挥效用,剪切蠕变本构模型为:
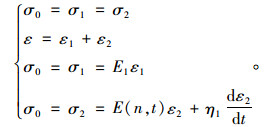
|
(23) |
当σ0>σL时,非线性黏塑性体发挥效用,剪切蠕变本构模型为:
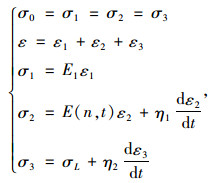
|
(24) |
式中,σ0为剪切荷载;σL为长期强度;E1,σ1为分别为胡克体的弹性模量和应力;η1,σ2为开尔文体黏滞系数和应力;η2,σ3为非线性黏塑性体黏滞系数和应力;dε2/dt为ε2对时间t的一阶导数;dε3/dt为ε3对时间t的一阶导数。
目前,除了Alonso[33]提出了岩石裂缝内晶体生长的模型外,现有的理论模型都没有考虑到含硬石膏的岩石中发生的化学迁移过程。正是这些过程导致化学膨胀岩与黏土质膨胀岩表现出根本不同的行为。当前,在一个正在进行的研究项目中,研究人员充分考虑硬石膏的溶解、石膏晶体的生长、扩散和对流运输以及水分蒸发等因素的影响,建立了硬石膏黏土岩膨胀的水力-机械-化学耦合模型[34],该模型考虑了硬石膏溶解和石膏沉淀引起的应变和应力。
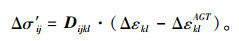
|
(25) |
其中
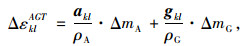
|
(26) |
式中,Δσ′ij为有效应力增量;D为刚度矩阵;ΔεklAGT为硬石膏转化为石膏化学过程的应变增量;Δεkl为应变增量;akl,gkl为与材料特性相关参数的张量;ΔmA,ΔmG为硬石膏和石膏单位体积的质量变化率。
连续介质力学类膨胀岩本构模型首先根据严谨的数学、力学等知识建立本构模型,然后结合膨胀岩试验确定本构模型中的膨胀参数。膨胀岩本构模型具有数学及力学知识基础,可实现对膨胀岩的膨胀进行建模分析及数值计算。
1.3 热力学定律类本构模型当前,热力学定律类本构模型主要是通过湿度应力场来表征膨胀现象。缪协兴等[11]受温度应力场理论的启发,提出了湿度应力场理论,白冰等[35]从热力学第一定律和建立本构方程的一般方法出发,对缪协兴提出的湿度应力场理论作了严格的证明,奠定了湿度应力场理论研究膨胀岩本构模型的数学及力学基础。膨胀岩湿度应力场理论主要研究的内容之一是研究含水率变化的岩石膨胀特性,即与湿度有关的膨胀岩本构方程[36]。从湿度场理论角度研究本构模型是膨胀岩本构模型研究的又一新思路。
含水率的变化使膨胀岩的泊松比、弹性模量、和屈服极限等力学性能发生变化,从而引起膨胀应力、塑性流动和随湿度场而变化的屈服准则等都相互耦合在一起。朱珍德等[37]考虑湿度场的影响并基于弹塑性理论,提出了基于湿度应力场理论的膨胀岩增量形式的弹塑性本构模型。
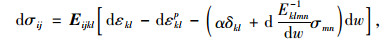
|
(27) |
式中,Eijkl为湿度影响下的弹性系数张量,是含水率的函数;α为膨胀系数,是含水率的函数;δij,δkl为Kronecker记号;w为湿度场;εij为总应变;εklp为塑性应变。
陈钒等[38]在传统的湿度应力场理论的基础上,运用硬石膏吸水结果建立了湿度状态一系列时变方程,最终建立了硬石膏岩含时间效应的湿度场本构模型。
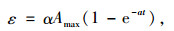
|
(28) |
式中,α为线膨胀系数;Amax为膨胀终止时刻的吸水率。
任松等[39]根据硬石膏岩试验结果改进了缪协兴等[40]基于湿度应力场提出的仅适用于黏土类膨胀岩的本构模型,并且,考虑了硬石膏膨胀性的时变特征,建立了含时间效应的硬石膏岩膨胀本构模型。
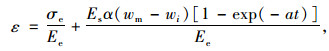
|
(29) |
式中,α为线膨胀系数;Ee为弹性模量;Es为膨胀模量;t为时间;wt为岩石在t时刻的吸水率;wi为岩石初始含水量;wm为岩石饱和吸水量;a为与岩石吸水性能有关的系数。
任松等[41]基于传统的湿度场本构模型,考虑时间效应、水压的影响后,改进后的硬石膏膨胀岩本构模型为:
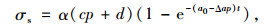
|
(30) |
式中,α为线膨胀系数;p为水压;c为反映岩石吸水能力的参数;d为无水压条件下岩石的最大吸水率;a为0 MPa水压下的吸水率;Δa为反映吸水系数随水压变化的参数;t为时间。
湿度应力场理论虽然有严谨的数学、力学基础,但是,湿度应力场理论仍然是建立在一定的假设前提下:如不考虑温度的影响、应变和湿度的变化不能太大、固体相的变形是弹性变形,忽略流体对固体相产生的耗散过程[35]。因此,基于湿度应力场的本构模型确定了一种理想物质模型,它是工程实际材料本构关系的一种理想化,需要工程实践进行检验、完善和发展。
此外,化学膨胀岩膨胀过程缓慢。硬石膏质黏土岩在实验室一个试验加载阶段的膨胀持续时间便可达数年[14]。湿度场理论多用于泥岩、页岩等含强吸水黏土矿物的物理膨胀岩,部分学者开始将湿度应力场理论应用于化学膨胀岩,并且,考虑到了化学膨胀岩的膨胀时变特性,建立了基于湿度应力场包含时间效应的化学膨胀岩本构模型。这类基于湿度应力场理论的化学膨胀岩本构模型的模型参数需要结合化学膨胀岩的膨胀试验结果确定。依据短期的实验室试验结果确定的化学膨胀岩本构模型的模型参数同长期实际工程的适用性有待考究。
化学膨胀岩的体积膨胀随时间变化且持续时间长,化学膨胀岩膨胀过程其实是流变过程[42],相比于传统的湿度应力场膨胀本构模型,考虑了时间效应的湿度应力场膨胀本构模型可将膨胀问题转化为流变问题,这对实际工程中的过程模拟和过程控制具有重要工程实践意义。将化学膨胀的时间效应与流变问题结合研究不失为研究膨胀岩本构模型的一种新思路。
2 讨论(1) 世界范围内应用最广的膨胀岩本构模型是Huder-Amberg一维膨胀岩本构模型,该模型被广泛应用于隧道仰拱的设计。Anagnostou膨胀岩本构模型考虑了渗流条件,可以计算隧道不同部位和随时间变化的膨胀,该模型在瑞士隧道设计建模分析中得到了较好的应用。国内外本构模型主要聚焦于实验室岩石尺度,实际工程尺度的本构模型研究及应用不足。
(2) 在采用半经验法本构模型时,需要先做一定的假设才能考虑长期应力应变关系;在应用连续介质力学本构模型时,虽然不需要事先假设长期应力应变关系,但是,任何不考虑渗流的连续介质力学模型都无法真实反映实际工程环境,考虑渗流又成为连续介质力学类本构模型的难点。运用基于热力学定律的湿度应力场理论研究膨胀岩的本构模型时假设忽略流体可能对固体相产生的耗散过程,而膨胀正是岩石-水相互作用的结果,这一假设对于膨胀岩流固相互作用过程可能是不合适的。
(3) 目前,国内外均对化学膨胀岩认识不足,研究较少,有很多问题需要解决。其中,较关键的是渗流对于化学膨胀岩的影响;地下水排水是否可以抑制膨胀;渗流运输过程对于膨胀的影响;水力边界条件的作用;晶体生长是否是化学类膨胀岩膨胀的主导机制。这些问题的解决对于认识化学膨胀岩至关重要。
(4) 对于化学膨胀岩,除了化学膨胀时间跨度长的问题,还有一个问题在于根据目前已有的实验室设备及条件进行化学膨胀岩的膨胀试验所得到的结果,并不能非常准确反映化学膨胀岩对实际工程膨胀问题影响的大小。因为,实验室一般的化学膨胀岩的试验条件控制方面,特别是水循环方面,实验室条件与工程现场条件相差很大,试验条件与实际工程环境相似性并不高。因此,由目前化学膨胀岩试验数据得到的膨胀岩本构模型应用于实际工程时的适用性有待考究。
3 未来展望为提高处理膨胀岩复杂工程地质条件下工程面临的实际问题的能力及减少膨胀岩带来的工程危害,本研究归纳、总结了国内外膨胀岩本构模型,以及分析了本构模型的不足。针对这些不足,对未来的本构模型的研究展望如下:
(1) 国内外对化学膨胀岩的研究均滞后于工程实际。因此,化学膨胀岩及化学膨胀本构模型研究是今后研究膨胀岩的重要方向之一。
(2) 化学膨胀岩的膨胀过程随时间变化且持续时间长,本构方程中考虑时间因素,将长期的膨胀问题结合流变问题分析是研究膨胀的新思路。湿度应力场理论具有严谨的数学、力学基础。力学基础基于弹塑性力学,弹塑性力学理论本身具有一定局限性,无法全面、真实、有效地反映膨胀岩吸湿过程中的膨胀岩应力应变关系及变化情况。进一步研究可以考虑结合流变问题,从黏弹塑性力学角度建立湿度应力场的膨胀岩本构模型。
(3) 对于本构模型的研究难点主要不在于数学、力学以及物理、化学等基础理论,难在对于膨胀的准确认识。目前,本构模型研究中大都只考虑单因素的影响,加深多因素耦合,重视实验室与工程现场实际环境之间差异的膨胀的本构模型研究是今后膨胀岩研究的难点,亦是热点。
(4) 多因素耦合、高精度、少干扰的新型膨胀岩试验装置研发不足。研发全新的、可靠的,专门应用于化学膨胀岩长期试验的新型试验装置具有广阔的前景。试验装置应可以同时进行一系列极慢和持久的膨胀试验及化学、力学试验,尤其是可以模拟不同工程现场实际环境。并且,可以尽量减少外部因素对试验的影响,如荷载调整、长期测量精度、仪器刚度、温度的影响,为化学膨胀岩本构模型研究提供可靠真实的试验数据。
| [1] |
PIMENTEL E, ANAGNOSTOU G. New Apparatus and Experimental Setup for Long-term Swelling Tests on Sulphatic Claystones[J]. Rock Mechanics and Rock Engineering, 2013, 46(6): 1271-1285. |
| [2] |
朱珍德, 张爱军, 张勇, 等. 基于湿度应力场理论的膨胀岩弹塑性本构关系[J]. 岩土力学, 2004, 25(5): 700-702. ZHU Zhen-de, ZHANG Ai-jun, ZHANG Yong, et al. Elastoplastic Constitutive Law of Swelling Rock Based on Humidity Stress Field Theory[J]. Rock and Soil Mechanics, 2004, 25(5): 700-702. |
| [3] |
范秋雁. 膨胀岩与工程[M]. 北京: 科学出版社, 2008. FAN Qiu-yan. Swelling Rock and Engineering[M]. Beijing: Science Press, 2008. |
| [4] |
HOFER R, CHIAVERIO F, KOVÀRI K. Chienbergtunnel Sissach-Tunnelhebung infolge Quellen[C]//Swiss Tunnel Congress 2007. Zurich: Fachtagung ftir Untertagbau, 2007: 95-100.
|
| [5] |
ANAGNOSTOU G. A Model for Swelling Rock in Tunnelling[J]. Rock Mechanics and Rock Engineering, 1993, 26(4): 307-331. |
| [6] |
WITTKE-GATTERMANN P, WITTKE M. Computation of Strains and Pressures for Tunnels in Swelling Rocks[J]. Tunnelling and Underground Space Technology, 2004, 19(45): 422-423. |
| [7] |
GYSEL M. Anhydrite Dissolution Phenomena: Three Case Histories of Anhydrite Karst Caused by Water Tunnel Operation[J]. Rock Mechanics and Rock Engineering, 2002, 35(1): 1-21. |
| [8] |
EINSTEIN H H. Tunnels in Opalinus Clayshale: A Review of Case Histories and New Developments[J]. Tunnelling and Underground Space Technology, 2000, 15(1): 13-29. |
| [9] |
ANAGNOSTOU G. Seepage Flow Around Tunnels in Swelling Rock[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1995, 19(10): 705-724. |
| [10] |
ANAGNOSTOU G. Untersuchungen zur statik des Tunnelbaus in Quellfähigem Gebirge[J]. Veroffentlichungen des instituts fur geotechnik, 1991, 185(2): 184-192. |
| [11] |
缪协兴, 茅献彪, 卢爱红. 湿度应力场理论在软岩巷道围岩稳定性控制中的应用[J]. 矿山压力与顶板管理, 2002, 19(3): 1-2, 5. MIAO Xie-xing, MAO Xian-biao, LU Ai-hong. Application of the Humid Stress Theory on the Soft Surrounding Rock Stability Control around Coal Mining Roadway[J]. Ground Pressure and Strata Control, 2002, 19(3): 1-2, 5. |
| [12] |
AMBERG J, HUDER G. Quellung in Mergel, Opalinuston und Anhydrit[J]. Schweizerische Bauzeitung, 1970, 88(43): 975-980. |
| [13] |
蒲文明, 陈钒, 任松, 等. 膨胀岩研究现状及其隧道施工技术综述[J]. 地下空间与工程学报, 2016, 12(增1): 232-239. PU Wen-ming, CHEN Fan, REN Song, et al. Research of Swelling Rock and Summarize of Tunnel Construction[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(S1): 232-239. |
| [14] |
MADSEN F, NUESCH R. The Swelling Behaviour of Clay-sulfate Rocks[C]//The 7th ISRM Congress. Aachen: International Society for Rock Mechanics and Rock Engineering, 1991: 285-288.
|
| [15] |
WITTKE W. Swelling Rock[M]. Hoboken: John Wiley and Sons, Ltd., 2014.
|
| [16] |
刘晓丽, 王思敬, 王恩志, 等. 含时间效应的膨胀岩膨胀本构关系[J]. 水利学报, 2006, 37(2): 195-199. LIU Xiao-li, WANG Si-jing, WANG En-zhi, et al. Study on Time-dependent Swelling Constitute Relation of Swelling Rock[J]. Journal of Hydraulic Engineering, 2006, 37(2): 195-199. |
| [17] |
刘跃东, 姜鹏飞. 基于湿度场理论的岩石膨胀本构模型研究[J]. 煤炭科学技术, 2018, 46(3): 61-66, 72. LIU Yue-dong, JIANG Peng-fei. Study on Rock Expansion Constitutive Model Based on Humidity Field Theory[J]. Coal Science and Technology, 2018, 46(3): 61-66, 72. |
| [18] |
邓建华, 黄醒春. 考虑时间因素的膏溶角砾岩膨胀本构关系[C]//第六届全国土木工程研究生学术论坛论文集. 北京: 中国土木工程学会, 2008: 128-133. DENG Jian-hua, HUANG Xing-chun. Study on Time-dependent Swelling Constitute Relation of Gypsum Breccia[C]//The 6th National Civil Engineering Graduate Academic Forum. Beijing: China Civil Engineering Society, 2008: 128-133. |
| [19] |
TB 10115-1998, 铁路工程岩石试验规程[S]. TB 10115-1998, Test Methods of Rocks for Railway Engineering[S]. |
| [20] |
HOELLRIGL M, BROETZ K, BUDIL A. Strenger Tunnel-Gebirgsdruck und Ausbau/Strenger Tunnel-support in Squeezing Rock[J]. Rock and Soil Engineering, 2004, 22(1): 39-43. |
| [21] |
GROB H. Swelling and Heave in Swiss Tunnels[J]. Bulletin of the International Association of Engineering Geology, 1975, 14(1): 55-60. |
| [22] |
BUTSCHER C, HUGGENBERGER P, ZECHNER E, et al. Relation between Hydrogeological Setting and Swelling Potential of Clay-sulfate Rocks in Tunneling[J]. Engineering Geology, 2011, 122(3/4): 204-214. |
| [23] |
WITTKE M. Begrenzung der Quelldrücke durch Selbstabdichtung beim Tunnelbau im Anhydritführenden Gebirge[J]. Geotechnik in Forschung und Praxis: Wbi-print, 2003(13): 3375-3379. |
| [24] |
左清军, 陈可, 谈云志, 等. 基于时间效应的富水泥质板岩隧道围岩膨胀本构模型研究[J]. 岩土力学, 2016, 37(5): 1357-1364. ZUO Qing-jun, CHEN Ke, TAN Yun-zhi, et al. A Time-dependent Constitutive Model of the Water-rich Argillaceous Slate Surrounding a Tunnel[J]. Rock and Soil Mechanics, 2016, 37(5): 1357-1364. |
| [25] |
左清军, 吴立, 袁青, 等. 软板岩膨胀特性试验及微观机制分析[J]. 岩土力学, 2014, 35(4): 986-990, 997. ZUO Qing-jun, WU Li, YUAN Qing, et al. Swelling Characteristics Test and Micromechanism of Soft Slate[J]. Rock and Soil Mechanics, 2014, 35(4): 986-990, 997. |
| [26] |
杨庆, 焦建奎, 栾茂田. 膨胀岩土侧限膨胀试验新方法与膨胀本构关系[J]. 岩土工程学报, 2001, 23(1): 49-52. YANG Qing, JIAO Jian-kui, LUAN Mao-tian. Study on a New Method of Confined Swelling Tests and Swelling Constitutive Relationship for Swelling Rocks[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(1): 49-52. |
| [27] |
傅学敏, 潘清莲. 软岩的膨胀规律和膨胀机理[J]. 煤炭学报, 1990(2): 31-38. FU Xue-min, PAN Qing-lian. Rules and Mechanism for Swelling of Weak and Soft Rocks[J]. Journal of China Coal Society, 1990(2): 31-38. |
| [28] |
BONINI M, DEBERNARDI D, BARLA M, et al. The Mechanical Behaviour of Clay Shales and Implications on the Design of Tunnels[J]. Rock Mechanics and Rock Engineering, 2009, 42(2): 361-388. |
| [29] |
陈宗基, 闻萱梅. 膨胀岩与隧洞稳定[J]. 岩石力学与工程学报, 1983(1): 1-10. CHEN Zong-ji, WEN Xuan-mei. Swelling Rocks and Stability of Tunnels[J]. Chinese Journal of Rock Mechanics and Engineering, 1983(1): 1-10. |
| [30] |
陈惠发, 萨里普A F, 余天庆, 等. 弹性与塑性力学[M]. 北京: 中国建筑工业出版社, 2004. CHEN Hui-fa, SARIPU A F, YU Tian-qing, et al. Elasticity and Plasticity[M]. Beijing: China Architecture & Building Press, 2004. |
| [31] |
ANAGNOSTOU G, SERAFEIMIDIS K, PIMENTEL E, et al. Modelling of Anhydritic Swelling Claystones[M]. Zurich: Bundesamt für Strassen, 2015.
|
| [32] |
李安润, 邓辉, 王小雪, 等. 饱水-失水循环条件下红层泥岩蠕变特性及本构模型研究[J]. 工程地质学报, 2020, 28(1): 1-9. LI An-run, DENG Hui, WANG Xiao-xue, et al. Research on Creep Characteristics and Constitutive Model of Red Bed Mudstone under Saturated-dehydrated Cycle[J]. Journal of Engineering Geology, 2020, 28(1): 1-9. |
| [33] |
ALONSO E E, BERDUGO I R, RAMON A. Extreme Expansive Phenomena in Anhydritic-gypsiferous Claystone: the Case of Lilla Tunnel[J]. Géotechnique, 2013, 63(7): 584-612. |
| [34] |
HUBER T, PIMENTEL E, ANAGNOSTOU G. Experimental Investigations for the Modelling of Chemo-mechanical Processes in Anhydritic Rock[J]. Energy Procedia, 2015, 76(3): 87-95. |
| [35] |
白冰, 李小春. 湿度应力场理论的证明[J]. 岩土力学, 2007, 28(1): 89-92. BAI Bing, LI Xiao-chun. Proof of Humidity Stress Field Theory[J]. Rock and Soil Mechanics, 2007, 28(1): 89-92. |
| [36] |
缪协兴. 用湿度应力场理论分析膨胀岩巷道围岩变形[J]. 中国矿业大学学报, 1995(1): 58-63. MIAO Xie-xing. Large Deformation Analysis of Surrounding Rock of a Tunnel in Swelling Rock Mass Based on the Humidity Stress Field Theory[J]. Journal of China University of Mining and Technology, 1995(1): 58-63. |
| [37] |
朱珍德, 张爱军, 张勇, 等. 基于湿度应力场理论的膨胀岩弹塑性本构关系[J]. 岩土力学, 2004, 25(5): 700-702. ZHU Zhen-de, ZHANG Ai-jun, ZHANG Yong, et al. Elastoplastic Constitutive Law of Swelling Rock Based on Humidity Stress Field Theory[J]. Rock and Soil Mechanics, 2004, 25(5): 700-702. |
| [38] |
陈钒, 吴建勋, 任松, 等. 基于湿度应力场理论的硬石膏岩膨胀试验研究[J]. 岩土力学, 2018, 39(8): 2723-2731. CHEN Fan, WU Jian-xun, REN Song, et al. The Swelling Tests of Anhydrite Based on the Humidity Stress Field Theory[J]. Rock and Soil Mechanics, 2018, 39(8): 2723-2731. |
| [39] |
任松, 欧阳汛, 吴建勋, 等. 含时间效应的硬石膏隧道弹-膨胀解析模型[J]. 浙江大学学报: 工学版, 2018, 52(5): 896-905. REN Song, OUYANG Xun, WU Jian-xun, et al. Elastic-swelling Analytical Model of Anhydrite Rock Considering Time-dependent Effect[J]. Journal of Zhejiang University: Engineering Science Edition, 2018, 52(5): 896-905. |
| [40] |
缪协兴, 杨成永. 膨胀岩体中的湿度应力场理论[J]. 岩土力学, 1993, 14(4): 49-55. MIAO Xie-xing, YANG Cheng-yong. Humidity Stress Field Theory in Swelling Rock Mass[J]. Rock and Soil Mechanics, 1993, 14(4): 49-55. |
| [41] |
任松, 吴建勋, 欧阳汛, 等. 压力水作用下硬石膏岩膨胀性研究[J]. 岩土力学, 2018, 39(12): 4351-4359. REN Song, WU Jian-xun, OUYANG Xun, et al. Influence of Pressured Water on the Swelling of Anhydrite Rock[J]. Rock and Soil Mechanics, 2018, 39(12): 4351-4359. |
| [42] |
王凯, 刁心宏. 膨胀岩湿度应力场本构模型二次开发研究[J]. 岩石力学与工程学报, 2015, 34(增2): 3781-3792. WANG Kai, DIAO Xin-hong. Secondary Development Study of Swelling Rock Humidity Stress Field Constitutive Model[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(S2): 3781-3792. |
 2021, Vol. 38
2021, Vol. 38