扩展功能
文章信息
- 许崇帮
- XU Chong-bang
- 公路隧道施工扰动分析方法探讨
- Discussion on Method for Analysing Construction Disturbance in Highway Tunnel
- 公路交通科技, 2021, 38(6): 11-16, 87
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(6): 11-16, 87
- 10.3969/j.issn.1002-0268.2021.06.002
-
文章历史
- 收稿日期: 2020-08-31
随着隧道工程的迅速发展,以及岩石力学、量测技术、数值计算方法、系统论、人工智能和非线性科学等理论与技术的建立、发展,隧道工程稳定性分析手段多样化,如力学分析法[1-4]、工程地质法[5-6]、物理模型试验法[7-8]等。研究人员利用这些研究手段对隧道工程稳定的研究主要侧重于两种隧道稳定判别依据的分析,一种是围岩强度判据[9],一种是围岩变形量或变形率判据[10]。但是,由于隧道屈服区域受泊松比影响很大,且隧道围岩泊松比很难确定,而围岩位移又在洞周各点各不同,其大小亦受围岩弹模和隧道形状的影响[11],使得两种判据难以满足工程需要[12-13]。近年来,郑颖人院士将有限元强度折减法应用到隧道稳定性分析中,提出了隧道的剪切安全系数和拉裂安全系数[11],对隧道的稳定性分析进行了有益的探索,但分析过程中未能反映出衬砌结构安全与隧道围岩安全系数的关系;此外,有限元强度折减法应用于隧道稳定分析尚处于起步阶段,量化评定指标还需要工程实例验证[14]。因此,研究施工对隧道围岩稳定影响的分析方法、评价指标、量化指标十分必要。
在隧道工程稳定性分析中,施工扰动是影响隧道工程稳定性的根本因素,是多种力学行为相互交织、作用和影响的结果,施工扰动下的力学行为可归结为隧道围岩应力和围岩变形两个指标状态[15]的变化,同时,影响制约这两个状态的主要因素有原岩应力和围岩自身承载能力及隧道衬砌结构(包括形式和强度)3个方面。可见,施工扰动下的隧道工程稳定性实际是围岩稳定性与衬砌结构稳定性的综合反映,换而言之,隧道施工扰动程度可通过围岩稳定状态和衬砌结构稳定状态进行反映,其中围岩稳定状态可用围岩变形(位移)和自身承载能力进行表述。因此,论文研究了隧道位移评判指标、围岩自承载能力的表述方式,以及基于隧道衬砌结构安全系数的衬砌安全度评判指标表述方式;在此基础上,进一步构建了隧道施工最小扰动评价方法,由隧道位移评判指标、围岩自承载能力评判指标和衬砌安全度评判指标的综合值表征隧道施工扰动程度,为隧道施工扰动分析提供了依据。
1 隧道施工最小扰动评价方法 1.1 隧道施工扰动指标研究(1) 隧道位移评判指标
隧道施工中位移监控项目主要有:地表下沉、围岩体内位移、拱顶下沉和周边位移[16]。其中,地表下沉位移和围岩体内位移可看作隧道围岩向临空面变形量沿径向的变化,是隧道拱顶下沉、周边位移在地表和围岩体内的表现形式。同时,地表下沉和围岩体内位移在隧道浅埋时可反映隧道围岩稳定状态的变化,但在隧道深埋时则对围岩稳定状态的敏感性降低;而拱顶下沉和周边位移则无论是浅埋还是深埋都能够直接反映隧道周边围岩变形趋势和隧道安全状态,是评价隧道围岩稳定状态关键性指标。因此,位移评判指标选取拱顶下沉、周边位移作为对象。
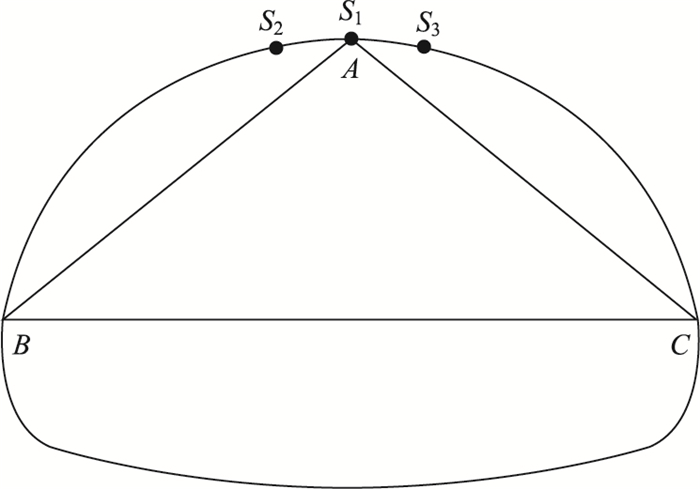
为了能较全面反映隧道位移情况,在隧道施工中,拱顶下沉一般在拱顶中间位置及左、右两侧一定距离处共布设3个测点(见图 1);隧道周边位移则一般布置3条测线(见图 1)。
|
| 图 1 拱顶下沉和周边收敛监测布置图 Fig. 1 Layout of monitoring arch crown settlement and surrounding convergence |
| |
拱顶下沉和周边收敛中反映隧道稳定性的有两指标:一是绝对沉降量/周边收敛值,反映施工扰动下隧道围岩整体的变形程度;二是隧道变形的不均度,反映施工扰动对围岩变形不利的影响程度。施工扰动影响应由这两个指标综合反映。同时,为避免隧道跨度影响,绝对变形值量采用其与隧道跨度的比值即相对沉降量代替。
拱顶下沉采用绝对沉降量和不均度综合反映施工扰动影响的表述形式,如式(1)所示。
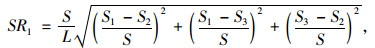
|
(1) |
式中,SR1为拱顶下沉评判指标;S1,S2,S3分别为拱顶监测点下沉位移;S为拱顶平均下沉值,S=(S1+S2+S3)/3;L为隧道跨度。
周边位移采用绝对沉降量和不均度综合反映施工扰动影响的表述形式如式(2)所示。
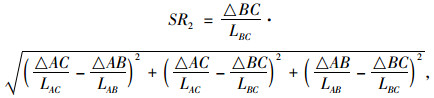
|
(2) |
式中,SR2为周边收敛评判指标;△AC,△AB,△BC分别为测线AC,AB,BC的位移收敛值;LAC,LAB,LBC分别为测线AC,AB,BC初始长度。
SR1,SR2反映了施工扰动对隧道沉降变形和收敛变形的影响程度,施工扰动位移评判综合指标则是SR1,SR2二者的综合体现,可按照式(3)进行计算得出:
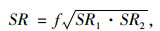
|
(3) |
式中,SR为隧道位移评判指标,SR值越大表明隧道施工扰动越大,越不利于隧道稳定,反之,则表示施工扰动越小,越有利于隧道稳定;f为修正系数。
根据《公路隧道施工技术规范》[17]、《公路隧道设计规范》[16]对各级围岩及不同埋深条件下隧道围岩变形量的规定,SR1,SR2的取值范围如表 1、表 2所示。
| 围岩级别 | 隧道埋深/m | ||
| < 50 | 50~300 | > 300 | |
| Ⅲ | 0~4.24E-03 | 0~7.07E-03 | 0~1.70E-02 |
| Ⅳ | 0~7.07E-03 | 0~1.70E-02 | 0~2.83E-02 |
| Ⅴ | 0~1.13E-02 | 0~2.26E-02 | 0~4.24E-02 |
| 围岩级别 | 隧道埋深/m | ||
| < 50 | 50~300 | > 300 | |
| Ⅲ | 0~1.27E-05 | 0~3.54E-05 | 0~2.04E-04 |
| Ⅳ | 0~3.54E-05 | 0~2.04E-04 | 0~5.66E-04 |
| Ⅴ | 0~9.05E-05 | 0~3.62E-04 | 0~1.27E-03 |
由于SR1,SR2值通常是一小于1的较小值,为使得SR值处于合理取值区间,修正系数f按照式(4)计算。

|
(4) |
式中,SR1max,SR2max分别为表 1、表 2中各埋深、围岩级别下的最大值。
则根据式(4)及表 1、表 2可得不同围岩级别及埋深条件下修正系数f值,见表 3。
| 围岩级别 | 隧道埋深/m | ||
| < 50 | 50~300 | > 300 | |
| Ⅲ | 6 087 | 2 829 | 761 |
| Ⅳ | 2 829 | 761 | 354 |
| Ⅴ | 1 398 | 494 | 192 |
(2) 隧道围岩自承载能力评判指标
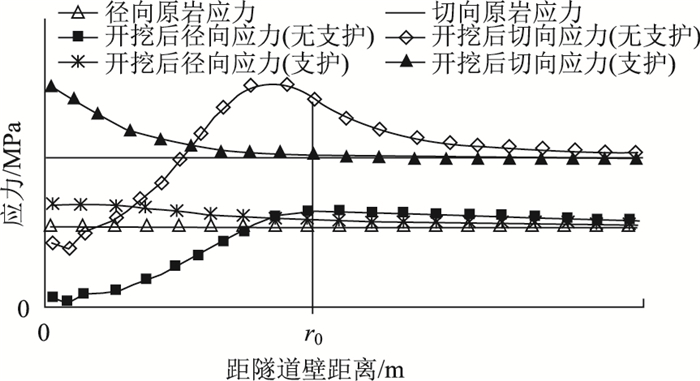
受隧道施工扰动影响,开挖后隧道围岩应力状态发生了显著变化(见图 2),且这种变化受隧道支护条件控制[18-19],并在隧道周边形成了一个主要的承载区域[20-22]。同时,该种围岩显著变化区域或承载区域一般在1倍隧道洞径范围内最为明显(见图 2),因此,将1倍隧道洞径范围内的围岩应力作为围岩自承载能力评判区域。
|
| 图 2 隧道围岩应力分布图 Fig. 2 Distribution of tunnel surrounding rock stresses |
| |
隧道围岩自承载能力不仅要反映围岩对原岩应力力学状态的继承能力,还应反映施工后围岩的安全状态。为此,对隧道围岩中某一质点i的自承载能力定义如下:
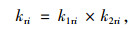
|
(5) |
式中,kri为自承载能力评判系数;k1ri为点i对原岩应力力学状态的继承能力的系数;k2ri为施工后点i的围岩安全状态系数。
其中,k1ri定义如下:
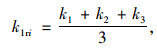
|
(6) |
式中,k1,k2,k3分别为点i第1主应力、第2主应力、第3主应力与原岩应力的接近度,取值如下:
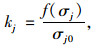
|
(7) |
式中,σj0为原岩应状态中第j(j=1,2,3)主应力值;kj根据弹塑性力学理论[1],最大值为3.0,故k1ri一般取0~3.0。
i点围岩施工后岩安全状态系数k2ri定义如下:
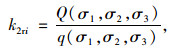
|
(8) |
式中,q(σ1, σ2, σ3)为i点实际围岩应力状态标识量;Q(σ1, σ2, σ3)为围岩屈服或破坏时应力状态标识量;若Q(σ1, σ2, σ3)/q(σ1, σ2, σ3)≤1,则k2ri=0,表示围岩失稳。q(σ1, σ2, σ3),Q(σ1, σ2, σ3)可用强度响应函数表示,Q(σ1, σ2, σ3)/q(σ1, σ2, σ3)则表示围岩i的最小安全系数,一般取值0~10.0。
1倍洞径范围内的围岩自承载能力评判指标定义如下:
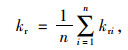
|
(9) |
式中,kr为围岩自承载能力评判指标,kr值一般为0~30.0,围岩自承载能力系数kr越大说明围岩自承载能力越强,围岩越稳定,施工扰动越小;n为1倍洞径范围内围岩单元数目。
(3) 隧道衬砌安全度评判指标
隧道衬砌安全系数作为评价衬砌参数选取是否合理的主要依据,一直是设计单位、施工单位评判隧道是否稳定的主要指标。为使隧道衬砌安全系数也能够反映围岩应力状况与衬砌安全的关系,对隧道衬砌安全系数修正如下:
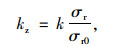
|
(10) |
式中,σr为隧道围岩与初期支护间压力,取值范围为0~σr0;σr0为洞壁处原岩应力;k为衬砌安全系数,考虑不同围岩级别下初期支护和二次衬砌功能不同,衬砌安全系数采用隧道二次衬砌安全系数进行表述;kz为隧道衬砌安全度评判指标,一般取值为0~15.0,衬砌安全系数评判指标kz值越大,表明隧道越稳定、施工扰动越小。
1.2 施工最小扰动分析方法量化与标准根据施工扰动中隧道位移评判指标SR、隧道围岩自承载能力指标kr和隧道衬砌安全度评判指标kz与施工扰动的关系可知:若施工扰动越大,则位移评判系数SR越大,围岩自承载能力系数kr越小,隧道衬砌安全系数kz越小。因此,施工扰动评价可用式(11)进行表述:
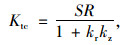
|
(11) |
式中Ktc为施工最小扰动综合评判系数。
由于隧道位移评判指标SR在实际工程通常在0~0.1之间分布广泛,因此,Ktc计算值一般小于0.1,为便于对施工扰动程度进行分级,将式(11)做如下变化:
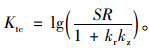
|
(12) |
则由式(12)可知,若施工最小扰动综合评判系数Ktc为负无穷时,施工扰动影响可以忽略,隧道稳定性为最理想状态;若Ktc为0时,则隧道稳定稳定性最差,即隧道处于失稳、破坏,施工扰动最为严重;对于二者之间状态做如表 2划分:
| 稳定状态 | 极佳 | 良好 | 稳定 | 较稳定 | 不稳定 |
| Ktc值 | <-3.0 | [-3.0, -0.7) | [-0.7, -0.3) | [-0.3,-0.15) | >-0.15 |
2 工程应用分析
福州机场二期高速公路工程中金鸡山隧道为双向八车道连拱隧道[23],采用有限元数值分析方法对金鸡山隧道Ⅴ级围岩段(埋深26.0 m)进行了双侧壁导坑法和CRD法计算分析。根据施工最小扰动分析方法,对两种施工方法的隧道位移评判指标SR、隧道围岩自承载能力评判指标kr、隧道衬砌安全度评判指标kz进行了计算。
(1) 位移评判指标SR
隧道单洞跨度(BC测线)18.20 m,AB测线、AC测线长12.14 m,两种施工方法的拱顶下沉和周边收敛如表 3所示。根据式(1)~式(3)可得两种施工方法的拱顶下沉评判指标SR1、周边位移评判指标SR2及位移评判指标SR如表 4所示。
| 名称 | 拱顶下沉量/mm | 周边位移/mm | |||||
| S1 | S2 | S3 | △ AB | △ AC | △ BC | ||
| CRD法 | 左洞 | 8.506 | 7.592 | 7.932 | 3.428 | 3.887 | 2.044 |
| 右洞 | 8.889 | 6.987 | 7.032 | 3.533 | 3.977 | 1.973 | |
| 双侧壁导坑法 | 左洞 | 7.793 | 7.056 | 6.914 | 3.261 | 3.773 | 2.275 |
| 右洞 | 7.835 | 6.823 | 6.498 | 3.229 | 3.707 | 2.123 | |
| 名称 | SR1 | SR2 | SR | |
| CRD法 | 左洞 | 6.36E-05 | 3.05E-08 | 1.946E-03 |
| 右洞 | 0.00015 | 3.12E-08 | 3.027E-03 | |
| 双侧壁导坑法 | 左洞 | 6.4E-05 | 2.98E-08 | 1.931E-03 |
| 右洞 | 9.3E-05 | 2.84E-08 | 2.274E-03 | |
(2) 隧道围岩自承载能力评判指标kr
隧道围岩自身承载能力评判选(拱腰)水平方向和(拱顶)竖向方向1倍(单)洞径内的围岩单元作为评判对象。利用式(5)~式(10)计算各部位围岩自承载能力评判指标,计算结果如表 5所示。
| 名称 | 拱顶 | 拱腰 | 平均值 | |
| CRD法 | 左洞 | 3.312 | 1.931 | 2.621 |
| 右洞 | 2.860 | 2.186 | 2.523 | |
| 双侧壁导坑法 | 左洞 | 3.229 | 2.287 | 2.758 |
| 右洞 | 3.015 | 2.796 | 2.906 | |
(3) 隧道衬砌安全度评判指标kz
隧道衬砌安全度评判选择左右洞拱顶和拱腰4个部位作为评判对象,4个特征部位根据式(10)计算衬砌安全度评判指标,计算结果如表 6所示。
| 名称 | 左洞 | 右洞 | |||||
| 拱顶 | 拱腰 | 平均值 | 拱顶 | 拱腰 | 平均值 | ||
| CRD | 0.34 | 2.29 | 1.32 | 0.28 | 3.62 | 1.95 | |
| 双侧壁导坑 | 1.59 | 7.28 | 4.44 | 1.95 | 6.87 | 4.41 | |
(4) 施工最小扰动综合评价指标Ktc
根据表 4~6的计算结果,利用式(12)可得到两种施工方法下左右洞的施工最小扰动综合评判指标,其计算结果如表 7所示。
| 名称 | SR | Kr | Kz | Ktc | |
| CRD法 | 左洞 | 1.95E-03 | 2.621 | 1.32 | -3.36 |
| 右洞 | 3.03E-03 | 2.523 | 1.95 | -3.29 | |
| 双侧壁导坑法 | 左洞 | 1.93E-03 | 2.758 | 4.44 | -3.84 |
| 右洞 | 2.27E-03 | 2.906 | 4.41 | -3.78 | |
由表 7可见,双侧壁导坑法和CRD法施工,隧道稳定性均属于良好级别。但二者相比较,双侧壁导坑法对隧道扰动程度小于CRD法,隧道施工采用双侧壁导坑比CRD法更有利于隧道稳定性。
3 结论(1) 将隧道围岩拱顶下沉和周边收敛的绝对变形值指标和各测点/测线变形的不均度指标作为基本指标,建立了反映施工扰动影响的隧道位移评判指标,并依据规范给出了拱顶下沉指标和周边收敛指标取值范围。
(2) 根据隧道施工后围岩应力变化,将1倍洞径内围岩作为自承载能力的评价对象,给出了考虑围岩对原岩应力力学状态的继承能力和围岩的安全状态的围岩自承载能力评判方法与公式。
(3) 根据隧道位移评判指标、隧道围岩自承载能力评判指标、隧道衬砌安全度评判指标构建了隧道施工最小扰动综合评判公式,给出了隧道施工扰动程度与隧道稳定程度量化指标的对应关系,及其稳定状态等级划分标准。
| [1] |
沈明荣. 岩体力学[M]. 上海: 同济大学出版社, 2000. SHEN Ming-rong. Rockmass Mechanics[M]. Shanghai: Tongji University Press, 2000. |
| [2] |
朱大勇, 钱七虎, 周早生, 等. 复杂形状洞室围岩应力的弹性解析分析[J]. 岩石力学与工程学报, 1999, 18(4): 402-404. ZHU Da-yong, QIAN Qi-hu, ZHOU Zao-sheng, et al. Elastic Solutionto Stresses of Rock Masses around Openings with Complex Shape[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(4): 402-404. |
| [3] |
朱大勇, 钱七虎, 周早生, 等. 复杂形状洞室映射函数的新解法[J]. 岩石力学与工程学报, 1999, 18(3): 279-282. ZHU Da-yong, QIAN Qi-hu, ZHOU Zao-sheng, et al. New Method for Calculating Mapping Function of Opening with Complex Shape[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(3): 279-282. |
| [4] |
许强, 黄润秋. 考虑地应力的洞室围岩块体稳定性分析的理论与实践[J]. 地质灾害与环境保护, 1996, 7(4): 1-6. XU Qiang, HUANG Run-qiu. The Theory and Application of Stability Analysis of Surrounding Rock in Consideration of Geostress[J]. Journal of Geological Hazards and Environment Preservation, 1996, 7(4): 1-6. |
| [5] |
冯玉国. 灰色优化理论模型在地下工程围岩稳定性分类中的应用[J]. 岩土工程学报, 1996, 18(3): 62-66. FENG Yu-guo. Application of Grey Optimal Theory Model in the Stability Classification of Adjoining Rock of Underground Construction[J]. Chinese Journal of Geotechnical Engineering, 1996, 18(3): 62-66. |
| [6] |
杨小永, 伍法权, 苏生瑞. 公路隧道围岩模糊信息分类的专家系统[J]. 岩石力学与工程学报, 2006, 25(1): 100-105. YANG Xiao-yong, WU Fa-quan, SU Sheng-rui. Expert System of Fuzzy Information for Classification of Surrounding Rock Mass in Highway Tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(1): 100-105. |
| [7] |
刘涛, 沈明荣, 陶履彬, 等. 连拱隧道动态施工模型试验与三维数值仿真模拟研究[J]. 岩石力学与工程学报, 2006, 25(9): 1802-1808. LIU Tao, SHEN Ming-rong, TAO Lü-bin, et al. Model Test and 3D Numerical Simulation Study on Excavation of Double-arch Tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(9): 1802-1808. |
| [8] |
陈秋南. 非对称连拱隧道动态施工力学模拟研究[D] 重庆: 重庆大学, 2005. CHEN Qiu-nan. Mechanics Simulation of Dynamic Construction of Asymmetric Double-arch Tunnel[D]. Chongqing: Chongqing University, 2005. |
| [9] |
蔡美峰. 岩石力学与工程[M]. 北京: 科学出版社, 2002. CAI Mei-feng. Rock Mechanics and Engineering[M]. Beijing: Science Press, 2002. |
| [10] |
李世辉, 宋军. 变形速率比值判据与猫山隧道工程验证[J]. 中国工程科学, 2002, 4(6): 85-91. LI Shi-hui, SONG Jun. Deformation Rate Ratio Criterion (DRRC) and Its Verification in Maoshan Tunnel Excavation[J]. Engineering Science, 2002, 4(6): 85-91. |
| [11] |
郑颖人, 邱陈瑜, 张红, 等. 关于土体隧洞围岩稳定性分析方法的探索[J]. 岩石力学与工程学报, 2008, 27(10): 1968-1980. ZHENG Ying-ren, QIU Chen-yu, ZHANG Hong, et al. Exploration of Stability Analysis Methods for Surrounding Rocks of Soil Tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(10): 1968-1980. |
| [12] |
陈先国. 隧道结构失稳及判据研究[D]. 成都: 西南交通大学, 2002. CHEN Xian-guo. Study on Failure and Criteria of Tunnel Structure[D]. Chengdu: Southwest Jiaotong University, 2002. |
| [13] |
王齐林. 地下结构失稳及可靠度研究[D]. 武汉: 武汉理工大学, 2007. WANG Qi-lin. Study on Failure and Reliability of Underground Structure[D]. Wuhan: Wuhan University of Technology, 2007. |
| [14] |
贾蓬, 唐春安, 杨天鸿, 等. 强度折减法在岩石隧道稳定性研究中的应用[J]. 力学与实践, 2007, 29(3): 50-55. JIA Peng, TANG Chun-an, YANG Tian-hong, et al. Application of Strength Reduction Method on the Stability Study of Rock Tunnel[J]. Mechanics in Engineering, 2007, 29(3): 50-55. |
| [15] |
孙钧, 周健, 龚晓南, 等. 受施工扰动影响土体环境稳定理论与变形控制[J]. 同济大学学报: 自然科学版, 2004, 32(10): 1261-1269. SUN Jun, ZHOU Jian, GONG Xiao-nan, et al. Theory of Soil Environment Stability and Deformation Control under Influence of Construction Disturbance[J]. Journal of Tongji University: Natural Science Edition, 2004, 32(10): 1261-1269. |
| [16] |
JTG D70-2004, 公路隧道设计规范[S]. JTG D70-2004, Code for Design of Road Tunnel[S]. |
| [17] |
JTJ 042-94, 公路隧道施工技术规范[S]. JTJ 042-94, Technical Specifications for Construction of Highway Tunnel[S]. |
| [18] |
杨超, 陆士良, 姜耀东. 支护阻力对不同岩性围岩变形的控制作用[J]. 中国矿业大学学报, 2000, 29(2): 170-173. YANG Chao, LU Shi-liang, JIANG Yao-dong. Controlling Effects of Support Resistance on Roadway Deformation under Different Rock Conditions[J]. Journal of China University of Mining & Technology, 2000, 29(2): 170-173. |
| [19] |
WANG W J. Study of Mechanical Principle of Reinforcing Sidewalls and Corners of Gateway to Control Floor Heave by Anchors[J]. Journal of Coal Science & Engineering, 2003, 9(1): 17-21. |
| [20] |
朱建明, 徐秉业, 任天贵, 等. 巷道围岩主次承载区协调作用[J]. 中国矿业, 2000, 9(2): 41-44. ZHU Jian-ming, XU Bing-ye, REN Tian-gui, et al. Coordination between Primary and Secondary Support Zones of Drift's Surrounding Rock[J]. China Mining Magazine, 2000, 9(2): 41-44. |
| [21] |
康红普. 巷道围岩的关键圈理论[J]. 力学与实践, 1997, 19(1): 34-36. KANG Hong-pu. Key-ring Theory for Surrounding Rock of Roadway[J]. Mechanics and Practice, 1997, 19(1): 34-36. |
| [22] |
卢汝绥, 钟世航. 隧道自承体系形成机理的分析[J]. 隧道及地下工程, 1997, 18(4): 5-9. LU Ru-sui, ZHONG Shi-hang. Analysis of Formation Mechanism of Self-supporting System of Tunnels[J]. Tunnels and Underground Engineering, 1997, 18(4): 5-9. |
| [23] |
许崇帮, 夏才初, 朱合华. 双向八车道连拱隧道施工方案优化分析[J]. 岩石力学与工程学报, 2009, 28(1): 66-73. XU Chong-bang, XIA Cai-chu, ZHU He-hua. Optimum Analysis of Construction Scheme of Multi-arch Tunnel with Eight Traffic Lanes[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(1): 66-73. |
 2021, Vol. 38
2021, Vol. 38
