扩展功能
文章信息
- 陈文强, 顾玉磊, 汪勇杰, 陈波
- CHEN Wen-qiang, GU Yu-lei, WANG Yong-jie, CHEN Bo
- 基于博弈决策的道路通行费最优定价模型研究
- Study on Optimal Pricing Model of Road Toll Based on Game Decision-making
- 公路交通科技, 2021, 38(5): 152-158
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(5): 152-158
- 10.3969/j.issn.1002-0268.2021.05.019
-
文章历史
- 收稿日期: 2020-09-26
2. 长安大学 汽车学院, 陕西 西安 710064
2. School of Automobile, Chang'an University, Xi'an Shaanxi 710064, China
随着中国经济的快速发展,交通拥堵问题已经扩散到各级城市,城市尺度的道路收费目标逐步由收费还贷转变为收费还贷与交通需求管理并重目标。交通需求管理目标之一,是通过拥堵定价增加沿线的出行成本来缓解路网拥堵,从而将交通流量从高峰时段转为非高峰时段,从拥挤路线改为拥挤程度较小的路线,或从私家车改为公共交通工具[1]。
拥挤定价理论的起源可以追溯到Pigou[2]和Knight[3],其以高速公路为例来解决外部性和最佳拥堵成本问题。此后,边际成本定价的概念,即净社会利益最大化而征收等于私人成本与道路社会成本之差的费用,已广泛应用于道路网络优化中[4-8]。拥堵定价涉及到管理者与交通出行者之间、交通出行者之间的相互反应,博弈论可以较好地处理主体间相互影响关系,利用博弈论研究拥堵收费的成果十分丰富。P.Ferrari [9]对道路网络收费和社会福利之间关系做了系统研究;N.Xiao[10]基于道路参与者互动原理提出了拥堵收费设计框架;Zhu和Ukkusuri[11]使用排队理论工具,将交通行为的动态和随机方面纳入边际拥堵成本的计算中,提出了一种基于距离的动态收费模型,并考虑了不确定的交通需求和供应状况,结果表明,收费通行的总行程时间比模拟运行减少了25%; AE Ohazulike[12]提出了拥堵收费的多主体博弈模型;Dusica Joksimovic[13]基于博弈理论,提出了不同政策目标下的拥堵收费定价模型;Theodore Tsekeris[14]提出了不同路网管理措施下的定价策略的综合评估框架,分析了道路交通拥堵的边际社会成本定价和收益最大化的道路通行费定价等情况;Wu和Huang[15]提出了在竞争性公路/交通系统中,考虑道路拥堵和瓶颈队列中的车辆拥堵,通过分析三种道路使用定价策略下的均衡来研究通勤者的出行方式;Z. Liu[16]提出了基于logit的随机用户均衡(SUE)约束的最优惠价格的通行费定价框架;Daganzo和Lehe[17]引入出行时间异质性,提出了一种基于使用情况的时变通行费,既减轻了拥堵,又优先考虑了短途出行。李浩、虞明远等[18-19]基于公共性差异化、车辆排放水平差异化视角研究了公路收费问题。
从目前检索到的成果看,除文献[17]引入了出行时间异质性外,其他涉及利用博弈理论研究拥堵收费的成果基本上将不同出行者的时间价值和出行效用做了无差别处理。而实际上,不同层次出行者的出行时间价值和出行效用是不同的,对于拥堵收费费率的敏感程度也会有差异,进而影响模型精度。本研究基于文献[13]提出的拥堵收费定价模型,基于管理者不同决策目标,将道路管理者和交通出行者看成是非合作静态博弈的双方,考虑不同出行者群体时间价值和出行效用差异性,建立双层规划模型,利用博弈论方法来诠释不同决策目标下的道路最优定价,以期提高模型精度,为城市道路通行费合理制定提供决策参考。
1 问题描述与建模交通网络中,管理者通过改变出行费率实现对出行者的引导,出行者基于出行效用选择出行路线,这是个典型的1+N双层博弈问题。上层是管理者1与N个交通出行者参与的最优决策问题,下层是N个交通出行者的交通均衡问题。
为研究方便,设公路网中任意两点间有多条线路可以通行,其中至少有一条为收费线路。出行者决策原则是出行收益大于出行成本,其中出行成本包括时间成本和财务成本。令cxi表示出行者i选择路线x的出行成本,则cxi可以表示为:
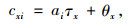
|
(1) |
式中,τx是选择x路线出行,完成全程所用的时间;θx是选择x路线出行支付通行费;αi是出行者i单位出行时间价值。
令uxi表示出行者i选择线路x的出行收益,其由出行效用u和选择线路x完成出行的出行成本cxi负数)构成,表达式为:
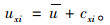
|
(2) |
根据出行线路决策原则,uxi>0,出行者出行;uxi<0,出行者放弃出行。
1.1 交通均衡模型令Si表示出行者i可以选择的策略集,si(θ)表示出行者i根据管理者决策(设通行费率为θ采取的策略集,其中si(θ)∈Si,s-i表示在此决策的基础上其他出行者i决策集,其中s-i=(si, …, si-1)。假设出行者是考虑到其他出行者合理选择的基础上单独进行决策来寻求收益最大,此时令Ji(s-i(θ), si(θ), θ)表示在给定的决策策略θ下,出行者i的收益。出行者收益包括出行效用和出行成本。出行者i收益表达式为:
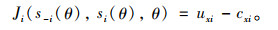
|
(3) |
此时,如果其他出行者采取对策s-i*,出行者i将采取对策si*(θ)来最大化其出行收益,表达式为:
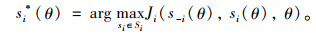
|
(4) |
如果式(4)涵盖所有的出行者,则si*(θ)≡(s-i*(θ), s*(θ))可以看成一个通行费率为θ的Nash-Wardrop均衡模型。
1.2 管理者决策模型管理者决策模型是由1个管理者和N个交通出行者作为局中人的非合作博弈模型。令ϕ代表管理者可能采取的定价策略集,设管理者采用通行费率为θ的策略(θ∈ϕ),出行者策略为si*(θ),管理者的收益为R(si*(θ), θ)。如果管理者希望通过θ*策略达到目标最优,表达式为:
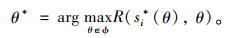
|
(5) |
假定式(4)、(5)适合所有局中人,则式(4)中θ=θ*。另外假定定价博弈模型是一个完全信息博弈模型,即每一位局中人对其他局中人信息、策略空间和收益函数有准确把握。则最优定价公式可以表示为:
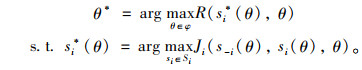
|
(6) |
此模型是一个典型的非合作静态Stackelberg博弈模型。
1.3 不同目标下的定价模型目标不同,最优定价策略也会有所不同:
(1) 总出行收益最大。交通管理者通过改变通行费率来平衡不同线路上的交通流量,以减少总的交通出行成本和因拥挤而产生的延迟,提高每条线路的利用率,使路网上交通总出行收益最大,其目标函数为:
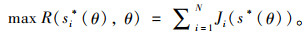
|
(7) |
(2) 通行费最大。交通管理者通过通行费率变化改变收费路网上交通量,使两者乘积最大。目标函数为:
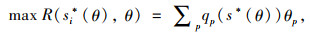
|
(8) |
式中,qp(s*),θp分别表示利用线路p的出行者数量和通行费率。
(3) 社会剩余最大。社会剩余最大即社会的总福利最大,是指生产者剩余和消费者剩余之和最大,本研究等同于通行费收与所有出行收益之和最大,目标函数表达式为:
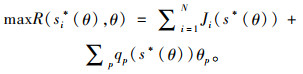
|
(9) |
双层规划模型,它是一种具有二层递阶结构的系统优化问题,上层决策者和下层决策者都有各自的目标函数和约束条件,上层先给定一个决策变量,下层各子系统以这个决策变量为参量,根据目标函数和约束条件,在可能的范围内求得一个最优值,并反馈给上层,上层再在下层的最佳反应的基础上,在可能的范围内求得整体上的最优解。基于本研究目标函数、约束条件特性和最优解特点(整数规划),论文采用分枝定界法进行模型求解[20]。求解步骤,先进行下层N个局中人的纳什-Wardrop均衡模型求解。纳什-Wardrop均衡可由Beckmann平衡分配模型及其F-W求解算法获得[21];在此基础上利用图解法进行上层N+1人的非合作静态Stackelberg博弈模型求解,最后对不同目标下的最优定价策略进行研究。
2 实证计算与结果分析假设交通出行者驾驶车辆从城市B点至C点上班,有p条线路可选,其中一条为收费线路,其余是免费线路。交通出行者i有三个出行方案可选择:收费线路、非收费线路和不出行。出行者i出行决策收益函数Ji(s-i(θ), si(θ), θ)与选择策略si(θ)、完成出行所获得的效用u、所耗费的时间τp、单位时间价值a及通行费θp有关。本例中出行者决策收益函数表达式为:
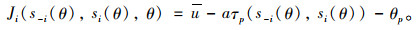
|
(10) |
通常情况下,不同出行者单位时间价值与出行效用是有差异的,出行目的、单位时间价值、出行效用各异。为方便研究,本节将出行者分为两组,“高单位时间价值组”和“低单位时间价值组”,假定两组出行者数量相同。经测算,高时间价值组出行者平均单位时间价值a=35元/h(按照月收入8 400元,每天工作8 h计算),低时间价值组出行者平均单位时间价值a=20元/h(按照月收入4 800元,每天工作8 h计算),高、低时间价值出行者在规定时间前到达C点,出行效用分别为u=35元/h×8 h=280元、20元/h×8 h=160元,迟到效用都为0,u=0。
根据交通工程理论,建成环境条件一定的情况下,车辆行驶速度(时间)与道路通行能力、交通流量有关。经调查,B点出行者在早高峰驾车到达C点一般预留36 min在途时间。经实地测定,任意一组在早高峰从B点至C点选择收费线路,收费线路和免费线路处于自由流阶段,经收费线路全程行驶时间为24 min(2/5 h),经免费线路全程行驶时间为36 min(3/5 h);两组都选择收费线路,全程行驶时间为36 min(3/5 h);两组都选择免费线路时,全程行驶时间为48 min(4/5 h)。数学描述为:
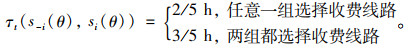
|
(11) |
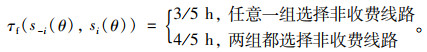
|
(12) |
利用函数式(10)、(11)、(12),结合上述测算值,通行费率为θ出行者收益如表 1所示。
| 出行组别 | 选择线路 | |||
| 低单位时间价值组 | ||||
| 收费道路 | 免费道路 | 不出行 | ||
| 高单位时间价值组 | 收费道路 | (259-θ, 148-θ) | (264-θ,148) | (264-θ,0) |
| 免费道路 | (259,152-θ) | (259,148) | (259, 0) | |
| 不出行 | (0,152-θ) | (0, 148) | (0,0) | |
基于决策收益,研究“最大出行收益”、“最大通行费”和“最大社会剩余”目标下的路网最优定价问题。
2.1 最大出行收益目标下的最优定价出行者总出行收益最大数学表达式为式(7),设管理者选择θ∈φ决策,决策收益如表 2所示。
| 出行组别 | 选择线路 | |||
| 低单位时间价值组 | ||||
| 收费道路 | 免费道路 | 不出行 | ||
| 高单位时间价值组 | 收费道路 | 407-2θ | 412-θ | 264-θ |
| 免费道路 | 411-θ | 407 | 259 | |
| 不出行 | 152-θ | 148 | 0 | |
由表 1可知,当0≤θ<5,根据收益最大原则,高单位时间价值组首选收费道路,因为选择收费道路收益(264-θ)大于选择免费线路收益259或不出行收益0;当0≤θ<4时,低单位时间价值出行者会选择收费道路出行,因为选择收费道路出行收益(152-θ)大于免费道路的收益148和不出行收益0。因此,当0≤θ<4时,双方都会选择收费道路出行,即s*={s低单位价值组(θ≠0), s高单位价值组(θ≠0)}此时实际收益为(407-2θ)。博弈结果见表 3。
| 出行组别 | 选择线路 | |||
| 低单位时间价值组 | ||||
| 收费道路 | 免费道路 | 不出行 | ||
| 高单位时间价值组 | 收费道路 | (259-θ, 148-θ) | (264-θ,148) | (264-θ,0) |
| 免费道路 | (259,152-θ) | (259,148) | (259, 0) | |
| 不出行 | (0,152-θ) | (0, 148) | (0,0) | |
当4≤θ≤5,高单位时间价值组首选收费道路,因为选择收费道路的收益(264-θ)大于等于选择免费道路收益259或不出行收益0;此时低单位时间价值组会选择免费道路出行,原因是选择免费道路收益148大于收费道路的收益(152-θ)或不出行0。因此,当4≤θ≤5时,两者博弈决策策略为s* ={s低单位价值组(θ=0), s高单位价值组(θ≠0)},实际收益为412-θ。博弈结果见表 4。
| 出行组别 | 选择线路 | |||
| 低单位时间价值组 | ||||
| 收费道路 | 免费道路 | 不出行 | ||
| 高单位时间价值组 | 收费道路 | (259-θ, 148-θ) | (264-θ,148) | (264-θ,0) |
| 免费道路 | (259,152-θ) | (259,148) | (259, 0) | |
| 不出行 | (0,152-θ) | (0, 148) | (0,0) | |
当θ>5,高单位时间价值组会选择免费道路出行,因为选择免费道路收益259大于收费道路收益264-θ和不出行收益0;低单位时间价值组会也会选择非收费道路出行,选择非收费道路收益148大于收费道路的收益152-θ或不出行收益0,两者博弈决策s*={s低单位价值组(θ=0), s高单位价值组(θ=0)},实际收益为407。博弈结果见表 5。
| 出行组别 | 选择线路 | |||
| 低单位时间价值组 | ||||
| 收费道路 | 免费道路 | 不出行 | ||
| 高单位时间价值组 | 收费道路 | (259-θ, 148-θ) | (264-θ,148) | (264-θ,0) |
| 免费道路 | (259,152-θ) | (259,148) | (259, 0) | |
| 不出行 | (0,152-θ) | (0, 148) | (0,0) | |
综上,不同通行费率θ下的出行者博弈决策结果和决策收益如式(13)、(14)所示:

|
(13) |
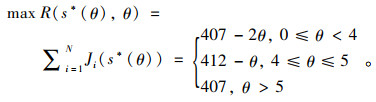
|
(14) |
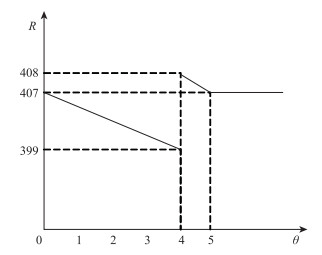
利用图解法将总出行收益最大为目标的管理者决策收益绘制成图(如图 1所示)。通过图 1可以看出,公路通行费率θ=4时,出行者总出行收益最大R=408。
|
| 图 1 基于最大总出行收益的决策收益示意图 Fig. 1 Schematic diagram of decision-making profit based on largest total travel profit |
| |
2.2 最大通行费目标下的最优定价
通行费最大数学描述如函数式(8),管理者选择θ∈ϕ决策,决策收益如式(15)所示:
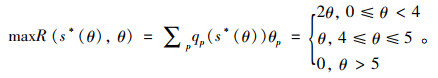
|
(15) |
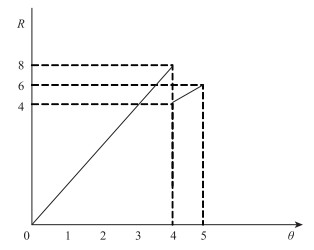
利用图解法将最大通行费下的管理者决策收益绘制成图(图 2)。
|
| 图 2 基于最大通行费收益的决策收益示意图 Fig. 2 Schematic diagram of decision-making profit based on largest toll |
| |
从图 2可以看出,当0≤θ<4,两组出行者同时选择收费公路,此区间通行费最大值趋于8;4≤θ≤5时,高单位时间组会选择收费公路,低单位时间价值组会选择免费道路,此区间通行费最大值为5。当θ>5,此区间通行费为0,由上述分析可知,通行费最大化目标下的公路最优定价θ趋于4,此时的管理者决策收益接近8。
2.3 最大社会剩余目标下的最优定价管理者剩余最大数学描述如函数式(9),管理者选择θ∈ϕ决策,决策收益如式(16)所示:
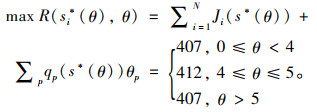
|
(16) |
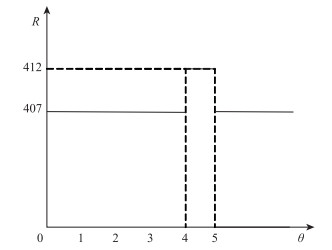
利用图解法将最大社会剩余最大的管理者决策收益绘制成图(图 3)。
|
| 图 3 基于最大社会剩余的决策收益示意图 Fig. 3 Schematic diagram of decision-making profit based on largest social surplus |
| |
从图 3可以看出,当0≤θ<4,最大社会剩余为407;4≤θ≤5时,最大社会剩余为412;当θ>5,最大社会剩余为407。可以看出,社会剩余最大化目标下最优定价为4≤θ≤5,此时决策收益为412。
3 结论与讨论本研究基于博弈论方法对不同决策目标下的道路通行费定价问题进行了研究,结果显示,基于博弈决策的道路通行费定价模型,可以表达和测算不同通行费率下道路参与者博弈过程和决策收益、不同决策目标下的最优通行费率。文中构建的出行情景中,通行费为θ=4时,出行者出行收益最大;通行费趋于4时,通行费最大;当通行费4≤θ≤5时,社会剩余最大。可以看出,本研究中构建的出行情景中通行费率为4时,出行者收益、通行费和社会剩余同时达到最大化,较好的满足决策目标。
为了验证模型的精度,本研究构建了出行情景,在出行情景下重点研究了上层交通参与者决策过程,对下层交通均衡问题研究做了简单处理,将交通参与者分为高价值组和低价值组,对每组的数量、道路通行能力等进行了假设,在此基础上给出交通均衡结果,这样处理的结果可能与现实中交通均衡问题有差异,但不影响论文研究目标的达成,这部分内容将在后续研究中补充完善。
| [1] |
ZHANG X. Editorial: Optimization Methods of Road Pricing[J]. European Journal of Transport and Infrastructure Research, 2014, 14(1): 1-6. |
| [2] |
PIGOU A C. The Economics of Welfare[M]. London: Macmillan Co., Ltd., 1920.
|
| [3] |
KNIGHT F H. Some Fallacies in the Interpretation of Social Cost[J]. The Quarterly Journal of Economics, 1924, 38(4): 582-606. |
| [4] |
YANG H, HUANG H J. Principle of Marginal-cost Pricing: How Does it Work in a General Road Network?[J]. Transportation Research Part A: Policy and Practice, 1998, 32(1): 45-54. |
| [5] |
NASH C. Marginal Cost and Other Pricing Principles for User Charging in Transport: A Comment[J]. Transport Policy, 2003, 10(4): 345-348. |
| [6] |
SWÄRDH J E, GENELL A. Marginal Costs of Road Noise: Estimation, Differentiation and Policy Implications[J]. Transport Policy, 2020, 88(C): 24-32. |
| [7] |
GAVANAS N, TSAKALIDIS A, PITSIAVA-LATINOPOULOU M. Assessment of the Marginal Social Cost due to Congestion Using the Speed Flow Function[J]. Transportation Research Procedia, 2017, 24: 250-258. |
| [8] |
VIERTH I, MERKEL A. Internalization of External and Infrastructure Costs Related to Maritime Transport in Sweden[M]//Research in Transportation Business & Management. [S. l. ]: Elsevier, 2020.
|
| [9] |
FERRARI P. Road Network Toll Pricing and Social Welfare[J]. Transportation Research Part B: Methodological, 2002, 36(5): 471-483. |
| [10] |
XIAO N, WANG X, XIE L, et al. Road Pricing Design Based on Game Theory and Multi-agent Consensus[J]. Journal of Automatica Sinica, 2014, 1(1): 31-39. |
| [11] |
ZHU F, UKKUSURI S V. A Reinforcement Learning Approach for Distance-based Dynamic Tolling in the Stochastic Network Environment[J]. Journal of Advanced Transportation, 2015, 49(2): 247-266. |
| [12] |
OHAZULIKE A E, STILL G, KERN W, et al. Multiple Stakeholders in Road Pricing: A Game Theoretic Approach[M]. Springer International Publishing: Berlin, 2015: 159-189, 2015.
|
| [13] |
JOKSIMOVIC D, BLIEMER M CJ, BOVY P H L et al. Different Policy Objectives in Road Pricing: A Game Theory Approach [C]//Bijdrage aan het Colloquium Vervoersplanologisch Speurwerk. Antwerpen: [s.n.], 2005.
|
| [14] |
TSEKERIS T, VOβ S. Design and Evaluation of Road Pricing: State-of-the-art and Methodological Advances[J]. NETNOMICS: Economic Research and Electronic Networking, 2009, 10(1): 5-52. |
| [15] |
WU W X, HUANG H J. Equilibrium and Modal Split in a Competitive Highway/Transit System under Different Road-use Pricing Strategies[J]. Journal of Transport Economics and Policy, 2014, 48(1): 153-169. |
| [16] |
LIU Z, WANG S, MENG Q. Toll Pricing Framework under Logit-based Stochastic User Equilibrium Constraints[J]. Journal of Advanced Transportation, 2013, 48(8): 1121-1137. |
| [17] |
DAGANZO C F, LEHE L J. Distance-dependent Congestion Pricing for Downtown Zones[J]. Transportation Research Part B: Methodological, 2015, 75: 89-99. |
| [18] |
李昊, 虞明远, 余艳春, 等. 基于车辆排放水平的差异化公路通行费率的分析[J]. 公路交通科技, 2018, 35(6): 137-144. LI Hao, YU Ming-yuan, YU Yan-chun, et al. Analysis on Differentiated Highway Toll Rate Based on Vehicle Emission Level[J]. Journal of Highway and Transportation Research and Development, 2018, 35(6): 137-144. |
| [19] |
徐瑛, 虞明远. 基于差异化公共性的公路收费问题解析[J]. 公路交通科技, 2012, 29(4): 149-152, 158. XU Ying, YU Ming-yuan. Analysis of Road Tolling Based on Differential Publicity[J]. Journal of Highway and Transportation Research and Development, 2012, 29(4): 149-152, 158. |
| [20] |
赵志刚, 顾新一, 李陶深. 求解双层规划模型的粒子群优化算法[J]. 系统工程理论与实践, 2007(8): 92-98. ZHAO Zhi-gang, GU Xin-yi, LI Tao-shen. Particle Swarm Optimization for Bi-level Programming Problem[J]. Systems Engineering Theory & Practice, 2007(8): 92-98. |
| [21] |
魏贤鹏, 战秋艳, 朝鲁. 基于Groebner基的Beckmann交通平衡分配模型新解法[J]. 动力系统与控制, 2016, 5(3): 96-104. WEI Xian-peng, ZHAN Qiu-yan, CHAO Lu. A New Method Based on Groebner Bases for Solving the Beckmann Traffic Equilibrium Assignment Model[J]. Dynamical Systems and Control, 2016, 5(3): 96-104. |
 2021, Vol. 38
2021, Vol. 38
