扩展功能
文章信息
- 刘韡, 郭银波
- LIU Wei, GUO Yin-bo
- 基于ABAQUS对钢纤维混凝土界面强度分析
- Analysis on Interfacial Strength of Steel Fiber Reinforced Concrete Based on ABAQUS
- 公路交通科技, 2021, 38(5): 65-72, 99
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(5): 65-72, 99
- 10.3969/j.issn.1002-0268.2021.05.008
-
文章历史
- 收稿日期: 2020-05-29
随着国民经济的持续猛涨,建筑工程的规模越来越大,然而钢纤维混凝土由于其强度高,抗弯、抗拉、抗冲击能力强、疲劳寿命长在结构工程、水利水电工程、桥面工程中得到了广泛的应用[1-3]。界面是钢纤维与混凝土之间的应力传递者,直接影响着钢纤维增强混凝土的力学性能[4],而两者之间的界面强度是主要因素[5]。从而,界面力学性能的研究对钢纤维增强混凝土具有重要意义。
近年来,国内外研究者对纤维混凝土界面的黏结性能从不同的角度进行了研究。王家赫等[6]通过对钢丝与混凝土黏结拔出行为进行了试验与模拟,探讨了钢丝埋置角度和深度对黏结强度的影响。结果表明:钢丝埋置长度越长,钢丝极限拔出荷载越大;钢丝拔出方向与埋入方向夹角越大,抗拔极限承载力越大。Abbas等[7]研究了钢纤维的嵌入深度和嵌入量对界面黏结强度的影响。结果表明:随着嵌入深度和嵌入量的增加,极限拉拔荷载显著增强。何桥敏等[8]研究了不同钢纤维掺量及黏结剂对混凝土性能的影响,结果表明:钢纤维混凝土的最佳钢纤维掺量为1.5%,在最佳掺量下,水泥净浆界面剂对界面黏结性能的改善比水泥砂浆界面剂好。陈沛然等[9]采用钢纤维单丝拉拔试验研究了基体强度对界面黏结性能的影响,结果表明:随着基体强度的增加,峰值拉拔荷载和最大黏结强度增大。张宝静等[10]讨论了有无黏结对预应力CFRP板加固受弯构件的影响,结果表明:在变黏结状态下,预应力CFRP板加固试验梁承载能力较无黏结加固有一定提高。
以上研究从基体、增强体以及有无黏结的角度对界面黏结性能进行了探讨,鉴于此,本研究应用内聚力单元来模拟界面的力学性能,结合混凝土的塑性本构关系,来研究混凝土和界面损伤、破坏过程,分析讨论界面的抗剪强度和抗拉强度对钢纤维混凝土黏结性能的影响,可以为钢纤维混凝土工程优化设计提供参考。
1 材料的本构模型 1.1 混凝土的本构关系在ABAQUS中混凝土最常用的本构模型是混凝土损伤塑性模型(CDP模型),为了合理地应用此模型,必须要确定混凝土应力应变曲线以及受拉损伤因子、受压损伤因子等参数。由于CDP模型采用的是等向强化模型[11],线弹性阶段的初始弹性模量就取为单轴受拉开裂时的割线模量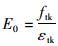
受拉时:
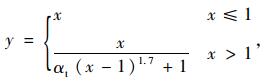
|
(1) |
式中,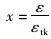
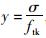
受压时:
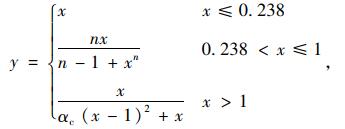
|
(2) |
式中,
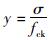
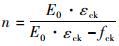
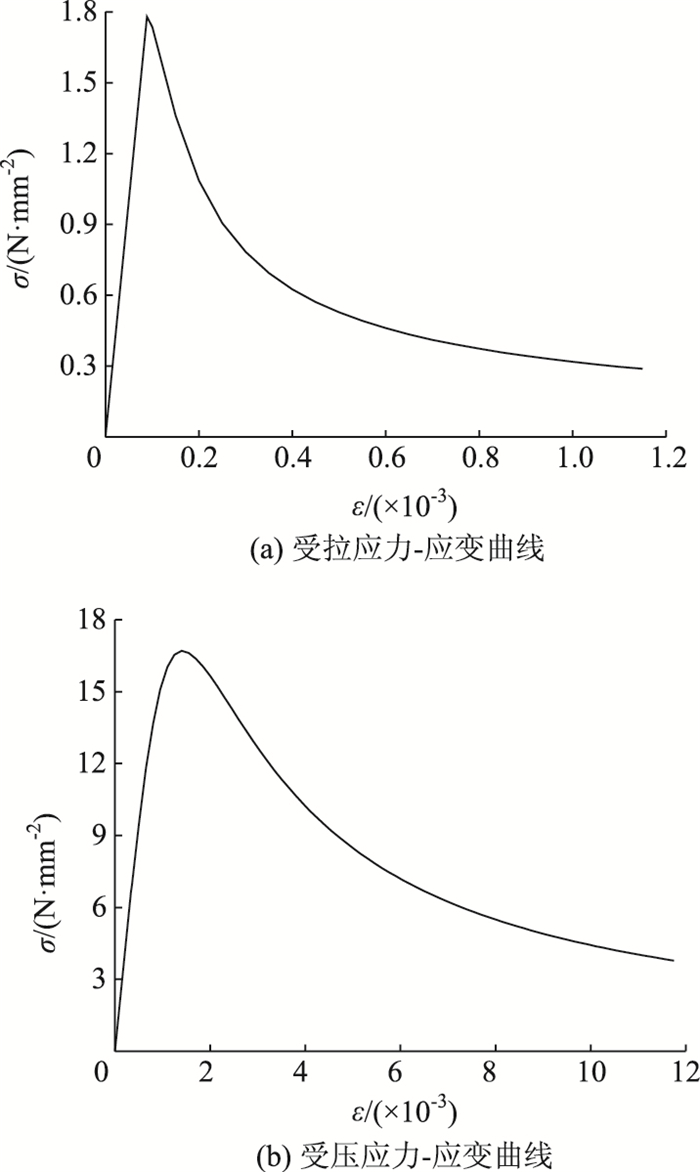
取C25混凝土,泊松比为0.2,其他参数见表 1。利用表 1中的参数以及式(1)和式(2)得到C25混凝土应力应变曲线如图 1所示。
| E0/ GPa |
ftk/ MPa |
εtk/ (×10-6) |
αt | fck/ MPa |
εck/ (×10-6) |
αc | n |
| 20 | 1.78 | 89 | 0.988 5 | 16.7 | 1 403 | 0.526 3 | 2.47 |
|
| 图 1 C25混凝土的应力应变曲线 Fig. 1 Stress-strain curves of concrete C25 |
| |
在ABAQUS中需要输入压应力、受压损伤因子与非弹性应变的关系,拉应力、受拉损伤因子与开裂应变的关系;令非弹性应变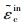
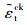
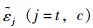
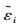
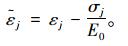
|
(3) |
文献[11]中也给出了损伤因子dj(j=t, c)的计算公式,令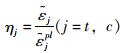

|
(4) |
在文献[14]中提供了ηj的取值范围,同时文献[11]中也给出了ηj的参考取值,在此就取ηc=0.6,ηt=0.9。根据以上公式计算出CDP模型的抗拉(压)强度-开裂应变(非弹性应变)关系及受拉(压)损伤因子-开裂应变(非弹性应变)关系,如表 2所示。除此之外,在CDP模型中还需定义屈服函数,流动法则,黏性特性相关参数[11],具体见表 3。表中,fb0/fc0为双轴与单轴抗压强度比值,K为受拉子午线与受压子午线第二应力状态不变量的比值。
| 抗压强度/ MPa |
非弹性应变/ (×10-3) |
受压损伤因子 | 抗拉强度/ MPa |
开裂应变/ (×10-3) |
受拉损伤因子 |
| 6.680 | 0.000 | 0.000 | 1.780 | 0.000 | 0.000 |
| 6.849 | 0.008 | 0.009 | 1.736 | 0.013 | 0.015 |
| 9.495 | 0.025 | 0.021 | 1.085 | 0.146 | 0.212 |
| 11.800 | 0.060 | 0.039 | 0.694 | 0.315 | 0.476 |
| 13.677 | 0.116 | 0.064 | 0.392 | 0.730 | 0.789 |
| 15.084 | 0.196 | 0.094 | 0.308 | 1.035 | 0.871 |
| 16.700 | 0.568 | 0.214 | 0.211 | 1.789 | 0.944 |
| 14.300 | 1.735 | 0.493 | 0.150 | 2.943 | 0.975 |
| 11.724 | 2.764 | 0.653 | |||
| 9.193 | 4.090 | 0.781 | |||
| 7.850 | 5.057 | 0.838 | |||
| 5.039 | 8.498 | 0.931 |
| 膨胀角 | 偏心率 | fb0/fc0 | K | 黏性系数 |
| 30° | 0.1 | 1.16 | 0.666 7 | 0.000 5 |
1.2 钢纤维的本构关系
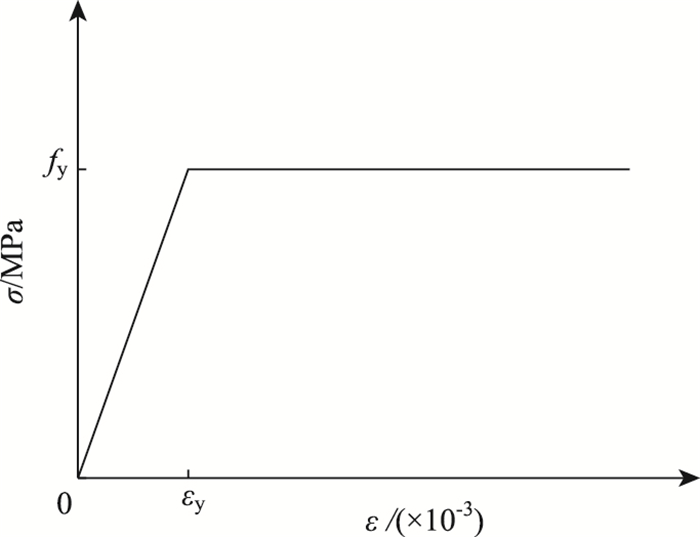
钢纤维的应力应变关系可以近似看成是钢筋的应力应变关系,钢筋的本构关系一般有3种模型[15]:理想弹塑性模型、弹性强化模型、弹塑性强化模型。由于本研究模拟界面的力学性能,并且钢纤维一般都是被拉出而不是被拔断,故钢纤维的本构关系采用理想弹塑性模型。钢纤维的弹性模量E=20 GPa,屈服强度fy=400 MPa,泊松比μ=0.25,钢纤维的应力应变关系如图 2所示。
|
| 图 2 钢纤维的理想弹塑性应力-应变关系 Fig. 2 Ideal elastic-plastic stress-strain relationship of steel fiber |
| |
1.3 内聚力单元的本构关系
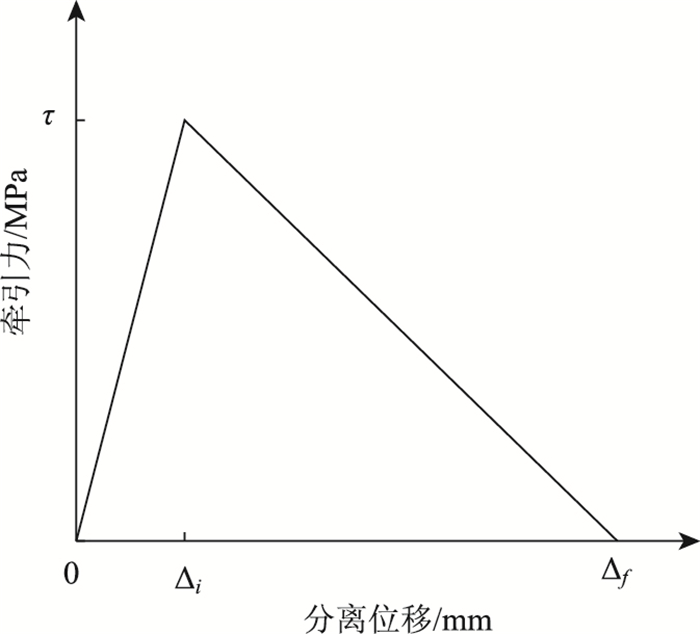
混凝土与钢纤维之间有非常薄的一层界面,采用内聚力单元对界面进行模拟;内聚力单元的本构关系就采用ABAQUS自身提供的双线性模型如图 3所示。图 3中,τ为损伤起始应力即界面的抗拉强度(抗剪强度);Δi为损伤起始位移;Δf为损伤失效位移。
|
| 图 3 内聚力单元的本构关系 Fig. 3 Constitutive relation of cohesive element |
| |
内聚力的损伤起始准则采用二次名义应力准则(Quads Damage):
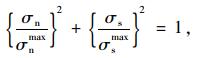
|
(5) |
式中,σnmax和σsmax分别为法向、切向的最大应力临界值;σn和σs分别为法向应力、切向应力。
内聚力的损伤演化准则采用基于能量的幂指数准则[16](Power Law Criterion):
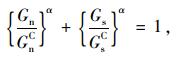
|
(6) |
式中,GnC和GsC分别为界面法向、切向的最大断裂能量;α为界面力学性能参数,一般取为1。
为了确定内聚力单元具体的本构关系,在ABAQUS中进行参数调试,一般可令Enn=Ess[17],Enn和Ess是根据建模的几何尺寸折算过来的,最终确定内聚力单元的参数如表 4所示。
| Enn/ MPa |
Ess/ MPa |
σn/ MPa |
σs/ MPa |
GnC/ (N·mm-1) |
GsC/ (N·mm-1) |
α |
| 100 | 100 | 2.5 | 2.5 | 0.2 | 0.2 | 1 |
2 数值模拟分析 2.1 模型的建立
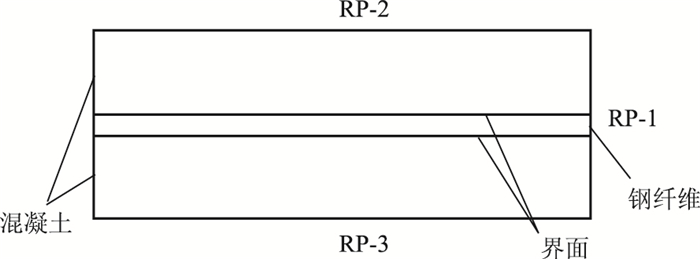
为了减少计算时间,提高收敛性,建立如图 4所示的二维有限元模型,尺寸为12 mm×4.52 mm,钢纤维的直径为0.5 mm,钢纤维与混凝土之间为界面层,厚度为0.01 mm。混凝土和钢纤维的网格精度为0.15 mm,单元类型为CPS4R;界面层的网格精度为0.01 mm,单元类型为COH2D4,采用扫掠技术沿着界面厚度进行网格划分。
|
| 图 4 钢纤维混凝土有限元模型 Fig. 4 FE model of SFRC |
| |
对钢纤维的右端耦合到参考点RP-1上,将混凝土层上端和下端分别耦合到参考点RP-2和RP-3上。进行界面抗剪模拟即单钢纤维拔出模拟时,在参考点RP-1上施加沿x方向的位移载荷,大小为0.02 mm,对混凝土层的左端和右端进行固定约束。进行界面抗拉模拟时,同样采用位移加载,在参考点RP-2沿y正方向施加的大小为0.002 mm,在参考点RP-3沿y负方向施加的大小为0.002 mm。材料属性参数的选取见表 1~表 4。
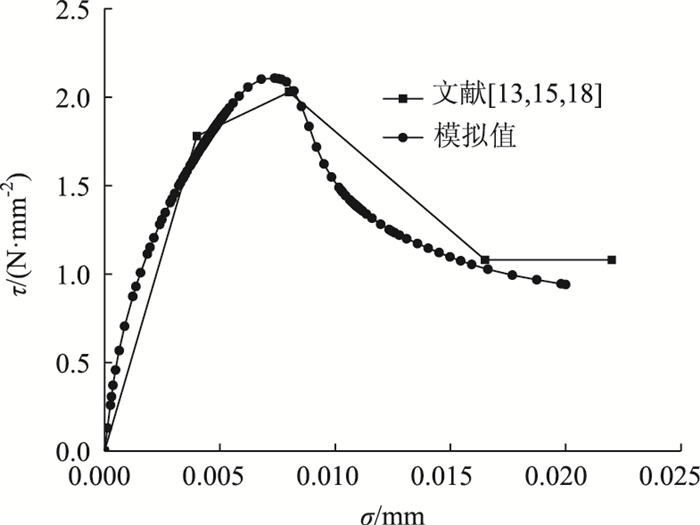
图 5为界面抗剪模拟下对得到的位移载荷曲线进行换算得到黏结应力滑移曲线模拟值,同时文献[13, 15, 18]提供了黏结应力滑移曲线的四段式模型,并稍加修正得到计算值。从图 5中可以看出上升段吻合较好,下降有误差但由于黏结应力与滑移的关系复杂性很大;并与文献[19]的试验结果(曲线分为3个阶段:完全黏结阶段、脱黏阶段和摩擦滑移阶段)相比较具有很好地一致性,故认为所建的模型是合理的。
|
| 图 5 黏结应力-滑移曲线 Fig. 5 Curves of bond stress vs. slip |
| |
2.2 界面抗剪强度影响分析
图 6给出了钢纤维拉拔最大载荷随界面抗剪强度的变化曲线,可以看出,随着界面抗剪强度的增大,最大拉力先增大后减小最后逐渐平稳;在界面抗剪强度达到2.4 MPa(1.35ftk)时,最大拉力达到最大值。

|
| 图 6 不同界面抗剪强度下的最大载荷 Fig. 6 Maximum loads under different interfacial shear strengths |
| |
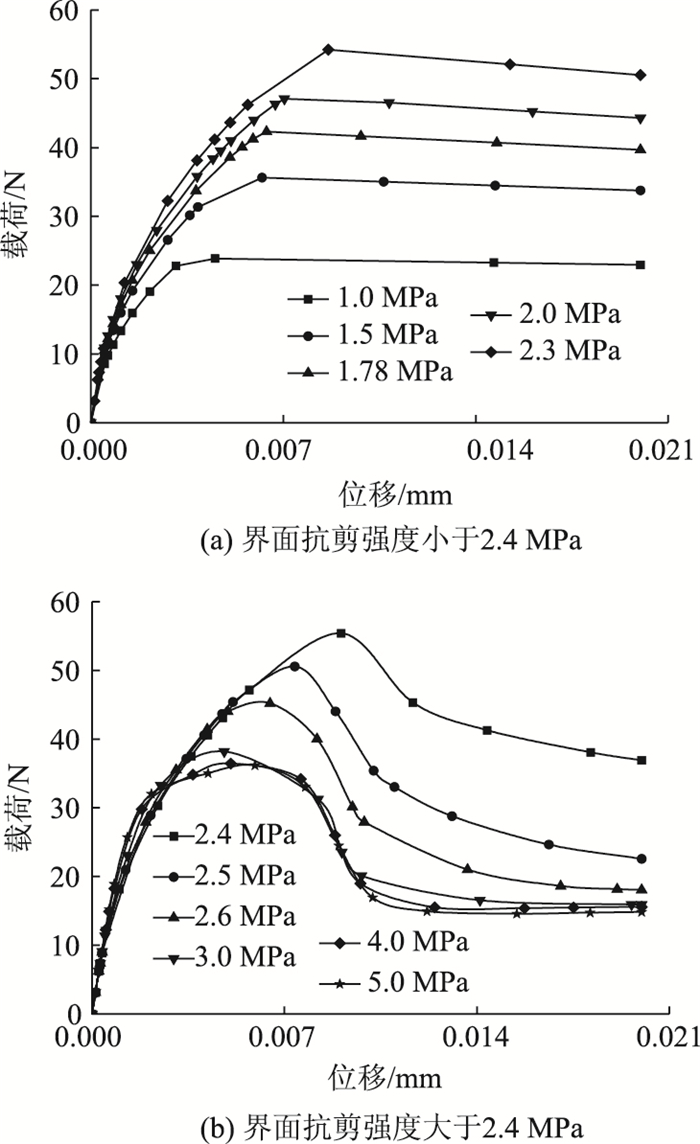
图 7(a)和图 7(b)分别为界面抗剪强度小于2.4 MPa和大于2.4 MPa的位移-载荷曲线。由图 7(a)可以看出,在相同位移载荷作用下,当界面抗剪强度小于2.4 MPa时,载荷达到最大值之后,随钢纤维拔出而平缓下降,这是由于裂纹首先在界面开始萌生,界面裂纹从右端缓慢向左端扩展,界面刚度逐渐退化,导致界面整体接近脱粘,但界面还存在一定的摩擦力;同时界面层附近的基体也出现了一定的损伤,与界面相比很微小。达到最大荷载的拔出位移也随界面抗剪强度的增大而增大。
|
| 图 7 不同界面抗剪强度的位移载荷曲线 Fig. 7 Displacement-load curves under different interfacial shear strengths |
| |
由图 7(b)可以看出,在相同位移载荷作用下,当界面抗剪强度大于2.4 MPa时,载荷达到最大值,随钢纤维的拔出在其附近出现平缓,之后急剧下降;拔出位移达到0.013 mm左右,载荷又趋于平缓。这是由于随位移载荷的缓慢增加,首先界面层右端局部出现损伤,但界面层的刚度退化微小,传递应力的性能影响不大,将纤维层的应力被传递到界面层附近的混凝土层。由于混凝土的抗拉强度小于界面抗剪强度,混凝土层迅速出现损伤,并沿着界面向左端扩展,刚度也随之退化,最终导致了界面附近的混凝土层几乎失效,但还具有非常微弱的承载能力。达到最大载荷的拔出位移也随界面抗剪强度的增大先减小后几乎保持不变。
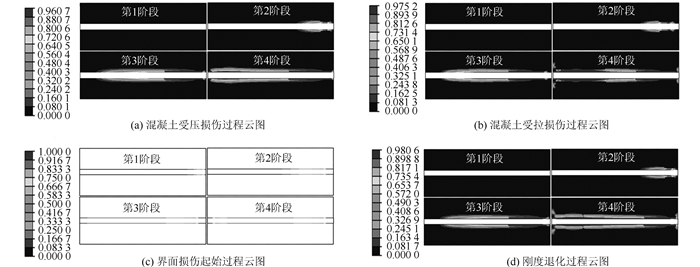
图 8显示了界面抗剪强度为5 MPa的钢纤维混凝土有限元模型在随位移变化的基体受拉、受压损伤,界面损伤起始,刚度退化云图分布情况。从各阶段的云图中可以看出首先由于界面附近的基体层受压造成损伤,并且界面右端有微弱的损伤起始;但基体层刚度也开始退化,而界面并没有退化。随着位移的增加,基体层损伤沿着界面附近从右端逐渐传递到左端,刚度退化主要是受拉损伤引起的;而界面局部出现损伤,并且在最右端也有了一定的刚度退化。
|
| 图 8 界面抗剪模拟试样损伤破坏过程 Fig. 8 Damage failure processes of interfacial shear simulation specimens |
| |
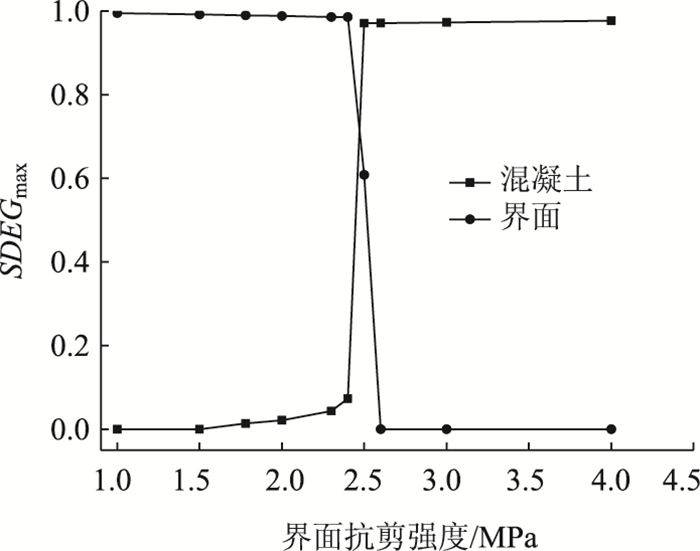
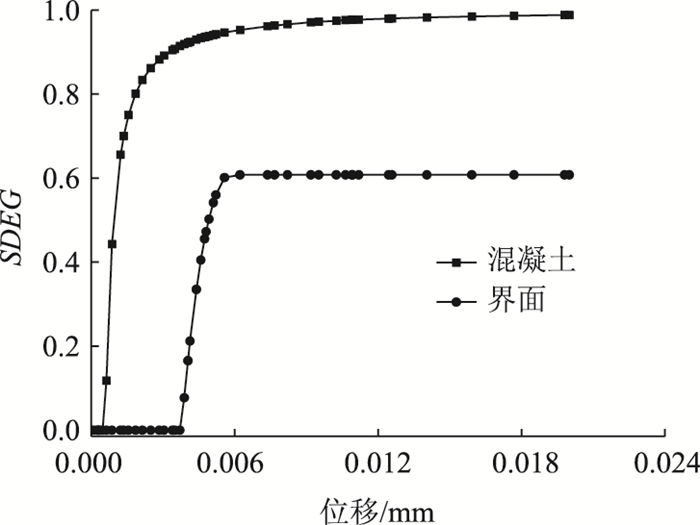
图 9是混凝土和界面某相邻节点的刚度退化参数(SDEG)的最大值随界面抗剪强度的变化关系,可以看出界面抗剪强度小于1.5 MPa(0.84ftk)时,混凝土层刚度没有退化,而界面的SDEG几乎达到1;界面抗剪强度在1.5~2.5 MPa(1.40ftk)之间,界面刚度仍然退化严重,混凝土层刚度有微弱的退化,但主要由于界面的失效造成钢纤维被拉出;界面抗剪强度大于2.5 MPa时,混泥土的SDEG接近于1,而界面刚度没有退化,这是因混凝土层失效而引起钢纤维被拉出。图 10显示了界面抗剪强度为2.5 MPa的混凝土和界面某相邻节点的SDEG随位移的变化,可以看出混凝土层首先开始损伤从而造成刚度退化,当SDEG即将达到0.9时,界面才开始出现刚度退化;随着钢纤维逐渐被拉出,界面刚度最终退化了60%,而混凝土层逐渐趋于0,这说明混凝土层的失效造成钢纤维被拉出。
|
| 图 9 某相邻节点的最大SDEG与界面抗剪强度关系 Fig. 9 Relationship between maximum SDEG and interfacial shear strength of an adjacent node |
| |
|
| 图 10 界面抗剪强度为2.5 MPa的刚度退化与位移关系 Fig. 10 Relationship between stiffness degradation and displacement when interfacial shear strength is 2.5 MPa |
| |
2.3 界面抗拉强度影响分析
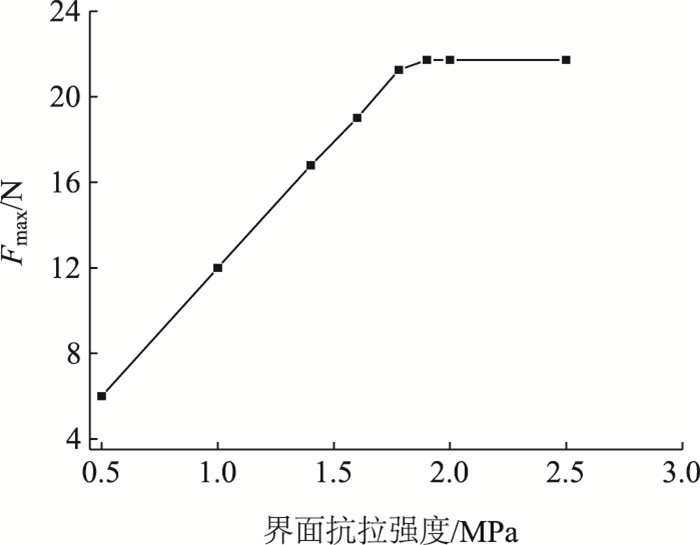
图 11显示的是最大横向载荷与界面抗拉强度的关系,可以看出在界面抗拉强度小于1.9 MPa(1.07ftk)时,最大横向载荷随界面抗拉强度增大呈线性增大;而界面抗拉强度大于1.9 MPa,最大横向载荷保持不变。
|
| 图 11 最大横向载荷与界面抗拉强度的关系 Fig. 11 Relationship between maximum transverse load and interfacial tensile strength |
| |
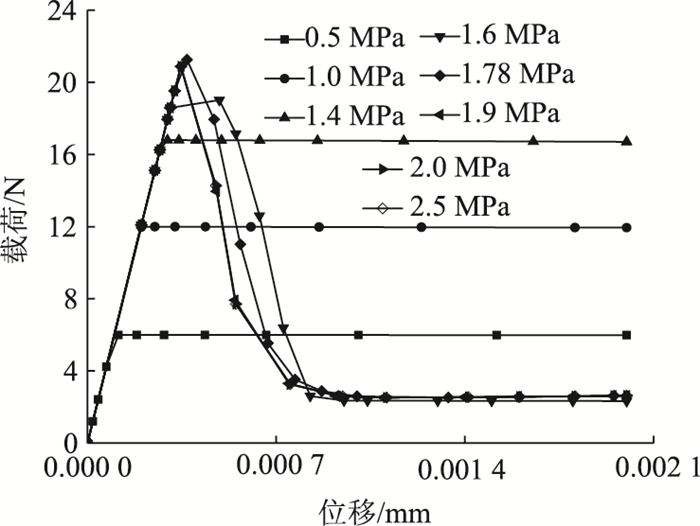
图 12给出了不同界面抗拉强度的位移-载荷曲线,在界面抗拉强度小于1.4 MPa(0.79ftk)时,载荷达到最大值之后平缓的下降,这是因为应力从上下两端传递到界面处,在混凝土层的四角出现了应力集中,由于界面抗拉强度不足,首先在界面中端出现损伤起始,并向界面两端扩展,直至界面层脱粘。在界面抗拉强度大于1.4 MPa时,载荷达到最大值急剧下降,之后又趋于平稳,这是由于混凝土层从产生应力集中的四角首先产生塑性变形而引起刚度退化,之后在混凝土层沿某一路径扩展造成刚度逐渐退化接近于0,最终造成混凝土层首先破坏。
|
| 图 12 不同界面抗拉强度的位移载荷曲线 Fig. 12 Displacement-load curves under different interfacial tensile strengths |
| |
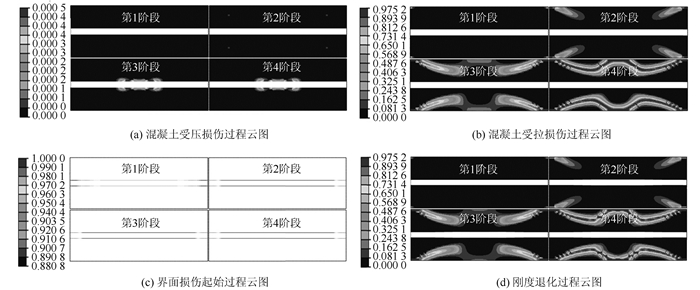
图 13显示了界面抗拉强度为1.78 MPa的钢纤维混凝土有限元模型在随位移变化的基体受拉、受压损伤,界面损伤起始,刚度退化云图分布情况。从以下各阶段云图可以看出,起初在界面和基体层都产生了损伤,但刚度退化首先是因基体层受拉损伤而引起的,微弱的受压损伤主要集中在界面附近。随着位移增加,由于基体受拉造成的裂纹沿着某一路径开始扩展,直至基体层失去承载能力,而界面的刚度退化很微小;此时基体受压损伤仍然集中在界面附近,且很微小。
|
| 图 13 界面抗拉模拟试样损伤破坏过程 Fig. 13 Damage failure processes of interfacial tensile simulation specimens |
| |
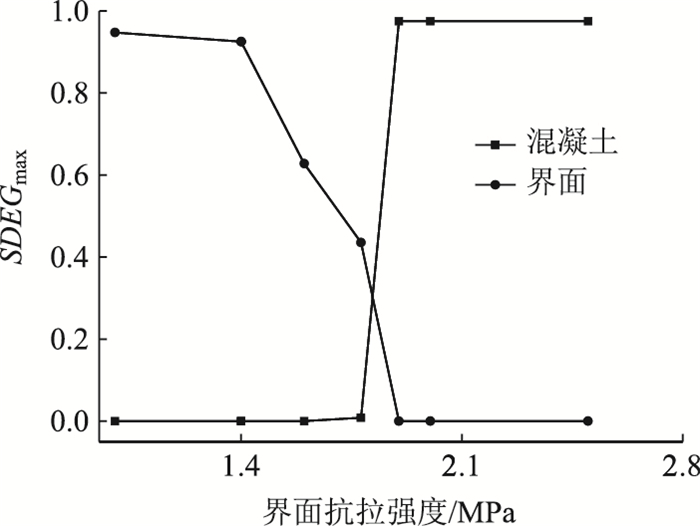
混凝土和界面某相邻节点的刚度退化参数最大值随界面抗拉强度的变化关系如图 14所示,可以看出,界面抗拉强度小于1.4 MPa时,界面的SDEG接近于1,而混凝土的SDEG为0;界面抗拉强度大于1.9 MPa时,混凝土的SDEG逼近于1,而界面的SDEG仍为0,这是由于混凝土的SDEG趋近1,造成材料整体承受荷载的能力急剧下降。图 15给出了界面抗拉强度为1.78 MPa的混凝土和界面的SDEG随位移的变化情况,可以看出首先是混凝土刚度开始退化的,之后界面刚度也逐渐退化,但混凝土刚度逐渐退化接近于0,而界面退化不到50%,这说明混凝土失去了承载能力导致材料整体失效。
|
| 图 14 某相邻节点的最大SDEG与界面抗拉强度关系 Fig. 14 Relationship between maximum SDEG and interfacial tensile strength of an adjacent node |
| |

|
| 图 15 界面抗拉强度为1.78 MPa的刚度退化与位移关系 Fig. 15 Relationship between stiffness degradation and displacement when interfacial tensile strength is 1.78 MPa |
| |
3 结论
本研究基于内聚力单元和CDP模型对单根纤维与混凝土基体之间界面的强度进行了模拟,讨论分析了钢纤维混凝土材料的损伤和破坏过程随界面抗拉强度和抗剪强度的变化规律。主要结论如下:
(1) 界面的抗剪强度为1.35ftk左右、抗拉强度为1.07ftk左右,钢纤维和混凝土的黏结效果最好,承载能力最强。
(2) 当界面抗剪强度小于0.84ftk时,界面发生失效,基体并没有损伤;在0.84ftk~1.40ftk之间主要是界面发生失效,但基体也有微弱的刚度退化;大于1.40ftk时,基体发生失效,界面层有微小的刚度退化。
(3) 当界面抗拉强度小于0.79ftk时,界面发生失效,基体并没有损伤;在0.79ftk~1.07ftk之间首先基体发生损伤并逐渐刚度退化为0,而界面也出现一定的刚度退化,但主要是由于基体发生失效;大于1.07ftk时,基体发生失效,界面有微小损伤起始但没有刚度退化。
(4) 本研究结果可为钢纤维混凝土的界面黏结优化设计提供参考,但在细观力学的基础上将混凝土仅视为单相材料,同时只考虑了圆直型钢纤维是本研究不足之处;今后可在本研究基础上,将混凝土视为三相材料:骨料、砂浆和两者之间界面,研究其他类型的钢纤维对界面强度以及界面断裂性能的影响等问题。
| [1] |
赵丹. 钢纤维混凝土性能及其应用[J]. 现代矿业, 2011, 27(10): 110-111. ZHAO Dan. Properties and Application of Steel Fiber Concrete[J]. Modern Mining, 2011, 27(10): 110-111. |
| [2] |
刘瑞. 钢纤维混凝土的性能及其应用[J]. 江西建材, 2016(14): 4, 7. LIU Rui. Properties and Application of Steel Fiber Concrete[J]. Jiangxi Building Materials, 2016(14): 4, 7. |
| [3] |
梅迎军, 赵翔, 代超, 等. 弯曲荷载作用下钢纤维聚合物混凝土疲劳寿命[J]. 公路交通科技, 2015, 32(9): 20-25. MEI Ying-jun, ZHAO Xiang, DAI Chao, et al. Fatigue Life of Steel Fiber Reinforced Polymer Concrete under Bending Load[J]. Journal of Highway and Transportation Research and Development, 2015, 32(9): 20-25. |
| [4] |
尚秀琳. 纤维增强水泥混凝土中纤维-基体界面区研究综述[J]. 建筑工程技术与设计, 2017(18): 3384-3384. SHANG Xiu-lin. Summary of Study on Fiber-matrix Interfaces in Fiber Reinforced Cement Concrete[J]. Architectural Engineering Technology and Design, 2017(18): 3384-3384. |
| [5] |
王术飞. 钢纤维在水泥基复合材料中黏结性能的研究进展[J]. 公路工程, 2019, 44(4): 279-284. WANG Shu-fei. Research Progress on Bonding Properties of Steel Fiber in Cement-based Composites[J]. Highway Engineering, 2019, 44(4): 279-284. |
| [6] |
王家赫, 张君, 于蕾, 等. 钢丝与混凝土黏结拔出行为的试验与模拟[J]. 工程力学, 2016, 33(6): 202-208. WANG Jia-he, ZHANG Jun, YU Lei, et al. Test and Simulation on Pull-out Behavior of Steel Wire in Concrete[J]. Engineering Mechanics, 2016, 33(6): 202-208. |
| [7] |
ABBAS M Y, KHAN M I. Fiber-matrix Interfacial Behavior of Hooked-end Steel Fiber-reinforced Concrete[J]. Journal of Materials in Civil Engineering, 2016, 28(11): 04016115. |
| [8] |
何桥敏, 周丽. 不同钢纤维掺量及黏结剂对混凝土性能的影响[J]. 中外公路, 2018, 38(5): 267-270. HE Qiao-min, ZHOU Li. Effect of Different Steel Fiber Contents and Binders on Concrete Properties[J]. Journal of China & Foreign Highway, 2018, 38(5): 267-270. |
| [9] |
陈沛然, 张亚芳, 李根. 基体强度对钢纤维单丝拉拔性能的影响[J]. 中山大学学报: 自然科学版, 2013, 52(6): 68-74, 80. CHEN Pei-ran, ZHANG Ya-fang, LI Gen. Effect of Matrix Strength on Properties of Steel Single Fiber Pull-out Test[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni: National and Science Edition, 2013, 52(6): 68-74, 80. |
| [10] |
张宝静, 尚守平. 变黏结预应力CFRP板加固受弯构件试验研究[J]. 公路交通科技, 2018, 35(11): 61-68. ZHANG Bao-jing, SHANG Shou-ping. Experimental Study on Flexural Member Strengthened with Variable Bonded Prestressed CFRP Plates[J]. Journal of Highway and Transportation Research and Development, 2018, 35(11): 61-68. |
| [11] |
刘巍, 徐明, 陈忠范. ABAQUS混凝土损伤塑性模型参数标定及验证[J]. 工业建筑, 2014, 44(增1): 167-171, 213. LIU Wei, XU Ming, CHEN Zhong-fan. Parameters Calibration and Verification of Concrete Damage Plasticity Model of ABAQUS[J]. Industrial Construction, 2014, 44(S1): 167-171, 213. |
| [12] |
张战廷, 刘宇锋. ABAQUS中的混凝土塑性损伤模型[J]. 建筑结构, 2011, 41(增2): 229-231. ZHANG Zhan-ting, LIU Yu-feng. Concrete Damaged Plasticity Model in ABAQUS[J]. Building Structure, 2011, 41(S2): 229-231. |
| [13] |
GB 500101—2010, 混凝土结构设计规范[S]. GB 500101—2010, Code for Design of Concrete Structures [S]. |
| [14] |
张劲, 王庆扬, 胡守营, 等. ABAQUS混凝土损伤塑性模型参数验证[J]. 建筑结构, 2008, 38(8): 127-130. ZHANG Jin, WANG Qing-yang, HU Shou-ying, et al. Parameters Verification of Concrete Damaged Plastic Model of ABAQUS[J]. Building Structure, 2008, 38(8): 127-130. |
| [15] |
过镇海. 钢筋混凝土原理[M]. 3版. 北京: 清华大学出版社, 2013. GUO Zhen-hai. Principle of Reinforced Concrete[M]. 3rd ed. Beijing: Tsinghua University Press, 2013. |
| [16] |
刘万雷, 常新龙, 张晓军, 等. 基于细观有限元方法的复合材料横向力学性能分析[J]. 材料工程, 2016, 44(11): 107-113. LIU Wan-lei, CHANG Xin-long, ZHANG Xiao-jun, et al. Analysis of Composite Transverse Mechanical Properties Based on Micromechanical Finite Element Method[J]. Journal of Materials Engineering, 2016, 44(11): 107-113. |
| [17] |
张洪峰. 内聚力单元参数影响因素研究[J]. 科技创新导报, 2018, 15(16): 4-8. ZHANG Hong-feng. Study on Influencing Factors of Cohesion Element Parameters[J]. Science and Technology Innovation Herald, 2018, 15(16): 4-8. |
| [18] |
袁敬. 钢纤维混凝土界面黏结机理及细观力学有限元分析[D]. 河北: 河北工业大学, 2007. YUAN Jing. Bonding Mechanism of SFRC Interface and FEM Analysis on Micromechanics[D]. Hebei: Hebei University of Technology, 2007. |
| [19] |
DENG F Q, DING X X, CHI Y, et al. The Pull-out Behavior of Straight and Hooked-end Steel Fiber from Hybrid Fiber Reinforced Cementitious Composite: Experimental Study and Analytical Modelling[J]. Composite Structures, 2018, 206: 693-712. |
 2021, Vol. 38
2021, Vol. 38
