扩展功能
文章信息
- 马瑞民, 姚立飞
- MA Rui-min, YAO Li-fei
- 基于双边理论的顺风车稳定匹配优化
- Optimization of Ride-sharing Stable Matching Based on Two-side Theory
- 公路交通科技, 2021, 38(4): 131-141
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(4): 131-141
- 10.3969/j.issn.1002-0268.2021.04.016
-
文章历史
- 收稿日期: 2020-06-10
2. 广东财经大学 地理与旅游学院, 广东 广州 510320
2. School of Geography and Tourism, Guangdong University of Finance and Economics, Guangzhou Guangdong 510320, China
私人小汽车保有量持续增加,座位占用率却一直很低下。截至2019年底,我国私人汽车拥有量达2.32亿辆,其中载客汽车1.89亿辆,但从平均保有量来讲相比美国等发达国家仍然较低,这意味着我国私人汽车保量很有可能将会持续增加。但是,目前私人小汽车出行的座位占用率仍然很低。据调查北京市在上下班高峰期80%的私家车上都只有一个人[1],整个交通网络中的私人汽车座位的使用率极低。由此可见,如果能够充分挖掘这部分交通网络中尚未使用交通运输能力,将对整个交通系统产生巨大的作用,而这也正是顺风车的兴起的契机。
移动互联平台、智能手机及GPS等技术的普及为顺风车提供了新的机遇,目前已经有很多平台提供顺风车出行服务,如美国的UberX和Lyft,欧洲的BlaBlaCar以及国内的滴滴出行和嘀嗒出行等等。顺风车出行是一种灵活的交通方式,平台中司机和乘客给出出发时间及起止点,有平台自动对其进行匹配并具有固定的费用计算规则,一旦匹配成功平台将对司乘双方告知信息。顺风车出行与传统的出租车出行是不同的,顺风车出行不以盈利为目的,旨在司乘双方的出行费用节省,且顺风车出行中司乘双方都是平台的顾客,双方都可根据其偏好自主选择一起出行。司机与乘客之间的匹配是顺风车出行中的一个关键问题。大多数研究将问题表述为具有不同系统优化目标的集中分配问题,如最小化总运行距离[2-4]、最小化总运行时间[5]、最大化系统匹配数量[6-7]等,且系统最优化匹配求解方法也是多种多样,有精确算法[8-9]、遗传算法[10]、贪婪算法[11]以及蜂群算法[12]等。但系统最优并不一定是参与者个人的最佳选择,在顺风车出行平台中参与者是独立的、利己的个体,如果他们相信存在更好的匹配,他们将拒绝平台给出的匹配方案,接着去寻找更好的匹配对象或直接转向其他的出行平台,即平台给出的匹配方案并不稳定。
稳定匹配的一个基本问题是众所周知的稳定婚姻问题(Stable Marriage Problem, SMP),它是由Gale和Shapley在1962年的开创性论文中首次提出的[13]。针对SMP提出了一种延迟接受算法(DA),该算法可以为任何稳定的婚姻问题找到至少一个稳定的匹配解。然后,越来越多的SMP变体被提出[14]。在本研究中,往往存在参与者中的某一方因时间窗约束不接受方案或因成本分配不接受方案,而这些参与者是不会出现在偏好列表中的,即在顺风车匹配问题中偏好列表是不完全的。此外,参与者在不同的匹配中可能获得相同的利益,并不严格地偏好其中一种匹配。综上,本研究将从参与者个体角度出发,引入稳定性概念,构建司乘双方稳定匹配模型,并提出相对应的启发式算法提高模型求解速度。
1 问题描述一些学者已经构建了相关的顺风车匹配系统最优化模型[2]:
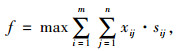
|
(1) |
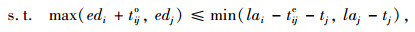
|
(2) |
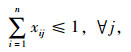
|
(3) |
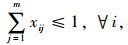
|
(4) |
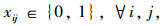
|
(5) |
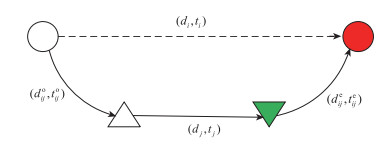
式(1)为目标函数,其中sij=(di+dj)-(dijo+dj+dije)表示司机i与乘客j拼车后所贡献的距离节省,di, dj分别表示司机i和乘客j起点到终点的原始距离;dijo为司机i起点到乘客j起点的距离;dije为乘客j终点到司机i终点的距离。式(2)为时间窗约束,每一对可行的匹配之间肯定存在以下的时间约束:(1) 司机的最大可用时间必须不能小于完成合乘路线所需要的总时间;(2) 司机行驶到乘客起点的时间窗与乘客出发的时间窗是有交叉的,即至少存在一个时间点能够满足司机顺利接到乘客,其中ti和tj分别为司机i和乘客j起点到终点的原始时间,tijo为司机i起点到乘客j起点的时间,tije为乘客j终点到司机i终点的时间,edi, lai和edj, laj分别表示司机i和乘客j最早出发时间和最晚到达时间。式(3)~(5)为0-1变量约束,该模型研究的是单司机单乘客匹配模型,即一个司机在同一时间只能搭载一个乘客,一个乘客在同一时间也只能乘坐一个司机的车。
上述模型旨在实现系统最优化的目标,即系统中所有车辆的总行驶距离最小化或系统中所有车辆总行驶时间最小化,但并未考虑匹配双方的成本分配,在系统最优模型的方案中有可能出现司机的匹配出行的成本还高于单独出行的成本的情况。从参与者个体角度来看,系统最优化模型给出的方案对参与者来说并不是最佳选择的选择。
2 顺风车出行稳定匹配模型首先建立稳定匹配问题的线性规划模型,并寻找出一个最优的稳定匹配解,记为fsta。对于平台而言,获利来源于匹配成功之后的距离节省s,假设平台从每一对成功匹配都得到一个固定比例的利润,令平台获利比例为η。
2.1 模型假设A1:一个司机只能载一个乘客,一个乘客也只能搭乘一个司机的车。
A2:乘客与司机的出行成本完全取决于车辆的行驶距离。
A3:如果参与者没有找到合适的匹配对象,将独自开车出行。
A4:参与者对成本理性,所有可行的匹配都是对参与者有成本节省的。
A5:参与者知道所有潜在匹配对象的信息。
2.2 参与者偏好序(1) 参与者效用函数构建
在本研究中共享出行参与者的成本分为两个部分:距离成本和时间机会成本。
假设(i, j)是最优稳定解中的一个匹配对,那么(i, j)的距离节省为sij,记平台获利为φij,那么平台因为司机i和乘客j匹配的获利为φij=α·η·sij。令司机i的时间机会成本为wti=ω·(tijo+tj+tije-ti),乘客j的时间机会成本为wtj=ω·max(0, edi+tj-edj),其中ω表示单位时间的工资水平,令ui(i, j), uj(i, j)分别代表匹配对(i, j)中司机i与乘客j的成本效用值,那么效用值计算式可以表示为:
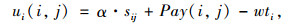
|
(6) |
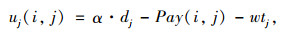
|
(7) |
式中α表示单位距离的成本;Pay(i, j)为乘客j向司机i支付的车费。而Pay(i, j)的确定必须考虑参与者之间的具体成本分配方式,不同的分配方式Pay(i, j)是不一样的。
目前关于单司机单乘客匹配模型中成本分配机制主要分为4种:(1) Geisberger等(2009) 提出平均分配司机与乘客合乘段的成本[15];(2)Kleiner等(2011)提出平均分配总的行驶距离[16];(3)Wang等(2013)提出平均分配可行匹配的成本节省[17];(4)Agtaz等(2011)按原始距离比例进行参与者之间的成本分配[2]。采用原始距离比例进行参与者之间的成本分配,则有:
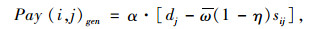
|
(8) |
式中ω为成本节省的分配比率,ω=dj/(di+dj)。
(2) 参与者效用值排序
由于参与者是理性的,即拼车出行成本必须小于自己驾驶出行的成本,令自己出行的效用值u(p, p)=0,即若参与者没有因为参与到共享出行平台而有所改变或获得利益,参与者将自己出行。
所有参与者最终有两种匹配结果,第1种是存在可行的匹配对象并且匹配成功,此时效用值ui(i, j)>0&uj(i, j)>0, ∀k∈I, l∈J;第2种是有可接受的匹配对象但是没有匹配成功或者没有接受的匹配对象,此时效用值不大于0,即-(ui(i, j)>0&uj(i, j)>0), ∀k∈I, l∈J,这一类匹配对象将会直接从该参与者的偏好序中删除。那么此时视为参与者与自己进行匹配。下面将参与者的偏好序定义为:
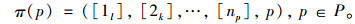
|
(9) |
π(p)是根据参与者p的效用值进行排序得到的一个偏好序列,下面以具体例子具体说明偏好序中各个符号的意义。例如用π(j)=([1l], [2k], …, [ni], j)为乘客j的偏好序,那么[1l]为司机l∈I处在乘客j偏好序的首位,即对乘客j来说,司机l就是其最佳选择;其中元素[ni]表示潜在的可接受的匹配对象处在列表π(j)的第n个位置,n也表示可行的匹配对象的数量。在偏好序的最后一个位置是参与者自己,表示如果参与者没有找到可行的匹配对象,那么他将独自开车出行或继续留在平台上等待匹配,直到他发布的出行信息过期(超出预计的出发时间)。令j≻ij′表示司机i严格偏好乘客j于j′,同理,i≻ji′表示司机j严格偏好乘客i于i′。如果司机i与乘客j之间的偏好关系满足i≻jj,那么对乘客j来说司机i是一个潜在的匹配对象,同理,j≻ii表示乘客j是司机i的潜在接匹配对象。如果司机i与乘客j之间的偏好关系满足i≻jj且j≻ii,那么(i, j)是一个可行的匹配对。
由上述分析我们可以对偏好序中的参与者分为两类,第1类是存在可行的匹配对象并且匹配成功,这一类的司机与乘客分别记为I(j)∈I和J(i)∈J;第2类是有可接受的匹配对象但是没有匹配成功或者没有接受的匹配对象,这一类分别的匹配对象就是参与者自己,记为{i}和{j}。令M=I(j)∪{j}表示乘客j, j∈J的策略空间,令W=J(i)∪{i}表示司机i, i∈I的策略空间。令ψ表示可行匹配对(i, j)的集合,其中i∈M,j∈W。
从上述分析中可以知道,对于任何一个匹配对(i, j)∈ψ(其中i∈M,j∈W)都是可行的,也就是说(i, j)满足了对应的时间窗口约束,同时考虑了司乘双方的成本分配问题,(i, j)也能满足匹配后的出行成本小于或等于匹配前的出行成本的成本约束。于是,可以将系统优化模型式(1)~(5)转化为:
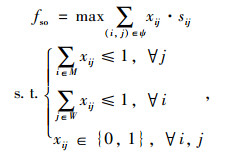
|
(10) |
式中fso是考虑参与者之间成本分配后的系统最优值,模型(10)能够保证参与者之间成本分配后个人成本节省是非负的,即保证了出行成本会有减少,但是并不能解决前文所提到的稳定匹配。
2.3 稳定优化模型对于参与者来说,系统可能会存在一些无差异偏好序列,即对着某个参与者来说,存在多个匹配对象的偏好一样。如此一来,这个参与者将有一个不严格偏好序,为了解决这个问题,Vate和Roth等提出的线性规划方法对该问题进行求解。稳定匹配模型如下[18-19]:
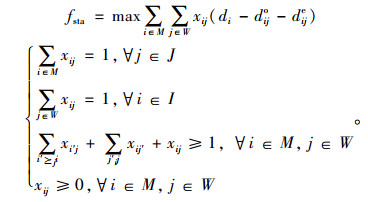
|
(11) |
对于小规模的匹配问题求解稳定最优解时,可以采用CPLEX进行求解,但是存在以下两个问题:(1) 本研究要处理的是顺风车共享出行参与者之间的匹配,涉及的参与者数量会比较大,而且要求匹配迅速及时。(2) Vate和Roth的优化模型中,仍然以系统最优化为目标,并没有考虑参与者个人的满意程度。因此,要将Vate和Roth等提出的线性规划方法应用到现实,就只能考虑将该线性规划模型的可行域空间尽可能地缩小,这正是本研究研究的重点问题。
3 模型求解 3.1 可行域空间缩减方法当参与者的数量较小时,可以对模型(11)直接进行最优解求解,但是本研究需要处理的是共享出行平台较大批量的司机与乘客的出行匹配,需要短时间进行大批量的匹配,如果不能对模型的可行域进一步地缩减,很难满足现实中的需求。
3.1.1 偏好列表相关理论定义1[19]: 一对一的司机乘客匹配可以定义为从参与者全集到参与者全集的一种单射关系,μ: M∪W→M∪W,对任意的i∈M和j∈W,满足以下关系:
(1) μ(i)=j当且仅当μ(j)=i,此时i和j是匹配对,记为(i, j);
(2) 如果μ(i)∉M,则μ(i)=i,此时i是没有匹配上的,记为(i, i);
(3) 如果μ(j)∉W,则μ(j)=j,此时j是没有匹配上的,记为(j, j)。
其中,根据μ确定的所有匹配对的集合称为匹配方案μ。
定义2: 一对一双边匹配μ: M∪W→M∪W,对任意的i∈I和j∈J,如果i和j满足i≻jμ(j)且j≻iμ(i),则称(i, j)是匹配方案μ的一个阻碍对。
定理1假设γ和γ′表示偏好结构,且满足γ′±Iγ。令μ和μ′表示相对应的稳定匹配,Mμ(Mμ′)表示偏好μ于μ′(偏好μ′于μ)的司机的集合,同样的道理,令Wμ (Wμ′)表示偏好μ于μ′ (偏好μ′于μ)的乘客的集合。那么,μ′和μ与Mμ′和Wμ之间是一种双射关系。
证明:假设i∈Iμ′。因为μ′≻iμ,则有μ′(i)≻iμ(i)≻ii,所以μ′(i)∈W。令j=μ′(i),因为μ, μ′是稳定匹配,那么在μ, μ′中是不会存在阻碍对(i, j)的,即μ′(j)≻jμ(j)是不成立的。因此j∈Wμ,μ′(Mμ′)⊂Wμ。
另一方面,假设j∈Wμ,同样的,有μ(j)≻jμ′(j)≻jj,因此μ(j)∈M。令μ(j)=i,因为μ, μ′是稳定匹配,那么在μ, μ′中是不会存在阻碍对(i, j)的,即μ(i)≻iμ′(i)是不成立的。因此i∈Mμ′,μ(Wμ)⊂Mμ′
由于μ′和μ都是单射,且Mμ′和Wμ都是有限集,则可以得出,μ′和μ与Mμ′和Wμ之间是一种双射关系。证毕。
定理2假设μ是任意的一个稳定匹配,S(μ)为与司机成功匹配的乘客的集合,n(μ)为与司机成功匹配的乘客的数量。则有,在所有的稳定匹配中,成功匹配的乘客的集合S(μ)和数量n(μ)都是一致的。
证明:采用反证法证明。假设偏好结构满足γ′=γ,司机i在稳定匹配μ′中是成功匹配的,但是不在匹配μ中。则有i∈Mμ′,根据定理1可知,μ(Wμ)⊂Mμ′,即Wμ通过μ与Mμ′形成一种映射关系,那么司机i也必然在稳定匹配μ中,这与假设矛盾,因此命题成立。证毕。
推论1:假设μ是通过GS算法司机-optimal求解的稳定匹配方案,(i, j)是μ中的一个匹配对,且j的偏好序列可以表示为:π(j)=([1],…,[i], [i]+1,…,[k], [nj], j),那么将位置[i]+1到位置[nj]+1之间的偏好信息从乘客j的偏好序中删除对匹配方案没有影响。同理,假设μ′通过GS算法乘客-optimal求解的稳定匹配方案,类似地对司机列表进行删减,对整个匹配方案没有影响。
证明:采用反证法证明。先证明通过司机-optimal的GS算法对乘客列表进行删减对匹配方案没有影响。令μ是通过GS算法司机-optimal求解的稳定匹配方案,(i, j)是μ中的一个匹配对,假设对乘客j的偏好序进行删减对匹配方案有影响,通过定理1和定理2,可以知道所有匹配中,在方案μ中匹配成功的个体,在其他稳定匹配方案中必然会匹配成功。那么说明在至少存在另一个稳定匹配方案μ′,使得(k, j)和(i, l)同时成立。因为在乘客j的偏好序中司机k的位置是在司机i后面的,则有i≻jk,而由于是通过GS算法实现的司机-optimal的匹配方案,那么u≻iu′,即j≻il,由此定义3可知,(i, j)将会是匹配方案μ′的一个阻碍对,这与假设矛盾。因此命题成立。
同理,通过乘客-optimal的GS算法对司机列表进行删减也不会对匹配方案产生影响。证毕。
3.1.2 Delete算子构建将DA算法应用到顺风车司机与乘客的匹配模型中,司机-Optimal延迟接受算法(DODA)得到的匹配方案对司机来说是最优的,但是对乘客来说却是最差的一种匹配方案。反之,乘客-Optimal延迟接受算法(RODA)的流程,得到的匹配方案对乘客来说是最优的。
(1) Delete算子
DA算法是Delete算子的核心组成组成部分,利用Delete算子可以对匹配双方的偏好列表有效地进行精简,记经过Delete算子精简之后的偏好序为π(p)gs。用一个列表来汇集所有司机的偏好序,这里称这个列表为司机偏好列表,记为pl(d),pl(d)=[π(1);π(2);…; π(i); …; π(m)], i∈I。同理记乘客的偏好列表为pl(r),则有pl(r)=[π(1);π(2);…; π(j); …; π(n)], j∈J。偏好序的精简过程如图 2所示。第1步,使用MODA算法后发现d3与r5成功匹配,那么根据推论1可知,将乘客r5偏好序中位于d3位置之后的元素(即排序在5以后的元素)删除,对匹配结果没有影响。因为乘客r5偏好序中位于d3位置之后的元素都已经删除,这意味着乘客r5与d3位置之后的司机都不可能进行匹配,反之,司机d2和d6也不可能与乘客r5进行匹配,即可以将r5从司机d2和d6的偏好序中删除。依此类推对所有乘客和司机的偏好序进行初次精简。第2步,使用WODA算法对司机偏好序进行精简,如图 2所示,此时(r4, d3)是WODA算法求解的稳定匹配方案中的一个匹配对,根据推论1可知,对司机d3偏好序中位于r4位置之后的元素进行删除,对匹配结果没有影响。与第一步精简方法同理,r4位置之后的元素r8, r7, r6的偏好序中也可以进一步将d3删除。
|
| 图 1 司机i与乘客j之间的拼车出行 Fig. 1 Carpooling between driver i and passengers j |
| |

|
| 图 2 Delete算子对偏好序精简过程 Fig. 2 Process of reduction of preference order by Delete operator |
| |
通过上述的两步基于GS算法的Delete算子,形成一个精简的乘客偏好列表,这里记为pl(r)gs=[π(1)gs, π(2)gs, …, π(j)gs, …, π(n)gs], j∈J;类似地,记精简之后司机偏好列表为pl(d)gs=[π(1)gs, π(2)gs, …, π(i)gs, …, π(m)gs], i∈I。令Mgs和Wgs分别表示通过Delete算子对司机和乘客的潜在可接受匹配对象进行删减之后的可行域。
3.1.3 算法流程第1阶段的主要目的是求得司机与乘客集匹配双方的偏好列表。根据式(2)判断司机i与乘客j之间是否满足时间窗口约束,如果满足时间窗口约束,则根据式(6)和(7)分别计算ui(i, j)和uj(i, j),如果u(i, j) < 0那么就是意味着,尽管匹配对(i, j)满足时间窗口约束,但是司机/乘客并不能通过匹配获得出行成本节省,这种匹配是不稳定的,只要某一方不能获得出行成本的节省,即匹配不可行的,此时令ui(i, j)=uj(i, j)=-K,K为一个足够大的正数。在求得所有司机与乘客的效用后,进一步对司机与乘客的效用值进行排序,这里采用最简单的冒泡法进行排序,最终输出司机与乘客双方的偏好列表,该偏好列表是按照效用值的大小从大到小依次排列的两个序列。
第2个阶段是对第1阶段得到的偏好列表进行精简,最终输出精简的偏好列表。
3.2 模型处理对参与者偏好列表进行精简之后,模型(11)转化为:
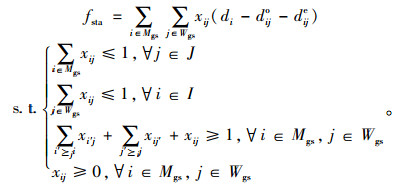
|
(12) |
定理3 模型(12)必然存在最优解[20]。
证明:本研究中参与者有两种配方式,一是与可行的潜在匹配对象进行匹配或参与者与自己匹配,那么集合Mgs和Wgs的大小都会远小于参与者的总数,即小于m+n。那么模型(12)为含有不超过m+n个变量的规划模型,故其最多具有2(m+n)2个可行解,即模型的可行解为有限多个。根据GS算法可知,本研究考虑的双边匹配问题必然存在稳定匹配解,即模型(12)至少存在一个可行解。因此模型(12)必然存在最优解。
4 算例分析顺风车的匹配成功与否往往与参与到顺风车平台的人数有关,故将研究城区繁华区域的顺风车匹配,由于实际的数据难以获得,这里将采用合理的数据模拟方法来产生相应的出行供给与出行需求。
4.1 参数设置假设城区繁华区域是一个长和宽都是20 km的一个正方形区域,且所有出行车辆在该区域内的平均行驶速度都为30 km/h,其中,乘客上下车的服务时间忽略不计,为了研究参与者的出行模式的影响,本研究将从研究两种不同的参与者起点与终点的分布入手:一种是所有的参与者的起止点都均匀随机地分布在区域内,另一种是参与者的起止点主要均匀随机地分布在2个中心。在后一种分布中,司机乘客的起点和终点分别位于两个不同的中心内,中心是一个圆形区域,半径为r。
系统中参与者的时间窗口的产生方法如下:为了提高顺风车的参与率,主要研究上班高峰期的出行。根据已有研究可知,出行者早上平均最晚出发时间为7:30 am,假设最晚出发时间是以7:30 am为均值,标准差为45 min的一个正态分布。将均值转化为分钟,则早上7:30可以记为450 min,即本研究的出行者最晚出发时间ldp是以450为均衡,45为标准差的一个正态分布,那么参与者p的最晚到达时间lap=ldp+tp,其中tp表示参与者p直接开车从起点到终点的时间。
弹性时间(Flexible Time):是指除去参与者从起点出发到终点的行驶时间外,可用的冗余时间。标记为FTp。
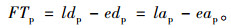
|
(13) |
假设弹性时间也是服从正态分布的,均值为一个给定的值FT min,标准差为4 min,那么根据式(13)可以求得edp=ldp-FTp,eap=lap-FTp。
为了计算简便,本研究假设车辆行驶单位距离的成本为固定的一个值α,α会随燃油价格的变化而变化,每天不同的时间段α的取值也会发生变化,如在滴滴顺风车服务中,夜间单位行驶距离的收费明显比白天高出很多,交通高峰期的收费也比非交通高峰期高,但是本研究是一种静态的顺风车匹配方案,故在某一个确定的时段,这里的α的取值也将会是一个固定的值。假设顺风车匹配平台将会向每一个成功匹配的匹配对(i, j)收取一定的费用φij,根据上文分析已知,平台收取的费用与匹配对的距离节省成正比,且比例记为η,为了计算方便,令η是一个固定值。此外,关于司机与乘客的时间机会成本wtp,本研究假设时间机会成本的系数ω已知,系数ω与参与者的工资水平成正相关,假设参与者p的工资为w元/年,假设每天工作时间是8 h,那么系数ω关系式可以表示为:ωp=w/(12×30×8×60)。为了便于计算,本研究假设所有参与者对时间机会成本的敏感程度是一致的,以北京年平均工资为例计算时间机会成本系数,根据国家统计年鉴,北京市2019年平均年工资为111 390元,那么ω≈0.645。
4.2 评价指标(1) 匹配成功率(Suc):匹配成功率定义为成功匹配上的参与者出行量除以参与者发布的总的出行需求量。假设稳定匹配模型求解的结果中,成功匹配的匹配对的数量为Ns,在平台中发布出行需求的司机数量为Nd,在平台中发布出行需求的乘客数量为Nr,那么匹配成功率为:
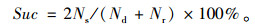
|
(2) 总行驶距离节省比率(Sav):总行驶距离节省比率定义为通过稳定匹配模型求解得到的系统总距离节省除以所有发布出行需求的司机与乘客直接从起点开车往终点的所有行驶距离之和,可以用公式表示为:
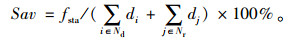
|
(3) 参与者个人出行平均节省比率(Si):参与者个人出行平均节省定义为参与者出行的个人距离节省除以其独自出行的行驶距离,再对所有成功匹配的参与者求平均值。根据不同的成本分配方式,Si的表达公式是不一样的,本研究主要讨论按比例分配方式。假设参与者按比例分配距离节省,那么Si的公式表达为:
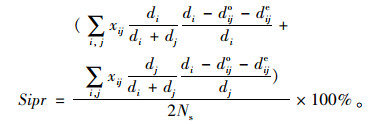
|
(4) 司机平均绕路比率(Dt):司机平均绕路比率定义为司机因为参与顺风车出行需要的额外行驶距离除以该司机单独出行的行驶距离,再对所有成功匹配的司机求取平均值。Dt的表达式如下:
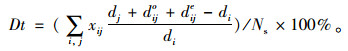
|
为了衡量本研究构建的稳定匹配模型以及提出的Delete算子的稳定性,本节进一步构建了如下指标来进行衡量模型的效果。
(5) Price of Anarchy (POA):根据前文定义,POA定义为稳定距离总节省偏离系统最优距离总节省的比例。POA表达式如下:
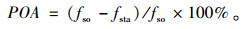
|
(6) 程序运行时间:本研究可以分为3种:直接求解系统最优值f已经对应的匹配方案的运行时间,记为RT;求解考虑参与者之间成本分配的系统最优值fso的运行时间,记为RTso;利用Delete算子对参与者偏好列表精简之后,求解稳定匹配值及对应的匹配方案的运行时间,记为RTsta。
4.3 结果分析(1) 参与者数量、聚集中心对匹配的影响
将Suc,Sav,Sipr,Dt,POA 5个指标对平台中潜在参与者数量和匹配区域中聚集中心对顺风车匹配结果的影响进行对比分析。如图 4所示,参与者数量变化区间为400~2 400,参与者弹性时间的均值为FT=30 min,弹性时间服从正态分布,标准差为4 min,平台向成功匹配的匹配对收取的费用比例η=10%,这里并不考虑参与者的时间机会成本,即ω=0,区域内所有司机单位行驶距离成本α为2元/km。
|
| 图 4 弹性时间、聚集中心对顺风车匹配的影响 Fig. 4 Influence of elastic time and gathering center on ridesharing matching |
| |
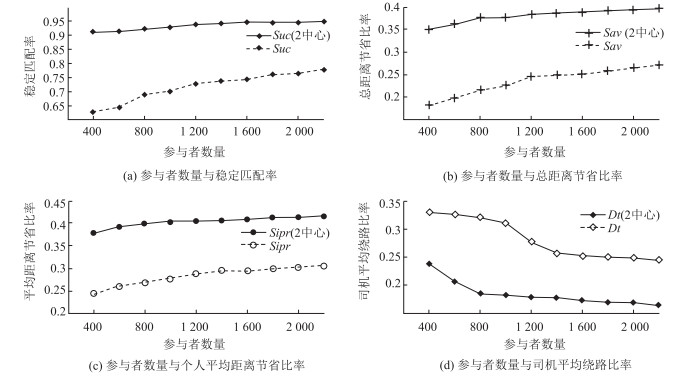
图 3(a)是参与者数量与稳定匹配率关系的对比图,从图中可以看到,有交通中心时的稳定匹配率远远高于没有交通中心时,当服务区内参与者数量仅为400时,有交通中心的顺风车稳定匹配率就已经达到了91.3%,此时,无交通中心的顺风车稳定匹配率仅仅为62.6%;而当服务区内参与者数量上升至2 400时,有交通中心的顺风车稳定匹配率达到了95%,无交通中心的顺风车匹配率仅为78%。图 3(b)是参与者数量与稳定匹配总距离节省比率关系的对比图,从图中可以看到,有交通中心时的距离节省比率也是远远高于没有交通中心时,从35.1%上升到39.9%,无交通中心的稳定匹配总距离节省比率随着参与者数量的变化从18.3%变动到27.2%。图 3(c)是参与者数量与稳定匹配个人平均出行距离节省比率关系的对比图,与图 3(a)和图 3(b)中的曲线有着类似的规律,随着参与者人数的不断增加,Sipr曲线不断上升,且有两个交通中心的个人平均距离节省比率远高于没有交通中心。图 3(d)是参与者数量与司机平均绕路比率关系的对比图,从图中可以看出,随着参与者数量的不断增加,司机的平均绕路比率不断下降,且有交通中心时司机的绕路比率是远低于没有交通中心时。当参与者人数上升至2 400时,在有两个交通中心的情况下,司机的绕路比率仅仅为16.1%,而此时,在没有交通中心的情况下,高比率为24.2%。此外需要指出的是,尽管在有两个交通中心的情况下,顺风车匹配的指标Suc, Sav, Sipr, Dt都展示出更好的指标值并一直保持着良好的稳定性能。Gap指标,也就是POA值,一直维持在6.4%到7.4%之间。由此可见,随着参与者人数的增加,本研究提出的稳定优化模型及算法都展示了良好,得到的稳定匹配解非常接近系统最优解。
|
| 图 3 参与者数量、聚集中心对顺风车匹配的影响 Fig. 3 Influence of number of participants and gathering center on ridesharing matching |
| |
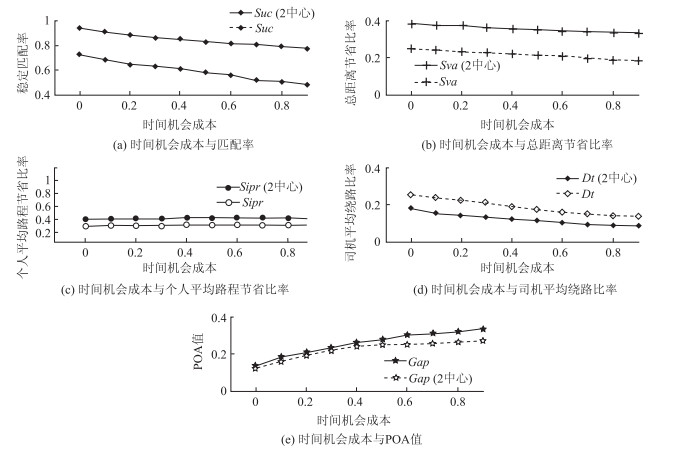
(2) 时间机会成本、聚集中心对匹配的影响
下面将对参与者时间机会成本和匹配区域中聚集中心对顺风车匹配结果的影响进行对比分析。其中参与者时间机会成本系数从0~0.9变化。参与者弹性时间的均值为FT=30 min,弹性时间服从正态分布,标准差为4 min,平台向成功匹配的匹配对收取的费用比例η=10%,区域内参与者人数为1 400,其中司机700,乘客700,区域内所有司机单位行驶距离成本α为2元/km。
图 4 (a)是参与者时间机会成本系数与稳定匹配率关系的对比图,从图中可以看到,无论服务区内有无聚集中心,稳定匹配率总是随着参与者时间机会成本系数的变大而不断下降,不同的是有两个聚集中心的情况下,稳定匹配率处于较高的状态。当参与者的时间机会成本系数增大到0.9时,匹配率依然高达77.6%,而此时没有聚集中心时的稳定匹配率仅仅为48.6%,匹配率较低。图 4(b)是参与者时间机会成本与稳定匹配总距离节省比率关系的对比图,与图(a)中的曲线有着类似的规律,随着参与者时间机会成本系数的不断增大,Sav曲线不断下降。图 4 (c)是参与者时间机会成本与稳定匹配个人平均出行距离节省比率关系的对比图,从图中可以发现,Sipr曲线不但没有随着时间机会成本系数的增加而下降,反而一直保持比较稳定的比率,并呈现略微的上升趋势,原因在于出行者对时间的敏感程度高,往往不接受需要花太多时间的匹配,即拒绝绕路距离较长的匹配,接受的大都是绕路时间短,且成本节省比率大的匹配,因而会使个人出行的平均距离节省比率呈现上升趋势。而这一点与图 4(d)中参与者时间机会成本与司机平均绕路比率关系是相呼应的,从图中可以看出,随着参与者时间机会成本系数的不断增加,司机的平均绕路比率是不断下降的。图 4(e)是参与者时间机会成本与稳定匹配POA值关系的对比图,如图所示,随着时间机会成本系数的增大,稳定匹配解与系统最优解之间的差距越来越大,原因如前所述,出行者时间敏感度高时,出行者很有可能会拒绝一些耗时而有距离节省的匹配,导致稳定匹配解与最优解之间的差距越来越大。但是需要指出的,对时间很敏感的人群参与到顺风车出行当中的比率相对较小。
(3) 算法效率
这里将对3种不同的求解方式的程序运行时间进行对比:第1种,假设参与者之间按原始出行距离的比例分配出行成本,可以保证得到的匹配方案中所有的成功匹配的司乘双方都有成本节省,对应模型为式(10),记对应的程序运行时间为RTso;第2种,为系统稳定匹配模型(11)对应的程序运行时间RTsta2,此时参与者的偏好列表并未进行精简;第3种,利用Delete算子对参与者偏好列表精简之后模型(12),求解稳定匹配值及对应的匹配方案的运行时间,记为RTsta1。
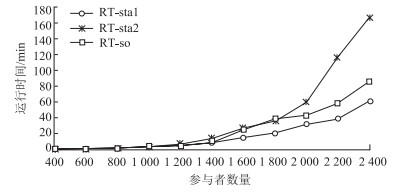
对RTsta1,RTsta2,RTso的比较可见图 5,如图中所示,随着参与者规模的不断增大,RTsta1,RTsta2,RTso的值都有着明显的增加,在参与者规模小于1 400时,求解模型(10)的程序运行时间RTso、求解没有精简偏好列表的模型(11)对应的程序运行时间RTsta2和使用精简列表的模型(12)的程序运行时间RTsta1差距很小,尤其是在小规模问题时,往往出现RTsta2 < RTsta1和RTso < RTsta1的情况,说明本研究提出的算法对解决小规模的顺风车匹配并未展现出优势,当参与者规模大于1 400后,RTsta1曲线的增长趋势相对而言是相当缓慢的;当参与者规模达到2 400时,RTsta2的值将近是RTsta1值的3.24倍,而RTso的值将近是RTsta1值的1.68倍。这意味着,本研究提出的Delete算子能够有效地对偏好列表进行精简,且精简之后使得模型的求解速度大幅度增加,说明该算法能够有效解决大规模的顺风车匹配问题。
|
| 图 5 各程序运行时间对比 Fig. 5 Comparison of running time of each program |
| |
5 结论
本研究构建了顺风车稳定匹配优化模型,并从参与者数量、参与者弹性时间、参与者时间机会成本、区域内有没有聚集中心和算法效率等5个方面对本研究提出的算法进行分析,其中衡量指标包含匹配率Suc、总距离节省比率Sav、参与者个人出行距离节省比率Sipr、司机绕路比率Dt以及稳定优化解和系统最优解之间的POA值。通过全面的试验和结果分析发现:(1) 无论服务区内有无聚集中心,随着参与者数量的增加,匹配率Suc、总距离节省比率Sav和参与者个人出行距离节省比率Sipr都不断上升,但服务区内有两个交通聚集中心时,Suc,Sav和Sipr都分别高于没有交通中心时,而随着参与者数量的增加,司机绕路比率Dt不断下降;(2) 无论服务区内有无交通聚集中心,随着参与者时间机会成本系数的增加,匹配率Suc、总距离节省比率Sav和司机绕路比率Dt是不断下降的,而随着参与者时间机会成本系数的增加,POA值不断增加的;(3) 随着参与者弹性时间的增加,对于服务区内无交通中心的情况,随着参与者数量的增加,匹配率Suc、总距离节省比率Sav和参与者个人出行距离节省比率Sipr都不断上升,司机绕路比率Dt是不断下降的;(4) 通过比较系统最优化模型、考虑参与者成本的系统优化模型和稳定匹配优化模型求解时间,发现本研究提出的偏好列表精简算法非常有效,能够有效地降低求解稳定匹配解的时间,使得本研究提出的稳定匹配优化模型能够应用到大型的顺风车匹配问题中。总而言之,本研究提出算法能够快速有效地解决单司机单乘客稳定匹配问题。
| [1] |
ZHOU G, HUANG K, MAO L. Design of Commute Carpooling Based on Fixed Time and Routes[J]. International Journal of Vehicular Technology, 2014(1): 1-9. |
| [2] |
AGATZ N A H, ERERA A L, SAVELSBERGH M W P, et al. Dynamic Ride-sharing: A Simulation Study in Metro Atlanta[J]. Transportation Research Part B: Methodological, 2011, 45(9): 1450-1464. |
| [3] |
MA S, WOLFSON O. Analysis and Evaluation of the Slugging Form of Ridesharing[C]//Proceedings of the ACM International Symposium on Advances in Geographic Information Systems. Orlando: ACM, 2013: 64-73.
|
| [4] |
RODIER C, ALEMI F, SMITH D. Dynamic Ridesharing: Exploration of the Potential for Reduction in Vehicle Miles Traveled[J]. Transportation Research Record, 2016, 2542: 120-126. |
| [5] |
HERBAWI W, WEBER M. The Ridematching Problem with Time Windows in Dynamic Ridesharing: A Model and a Genetic Algorithm[C]//2012 IEEE Congress on Evolutionary Computation (CEC). Brisbane: IEEE, 2012: 1-8.
|
| [6] |
邵增珍, 王洪国, 刘弘, 等. 多车辆合乘问题的两阶段聚类启发式优化算法[J]. 计算机研究与发展, 2013(11): 2325-2335. SHAO Zeng-zhen, WANG Hong-guo, LIU Hong, et al. Heuristic Optimization Algorithms of Multi-carpooling Problem Based on Two Stage Clustering[J]. Journal of Computer Research and Development, 2013(11): 2325-2335. |
| [7] |
WINTER S, NITTEL S. Ad Hoc Shared-ride Trip Planning by Mobile Geosensor Networks[J]. International Journal of Geographical Information Science, 2006, 20(8): 899-916. |
| [8] |
STIGLIC M, AGATZ N, SAVELSBERGH M, et al. The Benefits of Meeting Points in Ride-sharing Systems[J]. Transportation Research Part B: Methodological, 2015, 82: 36-53. |
| [9] |
ARSLAN A M, AGATZ N, KROON L, et al. Crowdsourced Delivery: A Dynamic Pickup and Delivery Problem with Ad Hoc Drivers[J]. Transportation Science, 2019, 53(1): 222-235. |
| [10] |
HERBAWI W, WEBER M. Evolutionary Multiobjective Route Planning in Dynamic Multi-hop Ridesharing[C]//European Conference on Evolutionary Computation in Combinatorial Optimization. Berlin: Springer, 2011: 84-95.
|
| [11] |
CALVO R W, DE LUIGI F, HAASTRUP P, et al. A Distributed Geographic Information System for the Daily Car Pooling Problem[J]. Computers & Operations Research, 2004, 31(13): 2263-2278. |
| [12] |
TEODOROVIC D, DELL'ORCO M. Bee Colony Optimization: A Cooperative Learning Approach to Complex Transportation Problems[J]. Advanced OR and AI methods in Transportation, 2005(1): 51-60. |
| [13] |
GALE D, SHAPLEY L S. College Admissions and the Stability of Marriage[J]. American Mathematical Monthly, 1962, 69(1): 9-15. |
| [14] |
IWAMA K, MIYAZAKI S. A Survey of the Stable Marriage Problem and Its Variants[C]//International Conference on Informatics Education and Research for Knowledge-circulating Society. Kyoto: IEEE, 2008: 131-136.
|
| [15] |
GEISBERGER R, LUXEN D, NEUBAUER S, et al. 10th Workshop on Algorithmic Approaches for Transportation Modelling, Optimization, and Systems (ATMOS'10)[J]. Dagstuhl, Germany: Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, 2010, 88-99. |
| [16] |
KLEINER A, NEBEL B, ZIPARO V A. A Mechanism for Dynamic Ride Sharing Based on Parallel Auctions[C]//Proceedings of the Twenty-second International Joint Conference on Artificial Intelligence. Palo alto: AAAI Press, 2011: 266-272.
|
| [17] |
WANG X, AGATZ N, ERERA A. Stable Matching for Dynamic Ride-sharing Systems[J]. Transportation Science, 2018, 52(4): 850-867. |
| [18] |
VATE J H V. Linear Programming Brings Marital Bliss[J]. Operations Research Letters, 1989, 8(3): 147-153. |
| [19] |
ROTH A E, ROTHBLUM U G, VANDE VATE J H. Stable Matchings, Optimal Assignments, and Linear Programming[J]. Mathematics of Operations Research, 1993, 18(4): 803-828. |
| [20] |
樊治平, 李铭洋, 乐琦. 考虑稳定匹配条件的双边满意匹配决策方法[J]. 中国管理科学, 2014(4): 112-118. FAN Zhi-ping, LI Ming-yang, YUE Qi. Decision Analysis Method for Two-sided Satisfied Matching Considering Stable Matching Condition[J]. Chinese Journal of Management Science, 2014(4): 112-118. |
 2021, Vol. 38
2021, Vol. 38
